1 Introduction

Thermal effects may play a crucial role in engineering structures at all scales. Considering micro-electro-mechanical systems (MEMS), i.e., mechanical systems at small scales and low temperatures, one faces the problem of heat propagation description. It has already been recognized that the classical theory of heat transfer based on the Fourier law has some limitations. These restrictions can include the infinite speed of heat, so nonclassical theories with finite thermal wave speed were proposed. In particular, Lord and Shulman proposed one of the most straightforward approaches, modifying the conventional Fourier law with relaxation time [1,2,3]. In this theory, the flux rate is applied in the form of the Fourier law. According to this theory, the heat equation of hyperbolic type ensures the displacement distributions and the finite speed of heat wave propagation. For other thermoelastic approaches, see [4,5,6,7,8,9,10,11,12,13]. Vattré and Pan [4] presented a three-dimensional thermoelastic study on the multilayered anisotropic plates in nonlocal media, including imperfection in interfaces. Allam et al. [5] used Green–Naghdi thermoelastic model to investigate electro-magneto-thermoelastic characteristics of a thick plate. Nobili and Pichugin [6] studied an asymptotic linear model using time-harmonic motion for a thermoelastic orthorhombic structure. Barretta et al. [7] proposed a stress-driven approach to study nonlocal beams by preparing thermoelastic coupling. In another study, Barretta et al. [8] investigated the thermo-mechanics of a laminated nonlocal beam supposed in a nonisothermal environment. Mahmoud Hosseini [9] selected the Green–Naghdi approach to probe the thermoelastic behavior of a small-scale MEMS/NEMS beam. Shakeriaski and Ghodrat [10] developed nonlinear forms of Lord–Shulman and Cattaneo-type thermoelastic models for media exposed to a laser shock. Othman and Lotfy [11] formulated Green–Lindsay and Lord–Shulman theories for studying wave propagation on a porous micropolar media. Sobhy and Zenkour [12] reported a new version for Green–Naghdi thermomechanics models to examine wave propagation of annular disks. Pourasghar and Chen [13] proposed a hyperbolic (non-Fourier) for heat conduction and calculated linear and nonlinear natural frequencies for a microbeam made of functionally graded materials reinforced by carbon nanotubes. Taati et al. [14] derived a couple stress thermomechanical model to address micro-size effects of shear-deformable beams based on a non-Fourier thermoelastic relation. Abouelregal et al. [15] established a study on the rotating thermoelastic nanobeams pertaining to a dynamic force and different heat sources.

It is worth mentioning that magnetic micro-particle (MMP) materials are used in molecular biology among various MEMS applications. MMPs can be used in many biomedical applications, including ribonucleic acid purification, magnetic cell separation, see, e.g., [16,17,18] and reference therein. One of the MMPs' most promising uses is to separate cancer cells from human blood cells.

Elements of MEMS such as micro-beams and micro-plates are widely used as accelerometer sensors, gyroscopes, and many others [19,20,21,22,23,24]. However, the most crucial challenge is the possible mechanical, magnetic, and thermal interactions. Therefore, accurate modeling of MEMS requires the proper description of these fields.

With the increasing use of intelligent structures, piezomagnetic characteristics as sensors and actuators have recently received particular attention from scientists. Piezomagnetic produces a magnetic field under the influence of mechanical stresses caused by external forces, in which there are changes in the direction and intensity of magnetization. The direct use of this property is in the construction of sensors such as accelerometers and strain gauges. An additional physical characteristic, which has magnetic particles or particular magnetic microsensors, is flexomagneticity. The main difference between the two properties is that flexomagneticity influences any materials having symmetries. What is more, piezomagneticity presents the coupling between strain and magnetization. For flexomagneticity, it is coupling between strain gradient and magnetization [25,26,27,28,29,30,31,32]. Furthermore, in microscale, the usage of flexomagneticity is significant in MMPs technology. That is why the interest in developing flexomagneticity property has been crucial in recent years.

Flexomagneticity (FM) effect is a novel discovery in the field of micro-/nanobeam technology. Recent studies have been done in the area of static and dynamics of piezomagnetic–flexomagnetic beams. Precursors in these fields are Sidhardh and Ray [33] and Zhang et al. [34]. In these preliminary studies, the authors focused on small-scale sensors and actuators, in which the flexomagneticity effect is observed. Zhang et al. focused on an actuator nanobeam subjected to static bending. The static bending calculation was considered according to the Euler–Bernoulli beam theory and the cantilever beam boundary conditions. The applied forces were applied uniformly and vertically to the length of the structure. Furthermore, surface elasticity was considered in this research. Moreover, the authors investigated both direct and converse magnetizations on different boundary conditions. The results of this study showed that flexomagnetic property is size-dependent. In addition to this, Sidhardh and Ray performed static bending on the piezomagnetic–flexomagnetic nanosize beam. The authors considered the clamped-free ends boundary conditions, and the calculations were performed according to the Euler–Bernoulli displacement kinematic field. Additionally, the direct and inverse magnetization effects were examined. Furthermore, the size dependency was discussed with the usage of the surface elasticity for the small beam. Finally, the results presented that the behavior of the flexomagnetic effect is scale-dependent, according to quantitative assessment. What is more, the authors ignored the piezomagnetic effect of nanostructures and achieved the same conclusion. On the other hand, Malikan and Eremeyev [35] performed a vibrational mode study on the Euler–Bernoulli piezomagnetic–flexomagnetic small-scale beam. According to the nonlocal stress-driven elasticity model, the size-dependent effect was analyzed for the linear frequency analysis. The attainments of this investigation illustrated that the flexomagneticity property is size-dependent.

Recently, Malikan and Eremeyev [36] performed a study on small-size structures with piezomagnetic–flexomagnetic properties. In this research, they examined the nonlinear calculation of natural structure frequencies. As a result, according to the nonlocal strain gradient elasticity model, they confirmed the size-dependency of the flexomagneticity phenomenon. What is more, the same authors Malikan and Eremeyev [37] examined nanosize beams with the piezo-flexomagnetic effect undergoing large deformations. The evaluation was performed with the usage of analytical–numerical solution procedures. Based on the results, it was concluded that the design should consider piezo-flexomagnetic properties in nano-electro-mechanical systems (NEMS). What is more, the flexomagnetic effect usage causes a reduction of the deformations of these structures. Additionally, Malikan et al. [38] explored piezo- and flexomagnetic effects in magnetic nanoparticles. The obtained results give new light and achievements in the smart nanosensor's design, as in this study, the structure's post-buckling behavior was scrutinized.

Lately, Malikan et al. [39] studied the porous states in a piezomagnetic–flexomagnetic beam structure considering the size effect's impact. Reached from their results, the flexomagnetic response of the structures is dependent on the porosity. Malikan et al. [40] investigated the temperature distribution in microresonators in micromedia. In this study, the structures were considered with piezomagnetic and flexomagnetic properties. It was found that piezomagnetic–flexomagnetic effects influence the thermal load distribution. Malikan and Eremeyev [41] presented FM in a small-scale plate. They obtained that the FM value can be affected by variations of the aspect ratio of the plate. Malikan and Eremeyev [42] reported a study to predict how surface elasticity can influence FM. Their achievements proved that surface elasticity could directly and strongly impress a nanomaterial's FM response. Malikan and Eremeyev [43] included shear deformations into a flexible nanoscale flexomagnetic beam to investigate the impact of shear deformations on the FM. Malikan et al. [44] studied thermal buckling and addressed the FM effect in FG-piezomagnetic micro-/nano-beams.

According to the recent research mentioned in the literature review, no thermoelastic study was performed on the piezomagnetic small particles containing flexomagnetic influence. Hereby, Lord–Shulman's dynamic thermoelastic model is evaluated in this study. For this purpose, the investigation of beam-shaped resonators with piezomagnetic and flexomagnetic properties is proposed. Additionally, according to a strain gradient model, the size-dependency is examined. Besides linear elastic strains, Euler–Bernoulli's thin beam theory is applied for kinematic displacements. The ease of this beam model is due to obtaining one equilibrium equation providing simpler, shorter, and possible mathematical modeling, particularly in micro-/nano-electro-magneto-thermoelasticity structures. If one uses higher-order beam displacements, there are many problems in order to describe governing equations of multi-physics problems. Thus, in terms of MEMS/NEMS, the Euler–Bernoulli displacement field has been highly recommended. After extracting the equations using the Hamilton principle, the resulting equations are discretized using the Navier method. What is more, the simply supported beam is considered as the boundary condition. Several combinations of main factors are examined to model the magnetic sensors adequately. Finally, the obtained analytically results are presented graphically by several images.

2 Theoretical model

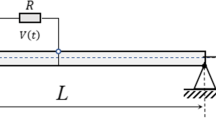
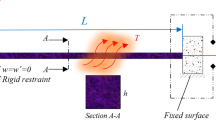
Let us consider small flexural displacements for the microbeam of thickness h (− h/2≤ z ≤ h/2), of width b (− b/2≤ y ≤ b/2), of length L (0< x ≤ L), as presented in Fig. 1, for simply supported beam conditions. The beam is subjected to a lateral magnetic field. A thermal source affects the beam vertically as well. Note that the pictured figure is only a schematic presentation of cobalt iron oxide (CoFe2O4) crystal microstructures, and the mathematical model is based on the continuum micro-mechanics. On the reason of assuming such a system, one can refer to microsensors used for measuring the temperature of the environments with high precision. Although the environment heat can be transferred into the sensor on the basis of various presumptions and models, this study utilizes the Lord–Shulman hypothesis together with the sinusoidal distribution of heat.

Fig. 1
figure 1

A square piezomagnetic–flexomagnetic microbeam lies in fully pivot ends

Full size image

As talked earlier, the classic beam model is employed [45, 46] to derive the thermoelastic model of vibration for the beam. Thus, the equation of motion for a piezomagnetic–flexomagnetic macro-beam located in the thermal and one-dimensional magnetic environments can be presented together as follows [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. First, the one-dimensional constitutive relation of the thermo-magneto-elastic stress component can be expressed as:

$$\sigma_{x} = - z\left( {C_{11} + \frac{{q_{31}^{2} }}{{a_{33} }}} \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} - C_{11} \alpha_{T} \theta \left( {x,z,t} \right)$$
(1)

where \(a_{33}\) represents the component of the second-order tensor of magnetic permeability,\(q_{31}\) is component of the third-order piezomagnetic tensor, \(C_{11}\) is Young's modulus, \(\alpha_{T}\) denotes the coefficient of linear thermal expansion, \(t\) is time, and \(w\) is the deflection.

The cross-sectional bending moment is shown below:

$$M_{x} = \int\limits_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\sigma_{x} } dz$$
(2)

Upon implementing Eq. (1) into Eq. (2), we get

$$M_{x} = - D\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} - C_{11} \alpha_{T} M_{T} \left( {x,z,t} \right)$$
(3)

where \(D = I_{z} \left( {C_{11} + \frac{{q_{31}^{2} }}{{a_{33} }}} \right)\).

The thermal moment can be defined by:

$$M_{T}^{{}} \left( {x,z,t} \right) = \int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\theta \left( {x,z,t} \right)zdz}$$
(4)

The transverse motion equation of the smart beam can be given as [33,34,35,36,37,38,39,40,41,42,43,44]:

$$\left( {D + g_{31} h} \right)\frac{{\partial^{4} w\left( {x,t} \right)}}{{\partial x^{4} }} + C_{11} \alpha_{T} \frac{{\partial^{2} M_{T} \left( {x,z,t} \right)}}{{\partial x^{2} }} - N^{{{\text{Mag}}}} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} + I_{0} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{4} w\left( {x,t} \right)}}{{\partial x^{2} \partial t^{2} }} = 0$$
(5)

and \(N^{{{\text{Mag}}}} = \psi q_{31}\), \(I_{z} = \int_{A}^{{}} {z^{2} dA}\), \(\left( {I_{0} ,I_{2} } \right) = \int\limits_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\rho \left( z \right)\left( {1,z^{2} } \right)dz}\). in which \(I_{z}\) is the moment of inertia, \(h\) is a thickness, \(g_{31}\) shows the corresponding component of the sixth-order gradient elasticity tensor, \(A\) is the cross-sectional area, and \(\rho\) is the mass density. It is necessary to note that the density is distributed constant along with the thickness. Thus, the first mass moment of inertia (\(I_{1}\)) disappeared.

The magnetic field engaged in the modeling is as follows:

$$\Psi = - \frac{{q_{31} }}{{2a_{33} }}\left( {z^{2} - \frac{{h^{2} }}{4}} \right)\frac{{d^{2} w}}{{dx^{2} }} + \frac{\psi }{h}\left( {z + \frac{h}{2}} \right)$$
(6)

which is available at [33,34,35,36,37,38,39,40,41,42,43,44] and was formulated on the basis of the converse FM effect and close circuit.

The Lord–Shulman (L-S) model presents thermoelasticity with one relaxation time. L-S model gives heat conduction relation as [50,51,52,53,54,55]:

$$\frac{\partial }{\partial x}\left( {\Gamma \left( \theta \right)\frac{{\partial \theta \left( {x,z,t} \right)}}{\partial x}} \right) + \frac{\partial }{\partial z}\left( {\Gamma \left( \theta \right)\frac{{\partial \theta \left( {x,z,t} \right)}}{\partial z}} \right) = \left( {1 + \tau_{0} \frac{\partial }{\partial t}} \right)\left( {\rho C_{v} \left( \theta \right)\frac{{\partial \theta \left( {x,z,t} \right)}}{\partial t} + \beta T_{0} \frac{{\partial e_{kk} }}{\partial t}} \right)$$
(7)

in which \(\Gamma \left( \theta \right)\) displays a thermal conductivity, \(C_{v} \left( \theta \right)\) is a specific heat at constant volume, \(T_{0}\) exhibits the environmental temperature in a nondeformed state, \(\tau_{0}\) is the thermal relaxation time, \(e_{kk} = \frac{{\partial u_{1} \left( {x,z,t} \right)}}{\partial x} + \frac{{\partial u_{2} \left( {x,z,t} \right)}}{\partial y} + \frac{{\partial u_{3} \left( {x,z,t} \right)}}{\partial z}\) is the volumetric strain. In addition, \(\beta = \frac{{C_{11} \alpha_{T} }}{1 - 2\nu }\) in which \(\nu\) is Poisson's ratio. Moreover, \(\theta \left( {x,z,t} \right) = T - T_{0}\) is a linear increment of the dynamical temperature of the sensor.

The derivative \({{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}\) will be equal to zero when the heat flow does not exist on the beam's upper and lower surfaces (\(z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}\)) [51].

Let us assume the increments of the temperature arise sinusoidally along the z-axis; hence,

$$\theta \left( {x,z,t} \right) = \theta_{1} \left( {x,t} \right)\sin \left( {\frac{\pi }{h}z} \right)$$
(8)

Equation (8) is consistent with the assumption that heat flux vanishes at the beam faces, i.e., for \(z = \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}\).

Using Eq. (8), one can obtain from Eq. (7)

$$\frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }}\sin \left( {\frac{\pi }{h}z} \right) - \left( {\frac{\pi }{h}} \right)^{2} \theta_{1} \sin \left( {\frac{\pi }{h}z} \right) = \left( {\frac{\partial }{\partial t} + \tau_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\frac{{\rho C_{v} }}{\Gamma }\theta_{1} \sin \left( {\frac{\pi }{h}z} \right) - \frac{{\beta T_{0} }}{\Gamma }z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(9)

Let us multiply both sides by z and then integrate on thickness direction, and a few simplifications give,

$$\frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} - \left( {\frac{\pi }{h}} \right)^{2} \theta_{1} = \left( {\frac{\partial }{\partial t} + \tau_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\varepsilon \theta_{1} - A_{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(10)

where

\(\varepsilon = \frac{{\rho C_{v} }}{\Gamma }\),

\(A_{2} = \frac{{\beta T_{0} \pi^{2} h}}{24\Gamma }\).

In what follows, let us consider Eq. (4) with the help of Eq. (8) as

$$M_{T} = \theta_{1} \left( {x,t} \right)\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\sin \left( {\frac{\pi }{h}z} \right)dz}$$
(11)

Here, Eq. (5) can be updated according to Eq. (11) as the following

$$\left( {D + g_{31} h} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} - N^{Mag} \frac{{\partial^{2} w}}{{\partial x^{2} }} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + C_{11} \alpha_{T} \frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }}\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {z\sin \left( {\frac{\pi }{h}z} \right)dz} = 0$$
(12)

Integrating from Eq. (12) simplifies it as follows:

$$\left( {D + g_{31} h} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} - N^{Mag} \frac{{\partial^{2} w}}{{\partial x^{2} }} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + A_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} = 0$$
(13)

in which \(A_{1} = C_{11} \alpha_{T} \frac{{2h^{2} }}{{\pi^{2} }}\).

Lastly, coupled thermoelastic governing equations can be justified upon Eqs. (10) and (13) as

$$\left( {D + g_{31} h} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} - N^{Mag} \frac{{\partial^{2} w}}{{\partial x^{2} }} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} + A_{1} \frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} = 0$$
(14)
$$\frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} - \left( {\frac{\pi }{h}} \right)^{2} \theta_{1} = \left( {\frac{\partial }{\partial t} + \tau_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\varepsilon \theta_{1} - A_{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(15)

To conveniently implement the scale effect for a micro-sized material, one can address the strain gradient elasticity [56,57,58,59,60,61,62,63,64] incorporating one length-scale parameter by expressing the following standard relationship,

$$\sigma_{ij}^{{}} = {\text{C}}_{{{\text{ijkl}}}} \left( {1 - l^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\varepsilon_{kl}^{{}}$$
(16)

where l is an extra microscale parameter.

Hereby and as a result of microstructural property, one can write the finalized governing equations as below:

$$\left( {D + g_{31} h} \right)\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - l^{2} \frac{{\partial^{6} w}}{{\partial x^{6} }}} \right) + A_{1} \left( {\frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} \theta_{1} }}{{\partial x^{4} }}} \right) - N^{Mag} \frac{{\partial^{2} w}}{{\partial x^{2} }} + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} = 0$$
(17)
$$\frac{{\partial^{2} \theta_{1} }}{{\partial x^{2} }} - \left( {\frac{\pi }{h}} \right)^{2} \theta_{1} = \left( {\frac{\partial }{\partial t} + \tau_{0} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\varepsilon \theta_{1} - A_{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(18)

As evident, Eq. (18) is identical to Eq. (15), which approved that the microstructural property is not included in the heat conduction equation.

Using the micro-dimensional constitutive equations is strenuous in light of the coupling problem among magnetic-thermal-elastic relations. To this, we introduce the following dimensionless quantities to skip toward nondimensional constitutive equations,

$$\begin{gathered} W = \frac{w}{L}, \, l^{*} = \frac{l}{L}, \, X = \frac{x}{L}, \, I_{0}^{*} = \frac{{I_{0} }}{\rho L}, \, I_{2}^{*} = \frac{{I_{2} }}{{\rho L^{3} }}, \, N^{*} = \frac{{N^{{{\text{Mag}}}} }}{{C_{11} L}}, \, \Lambda = \frac{t\xi }{L}, \, f = \frac{{L\xi C_{11} \alpha_{T} }}{\Gamma }, \, \hfill \\ \Omega = \frac{\omega L}{\xi }, \, \lambda = \pi S, \, D^{*} = \frac{D}{{C_{11} L^{3} }}, \, \xi = \sqrt {\frac{{C_{11} }}{\rho }} , \, g^{*} = \frac{{g_{31} h}}{{C_{11} L^{3} }}, \, \Theta = \frac{{\theta_{1} }}{{T_{0} }}, \, \tau^{*} = \frac{{\tau_{0} \xi }}{L}, \, \Upsilon = \frac{{2\alpha_{T} T_{0} }}{{\lambda^{2} }}, \, \hfill \\ C^{*} = \frac{{C_{v} }}{{\xi^{2} \alpha_{T} }}, \, S{ = }\frac{L}{h}, \, \delta = \frac{{\pi^{3} }}{{24\left( {1 - 2\nu } \right)}} \hfill \\ \end{gathered}$$

Hence,

$$\left( {D^{*} + g^{*} } \right)\left( {\frac{{\partial ^{4} W}}{{\partial X^{4} }} - l^{{*2}} \frac{{\partial ^{6} W}}{{\partial X^{6} }}} \right) + \Upsilon \left( {\frac{{\partial ^{2} \Theta }}{{\partial X^{2} }} - l^{{*2}} \frac{{\partial ^{4} \Theta }}{{\partial X^{4} }}} \right) - N^{*} \frac{{\partial ^{2} W}}{{\partial X^{2} }} + I_{0}^{*} \frac{{\partial ^{2} W}}{{\partial \Lambda ^{2} }} - I_{2}^{*} \frac{{\partial ^{4} W}}{{\partial X^{2} \partial \Lambda ^{2} }} = 0$$
(19)
$$\frac{{\partial^{2} \Theta }}{{\partial X^{2} }} - \lambda^{2} \Theta - f\left( {\frac{\partial }{\partial \Lambda } + \tau^{*} \frac{{\partial^{2} }}{{\partial \Lambda^{2} }}} \right)\left( {C^{*} \Theta - \frac{\delta }{\lambda }\frac{{\partial^{2} W}}{{\partial X^{2} }}} \right) = 0$$
(20)

As Eqs. (19) and (20) are of six order, there should also be six boundary conditions. One can see the assumed boundary conditions as follows,

$$\left. {{\text{U = }}W{ = }\Theta } \right|_{0}^{L} { = 0}, \, \left. {N_{x}^{{}} } \right|_{0}^{L} = N^{Mag} , \, \left. {M_{x}^{{}} } \right|_{0}^{L} \ne 0, \, \left. {T_{xxz} } \right|_{0}^{L} = 0$$
(21)

The boundary conditions \(N_{x}^{{}}\) and \(T_{xxz}\) are here additional in the case of a multi-physics problem. The magnetic force resulting from the magnetic field acted on both ends as axial compressive loads and generated force boundary conditions. In addition, the hyper stress resultant is an internal effect of the magnetic field and can be supposed zero on both ends of the domain as we are investigating rigid restraints. Moreover, \(M_{x}^{{}}\) denotes another force boundary condition.

3 Solution method

Let us assume vibrational modes as time-harmonic displacements. The boundary conditions are developed analytically to calculate the thermoelastic vibration behavior of the magnetic microscale beam. The frequency analysis based on the harmonic solution generally involves two sections: real and imaginary parts.

In a case, we investigate both ends of the beam with one rotational degree of freedom in the form of simply supported conditions. In the other case, however, both ends are supposed to be fully fixed in terms of clamped boundary conditions. The following equations demonstrate the mentioned procedure respecting the Navier method [65, 66],

$$W\left( {X,\Lambda } \right) = \sum\limits_{m = 1}^{\infty } {W_{m} X_{m} \left( X \right)\exp \left( {i\Omega \Lambda } \right)}$$
(22)
$$\Theta \left( {X,\Lambda } \right) = \sum\limits_{m = 1}^{\infty } {\Theta_{m} X_{m} \left( X \right)\exp \left( {i\Omega \Lambda } \right)}$$
(23)

in which we took into account the real part only. In the observed equations, \(X_{m}\) indicated in Eqs. (22) and (23) is required to be expressed,

$$X_{m} \left( X \right) = \sin \left( {m\pi X} \right)$$
(24)

Exerting Eqs. (22) and (23) on Eqs. (19) and (20) leads to generalized eigenvalue equations written in the matrix form as:

$$\left( {\left| {\begin{array}{*{20}c} {A_{11} } & {A_{12} } \\ {A_{21} } & {A_{22} } \\ \end{array} } \right| - \Omega^{2} \left| {\begin{array}{*{20}c} {B_{11} } & {B_{12} } \\ {B_{21} } & {B_{22} } \\ \end{array} } \right|} \right)\left\{ {\begin{array}{*{20}c} {W_{m} } \\ {\Theta_{m} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}$$
(25)

Then by further simplifying, one can get

$$\left| {\begin{array}{*{20}c} {K_{11} } & {K_{12} } \\ {K_{21} } & {K_{22} } \\ \end{array} } \right|\left\{ {\begin{array}{*{20}c} {W_{m} } \\ {\Theta_{m} } \\ \end{array} } \right\} = 0$$
(26)

where

$$\begin{gathered} K_{11} = \left( {D^{*} + g_{{}}^{*} } \right)\left( {\sum\limits_{m = 1}^{\infty } {\frac{{\partial^{4} X_{m} }}{{\partial X^{4} }}\exp \left( {i\Omega \Lambda } \right)} - l^{*2} \sum\limits_{m = 1}^{\infty } {\frac{{\partial^{6} X_{m} }}{{\partial X^{6} }}} \exp \left( {i\Omega \Lambda } \right)} \right) \hfill \\ - \left( {N^{*} - \Omega^{2} I_{2}^{*} } \right)\sum\limits_{m = 1}^{\infty } {\frac{{\partial^{2} X_{m} }}{{\partial X^{2} }}} \exp \left( {i\Omega \Lambda } \right) - \Omega^{2} I_{0}^{*} \sum\limits_{m = 1}^{\infty } {X_{m}^{{}} \exp \left( {i\Omega \Lambda } \right)} \hfill \\ \end{gathered}$$
$$K_{{12}} = \sum\limits_{{m = 1}}^{\infty } {\Upsilon \left( {\frac{{\partial ^{2} X_{m} }}{{\partial X^{2} }} - l^{{*2}} \frac{{\partial ^{4} X_{m} }}{{\partial X^{4} }}} \right)} \exp \left( {i\Omega \Lambda } \right)$$
$$K_{21} = \frac{f\delta }{\lambda }\sum\limits_{m = 1}^{\infty } {\frac{{\partial^{2} X_{m} }}{{\partial X^{2} }}} \left( {i\Omega - \tau^{*} \Omega^{2} } \right)\exp \left( {i\Omega \Lambda } \right)$$
$$K_{22} = \sum\limits_{m = 1}^{\infty } {\frac{{\partial^{2} X_{m} }}{{\partial X^{2} }}} \exp \left( {i\Omega \Lambda } \right) - f\left( {i\Omega C^{*} - C^{*} \tau^{*} \Omega^{2} + \frac{{\lambda^{2} }}{f}} \right)\sum\limits_{m = 1}^{\infty } {X_{m}^{{}} \exp \left( {i\Omega \Lambda } \right)}$$

As seen, the results will be time-dependent vibration with a thermal relaxation time. Notice that the numerical results are computed concerning the first mode of frequency. Equation (26) can be simplified and extracted via the below mathematical efforts for the first mode number (m = 1),

$$\det \left[ {\begin{array}{*{20}c} {\left( {D^{*} + g_{{}}^{*} } \right)\left( {\pi^{4} + l^{*2} \pi^{6} } \right) + \left( {N^{*} - \Omega^{2} I_{2}^{*} } \right)\pi^{2} - \Omega^{2} I_{0}^{*} } & { - \Upsilon \left( {\pi^{2} + l^{*2} \pi^{4} } \right)} \\ { - \frac{{\pi^{2} f\delta }}{\lambda }\left( {i\Omega - \tau^{*} \Omega^{2} } \right)} & { - \pi^{2} - f\left( {i\Omega C^{*} - C^{*} \tau^{*} \Omega^{2} + \frac{{\lambda^{2} }}{f}} \right)} \\ \end{array} } \right] = 0$$
(27)

The outcome of the above determinant will be a polynomial complex algebraic relation to which some mathematical efforts are applied. Indeed, this determinant leads to a fourth-order polynomial algebraic equation based on \(\Omega\).

$$\lambda_{1} \Omega^{4} + \lambda_{2} \Omega^{3} + \lambda_{3} \Omega^{2} + \lambda_{4} \Omega + \lambda_{5} = 0$$
(28)

where

$$\lambda_{1} = fC^{*} \tau^{*} \left( {I_{0}^{*} - I_{2}^{*} \pi^{2} } \right)$$
$$\lambda_{2} = ifC^{*} \left( {I_{2}^{*} \pi^{2} + I_{0}^{*} } \right)$$
$$\begin{gathered} \lambda_{3} = \pi^{2} I_{0}^{*} + I_{0}^{*} \lambda^{2} + \Omega^{2} I_{2}^{*} \lambda^{2} \pi^{2} + \Upsilon \tau^{*} \left( {\pi^{2} + l^{*2} \pi^{4} } \right)\frac{{\pi^{2} f\delta }}{\lambda } \hfill \\ + fC^{*} \tau^{*} \left[ {\left( {D^{*} + g_{{}}^{*} } \right)\left( {\pi^{4} + l^{*2} \pi^{6} } \right) + N^{*} \pi^{2} } \right] + I_{2}^{*} \pi^{4} \hfill \\ \end{gathered}$$
$$\lambda_{4} = \left[ { - i\Upsilon \left( {\pi^{2} + l^{*2} \pi^{4} } \right)\frac{{\pi^{2} f\delta }}{\lambda }} \right] - ifC^{*} \left[ {\left( {D^{*} + g_{{}}^{*} } \right)\left( {\pi^{4} + l^{*2} \pi^{6} } \right) + N^{*} \Omega \pi^{2} } \right]$$
$$\lambda_{5} = - \left[ {\left( {D^{*} + g_{{}}^{*} } \right)\left( {\pi^{6} + l^{*2} \pi^{8} } \right) + N^{*} \pi^{4} } \right] + \lambda^{2} \left[ {\left( {D^{*} + g_{{}}^{*} } \right)\left( {\pi^{4} + l^{*2} \pi^{6} } \right) + N^{*} \pi^{2} } \right]$$

The solution of this equation gives real and imaginary parts of natural frequency. In fact, as the system includes damping due to temperature, the roots of this algebraic equation should be complex in most cases, leading to attenuating the waves. It can be written as follows:

$$\Omega = {\text{Re}} \left( \Omega \right) + {\text{Im}} \left( \Omega \right)$$
(29)

The real section (decay rate) establishes phase shifting and gives an index of the system's damping and stability. Moreover, the imaginary part (oscillatory rate) measures the rate of the oscillations and predicts natural frequencies.

4 Solution validation

The presented theory's accuracy has been validated considering different conditions before performing the natural frequencies computations. The comparison of results obtained from different notable theories and the present work is presented in Tables 1 and 2. According to the previous research findings [67], the presented study results are high compliance. Furthermore, especially for thinner beams, the results coincide with the presented beam theory results, as shown in Table 1.

Table 1 Providing comparison for nondimensional natural frequencies of a macro-square beam \(\Omega = \omega_{n} L^{2} \sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {C_{11} I_{z} }}} \right. \kern-\nulldelimiterspace} {C_{11} I_{z} }}}\), E = 1TPa, υ = 0.3, h = 1 nm
Full size table
Table 2 Giving nondimensional natural frequencies for a small-scale square beam \(\Omega = \omega_{n} L^{2} \sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {C_{11} I_{z} }}} \right. \kern-\nulldelimiterspace} {C_{11} I_{z} }}}\), E = 30 × 106, υ = 0.3, h = 1, L/h = 10, ρ = 1
Full size table

A more comparison is associated here by means of Table 2. The analyzed specimen is a size-dependent square beam with a lack of magnetic properties. The dedicated reference for validation is [68], where two size-dependent models are under evaluation. These models are, respectively, strain gradient approach (SGT) and stress-driven integral model (SDM) [68,69,70]. Obviously, one can observe a bit of difference between the present paper results and those of the literature. However, while the parameter \(\lambda\) tends to be increased, the discrepancy is further. Nonetheless, there is an acceptable agreement among the results.

5 Practical examples

This section focuses on severe impacts on the microsensor's flexomagnetic response coming from the thermodynamic coupling consideration. Consequently, let us here discuss the determinative factors of the mathematical model. The time relaxation of heat, the initial temperature of the environment, mode numbers, length scale parameter, magnetic potential, thermal conductivity, and slenderness coefficient will be probed in depth. At the beginning, it is worth bearing in mind that the cobalt iron oxide as a piezomagnetic material is assigned to the microsensor. The physical and thermal properties of the microsensor are mentioned in Table 3 [71,72,73,74,75,76].

Table 3 Physical quantities for the analysis
Full size table

Studying the thermoelastic behavior of micro-materials and fine dimensions resulting from the coupling of an elastic problem with heat transfer gives more accurate results. Because the fundamental purpose of this research is to learn more about the thermoelastic behavioral differences between piezomagnetic micro-size beams in two cases, the first case is when the magnetic material has flexomagnetic properties (PFM) and the second case is a pure magnetic material without having a higher order of magnetic properties (PM). Note that the value of g* has been assumed as 4 × 10–4 for all computations.

First, as shown in Fig. 2, we, in summary, review the effect of heat source relaxation time (TRT). It should be noted that the retention time of temperature is minimal. As it turns out, increasing the kept time of the heat source in the vicinity of the beam slightly reduces the difference between the results of PM and PFM structures. In a point of fact, it can be said that thermal shocks make the flexomagnetic effect more. Furthermore, it can be practically concluded that if we apply thermal shock to the micro-material, a larger and more significant flexomagnetic effect can be extracted. On the other hand, as can be seen from the diagram, when the keeping time of the heat source increases, the natural frequencies of the system decrease. It could be discussed that the higher the holding time of the heat around the beam, the less stiffness the beam. It may be because the heat weakens the matter's molecular and atomic bonds after a time. Therefore, to have higher natural frequencies and to prevent resonance at lower excitation frequencies, the heat source should be kept around the magnetic microbeam for not a considerable time.

Fig. 2
figure 2

TRT versus dimensionless frequency for PM and PFM microstructures (ψ = 1 A, l* = 0.1, S = 20, m = 1)

Full size image

Figure 2 is examined while the initial ambient temperature was 293 K, which is a normal environment without cooling or heating effects on machine parts. But here, as shown in Fig. 3, we desire to change the initial temperature of the environment. Then, it is interesting to know what impact a warmer initial environment will have on the microbeam's thermoelastic behavior. For this purpose, we draw Fig. 3 for two different initial temperatures, 293 K and 333 K. With a simple look, it can be seen from the figure that when the earliest temperature of the environment becomes warmer, the natural frequencies would be more in a lower TRT. This outcome can be obtained from a distance between initial temperatures of 293 K and 333 K. On that account, it is logical to state that the initial temperature is a determining factor in microstructures' thermoelastic behavior. Thus, it should not be simply disregarded. However, in the case of large values of TRT, the commencing temperature's influence can be ignorable.

Fig. 3
figure 3

TRT versus dimensionless frequency for PM and PFM microstructures in different initial temperatures (ψ = 1 A, l* = 0.1, S = 20, m = 1)

Full size image

As shown in Fig. 4, we want to briefly study the effect of different frequency modes on the sensor's thermodynamic behavior. However, a wave propagation analysis of magnetic microstructures with the flexomagnetic effect requires a separate study. According to the results computed for this figure, it is evident that for the lower modes, the flexomagnetic effect remarkably affects the frequency results. For example, in the third frequency mode, the difference between the results of PM and PFM reaches less, which means that the magnetic microsensor with the flexomagnetic effect will have a lower normal frequency. Suppose we increase the TRT and get out of the range of thermal shocks; in that case, the amounts of frequency in all modes will go down. Another deduced point of this figure is that the effect of heat retention on higher modes is of further impact. This result was obtained from the lower and smoother slope of reducing results in the first mode compared to the rest.

Fig. 4
figure 4

TRT versus dimensionless frequency for PM and PFM microstructures in different mode numbers (ψ = 1 A, l* = 0.1, S = 20)

Full size image

Since this paper inspects the thermo-mechanical behavior of microstructures in the form of beams, the crucial point is having different values ​​of the parameter determining the microstructure behavior. The utilized parameter is the strain gradient length scale (SGLS) parameter. This parameter has no particular values for each specific structure [77]. For this purpose, we considered different values. In the first case, the problem is turned into a classical problem without considering the microscale effects, which in this form is l* = 0. All research records have shown that increasing the numerical values ​​of this parameter will positively affect the stiffness of the material and structure, and this theorem is also found in Fig. 5. However, the main conclusion that can be reported by plotting this figure is that the effect of heat retention on the material's stiffness is observable. Suppose the values of the SGLS parameter are lower ones for a microstructure; in that case, a shorter heat retention time further affects the behavior of that microscale structure.

Fig. 5
figure 5

TRT versus dimensionless frequency for PM and PFM microstructures in different SGLS parameter’s values (ψ = 1 A, S = 20, m = 1)

Full size image

Different amounts of magnetic potential have their unique effects. Research background has shown that increasing the magnetic potential’s positive values leads to an increase in the elastic stiffness of the material. Moreover, negative values ​​of this parameter lead to a decrease in the stiffness of the material and a weakening. According to Fig. 6, we assess the effects of changes in the amount of magnetic potential on the modeled microbeam's thermodynamic behavior. The results’ report shows that the TRT directly determines the impact of external magnetic potential on the microsensor. Short TRT brings about further noticeable magnetic potential. Furthermore, it is observed that the results for PM and PFM microsensors are closer to each other at larger values of magnetic potential. With this figure's help, it can be concluded that in the thermodynamic analysis of microstructures, the increase of positive magnetic potential leads to less importance of the flexomagnetic property.

Fig. 6
figure 6

TRT versus dimensionless frequency for PM and PFM microstructures within different magnetic amperes (l* = 0.1, S = 20, m = 1)

Full size image

In this section, utilizing Fig. 7, we explore the effect of cobalt iron oxide's thermal conductivity. In fact, we are looking to see if the flexomagnetic behavior of matter is affected by this coefficient and how different the FM effect will be at different values ​​of matter's thermal conductivity. In keeping with the results, it is conspicuous that if the thermal conductivity of the structure is increased, the flexomagnetic effect will be more crucial. However, this conclusion will be less significant in heat shocks. Therefore, if a microsensor made by cobalt iron oxide requires a more significant flexomagnetic effect, the material's thermal conductivity should be increased. This increase in heat conduction capacity can be achieved depending on the type of material how it is fabricated. Further, extra material can be added to the magnetic matrix, which is beyond the scope of this study.

Fig. 7
figure 7

Thermal conductivity versus dimensionless frequency for PM and PFM microstructures within different TRT (ψ = 1 A, l* = 0.1, S = 20, m = 1)

Full size image

Using Fig. 8, we will analyze the effects of parameter S on the microsensor's thermodynamic results. The dimensionless parameter S determines the slenderness coefficient of the beam. For this reason, we considered its values ​​from the zone of the ​​relatively thick beam to the thin beam. The most crucial point extracted from this figure can be that increasing the value of parameter S leads to an increase in the flexomagnetic effect. Therefore, in longer beams under thermodynamic loads, the material's flexomagnetic property severely impacts magnetic beam results. On the other, it is discernible that while the S has higher values, the effectiveness of the heat release time increases. This result means that increasing the values ​​of the beam slenderness ratio is determinative.

Fig. 8
figure 8

Slenderness ratio versus dimensionless frequency for PM and PFM microstructures within different TRTs (ψ = 1 A, l* = 0.1, m = 1)

Full size image

6 Conclusions

We have discussed the coupled dynamics of a beam-shaped specimen made of thermo-flexomagnetic material such as cobalt iron oxide. In order to take into account a size-effect and a finite speed of heat propagation, the Lord–Shulman model was applied, whereas, for the mechanical part, the linear Euler–Bernoulli kinematics was assumed. For brevity, we consider here simply supported beams. The coupled thermoelastic equations of motions are formulated concerning the following variables: magnetic induction function, thermoelastic functions, displacements, and linear stresses. Complex coupling behavior is originated from the influence of the second strain gradient on the thermoelastic equations of motion. The relevant relations corresponding to dimensionless phase and thermal relaxation time coefficients were determined. Considering coupling and the influence of heat conduction, we formulate the following conclusions, which could be helpful in the design and modeling of NEMS and MEMS:

  • The less relaxation time will lead to a sizeable flexomagnetic effect.

  • The initial temperature will be a decisive parameter for thermodynamic coupling analysis.

  • The lower frequency mode numbers will bring the momentous flexomagnetic influence.

  • The higher capacity of the heat conductivity will make a further noticeable flexomagnetic effect.

  • The larger the length, the more remarkable the flexomagnetic effect in a thermodynamic analysis.

The presented results significantly extended the previous pure elastic analyses. It was earlier shown that the increase or decrease in magnetic potential does not influence the flexomagnetic effect. Indeed, here we take into account the thermoelastic coupling, which essentially changes the behavior.