1 Introduction

The manipulation of elastic, acoustic and electromagnetic properties in materials using periodic structures referred to as phononic crystals or metamaterials has recently attracted the attention of researchers because of their unusual wave attenuation characteristics. This is caused by the existence of frequency ranges in the generated band structure where mechanical waves cannot propagate. These frequency ranges are known as stop bands or bandgaps which can be generated through two mechanisms known as Bragg scattering (BS) and local resonance (LR) mechanisms. The BS mechanism opens high-frequency bandgaps due to the periodicity of the structure and has a central frequency related to the wave velocity and lattice constant of a typical unit cell. The LR mechanism opens low-frequency stop bands and is generated by embedding several local resonators in the main structure which work against the excitation of the incident elastic wave to attenuate its vibration. The LR mechanism uses a small-size periodic structure because the central frequency of the stop bands is only related to the frequency of the resonator. Research on metamaterials has led to the development of several engineering applications such as noise and sound mitigation [1], structural vibration suppression [2], seismic protection [3], directional waveguides [4, 5], mechanical filters [6] and electromagnetic stealth cloaks [7].

In most of the studies related to stop band formation, the elastic metastructure is modeled as an infinite structure made of an infinite number of unit cells and the analysis is conducted on a single unit cell of the periodic structure. The formation of a stop band is typically depicted by obtaining the dispersion curves of the unit cell and identifying frequency regions where the real component of the wave number vanishes. Preliminary investigations on elastic metamaterials have focused on simple one-dimensional infinite periodic mass in mass units [8,9,10,11,12,13,14]. These studies have been extended to continuous structures such as rods [15, 16], beams [17,18,19,20,21,22,23], plates [24,25,26] and even more complex lattice structures consisting of origami and honeycomb structures [27, 28].

Different methods have been used to explore the stop band formation in a unit cell of an infinite periodic structure, which include the transfer matrix (TM) method [29,30,31], the spectral element method [32] and the homogenization method [21, 33, 34]. For practical vibration applications, however, the host structure is bounded by finite dimensions with applied boundary conditions, and therefore, the unit-cell modeling approach, which is commonly adopted to determine the stop band boundaries, may not be applicable to these finite structures [35]. To account for the finite dimensions of the host structure, recently a modal analysis approach was put forward by Sugino et al. [36, 37] to investigate the stop band formation in finite-length structural elements.

The main problem with local resonators that hinders its application in the industry is that resonators are rather heavy and will add mass to the primary structure. It was also observed that the obtained stop bands are rather narrow and cannot reach ultra-low frequencies. Few investigators have focused on reaching quasi-static ultra-low frequency stop bands in the neighborhood of almost zero frequency. To this end, two different techniques have been employed, namely, those which use inertial amplifier and those which utilize negative stiffness elements. A brief review of these studies is included in what follows. Yilmaz and co-workers [38,39,40] designed and validated experimentally the method of inertial amplification and proposed a number of mechanisms. Frandsen et al. [41, 42] designed a lightweight inertial amplification mechanism for continuous structures which was then validated experimentally on beam structures. Hu et al. [43] proposed both a metamaterial lumped and beam system with local resonators coupled by negative stiffness springs to generate ultra-low frequency bandgaps. Oh et al. [44, 45] designed a metamaterial with zero rotational stiffness capable of generating a quasi-static bandgap from almost zero frequency. In another study, the same authors proposed several ideas to create a stop band for broadband at low-frequency range [46]. Drugan [47] studied analytically the effect of negative stiffness components on elastic and elastic-dissipative wave propagation in an infinite chain made of elastic or elastic-dissipative components and demonstrated the generation of ultra-low bandgaps. Lin et al. [48] proposed a metamaterial with a unit cell made of a dynamic vibration absorber with negative stiffness spring, studied the bandgap behavior in an infinite and finite mass-spring chain, proved the existence of quasi-static broadband bandgap and suggested a conceptual model for a seismic metabarrier. Zhang et al. [49] designed a novel three-dimensional latticed elastic metamaterial with a wide and low-frequency stop band. Finally, Yang and Wang [50] proposed a new one-dimensional metamaterial model with both a negative effective moment of inertia and negative effective stiffness for generating an ultrawide-zero-frequency stop band.

Based on the above review and to the authors’ best knowledge, research on broadband and ultra-low quasi-static stop bands have is still quite limited and remains an important topic in the area of metamaterial-based vibration suppression. To fill this gap, the authors propose a new metamaterial to obtain the quasi-static stop band from zero frequency. The unit cell of the proposed metamaterial contains a resonator connected to bar-spring mechanism embedded in a host mass and also linked to a fixed substrate. The proposed metamaterial may be a suitable candidate in suppressing vibrations in low-frequency applications such as oil and gas piping systems [51]. The remainder of this paper is organized in four sections. In Section 2, the governing equations of the proposed metamaterial are derived by using the Lagrangian approach, and then Bloch’s theorem is used to derive the dispersion relation of the metamaterial with infinite lattice model. A finite metamaterial is considered in Sect. 3 and a closed-form relation for transmittance is obtained by using the matrix method [14]. In Sect. 4, several parametric studies are conducted to investigate the effects of various design parameters and concluding remarks are provided in Sect. 5.

2 Infinite metamaterial

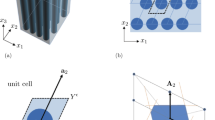
A unit cell of the proposed model is shown in Fig. 1a. The current model aims to generate quasi-static stop band from zero frequency. It is well known that the mathematical modeling of lumped parameter mass-spring systems translates the fundamental mechanisms of metamaterials. To this end, the proposed unit cell is simplified as a structure built with springs and masses, as shown in Fig. 1b. For the simplification, two oblique rods are modeled with rigid bar-spring mechanisms. Each unit cell of the new configuration is composed of an outer mass \(M_1\) and an inner mass \(m_1\) connected by a linear spring \(k_1\). In each unit cell, there are two symmetric elements which consist of rigid massless bars and linear vertical springs. One end of the vertical spring \(k_2\) is connected to the inner wall of mass \(M_1\), while the other end is connected to the massless bar. Furthermore, the other end of the bar is pinned to the mass \(m_1\). In addition, mass \(m_1\) is attached to the fixed substrate through spring with an elastic constant \(k_3\). It should be noted that positive stiffness springs are used in this model.

Fig. 1
figure 1

a Unit cell of the proposed elastic metamaterial and b spring-mass model

Full size image
Fig. 2
figure 2

Infinite lattice model of proposed metamaterial

Full size image

2.1 Equations of motion

A one-dimensional infinite mass-spring system, shown in Fig. 2, is considered in this section. As can be seen from the figure, the unit cells are uniformly placed with a periodic distance constant l and two neighboring unit cells interact with each other by a linear spring of stiffness K. The governing equations of motion are derived using Lagrange’s method. To this end, the Lagrangian for the infinite lattice is defined as follows:

$$\begin{aligned} \begin{aligned}&L = \frac{1}{2}\sum \limits _{j = - \infty }^\infty {M_1\left( {\frac{{du_j^{(1)} }}{{dt}}} \right) } ^2 + \frac{1}{2}\sum \limits _{j = - \infty }^\infty m_1 \left( {\frac{{du_j^{(2)} }}{{dt}}} \right) ^2 - \frac{1}{2}\sum \limits _{j = - \infty }^\infty {K\left( {u_{j + 1}^{(1)} - u_j^{(1)} } \right) ^2 } \\&\qquad -\frac{1}{2}\sum \limits _{j = - \infty }^\infty {k_1 } \left( {u_j^{(1)} - u_j^{(2)} } \right) ^2 - \sum \limits _{j = - \infty }^\infty {k_2 \left( {w_j } \right) ^2 }- \frac{1}{2}\sum \limits _{j = - \infty }^\infty {k_3 \left( {u_j^{(2)}} \right) ^2 } \end{aligned} \end{aligned}$$
(1)

where \(u_j^{(1)}\) and \(u_j^{(2)}\) denote the displacements of the masses \(M_1\) and \(m_1\) in the \(j ^\mathrm{{th}}\) unit cell, respectively. Furthermore, \(w_j\) is the vertical displacement of the vertical point of the bar. Assuming small displacements, the relationship between the displacements \(u_j^{(1)}\), \(u_j^{(2)}\) and \(w_j\) can be written as

$$\begin{aligned} {{w}_{j}}=\left( u_{j}^{(2)}-u_{j}^{(1)}\right) \tan {{\theta }_{0}} \end{aligned}$$
(2)

in which \(0<\theta _0<\pi /2\) is the angle between the bar and the vertical axis. The equations of motion in Lagrangian mechanics are Lagrange’s equations which can be written as follows:

$$\begin{aligned} \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial \dot{u}_j^{(1)} }}} \right) - \frac{{\partial L}}{{\partial u_j^{(1)} }}&= 0 \end{aligned}$$
(3a)
$$\begin{aligned} \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial \dot{u}_j^{(2)} }}} \right) - \frac{{\partial L}}{{\partial u_j^{(2)} }}&= 0 \end{aligned}$$
(3b)

The governing equations of motion for the \(j ^\mathrm{{th}}\) unit cell are derived by substituting Eqs. (1–2) into Eqs. (3aa,b) and can be expressed as

$$\begin{aligned} {{M}_{1}}\frac{{{d}^{2}}u_{j}^{(1)}}{d{{t}^{2}}}+K\left( 2u_{j}^{(1)}-u_{j-1}^{(1)}-u_{j+1}^{(1)}\right) +\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}\right) \left( u_{j}^{(1)}-u_{j}^{(2)}\right)&= 0 \end{aligned}$$
(4a)
$$\begin{aligned} {{m}_{1}}\frac{{{d}^{2}}u_{j}^{(2)}}{d{{t}^{2}}}+\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}\right) \left( u_{j}^{(2)}-u_{j}^{(1)}\right) +{{k}_{3}}u_{j}^{(2)}=&= 0 \end{aligned}$$
(4b)

2.2 Dispersion relations

Based on Bloch’s theorem, the displacements for the \(\left( {j + n} \right) ^{\mathrm{{th}}} \) unit cell can be assumed to be harmonic functions of time and wavenumber as follows:

$$\begin{aligned} u_{j + n}^{(1)}&= B^{(1)} \exp \left[ {i\left( {j\kappa l + n\kappa l - \omega t} \right) } \right] \end{aligned}$$
(5a)
$$\begin{aligned} u_{j + n}^{(2)}&= B^{(2)} \exp \left[ {i\left( {j\kappa l + n\kappa l - \omega t} \right) } \right] \end{aligned}$$
(5b)

where \(B^{(1)}\) and \(B^{(2)}\) are the complex wave amplitudes, \(\kappa \) is wavenumber, \(\omega \) is the angular frequency and \(i=\sqrt{-1}\) is the complex imaginary unit. By substituting Eqs. (5aa,b) into Eqs. (4aa,b) and then setting the determinant of the coefficient matrix equal to zero for a non-trivial solution of \(B^{(1)}\) and \(B^{(2)}\), the dispersion relation, i.e., the relation between the frequency and the wavenumber, of the proposed system is obtained as follows:

$$\begin{aligned} \begin{aligned}&{{m}_{1}}{{M}_{1}}{{\omega }^{4}}-{{\omega }^{2}}\left[ {{M}_{1}}\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}+{{k}_{3}}\right) +{{m}_{1}}\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}+4K{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) \right) \right] +\\&+\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}+4K{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) \right) \left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}+{{k}_{3}}\right) -{{\left( {{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}}\right) }^{2}}=0 \end{aligned} \end{aligned}$$
(6)

To simplify the analysis, the following dimensionless parameters are defined:

$$\begin{aligned} \Omega ^2 = \frac{{m_1 \omega ^2 }}{{k_1 }}, \quad \alpha = \frac{{m_1 }}{{M_1 }}, \quad \beta = \frac{{k_1 }}{K}, \quad \gamma = \frac{{k_2 }}{K},\quad \delta =\frac{{{k}_{3}}}{K} \end{aligned}$$
(7)

Substituting the above equations into Eq. (6) yields

$$\begin{aligned} \begin{aligned}&{{\Omega }^{4}}-{{\Omega }^{2}}\left[ \left( 1+\alpha \right) \left( 1+2\frac{\gamma }{\beta }\tan ^{2}{{\theta }_{0}}\right) +\frac{\delta }{\beta }+\frac{4\alpha }{\beta }{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) \right] +\\&\frac{\alpha }{\beta }\left[ \left( 4{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) +\delta \right) \left( 1+2\frac{\gamma }{\beta }\tan ^{2}{{\theta }_{0}}\right) +\frac{4\delta }{\beta }{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) \right] =0 \end{aligned} \end{aligned}$$
(8)

It should be noted that for \(\gamma =\delta =0\), the above equation is reduced to the dispersion equation of the conventional metamaterial proposed and validated experimentally by Yao et al. [52]. Based on the above equation, two branches of frequency \(\Omega \) can be obtained for a given dimensionless wavenumber \(\kappa l\). The roots of the above equation representing the two branches of the dispersion curve can be written as

$$\begin{aligned} {{\Omega }_{1}}&=\sqrt{\left( 1+\alpha \right) \left( \frac{1}{2}+\frac{\gamma }{\beta }\tan ^{2}{{\theta }_{0}}\right) +\frac{\delta }{2\beta }+\frac{2\alpha }{\beta }{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) -\sqrt{\Delta }} \end{aligned}$$
(9a)
$$\begin{aligned} {{\Omega }_{2}}&=\sqrt{\left( 1+\alpha \right) \left( \frac{1}{2}+\frac{\gamma }{\beta }\tan ^{2}{{\theta }_{0}}\right) +\frac{\delta }{2\beta }+\frac{2\alpha }{\beta }{{\sin }^{2}}\left( \frac{\kappa l}{2}\right) +\sqrt{\Delta }} \end{aligned}$$
(9b)

where

$$\begin{aligned} \Delta =\frac{1}{{4\beta ^2 }}\left\{ \begin{array}{l} \left[ {\left( {1 + \alpha } \right) \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) + \delta + 4\alpha \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) } \right] ^2 - \\ 4\alpha \left[ {\left( {4\sin ^2 \left( {\frac{{\kappa l}}{2}} \right) + \delta } \right) (\beta + 2\gamma \tan ^2 \theta _0 ) + 4\delta \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) } \right] \end{array} \right\} \end{aligned}$$
(10)

which can be written in a simplified form as follows:

$$\begin{aligned} \Delta =\frac{1}{{4\beta ^2 }}\left\{ \begin{array}{l} \left( {1 + \alpha } \right) ^2 \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) ^2 + \delta ^2 + 16\alpha ^2 \sin ^4 \left( {\frac{{\kappa l}}{2}} \right) + 2\delta \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) \left( {1 - \alpha } \right) \\ - 8\alpha \delta \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) - 8\alpha \left( {1 - \alpha } \right) \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) \end{array} \right\} \end{aligned}$$
(11)

Taking advantage of the following identity:

$$\begin{aligned} \begin{array}{l} \left[ {\left( {1 - \alpha } \right) \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) + \delta - 4\alpha \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) } \right] ^2 - \left( {1 - \alpha } \right) ^2 \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) ^2 \\ =\delta ^2 + 16\alpha ^2 \sin ^4 \left( {\frac{{\kappa l}}{2}} \right) + 2\delta \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) \left( {1 - \alpha } \right) - 8\alpha \delta \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) \\ -8\alpha \left( {1 - \alpha } \right) \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) \\ \end{array} \end{aligned}$$
(12)

Eq. (11) takes the following form after few simple manipulations:

$$\begin{aligned} \Delta = \frac{1}{{4\beta ^2 }}\left\{ {4\alpha \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) ^2 + \left[ {\left( {1 - \alpha } \right) \left( {\beta + 2\gamma \tan ^2 \theta _0 } \right) + \delta - 4\alpha \sin ^2 \left( {\frac{{\kappa l}}{2}} \right) } \right] ^2 } \right\} \end{aligned}$$
(13)

It can be observed that the parameter \(\Delta \) given by the above equation is always a positive quantity resulting in two positive real frequencies \(\Omega _1\) and \(\Omega _2\). Therefore, the displacements of the masses do not increase exponentially with time for any wavelength and the system stability is ensured.

Fig. 3
figure 3

Comparison between the proposed metamaterial and conventional metamaterial; (\(\alpha =2\), \(\beta = 0.3\) and \(\theta _0=\pi /4\))

Full size image

The dispersion curves of the proposed metamaterial are shown in Fig. 3 for two special cases and compared with the results of the conventional metamaterial \(\left( {\gamma =\delta = 0} \right) \). In the first case, we adopted \(\gamma =0.5\) and \(\delta = 0\), while we have \(\gamma =\delta = 0.5\) for the second case. For the numerical calculations, the following values were adopted for \(\alpha \), \(\beta \) and \(\theta _0\): \(\alpha =2\), \(\beta = 0.3\) and \(\theta _0=\pi /4\). As expected, there is one stop band, the frequency band through which the wave is not allowed to pass, in the range of \(0.963 \le \Omega \le 1.732\) for the conventional metamaterial. As it can be seen, there is one stop band in the frequency range 1.779 to 3.606, for the first case of the proposed metamaterial. This shows that the consideration of the vertical springs has only effect on the width of the stop band. However, it can be observed that for the second case of the proposed metamaterial, two stop bands appear in the frequency regions (0, 1.030) and (2.184, 3.688). The lower boundary of the first stop band is zero, and the first stop band is known as a quasi-static stop band. It can be concluded that the formation mechanism of generating the quasi-static stop band is the connection of mass \(m_1\) to the fixed substrate by the spring \(k_3\). A detailed parametric study to investigate the effects of various parameters on the stop band behavior based on the developed infinite lattice model is included in Sect. 4.1.

3 Finite metamaterial

In practical applications, the metamaterials are usually made of a finite number of unit cells. To this end, the main objective of this section is to develop a finite lattice model and to verify the stop band behavior predicted using the infinite lattice model. In this regard, a one-dimensional finite mass-spring system consisting of n unit cells, illustrated in Fig. 4, is considered in this section. The equations of motion of such system can be written as

$$\begin{aligned} {{M}_{1}}\frac{{{d}^{2}}u_{1}^{(1)}}{d{{t}^{2}}}+K(2u_{1}^{(1)}-u_{2}^{(1)}-{{u}_{in}})+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{1}^{(1)}-u_{1}^{(2)})&= 0 \end{aligned}$$
(14a)
$$\begin{aligned} {{m}_{1}}\frac{{{d}^{2}}u_{1}^{(2)}}{d{{t}^{2}}}+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{1}^{(2)}-u_{1}^{(1)})+{{k}_{3}}u_{1}^{(2)}&= 0 \end{aligned}$$
(14b)
$$\begin{aligned} {{M}_{1}}\frac{{{d}^{2}}u_{j}^{(1)}}{d{{t}^{2}}}+K(2u_{j}^{(1)}-u_{j-1}^{(1)}-u_{j+1}^{(1)})+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{j}^{(1)}-u_{j}^{(2)})&= 0 \quad j = 2,3,..., n-1 \end{aligned}$$
(14c)
$$\begin{aligned} {{m}_{1}}\frac{{{d}^{2}}u_{j}^{(2)}}{d{{t}^{2}}}+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{j}^{(2)}-u_{j}^{(1)})+{{k}_{3}}u_{j}^{(2)}&= 0\quad j = 2,3,..., n-1 \end{aligned}$$
(14d)
$$\begin{aligned} {{M}_{1}}\frac{{{d}^{2}}u_{n}^{(1)}}{d{{t}^{2}}}+K(2u_{n}^{(1)}-u_{n-1}^{(1)})+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{n}^{(1)}-u_{n}^{(2)})&= 0 \end{aligned}$$
(14e)
$$\begin{aligned} {{m}_{1}}\frac{{{d}^{2}}u_{n}^{(2)}}{d{{t}^{2}}}+({{k}_{1}}+2{{k}_{2}}\tan ^{2}{{\theta }_{0}})(u_{n}^{(2)}-u_{n}^{(1)})+{{k}_{3}}u_{n}^{(2)}&= 0 \end{aligned}$$
(14f)
Fig. 4
figure 4

Finite lattice model of proposed metamaterial

Full size image

where \(u_{in}\) is the input displacement. It is assumed that the input displacement, \(u_{in}\), and displacements of masses, \(u_j^{(\gamma )}\), are harmonic functions of time as follows:

$$\begin{aligned} u_{in}&= U_0 \exp \left( {i\bar{\omega }t} \right) \end{aligned}$$
(15a)
$$\begin{aligned} u_j^{(\gamma )}&= U_j^{(\gamma )} \exp \left( {i\bar{\omega }t} \right) \quad j = 1,2,..., n \end{aligned}$$
(15b)

where \(U_0\) and \(\bar{\omega }\) are, respectively, the amplitude and frequency of the external excitation. In addition, \(U_j^{(\gamma )} \) denotes the displacement amplitude. Substitution of the above equations into Eqs. (14a)–(14b) yields

$$\begin{aligned}&(2+\beta +2\gamma {{\tan }^{2}}{{\theta }_{0}}-\frac{\beta }{\alpha }{{\varpi }^{2}})U_{1}^{(1)}-U_{2}^{(1)}-{{U}_{0}}-(\beta +2\gamma {{\tan }^{2}}{{\theta }_{0}})U_{1}^{(2)}=0 \end{aligned}$$
(16a)
$$\begin{aligned}&U_{1}^{(2)}=\frac{1+2\frac{\gamma }{\beta }{{\tan }^{2}}{{\theta }_{0}}}{1+2\frac{\gamma }{\beta }{{\tan }^{2}}{{\theta }_{0}}+\frac{\delta }{\beta }-{{\varpi }^{2}}}U_{1}^{(1)} \end{aligned}$$
(16b)

where \(\varpi ^2 = \bar{\omega }^2 m_1 /k_1\). By eliminating \(U_1^{(2)}\) from the above equations yields

$$\begin{aligned} U_2^{(1)} = \Lambda U_1^{(1)} - U_0 \end{aligned}$$
(17)

in which

$$\begin{aligned} \Lambda =2+\beta +2\gamma {{\tan }^{2}}{{\theta }_{0}}-\frac{\beta }{\alpha }{{\varpi }^{2}}-\frac{{{(\beta +2\gamma {{\tan }^{2}}{{\theta }_{0}})}^{2}}}{\beta +2\gamma {{\tan }^{2}}{{\theta }_{0}}+\delta -\beta {{\varpi }^{2}}} \end{aligned}$$
(18)

In a similar manner, Eqs. (14c)–(14f) are reduced to

$$\begin{aligned} U_{j + 1}^{(1)}&= \Lambda U_j^{(1)} - U_{j - 1}^{(1)} \quad j = 2,3,...,n - 1 \end{aligned}$$
(19a)
$$\begin{aligned} U_{n - 1}^{(1)}&= \Lambda U_n^{(1)} \end{aligned}$$
(19b)

Equation (19a) can be written in a matrix form as follows:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {U_{j + 1}^{(1)} } \\ {U_j^{(1)} } \\ \end{array}} \right) = \mathbf{{[A]}}\left( {\begin{array}{*{20}c} {U_j^{(1)} } \\ {U_{j - 1}^{(1)} } \\ \end{array}} \right) \quad j = 2,3,...,n - 1 \end{aligned}$$
(20)

where

$$\begin{aligned} \mathbf{{[A]}} = \left[ {\begin{array}{*{20}c} \Lambda &{} { - 1} \\ 1 &{} 0 \\ \end{array}} \right] \end{aligned}$$

By using an iterative process, the above equation can be written as

$$\begin{aligned} \left( {\begin{array}{*{20}c} {U_{j + 1}^{(1)} } \\ {U_j^{(1)} } \\ \end{array}} \right) = [\mathbf{{A}}]^{j - 1} \left( {\begin{array}{*{20}c} {U_2^{(1)} } \\ {U_1^{(1)} } \\ \end{array}} \right) \quad j = 2,3,...,n - 1 \end{aligned}$$
(21)

Setting \(j= n-1\) in the above equation gives

$$\begin{aligned} \left( {\begin{array}{*{20}c} {U_n^{(1)} } \\ {U_{n - 1}^{(1)} } \\ \end{array}} \right) = [\mathbf{{A}}]^{n - 2} \left( {\begin{array}{*{20}c} {U_2^{(1)} } \\ {U_1^{(1)} } \\ \end{array}} \right) = \left[ {\begin{array}{*{20}c} {g_{11} } &{} {g_{12} } \\ {g_{21} } &{} {g_{22} } \\ \end{array}} \right] \left( {\begin{array}{*{20}c} {U_2^{(1)} } \\ {U_1^{(1)} } \\ \end{array}} \right) \end{aligned}$$
(22)

Combining and simplifying Eqs. (17), (19b) and (22) yields

$$\begin{aligned} U_n^{(1)} = \frac{{g_{11} g_{22} - g_{12} g_{21} }}{{\Lambda ^2 g_{11} + \Lambda \left( {g_{12} - g_{21} } \right) - g_{22} }}U_0 \end{aligned}$$
(23)

Finally, the transmittance \(\tau \) can be estimated as follows:

$$\begin{aligned} \tau = 20\log _{10} \left| {\frac{{U_n^{(1)} }}{{U_0 }}} \right| = 20\log _{10} \left| {\frac{{g_{11} g_{22} - g_{12} g_{21} }}{{\Lambda ^2 g_{11} + \Lambda \left( {g_{12} - g_{21} } \right) - g_{22} }}} \right| \end{aligned}$$
(24)

and is defined as the ratio of the amplitude of the outer mass in the last unit cell to the amplitude of the excitation.

Fig. 5
figure 5

a Dispersion curves computed using Eqs. (9a) and (9b); b Transmittance of a finite system with 20 units calculated using Eq. (24)

Full size image

For the sake of validation of the present formulations, Figs. 5a and 5b show, respectively, the dispersion curve of an infinite chain and transmittance spectrum of finite chain consisting of 20 cells as a function of frequency. For numerical calculation, the dimensionless parameters are \(\alpha = 0.4\), \(\beta = 1.5\) , \(\gamma = 0.5\), \(\delta =0.75\) and \(\theta _0 = \pi /6\). As can been seen from Fig. 5b, there are two frequency regions in the transmittance spectrum of finite chain in which the amplitude is considerably attenuated. These regions are stop bands presented in the dispersion curve of the infinite chain.

4 Parametric study on stop band behavior

4.1 Infinite metamaterial

This section studies the dispersion characteristics of the infinite chains when different dimensionless design parameters identified in Sect. 3 are varied. The first parameter \(\alpha \) is the ratio of the resonator mass to the outer mass which is varied from 0.1 to 2. The second parameter \(\beta \) is the ratio of the resonator spring stiffness to the spring stiffness between two unit cells that is varied from 0.25 to 2.5. The third parameter \(\gamma \) is the ratio of the vertical spring stiffness to the spring stiffness between two unit cells and whose value is varied between 0 and 2. \(\delta \) is the fourth dimensionless parameter varying between 0 and 2. All these parameters are defined in Eq. (7). The final design parameter is the angle \(\theta _0\) between the rigid link connecting the vertical spring element and the resonator mass which is varied from 0.05\(\pi \) to 0.4\(\pi \).

Figure 6 depicts the variation of the stop bands of the proposed metamaterial as a function of mass ratio \(\alpha \), with fixed values of \(\beta \), \(\gamma \), \(\delta \) and \(\theta _0\) equal to 0.8, 0.3, 0.6 and \(\pi /3\), respectively. It is observed that the width of the quasi-static stop band gets wider with an increase in the magnitude of \(\alpha \). However, the width of the second stop band first decreases and then slightly increases for increasing values of \(\alpha \). The variation of both stop bands with respect to the parameter \(\beta \) is shown in Fig. 7 for the following design parameters: \(\alpha =1.2\), \(\gamma =0.5\), \(\delta =0.5\) and \(\theta _0=\pi /10\). It can be seen that the width of the first bandgap decreases with increasing values of \(\beta \) whereas the second stop band has the opposite behavior.

Fig. 6
figure 6

Variation of stop bands of the proposed metamaterial with varying \(\alpha \); (\(\beta =0.8\), \(\gamma =0.3\), \(\delta =0.6\) and \(\theta _0=\pi /3\))

Full size image
Fig. 7
figure 7

Variation of stop bands of the proposed metamaterial with varying \(\beta \); (\(\alpha =1.2\), \(\gamma =0.5\), \(\delta =0.5\) and \(\theta _0=\pi /10\))

Full size image

The effect of the parameter \(\gamma \) on the stop band behavior of the metamaterial is illustrated in Fig. 8. In this figure, the remaining parameters are \(\alpha =1.5\), \(\beta =1\), \(\delta =0.1\) and \(\theta _0=\pi /6\). It can be concluded that increasing the magnitude of \(\gamma \) results in an increase of the second stop band and has no effect on the first stop band. Figure 9 displays the influence of the parameter \(\delta \) on the stop bands of the proposed metamaterial. For numerical calculations in this figure, we adapted \(\alpha =2\), \(\beta =1\), \(\gamma =0.1\) and \(\theta _0=\pi /4\). It can be observed that increasing the magnitude of \(\delta \) results in an increase and decrease of the first and second stop bands, respectively. Furthermore, it can be concluded that the lower and upper boundaries of the second band increase almost linearly with increasing values of \(\delta \). Finally, Fig. 10 illustrates the stop band behavior of the proposed metamaterial as a function of the angle \(\theta _0\) for fixed values of the following parameters: \(\alpha =1.5\), \(\beta =1.5\), \(\gamma =1\) and \(\delta =1.\) It is evident that the angle \(\theta _0\) can only alter the upper boundary of the second stop band and does not have any influence on the ending quasi-stop band as well as the lower boundary of the second stop band.

Fig. 8
figure 8

Variation of stop bands of the proposed metamaterial with varying \(\gamma \); (\(\alpha =1.5\), \(\beta =1\), \(\delta =0.1\) and \(\theta _0=\pi /6\))

Full size image
Fig. 9
figure 9

Variation of stop bands of the proposed metamaterial with varying \(\delta \); (\(\alpha =2\), \(\beta =1\), \(\gamma =0.1\) and \(\theta _0=\pi /4\))

Full size image
Fig. 10
figure 10

Variation of stop bands of the proposed metamaterial with varying \(\theta _0\); (\(\alpha =1.5\), \(\beta =1.5\), \(\gamma =1\)) and \(\delta =1\)

Full size image
Fig. 11
figure 11

Transmittances of the finite proposed metamaterial consisting of five cells with different values of \(\delta \)

Full size image

Figure 12 shows the transmittance spectrum of the proposed metamaterial with different numbers of unit cells (\(n=5\), 10 and 15). This figure was obtained by fixing the following values for the design parameters: \(\alpha =0.4\), \(\beta =0.8\), \(\gamma =0.4\), \(\delta =1\) and \(\theta _0=\pi /6\). Based on this figure, it can be concluded that the vibration suppression ability of the first attenuation region is significantly enhanced by increasing the number of unit cells. Therefore, the system parameters can be tuned such that the proposed metamaterial provides a way to achieve ultra-low frequency vibration suppression.

Fig. 12
figure 12

Transmittances of the finite proposed metamaterial consisting of different number of unit cells

Full size image

4.2 Finite metamaterial

This section studies the stop band behavior of a finite lattice model consisting of a certain number of unit cells and estimating the corresponding transmission spectrum. Figure 11 illustrates the transmittance spectrum of the proposed metamaterial consisting of five unit cells obtained for three different values of \(\delta \) (0, 0.4 and 0.8). The remaining design parameters are fixed as follows: \(\alpha =2\), \(\beta =1.5\) , \(\gamma =0\) and \(\theta _0=\pi /4\). It is important to note that a zero \(\delta \) coefficient corresponds to the case of a conventional metamaterial with a single attenuation zone observed around \(\varpi =1\) and this is associated with the locally resonant stop band and the negative effective mass region. For a nonzero \(\delta \) coefficient, three attenuation regions appear in the transmittance spectrum. Figure 11 depicts also very low transmittances predicted in the low frequency region thereby validating the formation of the quasi-static stop band. For example, this scenario occurs for the case where \(\delta =0.8\) with frequencies ranging from 0 to 0.665. In addition, it can be seen that the transmittance inside the first attenuation region decreases when the value of \(\delta \) increases. Furthermore, the width of the first attenuation region corresponding to the quasi-static stop band broadens when the value of \(\delta \) increases.

5 Conclusion

In this paper, we proposed and analyzed a new one-dimensional metamaterial to achieve the quasi-static stop band from zero frequency. On the basis of the infinite lattice model, the dispersion relation of the proposed metamaterial was obtained using Bloch’s theorem. The obtained numerical results demonstrated the existence of two stop bands in the dispersion curves in which the lower boundary of the first stop band is zero. This result is important because the proposed metamaterial can block all waves with frequencies lower than a certain value (upper band of quasi-static stop band). In addition, the finite unit cell model was established and a closed-form relation for transmittance was obtained. The attenuation behavior observed in the transmittance spectrum was in good agreement with the predictions from the dispersion curve of the infinite model. Finally, it should be noted that since a quasi-static stop band was achieved, the results of the present study can be helpful to design a new generation of vibration suppression devices.