1 Introduction

Micromechanical modeling of materials has sparked a lot of attention in recent years, as it is well known that many materials contain heterogeneous microstructures that play a dominating role in defining macro-mechanical behavior. Multiphase fiber and particle composites, ceramic and metal composites, poly-crystals (tungsten-carbide, zinc oxide, aluminia, zirconia), rocks, concrete, masonry structures and granular materials are examples of materials where this happens. These materials show microstructures that occur at a variety of length scales, from meters to nanometers. The micromechanical behaviors across distinct material phases have a profound influence on the response of such heterogeneous solids. A detailed discrete model, considering these materials as Lagrangian systems, is characterized by the expensive computational cost of the numerical model [1, 2] and for this, an alternative approach is preferable such as to adopt multiscale procedures for deriving equivalent homogenized continua. The capability of classical continuum mechanics theories to predict such phenomena is restricted, prompting the creation of a slew of novel micromechanical solids theories. There have been several instances where significant differences between theory and experimentation have been noticed. This refers, first and foremost, to stress situations with significant stress gradients. Stress concentrations in the vicinity of holes, notches, and fractures might be instances of such states. The disparity between the classical theory of elasticity and the tests is also noticeable in dynamical situations, such as elastic vibrations with high frequency and short wave lengths, such as ultrasonic waves [3,4,5,6,7,8]. More recently, different kind of continuum models have been proposed, in which the material response is dependent on certain microscale length parameters linked to the existence of inner degrees of freedom and non-local continuum behavior. ’Explicit’ non-local behavior refers to the fact that the stress at a given location is influenced not only by the strain at that location, but also by the stresses at nearby locations. This necessitates non-local descriptions that incorporate internal length parameters, ’implicit’ non-local description, with internal length and dispersion properties in wave propagation [3, 6, 9, 10], can be also obtained by adding extra degrees of freedom [11,12,13,14]. To explain the micromechanical behavior of materials, non classical and non-local theories based on higher-order gradients have been developed as well as micromorphic continua [9, 15]: the micropolar theory [16,17,18] is an example of ’implicit’ non-local descriptions, in which the rotation of the material point (microrotation), different from the classical local rigid rotation (macrorotation), is introduced as an additional kinematic parameter. This theory has been successfully used to a variety of composites with both periodic and random microstructure [19,20,21] as well as the couple stress theory [22, 23], in which the microrotation and the macrorotation coincide. Non-local ’explicit’ theories have been adopted for the modeling of heterogeneous materials [24, 25], such as composites with periodic microstructure [26] or random composites [27,28,29]. Given the extensive application of composite materials in many engineering structures, strong is the interest of researcher about the thermo-mechanical behavior of anisotropic materials [30, 31]. In particular, techniques based on homogenization have been widely exploited to study the mechanical behavior of materials: for example, the effects of micro-fractures and contact simulations on the macroscopic response of deformed composites, fiber-reinforced materials [32] and the failure and the damage of periodic masonry assemblies [33, 34] and of ceramic and advanced materials [35,36,37]. There are also many examples in which materials with voids [38,39,40] have been studied referring to Cosserat theory, such as foams [41,42,43,44], granular and geo-materials [45,46,47,48,49,50,51], cellular solids [52,53,54] and different kind of structures such as rods [55] and shells [56,57,58] or even multifield models with affine microstructure [5, 7]. In order to extend the numerical investigations about the microstructured composite materials made of rigid particles and elastic thin interfaces [59,60,61], the goal is to test the efficiency of the homogenization technique adopted [62, 63], to describe porous materials, not yet analyzed with this approach by the authors themselves [64,65,66]. The study is conducted both in static and dynamic conditions, varying the internal characteristics and then proposing a comparison between a discrete model and two continuous models, one micropolar and one classic. This is how the article is structured: we start from a brief description of the micropolar theory, especially referring to the 2D case (Sect. 2), then the homogenization technique used for the homogenization of the materials is mentioned (Sect. 3), the simulations will be illustrated both as regards the numerical implementation and both as regards the results (Sect. 4), and, finally, the conclusions will be remarked (Sect. 5).

2 Micropolar theory

Extra degrees of freedom are considered in micropolar theory, in particular, the microrotation of the material particles is considered together with the displacements. Therefore, the displacement field of a material particle in a micropolar continuum is characterized by displacements and rotations. In a 3D framework, there are three displacement and three rotation components, which reduce to two displacement and one rotation components in the 2D case. In the present study, we refer to 2D problems in a linearized kinematical framework, where, the displacement components being gathered in the vector \(\varvec{u}^{\top }=\begin{bmatrix} u_1&u_2&\omega \end{bmatrix}\), \(u_1\) and \(u_2\) being the displacement components, and \(\omega \) the micro-rotation. Note that the variable \(\omega \) is different from the macro-rotation \(\theta \), defined as the skew-symmetric part of the gradient of displacement. The strain vector is: \(\varvec{\varepsilon }^{\top }=\begin{bmatrix} {\varepsilon }_{11}&{\varepsilon }_{22}&{\varepsilon }_{12}&{\varepsilon }_{21}&{\kappa }_{1}&{\kappa }_{2} \end{bmatrix}\), where \(\varepsilon _{ij}\) (\(i,j=1,2\)) are the normal and shear strain components, and the microcurvatures are indicated by \(\kappa _1\) and \(\kappa _2\). Differently from the classical continuum, the strain components are not reciprocal \({\varepsilon }_{12} \ne {\varepsilon }_{21}\). The vector \(\varvec{\sigma }^{\top }=\begin{bmatrix} \sigma _{11}&\sigma _{22}&\sigma _{12}&\sigma _{21}&\mu _{1}&\mu _{2} \end{bmatrix}\) collects the stress components, where \(\sigma _{ij}\) (\(i,j=1,2\)) represents the normal and shear stress components, and \(\mu _1\), \(\mu _2\) are the microcouples. Due the presence of microcouples, differently from the classical continuum, the shear stress components are not reciprocal: \(\sigma _{12} \ne \sigma _{21}\). The couple stress components \(\mu _1\), \(\mu _2\) allow to satisfy the moment equilibrium of the micropolar body.

The operator \(\mathbf {D}\) is defined below:

$$\begin{aligned} \mathbf {D}^{\top } =\begin{bmatrix} \dfrac{\partial }{\partial x_1} &{} 0 &{} \dfrac{\partial }{\partial x_2} &{} 0 &{} 0 &{} 0 \\ 0 &{} \dfrac{\partial }{\partial x_2} &{} 0 &{} \dfrac{\partial }{\partial x_1} &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} -1 &{} \dfrac{\partial }{\partial x_1} &{} \dfrac{\partial }{\partial x_2} \end{bmatrix} , \end{aligned}$$
(1)

as consequence, is possible to write the kinematic compatibility relation between the vectors \(\varvec{u}\) and \(\varvec{\varepsilon }\):

$$\begin{aligned} \varvec{\varepsilon } = \mathbf {D} \, \varvec{u}\,, \end{aligned}$$
(2)

Using the Hamilton’s principle, the equilibrium of the body can be expressed as:

$$\begin{aligned} \delta \int _{t_1}^{t_2} (K-\Pi ) \, \mathrm{{d}}t=0\,, \end{aligned}$$
(3)

where the term K indicates the kinetic energy and \(\Pi \) is the total potential energy, which is defined by the sum of the strain energy U and the potential of external loads V:

$$\begin{aligned} \Pi =U+V. \end{aligned}$$
(4)

The variation of the kinetic energy is:

$$\begin{aligned} \delta K = \int _V \rho \delta \varvec{\dot{u}}^{\top } \varvec{\dot{u}} \, \mathrm{{d}}V= h \int _A \delta \varvec{\dot{u}}^{\top } \mathbf {m} \varvec{\dot{u}} \, \mathrm{{d}}A = -h\int _A \delta \varvec{u}^{\top } \mathbf {m} \varvec{\ddot{u}} \, \mathrm{{d}}A \,, \end{aligned}$$
(5)

h is the thickness of the body which can be assumed unitary and \(\mathbf {m}\) is mass matrix defined as:

$$\begin{aligned} \mathbf {m} = \begin{bmatrix} \rho h &{} 0 &{} 0 \\ 0 &{} \rho h &{} 0 \\ 0 &{} 0 &{} \rho J_c \end{bmatrix} \,, \end{aligned}$$
(6)

where \(\rho \) is the material density and \(J_c\) represents the rotary inertia of the material point. The variation of the strain energy is written in the form:

$$\begin{aligned} \delta U = \int _A \delta \varvec{\varepsilon }^{\top } \varvec{\sigma } \, \mathrm{{d}}A \,, \end{aligned}$$
(7)

and using Eq. (1):

$$\begin{aligned} \delta U = \int _A \delta \varvec{u}^{\top } \mathbf {D}^{\top } \, \varvec{\sigma } \, \mathrm{{d}}A \,. \end{aligned}$$
(8)

Below, the variation of the potential of external loads is reported:

$$\begin{aligned} \delta V= -\int _A \delta \varvec{u}^{\top } \varvec{b} \, \mathrm{{d}}A - \int _{\gamma _t} \delta \varvec{u}^{\top } \varvec{t} \, \mathrm{{d}}\gamma \,, \end{aligned}$$
(9)

where the body and surface forces are represented by the vectors \(\varvec{b}\) and \(\varvec{t}\), respectively.

At this point, the micropolar anisotropic constitutive equation can be reported:

$$\begin{aligned} \varvec{\sigma }=\mathbf {C} \, \varvec{\varepsilon } \,, \end{aligned}$$
(10)

where

$$\begin{aligned} \mathbf {C}= \begin{bmatrix} A_{1111} &{} A_{1122} &{} A_{1112} &{} A_{1121} &{} B_{111} &{} B_{112} \\ &{} A_{2222} &{} A_{2212} &{} A_{2221} &{} B_{221} &{} B_{222}\\ &{} &{} A_{1212} &{} A_{1221} &{} B_{121} &{} B_{122} \\ &{} &{} &{} A_{2121} &{} B_{211} &{} B_{212} \\ &{} &{} &{} &{} D_{11} &{} D_{12} \\ sym &{} &{} &{} &{} &{} D_{22} \end{bmatrix} = \begin{bmatrix} {\mathbb {A}} &{} {\mathbb {B}} \\ {\mathbb {B}}^{\top } &{} {\mathbb {D}} \end{bmatrix} \,. \end{aligned}$$
(11)

As hyperelastic media are considered, the stiffness matrix of the discrete system is symmetric, this yields that the continuum constitutive matrix \(\mathbf {C}\) is symmetric (\(\mathbf {C} \in Sym\)). Thus, \(A_{ijhk}=A_{hkij}\); \(B_{ijh}=B_{hij}\); \(D_{ij}=D_{ji}\) (\(i,j,h,k=1,2\)) and they are a fourth-order, third-order and second-order tensors, respectively [67]. On the basis of these assumptions, the Hamilton’s principle can be written as:

$$\begin{aligned} \int _{t_1}^{t_2} \left( \int _A \delta \varvec{u}^{\top } \left( \mathbf {m} \varvec{\ddot{u}} + \mathbf {D}^{\top } \, \mathbf {C}\mathbf {D}\varvec{u} \right) dA\, + \int _A \delta \varvec{u}^{\top } \varvec{b} \, dA + \int _{\gamma _t} \delta \varvec{u}^{\top } \varvec{t} \, d\gamma \right) \, dt = 0\,. \end{aligned}$$
(12)

3 Continuum model

3.1 Homogenization

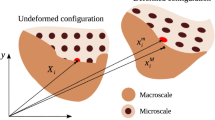
In this work, materials made of a rectangular microstructure and with the presence of voids (Fig. 1), representing to a porous medium, are taken into account: the blocks of the microstructure are assumed to be constant while the voids percentage v varies. In this case, two different size of the internal microstructure and three different percentage of the voids have been considered. In order to test the homogenization procedure for these kind of microstructured materials, we introduce a scale parameter s corresponding to the block lengths \(l_1\), \(l_2\) and consider two cases: \(s=1\), with \( l_1 = 0.8 \) \(\mu \)m and \( l_2 = 0.2 \) \(\mu \)m, and \(s=0.5\), with \(l_1 = 0.4 \) \(\mu \)m and \( l_2 = 0.1 \) \(\mu \)m. The scale parameter is intended as the ratio between the characteristic length of the macrostructure and the microstructure internal length of the material. The percentage of the voids can be defined through the ratio, indicated as v, between the length of the portion of the side in horizontal contact between the blocks and the total side of the block. Here, the ratios considered are: \(v=0.2/0.8=0.25\), \(v=0.4/0.8=0.5\) and \(v=0.6/0.8=0.75\), obviously, by changing the scale of the blocks the aforementioned ratios are constant.

Fig. 1
figure 1

Rectangular microstructures for the scale parameter \(s=1\) (a) \(v=0.25\), (b) \(v=0.5\), (c) \(v=0.75\)

Full size image

Three different voids size are considered, as reported in Fig. 2 where the representing volume element (RVE) is depicted. To apply the homogenization method to periodic assemblies, the RVE must be identified, as the volume element, made of the minimal number of elements and joints necessary to fully define the behavior of a discontinuous and heterogeneous material. The blocks are assumed rigid respect to the stiffness of the contact interfaces, and the elasticity of the microstructure is assumed to be concentrated in the joints between the blocks. For the interfaces, a linear elastic constitutive law is considered.

Fig. 2
figure 2

RVEs for the microstructure with scale parameter \(s=1\) with a voids percentage \(v=0.75\)

Full size image

As homogenization criterion, an energy equivalence criterion is adopted, based on the a generalized version of the so-called Cauchy–Born rule [68,69,70,71,72,73,74] that is a kinematic correspondence map between discrete and continuous fields proposed in [62, 63]. Non-classical continuous models of discrete systems of various kinds have been derived using revised discrete-continuum correspondence maps using this approach, always accounting for the internal size effect of the microstructure [75,76,77]. The feasibility of giving a macroscopic description for heterogeneous media has been widely studied within the framework of the homogenization or coarse graining theories [11]. The power equivalence approach provides a straightforward way to determine all the constitutive parameters of the continuous medium, the components of the matrix \(\mathbf {C}\) in Eq. 11, by establishing the elastic constants and the geometry of the discrete system. Finally, the constitutive matrix for the Cauchy model is derived from the previous Eq. 11 using the procedure in [78] as:

$$\begin{aligned} \mathbf {C}= \begin{bmatrix} A_{1111} &{} A_{1122} &{} 0\\ A_{2211} &{} A_{2222} &{} 0\\ 0 &{} 0 &{} \dfrac{1}{4}[A_{1212}+A_{2121}] + \dfrac{1}{2}A_{1221}\\ \end{bmatrix} \,. \end{aligned}$$
(13)

It should be remarked that Cauchy model does not keep memory of the internal length of the microstructure.

3.2 Finite element model

The continuum models have been solved with the finite element method that is based on the approximation of nodal displacements:

$$\begin{aligned} \varvec{u}={{\mathcal {N}}} \, \varvec{d}^e \,, \end{aligned}$$
(14)

The current implementation was carried out utilizing an in-house MATLAB code [79]. The kinematic displacement vector is arranged as follows:

$$\begin{aligned} \varvec{d}^{eT}=\begin{bmatrix} u_1^1&\ldots&u_1^4&u_2^1&\ldots&u_2^4&\omega ^1&\ldots&\omega ^4 \end{bmatrix} \,, \end{aligned}$$
(15)

there are 12 degrees of freedom overall (3 per node). The vector \(\mathbf {N}\), which gathers the Lagrangian shape functions, makes up the matrix of shape functions:

$$\begin{aligned} {{\mathcal {N}}}=\begin{bmatrix} \mathbf {N} &{} \mathbf {0} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {N} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} &{} \mathbf {N} \end{bmatrix} \,. \end{aligned}$$
(16)

By replacing the above expression of the displacement vector, in the Hamilton principle, the kinetic energy becomes:

$$\begin{aligned} \delta K = -\delta \varvec{d}^{eT} \int _A {{\mathcal {N}}}^{\top } \mathbf {m} {{\mathcal {N}}} \, \mathrm{{d}}A \, \varvec{\ddot{d}}^{\, e} \,. \end{aligned}$$
(17)

The mass matrix reads:

$$\begin{aligned} \mathbf {M}^e= \int _A {{\mathcal {N}}}^{\top } \mathbf {m} {{\mathcal {N}}} \, \mathrm{{d}}A \,. \end{aligned}$$
(18)

The internal work takes the form:

$$\begin{aligned} \delta U = \delta \varvec{d}^{eT} h \int _A (\mathbf {D} \, {{\mathcal {N}}})^{\top } \mathbf {C} (\mathbf {D} \, {{\mathcal {N}}}) \, \mathrm{{d}}A \, \varvec{d}^e = \delta \varvec{d}^{eT} h \int _A \mathbf {B}^{\top } \mathbf {C} \, \mathbf {B} \, \mathrm{{d}}A \, \varvec{d}^e\,, \end{aligned}$$
(19)

where \(\mathbf {B}=\mathbf {D} \, {{\mathcal {N}}}\), thus the element stiffness matrix is:

$$\begin{aligned} \mathbf {K}^e=\int _A \mathbf {B}^{\top } \mathbf {C} \, \mathbf {B} \, \mathrm{{d}}A \,, \end{aligned}$$
(20)

which must be integrated using a \(2\times 2\) Gauss integration for normal components and micro-couples, while reduced integration is used for shear components. Finally, the potential of external forces is:

$$\begin{aligned} \delta V= - \delta {\varvec{d}^e}^T\int _A {{\mathcal {N}}}^{\top } \varvec{b} \, \mathrm{{d}}A - \delta {\varvec{d}^e}^T \int _{\gamma _t} {{\mathcal {N}}}^{\top } \varvec{t} \, d\gamma = - \delta {\varvec{d}^e}^T \varvec{F} \,, \end{aligned}$$
(21)

where \(\varvec{F}\) is the global vector of volume and surface forces.

4 Numerical simulations

It is emphasized that the constitutive matrix of the continuum model, \(\mathbf {C}\) (Eq. 11), for all the cases here considered, with rectangular microstructure, is centrosymmetric and moreover orthotropic (Eqs. 22–27). Only the submatrix \(\mathbb {D}\) takes into account the internal scale of the microstructure of the material. In particular, due to the central symmetry, the submatrix \(\mathbb {B}= \mathbf {0}\) and there is no coupling between normal and shear stresses/strains with curvatures/micro-couples, moreover, due to the absence of dilatancy effect in the discrete original model, no Poisson effect is present.

A rectangular panel, of width \(L_x=12\) \(\mu \)m and height \(L_y=11.6\) \(\mu \)m, in the 2D plane stress case, both in static and in dynamic conditions, is studied. As a comparison, a lattice model as benchmark has been carried out in ABAQUS\(^{\circledR }\), and two continuum models, the Cosserat model and the Cauchy model, are compared with the latter. For the static case, the panel is subjected to a vertical load p applied at the top distributed in a foot print equal to \(a=L_x/4\) (Fig. 3). In the dynamic case, free vibrations are considered.

Fig. 3
figure 3

Static scheme for the static analyses

Full size image

4.1 Scale \(s=1\)

The constitutive matrix for the microstructure with the scale parameter \(s=1\) and voids size \(v= 0.25\) is:

$$\begin{aligned} \mathbf {C}_{v=0.25}^{s=1}=\begin{bmatrix} 0.9199 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.2944 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.1472 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1.8398 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0.1449 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0232 \\ \end{bmatrix} \,. \end{aligned}$$
(22)

In Fig. 4, the vertical displacement component is shown and due to the symmetry of the problem only half of the panel is reported (only the vertical component of displacements is reported, as the most significant of the case study). It can be noted that the contour plot of the micropolar continuum is in line with the discrete system. There are not evident differences among the Cauchy and Cosserat models, even if, this last is able to better distribute the level curves in comparison with the classical model. These differences have been shown to strongly increase when the load tip decreases [67].

The constitutive matrix for the microstructure with the scale parameter \(s=1\) and voids size \(v=0.5\) is:

$$\begin{aligned} \mathbf {C}_{v=0.5}^{s=1}= \begin{bmatrix} 0.8831 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.1962 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.0981 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1.7662 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0.1766 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0196\\ \end{bmatrix} \,. \end{aligned}$$
(23)

An increase in the size of the voids causes a decrease in the elastic contact among the rigid blocks of the microstructure, and this translates into a reduction in the elastic constants of the submatrix \(\mathbb {A}\), hence, in a loss of the stiffness. Differently, for the terms of the submatrix \(\mathbb {D}\), which depends, not only on the interface stiffness, but also on the internal size, there is an increment of the value of the term \(D_{11}\), while the term \(D_{22}\) decreases respect to the previous case. The lower stiffness led to an increase in the maximum displacements, and the classical model gives reliable results only for the static case (Fig. 4), although different from the discrete model which results are in agreement with the micropolar ones.

Finally, the constitutive matrix for the microstructure with the scale parameter \(s=1\) and the voids size \(v=0.75\) is:

$$\begin{aligned} \mathbf {C}_{v=0.75}^{s=1}= \begin{bmatrix} 0.6010 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.0981 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.0491 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1.2020 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0.1548 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0126\\ \end{bmatrix} \,. \end{aligned}$$
(24)

In the latter case, there is a further reduction in the elastic constants of the matrix \(\mathbb {A}\), while as regards the terms of the sub-matrix \(\mathbb {D}\), the term \(D_{11}\) decreases with respect to the case in which the dimensions of the voids are \(v = 0.5\), but it is greater than the case \(v = 0.25\), the term \(D_{22}\) is smaller in both cases. This implies an increase in the maximum displacement, and both continuous models provide a good characterization of the discrete model behavior (Fig. 4).

Fig. 4
figure 4

Vertical displacements for the microstructure with scale parameter \(s=1\). (a) \(v=0.75\) (b) \(v=0.5\) (c) \(v=0.75\)

Full size image

Regarding the dynamic analysis of the microstructure with a voids size \(v=0.75\) (Fig. 5), it can be observed as for the first three modes, both the classical and the micropolar continuum are able to detect the displacement plots. However, for this last model the maximum error, in the natural frequencies evaluation (Table 1), is around 3%, whereas for the Cauchy model the error is very high compared to the discrete system and only the axial vibration mode exhibits a good result (the errors reported are the relative errors of the continuous models computed with respect to the discrete system). Furthermore, only the micropolar model is capable of detecting the correct dynamic behavior (mode shape) of the fourth mode.

Fig. 5
figure 5

Vibration modes: microstructure with scale parameter \(s=1\) and voids size \(v=0.25\)

Full size image

From the dynamic analysis, the growth of the voids size highlights that the Cauchy model has worse results than the micropolar one, when compared to the discrete system and also with respect to the previous simulations with smaller voids percentage. Such large differences are noticed in terms of frequency (Table 1) and mode shapes (Fig. 6). The fourth mode of the Cauchy model, even if different from the previous case, does not match with the discrete one, and only the Cosserat model satisfactory represents the behavior of the benchmark.

Fig. 6
figure 6

Vibration modes: microstructure with scale parameter \(s=1\) and voids size \(v=0.5\)

Full size image

For the voids size \(v=0.75\) case, the micropolar model is still efficient as regards the representation of the displacement fields of the discrete model (Fig. 7). The estimation of frequencies for both continuous models deteriorated as the size of the voids has become larger (Tab. 1), even if the largest error threshold of the Cosserat model is about the 3.5%, and as a result, it continues to be reliable.

Fig. 7
figure 7

Vibration modes: microstructure with scale parameter \(s=1\) and voids size \(v=0.75\)

Full size image
Table 1 Natural frequencies (Mhz) for the microstructure with scale parameter \(s=1\)
Full size table

4.2 Scale \(s=0.5\)

The constitutive matrix for the microstructure with the scale parameter \(s=0.5\) and voids size \(v= 0.25\) is:

$$\begin{aligned} \mathbf {C}_{v=0.25}^{s=0.5}=\begin{bmatrix} 0.9199 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.2944 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.1472 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1.8398 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0.0362 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0058 \\ \end{bmatrix} \,. \end{aligned}$$
(25)

The scale parameter s is taken into account by the submatrix \(\mathbb {D}\), and, specifically, it can be seen that \(D_{ii}^{s=1}\approx 4D_{ii}^{s=0.5}\) (\(i=1,2\)). There is an improvement in the correspondence between the results of the discrete model and the micropolar model when the internal scale of the microstructure is reduced, as shown in the contour plots of the vertical displacements for the static case (Fig. 8).

The constitutive matrix for the microstructure with the scale parameter \(s=0.5\) and voids size \(v= 0.5\) is:

$$\begin{aligned} \mathbf {C}_{v=0.5}^{s=0.5}= \begin{bmatrix} 0.8831 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.1962 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.0981 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1.7662 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0.0442 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0049\\ \end{bmatrix} \,. \end{aligned}$$
(26)

Also in this case, the displacement field of the discrete model is well represented by the two continuous models, and the reduction in the scale favors the correspondence between the models; moreover, there is an increase in the maximum vertical displacement compared to the previous case (Fig. 8).

In the end, the constitutive matrix for the microstructure with the scale parameter \(s=0.5\) and the voids size \(v=0.75\) is:

$$\begin{aligned} \mathbf {C}_{v=0.75}^{s=0.5}= \begin{bmatrix} 0.6010 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.0981 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.0491 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1.2020 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0.0387 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.0032\\ \end{bmatrix} \,. \end{aligned}$$
(27)

With the decrease in the scale, as seen in the previous two cases, there is still a better correspondence between the continuous models and the discrete system (Fig. 8).

Fig. 8
figure 8

Vertical displacements for the microstructure with scale parameter \(s=0.5\). (a) \(v=0.75\) (b) \(v=0.5\) (c) \(v=0.75\)

Full size image

As regards the dynamic analysis, it is clear that only the micropolar model gives satisfactory results both in terms of plots (Fig. 9) and frequencies (Table 2). In particular, it has been noticed that the errors of the present results are smaller compared to the previous case with the scale parameter \(s=1\), in fact the the maximum error is around the \(0.70\%\).

Fig. 9
figure 9

Vibration modes: microstructure with scale parameter \(s=0.5\) and voids size \(v=0.25\)

Full size image

Also for case where the voids size is \(v=0.5\), the maximum error is reduced when the microstructure scale is reduced, which improves the natural frequencies evaluation for the micropolar model (Table 2); however, also in this case, the classical model is not able to predict the dynamic behavior of the benchmark and this is related to the orthotropic character of the material as well, except for the axial mode (Fig. 10).

Fig. 10
figure 10

Vibration modes: microstructure with scale parameter \(s=0.5\) and voids size \(v=0.5\)

Full size image

Finally, the dynamic study reveals that decreasing the scale parameter improves the outcomes and in general, it can be stated that with the increase in the voids size the evaluation of the frequencies presents some worsening; however, the Cosserat model still offers a good estimate of the dynamic response, the maximum error being around the 2% (Fig. 11 and Table 2).

Fig. 11
figure 11

Vibration modes: microstructure with scale parameter \(s=0.5\) and voids size \(v=0.75\)

Full size image
Table 2 Natural frequencies (Mhz) for the microstructure with scale parameter \(s=0.5\)
Full size table

5 Conclusions

In this paper, we have dealt with the numerical study of an orthotropic material, with the presence of voids, therefore assimilable to a porous medium. The comparisons among the discrete systems, assumed to be a micromechanical model of the material and supposed as the benchmark of the problem, and two continuous models were carried out through static and dynamic analyses. When the contact area between the blocks becomes significantly smaller than their geometric size, there is a worsening of the capability of the continuous model to represent the lattice system behavior. The differences between the Cosserat and Cauchy solutions arise as the scale ratio, understood as the ratio between the characteristic length of the macrostructure and the internal length of the material microstructure, increases because the Cauchy model cannot account for scale effects [80, 81]. The work highlights the possibility of describing porous media through this homogenization procedure, not yet previously detailed for these kinds of materials, and how the introduction of a new internal characteristic of the material, the size of the voids, involves a deterioration of the results compared to non-porous materials for the classical model [65]. As widely shown in earlier works [59, 62, 81], for orthotropic media the inadequacy of the a classical continuum arises even when the actual value of the length parameter of the internal microstructure can be considered small compared to the macroscopic characteristics. Only in the isotropic case, the classical model can provide results comparable with the results of the micropolar model when the internal length decreases. The numerical results show that the Cauchy model is not sufficient to adequately characterize problems in which material internal lengths play a significant role and the case of porous media analyzed in this work also contribute to highlight, both in the static and the dynamic case, this aspect. In this work, it has been particularly highlighted, from the dynamic analyses, not already performed in earlier papers, that the micropolar model, accounting for material size and anisotropy [67], makes an important contribution and allows us to accurately describe the mechanical behavior of the discrete system adopted to finely represent the material behavior.