Skip to main content
SpringerLink
Log in

2-D mathematical model of hyperbolic two-temperature generalized thermoelastic solid cylinder under mechanical damage effect

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

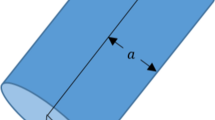
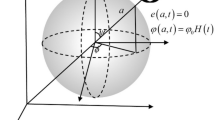
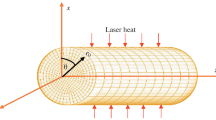
This paper presents the construction of a two-dimensional mathematical model of a thermoelastic, homogeneous, and isotropic solid cylinder with its bounding surface subjected to a thermal shock. It has been discovered that the governing differential equations may be constructed in the framework of the hyperbolic two-temperature generalized thermoelasticity theory based on the study of the damage mechanics variable. It has been demonstrated visually that different values of the two-temperature parameter, damage mechanics variable and cylindrical length may produce numerically significant increases in dynamical and conductive temperatures, strain, and the average of the major stress components. The two-temperature parameter, as well as the diameter of the cylindrical axis, has substantial effects on all the functions under consideration. The damage mechanics variable has very little impact on the conductive and dynamical temperatures, but it has large implications on the strain and stress distributions, as seen in the graphs. The thermal wave can propagate at a limited pace using the hyperbolic two-temperature theory. The hyperbolic two-temperature theory offers a finite speed of propagation to the thermal wave.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Data availability

Not applicable.

Abbreviations

\(C_{{\text{E}}}\) :

Specific heat at constant strain

\(c_{o} \,\,\) :

\(= \sqrt {\frac{\lambda + 2\,\mu }{\rho }}\) Longitudinal wave speed

D :

The mechanical damage variable

\(e_{ij}\) :

The strain components

\(K\) :

Thermal conductivity

\(T_{{\text{D}}} ,\,T_{{\text{C}}}\) :

Dynamical and conductive temperature, respectively

\(T_{o}\) :

Reference temperature

\(t\,,\tau_{0}\) :

Time and thermal relaxation time, respectively

\(u\,\) :

\(u\, = \left( {u_{r} ,u_{\psi } ,u_{z} } \right)\) The displacement functions

\(\alpha_{{\text{T}}}\) :

Coefficient of linear thermal expansion

\( \beta \) :

\( = \left( {\frac{{\lambda + 2\mu }}{\mu }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \)

\( \gamma \) :

\(= \left( {3\lambda + 2\mu } \right)\alpha _{T} \)

\(\varepsilon\) :

\(= \frac{\gamma }{{\rho \,C_{{\text{E}}} }}\) The mechanical coupling constant (dimensionless)

\(\varepsilon_{1}\) :

\(= \frac{{\gamma T_{o} }}{\mu }\) The thermoelastic coupling constant (dimensionless)

\(\eta\) :

\(= \frac{{\rho \,C_{{\text{E}}} }}{K}\) The thermal viscosity

\(\lambda \;,\;\mu \,\) :

Lamé’s constants

\(\rho \,\) :

Density

\(\sigma_{ij} \,\) :

Components of the stress tensor

References

  1. Lord, H.W., Shulman, Y.: A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15(5), 299–309 (1967). https://doi.org/10.1016/0022-5096(67)90024-5

    Article  MATH  Google Scholar 

  2. Abbas, I.A.: The effects of relaxation times and moving heat source on two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 93(5), 585–590 (2014). https://doi.org/10.1139/cjp-2014-0387

    Article  Google Scholar 

  3. Ezzat, M.A., Youssef, H.M.: Generalized magneto-thermoelasticity for an infinite perfect conducting body with a cylindrical cavity. Mater. Phys. Mech. 18, 156–170 (2013)

    Google Scholar 

  4. Othman, M.I., Mondal, S.: Memory-dependent derivative effect on 2D problem of generalized thermoelastic rotating medium with Lord–Shulman model. Indian J. Phys. (2019). https://doi.org/10.1007/s12648-019-01548-x

    Article  Google Scholar 

  5. Heydarpour, Y., Malekzadeh, P., Gholipour, F.: Thermoelastic analysis of FG-GPLRC spherical shells under thermo-mechanical loadings based on Lord–Shulman theory. Compos. B Eng. 164, 400–424 (2019). https://doi.org/10.1016/j.compositesb.2018.12.073

    Article  Google Scholar 

  6. Mondal, S.: Interactions of a heat source moving over a visco-thermoelastic rod kept in a magnetic field in the Lord–Shulman model under a memory dependent derivative. Comput. Math. Model. 31(2), 256–276 (2020). https://doi.org/10.1007/s10598-020-09490-y

    Article  MathSciNet  MATH  Google Scholar 

  7. Kiani, Y., Eslami, M.: Nonlinear generalized thermoelasticity of an isotropic layer based on Lord–Shulman theory. Eur. J. Mech. A Solids 61, 245–253 (2017). https://doi.org/10.1016/j.euromechsol.2016.10.004

    Article  MathSciNet  MATH  Google Scholar 

  8. Wang, Z.-W., Fu, L.-Y., Wei, J., Hou, W., Ba, J., Carcione, J.M.: On the green function of the Lord–Shulman thermoelasticity equations. Geophys. J. Int. 220(1), 393–403 (2020). https://doi.org/10.1093/gji/ggz453

    Article  Google Scholar 

  9. Alshaikh, F.: Effects of thermal relaxation times and porosity in a Lord–Shulman and refined multi-phase lags model of generalized thermoelasticity. Mech. Based Des. Struct. Mach. (2020). https://doi.org/10.1080/15397734.2020.1846129

    Article  Google Scholar 

  10. Chen, P.J., Gurtin, M.E.: On a theory of heat conduction involving two temperatures. Zeitschrift für angewandte Mathematik und Physik 19(4), 614–627 (1968). https://doi.org/10.1007/BF01594969

    Article  MATH  Google Scholar 

  11. Warren, W., Chen, P.: Wave propagation in the two temperature theory of thermoelasticity. Acta Mech. 16(1–2), 21–33 (1973). https://doi.org/10.1007/BF01177123

    Article  MATH  Google Scholar 

  12. Youssef, H.: Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 71(3), 383–390 (2006). https://doi.org/10.1093/imamat/hxh101

    Article  MathSciNet  MATH  Google Scholar 

  13. Abbas, I.A., Youssef, H.M.: Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 48(2), 331–339 (2013). https://doi.org/10.1007/s11012-012-9604-8

    Article  MathSciNet  MATH  Google Scholar 

  14. Youssef, H.M.: Two-temperature generalized thermoelastic infinite medium with cylindrical cavity subjected to moving heat source. Arch. Appl. Mech. 80(11), 1213–1224 (2010). https://doi.org/10.1007/s00419-009-0359-1

    Article  MATH  Google Scholar 

  15. Youssef, H.M.: Generalized thermoelastic infinite medium with cylindrical cavity subjected to moving heat source. Mech. Res. Commun. 36(4), 487–496 (2009). https://doi.org/10.1016/j.mechrescom.2008.12.004

    Article  MathSciNet  MATH  Google Scholar 

  16. Youssef, H.M., Abbas, I.A.: Thermal shock problem of generalized thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. Comput. Methods Sci. Technol. 13(2), 95–100 (2007)

    Article  Google Scholar 

  17. Youssef, H.: Generalized thermoelasticity of an infinite body with a cylindrical cavity and variable material properties. J. Therm. Stress. 28(5), 521–532 (2005). https://doi.org/10.1080/01495730590925029

    Article  Google Scholar 

  18. Youssef, H.M., El-Bary, A.A.: Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mech. 40, 158–171 (2018). https://doi.org/10.18720/MPM.4022018_4

    Article  Google Scholar 

  19. Youssef, H.M.: Problem of generalized thermoelastic infinite medium with cylindrical cavity subjected to a ramp-type heating and loading. Arch. Appl. Mech. 75(8–9), 553–565 (2006). https://doi.org/10.1007/s00419-005-0440-3

    Article  MATH  Google Scholar 

  20. El-Bary, A.A.: Hyperbolic two-temperature generalized thermoelasticity with fractional order strain of solid cylinder. J. Eng. Therm. Sci. (2021). https://doi.org/10.21595/jets.2021.21969

    Article  Google Scholar 

  21. Gross, D., Seelig, T.: Fracture Mechanics: With an Introduction to Micromechanics. Springer, Cham (2017)

    MATH  Google Scholar 

  22. Öchsner, A.: Continuum damage mechanics. In: Öchsner, A. (ed.) Continuum Damage and Fracture Mechanics, pp. 65–84. Springer, Singapore (2016). https://doi.org/10.1007/978-981-287-865-6_4

    Chapter  Google Scholar 

  23. Voyiadjis, G.Z.: Handbook of Damage Mechanics: Nano to Macro Scale for Materials and Structures. Springer, Berlin (2015)

    Google Scholar 

  24. Yao, Y., He, X., Keer, L.M., Fine, M.E.: A continuum damage mechanics-based unified creep and plasticity model for solder materials. Acta Mater. 83, 160–168 (2015). https://doi.org/10.1016/j.actamat.2014.09.051

    Article  Google Scholar 

  25. Voyiadjis, G.Z., Kattan, P.I.: Introducing damage mechanics templates for the systematic and consistent formulation of holistic material damage models. Acta Mech. 228(3), 951–990 (2017). https://doi.org/10.1007/s00707-016-1747-6

    Article  MathSciNet  MATH  Google Scholar 

  26. Khatir, A., Tehami, M., Khatir, S., Abdel Wahab, M.: Multiple damage detection and localization in beam-like and complex structures using co-ordinate modal assurance criterion combined with firefly and genetic algorithms. J. Vibroeng. 18(8), 5063–5073 (2016). https://doi.org/10.21595/jve.2016.17026

    Article  Google Scholar 

  27. Youssef, H.M.: Thermal shock problem of a generalized thermoelastic solid sphere affected by mechanical damage and thermal diffusion. J. Eng. Therm. Sci. 1(1), 1–16 (2021). https://doi.org/10.21595/jets.2021.21934

    Article  Google Scholar 

  28. Singh, A., Das, S., Craciun, E.-M.: Effect of thermomechanical loading on an edge crack of finite length in an infinite orthotropic strip. Mech. Compos. Mater. 55(3), 285–296 (2019). https://doi.org/10.1007/s11029-019-09812-1

    Article  Google Scholar 

  29. Craciun, E.-M., Soós, E.: Anti-plane states in an anisotropic elastic body containing an elliptical hole. Math. Mech. Solids 11(5), 459–466 (2006). https://doi.org/10.1177/1081286505044138

    Article  MathSciNet  MATH  Google Scholar 

  30. Tzou, D.Y.: A unified field approach for heat conduction from macro-to micro-scales. J. Heat Transf. 117(1), 8–16 (1995). https://doi.org/10.1115/1.2822329

    Article  Google Scholar 

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Mathematics Department, Faculty of Education, Alexandria University, Alexandria, Egypt

    Hamdy M. Youssef

  2. Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, 21955, Kingdom of Saudi Arabia

    Hamdy M. Youssef

  3. Mathematics Department, Al-Lith University College, Umm Al-Qura University, Al-Lith, Kingdom of Saudi Arabia

    Eman A. N. Al-Lehaibi

Authors
  1. Hamdy M. Youssef
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Eman A. N. Al-Lehaibi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hamdy M. Youssef.

Ethics declarations

Conflict of interest

All authors declare no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Youssef, H.M., Al-Lehaibi, E.A.N. 2-D mathematical model of hyperbolic two-temperature generalized thermoelastic solid cylinder under mechanical damage effect. Arch Appl Mech 92, 945–960 (2022). https://doi.org/10.1007/s00419-021-02083-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-02083-0

Keywords

Search

Navigation