Analytical solution of the uniaxial extension problem for the relaxed micromorphic continuum and other generalized continua (including full derivations)

Abstract

We derive analytical solutions for the uniaxial extension problem for the relaxed micromorphic continuum and other generalized continua. These solutions may help in the identification of material parameters of generalized continua which are able to disclose size effects.

1 Introduction

In this paper we continue our investigation of analytical solutions for the isotropic relaxed micromorphic model (and other isotropic generalized continuum models). It follows our recent exposition of analytical solutions for the simple shear [28], bending [25], and torsion problem [13, 27]. Here, we consider the uniaxial extension problem, which, in classical isotropic linear elasticity, allows to determine the size-independent longitudinal modulus $M_{\text {macro}}=\lambda _{\text {macro}}+2\mu _{\text {macro}}$.

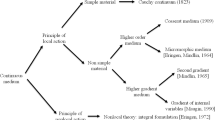
Here, we show the genealogy tree of the generalized continuum models:

The strain gradient theory and second gradient theory are equivalent [1, 17] and contain additionally the couple stress theory as a special case. Using the $\mathrm{Curl}$ as primary differential operator for the curvature terms allows a neat unification of concepts.

For some of the traditional models, uniaxial extension gives still rise to size effects in the sense that thinner samples are comparatively stiffer which can also be found experimentally [34,35,36]. In that case, the inhomogeneous response is triggered by the boundary conditions for the additional kinematic fields which are applied at the upper and lower surface. We refer the reader to the introduction of [25, 27, 28, 32] concerning the relevance of the scientific question as well as its importance for the determination of material parameters for generalized continua [33]. Indeed, the obtained analytical formulas can be used to determine size-dependent and size-independent material parameters. The notation follows that of [25, 27, 28]. We recapitulate shortly.

Fig. 1

Sketch of an infinite stripe of thickness h subjected to uniaxial extension boundary conditions

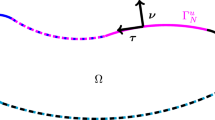
The paper is now structured as follows. We start with a recapitulation of the uniaxial extension problem in the classical linear elasticity. The solution is homogeneous and uniquely determines the longitudinal modulus $M_{\text {macro}}=\lambda _{\text {macro}}+2\mu _{\text {macro}}$. Then, we consider the isotropic relaxed micromorphic continuum. The boundary conditions for the additional nonsymmetric micro-distortion field $\varvec{P}$ derive from the so-called consistent coupling conditions

$$\begin{aligned} \text {D}\varvec{u}(\varvec{x})\times \varvec{\nu } = \varvec{P}(\varvec{x})\times \varvec{\nu }, \qquad \varvec{x} \in \Gamma \, , \end{aligned}$$

(1)

where $\varvec{\nu }$ is the normal unit vector to the upper and lower surface. It turns out that for zero Poisson modulus on the micro- and meso-scale, $\nu _{\text {micro}}=\nu _{\text {e}}=0$, respectively, the solution remains homogeneous and no size effects are observed. In the case with arbitrary $\nu _{\text {micro}},\nu _{\text {e}}\in \left[ -1,1/2\right]$ the solution will be inhomogeneous and size effects appear. The limiting stiffness as the ratio between the thickness and the characteristic length tends to zero ($h/L_{\text {c}}\rightarrow 0$) is given by $\overline{M} = \frac{M_{\text {e}} \, M_{\text {micro}}}{M_{\text {e}} + M_{\text {micro}}}$ which is both smaller than $M_{\text {micro}}=\lambda _{\text {micro}} + 2\mu _{\text {micro}}$ and $M_{\text {e}}$ as well greater than $M_{\text {macro}}=\lambda _{\text {macro}} + 2\mu _{\text {macro}}$.

1.1 Notation

We define the scalar product $\langle \varvec{a},\varvec{b} \rangle {:}{=}\sum _{i=1}^n a_i\,b_i \in \mathbb {R}$ for vectors $a,b\in \mathbb {R}^n$, the dyadic product $\varvec{a}\otimes \varvec{b} {:}{=}\left( a_i\,b_j\right) _{i,j=1,\ldots ,n}\in \mathbb {R}^{n\times n}$ and the Euclidean norm $\Vert {\varvec{a}}\Vert ^2{:}{=}\langle \varvec{a},\varvec{a} \rangle$. We define the scalar product $\langle \varvec{P},\varvec{Q} \rangle {:}{=}\sum _{i,j=1}^n P_{ij}\,Q_{ij} \in \mathbb {R}$ and the Frobenius-norm $\Vert {\varvec{P}}\Vert ^2{:}{=}\langle \varvec{P},\varvec{P} \rangle$ for tensors $\varvec{P},\varvec{Q}\in \mathbb {R}^{n\times n}$ in the same way. Moreover, $\varvec{P}^T{:}{=}(P_{ji})_{i,j=1,\ldots ,n}$ denotes the transposition of the matrix $\varvec{P}=(P_{ij})_{i,j=1,\ldots ,n}$, which decomposes orthogonally into the skew-symmetric part $\text {skew} \, \varvec{P} {:}{=}\frac{1}{2} (\varvec{P}-\varvec{P}^T )$ and the symmetric part $\text {sym} \, \varvec{P} {:}{=}\frac{1}{2} (\varvec{P}+\varvec{P}^T)$. The identity matrix is denoted by ${\mathbb {1}}$, so that the trace of a matrix $\varvec{P}$ is given by $\text {tr}\varvec{P} {:}{=}\langle \varvec{P},{\mathbb {1}} \rangle$, while the deviatoric component of a matrix is given by $\text {dev} \, \varvec{P} {:}{=}\varvec{P} - \frac{\text {tr}\left( \varvec{P}\right) }{3} \, {\mathbb {1}}$. Given this, the orthogonal decomposition possible for a matrix is $\varvec{P} = \text {dev} \,\text {sym} \, \varvec{P} + \text {skew} \, \varvec{P} + \frac{\text {tr}\left( \varvec{P}\right) }{3} \, {\mathbb {1}}$. The Lie-algebra of skew-symmetric matrices is denoted by $\mathfrak {so}(3){:}{=}\{\varvec{A}\in \mathbb {R}^{3\times 3}\mid \varvec{A}^T = -\varvec{A}\}$, while the vector space of symmetric matrices $\text {Sym}(3){:}{=}\{\varvec{S}\in \mathbb {R}^{3\times 3}\mid \varvec{S}^T = \varvec{S}\}$. The Jacobian matrix D$\varvec{u}$ and the curl for a vector field $\varvec{u}$ are defined as

$$\begin{aligned} \varvec{\text {D}u} =\! \left( \begin{array}{ccc} u_{1,1} &{}\quad u_{1,2} &{}\quad u_{1,3} \\ u_{2,1} &{}\quad u_{2,2} &{}\quad u_{2,3} \\ u_{3,1} &{}\quad u_{3,2} &{}\quad u_{3,3} \end{array} \right) \, , \qquad \text {curl} \, \varvec{u} = \varvec{\nabla } \times \varvec{u} = \left( \begin{array}{ccc} u_{3,2} - u_{2,3} \\ u_{1,3} - u_{3,1} \\ u_{2,1} - u_{1,2} \end{array} \right) \, . \end{aligned}$$

(2)

where $\times$ denotes the cross-product in $\mathbb {R}^3$. We also introduce the $\text {Curl}$ and the $\text {Div}$ operators of the $3\times 3$ matrix field $\varvec{P}$ as

$$\begin{aligned} \text {Curl} \, \varvec{P} =\! \left( \begin{array}{c} (\text {curl}\left( P_{11} , \right. P_{12} , \left. P_{13} \right) ^{{T}})^T \\ (\text {curl}\left( P_{21} , \right. P_{22} , \left. P_{23} \right) ^{T})^T \\ (\text {curl}\left( P_{31} , \right. P_{32} , \left. P_{33} \right) ^{T})^T \end{array} \right) \!, \qquad \text {Div} \, \varvec{P} =\! \left( \begin{array}{c} \text {div}\left( P_{11} , \right. P_{12} , \left. P_{13} \right) ^{T} \\ \text {div}\left( P_{21} , \right. P_{22} , \left. P_{23} \right) ^{T} \\ \text {div}\left( P_{31} , \right. P_{32} , \left. P_{33} \right) ^{T} \end{array} \right) \, . \end{aligned}$$

(3)

The cross-product between a second-order tensor and a vector is also needed and is defined row-wise as follows

$$\begin{aligned} \varvec{m} \times \varvec{b} = \left( \begin{array}{ccc} (b \times (m_{11},m_{12},m_{13})^{T})^T \\ (b \times (m_{21},m_{22},m_{23})^{T})^T \\ (b \times (m_{31},m_{32},m_{33})^{T})^T \\ \end{array} \right) = \varvec{m} \cdot \varvec{\epsilon } \cdot \varvec{b} = m_{ik} \, \epsilon _{kjh} \, b_{h} \, , \end{aligned}$$

(4)

where $\varvec{m} \in \mathbb {R}^{3\times 3}$, $\varvec{b} \in \mathbb {R}^{3}$, and $\varvec{\epsilon }$ is the Levi-Civita tensor. Using the one-to-one map $\text {axl}:\mathfrak {so}(3)\rightarrow \mathbb {R}^3$ we have

$$\begin{aligned} \varvec{A} \, \varvec{b} =\text {axl}(\varvec{A})\times \varvec{b} \quad \forall \, \varvec{A}\in \mathfrak {so}(3) \, , \quad \varvec{b}\in \mathbb {R}^3. \end{aligned}$$

(5)

The inverse of axl is denoted by Anti: $\mathbb {R}^3\rightarrow \mathfrak {so}(3)$.

2 Uniaxial extension problem for the isotropic Cauchy continuum

The strain energy density for an isotropic Cauchy continuum is

$$\begin{aligned} W \left( \text {D}\varvec{u}\right) = \mu _{\text {macro}} \left\Vert \text {sym} \text {D}\varvec{u} \right\Vert ^{2} + \dfrac{\lambda _{\text {macro}}}{2} \text {tr}^2\left( \text {D}\varvec{u}\right) \, , \end{aligned}$$

(6)

while the equilibrium equations without body forces are

$$\begin{aligned} \text {Div}\left[ 2\,\mu _{\text {macro}}\,\text {sym} \text {D}\varvec{u} + \lambda _{\text {macro}}\,\text {tr}\left( \text {D}\varvec{u}\right) {\mathbb {1}} \right] = \varvec{0}. \end{aligned}$$

(7)

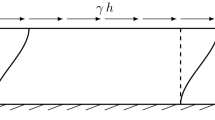
Since the uniaxial extensional problem is symmetric with respect to the $x_2$-axis, there will be no dependence of the solution on $x_1$ and $x_3$. The boundary conditions for the uniaxial extension problem are (see Fig. 1)

$$\begin{aligned} u_{2}(x_2=\pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, . \end{aligned}$$

(8)

The homogeneous displacement field solution $u_{2} (x_2)$, the gradient of the displacement $\text {D}\varvec{u}(x_2)$, and the strain energy $W(\varvec{\gamma })$ for the uniaxial extension problem are

$$\begin{aligned} u_{2} (x_2)&= \varvec{\gamma } \, x_{2} \, , \qquad \qquad \qquad \text {D}\varvec{u}(x_2) = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \varvec{\gamma } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, , \nonumber \\ W(\varvec{\gamma })&= \int _{-h/2}^{h/2} W(\text {D}\varvec{u}) = \frac{1}{2} \left( \lambda _{\text {macro}}+2\mu _{\text {macro}}\right) h \, \varvec{\gamma }^2 = \frac{1}{2} \, M_{\text {macro}} \, h \, \varvec{\gamma }^2 \, , \end{aligned}$$

(9)

where

$$\begin{aligned} M_{\text {macro}} = \lambda _{\text {macro}}+2\mu _{\text {macro}} \end{aligned}$$

(10)

is the extensional stiffness (or pressure-wave modulus, longitudinal modulus).

Here and in the remainder of this work, the elastic coefficients $\mu _i,\lambda _i$ are expressed in [MPa], the coefficients $a_i$ and the intensity of the displacement $\varvec{\gamma }$ are dimensionless, the characteristic lengths $L_{\text {c}}$ and the height h are expressed in meter [m].

3 Uniaxial extension problem for the isotropic relaxed micromorphic model

The general expression of the strain energy for the isotropic relaxed micromorphic continuum is

$$\begin{aligned} W \left( \varvec{\text {D}u}, \varvec{P},\text {Curl}\,\varvec{P}\right) =&\, \mu _{\text {e}} \left\Vert \text {sym} \left( \varvec{\text {D}u} - \varvec{P} \right) \right\Vert ^{2} + \frac{\lambda _{\text {e}}}{2} \text {tr}^2 \left( \varvec{\text {D}u} - \varvec{P} \right) + \mu _{\text {c}} \left\Vert \text {skew} \left( \varvec{\text {D}u} - \varvec{P} \right) \right\Vert ^{2} \nonumber \\&+ \mu _{\text {micro}} \left\Vert \text {sym}\,\varvec{P} \right\Vert ^{2} + \frac{\lambda _{\text {micro}}}{2} \text {tr}^2 \left( \varvec{P} \right) \nonumber \\&+ \frac{\mu \,L_{\text {c}}^2 }{2} \, \left( a_1 \, \left\Vert \text {dev sym} \, \text {Curl} \, \varvec{P}\right\Vert ^2 + a_2 \, \left\Vert \text {skew} \, \text {Curl} \, \varvec{P}\right\Vert ^2 + \frac{a_3}{3} \, \text {tr}^2 \left( \text {Curl} \, \varvec{P}\right) \right) \, , \end{aligned}$$

(11)

and the strictly positive definiteness conditions are¹

$$\begin{aligned}&\mu _{\text {e}}> 0, \qquad \kappa _{\text {e}} = \lambda _{\text {e}}+2/3 \, \mu _{\text {e}}> 0, \qquad \mu _{\text {micro}}> 0, \qquad \kappa _{\text {micro}}=\lambda _{\text {micro}}+2/3 \, \mu _{\text {micro}}> 0,\nonumber \\&\mu _{\text {c}}> 0, \qquad \mu> 0, \qquad L_{\text {c}}> 0, \qquad (a_1,a_2,a_3) > 0 \, . \end{aligned}$$

(12)

where we have the parameters related to the meso-scale, the parameters related to the micro-scale, the Cosserat couple modulus, the proportionality stiffness parameter, the characteristic length and the three dimensionless general isotropic curvature parameters, respectively. This energy expression represents the most general isotropic form possible for the relaxed micromorphic model. In the absence of body forces, the equilibrium equations are then

$$\begin{aligned}&\text {Div}\overbrace{\left[ 2\mu _{\text {e}}\,\text {sym} \left( \varvec{\text {D}u} - \varvec{P} \right) + \lambda _{\text {e}} \text {tr} \left( \varvec{\text {D}u} - \varvec{P} \right) {\mathbb {1}} + 2\mu _{\text {c}}\,\text {skew} \left( \varvec{\text {D}u} - \varvec{P} \right) \right] }^{{\widetilde{\sigma }}{:}{=}} = \varvec{0}, \nonumber \\&\widetilde{\sigma } - 2 \mu _{\text {micro}}\,\text {sym}\,\varvec{P} - \lambda _{\text {micro}} \text {tr} \left( \varvec{P}\right) {\mathbb {1}} \nonumber \\&\quad - \mu \, L_{\text {c}}^{2} \, \text {Curl} \big ({a_1 \, \text {dev sym} \, \text {Curl} \, \varvec{P} + a_2 \, \text {skew} \, \text {Curl} \, \varvec{P} + a_3 \, \text {tr} \left( \text {Curl} \, \varvec{P}\right) } \big ) = \varvec{0} \, . \end{aligned}$$

(13)

The ansatz for the micro-distortion $\varvec{P}(x_2)$, the displacement $\varvec{u}(x_2)$, and consequently the gradient of the displacement $\text {D}\varvec{u}(x_2)$ is

$$\begin{aligned} \varvec{u}(x_2)&= \left( \begin{array}{c} 0 \\ u_{2}(x_{2}) \\ 0 \end{array} \right) \, , \qquad \qquad \varvec{P}(x_2) = \left( \begin{array}{ccc} P_{11}(x_2) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad P_{22}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad P_{33}(x_2) \\ \end{array} \right) \, , \nonumber \\ \text {D}\varvec{u}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, . \end{aligned}$$

(14)

It is important to underline that, given subsequent ansatz (14), it holds that $\text {tr} \left( \text {Curl} \, \varvec{P}\right) =0$. This reduces immediately the number of curvature parameters appearing in the uniaxial extension solution.

The boundary conditions for the uniaxial extension are

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad P_{11}(x_{2} = \pm h/2) = 0 \, , \qquad \qquad P_{33}(x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(15)

Here, the constraint on the components of $\varvec{P}$ is given by the consistent coupling boundary condition

$$\begin{aligned} \varvec{P}\times \varvec{\nu } = \text {D}\varvec{u}\times \varvec{\nu } \, , \qquad \qquad \qquad \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad P_{11} \\ 0 &{}\quad 0 &{}\quad 0 \\ -P_{33} &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, , \end{aligned}$$

(16)

where $\varvec{\nu }$ is the normal unit vector to the upper and lower surface.

After substituting ansatz (14) into equilibrium equation (13) we obtain the following four differential equations

$$\begin{aligned} M_{\text {e}} \left( u_{2}''(x_{2})-P_{22}'(x_{2})\right) -\lambda _{\text {e}} \left( P_{11}'(x_{2})+P_{33}'(x_{2})\right)&= 0 \, , \nonumber \\ \frac{1}{2} \mu \, L_{\text {c}}^2 \left( (a_{1}+a_{2}) P_{11}''(x_{2})+(a_{2}-a_{1}) P_{33}''(x_{2})\right) \nonumber \\ -(M_{\text {e}}+M_{\text {micro}}) P_{11}(x_{2}) -(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{22}(x_{2})+P_{33}(x_{2})) +\lambda _{\text {e}} u_{2}'(x_{2})&= 0 \, , \nonumber \\ -(M_{\text {e}}+M_{\text {micro}}) P_{22}(x_{2})+M_{\text {e}} u_{2}'(x_{2}) -(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{11}(x_{2})+P_{33}(x_{2}))&= 0 \, , \nonumber \\ \frac{1}{2} \mu \, L_{\text {c}}^2 \left( (a_{2}-a_{1}) P_{11}''(x_{2})+(a_{1}+a_{2}) P_{33}''(x_{2})\right) \nonumber \\ -(M_{\text {e}}+M_{\text {micro}}) P_{33}(x_{2}) -(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{11}(x_{2})+P_{22}(x_{2}))+\lambda _{\text {e}} u_{2}'(x_{2})&= 0\, , \end{aligned}$$

(17)

where $M_{\text {e}}=\lambda _{\text {e}}+2\mu _{\text {e}}$ and $M_{\text {micro}}=\lambda _{\text {micro}}+2\mu _{\text {micro}}$. Being careful of substituting the system of differential equation with one in which Eq. (17)$_2$ and Eq. (17)$_4$ are replaced with their sum and their difference, respectively, we have

$$\begin{aligned} M_{\text {e}} \left( u_{2}''(x_{2})-P_{22}'(x_{2})\right) -\lambda _{\text {e}} f_{p}'(x_{2})&= 0 \, , \nonumber \\ a_{2} \, \mu \, L_{\text {c}}^2 \, f_{p}''(x_{2}) - (M_{\text {e}}+\lambda _{\text {e}}+M_{\text {micro}}+\lambda _{\text {micro}}) f_{p}(x_{2}) - 2 (\lambda _{\text {e}}+\lambda _{\text {micro}}) P_{22}(x_{2}) + 2 \lambda _{\text {e}} u_{2}'(x_{2})&= 0 \, ,\nonumber \\ - (M_{\text {e}}+M_{\text {micro}}) P_{22}(x_{2}) + M_{\text {e}} \, u_{2}'(x_{2}) - (\lambda _{\text {e}}+\lambda _{\text {micro}}) f_{p}(x_{2})&= 0 \, , \nonumber \\ a_{1} \, \mu \, L_{\text {c}}^2 \, f_{m}''(x_{2}) - (M_{\text {micro}} + M_{\text {e}} - \lambda _{\text {e}} - \lambda _{\text {micro}})f_{m}(x_{2})&= 0 \, , \end{aligned}$$

(18)

where $f_{p} (x_2){:}{=}P_{11}(x_2)+P_{33}(x_2)$ and $f_{m} (x_2){:}{=}P_{11}(x_2)-P_{33}(x_2)$. It is highlighted that Eq. (18)$_4$ is a homogeneous second-order differential equation depending only on $f_{m}(x_2)$ with homogeneous boundary conditions Eq. (15).

The fact that Eq. (18)$_4$ is an independent equation has its meaning in the symmetry constraint of the uniaxial extensional problem in the direction along the $x_2$- and $x_3$-axis, which requires that ${P_{11}(x_2)=P_{33}(x_2)}$. From Eq. (18) it is possible to obtain the following relation between $P_{22}(x_2)$ and $u_2(x_2)$

$$\begin{aligned} P_{22}(x_{2}) = \frac{ M_{\text {e}} \, u_{2}'(x_{2}) - (\lambda _{\text {e}}+\lambda _{\text {micro}}) f_{p}(x_{2}) }{ M_{\text {e}}+M_{\text {micro}} } \, , \end{aligned}$$

(19)

which, after substituting it back into Eq. (18), allows us to obtain the following system of three second-order differential equations in $u_2(x_2)$, $P_{22}(x_2)$, and $f_{p}(x_2)$

$$\begin{aligned} z_{1} \, f_{p}'(x_{2}) + z_{2} \, u_{2}''(x_{2})&= 0\, , \nonumber \\ a_{2} \, \mu \, L_{\text {c}}^2 \, f_{p}''(x_{2}) - z_{3} \, f_{p}(x_{2}) - 2 z_{1} \, u_{2}'(x_{2})&= 0\, , \nonumber \\ a_{1} \, \mu \, L_{\text {c}}^2 \, f_{m}''(x_{2}) - (M_{\text {e}} + M_{\text {micro}} - \lambda _{\text {e}} - \lambda _{\text {micro}}) f_{m}(x_{2})&= 0\, , \end{aligned}$$

(20)

where

$$\begin{aligned} z_1{:}{=}&\frac{ M_{\text {e}} \lambda _{\text {micro}}-\lambda _{\text {e}} M_{\text {micro}} }{ M_{\text {e}}+M_{\text {micro}} } \, , \qquad \qquad \qquad z_2{:}{=}\frac{ M_{\text {e}} M_{\text {micro}} }{ M_{\text {e}}+M_{\text {micro}} } \, , \nonumber \\ z_3{:}{=}&\frac{ \left( M_{\text {e}}-\lambda _{\text {e}}+M_{\text {micro}}-\lambda _{\text {micro}}\right) \left( M_{\text {e}}+2 \lambda _{\text {e}}+M_{\text {micro}} +2 \lambda _{\text {micro}}\right) }{ M_{\text {e}}+M_{\text {micro}} } \,. \end{aligned}$$

(21)

It is highlighted that due to positive definiteness conditions (12), $(z_2,z_3)>0$ and $z_1=0$ if and only if $\lambda _{\text {micro}}=\lambda _{\text {e}}=0$ (zero Poisson’s ratio case which is studied in Sect. 3.1) and $\frac{M_{\text {micro}}}{M_{\text {e}}}=\frac{\lambda _{\text {micro}}}{\lambda _{\text {e}}}$. If $z_1$ is zero, Eq. (20) uncouples completely into three independent differential equations in $u_2$, $f_{\text {p}}$, and $f_{\text {m}}$, respectively.

After applying boundary conditions Eq. (15), the solution in terms of $u_2(x_2)$, $P_{11}(x_2)$, $P_{22}(x_2)$, and $P_{33}(x_2)$ of system Eq. (20) is²

$$\begin{aligned} u_{2} (x_{2})&= \frac{ \frac{2 x_{2}}{h} -\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \, \text {sech}\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \sinh \left( \frac{f_{1} x_{2}}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} }{ 1-\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } \frac{\varvec{\gamma } h}{2} \, ,\nonumber \\ P_{22} (x_{2})&= \frac{ M_{\text {e}} + 2 \frac{z_1}{z_3} \left( \lambda _{\text {e}} + \lambda _{\text {micro}} \right) - \frac{z_1}{z_3} \left( M_{\text {e}}\frac{2z_1}{z_2} +2 \left( \lambda _{\text {e}} + \lambda _{\text {micro}} \right) \cosh \left( \frac{f_{1} h}{L_{\text {c}}}\right) \text {sech}\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \right) }{ \left( M_{\text {e}} + M_{\text {micro}} \right) \left( 1-\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) } \, \varvec{\gamma } \, , \nonumber \\ P_{11} (x_{2})&= P_{33} (x_{2}) = \frac{ \frac{z_{1}}{z_{3}} \left( \text {sech}\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \cosh \left( \frac{f_{1} x_{2}}{L_{\text {c}}}\right) -1\right) }{ 1-\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } \, \varvec{\gamma } \, , \qquad \qquad f_{1} {:}{=}\sqrt{\frac{z_{2} \, z_{3} - 2 z_{1}^2}{ \mu \, a_{2} \, z_{2}}} \, . \end{aligned}$$

(22)

In the above expressions all the quantities are real and well defined due to positive definiteness conditions Eq. (12). Indeed, since the coefficients $z_1$, $z_2$, and $z_3$ may be rewritten in terms of the meso- and micro-bulk and shear modulus as

$$\begin{aligned}&z_1 {:}{=}\frac{6 \kappa _{\text {micro}} \mu _{\text {e}}-6 \kappa _{\text {e}} \mu _{\text {micro}}}{3 \kappa _{\text {e}}+3 \kappa _{\text {micro}}+4 (\mu _{\text {e}}+\mu _{\text {micro}})} \, , \qquad z_2 {:}{=}\frac{(3 \kappa _{\text {e}}+4 \mu _{\text {e}}) (3 \kappa _{\text {micro}}+4 \mu _{\text {micro}})}{9 \kappa _{\text {e}}+9 \kappa _{\text {micro}}+12 (\mu _{\text {e}}+\mu _{\text {micro}})} \, ,\\&z_3 {:}{=}\frac{18 (\kappa _{\text {e}}+\kappa _{\text {micro}}) (\mu _{\text {e}}+\mu _{\text {micro}})}{3 \kappa _{\text {e}}+3 \kappa _{\text {micro}}+4 (\mu _{\text {e}}+\mu _{\text {micro}})} \, , \end{aligned}$$

we can write the expression of $f_1$ as follows

$$\begin{aligned} f_1 {:}{=}\sqrt{ \frac{ 6 \kappa _{\text {e}} \, \kappa _{\text {micro}} (\mu _{\text {e}}+\mu _{\text {micro}}) + 8 \mu _{\text {e}} \, \mu _{\text {micro}} (\kappa _{\text {e}} + \kappa _{\text {micro}}) }{ \mu \, a_2 (\kappa _{\text {e}}+\frac{4}{3} \mu _{\text {e}}) (\kappa _{\text {micro}}+\frac{4}{3} \mu _{\text {micro}}) } }, \end{aligned}$$

(23)

showing that the positive definiteness of energy (11) implies that $f_1$ is a strictly positive real number. Moreover, the function $g:(0,\infty )\rightarrow \mathbb {R}, \qquad g(x):= 1-\frac{4 z_{1}^2}{ z_{2} z_{3}}\,\frac{1}{x} \tanh \frac{x}{2}$ has the asymptotic behavior

$$\begin{aligned} \lim \limits _{x\rightarrow 0}g(x)=1-\frac{2\, z_{1}^2}{ z_{2} z_{3}}=f_1^2>0, \qquad \lim \limits _{x\rightarrow \infty }g(x)=1 \end{aligned}$$

(24)

and it is monotone increasing since its first derivative is given by

$$\begin{aligned} g'(x)=\frac{4 z_{1}^2}{ z_{2} z_{3}}\frac{\sinh x-x}{x^2 (\cosh x+1)} \end{aligned}$$

(25)

which it is positive for all $x\in (0,\infty )$. Hence, it follows that due to the positive definiteness of the elastic energy

$$\begin{aligned} g(x)>0 \qquad \forall \, x>0, \end{aligned}$$

(26)

which implies that

$$\begin{aligned} 1-\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h}>0 \qquad \forall \, L_{\text {c}}>0 \end{aligned}$$

(27)

which completes our proof that all the quantities from (22) are real and well-defined.

The strain energy associated with this solution is

$$\begin{aligned} W(\varvec{\gamma }) =&\int _{-h/2}^{h/2} W(\text {D}\varvec{u},\varvec{P},\text {Curl}\, \varvec{P})\nonumber \\ \, =&\frac{1}{2} \Bigg [ \frac{ \mu \, a_{2} \left( \frac{f_{1} z_{1} }{z_{3}} \right) ^2 \left( \frac{1}{f_{1}} \sinh \left( \frac{f_{1} h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} -1 \right) }{ \left( 1 -\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) ^2 \cosh ^2\left( \frac{f_{1} \, h}{2 L_{\text {c}}}\right) } + \frac{ \cosh ^2\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) -\frac{z_{1}^2}{z_{2} z_{3}} \left( \frac{3}{f_{1}} \sinh \left( \frac{f_{1} h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} -1 \right) }{ \left( 1 -\frac{4 z_{1}^2}{f_{1} z_{2} z_{3}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) ^2 \cosh ^2\left( \frac{f_{1} \, h}{2 L_{\text {c}}}\right) } \nonumber \\&\times \frac{z_{2}}{z_{3}} \left( M_{\text {e}} + M_{\text {micro}} + \lambda _{\text {e}} + \lambda _{\text {micro}} - \frac{2\lambda _{\text {e}}^2}{M_{\text {e}}} - \frac{2\lambda _{\text {micro}}^2}{M_{\text {micro}}} \right) \Bigg ] h \, \varvec{\gamma }^2 = \frac{1}{2} \, M_{\text {w}} \, h \, \varvec{\gamma }^2 \, . \end{aligned}$$

(28)

The plot of the extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$ is shown in Fig. 2.

Fig. 2

Relaxed micromorphic model. (left) Extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$. The stiffness is bounded as $L_{\text {c}} \rightarrow \infty$ ($h\rightarrow 0$). The values of the parameters used are: $\mu = 1$, $\lambda _{\text {e}}= 1$, $M_{\text {e}}= 2$, $\lambda _{\text {micro}}= 3$, $M_{\text {micro}}= 4$, $a_2= 1/5$; (right) Displacement profile across the thickness of the dimensionless $\overline{u}_2=u_2/\left( \gamma \, h\right)$ for different values of $L_{\text {c}}=\{0, 0.014, 0.0\overline{3}, 0.1\}$. The values of the other parameters used in order to maximize the nonhomogeneous behavior are $\mu = 1$, $\lambda _{\text {e}}=1$, $M_{\text {e}}=1$, $\lambda _{\text {micro}}=0.001$, $M_{\text {micro}}= 0.056$, $a_2=0.\overline{3}$

The values of $M_{\text {macro}}$ and $M_{\text {micro}}$ are

$$\begin{aligned} M_{\text {macro}} = \lim _{L_{\text {c}}\rightarrow 0} M_{\text {w}}&= \frac{M_{\text {e}}^2 M_{\text {micro}}+M_{\text {e}} \left( -2 \lambda _{\text {micro}}^2+M_{\text {micro}}^2+M_{\text {micro}} (\lambda _{\text {e}}+\lambda _{\text {micro}})\right) -2 \lambda _{\text {e}}^2 M_{\text {micro}}}{(M_{\text {e}}-\lambda _{\text {e}}-\lambda _{\text {micro}}+M_{\text {micro}}) (M_{\text {e}}+2 (\lambda _{\text {e}}+\lambda _{\text {micro}})+M_{\text {micro}})}\nonumber \\&= \frac{\kappa _{\text {e}} \, \kappa _{\text {micro}}}{\kappa _{\text {e}}+\kappa _{\text {micro}}} +\frac{4}{3}\frac{\mu _{\text {e}} \, \mu _{\text {micro}}}{\mu _{\text {e}}+\mu _{\text {micro}}} = \kappa _{\text {macro}} +\frac{4}{3} \mu _{\text {macro}} =M_{\text {macro}} \, , \nonumber \\ \overline{M} = \lim _{L_{\text {c}}\rightarrow \infty } M_{\text {w}}&= \frac{ M_{\text {e}} \, M_{\text {micro}} }{ M_{\text {e}} + M_{\text {micro}} } < {\left\{ \begin{array}{ll} M_{\text {micro}}\\ M_{\text {e}} \end{array}\right. } \, , \end{aligned}$$

(29)

where $M_{i}=\kappa _{i} + \frac{4}{3}\mu _{i}$ and $\lambda _{i}=\kappa _{i}-\frac{2}{3}\mu _{i}$ with $i=\{\text {macro},\text {micro},\text {e}\}$.³

It is highlighted that the structure $\frac{(\bullet )_{\text {e}} \, (\bullet )_{\text {micro}}}{(\bullet )_{\text {e}} + (\bullet )_{\text {micro}}}$ is applicable to evaluate the macro coefficients only for the shear and bulk modulus because of the orthogonal energy decomposition “sym dev/tr” of which they are related, and especially here it would be a mistake to use this structure for the coefficient $M_{\text {macro}}$ since it will give the value at the micro-scale. For more details about $\lim \limits _{L_{\text {c}}\rightarrow \infty } M_{\text {w}}$ see Appendix A.

3.1 Uniaxial extension problem for the isotropic relaxed micromorphic model with $\nu _e=\nu _{\text {micro}}=0$

A vanishing Poisson’s ratio at the meso- and micro-scale ($\nu _e=\nu _{\text {micro}}=0$) corresponds to a vanishing first Lamé parameter ($\lambda _{\text {e}}=\lambda _{\text {micro}}=0$). It is easy to see from Eqs. (21) and (22) that these conditions correspond to

$$\begin{aligned} \lambda _{\text {e}}=\lambda _{\text {micro}}=0 \Longleftrightarrow {\left\{ \begin{array}{ll} z_1 = 0 \, ,\\ z_2 = \dfrac{ M_{\text {e}} \, M_{\text {micro}} }{ M_{\text {e}}+M_{\text {micro}} } = \dfrac{ 2\mu _{\text {e}} \, \mu _{\text {micro}} }{ \mu _{\text {e}}+\mu _{\text {micro}} } \, ,\\ z_3 = M_{\text {e}}+M_{\text {micro}} = 2\left( \mu _{\text {e}}+\mu _{\text {micro}}\right) \, , \end{array}\right. } \end{aligned}$$

(30)

with $M_{i}=\lambda _{i} + 2\mu _{i} = 2\mu _{i}$ with $i=\{\text {micro},\text {e}\}$. Since the nonlinear terms in solution Eq. (22) vanish, we retrieve

$$\begin{aligned} u_{2} (x_{2})= \varvec{\gamma } \, x_2\, , \qquad \qquad \qquad P_{22} (x_{2})= \frac{\mu _{\text {e}}}{\mu _{\text {e}} + \mu _{\text {micro}}} \varvec{\gamma } \, , \qquad \qquad \qquad P_{11} (x_{2})=P_{33} (x_{2})= 0\, , \end{aligned}$$

(31)

which is a homogeneous elastic solution satisfying the equilibrium equation in the case of a constant micro-distortion tensor $\overline{\varvec{P}}$ (see Appendix D of [27] for further details)

$$\begin{aligned} \overline{\varvec{P}} = \frac{\mu _{\text {e}}}{\mu _{\text {e}}+\mu _{\text {micro}}} \, \left( \frac{1}{\left| \Omega \right| } \, \int _{\Omega } \varvec{\text {D}u} \, \text {d}V \right) \, . \end{aligned}$$

(32)

The strain energy associated with this solution is

$$\begin{aligned} W(\varvec{\gamma }) = \int _{-h/2}^{h/2} W(\text {D}\varvec{u}) = \frac{1}{2} \frac{2\mu _{\text {e}} \, \mu _{\text {micro}}}{\mu _{\text {e}}+\mu _{\text {micro}}} h \, \varvec{\gamma }^2 = \frac{1}{2} \, M_{\text {macro}} \, h \, \varvec{\gamma }^2 \, , \end{aligned}$$

(33)

where $M_{\text {macro}} = 2\mu _{\text {macro}} + \lambda _{\text {macro}} = 2\mu _{\text {macro}} = \frac{2\mu _{\text {e}} \, \mu _{\text {micro}}}{\mu _{\text {e}}+\mu _{\text {micro}}}$ is the macro-extensional stiffness, since $\lambda _{\text {macro}}=\nu _{\text {macro}}=0$.

4 Uniaxial extension problem for the isotropic micro-stretch model in dislocation format

In the micro-stretch model in dislocation format [5, 15, 20, 22, 30], the micro-distortion tensor $\varvec{P}$ is devoid from the deviatoric component $\text{ dev } \, \text{ sym } \, \varvec{P} = 0 \Leftrightarrow \varvec{P} = \varvec{A} + \omega {\mathbb {1}}$, $\varvec{A} \in \mathfrak {so}(3)$, $\omega \in \mathbb {R}$. The expression of the strain energy for this model in dislocation format can be written as [20]:

$$\begin{aligned}&W \left( \text{ D }\varvec{u}, \varvec{A},\omega ,\text{ Curl }\,\left( \varvec{A} - \omega {\mathbb {1}}\right) \right) \nonumber \\&\quad = \, \mu _{\tiny \mathrm{macro}} \left\Vert \text{ dev } \, \text{ sym } \, \text{ D }\varvec{u} \right\Vert ^{2} + \frac{\kappa _{\text {e}}}{2} \text{ tr}^2 \left( \text{ D }\varvec{u} - \omega {\mathbb {1}} \right) + \mu _{c} \left\Vert \text{ skew } \left( \text{ D }\varvec{u} - \varvec{A} \right) \right\Vert ^{2} + \frac{9}{2} \, \kappa _{\tiny \text{ micro }} \, \omega ^2 \nonumber \\&\quad \quad + \frac{\mu \,L_c^2}{2} \, \left( a_1 \, \left\Vert \text{ dev } \text{ sym } \, \text{ Curl } \, \varvec{A} \right\Vert ^2 + a_2 \, \left\Vert \text{ skew } \, \text{ Curl } \, \left( \varvec{A} + \omega {\mathbb {1}}\right) \right\Vert ^2 + \frac{a_3}{3} \, \text{ tr}^2 \left( \text{ Curl } \, \varvec{A} \right) \right) \, , \end{aligned}$$

(34)

since $\text{ Curl } \left( \omega {\mathbb {1}}\right) \in \mathfrak {so}(3)$. The equilibrium equations, in the absence of body forces, are then

$$\begin{aligned}&\text{ Div }\overbrace{\left[ 2\mu _{\tiny \text{ macro }}\,\text{ dev }\,\text{ sym } \, \text{ D }\varvec{u} + \kappa _{\text {e}} \text{ tr } \left( \text{ D }\varvec{u} - \omega {\mathbb {1}}\right) {\mathbb {1}} + 2\mu _{c}\,\text{ skew } \left( \text{ D }\varvec{u} - \varvec{A}\right) \right] }^{{\widetilde{\sigma }}{:}{=}} = \varvec{0} \, , \nonumber \\&2\mu _{c}\,\text{ skew } \left( \text{ D }\varvec{u} - \varvec{A}\right) \nonumber \\&\quad -\mu \, L_c^2 \, \text{ skew } \, \text{ Curl }\,\left( a_1 \, \text{ dev } \, \text{ sym } \, \text{ Curl } \, \varvec{A} \, + a_2 \, \text{ skew } \, \text{ Curl } \, \left( \varvec{A} + \, \omega {\mathbb {1}}\right) \, + \frac{a_3}{3} \, \text{ tr } \left( \text{ Curl } \, \varvec{A} \right) {\mathbb {1}} \, \right) = \varvec{0} \, , \nonumber \\&\text{ tr } \bigg [ 2\mu _{\tiny \text{ macro }}\,\text{ dev }\,\text{ sym } \, \text{ D }\varvec{u} \nonumber \\&\quad + \kappa _{\text {e}} \text{ tr } \left( \text{ D }\varvec{u} - \omega {\mathbb {1}}\right) {\mathbb {1}} - \kappa _{\tiny \mathrm{micro}} \text{ tr } \left( \omega {\mathbb {1}}\right) {\mathbb {1}} -\mu \, L_c^2 \, a_2 \, \text{ Curl }\, \text{ skew } \, \text{ Curl } \, \left( \omega {\mathbb {1}} + \varvec{A}\right) \bigg ] = \varvec{0} \,. \end{aligned}$$

(35)

According to the reference system shown in Fig. 1, the ansatz for the displacement and micro-distortion fields is

$$\begin{aligned} \varvec{u}(x_2)&= \left( \begin{array}{c} 0 \\ u_2(x_2) \\ 0 \end{array} \right) \, ,&\qquad \qquad \qquad \varvec{A}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 \quad &{} 0 \\ \end{array} \right) \, , \nonumber \\ \text {D}\varvec{u}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, ,&\omega \left( x_2\right) {\mathbb {1}}&= \left( \begin{array}{ccc} \omega \left( x_2\right) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \omega \left( x_2\right) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \omega \left( x_2\right) \\ \end{array} \right) \, . \end{aligned}$$

(36)

The boundary conditions at the free surface are then

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad \qquad \omega (x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(37)

Since the ansatz requires $\varvec{A}=0$, the micro-stretch model coincides with the micro-void model which will be presented in Sect. 6.

5 Uniaxial extension problem for the isotropic Cosserat continuum

The strain energy for the isotropic Cosserat continuum in dislocation tensor format (curvature energy expressed in terms of $\text {Curl} \varvec{A}$) can be written as [3, 8, 13, 14, 18, 21, 25, 28, 29]

$$\begin{aligned} W \left( \varvec{\text {D}u}, \varvec{A},\text {Curl}\,\varvec{A}\right) =&\, \mu _{\text {macro}} \left\Vert \text {sym} \, \varvec{\text {D}u} \right\Vert ^{2} + \frac{\lambda _{\text {macro}}}{2} \text {tr}^2 \left( \varvec{\text {D}u} \right) + \mu _{\text {c}} \left\Vert \text {skew} \left( \varvec{\text {D}u} - \varvec{A} \right) \right\Vert ^{2} \nonumber \\&+ \frac{\mu \, L_{\text {c}}^2}{2} \left( a_1 \, \left\Vert \text {dev} \, \text {sym} \, \text {Curl} \, \varvec{A}\right\Vert ^2 \, + a_2 \, \left\Vert \text {skew} \, \text {Curl} \, \varvec{A}\right\Vert ^2 \, + \frac{a_3}{3} \, \text {tr}^2 \left( \text {Curl} \, \varvec{A} \right) \right) \, , \end{aligned}$$

(38)

where $\varvec{A} \in \mathfrak {so}(3)$. The equilibrium equations, in the absence of body forces, are therefore the following

$$\begin{aligned} \text {Div}\overbrace{\left[ 2\mu _{\text {macro}}\,\text {sym} \, \varvec{\text {D}u} + \lambda _{\text {macro}} \text {tr} \left( \varvec{\text {D}u} \right) {\mathbb {1}} + 2\mu _{\text {c}}\,\text {skew} \left( \varvec{\text {D}u} - \varvec{A}\right) \right] }^{{\widetilde{\sigma }}{:}{=}}&= \varvec{0} \, , \nonumber \\ 2\mu _{\text {c}}\,\text {skew} \left( \varvec{\text {D}u} - \varvec{A}\right) -\mu \, L_{\text {c}}^2 \, \text {skew} \, \text {Curl}\, \left( a_1 \, \text {dev} \, \text {sym} \, \text {Curl} \, \varvec{A} \, + \frac{a_3}{3} \, \text {tr} \left( \text {Curl} \, \varvec{A} \right) {\mathbb {1}} \, \right)&= \varvec{0} \,. \end{aligned}$$

(39)

According to the reference system shown in Fig. 1 and ansatz (14), which has to be particularized as $\varvec{A} = \text {skew} \, \varvec{P} \in \mathfrak {so}(3)$, the ansatz for the displacement field and the micro-rotation for the Cosserat model is

$$\begin{aligned} \varvec{u}(x_2) = \left( \begin{array}{c} 0 \\ u_2(x_2) \\ 0 \end{array} \right) \, , \qquad \qquad \text {D}\varvec{u}(x_2) = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, , \qquad \qquad \varvec{A}(x_2) = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, . \end{aligned}$$

(40)

Since $\varvec{A}=\varvec{0}$, the Cosserat model is not able to catch any nonhomogeneous response for the uniaxial extension problem and classical solution (9) is retrieved.

The couple stress model [10, 11, 16, 19, 23], which appears by constraining $\varvec{A}=\text {skew} \, \varvec{\text {D}u} \in \mathfrak {so}(3)$ in the Cosserat model, is also not able to catch a nonhomogeneous response for the uniaxial extension problem since, due to the ansatz, we would have $\text {skew} \, \varvec{\text {D}u}=\varvec{0}$ as it can be seen in Eq. (40).

6 Uniaxial extension problem for the isotropic micro-void model in dislocation tensor format

The strain energy for the isotropic micro-void continuum in dislocation tensor format can be obtained from the relaxed micromorphic model by formally letting $\mu _{\text {micro}}\rightarrow \infty$ (while keeping $\kappa _{\text {micro}}$ finite) and can be written as [4, 28]

$$\begin{aligned} W \left( \varvec{\text {D}u}, \omega ,\text {Curl}\,\left( \omega {\mathbb {1}}\right) \right) =&\, \mu _{\text {macro}} \left\Vert \text {dev} \,\text {sym} \, \varvec{\text {D}u}\right\Vert ^{2} + \frac{\kappa _{\text {e}}}{2} \text {tr}^2 \left( \varvec{\text {D}u} - \omega {\mathbb {1}} \right) + \frac{\kappa _{\text {micro}}}{2} \text {tr}^2 \left( \omega {\mathbb {1}} \right) \nonumber \\&+ \frac{\mu \,L_{\text {c}}^2 }{2} \, a_2 \, \left\Vert \text {Curl} \, \left( \omega {\mathbb {1}}\right) \right\Vert ^2 \, . \end{aligned}$$

(41)

Here, $\omega : \mathbb {R}^3 \rightarrow \mathbb {R}$ is the additional scalar micro-void degree of freedom [4]. The equilibrium equations, in the absence of body forces, are

$$\begin{aligned} \text {Div}\overbrace{\left[ 2\mu _{\text {macro}} \, \text {dev} \, \text {sym} \, \varvec{\text {D}u} + \kappa _{\text {e}} \text {tr} \left( \varvec{\text {D}u} - \omega {\mathbb {1}} \right) {\mathbb {1}} \right] }^{{\widetilde{\sigma }}{:}{=}}&= \varvec{0}, \nonumber \\ \frac{1}{3}\text {tr} \left[ \widetilde{\sigma } - \kappa _{\text {micro}} \text {tr} \left( \omega {\mathbb {1}}\right) {\mathbb {1}} - \mu \, L_{\text {c}}^{2} \, a_2 \, \text {Curl} \, \text {Curl} \, \left( \omega {\mathbb {1}}\right) \right]&= 0. \end{aligned}$$

(42)

and the positive definiteness conditions are

$$\begin{aligned} \mu _{\text {macro}}> 0, \qquad \kappa _{\text {e}}> 0, \qquad \kappa _{\text {micro}}> 0, \qquad \mu> 0, \qquad L_{\text {c}}> 0, \qquad a_2 > 0 \, . \end{aligned}$$

(43)

According to the reference system shown in Fig. 1, the ansatz for the displacement field and the function $\omega (x_2)$ have to be

$$\begin{aligned} \varvec{u}(x_1,x_2)&= \left( \begin{array}{c} -x_2 \, x_3 \\ x_1 \, x_3 \\ 0 \end{array} \right) \, , \qquad \omega \left( x_2\right) {\mathbb {1}} = \left( \begin{array}{ccc} \omega \left( x_2\right) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \omega \left( x_2\right) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \omega \left( x_2\right) \\ \end{array} \right) \, , \nonumber \\ \text {D}\varvec{u}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, . \end{aligned}$$

(44)

The boundary conditions for the uniaxial extension are

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad \qquad \omega (x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(45)

After substituting ansatz (44) into equilibrium equations (42) we obtain the following two differential equations

$$\begin{aligned} \frac{1}{3} (3 \kappa _{\text {e}}+4 \mu _{\text {macro}}) \, u_{2}''(x_{2})-\kappa _{\text {e}} \, \omega '(x_{2})&= 0 \, ,\nonumber \\ \frac{2}{3} a_{2} \, \mu \, L_{\text {c}}^2 \, \omega ''(x_{2}) + 3 \kappa _{\text {e}} \, u_{2}'(x_{2}) - 3 (\kappa _{\text {e}}+\kappa _{\text {micro}}) \, \omega (x_{2})&= 0 \,. \end{aligned}$$

(46)

After applying boundary conditions Eq. (45), the solution in terms of $u_2(x_2)$ and $\omega (x_2)$ of system Eq. (46) is

$$\begin{aligned} u_{2} (x_{2})&= \frac{ \frac{x_{2}}{h} -\frac{z_{1}}{f_{1}} \text {sech}\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \sinh \left( \frac{f_{1}x_{2}}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} }{ 1 -\frac{2 z_{1}}{f_{1}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } h \, \varvec{\gamma } \, , \qquad \qquad \omega (x_{2}) = \frac{ z_{2} \left( 1-\text {sech}\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \cosh \left( \frac{f_{1} x_{2}}{L_{\text {c}}}\right) \right) }{ 1 -\frac{2 z_{1}}{f_{1}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } \varvec{\gamma } \, , \nonumber \\ f_1&{:}{=}\sqrt{ \frac{4 \mu _{\text {macro}} (\kappa _{\text {e}}+\kappa _{\text {micro}})+3 \kappa _{\text {e}} \kappa _{\text {micro}}}{2 \mu \, a_{2} (3 \kappa _{\text {e}}+4 \mu _{\text {macro}})} } \, , \quad z_1 {:}{=}\frac{3 \kappa _{\text {e}}^2}{(\kappa _{\text {e}}+\kappa _{\text {micro}}) (3 \kappa _{\text {e}}+4 \mu _{\text {macro}})} \, , \quad z_2 {:}{=}\frac{\kappa _{\text {e}}}{3 (\kappa _{\text {e}}+\kappa _{\text {micro}})} \, . \end{aligned}$$

(47)

where $f_1>0$, $z_1>0$, and $z_2>0$ are strictly positive in order to match positive definiteness conditions Eq. (43), and the same reasoning applied in the relaxed micromorphic model sections still holds. The strain energy associated with this solution is

$$\begin{aligned} W(\varvec{\gamma }) =&\int _{-h/2}^{h/2} W(\text {D}\varvec{u},\varvec{P},\text {Curl}\, \varvec{P})\nonumber \\ \, =&\frac{1}{2} \left[ \frac{ \mu \, a_{2} \, f_{1}^2 \, z_{2}^2 \left( \frac{1}{f_{1}} \sinh \left( \frac{f_{1} h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} -1 \right) }{ \left( 1- \frac{2 z_{1}}{f_{1}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) ^2 \cosh ^2\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) }+ \frac{ \left( 1 +z1 +\cosh \left( \frac{f_{1} h}{L_{\text {c}}}\right) -3 \frac{z_{1}}{f_{1}} \sinh \left( \frac{f_{1} h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) }{ 2\left( 1- \frac{2 z_{1}}{f_{1}} \tanh \left( \frac{f_{1} h}{2 L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} \right) ^2 \cosh ^2\left( \frac{f_{1} h}{2 L_{\text {c}}}\right) } \left( \frac{\kappa _{\text {e}} \kappa _{\text {micro}}}{\kappa _{\text {e}}+\kappa _{\text {micro}}} + \frac{4 \mu _{\text {macro}}}{3} \right) \right] h \, \varvec{\gamma }^2\nonumber \\ =&\frac{1}{2} \, M_{\text {w}} \, h \, \varvec{\gamma }^2 \, . \end{aligned}$$

(48)

The plot of the extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$ is shown in Fig. 3.

Fig. 3

Micro-void model. Extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$. The stiffness is bounded as $L_{\text {c}} \rightarrow \infty$ ($h\rightarrow 0$) by $M_{\text {e}}$. The values of the parameters used are: $\mu = 1$, $\lambda _{\text {e}}= 1$, $M_{\text {e}}= 2$, $\kappa _{\text {micro}}= 3$, $a_2= 1/5$

The values of the extensional stiffness $M_{\text {w}}$ for $L_{\text {c}}\rightarrow 0$ and $L_{\text {c}}\rightarrow \infty$ are

$$\begin{aligned} \lim _{L_{\text {c}}\rightarrow 0} M_{\text {w}}&= \frac{\kappa _{\text {e}} \, \kappa _{\text {micro}}}{\kappa _{\text {e}}+\kappa _{\text {micro}}} +\frac{4}{3}\mu _{\text {macro}} = \kappa _{\text {macro}} +\frac{4}{3} \mu _{\text {macro}} = 2\mu _{\text {macro}} + \lambda _{\text {macro}} =M_{\text {macro}} \, ,\nonumber \\ \lim _{L_{\text {c}}\rightarrow \infty } M_{\text {w}}&= \kappa _{\text {e}} +\frac{4}{3} \mu _{\text {macro}} = \kappa _{\text {e}} +\frac{4}{3} \mu _{\text {e}} = 2\mu _{\text {e}} + \lambda _{\text {e}} = M_{\text {e}} \, , \end{aligned}$$

(49)

where $\mu _{\text {macro}}=\mu _{\text {e}}$ for $\mu _{\text {micro}}\rightarrow \infty$, according to Eq. (29). We note that the extensional stiffness remains bounded as $L_{\text {c}}\rightarrow \infty$ ($h\rightarrow 0$).

7 Uniaxial extension problem for the classical isotropic micromorphic continuum without mixed terms

The expression of the strain energy for the classical isotropic micromorphic continuum [7, 17] without mixed terms (like $\langle \text {sym} \varvec{P}, \text {sym}\left( \text {D}\varvec{u} -\varvec{P}\right) \rangle$, etc.) and simplified curvature expression [25, 27] can be written as:

$$\begin{aligned} W \left( \text {D}\varvec{u}, \varvec{P}, \text {D}\varvec{P}\right) =&\, \mu _{\text {e}} \left\Vert \text {sym} \left( \text {D}\varvec{u} - \varvec{P} \right) \right\Vert ^{2} + \dfrac{\lambda _{\text {e}}}{2} \text {tr}^2 \left( \text {D}\varvec{u} - \varvec{P} \right) + \mu _{\text {c}} \left\Vert \text {skew} \left( \text {D}\varvec{u} - \varvec{P} \right) \right\Vert ^{2} \nonumber \\&+ \mu _{\text {micro}} \left\Vert \text {sym}\,\varvec{P} \right\Vert ^{2} + \dfrac{\lambda _{\text {micro}}}{2} \text {tr}^2 \left( \varvec{P} \right) \nonumber \\&+ \frac{\mu \, L_{\text {c}}^2}{2} \Bigg ( \widetilde{a}_1 \, \left\Vert \text {D}\left( \text {dev} \, \text {sym} \, \varvec{P}\right) \right\Vert ^2 + \widetilde{a}_2 \, \left\Vert \text {D}\left( \text {skew} \, \varvec{P}\right) \right\Vert ^2 + \frac{2}{9} \, \widetilde{a}_3 \left\Vert \text {D} \left( \text {tr} \left( \varvec{P}\right) {\mathbb {1}} \right) \right\Vert ^2 \Big ) \Bigg ) \end{aligned}$$

(50)

while the equilibrium equations without body forces are the following:

$$\begin{aligned}&\text {Div}\overbrace{\left[ 2\mu _{\text {e}}\,\text {sym} \left( \text {D}\varvec{u} - \varvec{P} \right) + \lambda _{\text {e}} \text {tr} \left( \text {D}\varvec{u} - \varvec{P} \right) {\mathbb {1}} + 2\mu _{\text {c}}\,\text {skew} \left( \text {D}\varvec{u} - \varvec{P} \right) \right] }^{{\widetilde{\varvec{\sigma }}}} = \varvec{0} \, , \nonumber \\&\widetilde{\sigma } - 2 \mu _{\text {micro}}\,\text {sym}\,\varvec{P} - \lambda _{\text {micro}} \text {tr} \left( \varvec{P}\right) {\mathbb {1}} \nonumber \\&\quad +\mu L_{\text {c}}^{2} \, \text {Div} \left[ \widetilde{a}_1 \, \text {D} \left( \text {dev} \, \text {sym} \, \varvec{P}\right) + \widetilde{a}_2 \, \text {D} \left( \text {skew} \, \varvec{P}\right) + \frac{2}{9} \, \widetilde{a}_3 \, \text {D} \left( \text {tr} \left( \varvec{P}\right) {\mathbb {1}} \right) \right] = \varvec{0} \, , \end{aligned}$$

(51)

where ($\mu _{\text {e}}$,$\kappa _{\text {e}}=\lambda _{\text {e}}+2/3 \, \mu _{\text {e}}$), ($\mu _{\text {micro}}$,$\kappa _{\text {micro}}=\lambda _{\text {micro}}+2/3 \, \mu _{\text {micro}}$), $\mu _{\text {c}}$, $L_{\text {c}} > 0$, and ($\widetilde{a}_1$,$\widetilde{a}_2$,$\widetilde{a}_3$)$> 0$ in order to guarantee the positive definiteness of the energy. According to the reference system shown in Fig. 1, the ansatz for the displacement field and the classical micromorphic model is

$$\begin{aligned} \varvec{u}(x_2)&= \left( \begin{array}{c} 0 \\ u_{2}(x_{2}) \\ 0 \end{array} \right) \, , \qquad \qquad \varvec{P}(x_2) = \left( \begin{array}{ccc} P_{11}(x_2) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad P_{22}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad P_{33}(x_2) \\ \end{array} \right) \, ,\nonumber \\ \text {D}\varvec{u}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, . \end{aligned}$$

(52)

The boundary conditions for the uniaxial extension are assumed to be

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad \qquad \varvec{P}(x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(53)

The calculations are deferred to micro-strain model Sect. 8 since the ansatz, the equilibrium equations, and the boundary conditions are the same; therefore, the solution will also be the same.

8 Uniaxial extension problem for the micro-strain model without mixed terms

The micro-strain model [9, 12, 31] is the classical Mindlin–Eringen [7, 17] model particular case in which it is assumed a priori that the micro-distortion remains symmetric, $\varvec{P}=\varvec{S}\in \text {Sym}(3)$.

The strain energy which we consider is [25, 27]

$$\begin{aligned} W \left( \varvec{\text {D}u}, \varvec{S}, \varvec{\text {D}S}\right) =&\, \mu _{\text {e}} \left\Vert \left( \text {sym} \, \varvec{\text {D}u} - \varvec{S}\right) \right\Vert ^{2} + \frac{\lambda _{\text {e}}}{2} \text {tr}^2 \left( \varvec{\text {D}u} - \varvec{S} \right) + \mu _{\text {micro}} \left\Vert \, \varvec{S} \right\Vert ^{2} + \frac{\lambda _{\text {micro}}}{2} \text {tr}^2 \left( \varvec{S} \right) \nonumber \\&+ \frac{\mu \, L_{\text {c}}^2}{2} \, \left( \widetilde{a}_1 \, \left\Vert \varvec{\text {D}} \left( \text {dev} \, \varvec{S}\right) \right\Vert ^2 + \frac{2}{9} \, \widetilde{a}_3 \, \left\Vert \text {D} \left( \text {tr} \left( \varvec{S}\right) {\mathbb {1}} \right) \right\Vert ^2 \right) \, . \end{aligned}$$

(54)

The chosen 2-parameter curvature expression represents a simplified isotropic curvature (the full isotropic curvature for the micro-strain model would still count 8 parameters [2]).

The equilibrium equations, in the absence of body forces, are therefore the following

$$\begin{aligned}&\text {Div}\overbrace{\left[ 2\mu _{\text {e}} \, \left( \text {sym} \, \varvec{\text {D}u} - \varvec{S}\right) + \lambda _{\text {e}} \, \text {tr} \left( \varvec{\text {D}u} - \varvec{S} \right) {\mathbb {1}} \right] }^{{\widetilde{\sigma }}{:}{=}} = \varvec{0}, \nonumber \\&2\mu _{\text {e}} \, \left( \text {sym} \, \varvec{\text {D}u} - \varvec{S}\right) + \lambda _{\text {e}} \, \text {tr} \left( \varvec{\text {D}u} - \varvec{S} \right) {\mathbb {1}} - 2 \mu _{\text {micro}} \, \varvec{S} - \lambda _{\text {micro}} \, \text {tr} \left( \varvec{S}\right) {\mathbb {1}} \, \, \nonumber \\&\quad + \, \mu \, L_{\text {c}}^{2}\, \text {sym} \, \text {Div} \, \left[ \widetilde{a}_1 \, \text {D} \left( \text {dev} \, \varvec{S}\right) + \frac{2}{9} \, \widetilde{a}_3 \, \text {D} \left( \text {tr} \left( \varvec{S}\right) {\mathbb {1}} \right) \right] = \varvec{0} \, , \end{aligned}$$

(55)

where ($\mu _{\text {e}}$,$\kappa _{\text {e}}=\lambda _{\text {e}}+2/3 \, \mu _{\text {e}}$), ($\mu _{\text {micro}}$,$\kappa _{\text {micro}}=\lambda _{\text {micro}}+2/3 \, \mu _{\text {micro}}$), $L_{\text {c}} > 0$, and ($\widetilde{a}_1$,$\widetilde{a}_3$)$> 0$ in order to guarantee the positive definiteness of the energy. The boundary conditions for the uniaxial extension are assumed to be

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad \qquad \varvec{S}(x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(56)

According to the reference system shown in Fig. 1, the ansatz for the displacement field and the micro-distortion is (which coincides with classical micromorphic model Eq. (52))

$$\begin{aligned} \varvec{u}(x_2)&= \left( \begin{array}{c} 0 \\ u_{2}(x_{2}) \\ 0 \end{array} \right) \, , \qquad \qquad \varvec{S}(x_2) = \left( \begin{array}{ccc} S_{11}(x_2) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad S_{22}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad S_{33}(x_2) \\ \end{array} \right) \, , \nonumber \\ \text {D}\varvec{u}(x_2)&= \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad u_{2,2}(x_2) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) \, . \end{aligned}$$

(57)

After substituting ansatz (57) into equilibrium equations (55) we obtain the following four differential equations

$$\begin{aligned}&M_{\text {e}} \left( u_{2}''(x_{2})-P_{22}'(x_{2})\right) -\lambda _{\text {e}} \left( P_{11}'(x_{2})+P_{33}'(x_{2})\right) = 0 \, , \nonumber \\&\quad -\frac{2}{9} \mu \, L_{\text {c}}^2 (3 \widetilde{a}_{1}+\widetilde{a}_{3}) P_{11}''(x_{2}) +\frac{1}{9} \mu \, L_{\text {c}}^2 (3 \widetilde{a}_{1}-2 \widetilde{a}_{3}) \left( P_{22}''(x_{2})+P_{33}''(x_{2})\right) \nonumber \\&\quad +(M_{\text {e}}+M_{\text {micro}}) P_{11}(x_{2}) +(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{22}(x_{2})+P_{33}(x_{2})) -\lambda _{\text {e}} u_{2}'(x_{2}) = 0 \, , \nonumber \\&\frac{1}{9} \mu \, L_{\text {c}}^2 \left( (3 \widetilde{a}_{1}-2 \widetilde{a}_{3}) P_{11}''(x_{2}) -2 (3 \widetilde{a}_{1}+\widetilde{a}_{3}) P_{22}''(x_{2}) +(3 \widetilde{a}_{1}-2 \widetilde{a}_{3}) P_{33}''(x_{2}) \right) \nonumber \\&\quad +(M_{\text {e}}+M_{\text {micro}}) P_{22}(x_{2}) -M_{\text {e}} u_{2}'(x_{2}) +(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{11}(x_{2})+P_{33}(x_{2})) = 0 \, , \nonumber \\&\frac{1}{9} \mu \, L_{\text {c}}^2 \left( (3 \widetilde{a}_{1}-2 \widetilde{a}_{3}) \left( P_{11}''(x_{2})+P_{22}''(x_{2})\right) -2 (3 \widetilde{a}_{1}+\widetilde{a}_{3}) P_{33}''(x_{2})\right) \nonumber \\&\quad +(M_{\text {e}}+M_{\text {micro}}) P_{33}(x_{2}) +(\lambda _{\text {e}}+\lambda _{\text {micro}}) (P_{11}(x_{2})+P_{22}(x_{2})) -\lambda _{\text {e}} u_{2}'(x_{2})&= 0 \, . \end{aligned}$$

(58)

Being careful of substituting the system of differential equation with one in which Eq. (58)$_2$ and Eq. (58)$_4$ are replaced with their sum and their difference, respectively, we have

$$\begin{aligned}&M_{\text {e}} \left( u_{2}''(x_{2})-P_{22}'(x_{2})\right) -\lambda _{\text {e}} f_{p}'(x_{2}) = 0 \, , \nonumber \\&\quad -\frac{1}{9} \mu \, L_{\text {c}}^2 \left( (3 \widetilde{a}_{1}+4 \widetilde{a}_{3}) f_{p}''(x_{2}) +2 (2 \widetilde{a}_{3}-3 \widetilde{a}_{1}) P_{22}''(x_{2}) \right) \nonumber \\&\quad +f_{p}(x_{2}) (M_{\text {e}}+\lambda _{\text {e}}+\lambda _{\text {micro}}+M_{\text {micro}}) +2 (\lambda _{\text {e}}+\lambda _{\text {micro}}) P_{22}(x_{2}) -2 \lambda _{\text {e}} u_{2}'(x_{2}) = 0 \, , \nonumber \\&\frac{1}{9} \mu \, L_{\text {c}}^2 \left( (3 \widetilde{a}_{1}-2 \widetilde{a}_{3}) f_{p}''(x_{2}) -2 (3 \widetilde{a}_{1}+\widetilde{a}_{3}) P_{22}''(x_{2}) \right) \nonumber \\&\quad +(M_{\text {e}}+M_{\text {micro}}) P_{22}(x_{2}) -M_{\text {e}} u_{2}'(x_{2}) +f_{p}(x_{2}) (\lambda _{\text {e}}+\lambda _{\text {micro}}) = 0 \, , \nonumber \\&f_{m}(x_{2}) (M_{\text {e}}-\lambda _{\text {e}}-\lambda _{\text {micro}}+M_{\text {micro}}) -\widetilde{a}_{1} \, L_{\text {c}}^2 \, f_{m}''(x_{2}) = 0 \, , \end{aligned}$$

(59)

where $f_{p} (x_2){:}{=}P_{11}(x_2)+P_{33}(x_2)$ and $f_{m} (x_2){:}{=}P_{11}(x_2)-P_{33}(x_2)$. It is highlighted that Eq. (59)$_4$ is a homogeneous second-order differential equation depending only on $f_{m}(x_2)$ with homogeneous boundary conditions Eq. (56).

Also here, the fact that Eq. (59)$_4$ is an independent equation has its meaning in the symmetry constraint of the uniaxial extensional problem in the direction along the $x_2$- and $x_3$-axis, which requires that ${P_{11}(x_2)=P_{33}(x_2)}$.

The solution and the measure of the apparent stiffness are too complicated to be reported here, but nevertheless, it is possible to plot how the apparent stiffness behaves while changing $L_{\text {c}}$ (see Fig. 4).

Fig. 4

Micro-strain model. (left) Extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$. The stiffness is bounded as $L_{\text {c}} \rightarrow \infty$ ($h\rightarrow 0$) and converges to $M_{\text {e}}$. The values of the parameters used are: $\mu = 1$, $\lambda _{\text {macro}}= 1$, $M_{\text {macro}}= 3$, $\lambda _{\text {micro}}= 9.69$, $M_{\text {micro}}= 12$, $\widetilde{a}_1= 1/5$, $\widetilde{a}_3= 1/6$; (right) Displacement profile across the thickness of the dimensionless $\overline{u}_2=u_2/\left( \gamma \, h\right)$ for different values of $L_{\text {c}}=\{0, 3, 5, 10, \infty \}$. The values of the other parameters used in order to maximize the nonhomogeneous behavior are $\mu = 1$, $\lambda _{\text {e}}= 11$, $M_{\text {e}}= 33$, $\lambda _{\text {micro}}= 1.1$, $M_{\text {micro}}= 3.3$, $\widetilde{a}_1= 1$, $\widetilde{a}_3= 1/6$

We note that the extensional stiffness remains bounded as $L_{\text {c}}\rightarrow \infty$ ($h\rightarrow 0$) and converges to $M_{\text {e}}$. The solution obtained for the micro-strain model for the uniaxial extension problem also holds for the classical micromorphic problem presented in Sect. 7.

9 Uniaxial extension problem for the second gradient continuum

Fig. 5

Second gradient model. (left) Extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$. For the second gradient model (solid curve) the stiffness is unbounded as $L_{\text {c}} \rightarrow \infty$ ($h\rightarrow 0$), while for the micro-strain model (dashed curve) the stiffness is bounded. The second gradient model can be obtained from the micro-strain model by formally letting $\mu _{\text {e}},\lambda _{\text {e}}\rightarrow \infty$. The values of the parameters used are: $\mu = 1$, $\mu _{\text {macro}}= 1$, $\lambda _{\text {macro}}= 2$, $\widetilde{a}_3= 4$; (right) Displacement profile across the thickness of the dimensionless $\overline{u}_2=u_2/\left( \gamma \, h\right)$ for different values of $L_{\text {c}}=\{0, 0.1, 0.2, 0.35, \infty \}$. The values of the other parameters used in order to maximize the nonhomogeneous behavior are $\mu = 1$, $\lambda _{\text {micro}}=1$, $M_{\text {micro}}= 1$, $\widetilde{a}_3=2$

The strain energy density for the isotropic second gradient with simplified curvature [1, 6, 17, 25, 27] is

$$\begin{aligned}&W \left( \varvec{\text {D}u}, \varvec{\text {D}^2 u}\right) = \, \mu _{\text {macro}} \left\Vert \text {sym}\,\varvec{\text {D}u} \right\Vert ^{2} + \frac{\lambda _{\text {macro}}}{2} \text {tr}^2 \left( \varvec{\text {D}u} \right) \nonumber \\&\quad + \frac{\mu \, L_{\text {c}}^2}{2} \left( \widetilde{a}_1 \, \left\Vert \text {D} \Big (\text {dev} \, \text {sym} \, \varvec{\text {D} u}\Big ) \right\Vert ^2 + \widetilde{a}_2 \, \left\Vert \text {D} \Big (\text {skew} \, \varvec{\text {D} u}\Big ) \right\Vert ^2 + \frac{2}{9} \, \widetilde{a}_3 \, \left\Vert \text {D} \Big ( \text {tr} \left( \varvec{\text {D} u}\right) \, {\mathbb {1}} \Big ) \right\Vert ^2 \right) \, , \end{aligned}$$

(60)

while the equilibrium equations without body forces are the following:

$$\begin{aligned}&\text {Div}\bigg [ 2 \mu _{\text {macro}} \,\text {sym}\,\varvec{\text {D}u} + \lambda _{\text {macro}} \text {tr} \left( \varvec{\text {D}u}\right) {\mathbb {1}} \nonumber \\&\quad - \mu L_{\text {c}}^{2} \, \left( \widetilde{a}_1 \, \text {dev} \, \text {sym} \, \varvec{\Delta } \left( \varvec{\text {D}u}\right) + \widetilde{a}_2 \, \text {skew} \, \varvec{\Delta } \left( \varvec{\text {D}u}\right) + \frac{2}{9} \, \widetilde{a}_3 \, \text {tr} \left( \varvec{\Delta } \left( \varvec{\text {D}u}\right) \right) {\mathbb {1}} \right) \bigg ] = \varvec{0} \, , \end{aligned}$$

(61)

where $(\mu _{\text {macro}},\kappa _{\text {macro}},\mu ,\widetilde{a}_1,\widetilde{a}_3)>0$ in order to guarantee the positive definiteness of the energy. Due to the uniaxial extension problem symmetry the following structure of $\varvec{u} = \left( 0,u_{2}(x_{2}), 0\right) ^T$ has been chosen, which results in having only the component $u_{2,2}$ different from zero in the gradient of the displacement $\text {D}\varvec{u}$. The boundary conditions for the uniaxial extension are (see Fig. 1) assumed to be

$$\begin{aligned} u_{2}(x_{2} = \pm h/2) = \pm \frac{\varvec{\gamma } \, h}{2} \, , \qquad \qquad \qquad u'_{2}(x_{2} = \pm h/2) = 0 \, . \end{aligned}$$

(62)

After substituting the expression of the displacement field in Eq. (61), the nontrivial equilibrium equation reduces to

$$\begin{aligned} (\lambda _{\text {micro}}+2 \mu _{\text {micro}}) \, u_{2}''(x_{2})-\frac{1}{3} \widetilde{a}_{3} \, \mu \, L_{\text {c}}^2 \, u_{2}^{(4)}(x_{2}) = 0 \, . \end{aligned}$$

(63)

After applying the boundary conditions to the solution of Eq. (63), it results that $u_{2}(x_2)$ is given by [24, 26]

$$\begin{aligned} u_{2}(x_{2}) = \frac{ \frac{2x_2}{h} - \frac{2}{f_1} \sinh \left( f_1\frac{x_2}{L_{\text {c}}}\right) \text {sech}\left( \frac{f_1}{2}\frac{h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} }{ 1 - \frac{2}{f_1} \tanh \left( \frac{f_1}{2}\frac{h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } \frac{\varvec{\gamma } h}{2} \, , \qquad \qquad f_1 := \sqrt{\frac{\lambda _{\text {macro}}+2 \mu _{\text {macro}}}{\mu \, \widetilde{a}_{3}/3 }} \, . \end{aligned}$$

(64)

where $f_1>0$ is strictly positive in order to match the positive definiteness conditions and the same reasoning applied in the relaxed micromorphic model sections still holds. Strain energy (61) becomes then

$$\begin{aligned} W(\varvec{\gamma }) = \int _{0}^{h} W \left( \varvec{\text {D}u}, \varvec{\text {D}^2 u}\right) = \frac{1}{2} \left[ \frac{ \overbrace{\lambda _{\text {macro}} + 2\mu _{\text {macro}}}^{M_{\text {macro}}} }{ 1-\frac{2}{f_1} \tanh \left( \frac{f_1}{2}\frac{h}{L_{\text {c}}}\right) \frac{L_{\text {c}}}{h} } \right] h \, \varvec{\gamma }^2 = \frac{1}{2} \, M_{\text {w}} \, h \, \varvec{\gamma }^2 \, . \end{aligned}$$

The plot of the extensional stiffness $M_{\text {w}}$ while varying $L_{\text {c}}$ is shown in Fig. 5.

10 Conclusions

Only the second gradient formulation produces an unbounded apparent stiffness as $L_{\text {c}}\rightarrow \infty$ ($h\rightarrow 0$), while for the other models different bounded limit stiffnesses are observed. For the second gradient model, because of its unboundedness stiffness, it can be more likely to have an instability in the parameters’ fitting process on real structures: while being at a scale close to the singularity, a small changes in the geometrical or material properties of the sample may technically cause an arbitrarily large change in the values of the elastic coefficients. Therefore, the use of the second gradient model (or the classical micromorphic model in bending or torsional tests [25, 27]) should be done with great care as regards the stable identification of parameters. These problems are avoided for the relaxed micromorphic model. The relaxed micromorphic model determines $\overline{M} = \frac{M_{\text {e}} \, M_{\text {micro}}}{M_{\text {e}} + M_{\text {micro}}}$, which is less than $M_{\text {micro}}$ and $M_{\text {e}}$, while the micro-strain model determines $M_{\text {e}}$ as limit stiffness. The Cosserat model is not able to catch a nonhomogeneous solution and provides no size effect. The different limit stiffnesses for the relaxed micromorphic model versus the full micromorphic and micro-strain model approach, respectively, suggest that the meaning of classical experimental tests does not have an unambiguous deformation and micro-deformation solution field anymore, and this is due to the fact that we can have different boundary conditions on the components of the micro-distortion tensor depending on what each model requires to constrain. This allows the existence of different uniaxial extension-like problems and not just one like for a classical Cauchy material.

The limit \(L_{\text {c}} \rightarrow \infty \) for the relaxed micromorphic model

The limit of the energy, Eq. (11), for $L_{\text {c}} \rightarrow \infty$, requires that $\left\Vert \text {Curl}\,\varvec{P} \right\Vert = 0$, which implies that $\varvec{P} = \text {D} \varvec{\zeta }$, for some $\zeta : \Omega \rightarrow \mathbb {R}^3$. Energy Eq. (11) now becomes

$$\begin{aligned} W \left( \varvec{\text {D} u}, \varvec{\text {D} \zeta }\right) =&\, \mu _{\text {e}} \left\Vert \text {sym} \left( \varvec{\text {D} u} - \varvec{\text {D} \zeta } \right) \right\Vert ^{2} +\dfrac{\lambda _{\text {e}}}{2} \text {tr}^2 \left( \varvec{\text {D} u} - \varvec{P} \right) + \mu _{\text {micro}} \left\Vert \text {sym}\,\varvec{\text {D} \zeta } \right\Vert ^{2} + \dfrac{\lambda _{\text {micro}}}{2} \text {tr}^2 \left( \varvec{\text {D} \zeta } \right) \, , \end{aligned}$$

(65)

and that Eq. (13) turns into

$$\begin{aligned} \begin{array}{rr} \text {Div} \overbrace{ \left[ 2\mu _{\text {e}}\,\text {sym} \left( \varvec{\text {D} u} - \varvec{\text {D} \zeta } \right) + \lambda _{\text {e}} \text {tr} \left( \varvec{\text {D} u} - \varvec{\text {D} \zeta } \right) {\mathbb {1}} \right] }^{{\widetilde{\varvec{\sigma }}{:}{=}} } &{}= \varvec{0} \, ,\\ \widetilde{\sigma } - 2 \mu _{\text {micro}}\,\text {sym}\,\varvec{\text {D} \zeta } - \lambda _{\text {micro}} \text {tr} \left( \varvec{\text {D} \zeta }\right) {\mathbb {1}} &{}= \varvec{0} \, , \end{array} \end{aligned}$$

(66)

with consistent coupling boundary condition $\text {D}\,\varvec{u} \cdot \varvec{\tau } = \text {D} \varvec{\zeta } \cdot \varvec{\tau }$. Given Eq.  (66)$_1$, Eq. (66)$_2$ reduces to be

$$\begin{aligned} \text {Div}\left[ 2 \mu _{\text {micro}}\,\text {sym}\,\varvec{\text {D} \zeta } + \lambda _{\text {micro}} \text {tr} \left( \varvec{\text {D} \zeta }\right) {\mathbb {1}} \right] = \varvec{0} \, , \end{aligned}$$

(67)

which, for the uniaxial extension problem with boundary condition $u_{2} \left( x_2 = \pm h/2 \right) = \pm \varvec{\gamma } \, h/2$, is equivalent to

$$\begin{aligned} \text {D} \varvec{\zeta } = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad a &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right) \, , \quad \text {D} \varvec{u} = \left( \begin{array}{ccc} 0 &{}\quad \varvec{\gamma } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right) \, , \end{aligned}$$

(68)

where a is an arbitrary constant. This solution to Eq. (66) is therefore not unique. Inserting $\text {D} \varvec{u}$ and $\text {D} \varvec{\zeta }$ from Eq. (68) in Eq. (65), the following energy expression is recovered

$$\begin{aligned} I \left( a\right) = \frac{1}{2} \left( 2 a^2 M_{\text {micro}} +2 M_{\text {e}} (a-\varvec{\gamma } )^2 \right) \, , \end{aligned}$$

(69)

which has to be minimized with respect to a in order to remove the nonuniqueness of equilibrium system Eq. (66), which means that the following relation

$$\begin{aligned} \dfrac{\partial }{\partial a} \left( a^2 M_{\text {micro}} +M_{\text {e}} (a-\varvec{\gamma } )^2 \right) = 2 a (M_{\text {e}}+M_{\text {micro}}) -2 \varvec{\gamma } \, M_{\text {e}} = 0 \end{aligned}$$

(70)

has to be satisfied. The solution of Eq. (70) is $a_{\text {min}} = \dfrac{M_{\text {e}}}{M_{\text {e}} + M_{\text {micro}}} \varvec{\gamma }$. Finally it is possible to substitute $a_{\text {min}}$ into Eq. (68) obtaining

$$\begin{aligned} \text {D} \varvec{\zeta } = \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \dfrac{M_{\text {e}}}{M_{\text {e}} + M_{\text {micro}}} \varvec{\gamma } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right) , \quad \text {D} \varvec{u} = \left( \begin{array}{ccc} 0 &{}\quad \varvec{\gamma } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right) . \end{aligned}$$

(71)

Solution Eq. (71) satisfies the equilibrium equations, the boundary conditions, and the minimum energy requirement. The expression of the energy now becomes

$$\begin{aligned} W(\varvec{\gamma }) = \int _{-h/2}^{h/2} W(\text {D} \varvec{u},\text {D} \varvec{\zeta }) = \frac{1}{2} \dfrac{M_{\text {e}} \, M_{\text {micro}}}{M_{\text {e}} + M_{\text {micro}}} h \, \varvec{\gamma }^2 = \frac{1}{2} \overline{M} h \, \varvec{\gamma }^2 \, , \end{aligned}$$

(72)

with $\overline{M}=\dfrac{M_{\text {e}} \, M_{\text {micro}}}{M_{\text {e}} + M_{\text {micro}}}$ the extensional stiffness for the relaxed micromorphic when $L_{\text {c}} \rightarrow \infty$.