1 Introduction

Nowadays, one of the constant challenges of mechanical systems is to design new reinforcement techniques for existing structures so that they offer a real comfort of safety for their occupant while ensuring the lifespan of the structure [1, 2]. Amongst that, many phenomenological models using hysteresis force for modelling or control of mechanical systems have been proposed [4,5,6,7,8]. It is well known that hysteresis is a typical nonlinear phenomenon. This nonlinear behaviour is encountered in a wide variety of processes in which the input–output dynamic relations between variables involve memory effects.

The idea of employing negative stiffness springs, or ‘anti-springs’, for the dissipation of a large fraction of the energy initially induced into the system can be traced in civil engineering [9,10,11,12] and the innovative paper by George Tsiatasa and Aristotelis Charalampakis [13]. This spring can easily obtain negative stiffness for negative values of its parameter \(\alpha \), leading to a true softening behaviour.The central concept of these approaches is to significantly reduce the stiffness of the isolator and consequently of the natural frequency of the system even at almost zero levels.

This paper deals with the predictions of conditions for which horseshoe chaos appears in a class of systems with Bouc–Wen hysteresis. In fact, due to the strongly nonlinearity of the Bouc–Wen model, no analytical investigation has been done until now. Predicting the appearance of some dynamic states in the space parameters of the system remains a challenge for engineering application. If force is the input function, and total force versus displacement is considered, then the reduction of the hysteretic force results in total stiffness degradation only, whereas both total strength and total stiffness degrade if displacement is the independent variable. In fact, the hysteretic energy increases with linearly increasing force, the system degrades nonlinearly and is quite sensitive to the shape parameters of the systems. This sensitivity can give rise to the appearance of separatrix, meaning that the transverse intersection between the perturbed and unperturbed heteroclinic orbits can occur, thus the presence of horseshoe chaos [3, 16,17,18,19,20]. The appearance of horseshoe chaos in a physical system guarantees transient chaotic behaviour of the system. The control of this disturbance is fundamental to design an operation of these physical systems. This paper shows that by playing only on the shape parameters of the Bouc–Wen hysteresis one can predict and suppress the appearance of chaotic motion.

After the derivation of the equation, we show using some mathematical tools the transition from the nondegenerated to degenerated potential and then focus on the conditions for which horseshoe chaos can be suppressed on the system.

2 Mathematical modelling and analytical investigation

Equation of motion for single degree of freedom system consisting of a mass (\(m>0\)) connected in parallel to a viscous damper (\(c>0\)) with Bouc–Wen hysteretic spring is described by:

$$\begin{aligned} m\ddot{x}\left( t \right) + c\dot{x}\left( t \right) + H\left( {x,z,t} \right) = F\left( t \right) \end{aligned}$$
(1)

where \(x,\dot{x}\) and \(\ddot{x}\) are displacement, velocity and acceleration, respectively, and the nondamping restoring force, H, is composed of both linear and hysteretic restoring forces. H is given by:

$$\begin{aligned} H\left( {x,z,t} \right) = \alpha kx\left( t \right) + k \left( {1 - \alpha } \right) z\left( t \right) \end{aligned}$$
(2)

k is a stiffness, \(\alpha \) the rigidity ratio of post-yield to pre-yield and z the hysteretic displacement. The relative input of the hysteretic part is therefore controlled by the parameter \(\alpha \) . The nonlinear restoring force is thus a function of the fictitious hysteretic displacement z rather than the total displacement x. At larger displacements, for a nonpinching, nondegrading system the so-called Bouc–Wen model represents the true hysteresis in the form [5, 7, 14]:

$$\begin{aligned} \dot{z} = D^{-1}(A\dot{x} - \beta \left| {\dot{x}} \right| \left| z \right| ^{n - 1} z - \gamma \dot{x}\left| z \right| ^n) \end{aligned}$$
(3)

where \(\dot{z}\) denotes the time derivative, \(n>1\), \(D>0\), \(k>0\) and \(A>0\). A is the parameter controlling hysteresis amplitude \(\beta \), \( \gamma \) and n are parameters describing shape and amplitude of hysteresis. In this study, thermodynamic admissibility issues impose the following inequality [23,24,25]:

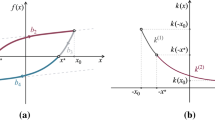
$$\begin{aligned} \beta \ge \gamma \end{aligned}$$
(4)

Based on (4), the hysteretic loop assumes a bulge shape (see Fig. 1) as opposed to a slim-S one (see Fig. 2).

$$\begin{aligned} \beta + \gamma \ge 0 \end{aligned}$$
(5)

Equation (5) is a sufficient and necessary condition for strain-softening behaviour. The combination of \(\beta \) and \( \gamma \) dictates whether the model describes a softening (see Fig. 1) or hardening (see Fig. 2) load–slip relation.

Fig. 1
figure 1

Softening hysteresis loop generated by the model for \(D = 1\), \(n=2, A=1, \gamma =0.05\) and \(\beta =0.95\)

Full size image

These results are obtained assuming that the external excitation is harmonic, i.e. \(F\left( t \right) = F_0 \sin \left( {\varOmega t} \right) \), where \( F_0 \) and \(\varOmega \) are, respectively, the amplitude and frequency of the excitation. To derive the total energy of the system, it is convenient to rewrite the system equation in the form [4]:

$$\begin{aligned}&\ddot{x}\left( t \right) + 2\varsigma \omega \dot{x} \left( t \right) + \alpha \omega ^2 x\left( t \right) + \omega ^2 \left( {1 - \alpha } \right) z\left( t \right) = F\left( t \right) \nonumber \\&\omega = \sqrt{\frac{k}{m}} \,\,,\,\,\,\varsigma =\frac{c}{{2m\omega }}. \end{aligned}$$
(6)

where \( \omega \) is a pre-yield natural frequency of the system and \( \varsigma \) a linear viscous damping ratio. The evolution of the hysteretic displacement z given by the following constitutive differential equation:

$$\begin{aligned} \dot{z} =D^{-1} \left[ {A - \left( {\gamma + sgn \left( {\dot{x}} \right) sgn\left( z \right) \beta } \right) \left| z \right| ^n } \right] \dot{x} \end{aligned}$$
(7)
Fig. 2
figure 2

Hardening hysteresis loop generated by the model for \(D=1\), \(n=2, A=1, \gamma =-0.65\) and \(\beta =0.35\)

Full size image

We note that the phase space of the Bouc–Wen oscillator is three dimensional and is spanned by \(\left( {x,\dot{x},z} \right) \). Setting \(\varepsilon = {\mathrm{sgn}} \left( {\dot{x}} \right) {\mathrm{sgn}} \left( z \right) = \pm 1 \) with Sgn denotes the Signum function; in order to integrate z, (7) can be rewritten in the following form:

$$\begin{aligned} dz =D^{-1} \left[ {A - \left( {\gamma + \varepsilon \beta } \right) \left| z \right| ^n } \right] dx \end{aligned}$$
(8)

3 Appearance of separatrix and Melnikov analysis

Equations (6) and (8) can be recast in state space form as:

$$\begin{aligned}&\dot{x} = y \nonumber \\&\dot{y} = - 2\varsigma y - \alpha \omega _0 ^2 x -\left( {1 - \alpha } \right) \omega _0 ^2 z \nonumber \\&\dot{z} = D^{-1}\left[ {A - \left( {\gamma + \varepsilon \beta } \right) \left| z \right| ^n }\right] y. \end{aligned}$$
(9)

For \(D=1\) and \(n=2\), one obtains three fixed points \(\left( {0\,,\,0\,,\,0} \right) \);

\(\left( { - \frac{{\left( {1 - \alpha } \right) }}{\alpha }\sqrt{\frac{A}{{\gamma + \varepsilon \beta }}};\,\,0\,\,; \sqrt{\frac{A}{{\gamma + \varepsilon \beta }}} } \right) \) and \(\left( {\frac{{\left( {1 - \alpha } \right) }}{\alpha } \sqrt{\frac{A}{{\gamma + \varepsilon \beta }}};\,\,0\,\,; -\sqrt{\frac{A}{{\gamma + \varepsilon \beta }}} } \right) \)

Taking into account the influence of the hysteretic force, the potential energy of the system, is given by:

$$\begin{aligned} V\left( x \right) = \frac{1}{2}\alpha \omega ^2 x^2 + \omega ^2 \left( {1 - \alpha } \right) \int _{x\left( 0 \right) }^{x \left( t \right) } {zdx} \end{aligned}$$
(10)

The energy absorbed by the hysteretic element is thus the continuous integral of the hysteretic force and the total energy displacement.

Equation (8) is integrated for \(D=1\) and \(n=2\). The initial conditions x(0) , \( \dot{x}(0) \) , z(0) are known. For the sake of simplicity, it is assumed that \( x(0)=\dot{x}(0)=z(0)=0 \). It is claimed that the hysteretic displacement z can thus be derived explicitly and given by:

$$\begin{aligned} z = \frac{{\sqrt{A}}}{{\sqrt{\left( {\gamma +\varepsilon \beta } \right) } }}\tanh \left( {\sqrt{A\left( {\gamma + \varepsilon \beta } \right) } x} \right) \end{aligned}$$
(11)

Then the complete potential of the system, taking into account the hysteresis component (see Fig. 3a) is given by:

$$\begin{aligned} V\left( x \right) = \frac{1}{2}\alpha \omega ^2 x^2 + \omega ^2 \frac{{\left( {1 - \alpha } \right) \sqrt{A} }}{{\sqrt{\left( {\gamma + \varepsilon \beta } \right) } }} {\ln }\cosh \left( {\sqrt{A\left( {\gamma + \varepsilon \beta }\right) } x} \right) \end{aligned}$$
(12)

The critical amplitude \(x_u\) is obtained when the following conditions are satisfied:

$$\begin{aligned} V^{'}\left( x \right) = 0 \,\,\,and\,\,V^{''}\left( x \right) \ge 0 \end{aligned}$$
(13)

But obtaining the analytical expression using the form given by (11) is quite impossible. To find an approximation solution, we carry out the expansion of \(\tanh \left( {\sqrt{A\left( {\gamma + \varepsilon \beta } \right) } x} \right) \) and assume that \(\beta = \xi \bar{\beta } \) and \(\gamma = \xi \bar{\gamma } \) where \(\xi \) is a small positive constant. An expansion in power series of \(\xi \) allows to obtain an approximate description of the hysteresis loop by neglecting the \(\xi ^3\) and higher powers, and by integration of (10), one obtains:

$$\begin{aligned} V_{ap}\left( x \right) =\frac{1}{2}(\omega ^2 \left( {\alpha +\left( {1 - \alpha } \right) A} \right) )x^2 - \frac{1}{{12}} (\omega ^2 A^2 \left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) )x^4 \end{aligned}$$
(14)

The representation of this potential shows that the presence of hysteretic force describes the unbounded monostable potential (see Fig. 3b).

Equation of the dynamic of this system is given by :

$$\begin{aligned} \ddot{x}\left( t \right) + 2\varsigma \omega \dot{x} \left( t \right) + \left( {\alpha \omega ^2 \left( t \right) + \omega ^2 \left( {1 - \alpha } \right) A} \right) x \left( t \right) - \frac{1}{3}\omega ^2 A^2 \left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) x^3 \left( t \right) =F_0 \sin \left( {\varOmega t} \right) \end{aligned}$$
(15)
Fig. 3
figure 3

a Phase space. b Potential curves of system for \(\varepsilon =1\)

Full size image

Figure 3 also shows that we have three fixed points: one stable (0, 0) and the other two unstable \(\left( { \pm \sqrt{\frac{{3\left( {\alpha + \left( {1 - \alpha } \right) A} \right) }}{{\left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) A^2 }}} ,0} \right) \) leading to the appearance of heteroclinic orbit (see Fig. 4). In this case, the separatrix appears leading to the possible transverse intersection between perturbed and unperturbed heteroclinic orbit. This means that the shape parameters of the hysteresis force have a direct link with the appearance of horseshoe chaos in the system. The presence of horseshoe chaos means the existence of a starting point for successive route to chaotic dynamics. This can be detected analytically using Melnikov theory.

Fig. 4
figure 4

Heteroclinic orbit of unbounded monostable potential

Full size image

4 Melnikov analysis

In the present section, we apply the Melnikov method [16, 21, 22, 26] to detect analytically the effects of Bouc–Wen model parameters on the threshold condition for the inhibition of horseshoe chaos in the system and on the fractal basin boundaries. To apply this method, we introduce a small \(\mu \) parameter in (15) and rewrite the governing system as the following set of first-order differential equations :

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}\left( \tau \right) = y\left( \tau \right) \\ \dot{y}\left( \tau \right) = - \omega ^2 \left( {\alpha + \left( {1 - \alpha } \right) A} \right) x\left( \tau \right) + \frac{1}{3}A^2 \omega ^2 \left( {\gamma + \varepsilon \beta } \right) \left( {1 - \alpha } \right) x^3 \left( \tau \right) + \mu \varGamma \left( t \right) \\ \end{array}\right. \end{aligned}$$
(16)

With \(\varGamma \left( \tau \right) = - 2\varsigma \omega y\left( \tau \right) + F_0 \cos \left( {\varOmega \tau } \right) \). For \( \mu =0\) and after assuming that : \(x = x\left( \tau \right) ; y = y\left( \tau \right) \) the system of (16) is the Hamiltonian system with Hamiltonian function.

$$\begin{aligned} H\left( {x,y}\right) =\frac{1}{2}y^2 + \frac{1}{2}\omega ^2 \left( {\alpha + \left( {1 - \alpha }\right) A} \right) x^2 -\frac{1}{4}\left( {\frac{1}{3}\left( {1 - \alpha }\right) \left( {\gamma + \varepsilon \beta }\right) \omega ^2 A^2}\right) x^4 \end{aligned}$$
(17)

The saddle points (see Fig. 3) \( x_{u1}\) and \( x_{u2}\) are connected by heteroclinic orbits (see Fig. 4) that satisfied the following equation:

$$\begin{aligned}&x_{het} = \pm \sqrt{\frac{{3\left( \alpha +\left( 1-\alpha \right) A\right) }}{{\left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) A^2 }}} \tanh \left( {\omega \sqrt{\frac{{\alpha +\left( {1 - \alpha } \right) A}}{2}} \tau } \right) \nonumber \\&y_{het} = \pm \frac{{3\left( {\alpha + \left( {1 - \alpha } \right) A} \right) \omega }}{{\left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) A^2 }}\sqrt{\frac{{\alpha +\left( {1 - \alpha } \right) A}}{2}} {{\text {sech}}^2} \left( {\omega \sqrt{\frac{{\alpha + \left( {1 - \alpha } \right) A}}{2}} \tau } \right) \end{aligned}$$
(18)

The Melnikov theory defines the condition for the appearance of the so-called transverse intersection points between the perturbed and the unperturbed separatrix or the appearance of the fractality on the basin of attraction. This theory can be applied in the case of (15) by using the formula given by Wiggins [26] as follows:

$$\begin{aligned} M_Y \left( {\tau _0 } \right)&= \int _{ - \infty }^{ + \infty } {g_0 \left( {u_{het} \left( \tau \right) } \right) } {\times } g_p \left( {u_{het} \left( \tau \right) ,\tau + \tau _0 } \right) d\tau \nonumber \\&= - 2\varsigma \omega \int _{ - \infty }^{ + \infty } {y_{het}^2 } \left( \tau \right) d\tau + F_0 \int _{ - \infty }^{ + \infty } {y_{het} } \left( \tau \right) \sin \left( {\varOmega \left( {\tau + \tau _0 } \right) } \right) d\tau \nonumber \\&= I \pm Z\left( {\tau _0 } \right) \end{aligned}$$
(19)

where

$$\begin{aligned} I = - 24\varsigma \omega ^{2} \sqrt{\frac{\alpha +\left( 1-\alpha \right) A}{2}} \left( {\frac{{\alpha + \left( {1 - \alpha } \right) A}}{{\left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) A^2 }}} \right) ^2 \end{aligned}$$

and

$$\begin{aligned} Z\left( {\tau _0 } \right) = \frac{{3F_0 \varOmega \pi \left( {\alpha + \left( {1 - \alpha } \right) A} \right) \sin \left( {\varOmega \tau _0 } \right) }}{{\omega \left( {1 - \alpha } \right) \left( {\gamma + \varepsilon \beta } \right) A^2 \sqrt{\frac{{\alpha + \left( {1 - \alpha } \right) A}}{2}} {\sinh }\left( {\frac{{\varOmega \pi }}{{2\omega \sqrt{\frac{{\alpha + \left( {1 - \alpha } \right) A}}{2}}}}}\right) }} \end{aligned}$$

When the Melnikov function has a simple zero point, the stable manifold and the unstable manifold intersect transversally, and chaos in the sense of Smale horseshoe transform occurs. So let \(M_Y \left( {\tau _0 } \right) = 0\), one concludes that Melnikov chaos appears when:

$$\begin{aligned} F_0 \ge F_{{CR}} = \left| {\frac{{4\varsigma \omega ^3 \left( {\alpha + \left( {1 - \alpha } \right) A} \right) ^2}}{{\left( {\left( {\gamma + \varepsilon \beta } \right) \left( {1 - \alpha }\right) A^2 } \right) \varOmega \pi \sin \left( {\varOmega \tau _0 }\right) }}{\sinh } \left( {\frac{{\varOmega \pi }}{{2\omega \sqrt{\frac{{\alpha +\left( {1 - \alpha }\right) A}}{2}}}}}\right) }\right| \end{aligned}$$
(20)
Fig. 5
figure 5

Evolution of the critical amplitude \( F_{CR}\) as a function of : \(\varOmega \) (a), (c) and (e) ; \(\alpha \) (b); \(A\ (d)\) and \((\gamma + \varepsilon \beta )\ (f)\) with \(\varepsilon =1\)

Full size image

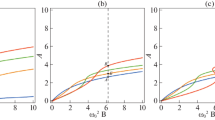
The criterion in Eq. (20) defines the threshold value of \(F_{CR}\) for the appearance of a transverse intersection between the perturbed and the unperturbed manifolds. Such a condition is known as necessary for the existence of chaos. The threshold condition is plotted in Fig. 5 as a function of the driving frequency \(\varOmega \) for different values of \(\alpha \) (see Fig. 5a), A (see Fig. 5c) and (\(\gamma + \varepsilon \beta \)) (see Fig. 5e) , as function of the parameter \(\alpha \) (see Fig. 5b), as function of A (see Fig. 5d) and as function of the parameters (\(\gamma + \varepsilon \beta \)) (see Fig. 5f).

Figure 5a shows in the space (\(\varOmega \), \(F_{CR}\)), the lower bound for the appearance of heteroclinic bifurcation for several cases of \(\alpha \) parameter. For (\(\varOmega \), \(F_{CR}\)) taken below the lower bound line, the system displays a periodic motion, while possible chaotic motion is observed in the upper domain. It appears that: when \(\alpha \) decreases, the surface of the critical force increases; consequently, critical force decreases.

Figure 5b illustrates the effects of negative stiffness on the threshold value of \(F_{CR}\), for \( -1<\alpha <0 \), the threshold increases, it appears that the control effect increases as \(\alpha \) increases, this is a sign of the reinforcement of effectiveness of the control. The variations of the critical force as a function of \(\alpha \) show that the parameter \(\alpha \) plays a preponderant role in its efficiency.

Fig. 6
figure 6

Basins of attraction showing the confirmation of the analytical prediction for \(\varepsilon =1\), \(\alpha =-0.5\), \(\beta =0.95\), \(\gamma =0.05\), \(\varsigma =0.02\) and \(A=1\)

Full size image

Figure 5c and e shows the critical external forcing amplitude for different values of A and (\(\gamma + \varepsilon \beta \)), respectively. One can see (Fig. 5c) that when the value of the parameter A increases, the thresholds of the critical values for heteroclinic bifurcation of the harmonic excitation \(F_{CR}\) decrease. The same effect is observed with the parameters (\(\gamma + \varepsilon \beta \)) (Fig. 5e). We conclude that the parameters A and (\(\gamma + \varepsilon \beta \)) have the same effect on the critical value for chaotic motions.

Figure 5d highlights the fact that as A increases the amplitude of the critical force decreases. Consequently, the choice of the parameter A relating to the reduction of the speed and amplitude of vibration or to the increase of the stability basin may be the starting point of a route leading to unpredictable behaviour. The same investigations are made in the case of Fig. 5f.

5 Numerical investigation

The existence of a homoclinic or heteroclinic orbit for the detection of horseshoe chaos in physical systems is of paramount importance. Indeed, the choices of control parameters for obtaining the basin of attraction are not done in a random manner. Moreover, it is possible to determine the conditions for which heteroclinic orbit appears, while defining the limits of values of model parameters for which basins can be obtained. Of Eq. (18), it is possible to find the conditions (see Eq. 21) for which the parameters of the Bouc–Wen model will allow to obtain each time a heteroclinic orbit. Thus, if the conditions (I) and (II) are satisfied, horseshoe chaos in the system can be predicted.

$$\begin{aligned} A> 0\,;\,\,\,-1< \alpha<0\,\,\,with \,\,\left| \begin{array}{l} (I)\left\{ \begin{array}{l} \beta + \gamma> 0 \\ \gamma - \beta < 0 \\ \end{array}\right. \\ (II)\left\{ \begin{array}{l} \beta + \gamma> \beta - \gamma \\ \beta - \gamma > 0 \\ \end{array}\right. \\ (III) All\,\,other\,cases\,\,\,\,\,\,\emptyset \\ \end{array} \right. \end{aligned}$$
(21)

To validate the accuracy of the proposed analytical predictions, we solve numerically Eq. 9 by means of fourth-order Runge–Kutta algorithm. A particular characteristic of the Melnikov theory is the fractality [15, 17, 21] of the basin of attraction and the resulting unpredictability due to the dependence on the initial conditions.

The limit \(F_{CR}\) given by (20) is shown in Fig. 6. These figures display the basin of attraction according to the evolution of external forces. Thus, it appears that the basin has a regular geometry (see Fig. 6a), and completely fractal (see Figs. 6b, c) for higher values, sign of the establishment of chaos. In addition, from the appropriate parameters of the Bouc–Wen model, we can also control the appearance of chaos in the SDOF system (see Fig. 7).

Figure 7 shows how when playing with the parameters of Bouc–Wen model it is possible to control system or to cause chaos. Thus, for the same value of critical amplitude and for different parameters of the Bouc–Wen model, the attraction basin is chaotic (see Fig. 6c); in Fig. 7 the attraction basin can be controlled. It is viewed that for a small amplitude of the external force, the limits of the basin are regular. In the case of the soft system, the heteroclinic orbit is clear. Above a certain value, it becomes irregular, meaning the presence of Melnikov chaos in the case of the soft system.

Fig. 7
figure 7

Effect of parameters \( (\gamma + \varepsilon \beta )\), A and \(\alpha \), on the basins of attraction for \(\varOmega =1\), \(\alpha =-0.4\), \(\gamma + \varepsilon \beta =0.9\) and \(A=0.7\)

Full size image
Fig. 8
figure 8

Response of Bouc–Wen model under cyclic excitation, with parameters used in Fig. 6 without control and Fig. 7 with control: − without control; \(\dots \) with control

Full size image

To validate the accuracy of the restoring force, (2) is plotted in Fig. 8; by comparing the curves in this figure, we show that the energy dissipated by the system can be considerably reduced when the system is controlled.

6 Conclusion

We have presented an analytical and numerical solution to describe the link between the presence of horseshoe chaos and hysteretic loop in a SDOF system. The hysteretic behaviour has been modelled by the constitutive differential equation of the first-order so-called Bouc–Wen model. Based on Melnikov theory, the approximate analytical solution has been obtained and we have studied the effects of some main parameters of the system such as \( \alpha \), A, \( \beta \) and \( \gamma \) on the chaotic dynamic of the system on its stability. It appears after dynamics analysis that the shape parameters of the hysteresis force play a key role in the occurrence of chaotic dynamics so-called horseshoe chaos. Thus, taking into consideration a selective situation on the hysteresis function one could be able to quench the appearance of Melnikov chaos in the system. Those predictions are confirmed and complemented by the numerical simulations from which we illustrate the regular nature of the basin of attraction. The analysis has also allowed to estimate the condition for the possible appearance of horseshoe chaos in the system. The main conclusion is that this condition depends strongly of Bouc–Wen parameters in the case of softening system.