1 Introduction

Rotary swaging is an established incremental cold forming manufacturing process for axisymmetric workpieces [1]. The incremental forming influences not only the geometry but also static and dynamic mechanical properties by work hardening and residual stresses that may develop through the process. Amely et al. presented investigations of residual stresses after cold radial forging. They found that the distribution of residual stresses at the inner and outer surfaces in the axial direction of tubes was uniform and became tensile at the outer surface of the tube and compressive at the inner surface [2]. In another study, Ghaei et al. found a dependence of the die geometry on the radial forging force [3]. In the following studies, he showed in FE simulation that the die geometry is influencing the axial stresses in steel tubes [4]. Liu studied the material flow in his finite element rotary swaging simulation. At the beginning and the end of tube reduction zone, the local plastic deformation is higher than in other tube zone. Moreover, these most active regions of strain are located on the inner and outer surfaces [5]. Darki performed a numerical analysis of the radial forging with two passes [6] and determined that in addition to the uniform distribution of the residual stresses at the outer and inner surfaces, the maximum range of residual stresses occurred in the first pass. Neutron diffraction analyses of cold rotary swaged tungsten heavy alloy showed that the distribution of residual stresses within the swaged workpiece was not homogeneous and fluctuated between positive and negative values, especially in the center of the workpiece [7].

The formation of the intrinsic properties by rotary swaging depends on the material flow [8]. During the process, the material is stretched and upset as well [9], resulting in a complex material flow. In such a process, the internal properties of the part, such as its microstructure, hardness and residual stresses components, are relevant for the mechanical properties of the workpieces [10]. Thus, modifications of rotary swaging influence the material flow history, in particular the generation of residual stress and thus the resulting component properties [11]. In order to improve the mechanical properties of the workpieces, it is not always necessary to eliminate or avoid the residual stresses, but it could be sufficient to control their level and distribution.

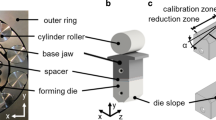
In infeed rotary swaging, the part is fed axially into the swaging head, see Fig. 1a, and the diameter is reduced incrementally by revolving and oscillating dies [12]. If the workpiece is fed deep enough that the complete die is in contact, a steady-state phase is assumed. The die features a reduction zone with a die angle α (conventional 5° ≤ α ≤ 15°) in which the main deformation is occurring. In the adjacent calibration zone (conventional length lc = 20 mm), the final geometry is generated with narrow tolerances. The reduction zone and the calibration zone are connected with a transition radius. In the exit zone, the workpiece is smoothly unloaded. These zones are conventionally equipped with a round shape [13], but also flat dies were already used to produce round [14] as well as polygonal cross sections [15]. Therefore, the stroke following angle Δϕ must be controlled, which is the relative rotation angle of workpiece and die between two consecutive strokes.

Fig. 1
figure 1

Infeed rotary swaging: a swaging head, b a pressure column, c flat swaging die, d die assembly

Full size image

These strokes are initiated by the oscillation of the dies due to the cylinder roller and the base jaw with a cam. With every overrunning of the cam by cylinder roller the base jaw, the spacer and the die are pushed inward until the dies are completely closed (see Fig. 1d). These four components represent together one single system between the workpiece and the outer ring which is called pressure column, see Fig. 1b. The generated closing time depends on the rotational speed of the swaging axle as well as the base jaws with a cam and die dimensions and can be varied by the height of the spacers. Figure 2 visualizes the radial die position for one full stroke. For the same stroke period T, the time of contact between the die and the workpiece tK and closing time of the die tS change depending on the spacer height hS. By increased spacer height hS2 (blue line), the stroke time tH remains constant; however, the contact time tK2 and the closing time tS2 increase compared to tK1 and tS1 at less spacer height hS1 (black line). This simplified kinematic consideration disregards elasto-dynamic effects like rebounding of and within the pressure column.

Fig. 2
figure 2

Radial die position for two full strokes and resulting times

Full size image

However, not only die dimensions influence the closing pressure. All machine components feature technical tolerances. Thus, the geometrical deviations of the pressure columns at each individual stroke create a scattering within the impact on the workpiece surface. The influence of fluctuating process parameters on residual stresses distribution was already investigated in [15]. It was shown that the residual stresses distribution at the surface of the workpiece was influenced by each stroke during the process. Moreover, for the workpieces swaged with conventional round dies, residual stresses fluctuated strongly between positive and negative values. However, beneath the surface in a depth of 30 µm they shifted to tensile stress and became homogeneous, which means that the effects were limited to the very surface of the workpieces.

The fluctuations of residual stresses could be significantly reduced by the use of flat dies, which exhibits a flat surface in the reduction as well as in the calibration zone, see Fig. 1c. In the case of four dies in the swaging head, closed flat shaped dies form a square, see Fig. 1d and in a combination with a stroke following angle of Δϕ = 0°, the formed workpiece shows also a square cross section. For this purpose, the workpiece is clamped in in a way that it rotates synchronously with the dies; hence, no torsion moments will occur. When the dies are open, the workpiece still rotates with the dies, resulting in that the diagonal of the rectangular cross section of the workpiece is larger than the free space between the opened dies. This results in a stroke following angle ∆ϕ between the dies and the workpiece equal to zero. Such process design led to homogeneous residual stresses at the surface of the square parts [15].

The aim of the present investigation is a targeted of residual stresses through definite settings in rotary swaging of tubes without mandrel. The main question in this work is whether the residual stresses can be influenced without changing the degree of forming but only by changing of the spacer height hS and correspondingly changing of the closing time tS. A validated FE simulation was used to reproduce the development of the residual stresses during the process, as they are difficult to trace in rotary swaging experiments. Furthermore, the influence of the die geometry was investigated, which gives the opportunity to verify and refine the existing model. Thus, the length of calibration zone of the die lc and the die angle α were varied.

2 Materials and methods

2.1 Rotary swaging setup

Experiments were carried out using four flat swaging dies, made of 1.2379 steel. The flat dies featured a die angle of α = 10° and a flat surface in the reduction as well as in the calibration zone. Due to such geometry, the four closed dies are forming a square, which has an inner circle diameter of 15 mm. The stroke frequency of the die was kept constant at fst = 35 Hz, and the ideal stroke height was defined from a cam height and equally set to hT = 1 mm. The feed per stroke was set to lst = 0.46 mm/stroke. During infeed rotary swaging, the stroke following angle of Δϕ = 0° was used and remained constant throughout the process. To achieve this, the workpiece was rotated with the same angular velocity as the dies. Workpieces used in this investigation were cold drawn steel tubes E355 (1.0580) with an initial length of L0 = 300 ± 0.85 mm, and a diameter of d0 = 20 ± 0.30 mm with a wall thickness of s0 = 3 mm (specified by the manufacturer). Each workpiece was heat-treated in a vacuum furnace at 890 °C for 5 h to eliminate existing residual stresses and work hardening before rotary swaging.

Intermediate spacers with two different thickness values hS1 = 5.08 mm (setting 1) and hS2 = 5.16 mm (setting 2) were used in this investigation to generate different closing pressures and closing times, see Fig. 2. All experiments were conducted at room temperature, using mineral oil Condocut KNR 22 for lubrication. Contact time between workpiece and dies was measured indirectly using electric current that was only flowing when the circuit was shortened. While dies and the workpiece were in contact, the current could flow and the time between rising and falling edge was measured.

2.2 Residual stress measurement

The residual stresses state of the processed tubes was measured in the steady-state region along a path of 40 mm on the outer surface of the tubes from point A to point B, see. Figure 3. An X-ray diffractometer type MZ IV from GE Inspection technologies (Ahrensburg, Germany) equipped with a position-sensitive detector and Vanadium-filtered Cr-Kα radiation source was used. The iron α {211} peak was recorded along 13 χ-angles between − 45° and + 45° at the surface of the processed samples using an aperture of 1 mm and a step size of 1 mm along a line of 40 mm in length, see Fig. 3. The residual stresses were calculated using the standard sin2ψ-method using X-ray elastic constants ½ S2 = 5.81 × 10–6 MPa−1 [16]. Because of the systematically observed shift of the tangential residual stresses and the similarity to the axial residual stresses [17], only the axial residual stresses were measured. Moreover, the axial residual stresses depth profile was evaluated in the middle of the steady-state area started in point C using a semi-destructive method by successively removing layers of material by electrochemical etching using a solution of H3PO4 and H2SO4 to access the material below the surface.

Fig. 3
figure 3

Sketch of a swaged workpiece showing the position of outer surface residual stress measurements

Full size image

2.3 Modeling and simulation

In this study, a 2D axisymmetric model was built using two components—a die (rigid body) and a workpiece (deformable body). In order to consider the Bauschinger effect [18] caused by the cyclic loading, a nonlinear strain hardening model was selected in ABAQUS. According to the Chaboche approach [19], a combined kinematic and isotropic strain hardening model was applied. The required coefficients of isotropic hardening were obtained from cyclic tensile-compression tests with annealed hourglass samples, which were used to simulate the cyclic test to validate the resulting material model [17]. The initial yield strength was σ0 = 357.3 MPa. For the isotropic hardening, the coefficients Q = 104.08 MPa and b = 2.78 were determined. For the kinematic hardening by means of the data type “Half Cycle” with three back stresses [20], a flow curve obtained from a tensile test on annealed samples was used. Contact conditions between the workpiece and the die were simplified in the simulation by using Coulomb’s law with a constant coefficient of friction value μ = 0.1 with the “penalty” contact method [21].

The workpiece geometry was identical to the real tube with an initial diameter of d0 = 20 mm, a wall thickness of S0 = 3 mm as well as an initial length L0 = 300 mm (see Fig. 4). The initial state of the workpiece was stress-free. For the FEM analysis, a CAX4R mesh was set up with a mesh size of 0.15 mm in axial and radial directions. In order to take into account a back throw of the workpiece (negative material shifting) [13], an additional fixed holder was connected to the workpiece by two springs with a stiffness of 33,075 N/m. The relative movement as in the real process between the workpiece and the die was realized by axial movement of the die in Z’ direction. The simulation was performed by a dynamic explicit analysis with 140 strokes of the die in radial direction and a feed per stroke of the die with lst = 0.46 mm in axial direction. For evaluation and visualization purposes of residual stresses during the process, dies were removed at the end of each stroke and the simulation was proceeded by a static general step to release the spring-back [22].

Fig. 4
figure 4

Principle of the 2D axisymmetric model

Full size image

In the simulation, the difference in thickness of the intermediate spacer was realized by the die path during a single stroke. A difference in the closing time tS between the die and the workpiece was set in simulation by tabular values, which are visualized in Fig. 5. A low closing time (tS1 = 3.0 ms) corresponding to the use of spacer thickness of hS1 = 5.08 mm and a high closing time (tS2 = 4.4 ms) corresponding to the use of spacer thickness of hS2 = 5.16 mm were implemented. Simulation parameters are presented in Table 1.

Fig. 5
figure 5

Square-shaped cross section: a experiment 1, b experiment 2, c table of geometrical values

Full size image
Table 1 Simulation parameters
Full size table

Contact time between the workpiece and the die was estimated from the last stroke of the finished simulation. The stroke time was calculated between the first contact until detach of the workpiece and the die.

3 Results

3.1 Experiments

By using flat dies in combination with the stroke following angle of Δϕ = 0°, the produced workpieces had a square-shaped cross section, see Fig. 5. The produced workpiece showed an increased tube wall thickness when a spacer with a higher thickness was used. Dependent on the spacer height hS, the wall thickness s1 and the height of the squares h1 of the formed tubes were modified, see Fig. 5c. Thicker spacer (hS2 = 5.16 mm) led to a greater height reduction h1 but also to a growth in the wall thickness s1 in a middle of the workpiece wall. Moreover, sharper corner at the inner wall of the workpiece can be seen after forming with hS1 = 5.08 mm.

The axial residual stresses of not swaged annealed tubes were measured as 7 ± 5 MPa which can be assumed to be zero. The axial residual stresses measured for both conditions are shown for two representative samples in Fig. 6. The distribution of residual stresses at the outer surface along the workpieces in the area from point A to point B is quite homogenous and stays constant within the measured length of 40 mm, see Fig. 6a. Slight bending at the wall of the workpiece swaged with hS = 5.16 mm (see Fig. 5b) should lead to a higher compressive stresses; nevertheless, increasing the spacer thickness hS resulted in an increase in tensile residual stresses of about 100 MPa. This increase could not be explained by a change in the degree of forming. There is no clear dependence between the spacer thickness hS, the height of the squares h1 and the wall thickness s1. The change of each spacer thickness ∆hS = 0.08 mm (in diameter ∆hS = 0.16 mm) leads to the difference in the squares height of about ∆h1 = 0.04 mm and a difference in the wall thickness of about ∆s1 = 0.07 mm. However, the increase in axial residual stresses occurred with the higher spacer thickness hS and thus with the higher closing time tS. These results are validated by the simulation in chapter 3.2, Fig. 8b. The increase in the axial residual stresses can also be observed in the measurements of the depth profiles, see Fig. 6b (simulation compare Fig. 9). There, a significant drop of the axial residual stresses can be seen along the first 0.03 mm under the surface for both settings, and then, they stabilized to a value of 300 MPa at 0.3 mm under the surface. This indicates that the difference due to the different spacer height only concerned the material state in the first few microns.

Fig. 6
figure 6

Axial residual stresses for both experiments: a at the surface, b depth profile

Full size image

The contact time tK between the workpiece and the dies is presented in Fig. 7 as an upper envelope of the measured time at every stroke. The contact time tK_sim obtained by the simulation is shown by horizontal lines. It can be seen that the experimental measurement is in agreement with the simulated contact time. The values of the contact time are higher in the process with the higher spacer thickness hS2 = 5.16 mm. In the simulation, the difference in spacer thickness was numerically coded by the die path and can be differed by the closing time tS. Contact time tK1_sim by low closing time (tS1 = 3.0 ms) corresponds to the experimental contact time at hS1 = 5.08 mm. For the simulation with high closing time at tS2= 4.4 ms, tK2_sim is higher as the measured contact time at hS2 = 5.16 mm. An increase in the spacer thickness by only 1.5% resulted in an increase in contact time by 16% und closing time by 46%.

Fig. 7
figure 7

Contact time of experiment and simulation: a setting 1 and simulation No. 1, b setting 2 and simulation No. 2

Full size image

3.2 Simulation

Further analysis of the simulation results reflected the comparison of the axial residual stresses distribution after 140th strokes for two die motions with different contact and closing time values (Nos. 1 and 2), see Fig. 8. Similar to the experimental results, a higher closing time led to higher axial residual stresses at the workpiece surface (area between points A and B). Figure 8b shows the axial residual stresses of both simulations at the surface of the workpiece. The development of axial residual stresses at the tip (T) and end (E) of the workpiece is very similar. In contrast, the residual stresses differ significantly in the entrance of the dies and the entrance of the calibration zone.

Fig. 8
figure 8

Axial residual stresses for simulation No. 1 and simulation No. 2: a within the material, b on the surface

Full size image

In the middle of the steady-state area between points A and B, the depth distribution in point C was also analyzed considering the axial residual stresses, see Fig. 9. The course goes from positive values on the surface to negative ones on the inner side of the tube. Moreover, the values at the first 0.5 mm under the surface of 300 MPa corresponded to the axial residual stresses measured in depth after the experiments. However, in a depth from 0.3 to 0.5 mm the experimentally measured residual stresses were remarkably higher. This discrepancy can be explained by surface effects, such as scratching and peeling. The contact between the workpiece and dies was simplified in the simulation, and thus, simulated residual stresses have smoother distribution toward the surface.

Fig. 9
figure 9

Simulated axial residual stresses depth profiles for different closing time values

Full size image

The difference between the distribution of residual stresses at low and high closing time values is more pronounced on the inner side of the tube. Moreover, in this region a longer closing time led to higher compressive stresses.

The development of axial residual stresses along the workpiece with increasing number of strokes is visualized in Fig. 10a for the whole process. For this simulation, the short closing time tS = 3.0 ms was chosen. At the displayed stroke 5 and stroke 17, the workpiece is still filled only in the reduction zone and the change of the axial residual stresses is observed in the region before the workpiece was reduced. Further simulation does not show any changes in residual stresses; thus, axial residual stresses were completely removed in the reduction zone, see stroke 45. However, behind the transition zone, tensile residual stresses were built at the surface of the tube and compressive residual stresses formed at the inner surface. This distribution remains in development of residual stresses since stroke 45. The values of the residual stresses in positive and negative areas are more pronounced after the change from the reducing part to the already calibrated part of the workpiece (see stroke 50) and reach there the largest (400 MPa) and the smallest (− 400 MPa) values. In further progress, the residual stresses are slightly reduced to 300 MPa at the surface and to − 300 MPa at the inner surface of the workpiece in the steady-state area. Such distribution stays till the end of the process at stroke 140. Hence, the transition zone from the reduction to the calibration of the workpiece had a very strong influence on the residual stress distribution. Moreover, a reduction of residual stresses within the calibration zone indicates that in addition to the geometry in the transition area, the length of the calibration zone is also decisive.

Fig. 10
figure 10

Development of axial residual stresses: a at workpiece over 140 strokes for simulation No. 1 with reference die geometry, b with increased die angle of α = 15°, c with reduced calibration zone of the die

Full size image

Thus, the possibilities to influence residual stresses are shown in Fig. 10a and Fig. 10b. By modifications of the geometry of the forming die to α = 15°, a change of the residual stresses can be observed, compared with the reference die geometry. The higher die angle α led to an increased degree of forming per stroke and thus an increase in the forming force at the dies (rigid body) in the simulation. This introduced more stress into the process. Moreover, the formation of residual stresses in the calibration zone dominates, especially after the change from the reduced part to the already calibrated part of the workpiece, where the values change from 445 MPa at the outer and − 482 MPa at the inner surface of the workpiece. Further distribution of the axial residual stresses at stroke 140 reflects more explicit positive and negative values of the residual stresses in the steady-state area than in the conventional process.

Another modification of the forming die such as the reduction of the calibration zone from lc = 20 mm to 8 mm led to very similar development of the residual stresses as in the reference process with α = 10° and lc = 20 mm. However, at stroke 140 very pronounced tensile and compression stresses after the reduced zone of the workpiece as well as a reduction of the residual stresses in the depth of the tube wall are observed, see Fig. 10c. Forming with a shorter calibration zone of the die led to the significant decrease in the tensile residual stresses as well as an increase in the compressive axial residual stresses compared to the reference die geometry or to the increase in the die angle to α = 15°.

Quantitative comparison of the residual stresses distribution in the depth for different simulated process setups was made in the middle of the steady-state area (position C), compare Fig. 10. The trends in the depth distributions differ from each other depending on the die geometry, see Fig. 11a. The difference to the depth profile of the workpiece swaged with reference dies (depth profile α = 0°, lc = 20 mm) is shown in Fig. 11b. At the outer surface, all values of residual stresses are almost identical. Both variations of the die geometry just led to a small drop. The workpiece produced by the die with the shorter calibration zone of lc = 8 mm shows an axial residual stresses decrease in the first millimeter depth of the workpiece (maximum difference − 65 MPa). Next, the residual stresses change from a negative to a positive difference. For the last millimeter, the residual stresses exhibit just slightly higher values than the workpiece swaged with the reference die geometry. For the simulation with the higher die angle, the difference is the other way around. First, the residual stresses are higher (maximum difference 80 MPa) and in the middle of the wall thickness, the residual stress values started to become lower. At the inner surface of the wall, the residual stresses remain low.

Fig. 11
figure 11

Simulated trends in the depth profile a for different simulation settings b compared to the reference setting (No. 1)

Full size image

Thus, for the die geometry it can be concluded that with the shorter calibration zone lower tensile residual stresses can be achieved near the outer surface and the main influence is restricted in the outer part of the wall thickness. On the other hand, with the higher die angle, changes are present over the complete wall thickness. Therefore, the residual stress is higher at the outer half and lower at the inner half of the wall thickness.

4 Conclusion

In this study, the development of the residual stresses by infeed rotary swaging of E355 steel tubes without mandrel was analyzed. The experimental results were compared with the FEM process simulation. The following conclusions could be drawn:

  • Higher spacer thickness hS2 led to higher tensile residual stresses at the outer surface of the workpiece in the axial direction although the degree of forming was not changed. In the depth up to half millimeter, the residual stresses remained almost identical at values around + 300 MPa for both spacer heights hS.

  • The contact time could be controlled by the spacer height hS, which was confirmed by experiment and simulation.

  • Both FEM and measurement results showed homogeneous development of tensile residual stresses in the axial direction along the outer surface of tubes, which decreases in the material depth to compressive residual stresses toward the inner surface of the wall.

  • Before entering the dies, significant axial residual stresses were generated in the tube. They were reduced almost to zero in the subsequently passed reduction zone. In the calibration zone, residual stresses were generated again to their final values in the steady-state zone.

  • The depth distributions revealed a dependence of the process modifications on the residual stresses. An increase in the die angle caused an increase in the tensile residual stresses with a simultaneous decrease in the compressive residual stresses compared to the reference process parameters. However, the tensile residual stresses could be lowered by a shorter calibration zone with almost unchanged compressive stresses.

  • The results support the goal of controlling the residual stresses profiles in parts by adjusting the settings of rotary swaging process. On the other hand, possible settings are restricted by demands of geometric tolerances and surface quality. Therefore, new optimization strategies must be found in future work to produce efficient combinations of external and internal product properties.