Abstract
The geometrical nonlinear effects caused by large displacements and rotations over the cross section of composite thin-walled structures are investigated in this work. The geometrical nonlinear equations are solved within the finite element method framework, adopting the Newton–Raphson scheme and an arc-length method. Inherently, to investigate cross-sectional nonlinear kinematics, low- to higher-order theories are employed by using the Carrera unified formulation, which provides a tool to generate refined theories of structures in a systematic manner. In particular, beams and shell-like laminated composite structures are analyzed using a layerwise approach, according to which each layer has its own independent kinematics. Different stacking sequences are analyzed, to highlight the influence of the cross-ply angle on the static responses. The results show that the geometrical nonlinear effects play a crucial role, mainly when higher-order theories are utilized.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Composite materials have encountered great success during recent decades. Their usage on sophisticated structural components has drastically grown in many engineering fields, such as automotive and aerospace, among the others. This aspect is mainly due to their outstanding structural performances, in terms of stiffness and strength properties, compared with traditional metal alloys. The adoption of composite laminated structures in engineering applications continues to grow, as, for example, shown by Zhang et al. [1] for the aerospace field. However, challenging issues in numerical modeling arise due to their heterogeneous mechanical properties.
A large number of one-dimensional (1D) models for slender structures have been developed in history. Classical theories such as the Euler–Bernoulli beam [2] are widely applied in numerical simulations, although it lacks the ability to accurately predict the transverse shear over the cross sections of beams, for which the shear effects play a crucial role in their mechanical behavior. To overcome this problem, many other models have been developed to carry out reliable results, especially in the case of composite structures. A comprehensive review of the modeling of laminated materials for 1D structures can be found in Kapania and Raciti [3, 4]. Based on the Timoshenko beam theory [5], which considers a constant distribution of the shear stress along the cross section, the first-order shear deformation theory (FSDT) has been developed. This model has been adopted by engineers for their study on the analysis of laminated structures. For instance, Kapania and Raciti [6] worked in the framework of the nonlinear finite element method (FEM), which is the main focus of the proposed research. They developed a simple 1D model for the nonlinear analysis of symmetrically and asymmetrically laminated composite beams, including shear deformation, bending–stretching coupling, and twisting. Gupta et al. [7] presented a formulation for the post-buckling behavior of composite beams with axially immovable ends. Lanc et al. [8] discussed a beam finite element (FE) model for the post-buckling analysis of composite laminated structures in the framework of an updated Lagrangian incremental formulation. Even though the FSDT ensures reliable accuracy for a wide range of problems, it has its own limitations. In fact, when higher-order phenomena arise within the structure, an accurate evaluation of the stress distribution may be necessary, so that theories based on classical approach could lack the ability to perform an accurate stress analysis. For this reason, refined kinematics were suggested by researchers. Stephen and Levinson [9] developed a higher-order theory starting from the Timoshenko beam equation and taking into account the shear curvature, through the introduction of new coefficients.
The need for the adoption of refined mathematical models arises when dealing with large displacements and rotations, in order to be able to catch higher-order phenomena. For this reason, refined kinematics were suggested during the last decades. In the following some major contributions in the geometrical nonlinear analysis of beams are reviewed for completeness sake. Vo and Lee [10] analyzed the geometrical nonlinear behavior of thin-walled composite beams, considering various stacking sequences and loading conditions. The governing equations were derived with a Newton–Raphson linearization and von Kármán approximations. Both updated and total Lagrangian approach were adopted by Bathe and Bolourchi [11] to evaluate the large displacement field of three-dimensional beam elements. Chan and Kitipornchai [12] conducted an investigation about the geometrical nonlinear analysis asymmetric thin-walled beam columns, with an updated Lagrangian formulation and the arc-length method. Emam [13] evaluated the post-buckling behavior of composite beams comparing different approaches, from classical to higher-order beam models accounting for shear deformation theories. Obst and Kapania [14] developed a 1D higher-order beam model with a parabolic shear distribution. Mororó et al. [15] developed a three-dimensional frame FE for geometrical nonlinear analysis of thin-walled laminated composite beams is presented. Simo and Vu-Quoc [16, 17] developed spatial beam FEs, based on strain measures derived from the principle of virtual work. Experimental study were conducted about the nonlinear response of composite structures, for instance, for static [18, 19], dynamics [20] and stress analysis [21] of polymer composite panels. Cross-sectional deformation of thin-walled composite structure found a great interest in the literature. For instance, Cesnik and Hodges [22] developed the VABS approach for the modeling of cross section of laminated rotor blades and Pollay and Yu [23] used the same approach for the matrix cracking modeling. Moreover, Garcea et al. [24] studied the post-buckling behavior of thin-walled structure through a Koiter semi-analytic approach, Gabriele et al. [25] developed a 1D beam model able to account for cross-sectional in-plane deformation, and the same was done also by Gonçlaves et al. [26], including finite rotations.
This paper intends to investigate the need for higher-order (nonlinear) kinematics in the case of geometrical nonlinear problems. As a matter of fact, many papers in the literature combine classical structural theories (mainly with linear kinematics) with nonlinear geometrical relations (Green–Lagrange or von Kármán). This may shrink the consistency of the formulation and bring to inaccurate (inappropriate) results. Thus, the relation between a higher-order model and the adoption of geometrical nonlinear relations is investigated with practical examples. In other words, the problem we address in this work is if the nonlinear kinematic equations are strictly mandatory even if an higher-order model is adopted for the structural analysis and which level of accuracy is reached, considering various cross section shapes, from compact to thin-walled ones. In the case of structures made by isotropic material, the answers of the aforementioned questions can be found in Carrera et al. [27]. According to the work, even if the beam model adopted is achieved using a higher-order theory, the geometrical nonlinear relations must be considered to evaluate the correct displacement field. Clearly, in order to make such analyses, the development of beam models considering low- from higher-order theories is needed to investigate the influence of the order of the mathematical model on the geometrical nonlinear behavior of the structure. An efficient method to perform such analyses is represented by the Carrera Unified Formulation (CUF) [28]. CUF is a hierarchical formulation which allows introducing, as an input of the analysis, any theory order, so any beam model can be developed for a given problem. Because composite structures are investigated in this paper, particular emphasis is given to layerwise approaches. It is defined as a modeling technique in which the different layers of a composite material are individually and independently modeled by means of a unique formulation. This methodology was devised using CUF in [29] and then further extended to a vast number of application, for instance for progressive damage analysis [30], meshless analysis [31], dynamic analysis [32, 33] and stress evaluation [34], among the others.
This paper is organized as follows: (i) first, the formulation of the adopted refined beam theory is presented in Sect. 2; (ii) subsequently, Sect. 3 introduces the geometrical relations and the constitutive expressions for composite materials; (iii) Sect. 4 describes the derivation of the nonlinear governing relations and the FNs of secant and tangent matrices for the solution of the geometrical nonlinear problem; (iv) then, different loading and structural cases are considered as numerical results in Sect. 5; (v) finally, the main conclusions are given.
2 Unified formulation of composite beams
2.1 Kinematics and finite element approximation
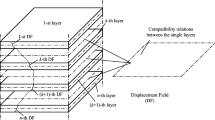
Consider a generic one-dimensional (1D) structure, as depicted in Fig. 1. A Cartesian coordinate system is adopted, oriented so that x and z are the coordinate of the cross section \(\Omega \) and y is orthogonal and lays along the beam axis. In this work, the three-dimensional (3D) displacement field \(\varvec{\mathbf {u}}(x,y,z) = \left\{ u_{x} \; u_{y} \; u_{z}\right\} ^{T}\) is expressed in the framework of the Carrera Unified Formulation (CUF) and, in the case of a 1D structure, it is:
where \(F_{s}\) are the expansion functions of order M of the cross section with coordinate x and z and \(\varvec{\mathbf {u}}_{s}\) are the generalized displacement vector. The choice of \(F_{s}\) and M is arbitrary and it is according to the theory adopted to model the structure. Many options are available for the expansion functions, i.e. Taylor polynomials [35], Chebyshev polynomials [36], Lagrange expansion [37] and Legendre polynomials [38], among the others. In this work, Lagrange polynomials are adopted to discretize the displacement field over the cross section. This choice allows to adopt a layerwise approach to analyze the composite structure. A comprehensive review about layerwise theories developed was made by Carrera [29]. The layerwise theory treats each layer individually and both displacement and transverse shear stress continuity may be satisfied between each layer; therefore, it yields results compatible to 3D elasticity solutions. According to the layerwise approach, each layer has its own kinematic described by a own Lagrange polynomial, as shown in Fig. 1. That figure shows also the Lagrange polynomials adopted in this work, which are, with increasing higher-order capabilities, a linear (L4), quadratic (L9) and cubic (L16) polynomial.
Multiple Lagrange polynomials can be assembled above the cross section imposing the displacement continuity at the interface nodes, so any type of cross section, from compact to thin-walled shapes, can be analyzed.
As far as the displacements along the beam axis are concerned, the finite element method (FEM) is adopted to approximate the vector \(\varvec{\mathbf {u}}_{s}(y)\), as follows:
where \(N_{j}\) and j represent the shape function and the order of the shape function, respectively, and \(\varvec{\mathbf {q}}_{s j}\) is the FE nodal parameters vector \(\left\{ \begin{array}{ccc} q_{x_{s j}}&q_{y_{s j}}&q_{z_{s j}} \end{array}\right\} ^{T}\). Interested readers can refer to Bathe [39] and to Carrera et al. [40] for the complete form of the shape functions \(N_{j}\), not reported here for the sake of brevity. In this work, classical 1D FEs with four nodes (B4) are adopted, i.e. a cubic approximation along the y axis is considered. Finally, introducing Eq. (2) into Eq. (1), the explicit form of the 3D displacement field can be obtained:
3 Geometrical and constitutive relations
To introduce the geometrical and constitutive relations, consider the beam structure shown in Fig. 1. The strain \(\varvec{\mathbf {\epsilon }}\) and stress \(\varvec{\mathbf {\sigma }}\) components are written in vectorial form, and the transposed vectors are introduced in the following:
As far as the geometrical relations are concerned, the full Green–Lagrange strains are taken into account. The relation between the strain \(\varvec{\mathbf {\epsilon }}\) components and the displacement vector \(\varvec{\mathbf {u}}(x,y,z)\) is
Equation (5) may read:
where \(\varvec{\mathbf {b}}_l\) and \(\varvec{\mathbf {b}}_{nl}\) are the linear and nonlinear differential operators, whose complete form are reported in [41]. Finally, the strain vector \(\varvec{\mathbf {\epsilon }}\) in Eq. (6) can be written in terms of the generalized nodal unknowns \(\varvec{\mathbf {q}}_{s j}\) by employing Eq. (3).
where \(\varvec{\mathbf {B}}_l^{sj}\) and \(\varvec{\mathbf {B}}_{nl}^{sj}\) represent the algebraic form of the differential operators \(\varvec{\mathbf {b}}_l\) and \(\varvec{\mathbf {b}}_{nl}\). Complete form of the algebraic matrices is not reported here for the sake of brevity, but can be found in [41]. ’
As far as the constitutive relations are considered, we assume linear elastic material in this work; thus, the Hooke law can be employed:
where \(\varvec{\mathbf {C}}\) is the material matrix, whose complete form can be found in [42]. The coefficients of the material matrix depend only on the material properties and the geometrical properties of the fibers. Explicit form of the coefficients can be found in many books, see [43].
4 Nonlinear governing FE equations
Once the strain \(\varvec{\mathbf {\epsilon }}\) and stress \(\varvec{\mathbf {\sigma }}\) tensors are defined, the nonlinear governing equations of an elastic body can be calculated. In this work, they are derived using the principle of virtual work, that is expressed in the following:
where \(\delta L_\mathrm {int}\) is the virtual variation of the strain energy and \(\delta L_\mathrm {ext}\) is the virtual variation of the work of the external loads. Consider each term of Eq. (9) separately. The first term can be written as:
where V is the volume domain of the body. Introducing the geometrical [Eq. (7)] and the constitutive relations [Eq. (8)] into Eq. (10), one can write:
Equation (11), and in particular the argument of the integral, can be written in terms of four fundamental nuclei (FN). \(\varvec{\mathbf {K}}_0^{i j \tau s} = \displaystyle \int _{V}\varvec{\mathbf {B}}_l^{sj} \, \varvec{\mathbf {C}} \, \varvec{\mathbf {B}}_l^{\tau i} \;\mathrm {d}V\) is the linear contribution, \(\varvec{\mathbf {K}}_{lnl}^{i j \tau s} = \displaystyle \int _{V}\varvec{\mathbf {B}}_l^{sj} \, \varvec{\mathbf {C}} \, \varvec{\mathbf {B}}_{nl}^{\tau i} \;\mathrm {d}V\) and \(\varvec{\mathbf {K}}_{nll}^{i j \tau s} = \displaystyle \int _{V}2 \, \varvec{\mathbf {B}}_{nl}^{sj} \, \varvec{\mathbf {C}} \, \varvec{\mathbf {B}}_l^{\tau i} \;\mathrm {d}V\) are the nonlinear contribution of order 1 and \(\varvec{\mathbf {K}}_{nlnl}^{i j \tau s} = \displaystyle \int _{V}2 \, \varvec{\mathbf {B}}_{nl}^{sj} \, \varvec{\mathbf {C}} \, \varvec{\mathbf {B}}_{nl}^{\tau i} \;\mathrm {d}V\) is the nonlinear contribution of order 2. The result of the sum of these 4 contributions is the secant stiffness matrix \(\varvec{\mathbf {K}}_S^{i j \tau s}\). Thus, we can write Eq. (11) as:
Next, consider the second term of Eq. (9), \(\delta L_\mathrm {ext}\). Omitting some mathematical steps that can be found in Carrera et al. [28], one can write:
where \(\varvec{\mathbf {P}}\) is a generic concentrated load \(\varvec{\mathbf {P}}(x,y,z) =\left\{ P_{{x}} \; P_{{y}} \; P_{{z}}\right\} ^{\mathrm {T}}\). Introducing the 3D displacement field, expressed in Eq. (3), into Eq. (13), it can be written as:
where it is assumed that \(\varvec{\mathbf {P}}\) is applied at \([x_{p}, \; y_{p}, \; z_{p}]\) and \(\varvec{\mathbf {p}}_{\tau i}\) is the FNs of the vector of the nodal loadings. Finally, introducing Eqs. (12) and (14) into Eq. (9), it reads as:
and then,
Equation (16) can be arbitrarily expanded to reach any desired theory, from low- to higher-order ones, by choosing the values for \(\tau ,s=1,2,\ldots ,M\) and \(i,j=1,2,\ldots ,p+1\), to give:
where \(\varvec{\mathbf {K}}_{S}\), \(\varvec{\mathbf {q}}\), and \(\varvec{\mathbf {p}}\) are the global, assembled finite element arrays of the final composite structure.
Equation (17) represents the starting equation for the resolution of the geometrical nonlinear problem. The authors refer to the work by Pagani and Carrera [41] for an exhaustive description of the applied method for the resolution of the nonlinear equations. The geometrical nonlinear problem is solved using the Newton–Raphson method, according to which Eq. (17) can be linearized using Taylor’s expansion around a known solution. What comes out from the linearization of the internal work is the so-called tangent stiffness matrix \(\varvec{\mathbf {K}}_{T}\).
where \(\varvec{\mathbf {K}}_{T}^{i j \tau s}\) represent the FN of the tangent stiffness matrix. Note that \(\varvec{\mathbf {K}}_{T}^{i j \tau s} = \varvec{\mathbf {K}}_{0}^{i j \tau s} + \varvec{\mathbf {K}}_{T_1}^{i j \tau s} + \) \(\varvec{\mathbf {K}}_{\sigma }^{i j \tau s}\). \(\varvec{\mathbf {K}}_{0}^{i j \tau s}\) is the linear contribution, \(\varvec{\mathbf {K}}_{T_1}^{i j \tau s}\) equals to \(2 \varvec{\mathbf {K}}_{lnl}^{i j \tau s}+\varvec{\mathbf {K}}_{nll}^{i j \tau s}+2 \varvec{\mathbf {K}}_{nlnl}^{i j \tau s}\), and \(\varvec{\mathbf {K}}_{\sigma }^{i j \tau s}\) represents the so-called geometrical stiffness [44]. It takes into account both linear and nonlinear pre-stress states. The resulting system of equations needs to be constrained. In this work, an opportune arc-length path-following constraint is adopted. More detail about the arc-length method adopted can be found in the works by Carrera [45] and Crisfield [46, 47].
5 Numerical results
To show the relationship between the order of the theory and the nonlinear displacement–strain equations, various problems are addressed hereafter. After an assessment of the proposed nonlinear model through comparison with literature results and ABAQUS, compact, thin-walled and box cross section composite beams are considered, with [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] and [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)] stacking sequences. Large displacements and rotations are enforced by imposing loads on the cross section of the beams, and linear and nonlinear analyses are carried out using from low- to higher-order theories.
5.1 Assessment
A preliminary assessment analysis was conducted in order to validate the proposed geometrical nonlinear model. We consider the same analysis case presented by Emam [13] about the post-buckling of a simply supported [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] cross-ply beam, with \(E_{1}\)/\(E_{2}\) = 10, \(G_{12}\) = 0.6\(E_{2}\), \(G_{23}\) = 0.6\(E_{2}\), \(G_{13}\) = \(G_{12}\) \(\nu _{12}\) = 0.25 and \(\nu _{13}\) = \(\nu _{12}\). The ratio between the length of the beam and the side of the square cross section equals 50 and the layers have the same thickness. The same analysis was performed using 1D, 2D and 3D elements with ABAQUS. The vertical displacement component vs the applied load is given in Fig. 2, showing a good match between the proposed model and the 3D elements of ABAQUS.
5.2 Compact cross section composite beam
In the second analysis case, a square compact cross section of a cantilever beam was considered. The beam is made of three layers of an orthotropic material with Young moduli \(E_{1}=155\) GPa, \(E_{2}=E_{3}=15.5\) GPa, Poisson’s ratios \(\nu =0.25\) and shear moduli \(G_{12}=G_{13}\)=9.3 GPa, \(G_{12}=G_{23}=7.75\) GPa. Figure 3 shows the loading condition of the proposed analysis case, along with the cross section of the beam. Each layer has the same thickness t/3, where t is the side of the square cross section, and the length-to-side ratio is 10.
For this and all the subsequent discussions, 10 cubic elements were used for the beam axis discretization. Figure 4 shows the discretization employed per layer, namely L4, L9 and L16 Lagrange polynomials. Two stacking sequences were analyzed: [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] and [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)].
The linear and nonlinear equilibrium curves of the [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] configuration are given in Fig. 5a, where the displacement in the z-direction was evaluated for each kinematic approximation. Then, the percentage difference between linear and nonlinear solutions is reported in Fig. 5b. The results show that the greater is the order of the employed theory, the higher is the difference between linear and geometrical nonlinear analyses, although the L9 and L16 curves are very close to each other. Despite the results shown in Carrera et al. [27] for a compact case of an isotropic beam, Fig. 5 demonstrates that the values of the percentage differences are relevant when composite materials are considered; hence, linear analyses could not be considered accurate for the given problem. In fact, even for the lowest order theory, the difference between linear and nonlinear solution reaches a not negligible value, near 5%. The same conclusions can be drawn from the [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)] stacking sequence case, whose results are reported in Fig. 6. The percentage difference between linear and nonlinear solutions reaches higher values for the L16 approximation, until near 20% for the last considered external load.
a Linear and nonlinear equilibrium curves for the z-component of the displacement of the point “A” for the compact square cross section beam. b Percentage difference between linear and geometrical nonlinear analyses. Percentage difference \(u^{*}= \dfrac{u_{nl}-u_{l}}{u_{nl}} \times 100\). \(t^{*}= \dfrac{t}{3}\)
a Linear and nonlinear equilibrium curves for the z-component of the displacement of the point “A” for the compact square cross section beam. b Percentage difference between linear and geometrical nonlinear analyses. Percentage difference \(u^{*}= \dfrac{u_{nl}-u_{l}}{u_{nl}} \times 100\). \(t^{*}= \dfrac{t}{3}\)
5.3 Thin-walled composite beam
The next analysis dealt with a thin-walled channel-section beam. The geometry is shown in Fig. 7, and w\(=\)h, h/t \(=\) 10 and length-to-side ratio is 20. The material adopted is orthotropic, with \(E_{1}=155\) GPa, \(E_{2}=E_{3}=15.5\) GPa, \(\nu =0.25\), \(G_{12}=G_{13}=9.3\) GPa and \(G_{12}=G_{23}=7.75\) GPa. Two different stacking sequences were considered, [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] and [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)].
Three different higher-order models were used to define the channel section and to approximate the displacement field. In detail, as shown in Fig. 8, 18L4, 18L9 and 18L16 Lagrange polynomials were implemented. Increasing forces were applied as shown in Fig. 7, and in this scenario, static analysis using linear and nonlinear strain–displacement relations was performed, and the displacement of the points “A” and “B” along the x-axis and of the point “C” along the z-axis was calculated. Then, the difference between linear and nonlinear solutions was calculated.
In Fig. 9, both linear and nonlinear solutions are displayed, using the L4, L9 and L16 Lagrange polynomials.
The percentage difference for the [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] stacking sequence is shown too, along with some of the deformed configurations. It can be noticed that increasing the external loading, the percentage difference increases as well. The greater the order of the beam theory is, the higher the differences between linear and geometrical nonlinear analyses are. This behavior can be assessed in Table 1, where some values of both linear and nonlinear solution are reported. The highest values of the difference percentages are reported in bold in the table, going from 3.15 for a first-order beam model to 30.12 for a quadratic beam model and to 33.08 for a cubic theory. It is clear that the adoption of geometrical nonlinear relations is required for thin-walled problems. Figure 10 shows the results of the same analyses for the point “C.” A hardening behavior of the nonlinear analysis can be noticed until a certain load, and then a softening trend appears. For example, for the cubic interpolation mathematical model, the percentage difference changes the sign after a load \(P=16\) kN, as clearly reported in Table 2. The same trend is evident for the L9 solution, but in this case, the load of the changing trend is higher, near 20 kN. Finally, the L4 solution leads to a hardening behavior.
As far as the [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)] cross-ply lamination is concerned, Fig. 11 shows the percentage difference between linear and nonlinear solutions, along with both static solutions for point “A.” As noticed in the previous case, it can be observed that the percentage difference increases with the external loading. The values of the percentage difference are greater than the ones of the [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] stacking sequence case. Table 3 reports values of the displacement for points point “A” and in bold are quoted the highest values. For the point “A,” they go from 1.99 for a first-order beam model to 25.30 for a quadratic beam model and to 29.63 for a cubic theory. Its results evident that for the thin-walled problems, the adoption of geometrical nonlinear relations is needed. Finally, the z-displacement of the point “C” is analyzed as well. The curves and values are reported in Fig. 12 and Table 4, respectively, and they show a similar trend of those of the “C” point for the [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] stacking sequence case.
5.4 Pinched box beam
As a final example, a box pinched beam was analyzed. The material properties are the same as in the previous example, with \(E_{1}=155\) GPa, \(E_{2}= E_{3}=15.5\) GPa, \(\nu =0.25\), \(G_{12}=G_{13}=9.3\) GPa and \(G_{12}=G_{23}=7.75\) GPa. [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] and a [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)] stacking sequences were analyzed. Geometrical data are similar to the previous analysis case, and they are shown in Fig. 13, with \(w=h\), \(h/t = 10\) and length-to-side ratio 20. Three different higher-order beam models were utilized to evaluate the displacement field over the cross section, which pattern is described in Fig. 14.
Both static linear and nonlinear analyses were performed and the difference between the two solutions has been evaluated for the displacement along x-axis of the point “A” and the displacement along z-axis of the point “B” (points “A” and “B” are reported in Fig. 13). In Fig. 15, the z component of the displacement of point “A” for the cross-ply lamination [\(0^\circ \)/\(90^\circ \)/\(0^\circ \)] is considered. In Fig. 15a both static linear and nonlinear solutions are reported, whereas in Fig. 15b the difference between the two solutions is shown. The L9 and L16 polynomials lead to higher differences than L4 polynomial, and L16 leads to higher values, as pointed out in the previous analysis case for the thin-walled cross section beam. The same trend is highlighted in (Fig. 16) that considers the point “B” for the same stacking sequence case. Moreover, for all the L9 and L16 polynomials, the percentage difference is null for some positions on the cross sections. The reason is that, before this value, the displacement from the nonlinear solution is higher than the linear one, while it becomes less increasing the external load. Tables 5 and 6 report values for displacement and percentage difference for the points “A” and “B,” respectively.
Finally, a [\(0^\circ \)/\(45^\circ \)/\(0^\circ \)] cross-ply lamination case was considered. The displacement along z-axis of the point “A” and the displacement along x-axis of the point “B” has been considered, and the results are shown, respectively, in Figs. 17 and 18. The main difference from the previous cases arises looking at the point “B.” In fact, after the external load P reaches the value of 100 kN, the L9 polynomial leads to higher differences between linear and nonlinear solution than the L16 polynomial (while the L4 polynomial brings lower values as already noticed for the previous cases). Tables 7 and 8 report correspondent values.
6 Conclusions
This paper investigates the importance of considering geometrical nonlinearities in the case of high-order nonlinear theories of structures. Thanks to the Carrera Unified Formulation (CUF), from low- to higher-order theories have been addressed in the domain of linear and nonlinear elasticity. Compact, thin-walled and box cross sections have been analyzed. In particular, it has been shown that the geometrical nonlinear kinematic relations can be very significant in the selected analysis cases. It has been proved that in many problems the adoption of the geometrical nonlinear relations may be mandatory to correctly capture the deformed state of the given structure, especially when refined models are employed.
References
Zhang, X., Chen, Y., Hu, J.: Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 97, 22–34 (2018)
Euler, L.: Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti, vol. 1. Springer, Berlin (1952)
Kapania, R.K., Raciti, S.: Recent advances in analysis of laminated beams and plates, Part I: shear effects and buckling. AIAA J. 27(7), 923–935 (1989)
Kapania, R.K., Raciti, S.: Recent advances in analysis of laminated beams and plates, Part II: Vibrations and wave propagation. AIAA J. 27(7), 935–946 (1989)
Timoshenko, S.P.: On the transverse vibrations of bars of uniform cross section. Philos. Mag. 43, 125–131 (1922)
Kapania, R.K., Raciti, S.: Nonlinear vibrations of unsymmetrically laminated beams. AIAA J. 27(2), 201–210 (1989)
Gupta, R.K., Gunda, J.B., Janardhan, G.R., Rao, G.V.: Post-buckling analysis of composite beams: simple and accurate closed-form expressions. Compos. Struct. 92(8), 1947–1956 (2010)
Lanc, D., Turkalj, G., Pesic, I.: Global buckling analysis model for thin-walled composite laminated beam type structures. Compos. Struct. 111, 371–380 (2014)
Stephen, N.G., Levinson, M.: A second order beam theory. J. Sound Vib. 67(3), 293–305 (1979)
Vo, T.P., Lee, J.: Geometrical nonlinear analysis of thin-walled composite beams using finite element method based on first order shear deformation theory. Arch. Appl. Mech. 81(4), 419–435 (2011)
Bathe, K.-J., Bolourchi, S.: Large displacement analysis of three-dimensional beam structures. Int. J. Num. Methods Eng. 14(7), 961–986 (1979)
Chan, S.L., Kitipornchai, S.: Geometric nonlinear analysis of asymmetric thin-walled beam-columns. Eng. Struct. 9(4), 243–254 (1987)
Emam, S.A.: Analysis of shear-deformable composite beams in postbuckling. Compos. Struct. 94(1), 24–30 (2011)
Obst, A.W., Kapania, R.K.: Nonlinear static and transient finite element analysis of laminated beams. Compos. Eng. 2(5–7), 375–389 (1992)
Mororó, L.A.T., Melo, A.M.C., Parente Junior, E.: Geometrically nonlinear analysis of thin-walled laminated composite beams. Latin Am. J. Solids Struct. 12(11), 2094–2117 (2015)
Simo, J.C., Vu-Quoc, L.: A three-dimensional finite-strain rod model. Part ii: Computational aspects. Comput. Methods Appl. Mech. Eng. 58(1), 79–116 (1986)
Simo, J.C., Vu-Quoc, L.: A geometrically-exact rod model incorporating shear and torsion-warping deformation. Int. J. Solids Struct. 27(3), 371–393 (1991)
Pandey, H.K., Agrawal, H., Panda, S.K., Hirwani, C.K., Katariya, P.V., Dewangan, H.C.: Experimental and numerical bending deflection of cenosphere filled hybrid (glass/cenosphere/epoxy) composite. Struct. Eng. Mech. 73(6), 715–724 (2020)
Mehar, K., Panda, S.K., Mahapatra, T.R.: Large deformation bending responses of nanotube-reinforced polymer composite panel structure: numerical and experimental analyses. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 233(5), 1695–1704 (2019)
Hirwani, C.K., Panda, S.K., Mahapatra, T.R., Mahapatra, S.S.: Numerical study and experimental validation of dynamic characteristics of delaminated composite flat and curved shallow shell structure. J. Aerosp. Eng. 30(5), 04017045 (2017)
Hirwani, C.K., Panda, S.K.: Numerical and experimental validation of nonlinear deflection and stress responses of pre-damaged glass-fibre reinforced composite structure. Ocean Eng. 159, 237–252 (2018)
Cesnik, C.E.S., Hodges, D.H.: Vabs: a new concept for composite rotor blade cross-sectional modeling. J. Am. Helicop. Soc. 42(1), 27–38 (1997)
Pollayi, Hemaraju, Wenbin, Yu.: Modeling matrix cracking in composite rotor blades within vabs framework. Compos. Struct. 110, 62–76 (2014)
Garcea, G., Leonetti, L., Magisano, D., Gonçalves, R., Camotim, D.: Deformation modes for the post-critical analysis of thin-walled compressed members by a Koiter semi-analytic approach. Int. J. Solids Struct. 110, 367–384 (2017)
Gabriele, S., Rizzi, N., Varano, V.: A 1d nonlinear TWB model accounting for in plane cross-section deformation. Int. J. Solids Struct. 94, 170–178 (2016)
Gonçalves, R., Ritto-Corrêa, M., Camotim, D.: Incorporation of wall finite relative rotations in a geometrically exact thin-walled beam element. Comput. Mech. 48(2), 229–244 (2011)
Carrera, E., Pagani, A., Augello, R.: Evaluation of geometrically nonlinear effects due to large cross-sectional deformations of compact and shell-like structures. Mech. Adv. Mater. Struct. (2018). https://doi.org/10.1080/15376494.2018.1507063
Carrera, E., Giunta, G., Petrolo, M.: Beam structures: classical and advanced theories. Wiley, New York (2011)
Carrera, E.: C\(_{z}^{0}\) requirements-models for the two dimensional analysis of multilayered structures. Compos. Struct. 37(3–4), 373–383 (1997)
Nagaraj, M.H., Reiner, J., Vaziri, R., Carrera, E., Petrolo, M.: Progressive damage analysis of composite structures using higher-order layer-wise elements. Compos Part B Eng,. 190, 107921 (2020). https://doi.org/10.1016/j.compositesb.2020.107921
Yan, Y., Carrera, E., de Miguel, A.G., Pagani, A., Ren, Q.-W.: Meshless analysis of metallic and composite beam structures by advanced hierarchical models with layer-wise capabilities. Compos. Struct. 200, 380–395 (2018)
Yan, Y., Pagani, A., Carrera, E.: Exact solutions for free vibration analysis of laminated, box and sandwich beams by refined layer-wise theory. Compos. Struct. 175, 28–45 (2017)
Carrera, E., Pagani, A., Augello, R.: Effect of large displacements on the linearized vibration of composite beams. Int. J. Non-Linear Mech. 120, 103390 (2020)
Pagani, A., Augello, R., Carrera, E.: Evaluation of in-plane and out-of-plane stresses in composite structures subjected to large displacements/rotations. In ASME International Mechanical Engineering Congress and Exposition, vol. 52002, p. V001T03A035. American Society of Mechanical Engineers, 2018
Carrera, E., Giunta, G.: Refined beam theories based on a unified formulation. Int. J. Appl. Mech. 2(1), 117–143 (2010)
Filippi, M., Pagani, A., Petrolo, M., Colonna, G., Carrera, E.: Static and free vibration analysis of laminated beams by refined theory based on chebyshev polynomials. Compos. Struct. 132, 1248–1259 (2015)
Carrera, E., Petrolo, M.: Refined beam elements with only displacement variables and plate/shell capabilities. Meccanica 47(3), 537–556 (2012)
Carrera, E., de Miguel, A.G., Pagani, A.: Hierarchical theories of structures based on legendre polynomial expansions with finite element applications. Int. J. Mech. Sci. 120, 286–300 (2017)
Bathe, K.J.: Finite element procedure. Prentice Hall, New Jersey (1996)
Carrera, E., Cinefra, M., Petrolo, M., Zappino, E.: Finite element analysis of structures through unified formulation. Wiley, New York (2014)
Pagani, A., Carrera, E.: Unified formulation of geometrically nonlinear refined beam theories. Mech. Adv. Mater. Struct. 25(1), 15–31 (2018)
Carrera, E., Filippi, M.: Variable kinematic one-dimensional finite elements for the analysis of rotors made of composite materials. J. Eng. Gas Turbines Power 136(9), 092501 (2014)
Ochoa, O.O., Reddy, J.N.: Finite element analysis of composite laminates. Springer, Berlin (1992)
Zienkiewicz, O.C., Taylor, R.L.: The finite element method for solid and structural mechanics. Elsevier, Amsterdam (2005)
Carrera, E.: A study on arc-length-type methods and their operation failures illustrated by a simple model. Comput. Struct. 50(2), 217–229 (1994)
Crisfield, M.A.: A fast incremental/iterative solution procedure that handles “snap-through”. Comput. Struct 13, 55–62 (1981)
Crisfield, M.A.: An arc-length method including line searches and accelerations. Int. J. Numer. Methods Eng. 19(9), 1269–1289 (1983)
Funding
Open access funding provided by Politecnico di Torino within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carrera, E., Pagani, A. & Augello, R. On the role of large cross-sectional deformations in the nonlinear analysis of composite thin-walled structures. Arch Appl Mech 91, 1605–1621 (2021). https://doi.org/10.1007/s00419-020-01843-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-020-01843-8