1 Introduction

Mechanical metamaterials are of growing interest due to their extraordinary mechanical properties for engineering applications [13, 16, 30, 51]. Mechanical metamaterials are designed with well-defined microstructures in order to achieve controllable properties. Consequently, it is not only the composition of materials but also the microstructures that govern the behavior of metamaterial [39]. Most of the existing designs of mechanical metamaterials are achieved either by utilizing origami and kirigami deformation mechanisms [17, 52] or by tailoring the topology of the lattice cells and by arranging them periodically at the microscale [64]. For example, so-called pantographic microstructures [25,26,27, 53, 56, 65] are constituted by two parallel arrays of beams connected by small internal cylinders (pivots) and display novel functionalities. Their mechanical properties are reported to be usually size dependent [4]. In other words, remarkable size effects are observed when metamaterials are tested. For example, in the experiments of [4, 45] the samples become stiffer with decreasing sample size. But smaller is not always stiffer. For example, a softening effect is observed in the studies of [59].

In order to capture the size-dependent behaviors completely, a direct finite element computation with a detailed mesh and an appropriate constitutive relation connecting stress and strains is always possible [62] and usually provides good accuracy. However, due to the complexity of the microstructures, it carries too much computational burden even for modern computer technology. The homogenization method [5, 12, 20,21,22, 32, 34, 36, 37, 42, 63] is thus used as an alternative way to model metamaterials as an equivalent effective homogeneous continuum. The homogenization modeling method is also motivated by the desire for an increasing understanding of the micromechanical mechanism behind the peculiar behaviors of metamaterials [28]. Despite the efficiency of the homogenization method when applied in practice, it shows a limitation. Metamaterials were homogenized into a Cauchy continuum in past studies [35]. However, the size-dependent behaviors could not be captured by such method. This is because the classical Cauchy theory lacks an internal length scale of the microstructure. Hence, it is unable to predict the size effects.

Consequently, homogenization in the framework of generalized mechanics such as micropolar theory [41] and strain gradient theory [15, 19, 47] was employed. The problem of getting homogenized constitutive equations for generalized continua is rather difficult, and many debates are active in the literature. Kumar and McDowell [41] derived the effective material parameters based on an energy equivalence assumption by means of micropolar elasticity. Dos Reis and Ganghoffer [28] used the asymptotic method and homogenized metamaterials to micropolar media. An effective couple-stress continuum model was built by Liu and Su [46]. The effective moduli are obtained based on a selected representative volume element (RVE) under certain boundary conditions. Many efforts have been made to develop strain gradient continua. Dell’Isola and colleagues developed second gradient homogenization techniques for the so-called pantographic structures which has been extensively studied, for example, in [3, 9, 11, 23,24,25,26,27, 55]. Boutin et al. [18] obtained high-order continuum model by means of a micro/macro-identification procedure based on the asymptotic homogenization method of discrete media. Misra and Poorsolhjouy [48] identified higher-order elastic constants for grain assemblies based on granular micromechanics. Abdoul-Anziz and Seppecher [2] determined the effective behavior of 1D, 2D and 3D periodic structures through a \(\varGamma \)-convergence theorem. By means of homogenization, Li [43] established a strain gradient constitutive law. In [8, 44], a fast Fourier transform (FFT) and an FEM approach have been used to deliver the effective classical stiffness tensor as well as strain gradient stiffness tensor. In [67], the effective metamaterial parameters are derived based on quadratic boundary conditions. Effective moduli were presented for metamaterials of different symmetries. In [61], based on an assumption of strain energy equivalence at micro- and macroscale of an RVE, a computational solution was provided for determining parameters of metamaterials. It is also shown that the strain gradient stiffness tensor determined in [61] vanishes when the structure is purely homogeneous, and it is insensitive to a repetition of the basic cells. Many authors compare direct FEM computations to equivalent generalized homogeneous continua. For example, in a recent study [66] size effects of lattice structures were examined by comparing direct FEM computations with an equivalent micropolar elastic model. It was found that size effects are not captured in the micropolar model.

The aim of the present paper is to provide quantitative comparative studies for metamaterials constructed by repetitive planar lattice structures between direct FEM computations, which are understood as correct solutions, and equivalent effective strain gradient continua. These simulations will examine size effects directly for metamaterials under different boundary conditions, of different aspect ratios, constructed by different unit cells and by different topologies. A second-order asymptotic analysis (presented in Sect. 2) is used to model the metamaterials by equivalent effective strain gradient continua. In this paper, it is intended to investigate the mechanism of size effects and to answer the following question: Do the metamaterial parameters derived by using the second-order asymptotic analysis allow to capture size effects accurately including both stiffening and softening effects?

2 Second-order asymptotic homogenization method based on strain gradient theory

Consider a two-dimensional periodic metamaterial \(\varOmega \), which is constructed by a finite number of representative volume elements (RVEs) \(\varOmega _P^\text {m}\) at the microscale, namely:

$$\begin{aligned} \cup \varOmega _P^\text {m} = \varOmega \ , \qquad \varOmega _P^\text {m} \cap \varOmega _Q^\text {m} = \emptyset \ , \qquad P,Q = 1,2,3,...M, P \ne Q \ . \end{aligned}$$
(1)

We remark that the RVE at the microscale \(\varOmega _P^\text {m}\) represents the detailed microstructure, such as the fibers and the matrices in a composite material. The same RVE at the macroscale \(\varOmega _P^\text {M}\) is modeled homogeneously. The equivalence of the strain energies for an RVE at the micro- \(\varOmega _P^\text {m}\) and at the macroscale \(\varOmega _P^\text {M}\) is postulated. The definitions of the micro- (“\(\text {m}\)”) and of the macroscale (“\(\text {M}\)”) energy density, \( w^\text {m}\) and \( w^\text {M}\), respectively, read

$$\begin{aligned} \int _{\varOmega _P^\text {m}} { w^\text {m}} \, \mathrm {d} V^\text {m}= & {} \int _{\varOmega _P^\text {M}} { w^\text {M}} \, \mathrm {d} V^\text {M} \ \Longleftrightarrow \nonumber \\ \int _{\varOmega _P^\text {m}} \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm {d} V^\text {m}= & {} \int _{\varOmega _P^\text {M}} \frac{1}{2} \big ( C^\text {M}_{ijkl} u^\text {M}_{i,j} u_{k,l}^\text {M} + D_{ijklmn}^\text {M} u_{i,jk}^\text {M} u_{l,mn}^\text {M} \big ) \, \mathrm {d} V^\text {M} \ , \end{aligned}$$
(2)

where first-order theory is used at the microscale and second-order theory at the macroscale. \(C^\text {m}_{ijkl}\) is defined in every material point of the heterogeneous structure. \(C^\text {M}_{ijkl}\) and \(D^\text {M}_{ijklmn}\) are the homogenized classical stiffness tensor and strain gradient stiffness tensor of the corresponding equivalent continua. The use of a displacement gradient in Eq. (2) will bring simplicity. Indeed, it can be replaced by the linear strain tensor. A discussion of objectivity of the strain energy can be found in [61]. In what follows, two different cases are demonstrated: a heterogeneous case at the microscale with known material properties versus a homogeneous case at the macroscale with sought effective parameters.

2.1 The macroscale energy for an RVE

Consider the macroscale case for an RVE \(\varOmega _P^\text {M}\). As it is customary in spatial averaging, we define the geometric center \(\overset{\text {c}}{\varvec{X}}\) of the RVE. Then, we approximate the macroscale displacement by a Taylor expansion around the value at the geometric center by truncating after quadratic terms (in order to account for the strain gradient effect) and then calculate displacement gradients of this approximation:

$$\begin{aligned}&\displaystyle u_i^\text {M}(\varvec{X}) =u^\text {M} _i\Big |_{\overset{\text {c}}{\varvec{X}}} + \langle {u}_{i,j}^\text {M} \rangle (X_j-\overset{\text {c}}{X}_j) + \frac{1}{2} \langle {u}_{i,jk}^\text {M} \rangle (X_j-\overset{\text {c}}{X}_j) (X_k-\overset{\text {c}}{X}_k) \ , \nonumber \\&\displaystyle u^\text {M} _{i,j}(\varvec{X}) = \langle {u}_{i,j}^\text {M} \rangle + \langle {u}_{i,jk}^\text {M}\rangle (X_k-\overset{\text {c}}{X}_k) \ , \nonumber \\&\displaystyle u^\text {M}_{i,jk}(\varvec{X}) = \langle {u}_{i,jk}^\text {M} \rangle \ , \end{aligned}$$
(3)

where according to [61]

$$\begin{aligned} \langle {u}_{i,j}^\text {M} \rangle&=\frac{1}{V^\text {M}}\displaystyle \int _{\varOmega _P^\text {M}} u^\text {M} _{i,j} \, \mathrm {d} V^\text {M} = u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{\varvec{X}}} \ , \qquad \langle {u}_{i,jk}^\text {M} \rangle =\frac{1}{V^\text {M}}\displaystyle \int _{\varOmega _P^\text {M}} u^\text {M} _{i,jk}\, \mathrm {d} V^\text {M} = u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{\varvec{X}}} \ . \end{aligned}$$
(4)

The macroscale energy of an RVE reads as follows (the detailed derivation can be found in [61]), as the macroscale stiffness tensors are constant in space,

$$\begin{aligned}&\int _{\varOmega _P^\text {M} } \frac{1}{2} \big ( C^\text {M}_{ijlm} u^\text {M}_{i,j} u^\text {M}_{l,m} + D^\text {M}_{ijklmn} u^\text {M}_{i,jk} u^\text {M}_{l,mn} \big ) \, \mathrm {d} V^\text {M} \ , \nonumber \\&\quad = \frac{1}{2}V^\text {M} \Big ( C^\text {M}_{ijlm} \langle {u}_{i,j}^\text {M}\rangle \langle {u}_{l,m}^\text {M}\rangle + ( C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn} ) \langle {u}_{i,jk}^\text {M}\rangle \langle {u}_{l,mn}^\text {M}\rangle \Big ) \ , \end{aligned}$$
(5)
$$\begin{aligned}&\bar{I}_{kn} = \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {M}} (X_k-\overset{\text {c}}{X}_k)(X_n-\overset{\text {c}}{X}_n) \, \mathrm {d} V^\text {M} \ . \end{aligned}$$
(6)

Therefore, the macroscale energy of an RVE is expressed in terms of the gradient of macroscopic deformation. In what follows, it will be presented by using asymptotic homogenization method that the microscale energy can be expressed in terms of the gradient of macroscopic deformation. This will also lead to connections between the parameters.

2.2 The microscale energy for an RVE

Following the asymptotic homogenization method presented in [61], we reformulate the left-hand side of Eq. (2). The asymptotic homogenization method decomposes length scales by making use of global coordinates, \(\varvec{X}\), depicting the global variations, and by using local coordinates, \( \varvec{y}\), presenting the local fluctuation. The local coordinates are introduced as:

$$\begin{aligned} y_j= \frac{1}{\epsilon }( X_j - \overset{\text {c}}{X}_j ) \ , \end{aligned}$$
(7)

where \(\epsilon \) is a homothetic ratio connecting global and local coordinates. Following [61], the displacement field of an RVE, \(\varOmega _P^\text {m}\), at global coordinates, \(\varvec{X}\), is approximated by an asymptotic expansion with regard to \(\epsilon \),

$$\begin{aligned} \varvec{u }^\text {m}(\varvec{X}) = \overset{0}{\varvec{u}}( \varvec{X}, \varvec{y}) + \epsilon \overset{1}{\varvec{u}}(\varvec{X},\varvec{y}) + \epsilon ^2 \overset{2}{\varvec{u}}(\varvec{X}, \varvec{y}) + \dots \ . \end{aligned}$$
(8)

Please note that the governing equation within the RVE must be fulfilled

$$\begin{aligned} \big ( C_{ijkl}^\text {m} u^\text {m}_{k,l} \big )_{,j} + f_{i} = 0 \ , \end{aligned}$$
(9)

where \( f_i\) is body forces. Substituting Eq. (8) to Eq. (9) and gathering terms having the same order in \(\epsilon \) lead to the following equations:

  • in the order of \(\epsilon ^{-2}\)

    $$\begin{aligned} \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{0}{u}_k}{\partial y_l} \Big ) = 0 \ ; \end{aligned}$$
    (10)

  • in the order of \(\epsilon ^{-1}\)

    $$\begin{aligned} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{0}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \overset{0}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big ) = 0 \ ; \end{aligned}$$
    (11)

  • in the order of \(\epsilon ^{0}\)

    $$\begin{aligned} \big ( C_{ijkl}^\text {m} \overset{0}{u}_{k,l} \big )_{,j} + \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{1}{u}_k}{\partial y_l} \Big )_{,j} + \frac{\partial }{\partial y_j} \big ( C_{ijkl}^\text {m} \overset{1}{u}_{k,l} \big ) + \frac{\partial }{\partial y_j} \Big ( C_{ijkl}^\text {m} \frac{\partial \overset{2}{u}_k}{\partial y_l} \Big ) + f_i = 0 \ . \end{aligned}$$
    (12)

Indeed, the solution in the order of \(\epsilon ^{-2}\) can be given as

$$\begin{aligned} \overset{0}{u}_i = \overset{0}{u}_i(\varvec{X}) \ . \end{aligned}$$
(13)

\(\overset{0}{u}_i(\varvec{X})\) depends only on the macroscopic coordinates. It is assumed to be the known macroscopic displacement \(\overset{0}{u}_i(\varvec{X}) =u^\text {M}_i(\varvec{X})\). Likewise, the solutions for the order of \(\epsilon ^{-1}\) and \(\epsilon ^{0}\) can be obtained [61]. Therefore, the microscale displacement field can be rewritten as:

$$\begin{aligned} u^\text {m}_i(\varvec{X},\varvec{y}) = {u}_i^\text {M} (\varvec{X}) + \epsilon \varphi _{abi}(\varvec{y}) {u}_{a,b}^\text {M}(\varvec{X}) + \epsilon ^2 \psi _{abci}(\varvec{y}) {u}_{a,bc}^\text {M}(\varvec{X}) + \dots \ , \end{aligned}$$
(14)

where \(\varphi _{abi}(\varvec{y})\) and \(\psi _{abci}(\varvec{y})\) are assumed to be \(\varvec{y}\)-periodic. They are the solutions of the following two partial differential equations [61]

$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ak} \delta _{bl} \Big ) \bigg ) = 0 \ , \end{aligned}$$
(15)
$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \Big ( \frac{\partial \psi _{abck}}{\partial y_l} + \varphi _{abk} \delta _{lc} \Big ) \bigg ) + C_{ickl}^\text {m} \Big ( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ka} \delta _{lb} \Big ) - {C}_{icab}^\text {M} = 0 \ . \end{aligned}$$
(16)

We refer to [61] for a derivation of Eq. (15) and Eq. (16).

By using Eq. (14) and the latter on the left-hand side of Eq. (2), the microscale energy becomes

$$\begin{aligned} \int _{\varOmega _P^\text {m}} \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm {d} V^\text {m} = \frac{V^\text {M}}{2}\Big ( \bar{C}_{abcd} \langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,d}^\text {M}\rangle + \bar{D}_{abcdef}\langle {u}_{a,bc}^\text {M}\rangle \langle {u}_{d,ef}^\text {M}\rangle + \bar{G}_{abcde}\langle {u}_{a,b}^\text {M}\rangle \langle {u}_{c,de}^\text {M}\rangle \Big ) \ \end{aligned}$$
(17)

with

$$\begin{aligned} \bar{C}_{abcd}= & {} \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm {d} V^\text {m} \ , \nonumber \\ \bar{D}_{abcdef}= & {} \frac{\epsilon ^2}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm {d} V^\text {m} \ , \nonumber \\ \bar{G}_{abcde}= & {} \frac{2\epsilon }{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} M_{cdekl} \, \mathrm {d} V^\text {m} \ , \end{aligned}$$
(18)
$$\begin{aligned} L_{abij}= & {} \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \ , \nonumber \\ M_{abcij}= & {} y_{c} \Big ( \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \Big ) + \Big ( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \Big ) \ . \end{aligned}$$
(19)

Note that the rank 5 tensor vanishes for centrosymmetric materials, \(\bar{\varvec{G}}=0\).

2.3 The equivalence of the macro- and microscale strain energy for an RVE

Based on Eq. (2), the effective parameters including the classical Cauchy stiffness tensor as well as the strain gradient ones can be calculated by:

$$\begin{aligned} C^\text {M}_{abcd}= & {} \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm {d} V^\text {m} \ , \nonumber \\ D^\text {M}_{abcdef}= & {} \frac{\epsilon ^2}{V^\text {M}} \Bigg ( \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm {d} V^\text {m} - C^\text {M}_{abef} \int _{\varOmega _P^\text {m}}y_c y_d \, \mathrm {d} V^\text {m} \Bigg )\ , \end{aligned}$$
(20)

after computing \(\varvec{\varphi }\) and \(\varvec{\psi }\) from Eqs. (15) and (16) in an RVE. Indeed, Eqs. (15) and (16) are solved numerically by means of the FEM [61].

3 Computational study

Size effects of metamaterials constructed by lattice-based microstructures are computationally examined. A quantitative assessment of the capability to capture size effects by means of the second-order homogenization method is conducted in this section.

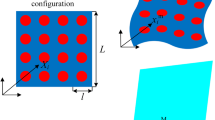
Three types of computations as indicated in Fig. 1 are conducted in this section. The first simulation is a direct computation with the detailed mesh of the metamaterials. The metamaterials are “made” from an isotropic materials with Young’s modulus \(E= 100 \)MPa and Poisson’s ratio \(\nu = 0.3\). The second and third ones are the corresponding homogenized classical continua as well as homogenized strain gradient continua with the same sizes, boundary conditions as in the first simulations. The stiffness tensor \(C_{ijkl}^\text {M}\) is needed for the second simulation. Both \(C_{ijkl}^\text {M}\) and \(D^\text {M}_{ijklmn}\) are required for the third one. These two tensors are delivered by using the method that was outlined above.

Fig. 1
figure 1

The lattice structure and its equivalent homogenized continuum

Full size image

The first and second simulations are conducted by means of standard FEM. A discretization with a quadratic Lagrange shape function was carried out. The implementation of strain gradient elasticity was achieved based on isogeometric analysis (IGA) in order to ensure an at least \(C^1\) continuity [38, 40, 54]. A verification of the used IGA codes with analytical solutions can be found in [60]. All of the computations are done in the open source platform FEniCS [1, 14, 38, 49]. The total strain energies in Eq. (21) are calculated to assess the computations.

$$\begin{aligned} W^L= & {} \int _{\varOmega } \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm {d} V \ , \nonumber \\ W^C= & {} \int _{\varOmega } \frac{1}{2} C^\text {M}_{ijkl} u^\text {M}_{i,j} u_{k,l}^\text {M} \, \mathrm {d} V \ , \nonumber \\ W^{SG}= & {} \int _{\varOmega } \frac{1}{2} \big ( C^\text {M}_{ijkl} u^\text {M}_{i,j} u_{k,l}^\text {M} + D_{ijklmn}^\text {M} u_{i,jk}^\text {M} u_{l,mn}^\text {M} \big ) \, \mathrm {d} V \ . \end{aligned}$$
(21)

The relative errors are defined in Eq. (22). They serve for evaluation of the accuracy of different approaches:

$$\begin{aligned} R^{C} = \left| \frac{W^L - W^{C}}{W^L} \right| \ , \ R^{SG} = \left| \frac{W^L - W^{SG}}{W^L} \right| \ . \end{aligned}$$
(22)

Figure 1 presents an example of the square lattice and its homogenized continua. In order to understand the mechanism of size effects better, a number of factors (boundary conditions, aspect ratios of lattice structures, different unit cells, different microstructural topologies) are investigated in what follows.

3.1 Examination of size effects for different boundary conditions

Square lattice structures (width = length = 4 mm) as shown in Fig. 2 are investigated here for different boundary conditions. The left sides of the structures are fixed, and on the right sides, prescribed displacements are imposed, resulting in extension, shear and torsion tests. The material parameters are displayed in Table 1, where \(V_f\) denotes the volume ratio (the volume of ligaments over the whole cell), t is the thickness of the ligament, and l is the length of the cell. The square lattice structure is of cubic symmetry. There are 3 and 6 independent parameters in the classical stiffness tensor and strain gradient stiffness tensor [6, 7], respectively, as shown in the following:

$$\begin{aligned} \varvec{C}^\text {M}= & {} \begin{pmatrix} C_{1111} &{} C_{1122} &{} 0 \\ &{} C_{1111} &{} 0 \\ \text {sym.} &{} &{} C_{1212} \\ \end{pmatrix} \ , \nonumber \\ {\varvec{D}}^\text {M}= & {} \begin{pmatrix} D_{111111}&{} D_{111221} &{} D_{111122} &{}0 &{} 0 &{} 0 \\ &{} D_{221221} &{} D_{221122} &{} 0 &{} 0 &{} 0 \\ &{} &{} D_{122122} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} D_{111111} &{} D_{111221} &{} D_{111122} \\ &{}\text {sym.} &{} &{} &{} D_{221221} &{} D_{221122} \\ &{} &{} &{} &{} &{} D_{122122} \\ \end{pmatrix} \ . \end{aligned}$$
(23)
Fig. 2
figure 2

Examination of size effects in cases of different boundary conditions

Full size image

The numerical results are compiled in Figs. 3 and 4. The following observations and interpretations can be made:

  • In the torsion test, the direct computation shows a deviation (stiffening) from the homogenized Cauchy continuum. This difference is known as a (stiffening) size effect.

  • No significant size effects are observed in extension and shear tests. Homogenized Cauchy continua are accurate enough for these cases.

  • With the homogenized strain gradient continuum, the size effect can be fully captured.

Table 1 Geometry and material parameters for square lattice cell
Full size table
Fig. 3
figure 3

Comparison of strain energies for square lattice structures under different boundary conditions

Full size image
Fig. 4
figure 4

Relative errors for the Cauchy and the strain gradient continuum under different boundary conditions

Full size image

3.2 Examination of size effects for different aspect ratios of the samples

The size effects are investigated further by varying the aspect ratio of the samples under torsion boundary conditions as shown in Fig. 5.

Fig. 5
figure 5

Selected aspect ratios for the square lattice

Full size image

As indicated in Figs. 6 and 7, we find:

  • With increasing aspect ratio, the microstructural effects become more important and the size effects become more pronounced.

  • Strain gradient continua show good agreement with direct computation, and the size effects can be grasped well even for the large aspect ratio value of 50.

Fig. 6
figure 6

Comparison of strain energies for square lattice structures with different aspect ratios

Full size image

3.3 Examination of size effects for different unit cells (closed or open cells)

The square lattices constructed by two different unit cells shown in Fig. 8, closed cells and open cells are studied herein. The differences are that closed cells possess a closed surface without intersecting by voids, and the open cells are cut by voids leading to zigzag surfaces. The closed and open cells are essentially the same lattices when the length of the lattices is very large or the length of the cells is very small so that the differences between cells can be ignored.

The material parameters for the closed and open cells can be found in Tables 1 and 2. The classical stiffness tensor \(\varvec{C}^\text {M}\) is the same for closed and open cells. However, the strain gradient stiffness tensor \(\varvec{D}^\text {M}\) is different indicating the microstructural differences for closed and open cells.

Table 2 Geometry and material parameters for the open cell
Full size table
Fig. 7
figure 7

Relative errors for the Cauchy and strain gradient continuum for different aspect ratios

Full size image
Fig. 8
figure 8

Lattices constructed from closed and open cells

Full size image

From numerical experiments (torsion boundary conditions) indicated in Fig. 8, we find from Figs. 9, 3c, 6b:

  • Structures constructed from closed cells show a stiffening size effect, and open cell constructs show a softening effect.

  • Strain gradient continua are able to grasp both stiffening and softening effects.

Fig. 9
figure 9

Comparison of strain energies for square lattice structures with open cells

Full size image

3.4 Examination of size effects for different topologies of microstructures

The three topologies of lattices shown in Fig. 10, which have been intensively studied in [41, 46, 66], are used. The volume ratio of the lattices is set to be equal leading to a difference of the thickness of ligaments. The material parameters are shown in Table 3. Two kinds of numerical experiments (either applying prescribed displacement or tractions) were performed.

3.4.1 Numerical tests under prescribed displacements

Torsion tests for \(4 \times 4\) lattice structures under prescribed displacements (torsion boundary conditions) as shown in Fig. 10 were conducted.

Fig. 10
figure 10

The square lattice, mixed triangle lattice A and mixed triangle lattice B

Full size image

From the numerical experiments, we see in Figs. 11 and12:

  • Stiffening size effects are found for all three lattices. Strain gradient continua are able to grasp the stiffening effects accurately in all cases.

  • The stiffening size effects gradually decay from the square lattice, the mixed triangle A lattice, to the mixed triangle B lattice.

Table 3 Geometry and elastic parameters for lattice cells of different topologies
Full size table
Fig. 11
figure 11

Comparison of strain energies for lattice structures with different topologies

Full size image
Fig. 12
figure 12

Relative errors for the Cauchy and the strain gradient continuum for different microstructural topologies

Full size image

3.4.2 Numerical tests for prescribed tractions

As displayed in Fig. 13, lattices (50 mm \( \times \) 1 mm) with different microstructural topologies were investigated.

Fig. 13
figure 13

The square lattice, mixed triangle lattice A and mixed triangle lattice B

Full size image

The left sides are clamped, and to the right sides, tractions are applied. The results for total displacements, total strain energies and the relative energies can be found in Figs. 14, 15 and 16. The following observations can be made:

  • The direct computations for lattices show smaller total displacements and larger total strain energies than the Cauchy continuum. This stiffening size effect is observed for all three lattices.

  • A good match between strain gradient continua and direct computations is visible for both total displacements and total strain energies. Strain gradient continua are able to grasp stiffening effects accurately in all of the cases.

  • The topologies of the microstructures have a big influence on the size effects.

Fig. 14
figure 14

Comparison of total displacement for lattice structures with different microstructural topologies

Full size image
Fig. 15
figure 15

Comparison of strain energies for lattice structures with different microstructural topologies

Full size image
Fig. 16
figure 16

Relative errors for the Cauchy and strain gradient continuum for different microstructural topologies

Full size image

4 Discussions

The results show that equivalent homogeneous strain gradient continua can be used as a replacement for metamaterials with lattice microstructures. Stiffening or softening size effects of metamaterials are both captured by strain gradient continua. The reason for the stiffening size effects is mainly due to

  • Beam bending effects

From the extension and shear tests conducted in Sect. 3.1, it is concluded that the bending energies are negligible. Hence, no size effects are detected. In the case of torsion tests, beam bending energies cannot be ignored, resulting in a stiffening size effect. This size effect grows with increasing aspect ratios of the lattices as shown in Sect. 3.2. Size effects shown in different topologies of microstructures are originated from beam bending, as well. As shown in Sect. 3.4, the size effects are more distinct in square lattice than in mixed triangle A and B lattices due to the fact that the square lattice is a bending dominated lattice and the others are stretch dominated [5]. The reason for the softening size effects is mainly due to

  • Zigzagging edge arrangements contributing less stiffness than the interior.

The Cauchy theory does not have the capability to take the microstructural information into account. However, the differences of geometries and topologies of microstructures and edge arrangement can be described by strain gradient theory with additional constitutive parameters.

Another issue is the positive definiteness of the strain energy for the homogenized strain gradient continua since some negative values are observed in the strain gradient stiffness tensors. Indeed, in this paper, the assumption of equivalence of strain energies for one RVE is used. This means at the macroscale that the homogenized strain energies of the continua are equal to that at the microscale, where the constituents of the RVE are linear elastic ensuring a positive strain energy. For the FEM implementation, if the size of the FEM element is larger than or equal to that of the RVE, an outcome of positive energy for the FEM computation is ensured. This was demonstrated also in [8, 41, 44]. Fortunately, in the present work, isogeometric analysis was used, and it is possible to specify relatively large sized elements: So convergence of computations is assured by setting a higher polynomial degree of NURBS. Note that choosing a larger size of elements than RVE in FEM is a sufficient but not a necessary condition to ensure the positive definite of the effective material parameters.

5 Conclusions

A second-order asymptotic homogenization was used to model metamaterials of lattice-based microstructures as effective homogeneous strain gradient continua. Size effects of metamaterials under different boundary conditions, different aspect ratios, different unit cells (closed or open cells), different topologies were examined. It was shown that both stiffening and softening size effects can be fully captured by effective strain gradient continua. Stiffening size effects are attributed to beam bending, and softening size effects are found due to the zigzag edge arrangements. It should be remarked that the presented homogenized model can produce the symmetry properties considered in [6, 7, 29, 50].

Finally, it is possible to envision for the near future the following extensions of this work:

  • The extension to 3D cases will be conducted in order to be able to predict out-of-plane deformations [11, 23, 33] and to study 3D metamaterials.

  • The application of the homogenization method to the analysis of pantographic (bi-pantographic) structures will be explored [9, 10, 26, 27].

  • A comparative study will be undertaken between the presented computational homogenization method and that shown in [23, 31]. Indeed, in [31], the constitutive parameters of macro-homogenized model are identified by a fitting procedure to get the best possible agreement with micromodel. The homogenization is made “globally” and conjecturing the macro-continuum model “a priori.” On the other hand, in the current work, the structure of the homogenized description and its parameters are explicitly deduced from an RVE. It will be interesting to investigate differences of the identified parameters by means of these two methods.

  • Hencky-type discrete models are the fundamental building block for continuum models [57, 58]. Physical systems studied in the present paper can be also modeled by the so-called Hencky-type models. Future investigations will also address this point.

  • Comparisons with the results presented in [2, 18, 29, 48] will be beneficial to highlight the physical meaning of the identified higher-order constitutive parameters.