A variational method for post-buckling analysis of end-supported nanorods under self-weight with surface stress effect

Abstract

In this paper, the formulation of post-buckling of end-supported nanorods under self-weight was developed by the variational method. The surface stress effect was considered following the surface elasticity theory of Gurtin–Murdoch. The variational formulation involving the strain energy in the bulk material, the strain energy of the surface layer, and the potential energy due to self-weight was expressed in terms of the intrinsic coordinates. The variational formulation was accomplished by introducing the Lagrange multiplier technique to impose the boundary conditions. The finite element method was used to derive a system of nonlinear equations resulting from the stationary of the total potential energy, and then, Newton–Raphson iterative procedure was applied to solve this system of equations. The post-buckled configurations of nanorods under self-weight due to various boundary conditions were presented and demonstrated that the variational formulation expressed in terms of intrinsic coordinate is highly recommended for post-buckling analysis of end-supported nanorods. In addition, the surface stress effect significantly influenced the post-buckling response of nanorods and exhibited higher stiffness in comparison with nanorods without surface stress. The model formulation presented in this study is of special interest in the design and application of advanced technological devices.

Appendix

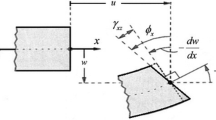
In order to validate the accuracy of formulation in this work, Eq. (8) is confirmed by the governing equation from considering the equilibrium of a nanorod under self-weight as shown in Fig. 12. The moment equilibrium from the free-body diagram of an infinitesimal segment (Fig. 12b) can be obtained as

$$\begin{aligned} \frac{\mathrm{d}M}{\mathrm{d}s}+\int \limits _\Gamma {T_{\xi } \eta \mathrm{d}\Gamma -Q=0} \end{aligned}$$

(A1)

Fig. 12

Schematic of a nanorod under self-weight: a equilibrium of a nanorod; b free-body diagram of an infinitesimal segment

where $\Gamma$ is the perimeter of a nanorod cross-section and $T_{\xi } =(2\mu _\mathrm{s} +\lambda _\mathrm{s} )\eta \frac{d^{2}\theta }{\mathrm{d}s^{2}}$ is the contract tractions exist on the contact surface between the bulk part and surface layer [19]. Substitution of the contract tractions into Eq. (A1) gives

$$\begin{aligned} \frac{\mathrm{d}M}{\mathrm{d}s}+(2\mu _\mathrm{s} +\lambda _\mathrm{s} )I^{s}\frac{d^{2}\theta }{\mathrm{d}s^{2}}-Q=0 \end{aligned}$$

(A2)

where $I^{s}=\int _\Gamma {\eta ^{2}} \mathrm{d}\Gamma$. By considering the free-body diagram of the segment of a nanorod as shown in Fig. 12(a), a summation of force in the normal direction ($\eta$) gives

$$\begin{aligned} Q+\int \limits _\Gamma {\sigma _{\xi \eta }^{s} \mathrm{d}\Gamma \,} +w_\mathrm{s} (L-s)\sin \theta +R_{\mathrm{BY}} \cos \theta =0 \end{aligned}$$

(A3)

where $\sigma _{\xi \eta }^{s}$ is the shear stress at the cross-section and $\int \limits _\Gamma {\sigma _{\xi \eta }^{s} \mathrm{d}\Gamma \,} =-\tau _\mathrm{s} p^*\theta$ [19]. Substitution of Eq. (A3) into Eq. (A2) yield

$$\begin{aligned} \frac{\mathrm{d}M}{\mathrm{d}s}+(2\mu _\mathrm{s} +\lambda _\mathrm{s} )I^{s}\frac{d^{2}\theta }{\mathrm{d}s^{2}}-\tau _\mathrm{s} p^*\theta +w_\mathrm{s} (L-s)\sin \theta +R_{\mathrm{BY}} \cos \theta =0 \end{aligned}$$

(A4)

Assuming a homogenous isotropic material, the relevant bulk stress for an Euler beam can be expressed as

$$\begin{aligned} \sigma _{\xi \xi } =E\varepsilon _{\xi \xi } +\nu \sigma _{\eta \eta } \end{aligned}$$

(A5)

where $\varepsilon _{\xi \xi } =\eta \frac{\mathrm{d}\theta }{\mathrm{d}s}$ is the bulk strain. The exact moment-curvature relationship for a nanorod with surface energy effect can be obtained as

$$\begin{aligned} M=\int _A {\sigma _{\xi \xi } \eta dA} =\left[ {EI-\frac{2vI\tau _\mathrm{s} }{H}} \right] \frac{\mathrm{d}\theta }{\mathrm{d}s} \end{aligned}$$

(A6)

where $I=\int _A {\eta ^{2}dA}$. By differentiating Eq. (A6) with respect to arc lengths, and then substitution into Eq. (A4), yields the governing differential equation as

$$\begin{aligned} \left[ {EI-\frac{2vI\tau _\mathrm{s} }{H}+(2\mu _\mathrm{s} +\lambda _\mathrm{s} )I^{s}} \right] \frac{d^{s}\theta }{\mathrm{d}s^{2}}-\tau _\mathrm{s} p^*\theta +w_\mathrm{s} (L-s)\sin \theta +R_{\mathrm{BY}} \cos \theta =0 \end{aligned}$$

(A7)

Equation (A7) identical to Eq. (8) that is confirmed the accuracy of formulation in this work. To identify the physical meaning of the multiplier $\lambda$ in Eq. (8), the multiplier is identified as the constraint reaction force at the support, as follows

$$\begin{aligned} \lambda =R_{\mathrm{BY}} =R_{\mathrm{AY}} =\frac{1}{L}\int \limits _0^L {w_\mathrm{s} y\mathrm{d}s} \end{aligned}$$

(A8)