Bifurcations and post-critical behaviors of a nonlinear curved plate in subsonic airflow

Abstract

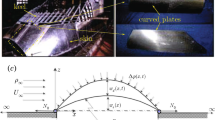
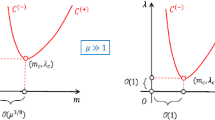
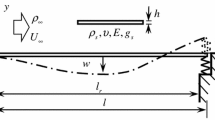
This paper visits the stability, bifurcations and post-critical behaviors of a nonlinear curved plate in a subsonic axial flow. The curved plate is simply supported and subjected to an initial horizontal tension. The plate is initially curved, and the initial shape is modeled by a shallow shell with constant curvature. The airflow is assumed incompressible, and the fluid force is considered as the sum of two parts: One is due to the plate deformation, and the other is to the plate initial shape. The Laplace’s equation is solved for the fluid force by placing a series of time-independent sources on the plate. The nonlinear axial strain due to large deformation is considered for the potential energy of the plate. Results show that the system has a fundamental and four bifurcated equilibrium solutions. The fundamental bifurcation is always supercritical; however, the secondary bifurcation is either supercritical or subcritical. The bifurcation regions are analyzed in parametric planes, and eight typical bifurcation processes are explored. There appear jump phenomena between the two stable states of system after the fundamental bifurcation. The combinations of designed parameters, including the plate initial curvature, horizontal tension and flow velocity, highly influence the bifurcation behaviors of the plate.

Appendix

The expression of $\Delta _1$ in Eq. (3.3) is:

$$\begin{aligned} \begin{aligned} {\Delta _1}\left( {\lambda ,\gamma ,{R}} \right)&= {b_0}+{b_1}{\lambda ^3} + {b_2}{\lambda ^2} + {b_3}\lambda + {b_4}{\gamma ^2}\lambda + {b_5}{\gamma ^4}\lambda + {b_6}{\gamma ^2}{\lambda ^2}\\&\quad + {b_7}{\gamma ^6} + {b_8}{\gamma ^4} + {b_9}{\gamma ^2} + {b_{10}}R^3 + {b_{11}}R^2 + {b_{12}}R^2{\gamma ^2} + {b_{13}}R^2\lambda \\&\quad + {b_{14}}{R}{\gamma ^2}\lambda + {b_{15}}{R}\lambda + {b_{16}}{R}{\gamma ^2} + {b_{17}}{R}{\gamma ^4} + {b_{18}}{R}{\lambda ^2} + {b_{19}}{R} \end{aligned} \end{aligned}$$

(A.1)

where

$$\begin{aligned} \begin{aligned} {b_0}&=1.3676e{-3},{b_1}=-1.012e{-8},{b_2}=2.463{-6},{b_3}=-1.005e{-4},{b_4}=6.566e{-4};\\ {b_5}&=-4.256e{-3},{b_6}=-0.788e{-6},{b_7}=-4.475e{-3},{b_8}=4.20e{-2},{b_9}=1.64e{-2};\\ b_{10}&=-1.428e{-6},b_{11}=4.226e{-5},b_{12}=1.08e{-3},b_{13}=-1.034e{-6},b_{14}=-6.799e{-5};\\ b_{15}&=2.039e{-5},b_{16}=-9.324e{-3},b_{17}=-4.256e{-3},b_{18}=-2.499e{-7},b_{19}=-4.170e{-4}. \end{aligned} \end{aligned}$$

The expression of $\Delta _2$ in Eq. (3.3) is:

$$\begin{aligned} \begin{aligned} {\Delta _2}\left( {\lambda ,\gamma ,{R}} \right)&={c_0} + {c_1}{R_0} + {c_2}\lambda + {c_3}\lambda {R} + {c_4}{\lambda ^2} + {c_5}{\gamma ^2}{R} + {c_6}{\lambda ^3} + {c_7}{\gamma ^2}\\&\quad + {c_8}{\lambda ^2}{R} + {c_9}{\gamma ^2}R^2 + {c_{10}}{\gamma ^2}\lambda + {c_{11}}{\gamma ^2}\lambda {R} + {c_{12}}{\lambda ^2}{\gamma ^2}\\&\quad + {c_{13}}{\lambda }{\gamma ^2}+ {c_{14}}{R}{\gamma ^4}+ {c_{15}}{\gamma ^4} + {c_{16}}{\lambda }R^2 +{c_{17}}R^3+{c_{18}}R^2 \end{aligned} \end{aligned}$$

(A.2)

where

$$\begin{aligned} \begin{aligned} {c_0}&=-2.8465e4,{c_1}=7.21e3,{c_2}=1.74e{2},{c_3}=2.08e{-2},{c_4}=5.0284e{-3},\\ {c_5}&= 7.168e3,{c_6}=3.63e-8,{c_7}=-1.010e5,{c_8}=1.508e{-7};{c_9}=-1.037e{2},\\ c_{10}&=-8.8165,c_{11}=2.74e{-1},c_{12}=-5.642e5;c_{13}=-0.4102e{-6};\\ c_{14}&=0.370e{-3}; c_{15}=0.73e{-3};c_{16}=1.64e{-10};c_{16}=4.502e{-13};c_{16}=1.13e{-5} \end{aligned} \end{aligned}$$

The expression of b in Eq. (3.19) and the coefficients in Eq. (3.20) are:

$$\begin{aligned} b=\gamma (a_3{\gamma ^2} +a_2\lambda _c^1 + a_1R +a_0) \end{aligned}$$

(A.3)

where

$$\begin{aligned} a_3=4.9536e{-5};a_2= -7.887{-5};a_1=6.9760e{-2};a_0=-3.437e{-1}. \end{aligned}$$