Skip to main content
SpringerLink
Log in

Studying the field-controlled change of shape and elasticity of magnetic gels using particle-based simulations

  • SPECIAL
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

Ferrogels are soft elastic materials into which magnetic particles are embedded. The resulting interplay between elastic and magnetic interactions and the materials’ response to external fields makes them promising candidates for applications such as actuation and drug delivery. In this article, after providing a very brief introduction to particle-based simulation methods, we give an overview on how they can be applied to magnetic gels. We focus on the different mechanisms by which ferrogels can deform in an external magnetic field. Based on examples from our previous work, we show how these mechanisms can be captured by particle-based simulations. Lastly, we provide some links to simulation techniques on larger length scales.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Reprinted from Ref. [43] with permission from Elsevier. (Color figure online)

Fig. 2

Reprinted from Ref. [43] with permission from Elsevier

Fig. 3

(Based on data from Ref. [45])

Fig. 4

This figure is based on data from Ref. [44]. (Color figure online)

Fig. 5

(Figure adapted from Ref. [51])

Fig. 6

(Reproduced from Ref. [51])

Fig. 7
Fig. 8

(Figure adapted from Ref. [57]—published by the Royal Society of Chemistry)

Similar content being viewed by others

References

  1. Zrinyi, M., Barsi, L., Büki, A.: Deformation of ferrogels induced by nonuniform magnetic fields. J. Chem. Phys. 104, 8750 (1996)

    Article  Google Scholar 

  2. Barsi, L., Büki, A., Szabo, D., Zrinyi, M.: Gels with magnetic properties. Prog. Colloid Polym. Sci. 102, 57 (1996)

    Article  Google Scholar 

  3. Varga, Z., Feher, J., Filipcsei, G., Zrinyi, M.: Smart nanocomposite polymer gels. Macromol. Symp. 200, 93 (2003)

    Article  Google Scholar 

  4. Gollwitzer, C., Turanov, A., Krekhova, M., Lattermann, G., Rehberg, I., Richter, R.: Measuring the deformation of a ferrogel in a homogeneous magnetic field. J. Chem. Phys. 128, 164709 (2008)

    Article  Google Scholar 

  5. Odenbach, S.: Microstructure and rheology of magnetic hybrid materials. Arch. Appl. Mech. 86, 1–11 (2016)

    Article  Google Scholar 

  6. Weeber, R., Hermes, M., Schmidt, A.M., Holm, C.: Polymer architecture of magnetic gels: a review. J. Phys. Condens. Matter 30(6), 063002 (2018)

    Article  Google Scholar 

  7. Bellan, C., Bossis, G.: Field dependence of viscoelastic properties of mr elastomers. Int. J. Mod. Phys. B 16, 2447 (2002)

    Article  Google Scholar 

  8. Ramanujan, R., Lao, L.: The mechanical behavior of smart magnet-hydrogel composites. Smart Mater. Struct. 15(4), 952 (2006)

    Article  Google Scholar 

  9. Monz, S., Tschöpe, A., Birringer, R.: Magnetic properties of isotropic and anisotropic CoFe\(_2\)O\(_4\)-based ferrogels and their application as torsional and rotational actuators. Phys. Rev. E 78(2), 021404 (2008)

    Article  Google Scholar 

  10. Zimmermann, K., Naletova, V., Zeidis, I., Böhm, V., Kolev, E.: Modelling of locomotion systems using deformable magnetizable media. J. Phys. Condens. Matter 18(38), S2973 (2006)

    Article  Google Scholar 

  11. Zimmermann, K., Böhm, V., Zeidis. I.: Vibration-driven mobile robots based on magneto-sensitive elastomers. In: 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), pp. 730–735. IEEE (2011)

  12. Schmauch, M.M., Mishra, S.R., Evans, B.A., Velev, O.D., Tracy, J.B.: Chained iron microparticles for directionally controlled actuation of soft robots. ACS Appl. Mater. Interfaces 9(13), 11895–11901 (2017)

    Article  Google Scholar 

  13. Volkova, T.I., Böhm, V., Kaufhold, T., Popp, J., Becker, F., Borin, D.Y., Stepanov, G.V., Zimmermann, K.: Motion behaviour of magneto-sensitive elastomers controlled by an external magnetic field for sensor applications. J. Magn. Magn. Mater. 431, 262–265 (2017)

    Article  Google Scholar 

  14. Volkova, T.I., Böhm, V., Naletova, V.A., Kaufhold, T., Becker, F., Zeidis, I., Zimmermann, K.: A ferrofluid based artificial tactile sensor with magnetic field control. J. Magn. Magn. Mater. 431, 277–280 (2017)

    Article  Google Scholar 

  15. Qin, J., Asempah, I., Laurent, S., Fornara, A., Muller, R.N., Muhammed, M.: Injectable superparamagnetic ferrogels for controlled release of hydrophobic drugs. Adv. Mater. 21(13), 1354–1357 (2009)

    Article  Google Scholar 

  16. Alexiou, C., Jurgons, R., Schmid, R.J., Bergemann, C., Henke, J., Erhard, W., Huenges, E., Parak, F.: Magnetic drug targeting–biodistribution of the magnetic carrier and the chemotherapeutic agent mitoxantrone after locoregional cancer treatment. J. Drug Target. 11(3), 139–149 (2003)

    Article  Google Scholar 

  17. Babincová, M., Leszczynska, D., Sourivong, P., Čičmanec, P., Babinec, P.: Superparamagnetic gel as a novel material for electromagnetically induced hyperthermia. J. Magn. Magn. Mater. 225(1), 109–112 (2001)

    Article  Google Scholar 

  18. Lao, L., Ramanujan, R.: Magnetic and hydrogel composite materials for hyperthermia applications. J. Mater. Sci. Mater. Med. 15(10), 1061–1064 (2004)

    Article  Google Scholar 

  19. Stolbov, O.V., Raikher, Y.L., Balasoiu, M.: Modelling of magnetodipolar striction in soft magnetic elastomers. Soft Matter 7, 8484–8487 (2011)

    Article  Google Scholar 

  20. Kalina, K.A., Metsch, P., Kästner, M.: Microscale modeling and simulation of magnetorheological elastomers at finite strains: a study on the influence of mechanical preloads. Int. J. Solids Struct. 102, 286–296 (2016)

    Article  Google Scholar 

  21. Metsch, P., Kalina, K.A., Spieler, C., Kästner, M.: A numerical study on magnetostrictive phenomena in magnetorheological elastomers. Comput. Mater. Sci. 124, 364–374 (2016)

    Article  Google Scholar 

  22. Attaran, A., Brummund, J., Wallmersperger. T.: Development of a continuum model for ferrogels. J. Intell. Mater. Syst. Struct. https://doi.org/10.1177/1045389X16672564 (2016)

  23. Kubo, R.: The fluctuation-dissipation theorem. Rep. Prog. Phys. 29(1), 255–284 (1966)

    Article  MATH  Google Scholar 

  24. Frenkel, D., Smit, B.: Understanding Molecular Simulation, 2nd edn. Academic Press, San Diego (2002)

    MATH  Google Scholar 

  25. Biller, A., Stolbov, O., Raikher, Y.L.: Modeling of particle interactions in magnetorheological elastomers. J. Appl. Phys. 116(11), 114904 (2014)

    Article  Google Scholar 

  26. Weeks, J.D., Chandler, D., Andersen, H.C.: Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 54, 5237 (1971)

    Article  Google Scholar 

  27. Weis, J.J., Levesque, D., Zarragoicoechea, G.J.: Orientational order in simple dipolar liquid-crystal models. Phys. Rev. Lett. 69(6), 913–916 (1992)

    Article  Google Scholar 

  28. Stevens, M.J., Grest, G.S.: Coexistence in dipolar fluids in a field. Phys. Rev. Lett. 72(23), 3686–3689 (1994)

    Article  Google Scholar 

  29. Camp, P.J., Shelley, J.C., Patey, G.N.: Isotropic fluid phases of dipolar hard spheres. Phys. Rev. Lett. 84(1), 115–118 (2000)

    Article  Google Scholar 

  30. Kantorovich, S., Cerdà, J.J., Holm, C.: Microstructure analyisis of monodisperse ferrofluid monolayers: theory and simulation. Phys. Chem. Chem. Phys. 10(14), 1883–1895 (2008)

    Article  Google Scholar 

  31. Jordanovic, J., Klapp, S.H.L.: Field-induced layer formation in dipolar nanofilms. Phys. Rev. Lett. 101, 038302 (2008)

    Article  Google Scholar 

  32. Donaldson, J.G., Kantorovich, S.S.: Directional self-assembly of permanently magnetised nanocubes in quasi two dimensional layers. Nanoscale 7(7), 3217–3228 (2015)

    Article  Google Scholar 

  33. Alvarez, C.E., Klapp, S.H.L.: Percolation and orientational ordering in systems of magnetic nanorods. Soft Matter 8, 7480–7489 (2012)

    Article  Google Scholar 

  34. Weeber, R., Klinkigt, M., Kantorovich, S., Holm, C.: Microstructure and magnetic properties of magnetic fluids consisting of shifted dipole particles under the influence of an external magnetic field. J. Chem. Phys. 139(21), 214901 (2013)

    Article  Google Scholar 

  35. Yener, A.B., Klapp, S.H.: Self-assembly of three-dimensional ensembles of magnetic particles with laterally shifted dipoles. Soft Matter 12(7), 2066–2075 (2016)

    Article  Google Scholar 

  36. Puljiz, M., Huang, S., Auernhammer, G.K., Menzel, A.M.: Forces on rigid inclusions in elastic media and resulting matrix-mediated interactions. Phys. Rev. Lett. 117(23), 238003 (2016)

    Article  Google Scholar 

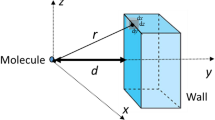
  37. Menzel, A.M.: Force-induced elastic matrix-mediated interactions in the presence of a rigid wall. Soft Matter 13(18), 3373–3384 (2017)

    Article  Google Scholar 

  38. Barbucci, R., Pasqui, D., Giani, G., De Cagna, M., Fini, M., Giardino, R., Atrei, A.: A novel strategy for engineering hydrogels with ferromagnetic nanoparticles as crosslinkers of the polymer chains. Potential applications as a targeted drug delivery system. Soft Matter 7(12), 5558–5565 (2011)

    Article  Google Scholar 

  39. Messing, R., Frickel, N., Belkoura, L., Strey, R., Rahn, H., Odenbach, S., Schmidt, A.M.: Cobalt ferrite nanoparticles as multifunctional cross-linkers in PAAm ferrohydrogels. Macromolecules 44(8), 2990–2999 (2011)

    Article  Google Scholar 

  40. Roeder, L., Bender, P., Kundt, M., Tschöpe, A., Schmidt, A.M.: Magnetic and geometric anisotropy in particle-crosslinked ferrohydrogels. Phys. Chem. Chem. Phys. 17(2), 1290–1298 (2015)

    Article  Google Scholar 

  41. Ilg, P.: Stimuli-responsive hydrogels cross-linked by magnetic nanoparticles. Soft Matter 9(13), 3465–3468 (2013)

    Article  Google Scholar 

  42. Arnold, A., Lenz, O., Kesselheim, S., Weeber, R., Fahrenberger, F., Röhm, D., Košovan, P., Holm, C.: ESPResSo 3.1—molecular dynamics software for coarse-grained models. In: Griebel, M., Schweitzer, M.A. (eds.) Meshfree Methods for Partial Differential Equations VI. Lecture Notes in Computational Science and Engineering, vol. 89, pp. 1–23. Springer, Berlin (2013)

    Chapter  Google Scholar 

  43. Weeber, R., Kantorovich, S., Holm, C.: Ferrogels cross-linked by magnetic nanoparticles—deformation mechanisms in two and three dimensions studied by means of computer simulations. J. Magn. Magn. Mater. 383, 262–266 (2015)

    Article  Google Scholar 

  44. Weeber, R., Kantorovich, S., Holm, C.: Deformation mechanisms in 2d magnetic gels studied by computer simulations. Soft Matter 8, 9923–9932 (2012)

    Article  Google Scholar 

  45. Weeber, R., Kantorovich, S., Holm, C.: Ferrogels cross-linked by magnetic particles: field-driven deformation and elasticity studied using computer simulations. J. Chem. Phys. 143, 154901 (2015)

    Article  Google Scholar 

  46. Wood, D.S., Camp, P.J.: Modeling the properties of ferrogels in uniform magnetic fields. Phys. Rev. E 83, 011402 (2011)

    Article  Google Scholar 

  47. Dudek, M., Grabiec, B., Wojciechowski, K.: Molecular dynamics sumulations of auxetic ferrogel. Rev. Adv. Mater. Sci. 14, 167–173 (2007)

    Google Scholar 

  48. Raikher, Y.L., Stolbov, O.V.: Magnetodeformational effect in ferrogel samples. JMMM 258/259, 477 (2003)

    Article  Google Scholar 

  49. Zubarev, A.Y.: On the theory of the magnetic deformation of ferrogels. Soft Matter 8(11), 3174–3179 (2012)

    Article  Google Scholar 

  50. Ivaneyko, D., Toshchevikov, V., Saphiannikova, M., Heinrich, G.: Effects of particle distribution on mechanical properties of magneto-sensitive elastomers in a homogeneous magnetic field. Condens. Matter Phys. 15(3), 33601 (2012)

    Article  Google Scholar 

  51. Weeber, R., Holm, C.: Interplay between particle microstructure, network topology and sample shape in magnetic gels—a molecular dynamics simulation study. arxiv:1704.06578 (2017)

  52. Annunziata, M.A., Menzel, A.M., Löwen, H.: Hardening transition in a one-dimensional model for ferrogels. J. Chem. Phys. 138(20), 204906 (2013)

    Article  Google Scholar 

  53. Pessot, G., Schümann, M., Gundermann, T., Odenbach, S., Löwen, H., Menzel, A.M.: Tunable dynamic moduli of magnetic elastomers: from characterization by x-ray micro-computed tomography to mesoscopic modeling. J. Phys. Condens. Matter 30, 125101 (2018)

    Article  Google Scholar 

  54. Backes, S., Witt, M.U., Roeben, E., Kuhrts, L., Aleed, S., Schmidt, A.M., von Klitzing, R.: Loading of pnipam based microgels with cofe2o4 nanoparticles and their magnetic response in bulk and at surfaces. J. Phys. Chem. B 119(36), 12129–12137 (2015)

    Article  Google Scholar 

  55. Minina, E.S., Sánchez, P.A., Likos, C.N., Kantorovich, S.S.: The influence of the magnetic filler concentration on the properties of a microgel particle: zero-field case. J. Magn. Magn. Mater. 459, 226–230 (2018)

    Article  Google Scholar 

  56. Pessot, G., Weeber, R., Holm, C., Löwen, H., Menzel, A.M.: Towards a scale-bridging description of ferrogels and magnetic elastomers. J. Phys. Condens. Matter 27(32), 325105 (2015)

    Article  Google Scholar 

  57. Huang, S., Pessot, G., Cremer, P., Weeber, R., Holm, C., Nowak, J., Odenbach, S., Menzel, A.M., Auernhammer, G.K.: Buckling of paramagnetic chains in soft gels. Soft Matter 12(1), 228–237 (2016)

    Article  Google Scholar 

  58. Cremer, P., Löwen, H., Menzel, A.M.: Tailoring superelasticity of soft magnetic materials. Appl. Phys. Lett. 107(17), 171903 (2015)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful for financial support from the German Science Foundation (DFG) through the priority program SPP 1681 through the Grant HO 1108/23-2. Additionally, R. W. and C. H. acknowledge funding through the cluster of excellence EXC 310, SimTech, and access to the computer facilities of the HLRS and BW-Unicluster.

Author information

Authors and Affiliations

  1. Institut für Computerphysik, Universität Stuttgart, Allmandring 3, 70569, Stuttgart, Germany

    Rudolf Weeber, Patrick Kreissl & Christian Holm

Authors
  1. Rudolf Weeber
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Patrick Kreissl
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christian Holm
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rudolf Weeber.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Weeber, R., Kreissl, P. & Holm, C. Studying the field-controlled change of shape and elasticity of magnetic gels using particle-based simulations. Arch Appl Mech 89, 3–16 (2019). https://doi.org/10.1007/s00419-018-1396-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-018-1396-4

Keywords

Search

Navigation