Skip to main content
SpringerLink
Log in

Nonlinear response and stability of a spindle system supported by ball bearings

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

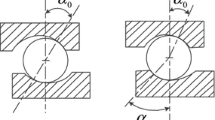
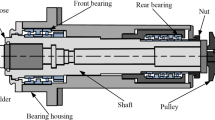
In this effort, the nonlinear responses and stability of a spindle system supported by ball bearings are presented. The dynamics of this system is described by a set of second order differential equations with a nonlinear piecewise smooth force. The Floquet theory is applied to investigate the stability of the periodic solution. Due to the loss of contact between the raceways and balls in the ball bearing, the bending of the frequency response curves switch to the left at the weak resonance region, which is similar to the frequency response curves of a system with a soft spring. With the decrease of the bearing clearance, the bending of the frequency response curves switch to the right, which is similar to the frequency response curves of a system with a hard spring. Increase of the frequency ratio, the bending of frequency response curves transforms from left to right. The route to chaos through a period doubling process is also observed in this spindle-bearing system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Yamamoto Y.: On the vibration of a shaft supported by bearing having radial clearance. Trans. Jpn. Soc. Mech. Eng. 21, 182–192 (1995)

    Google Scholar 

  2. Tiwari M., Gupta K., Prakash O.: Dynamic response of an unbalanced rotor supported on ball bearings. J. Sound Vib. 238(5), 757–779 (2000)

    Article  Google Scholar 

  3. Harsha S.P., Sandeep K., Prakash R.: The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings. Int. J. Mech. Sci. 45, 725–740 (2003)

    Article  Google Scholar 

  4. Bercea I., Nélias D., Cavallaro G.: A unified and simplified treatment of the non-linear equilibrium problem of double-row rolling bearings, Part 1: rolling bearing model. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribol. 217, 205–212 (2007)

    Article  Google Scholar 

  5. Sopanen J., Mikkola A.: Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 1: theory. Proc. Inst. Mech. Eng. Part K: J. Multi-body Dyn. 217, 201–212 (2003)

    Google Scholar 

  6. Sopanen J., Mikkola A.: Dynamic model of a deep-groove ball bearing including localized and distributed defects, Part 2: implementation and results. Proc. Inst. Mech. Eng. Part K: J. Multi-body Dyn. 217, 213–223 (2003)

    Google Scholar 

  7. Lee B.H.K., Gong L., Wong Y.S.: Analysis and computation of nonlinear dynamic response of a two-degree-of-freedom system and its application in aeroelasticity. J. Fluids Struct. 11, 225–246 (1997)

    Article  Google Scholar 

  8. Ferreira J.V., Serpa A.L.: Application of the arc-length method in nonlinear frequency response. J. Sound Vib. 284, 133–149 (2005)

    Article  Google Scholar 

  9. Franceschini G., Flori R.: Vibrations of a body supported by shear mountings of incompressible material with memory. Int. J. Eng. Sci. 39, 1013–1031 (2001)

    Article  Google Scholar 

  10. Wang L.H., Zhao Y.Y.: Nonlinear interactions and chaotic dynamics of suspended cables with three-to-one internal resonances. Int. J. Solids Struct. 43, 7800–7819 (2006)

    Article  MATH  Google Scholar 

  11. Zhao Y.Y., Wang L.H.: On the symmetric modal interaction of the suspended cable: three-to-one internal resonance. J. Sound Vib. 294, 1073–1093 (2006)

    Article  Google Scholar 

  12. Amer, Y.A., Bauomy, H.S.: Vibration reduction in a 2DOF twin-tail system to parametric excitations. Commun. Nonlinear Sci. Numer. Simul. (2007). doi:10.1016/j.cnsns.2007.10.005

  13. Lin C.W., Tu J.F., Kamman J.: An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation. Int. J. Mach. Tools Manuf. 43, 1035–1050 (2003)

    Article  Google Scholar 

  14. Harris T.A.: Rolling Bearing Analysis. Wiley, New York (1984)

    Google Scholar 

  15. Kramer E.: Dynamics of Rotors and Foundations. Springer, New York (1993)

    Google Scholar 

  16. Abdelhak, F., Mohamed, B.: Effect of fast harmonic excitation on frequency-locking in a van der Pol–Mathieu–Duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. (2007). doi:10.1016/j.cnsns.2007.07.010

  17. Ambarisha V.K., Parker R.G.: Nonlinear dynamics of planetary gears using analytical and finite element models. J. Sound Vib. 302, 577–595 (2007)

    Article  Google Scholar 

  18. Kang B., Tan C.A.: Nonlinear response of a beam under distributed moving contact load. Commun. Nonlinear Sci. Numer. Simul. 11, 203–232 (2006)

    Article  MATH  Google Scholar 

  19. Gao S.H., Long X.H., Meng G.: Nonlinear response and non-smooth bifurcations of an unbalanced machine-tool spindle-bearing system. Nonlinear Dyn. 54, 365–377 (2008)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, 800 Dongchuan RD, 200240, Shanghai, People’s Republic of China

    S. -H. Gao, X. -H. Long & G. Meng

Authors
  1. S. -H. Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. -H. Long
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to X. -H. Long.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gao, S.H., Long, X.H. & Meng, G. Nonlinear response and stability of a spindle system supported by ball bearings. Arch Appl Mech 80, 1069–1081 (2010). https://doi.org/10.1007/s00419-009-0358-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-009-0358-2

Keywords

Search

Navigation