Introduction

At ambient conditions, a mineral inclusion in a mineral host can display a pressure that significantly differs from the external one due to the difference in the thermal expansion (\(\Delta \mathrm{\alpha }={\mathrm{\alpha }}_{\mathrm{inclusion}}-{\mathrm{\alpha }}_{\mathrm{host}}\)) and compressibility (\(\Delta\upbeta ={\upbeta }_{\mathrm{inclusion}}-{\upbeta }_{\mathrm{host}}\)) coefficients between the inclusion and the host (e.g. Rosenfeld and Chase 1961). The precise quantification of the inclusion pressure (Pinc) is of great interest in mineralogy and petrology, because it can provide information on the inclusion entrapment pressure (Ptrap) and temperature (Ttrap) and thus on its metamorphic history. This is the subject of elastic thermobarometry. This method appears particularly attractive, because it does not depend on chemical equilibrium and hence represents a good alternative, or a complementary tool, to classical thermobarometry based on thermodynamic equilibrium (e.g., Angel et al. 2015; Kohn et al. 2023). During the last few years, elastic thermobarometry has considerably advanced. The effect of host-inclusion geometry, in terms of inclusion shape, size, and position in the host, as well as the intrinsic anisotropy in the elastic properties of the crystalline inclusion and the host have been implemented in the model (e.g., Mazzucchelli et al. 2018; Campomenosi et al. 2018; Murri et al. 2018; Zhong et al. 2020; Alvaro et al. 2020; Moulas et al. 2020; Gilio et al. 2021; Gonzalez et al. 2021).

Quartz-in-garnet (QuiG) and zircon-in-garnet (ZiG) are among the most used inclusion-host systems in elastic thermobarometry, because they can be found in many metamorphic rocks (e.g. Zhong et al. 2019; Gilio et al. 2022). As QuiG systems show ∆α < ∆β, they are more sensitive to changes in pressure P and, therefore, they are good barometers. On the other hand, for ZiG systems ∆α > ∆β, making them chiefly sensitive to changes in temperature T and, consequently, good thermometers (e.g. Kohn 2014; Thomas and Spear 2018; Bonazzi et al. 2019).

Raman spectroscopy is a powerful method to obtain Pinc at atmospheric P and room T. Moreover, it provides the opportunity to study host-inclusion systems at non-ambient conditions. For instance, since ZiG systems are sensitive to temperature changes, we recently demonstrated that in situ Raman spectroscopy at high temperatures and ambient pressure can be used to reach the conditions of mechanical equilibrium between zircon and garnet (Campomenosi et al. 2023). In addition, we have shown that at higher temperatures, zircon inclusions experience a tensile strain imposed by the host, leading to a negative Pinc, which triggers ZiG systems to instantaneous plastic relaxation. Consequently, the Pinc of zircon inclusions measured after a heating–cooling cycle are representative of the conditions explored via the experiments rather than the conditions of original entrapment. The possibility of instantaneous elastic resetting of the inclusion when Pinc is lower than the external pressure has important implications in petrology, because it shows that ZiG systems can be very sensitive to different exhumation P–T paths (Campomenosi et al. 2023). However, we also demonstrated that when the ZiG system behaves elastically, the elastic models used within the framework of the elastic thermobarometry correctly reproduce the Pinc measured in natural samples also at non-ambient conditions.

By the same logic, since QuiG systems are good barometers, here we show that in situ Raman spectroscopy at high pressure and room temperature, using the diamond-anvil-cell (DAC) technique, can provide valuable information about the elastic interaction between the two minerals under non-ambient conditions. Our results validate the current elastic models and EoS used to predict entrapment conditions of QuiG systems in the investigated pressure range (up to 2.5 GPa). In addition, we have performed experiments up to 7 GPa on a QuiG system in which the inclusion was only partially shielded from the external pressure to explore the host-inclusion geometry effects.

Theoretical background: a recap on residual strain and Pinc in host-inclusion systems

In this study, we are concerned only with the elastic deformation of the inclusion developed from its entrapment to its final state after the rock exhumation (Angel et al. 2014a, b; 2015; Mazzucchelli et al. 2019), without considering possible visco-plastic deformation (e.g. Zhong et al. 2020).

The volume equation-of-state (EoS), V(P), provides a tool to calculate the volume strain εV. To take into account the elastic anisotropy of the system, we should use the strain tensor εij, which can be calculated from the axial EoSs, li(P), where li represents the corresponding unit-cell parameter. However, the EoSs do not include the elastic relaxation process to restore the mechanical equilibrium between the host and the inclusion at the final state. Therefore, the calculation of the true residual strain is a two-step procedure (Fig. 1), which for QuiG systems is (Mazzucchelli et al. 2019).

  1. 1)

    the unrelaxed strain \({\upvarepsilon }_{\mathrm{ij}}^{\mathrm{unrel}}\) is calculated as

    $$\varepsilon _{{\text{ij}}({\text{qz}})}^{{\text{unrel}}} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{{{\text{V}}_{{\text{gr}}}^{{\text{end}}}}}{{{\text{V}}_{{\text{gr}}}^{{\text{trap}}}}}} \right)}^{1/3}}\frac{{l_{{\text{i}},{\text{qz}}}^{{\text{trap}}}}}{{l_{{\text{j}},{\text{qz}}}^{{\text{end}}}}} - 1,}&{{\text{i}} = {\text{j}}} \\ {0,}&{{\text{i}} \ne {\text{j}}} \end{array}} \right.$$
    (1)

where Vgr is the volume of garnet at the entrapment (trap) and final (end) conditions, while li,qz is the corresponding unit-cell parameter of quartz, derived from EoSs.

Fig. 1
figure 1

Sketch of the real P–T path experienced by a cubic host (blue solid line) subjected to an external pressure Pext, i.e., Phost = Pext, as well as of different P–T paths of an anisotropic inclusion from the entrapment (Ttrap, Ptrap) to the final state (Tend, Pend), while the host experiences an external pressure Pext; the dashed line corresponds to the virtual unrelaxed P–T path of an inclusion forced to fit the cavity of the host during the exhumation. The grey solid line corresponds to the real relaxed P–T path experienced by the inclusion upon exhumation. \({{P}}_{\mathrm{inc}}^{\mathrm{unrel}}\) and \({{P}}_{\mathrm{inc}}^{\mathrm{rel}}\) are derived from the unrelaxed and relaxed residual strain, respectively

Full size image
  1. 2)

    the relaxed strain \({\upvarepsilon }_{\mathrm{kl}}^{\mathrm{rel}}\) is calculated aswhere Rklij is the fourth-rank relaxation tensor, specific for a given host-inclusion system (Mazzucchelli et al. 2019), because it depends on the elastic properties of both the host and inclusion as well as their relative crystallographic orientation.

    $${\varepsilon }_{\mathrm{kl}(\mathrm{qz})}^{\mathrm{rel}}={\mathrm{R}}_{\mathrm{klij}}{\varepsilon }_{\mathrm{ij}(\mathrm{qz})}^{\mathrm{unrel}},$$
    (2)

Knowing the residual strain tensor, we can then calculate the stress tensor σmn as

$${\sigma }_{\mathrm{mn}(\mathrm{qz})}={\mathrm{c}}_{\mathrm{mnkl}(\mathrm{qz})}{\varepsilon }_{\mathrm{kl}(\mathrm{qz})},$$
(3)

where \({\mathrm{c}}_{\mathrm{mnkl}(\mathrm{qz})}\) is the fourth-rank elastic stiffness tensor of quartz, and finally, the inclusion residual pressure Pinc is

$${{P}}_{\mathrm{inc}}=-\frac{\left({\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}\right)}{3}.$$
(4)

Note that the Einstein summation convention is used in Eqs. 2 and 3.

The important difference between Pinc calculated from unrelaxed and relaxed residual strains can be understood by introducing the concept of the entrapment isomeke (Adams et al. 1975): a line in P–T space along which the inclusion volume perfectly matches the volume cavity in the host. Along the entrapment isomeke, the pressure in the inclusion is equal to that of the host Phost, which in turn is identical to the external pressure Pext (see Fig. 1). The pressure on the entrapment isomeke at Tend is called Pfoot and it can be either positive or negative depending on the entrapment conditions. For Pfoot ≠ 0, \(\left|{{P}}_{\mathrm{foot}}\right|>\left|{{P}}_{\mathrm{inc}}^{\mathrm{unrel}}\right|>\left|{{P}}_{\mathrm{inc}}^{\mathrm{rel}}\right|\)(Fig. 1). The last, \({{P}}_{\mathrm{inc}}^{\mathrm{rel}}\), is the relaxed inclusion pressure (hereafter referred to as Pinc) that we can measure experimentally. Null or negative Pinc at ambient conditions may develop in natural quartz inclusions that were trapped (or reset) toward or within the granulite facies (e.g., Kouketsu et al. 2014).

The room-temperature Pinc can be derived from the Raman-peak positions via two methods: (i) the hydrostatic approach, using experimentally established ω(P) trends on reference free crystals (e.g. Enami et al. 2007; Kohn 2014; Kouketsu et al. 2014; Zhong et al. 2019), and (ii) the mode Grüneisen tensor approach, based on the relation (e.g., Angel et al. 2019 and references therein)

$$-\frac{\Delta {\omega }^{\mathrm{m}}}{{\omega }_{0}^{\mathrm{m}}}= {{\varvec{\gamma}}}^{\mathbf{m}}:{\varvec{\upvarepsilon}},$$
(5)

where \({{\varvec{\gamma}}}^{\mathbf{m}}\) is the Grüneisen tensor of phonon mode m, \(\frac{\Delta {\omega }^{\mathrm{m}}}{{\omega }_{0}^{\mathrm{m}}}\) is the relative change in the wavenumber ω of a phonon mode m measured in the inclusion with respect to a free crystal at a given temperature and pressure, and “:” represents a double-scalar product. For uniaxial crystals like quartz, the non-zero independent strain-tensor components are ε11 and ε33, and therefore, Eq. 5 becomes

$$-\frac{\Delta {\omega }^{\mathrm{m}}}{{\omega }_{0}^{\mathrm{m}}}={2\gamma }_{11}^{\mathrm{m}}{\varepsilon }_{11}+{\gamma }_{33}^{\mathrm{m}}{\varepsilon }_{33}.$$
(6)

The Grüneisen tensor components can be calculated from density-functional-theory (DFT) simulations (e.g., Murri et al. 2018; Stangarone et al. 2019), and once we measure ∆ω, we can calculate the relaxed strain tensor and, therefore, the relaxed Pinc by applying Eqs. 3 and 4.

The hydrostatic approach is easy-to-handle and requires only one Raman peak to be measured, but it assumes negligible deviatoric stress in the host-inclusion system. The Grüneisen tensor approach considers the elastic anisotropy, but the minimum number of Raman peaks to be measured should be equal to the non-zero independent strain-tensor components; that is, for quartz inclusions at least two Raman peaks should be used.

Materials and methods

Sample description

Three natural garnet samples (S3, S4, and S5), each containing a single natural quartz inclusion, were manually extracted from a double-polished section of a garnet-bearing para-gneiss coming from the Fjortoft island (62°42′43.4ʺN 6°24′54.7ʺE, Western-Gneiss-Region, Norway). The chemical composition of the host garnet is (Fe1.7Mg0.9Mn0.02Ca0.2)(Al1.95)(SiO4)3 thus consisting of ~ 56 mol% almandine, ~ 35 mol% pyrope, ~ 8 mol% grossular, and ~ 1 mol% spessartine as major end-members.

The QuiG specimens (Fig. 2) were loaded in a Boehler-Almax DAC equipped with diamond culets of 600 µm in diameter. Stainless steel gaskets with a thickness of 250 µm were drilled using an Almax-easyLab spark eroder with a tungsten carbide tip of 300 µm. Gasket pre-indentation, sample dimensions, and initial Pinc are shown in Table 1. It should be noticed that according to previous studies (Mazzucchelli et al. 2018; Campomenosi et al. 2018; Zhong et al. 2020), the inclusion in sample S5 is too close to the external surfaces of the host for it to be elastically isolated. However, the thinner host of S5 allowed us to study this QuiG specimen to higher external pressures and to explore the effects of reduced shielding of the inclusion.

Fig. 2
figure 2

The three QuiG samples loaded in the diamond-anvil cell and a representative Raman spectrum showing the three Raman active modes used in this study to calculate residual strain and Pinc. Peak labels indicate the irreducible representation of the corresponding vibrational mode (Mulliken notation) and their wavenumber measured on a free crystal at ambient conditions (superscript). Raman spectra measured from different points in garnet were identical, indicating no inhomogeneous strain developed in the hosts, indicating that in all three cases, the host was under hydrostatic pressure

Full size image
Table 1 Gasket pre-indentation and host-inclusion size and characterization
Full size table

The pressure-transmitting medium used was a mixture of methanol, ethanol, and distilled water with proportion 16:3:1, respectively, providing hydrostatic pressure up to 10 GPa (Angel et al. 2007). The external P applied on the QuiG was determined via the ruby photoluminescence R1 line (Munro et al. 1985) with a precision of ~ 0.1 GPa.

Raman spectroscopy

Raman spectra were collected using a Horiba Jobin–Yvon T64000 triple-grating monochromator spectrometer (1800 gr/mm) equipped with a Symphony LN2-cooled CCD detector and an Olympus BH41 microscope with a 50 × long-working-distance objective (N.A. 0.5). Raman scattering was excited with the 488.0-nm line of a Coherent Innova 90C FreD Ar + laser. The resulting spectral resolution was ~ 2 cm−1 and the instrumental precision in determining the peak position was 0.35 cm−1. The acquisition time for each spectrum was between 60 s (sample S3 and S4) and 90 s (sample S5) averaged over 10 accumulations (i.e., total acquisition time of 600 and 900 s respectfully) to improve the signal–background ratio. The spectral range set for quartz and garnet Raman spectra was between 50 and 1250 cm−1. Instrumental drift was monitored by collecting the Raman spectra of a free quartz crystal at each pressure step and the resulting average standard deviation in the peak positions was ~ 0.2 cm−1. A background spectrum was measured alongside the samples and then subtracted from the sample spectrum during data evaluation. In addition, the spectra were temperature-reduced according to the Bose–Einstein phonon population factor (e.g., Kuzmany 2009). The OriginPro® 2021 software package was used for data evaluation. Peak position (ω, full-width at half-maximum (FWHM) and integrated intensity were determined by fitting the Raman spectra with a pseudo-Voigt function \(\mathrm{PV}=\mathrm{qL}+\left(1-\mathrm{q}\right)\mathrm{G}\) where L and G are the Lorentz and Gauss peak-shape functions, respectively, and q is a weight coefficient.

Estimating inclusion residual strain and pressure from Raman spectra

The residual pressure Pinc of quartz inclusions was calculated with respect to a free quartz crystal at atmospheric pressure, i.e., at Pext ~ 0 GPa. In addition, to reveal better the effect of the garnet host, the residual pressure of the inclusion was also calculated with respect to a free quartz crystal at the same external pressure as that applied to the host, i.e., the pressure in the DAC. For clarity, we will refer to this pressure hereafter as to ∆P, which is the difference between Pinc and Pext. Both Pinc and ∆P were determined using both the hydrostatic approximation and the Grüneisen tensor approach. For the hydrostatic approximation, we used the P calibration of Morana et al. (2020) for the Raman peaks generated by the E mode near 128 cm−1, the A1 mode near 207 cm−1, and A1 mode near 464 cm−1 (hereafter designated as \({\mathrm{E}}^{128}\), \({\mathrm{A}}_{1}^{207},\) and \({\mathrm{A}}_{1}^{464}\), respectively). For the second approach, we used the same phonon modes with the Grüneisen tensor components calculated via DFT simulations (Murri et al. 2018). The residual stress and, subsequently, the residual Pinc at ambient conditions, were calculated from the strain, using the elastic stiffness tensor c of quartz reported by Lakshtanov et al. (2007) normalized to the isothermal bulk modulus of quartz (Angel et al. 2017). The corresponding cijkl values are available on the EntraPT online platform (Mazzucchelli et al. 2021). At high pressures, the same calculations were carried out, but employed a modified c tensor components according to the dcijkl/dP values obtained from linear fits to the available experimental data points of cijkl(P) at room temperature (Wang et al. 2015).

Predicting inclusion residual strain and pressure from available EoS

The prediction of inclusion residual strain and Pinc according to the available EoS was performed using the EoSFit-7c software (Angel et al. 2014a, b) available at www.rossangel.net. For the quartz inclusions, we used the EoS of Angel et al. (2017), while for the garnet host, we used the pure-almandine EoS (Angel et al. 2022), because the exact garnet composition has negligible effects in the case of QuiG (Angel et al. 2022).

The output of Eosfit-7c (from the EPTH command in the HOSTINC utility) is the unrelaxed residual strain, from which the relaxed strain was calculated using the relaxation tensor approach (Mazzucchelli et al. 2019). Then, the relaxed stress components and Pinc were calculated, using the c tensor specified in the previous subsection. We employed a relaxation tensor R for quartz-in-pyrope, because R for the quartz-in-almandine system is not available. To verify that the garnet composition has negligible effect on the strain relaxation, we performed the same calculations with the available quartz-in-grossular R tensor; the difference in the relaxed volume strains was ~ 0.00015, corresponding to differences in Pinc of ~ 0.005 GPa. We further assumed that dR(P)/dP = 0 for calculations at high pressures. Error propagation in the resulting Pinc at high pressure was estimated following the approach of Mazzucchelli et al. (2021). A worked example of this calculation of strains and Pinc from EoSs is given in the appendix.

The entrapment conditions (Ptrap and Ttrap) used to predict Pinc were chosen to fit (within error) the inclusion volume strain and Pinc measured at ambient conditions: Ptrap and Ttrap of 1.5 GPa and 1173 K for the sample S3 and of 1.4 GPa and 1173 K for the samples S4 and S5. Note that these entrapment conditions are consistent with the metamorphic history of rocks coming from the same area (Gilio et al. 2022).

Results and discussion

Main Raman spectral features: QuiG vs free quartz

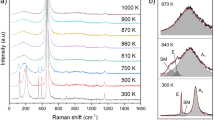
For all the analysed samples, the quartz Raman peaks generated by the \({\mathrm{E}}^{128}\), \({\mathrm{A}}_{1}^{207}\), and \({\mathrm{A}}_{1}^{464}\) modes were very well resolved in the entire pressure range investigated (Fig. 3A); thus, we will focus on these three phonon modes. Figure 3 B shows the pressure dependence ω(P) for QuiG and a free quartz. As can be seen, the pressure derivatives \({(\partial \omega /\partial {P})}_{\mathrm{T}}\) are significantly smaller for QuiG than for a free quartz crystal (Fig. 3 B). This clearly demonstrates the shielding effect of the host garnet: the wavenumber of the quartz inclusion is not a function of the external pressure (Pext), but rather of the strain imposed by the host at that Pext. Because garnet is stiffer than quartz, the inclusion experiences an effectively lower pressure than the actual external pressure acting on the host. The shielding effect of the host is also responsible for the significant difference in FWHM shown by the \({\mathrm{A}}_{1}^{207}\) mode measured in the inclusion with respect to that of a free crystal. At ambient pressure, this mode is involved in strong phonon–phonon interactions, leading to a large FWHM (Jayaraman et al. 1987). Upon a pressure increase, the phonon–phonon interactions weaken, and consequently, the FWHM strongly decreases (e.g., Morana et al. 2020). Hence, the systematically larger FWHM for the \({\mathrm{A}}_{1}^{207}\) mode measured in the inclusion than the free crystal implies that Pinc < Pext.

Fig. 3
figure 3

A Representative Raman spectra of QuiG (sample S3) collected at different pressures. B Wavenumber ω and FWHM vs external pressure for the \({\mathrm{E}}^{128}\), \({\mathrm{A}}_{1}^{207},\) and \({\mathrm{A}}_{1}^{464}\) modes measured in QuiG and compared to a free quartz crystal under hydrostatic pressure (data from Morana et al. 2020). ∆ω = ωinclusion−ωfree is mostly < 0, if determined with respect to a free crystal at the same external conditions, while it is mostly > 0 when determined with respect to a free crystal at ~ 0 GPa. Note that the FWHMs are expected to be constant with pressure, because the phonon decay is not expected to change with pressure if phonon–phonon interactions are negligible (Morana et al. 2020 and references therein)

Full size image

Quantifying Pinc: the hydrostatic approach

Figure 4A and Table S1 show the Pinc calculated from the difference in wavenumber of the inclusions with respect to a free crystal at ~ 0 GPa, ∆ω0, and the hydrostatic P(ω) relations (Morana et al. 2020). The Pinc inferred from the three different modes agree within 0.1 GPa for all the three samples. Samples S3 and S4 also show a relatively good agreement with EoS predictions across the full pressure range investigated, whereas sample S5 does not. The Pinc in sample S5 are shifted from the pressures predicted by the elastic model of isolated inclusions toward the external pressure (blue line in Fig. 4 A). This reflects a lower degree of elastic isolation of the inclusion in sample S5 from the external environment, due to it being closer to the external surface of the host (Table 1). Nevertheless, all three quartz inclusions show Pinc significantly smaller than the external pressure, thus demonstrating the shielding effect of the host garnet. Figure 4A also shows the possibility to directly determine Pfoot by high-pressure experiments as the pressure at which Pinc = Pext, thus providing the locations of the entrapment isomeke.

Fig. 4
figure 4

Residual pressure Pinc (A) and ∆P (B) according to the hydrostatic calibration of Morana et al. (2020). Red solid line corresponds to EoS predictions according to Eqs. 1, 2, 3, 4. Black dashed lines represent Pfoot. Blue solid lines show the expected trends in a free quartz crystal (Free qz). The disagreement in ∆P between different modes shown in B arises from the non-linearity of the behaviour of the E128 and \({\mathrm{A}}_{1}^{207}\) modes with pressure (see text)

Full size image

An alternative way to demonstrate the shielding effect of garnet would be to calculate ∆P (Table S2), which is the difference between the pressure in the inclusion and the external pressure. One might think to calculate ∆P from the ∆ωext with respect to a free quartz crystal at Pext (Fig. 4 B) using the same hydrostatic P(ω) relations (Morana et al. 2020). In this way, the three modes yield negative ∆P, emphasizing that the stiffer garnet host effectively reduces the pressure acting on the softer quartz inclusion. However, only the \({\mathrm{A}}_{1}^{464}\) mode gives results that are consistent with the EoS predictions (sample S3 and S4), while for Pext > 0.5 GPa, the pressures derived from the \({\mathrm{E}}^{128}\) and \({\mathrm{A}}_{1}^{207}\) modes strongly deviate from the EoS results. This discrepancy can be understood by considering the non-linearity of the phonon wavenumbers with respect to pressure. The \({\mathrm{A}}_{1}^{464}\) mode shows linear behaviour of the wavenumber with increasing pressure, whereas the other two modes show a non-linear behaviour (Schmidt and Ziemann 2000; Morana et al. 2020). The latter makes the \({\mathrm{E}}^{128}\) and \({\mathrm{A}}_{1}^{207}\) phonon modes unsuitable to calculate ∆P directly from the measured ∆ωext using the hydrostatic calibration with respect to a free quartz crystal at Pext. A more correct approach is to obtain dP/dω at Pext from the hydrostatic calibration, and apply that to obtain ∆P = ∆ωext. dP/dω, and this yields values consistent with the Pinc, as shown in Fig. 4A. In practical terms, this means that one should take into account ad-hoc polynomial equations obtained by fitting the data collected under hydrostatic pressure starting from the external pressure at which the ∆P has to be determined rather than from ambient conditions. Consequently, each ∆P point in the diagram would require a different hydrostatic calibration.

Quantifying residual volume strain and Pinc: the anisotropic approach

The volume strain of the inclusion \({\varepsilon }_{V}^{inc}\) calculated with respect to a free quartz at ~ 0 GPa and, consequently, the Pinc determined by the Grüneisen tensor approach are also in a good agreement with the EoS predictions within the investigated pressure range (Figs. 5A and 6A, Table S3). On the other hand, when considering the difference between the volume strain of the inclusion and the volume strain of a free quartz at Pext (i.e. \({\Delta \varepsilon }_{V}\)) and the corresponding ∆P, (Fig. 5B and 6B), the Grüneisen approach gives consistent results with EoS predictions up to Pext ~ 1.2 GPa for samples S3 and S4. The good agreement obtained in quantifying \({\Delta \varepsilon }_{V}\) and ∆P with the anisotropic approach employing the mode Grüneisen tensor of all the three modes is because the Grüneisen tensor components γij of quartz can be considered as constant up to ca. 2 GPa (Murri et al. 2019). Consequently, the observed disagreement between EoS and our data at Pext > 1GPa may indicate that at high pressures, γij become strain-dependent. In addition, Murri et al. (2018, 2019) and Morana et al. (2020) have already pointed out the limitation of the Grüneisen-tensor approach in predicting the correct ∆ω for the \({\mathrm{A}}_{1}^{207}\) mode above 2.5 GPa on a free quartz crystal under hydrostatic conditions due to the relatively strong phonon–phonon interactions this mode experiences. However, test calculations of \({\Delta \varepsilon }_{V}\) carried out without this mode did not improve the agreement between ∆P derived from Raman data and from EoS.

Fig. 5
figure 5

Residual volume strain of quartz inclusions \({\upvarepsilon }_{V}^{inc}\) calculated with respect to a free crystal at ~ 0 GPa (A) and difference between volume strain of the inclusion and of a free quartz crystal at Pext ∆εV (B) according to the anisotropic approach using the mode Grüneisen tensors of the E128, \({\mathrm{A}}_{1}^{207}\) and \({\mathrm{A}}_{1}^{464}\) modes. Red solid line corresponds to EoS predictions according to Eqs. 1, 2, 3, 4. Blue solid lines correspond to trends expected for a free quartz crystal

Full size image
Fig. 6
figure 6

The residual pressure Pinc of quartz inclusions calculated with respect to a free crystal at ~ 0 GPa (A) and the difference ∆P between the inclusion Pinc and Pext calculated according to the anisotropic approach using the mode Grüneisen tensor of the E128, \({\mathrm{A}}_{1}^{207}\), and \({\mathrm{A}}_{1}^{464}\) modes and Eqs. 4, 5. Red solid lines corresponds to EoS predictions according to Eqs. 1, 2, 3, 4. Black dashed lines represent Pfoot. Blue solid lines correspond to trends expected for a free quartz crystal (Free qz)

Full size image

Modified metastability of quartz and symmetry breaking

Previous studies on free quartz at high pressures revealed that the change in the pressure dependence of the FWHM of the \({\mathrm{A}}_{1}^{207}\) mode reflects the metastability of quartz as it enters the thermodynamic stability field of coesite (Morana et al. 2020) at ~ 2.4 GPa at 298 K (Bose and Ganguly 1995). As described above, all samples studied here show an FWHM of this mode larger than that of a free crystal at the same Pext (Fig. 3), suggesting that quartz inclusions become metastable with respect to coesite at an external pressure higher than that for a free quartz crystal because of the shielding effect of garnet. This hypothesis can be demonstrated by exploring quartz inclusions at higher pressure.

The thinner sample S5 (see Table 1) allowed us to analyse the quartz inclusion up to 7 GPa, i.e. far beyond the pressure at which coesite becomes thermodynamically stable with respect to quartz under hydrostatic stress. The pressure dependence of the FWHM of the \({\mathrm{A}}_{1}^{207}\) mode indicates that the quartz inclusion in sample S5 becomes metastable with respect to coesite at Pext of ~ 4.4 GPa, i.e. apparently 2 GPa above the quartz–coesite phase boundary (Fig. 7A). However, this external pressure corresponds to an inclusion pressure Pinc of ~ 2.4 GPa (Figure S1), which is the pressure of the quartz–coesite phase boundary at room temperature (Bose and Ganguly 1995). This result confirms that the difference in the observed Pext at which the quartz metastability begins is almost entirely the shielding effect of the host garnet. In natural systems, this shielding effect means that quartz inclusions in a garnet core remain thermodynamically stable even on prograde paths that take the garnet into the stability field of coesite. If further growth of the garnet occurs in the coesite field then the recovered garnets have quartz inclusions in their cores together with coesite inclusions in the rim of the same garnet (e.g. Reinecke 1998; Parkinson 2000).

Fig. 7
figure 7

A Pressure dependence of the FWHM of the \({\mathrm{A}}_{1}^{207}\) mode for a free quartz (red triangles, data from Morana et al. 2020) and for a QuiG (sample S5). The changes in slope are interpreted as indicating the conditions under which quartz (qz) becomes metastable with respect to coesite (coe). The quartz inclusion metastability begins at Pext of ~ 4.4 GPa about 2 GPa above the free crystal. B Pressure dependence of the peak position of the E128 mode for the QuiG sample S5. Above ~ 4.4 GPa, this peak splits in two non-degenerate components (see the blue and green pseudo-Voigt functions in the inset). Red dashed lines represent the pressure of the quartz–coesite thermodynamic phase boundary at ~ 300 K according to Bose and Ganguly (1995). Grey solid lines represent the Pext interpreted as the beginning of quartz metastability with respect to coesite for this sample according to the pressure dependence of the FWHM of the \({\mathrm{A}}_{1}^{207}\) mode

Full size image

In addition, at Pext > 4.4 GPa, the doubly degenerate E128 mode of sample S5 splits into two non-degenerate components, with a wavenumber difference of ~ 3 cm−1 (Fig. 7B). The lifting of mode degeneracies is a result of the so-called morphic effect: a symmetry reduction of the crystal point group due to an external anisotropic field (e.g., electric field, uniaxial stress field, and magnetic field) (Gregora 2006). Since we apply pressure on the QuiG system, the observed symmetry reduction of the quartz inclusion is caused by stress-induced morphic effects. The effect of symmetry-breaking stress on the Raman scattering of quartz has been investigated in several studies using both experimental and theoretical approaches (Tekippe et al. 1973; Briggs and Ramdas 1977; Murri et al. 2019, 2022). According to Tekippe et al. (1973), if quartz undergoes a stress-induced symmetry reduction from trigonal to monoclinic (D3 → C2; Schönflies notation), the splitting magnitude of the E128 mode observed in our experiment would correspond to a deviatoric stress of ~ 0.7 GPa, acting perpendicularly to the trigonal c-axis on the quartz inclusion. It is worth noting that the splitting of the doubly degenerate \({\mathrm{E}}^{128}\) mode and the change in the slope of the pressure dependence of FWHM of the \({\mathrm{A}}_{1}^{207}\) mode for QuiG occur at the same external pressure. This suggests that in the presence of symmetry-breaking stresses, quartz undergoes a crossover to a lower-symmetry state when it becomes thermodynamically metastable with respect to coesite.

Given that garnet under hydrostatic stress undergoes isotropic strain, a fully isolated quartz inclusion keeps the original symmetry unchanged. Thus, the main source of stress-induced symmetry breaking in our experiment is the effects of host-inclusion geometry, namely the position of the inclusion inside the host. The distance between the inclusion boundary and the surface of the host is different along the directions perpendicular and parallel to the diamond culets (see Fig. 1 and Table 1), leading to an anisotropic shielding of the inclusion by the host subjected to the external hydrostatic pressure (e.g., Mazzucchelli et al. 2018; Zhong et al. 2020). That the host-inclusion geometry of sample S5 (Table 1) does not fully meet the requirements for perfectly isolated inclusions, can also be deduced from the deviation in \({\varepsilon }_{V}^{inc}\) and Pinc from the corresponding EoS predictions (Figs. 5, 6A). Nevertheless, our results still represent possible natural processes, because during the garnet crystallization, the inclusion cannot be fully isolated from the surrounding environment. For instance, host-inclusion geometry effects and the consequent anisotropic stress state developed in the inclusion can be very important during quartz entrapment close to the coesite stability field at high temperature (e.g. Richter et al. 2016). Therefore, the interpretation of quartz and coesite inclusions, especially when trapped within the same garnet host but at different stages of growth (e.g. Parkinson 2000), can be quite complex and the elastic anisotropy together with the evolving geometry of the host-inclusion system should not be neglected.

Conclusions

The analysis of residual volume strain and Pinc of quartz inclusions within garnet (QuiG) at high external pressures reported in this study demonstrates the shielding effect of the host garnet and the applicability of Raman spectroscopy to determine the Pinc even when the host is not at atmospheric pressure. For geobarometers like QuiG, in situ Raman spectroscopy at high pressure can be used to directly determine Pfoot by determining when the volume strain and residual pressure of the inclusion match those of a free quartz crystal included inside the DAC.

We further show that the apparent metastability of quartz inclusions with respect to coesite at room temperature is simply the result of the shielding effect of the garnet host; quartz metastability indicated by sharpening of the \({\mathrm{A}}_{1}^{207}\) mode actually occurs at inclusion pressures corresponding to the equilibrium phase boundary at the temperature of the experiment. Moreover, the development of non-hydrostatic stresses due to the host-inclusion geometry may lead to a reduced symmetry state of quartz inclusions to adopt to the metastability of quartz with respect to coesite at high pressure. Finally, because under geologically relevant pressure and temperature conditions, symmetry-breaking stresses may also affect the mean pressure at which quartz transforms into coesite, the partial shielding of the garnet host may have important consequences in the formation of coesite inclusions.