Introduction

Volcanic eruptions feature among the most dangerous natural hazards on Earth (Wendee 2022), and can range in style from effusive lava-fed fountains to explosive eruptions that are capable to generate pyroclastic flows and destructive ashfalls (Gonnermann et al. 2017; La Spina et al. 2020). Eruptive style is mainly controlled by the decompression rate and by the ability of the gas phase to escape the magma (Mueller et al. 2008; Degruyter et al. 2012; Cashman and Scheu 2015; Gonnermann 2015; Cassidy et al. 2018), with viscosity modulating the decoupling between magma and gas phase and the overall transport mechanism (Webb and Dingwell 1990; Zhang 1999; Koyaguchi and Mitani 2005; Lautze and Houghton 2007; Vona et al. 2011; Gonnermann 2015; Di Genova et al. 2017b). Therefore, viscosity is arguably the most important physical property controlling magma dynamics and eruptive styles (Sparks 2003; Giordano et al. 2008). Magma viscosity strongly depends on the composition of the molten phase (including dissolved volatile phases), temperature, bubble content and crystal cargo (Friedman et al. 1963; Richet et al. 1996; Ishibashi and Sato 2007; Vetere et al. 2007; Vona et al. 2011; Gonnermann and Manga 2012; Robert et al. 2013; Sehlke et al. 2014; Chevrel et al. 2015; Campagnola et al. 2016; Di Genova et al. 2017a, 2018; Cassidy et al. 2018; Romano et al. 2020). Previous experimental studies have extensively investigated the dependence of melt viscosity on composition and temperature (Hui and Zhang 2007; Giordano et al. 2008, 2009; Misiti et al. 2009, 2011). However, recent works have demonstrated that volcanic melts are prone to nano-crystallization and dehydration during viscosity measurements (Di Genova et al. 2017a, 2020b; Kleest et al. 2020; Okumura et al. 2022; Scarani et al. 2022). These effects may hinder the accurate determination of melt viscosity, directly affecting the reliability of the resulting models assessing magma transport (Scarani et al. 2022), and therefore preventing effective numerical modelling of magma dynamics upon decompression.

In this work, we investigated the viscosity of Stromboli basalt as a function of temperature and dissolved water content, developing a novel and accurate viscosity model based on the Mauro-Yue-Ellison-Gupta-Allan (MYEGA) parametrization (Mauro et al. 2009). Combining conventional and flash differential scanning calorimetry (C-DSC and F-DSC), viscometry, Raman and Brillouin spectroscopy, we demonstrate that the hydrous Stromboli melt is prone to nano-crystallization during viscosity measurements and that its viscosity is significantly lower than expected based on literature models (Hui and Zhang 2007; Giordano et al. 2008, 2009; Langhammer et al. 2022).

Stromboli is the northernmost volcanic island of the Aeolian archipelago in the Tyrrhenian Sea (Italy), formed by the subduction of the African plate under the Eurasian plate (Revil et al. 2011). It reaches an elevation of 924 m above sea level and constitutes the exposed portion of a substantial stratovolcano measuring approximately 2500 m in height (Bertagnini et al. 2003). Stromboli volcano is known for its persistent strombolian activity and its sporadic paroxysmal events (Métrich et al. 2009; Vona and Romano 2013; Andronico et al. 2021; Mattia et al. 2021), the latter being responsible for the most hazardous eruptions. This behaviour has been associated with a sudden rapid rise of the magma (Métrich et al. 2009; Misiti et al. 2009; Pichavant et al. 2013; Le Gall and Pichavant 2016a; Andronico et al. 2021; Ripepe et al. 2021a, b), with ascent rates that can only be reliably estimated provided that a correct parametrization of magma viscosity is available. Due to the noticeably lower melt viscosity emerging from our experimental data with respect to previous studies, numerical models of magma ascent at Stromboli should therefore consider noticeably higher ascent rates, with implications for the outgassing dynamics upon decompression. Consequently, our findings are anticipated to improve numerical simulations, providing enhanced constraints on magma ascent time-scales and on the evolution of magma rheology resulting from decompression and degassing.

The current understanding of how the viscosity of volcanic melts is affected by the formation of nanocrystals

Various authors have recently focused their investigations on nanocrystallization processes occurring in volcanic melts, demonstrating that these processes may have a critical effect on rheology, namely an increase in the effective viscosity of magmas. Based on such literature, two parallel mechanisms can be identified to be responsible for this increase in viscosity.

The first mechanism dominates around the glass transition temperature, in the high viscosity interval (108 Pa s \(\lesssim\)η \(\lesssim\)1013 Pa s). Several studies that focused on a wide range of melt compositions, including basaltic (Bouhifd et al. 2004; Di Genova et al. 2020b; Scarani et al. 2022), andesitic (Richet et al. 1996; Liebske et al. 2003; Vetere et al. 2006; Okumura et al. 2022), tephri-phonolitic-foiditic (Kleest et al. 2020), and rhyolitic melts (Di Genova et al. 2017a) clarified that the increase in viscosity can be attributed to the diffusion of iron and titanium within the initially homogenous melt to form oxide (nano)crystals. For instance, Okumura et al. (2022) proposed that the increase of the anhydrous viscosity due to magnetite nanocrystallization in andesitic magmas is well-explained by the complete depletion of iron in the melt phase. Therefore, this process is crucially dependent on the (continuously evolving) composition of the melt phase. The gradual clustering of iron and titanium takes place, initially in an amorphous state, eventually resulting in the formation of Fe-Ti-enriched (nano)crystals (Scarani et al. 2022).

The second mechanism operates in the undercooled melt at high temperatures, where the low viscosity (10−3 Pa s \(\lesssim\) η \(\lesssim\) 103 Pa s) of the melt is thought to promote nanolite aggregation and melt entrapment within these aggregates (Di Genova et al. 2020a). Although nanolites may be present in very low volume fractions (typically far less than 10 vol%, i.e., at fractions deemed to be uninfluential in the case of microlite suspensions;Mueller et al. 2011b; Vona et al. 2011), the melt entrapment within aggregates could result in an increased effective volume of the solid, which, in turn, increases the overall viscosity of the magma. Nanolite aggregation was observed in the laboratory, examining in situ a Mt. Etna trachybasalt, and in the eruptive products of the Plinian eruption of Mt. Etna 122 CE (Di Genova et al. 2020a). Notably, this melt entrapment mechanism is not necessarily restricted to the nano-sized domain; in-situ high-temperature 4D studies of crystal growth kinetics and textural evolution during crystallization of Mt. Etna trachybasaltic magma under water-saturated conditions showed a rapid dendritic crystallization that favoured the entrapment of melt between microlite branches (Arzilli et al. 2022).

Finally, the role of nanocrystallization reaches beyond the liquid and crystalline fractions of the magma, as nano-sized Fe-Ti nanolite oxides have been shown to promote heterogeneous bubble nucleation (Cáceres et al. 2020; Di Genova et al. 2020a) that might be crucial for the fragmentation of the magma (Knafelc et al. 2022; Yoshida et al. 2023).

Materials and methods

Synthesis of Stromboli glasses

The starting materials used in this work are ash-to-lapilli-sized pyroclasts corresponding to the low porphyritic (LP) deposit from the July–August 2019 eruption of Stromboli volcano, Italy. Firstly, a homogeneous anhydrous crystal- and bubble-free glass was produced by crushing and melting the natural samples in a Pt crucible at 1400 ℃ for 4 h. The obtained glass was crushed to powder size and mixed before a second melting was performed at the same conditions for chemical homogenization. A fraction of the glass material was subjected to grinding, resulting in a powdered form, which was subsequently divided into two different grain sizes through the process of sieving. (i.e., < 100 μm and 100–250 μm diameter). Subsequently, the two powder sizes were mixed at a 1:1 weight ratio to minimize porosity during the high-temperature and -pressure synthesis of water-bearing glasses. The remaining glass was kept to perform viscosity measurements and Brillouin spectroscopy of the anhydrous sample. Water-bearing glasses, from 0.9 ± 0.03 to 4.7 ± 0.26 wt% H2O, were synthesized using a piston-cylinder apparatus at the Bayerisches Geoinstitut in Bayreuth (University of Bayreuth, Germany), in addition to an internally heated pressure vessel (IHPV) equipment at the Institute of Mineralogy in Göttingen (University of Göttingen, Germany). For the piston-cylinder experiments, hydrous samples were prepared by adding distilled water stepwise to the dry powder in Au80Pd20 capsules (4.6 mm inner diameter; 10–12 mm length), which have been shown to minimize iron loss during the synthesis of starting materials (Pichavant et al. 2013). After welding the capsules, they were weighed and then left overnight in a furnace at 150 ℃ to check for possible water loss. The capsules that did not show weight loss after this treatment were used for the hydrous synthesis using a talc-pyrex-Al2O3 assembly at 1200 ℃ and 5–10 kbar at intrinsic reduced oxygen fugacity conditions (\({f}_{{O}_{2}}\) < NNO + 0), with a 24 h dwell to ensure water homogenization within the sample. Eventually, a rapid cooling process with a rate of approximately 100 K s−1 was applied to the melt. This was achieved by deactivating the heating power and employing an automatic pressure controller to maintain the pressure within nominal levels throughout the cooling phase. Samples were slowly decompressed to ambient pressure to avoid fractures. Additionally, one extra anhydrous glass was synthesised at 1250 ℃ and 5 kbar to account for the effect of pressure in the synthesis of our glasses. For the IHPV experiments, dry glass powder and an appropriate amount of distilled water were loaded in Au80Pd20 capsules (3 mm inner diameter; 15 mm length). All samples were stacked together and the synthesis was run at 5 kbar and 1250 ℃ for 24 h at relatively oxidizing conditions (\({f}_{{O}_{2}}\) = NNO + 3 ± 1) as determined by Schuessler et al. (2008). Samples were rapidly quenched with a cooling rate of ~ 150 K s−1 at isobaric pressure. Throughout the manuscript, all samples are renamed based on their measured water content in wt% (e.g., S_0 for the anhydrous material and S_3.36 for a sample with 3.36 ± 0.01 wt% H2O).

Electron microprobe analyses

The major elemental composition (Si, Ti, Al, Fetot., Mn, Mg, Ca, Na, K, and P) was determined using a JEOL JXA-8200 electron microprobe at the Bayerisches Geoinstitut (University of Bayreuth, Germany) (Supplementary Table 1). The anhydrous and hydrous glasses were embedded in epoxy, polished, and carbon coated. Measurements were performed using 15 kV voltage, 5 nA current, and 20 s of counting time. A defocused 10 μm beam was used for all elements. Between 20 and 30 points per sample were measured to account for heterogeneities. Synthetic wollastonite (Ca, Si), periclase (Mg), hematite (Fe), spinel (Al), orthoclase (K), albite (Na), manganese titanate (Mn, Ti), and apatite (P) were used as calibration standards. Sodium and potassium were analysed first to prevent alkali migration effects (Hughes et al. 2019). The findings from this analysis, as presented in Supplementary Material Table 1, provided confirmation that the composition of our anhydrous glass closely corresponded, within the margin of uncertainty, to previous studies that investigated the melt viscosity of Stromboli basalt (Giordano et al. 2006; Misiti et al. 2009).

Table 1 Glass transition (Tg), water speciation, total water concentrations and K/G factors of Stromboli glasses
Full size table

Water content determination

The water content of Stromboli glasses was measured using Fourier-transform infrared spectroscopy (FTIR) at the Bayerisches Geoinstitut (University of Bayreuth, Germany). We used a Bruker IFS 120 spectrometer connected to a Bruker IR microscope. Spectra were acquired using a tungsten light source with a Si-coated CaF2 beam-splitter and a narrow-band MCT (mercury; cadmium; telluride) detector. FTIR measurements were acquired between 1000 to 6000 cm−1 on doubly polished samples (⁓0.2–0.3 mm thickness). The analysed spot was 100 μm in diameter with a spectral resolution of 4 cm−1. For each spectrum, 200 scans were accumulated. All hydrous glasses were measured at least three times at different spots to account for possible heterogeneity. The total water content was derived using the peak areas of the OH− and H2O bands (⁓4500 cm−1 and 5200 cm−1, respectively), which correspond to the combination of the stretching and bending modes of OH− groups and water molecules. To determine the peak area values, an appropriate baseline under the OH− and H2O bands was defined using the “two Gaussians” (GG) baseline and the “GGpar” integral molar absorption coefficients (εOH- = 0.62; εH2O = 0.71) following Ohlhorst et al. 2001. This approach is more suitable than other methods (e.g., “straight line” (TT) baseline) for determining water concentration in basalts because the superimposition of bands resulting in a curved baseline is considered (Ohlhorst et al. 2001).

Raman spectroscopy

Stromboli glasses subjected to C-DSC, F-DSC and micropenetration were characterized before and after experimental measurements to account for potential modifications (i.e., crystallization and/or water loss). We used a confocal Raman imaging microscope at the Institute of Non-Metallic Materials, TU Clausthal (alpha300R, WITec GmbH), and a Dilor XY spectrometer at the Bayerisches Geoinstitut (Horiba Jobin Yvon Inc.). Spectra were acquired with a 100 × objective in the ranges between 200–1300 cm−1 for the silicate region and between 2700–4000 cm−1 for the water region. The integration time was 7 s (3 accumulations, 13 mW laser power), and 30 s (2 accumulations, 2 mW laser power) for the Dilor XY spectrometer. Additionally, spectra acquired by the Dilor XY spectrometer were background-corrected due to an interference between the interferometer node and the filter glass. All spectral intensities were further corrected for temperature and frequency-dependence scattering according to Tsyganenko and Smirnov (1995). Then, we subtracted the background using cubic splines fit through intervals in the silicate (from 200 to 300, and from 1240 to 1300 cm−1) and water (from 2700 to 3100, and from 3750 to 3900 cm−1) regions. In conclusion, all spectra were subjected to a smoothing process in order to minimize noise.

Micropenetration viscometry

We subjected polished plane-parallel glass chips (3 mm thick) to micropenetration viscometry measurements using a vertical dilatometer (Bähr VIS 404) at the Institute of Non-Metallic Materials, TU Clausthal. We measured the indentation rate of a sapphire sphere (r = 0.75 mm) during isothermal dwells at temperatures controlled using an S-type thermocouple (Pt-PtRh) placed at ~ 2 mm from the sample surface. The temperature error is estimated to be ± 5 K considering the accuracy of the S-type thermocouple and its distance from the sample (Behrens et al. 2018). We followed standard procedures (Di Genova et al. 2014a, 2020b; Scarani et al. 2022) to achieve thermal equilibration of the sample at the target temperature. The indentation depth was measured as a function of time and the viscosity curve was determined according to Eq. 1 (Douglas et al. 1965):

$$\begin{array}{c}\eta =\frac{9F}{32 \sqrt{2r} \sqrt{{L}^{3}}}t\end{array}$$
(1)

where η is the Newtonian viscosity (Pa s), F is the applied force (N), t is the time (s), r is the radius of the sphere (m) and L is the indentation depth (m). Viscosity measurements of the standard glass DGG-1 were used to calibrate the vertical dilatometer, reproducing the certified viscosity data (Meerlender 1974) with a deviation of ± 0.1 in log units. As the effect of a uniform (hydrostatic) pressure on the liquid viscosity of silicate melts is relatively small at around glass transition (0.1 log units per 100 MPa; Del Gaudio et al. 2007), micropenetration experiments at ambient pressure were used to model the dynamic behaviour of silicate melts under eruptive conditions.

Differential scanning calorimetry

Differential Scanning Calorimetry (DSC) measurements were performed at the Institute of Non-Metallic Materials (TU Clausthal) using two apparatuses. We used 20 ± 5 mg of glass in a PtRh20 crucible under a constant N2 5.0 flow rate (20 ml min−1) in a conventional differential scanning calorimeter (C-DSC, 404 F3 Pegasus, Netzsch), which allowed the measurement of the heat flow at a heating rate (qh) between 5 and 30 K min−1. Moreover, we used ~ 50 ng of glass for the analyses performed with a flash calorimeter (F-DSC, Flash DSC 2 + , Mettler Toledo) equipped with UFH 1 sensors, under constant Ar 5.0 flow (40 ml min−1), which allowed the measurement of the heat flow at a heating rate (qh) between 100 and 30,000 K s−1 (6,000 and 1,800,000 K min−1). The C-DSC was calibrated using melting temperatures and enthalpy of fusion of reference materials (pure metals: In, Sn, Bi, Zn, Al, Ag, and Au). The F-DSC was calibrated using the melting temperature of aluminium (melting temperature 933.6 K) and indium (melting temperature 429.8 K).

For C-DSC measurements, we followed the methodology presented by Stabile et al. (2021). Namely, we initially erased the thermal history of the glass via a two-step thermal treatment: we heated the sample at a rate qh = 20 K min−1 up to a few degrees above Tpeak (the undershoot of the heat flow curve in the glass transition region, see Fig. 1) and subsequently cooled the melt to 100 °C at a rate qc = 10, 15, 20, or 30 K min−1. We then performed the actual C-DSC measurement using the rate-matching method, by performing an additional upscan (i.e., heating segment at qh) at a rate matching that of the previous downscan (i.e., cooling at qc), i.e., qh = qc. From the measured heat flow during the second upscan, we extracted the characteristic temperatures Tonset and Tpeak as indicated in Fig. 1: Tpeak corresponds to the above-mentioned undershoot of the heat flow curve, while Tonset represents the intercept between the tangent to the heat flow curve of the glass (i.e., before the fictive temperature) and the tangent to the inflection point during the glass transition. For the F-DSC measurements, we used the same procedure mentioned above, but at higher qh,c (Di Genova et al. 2020b; Al-Mukadam et al. 2021; Stabile et al. 2021; Scarani et al. 2022). Finally, viscosity was calculated from C- and F-DSC data using the relationship between the matching heating rate (qh) of the measurement and the shift factors Konset and Kpeak (Di Genova et al. 2020b; Stabile et al. 2021) expressed in Eq. 2:

$$\begin{array}{c}{log}_{10}\eta \left({T}_{onset,peak}\right)={K}_{onset,peak}-{log}_{10}\left({q}_{h}\right)\end{array}$$
(2)

where Konset = 11.20 ± 0.15 and Kpeak = 9.84 ± 0.20 (Di Genova et al. 2020b; Stabile et al. 2021). Notably, when qh is 10 K min−1, η(Tonset) ≈ 1012 Pa s, and therefore, Tonset ≈ Tg.

Fig. 1
figure 1

Heat flow of anhydrous Stromboli glasses measured as a function of temperature using a conventional DSC. The red and black lines correspond to the second upscan during measurements performed at 30 and 15 K min−1 using the rate-matching method (Di Genova et al. 2020b; Stabile et al. 2021), respectively

Full size image

Brillouin spectroscopy

Brillouin spectroscopy (BLS) measurements were performed at the Bayerisches Geoinstitut in Bayreuth, Germany. Plane-parallel polished glass samples of ⁓50 μm thickness were measured using a solid-state Nd:YVO4 laser source with a wavelength of 532 nm, with a power at the source of 50 mW. The Brillouin frequency shift was quantified using a six-pass Fabry–Perot interferometer (Whitfield et al. 1976) combined with a single-pixel photon counter detector. The experiments were conducted using a symmetric forward scattering geometry (Whitfield et al. 1976; Cassetta et al. 2021) with a scattering angle of θ = 79.8°. The scattering angle was calibrated using a silica reference glass. Frequency shifts (Δω) were converted to longitudinal (vp) and shear (vs) sound velocities using Eq. 3:

$$\begin{array}{c}v=\frac{\Delta \omega \lambda }{2sin\left(\theta /2\right)}\end{array}$$
(3)

where λ is the laser wavelength and θ is the angle between the incident and scattered beams (Whitfield et al. 1976; Sinogeikin et al. 2006). We collected between 4 and 8 spectra for each sample at different rotation angles (from -180° to + 180°) to account for uncertainties. Finally, we calculated the K/G ratio using the longitudinal (vp), and shear (vs) acoustic velocities using Eq. 4:

$$\begin{array}{c}\frac{K}{G}={\left(\frac{{v}_{p}}{{v}_{s}}\right)}^{2}-\frac{4}{3}\end{array}$$
(4)

Viscosity modelling

The combination of C-DSC and Brillouin spectroscopy (BLS) enabled the parameterization of the melt viscosity of hydrous and anhydrous samples as a function of temperature η(T), via the Mauro–Yue–Ellison–Gupta–Allan (MYEGA) equation (Eq. 5) (Mauro et al. 2009):

$$\begin{array}{*{20}c} {log_{{10}} \eta \left( T \right) = log_{{10}} \eta _{\infty } + \left( {12 - log_{{10}} \eta _{\infty } } \right)\frac{{T_{g} }}{T}exp\left[ {\left( {\frac{m}{{12 - log_{{10}} \eta _{\infty } }} - 1} \right)\left( {\frac{{T_{g} }}{T} - 1} \right)} \right]} \\ \end{array}$$
(5)

where \({log}_{10}{\eta }_{\infty }=-2.93\pm 0.3\) is the logarithmic viscosity at infinite temperature (Mauro et al. 2009; Langhammer et al. 2021), \({T}_{g}\) is the glass transition temperature determined by C-DSC (Tonset at qh,c = 10 K min−1) and m is the melt fragility defined in Eq. 6 (Angell 1995) as the slope of viscosity curve evaluated at Tg:

$$\begin{array}{c}m={\left.\frac{\partial {log}_{10}\eta }{\partial {T}_{g}/T}\right|}_{T={T}_{g}}\end{array}$$
(6)

Simultaneously, the melt fragility parameter, m, can be obtained from BLS measurements using the empirical relationship introduced in Cassetta et al. (2021) (Eq. 7). This relationship has also been recently validated for peridotitic melts by Di Genova et al. (2023):

$$\begin{array}{c}m=43\cdot \frac{K}{G}-31\end{array}$$
(7)

To describe the dependence of \({T}_{g}\) from total water content, we use the model proposed by Schneider et al. (1997), according to Langhammer et al. (2021) (Eq. 8):

$$\begin{array}{c}{T}_{g}\left({x}_{{H}_{2}\mathrm{O}}\right)= {w}_{1}{T}_{g,{H}_{2}\mathrm{O}}+{w}_{2}{T}_{g,d}+c{w}_{1}{w}_{2}\left({T}_{g,d}-{T}_{g,{H}_{2}\mathrm{O}}\right)+d{w}_{1}{{w}_{2}}^{2}\left({T}_{g,d}-{T}_{g,{H}_{2}\mathrm{O}}\right), \end{array}$$
(8)

with

$$\begin{array}{c}{w}_{1}= \frac{{x}_{{H}_{2}\mathrm{O}}}{b\left(100-{x}_{{H}_{2}\mathrm{O}}\right)+{x}_{{H}_{2}\mathrm{O}}}\, and\, {w}_{2}= \frac{b\left(100-{x}_{{H}_{2}\mathrm{O}}\right)}{b\left(100-{x}_{{H}_{2}\mathrm{O}}\right)+{x}_{{H}_{2}\mathrm{O}}},\end{array}$$
(9)

where \({X}_{{H}_{2}O}\) is the mol% of dissolved water, \({T}_{g,d}\) is the glass transition temperature of the anhydrous composition and \({T}_{g,{H}_{2}O}\) is the glass transition of pure water equal to 136 K (Kohl et al. 2005). Note that b, c, and d, are fitting parameters. As such, our melt viscosity model for Stromboli basalts incorporates the effect of water on η(T) via \({T}_{g}\).

Results

Scanning electron microscopy, Raman and FTIR analyses

Scanning electron microscopy imaging in backscattered electron (BSE) mode (Supplementary Material Fig. 1) and Raman spectra analysis (Fig. 2) were used to verify the pristine glass nature of the samples before and after viscosity and calorimetric measurements (Di Muro et al. 2009; Di Genova et al. 2016). Indeed, previous research (Di Genova et al. 2017a, b, 2020a, b; Giordano et al. 2021; Kleest and Webb 2022; Scarani et al. 2022) has demonstrated that BSE imaging alone cannot conclusively confirm the presence or absence of nanolites, since the spatial resolution of this technique is insufficient to identify objects exhibiting a size of only few tens of nanometers. Conversely, its combination with Raman spectroscopy represents a more reliable approach for detecting Fe-Ti nanolites, even when BSE images are unable to show crystals that are instead indisputably visible using transmission electron microscopy (Di Genova et al. 2017a, b, 2020a, b; Scarani et al. 2022).

Fig. 2
figure 2

Raman spectra of anhydrous and hydrous glasses before C-DSC and viscosity measurements. The spectral range (650–730 cm−1) most prominently affected by the presence of Fe-Ti-oxides is shaded in gray, with a dashed line marking the usual maximum (~ 690 cm−1) of the peak assigned to these phases (Di Genova et al. 2020b; Stabile et al. 2021). Samples labelled with asterisk were synthesized using IHPV, while the rest were synthesized under piston-cylinder experiments

Full size image

In the case of our samples, BSE analyses (Supplementary Material Fig. 1) show no evidence of crystals or bubbles before and after viscosity experiments. As for Raman spectra (Fig. 2), they confirmed first-of-all the crystal-free amorphous nature of our initial anhydrous and hydrous samples (Di Muro et al. 2009; Di Genova et al. 2016). This confirmation arises from the absence of characteristic features in the 650–730 cm−1 range, associated with the most prominent signal of Fe-Ti-oxides, which typically peaks around ~ 690 cm−1 (Di Genova et al. 2020a, b). In contrast, and regardless of the fact that no nanolites were observed by BSE, Raman spectra acquired in the low-wavenumber range (< 1300 cm−1) post-DSC and post-micropenetration measurements (Fig. 3) evidence that samples with H2O content greater than 1 wt% underwent a certain degree of crystallization of Fe–Ti-oxide nanolites during such high-temperature analyses. We identified two groups of nanolite-bearing glasses post-experiments: (i) samples showing a low-to-moderate degree of nanolitization (Fig. 3a), except for S_0.91 that did not experience nanolite crystallization, and (ii) samples that present a more prominent Raman feature peaking at ~ 690 cm−1, suggesting a substantial compositional modification of the residual melt during C-DSC experiments (Fig. 3b). We observed that this difference is associated with the oxidation conditions of the starting materials. Samples synthesized using the relatively oxidizing IHPV method experienced the highest changes after DSC and viscosity measurements, compared to the ones synthesized by piston-cylinder experiments.

Fig. 3
figure 3

Raman spectra of hydrous glasses after C-DSC analyses and micropenetration measurements (MP). The spectral range (650–730 cm−1) most prominently affected by the presence of Fe-Ti-oxides is shaded in gray, with a dashed line marking the usual maximum (~ 690 cm−1) of the peak assigned to these phases (Di Genova et al. 2020b; Stabile et al. 2021). The heating rate used during DSC measurements is reported in the legend. a Samples synthesized using piston-cylinder. Raman spectra show a low to moderate degree of nanolitization b Samples synthesized using IHPV. Raman spectra show a strong contribution in the 650–730 cm−1 region associated with the crystallization of Fe-Ti-oxides

Full size image

To account for possible loss of water during experiments, we acquired FTIR and Raman spectra of hydrous samples before and after DSC, as well as before and after micropenetration measurements (Fig. 4).

Fig. 4
figure 4

a FTIR comparison of water spectral bands before and after C-DSC measurements. Red arrows show the formation of a new peak at ⁓4300 cm−1 after C-DSC measurements that might be attributed to the apparition of free hydroxyl groups (Bondar et al. 2022). b, c, and d correspond to the comparison of the Raman water region before and after C-DSC measurements. Blue arrows show the development of a shoulder at ⁓3700 cm−1 associated to free OH species (Larre et al. 2020)

Full size image

FTIR analyses show that the area of the molecular H2O bands (5200 cm−1) did not vary significantly after DSC measurements. However, for samples with the highest water content (S_3.36, S_4.32 and S_4.69), a new contribution at ⁓4300 cm−1 was observed (Fig. 4a). This new feature might be related to the formation of free hydroxyl species: as recently suggested by Bondar et al. (2023), such OH groups could be associated to alkaline earth cations (e.g., Ca and Mg) rather than to tetrahedrally coordinated network formers (such as Al and Si), thereby playing a markedly different structural role. For the other samples characterized by a lower water content (< 3 wt%), the area of the OH− bands did not show significant changes.

Concerning Raman data, we normalized the intensity of the water band area at high wavenumber (HW; 2700–4000 cm−1) to the area of the silicate region at low wavenumber (LW; 200–1300 cm−1) to check for possible water loss (Di Genova et al. 2017b). The comparison between the HW/LW ratio before and after DSC experiments showed a significant decrease for the sample with the highest water content (S_4.69). Nevertheless, the quantification of water content depletion was not performed using Raman spectroscopy due to previous studies indicating that this technique is not reliable for glasses that contain nanolites (Di Genova et al. 2017b). Importantly, and for the same three samples mentioned (S_3.36, S_4.32 and S_4.69) above for FTIR analysis, we observed the development of a Raman shoulder at ⁓3700 cm−1 (blue arrows in Fig. 4). This contribution was previously associated with the formation of free OH species, as suggested by Larre et al. (2020). Therefore, by combining FTIR and Raman spectra, we deduce that samples with a water content exceeding 3.3 wt% underwent both nanocrystallization and possibly the generation of free hydroxyls during the experiments. In general, regardless of the synthesis method employed, we observed more pronounced structural modifications as the water content increased, particularly following DSC and micropenetration experiments.

Viscosity, fragility, and glass transition temperature of the anhydrous melt

C-DSC- and F-DSC-derived anhydrous melt viscosity are reported as a function of temperature in the Supplementary Material Table 2 and shown together with literature data in Fig. 5. To accurately characterize the anhydrous viscosity of Stromboli basalt, we used the MYEGA parametrization (Eq. 5), fixing log10η∞ = -2.93 (Mauro et al. 2009; Langhammer et al. 2021; Scarani et al. 2022), to fit our anhydrous C-DSC-derived viscosity (10.1 < log η < 11.98) together with micropenetration (7.8 < log η < 10.5) and concentric cylinder data (0.8 < log η < 1.9) from Scarani et al. (2022) to fully constrain the melt fragility index (m = 40.7 ± 0.7) and glass transition temperature (Tg = 666.9 ± 0.8 ℃). Our fragility estimates are slightly lower compared to the empirical viscosity model proposed by Giordano et al. (2009) for Stromboli composition (m = 42 and Tg = 662.5 ℃), who nevertheless used a Vogel-Fulcher-Tammann (VFT) parameterization, \({log}_{10}\eta \left(T\right)= {log}_{10}{\eta }_{\infty }+\frac{B}{T-C},\) intrinsically involving a different viscosity at infinite temperature (\({log}_{10}{\eta }_{\infty }=-4.55\)) (Russell et al. 2003; Misiti et al. 2009; Langhammer et al. 2021). When we used the VFT parametrization and assuming \({log}_{10}{\eta }_{\infty }=-4.55\) to fit our dataset, we obtained Tg = 667.4 ± 0.8 ℃ and m = 42 ± 0.7, which is in excellent agreement with Giordano et al. (2009). Therefore, the viscosity formulation (MYEGA or VFT), and the resulting choice of \({log}_{10}{\eta }_{\infty }\), have a negligible effect on the estimations of m and Tg. Finally, we found that our anhydrous F-DSC-derived viscosity (6.4 < log < 8.5), which was not used to constrain our MYEGA parameterization, is in excellent agreement with our fit, suggesting that F-DSC-derived viscosity can be used to accurately derive viscosity of volcanic melts.

Fig. 5
figure 5

Viscosity of anhydrous Stromboli melt as a function of temperature. The black line corresponds to the best fit of the data using the MYEGA equation (Eq. 5) combining our C-DSC data with micropenetration and concentric cylinder data from Scarani et al. (2022). The same data were also fit using the VFT formulation (dashed grey line, see text for details). F-DSC data were not used to constrain the MYEGA and VFT fits. For comparison purposes, we report viscosity data from Misiti et al. (2009) and Giordano et al. (2006) who examined the same composition

Full size image

Viscosity, fragility, and glass transition temperature of the hydrous melt

The DSC-derived and measured hydrous viscosity are reported in Table 3 of the Supplementary Material and shown in Fig. 6. Raman spectroscopy results showed that almost all our hydrous glasses, except for S_0.91 and S_4.32 after F-DSC, crystallized Fe-Ti-oxide nanolites during viscosity measurements. On the other hand, we also observe that samples with water content higher than 3.3 wt% suffered occasional loss of total water content, with the parallel formation of free OH species during viscosity experiments. Previous studies (Stabile et al. 2021; Okumura et al. 2022; Scarani et al. 2022) have shown that the removal of Fe-Ti-oxides from volcanic melts during nanocrystallization induces a non-trivial increase in the viscosity of the residual melt. As such, we infer that our hydrous viscosity results do not represent the viscosity of the pure hydrous melt, which is expected to be lower, especially at high water contents. Nevertheless, measurements performed at the glass transition temperature Tg (η = 1012 Pa s) were virtually unaffected by nanocrystallization, while the instability of the samples was more and more evident as the temperature increased. We remark that the timescale of nanocrystallization during C-DSC experiments seems to be in the order of seconds to a few minutes, occurring as soon as the temperature of the sample crosses Tg. We observe that considering these increasingly nanolite-bearing measurements as valid data points would misleadingly result in an apparent decrease of m, as inferred by the slopes of the dashed lines in Fig. 6. Conversely, when considering only nanolite-free measurements (i.e., S_0.91 and S_4.32 dashed lines in Fig. 6), we observe that the slope of the dashed lines does not exhibit a marked dependence on water content. The instability of hydrous samples during the measurements is reaffirmed by the data acquired by micropenetration. For example, when measuring sample S_4.32, we observed a time-dependent increase in viscosity from 1010.38 to 1011.67 Pa s in 60 min (orange arrow in Fig. 6) during the micropenetration measurement between 459 and 461 ℃ (i.e., ⁓50 ℃ above Tg), resulting in a viscosity almost two orders of magnitude greater than C-DSC-derived estimations. Also, for sample S_1.97, we observed a considerable difference between micropenetration and C-DSC-derived viscosities, with η = 1011.88 and 1010.62 Pa s (546 ℃), respectively. We attribute the observed variation to the occurrence of nanocrystallization and water loss during micropenetration measurements, which are conducted for longer durations above Tg compared to DSC (differential scanning calorimetry) experiments.

Fig. 6
figure 6

Experimental viscosity of hydrous Stromboli melt. Water contents are labeled by color. Circles, diamonds, and triangles represent C-DSC, F-DSC, and MP measurements, respectively. Filled symbols correspond to nanolite-free measurements. Dashed lines are a guide for the eye. The arrow shows the increase in viscosity during MP measurements

Full size image

The glass transition temperature (Tg) was either directly derived (Tonset at qc,h = 10 K min−1, see methodology paragraphs for further details) or linearly extrapolated using the measured Tonset at qc,h = 15 and 30 K min−1 (Table 1). As expected (Giordano et al. 2008; Misiti et al. 2009; Bouhifd et al. 2013), Tg decreases with water content (Fig. 7), from 664.1 ℃ at anhydrous conditions to 400.4 ℃ when H2O = 4.69 ± 0.26 wt%. We used Eq. 8 and 9 to parameterize Tg as a function of water content (dashed line in Fig. 7) using only the measured Tg data (i.e., Tonset at qc,h = 10 K min−1) and we obtained the fit parameters b = 0.235, c = 1.234 and d = -1.47. Note that this model well-predicts our extrapolated Tg values (i.e., Tonset at qc,h = 15 and 30 K min−1) and it is in good agreement (Fig. 7) with Tg values from Misiti et al. (2009), similarly calculated by the linear extrapolation of the two closest viscosity data points (i.e., around η = 1012 Pa s). Additionally, we converted the polynomial relationship from mol% to wt% for Stromboli composition, to be able to calculate Tg for H2O contents up to 10 wt% (see Supplementary Material Fig. 2).

Fig. 7
figure 7

Glass transition temperature (Tg) as a function of water content (wt%). The dashed line corresponds to the best fit solution using Eqs. 8 and 9 (Schneider et al. 1997). Tg measured corresponds to Tonset at qc,h = 10 K min−1, Tg extrapolated corresponds to values obtained from linear regression of Tonset at qc,h = 15 and 30 K min−1. Extrapolated Tg from the literature are also reported (Misiti et al. 2009)

Full size image

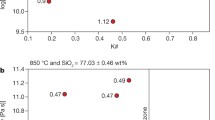
Using Eq. 4 and Brillouin spectroscopy data (BLS), we calculated the K/G ratio for our anhydrous and hydrous samples (Table 1). We found that the K/G ratio is independent on the total water concentration between 0 and ⁓5 wt% (K/G = 1.73 ± 0.02) and that the effect of pressure is negligible when comparing samples synthesized up to 5 kbar. Additionally, our data are in good agreement with Cassetta et al. (2021) who calculated, using BLS data from the literature (Whittington et al. 2012), K/G = 1.74 and 1.68 for an anhydrous and hydrous (H2O = 3.02 wt%) basalt, respectively. As such, based on the empirical relationship between K/G and m (Eq. 7) (Cassetta et al. 2021), we deduce here that, within the uncertainty, the fragility index (m) of the water-bearing melts equals m of the anhydrous melt (m = 40.7 ± 0.7), which is reliably constrained by viscosity data over a large temperature interval (Fig. 5). We test this hypothesis in the discussion section using an independent set of data.

Discussion

The remarkable agreement between our anhydrous viscosity and literature data (Giordano et al. 2006; Misiti et al. 2009; Scarani et al. 2022), together with the virtual absence of Raman spectral features between 650 and 730 cm−1, demonstrate that the anhydrous Stromboli melt is not prone to nanocrystallization during viscosity and DSC measurements. This agrees with the recent findings of Scarani et al. (2022) who showed that the overall FeOtot + TiO2 content modulates the nanocrystallization of basaltic melts: the comparatively lower content in transition metal oxides of the Stromboli anhydrous composition results in a more stable melt with respect to, for instance, Mt. Etna trachybasalt. Moreover, the excellent agreement of our F-DSC-derived viscosity (6.4 < log η < 8.5) with the parameterization of anhydrous Stromboli basalt proposed by this work, as well as by previous studies (Giordano et al. 2008, 2009; Misiti et al. 2009; Scarani et al. 2022), demonstrates that the F-DSC approach represents a valuable tool for accessing unprecedented viscosity ranges, commonly restricted by melt crystallization and gas exsolution (Dingwell et al. 2004; Al-Mukadam et al. 2020; Langhammer et al. 2021; Di Genova et al. 2023).

In contrast, Raman spectra of hydrous glasses (Figs. 2 and 3) suggest that Stromboli hydrous melts with H2O contents greater than 1 wt% are prone to Fe-Ti-oxide nanolite crystallization during viscosity and C-DSC measurements. Moreover, for samples with water content higher than 3.3 wt%, Raman and FTIR spectra suggest the formation of free hydroxyl (Fig. 4). These changes induce non-trivial chemical and structural modifications in the melt that are known to result in an overestimation of melt viscosity at temperatures above Tg (Di Genova et al. 2017a, b; Di Genova et al. 2020b; Liebske et al. 2003).

In general, Raman spectral signatures (Fig. 3) suggest an increasing degree of nanocrystallization as water content increases, which is in good agreement with previous studies (Davis et al. 1997). For instance, for low water content (S_1.25), micropenetration results show a relatively good agreement with C-DSC-derived viscosity data (Fig. 5), as supported by the comparison of Raman spectra acquired before and after the measurements that suggests moderate nanocrystallization (Figs. 2 and 3a). For higher water contents (e.g., S_2.08, S_3.36, S_4.01, S_4.32, and S_4.69), we observed stronger Raman intensity at ~ 650–730 cm−1 (Fig. 3) and an evident time-dependent increase in viscosity during micropenetration measurements (Fig. 6). As such, the hydrous Stromboli basalt becomes more and more unstable during measurements as water content increases. Finally, the inspection of Raman spectra in Fig. 3 indicates that, for comparable water contents, a relatively more oxidized starting material (i.e., samples synthesised with IHPV apparatus) led to a higher degree of nanocrystallization during the experiments.

Since C-DSC measurements of Tg (η = 1012 Pa s) involve the lowest/shortest operatively achievable excursion to high temperatures, thereby minimizing the risk of nanocrystallization in the samples, we argue that our Tg values (Fig. 7) represent the most accurate starting point for a reliable description of the viscosity of the hydrous Stromboli melt. We therefore combined our Tg parameterization as a function of H2O content (Fig. 7 and Table 1) with the estimated and constant fragility index m = 40.7 ± 0.7, entering them into the MYEGA parametrization (Eq. 5) to model the viscosity of Stromboli melt as a function of temperature and water content. We note that while our BLS results and the remarkable prediction of the F-DSC-derived hydrous viscosity (Fig. 9) support the hypothesis that m is not dependent on H2O content and equals the value of the anhydrous melt (m = 40.7 ± 0.7), the empirical viscosity model proposed by Giordano et al. (2009) for Stromboli composition predicts conversely that m should decrease significantly with increasing water content from 42 (anhydrous melt) to 36.5 (H2O = 5 wt%). Keeping all other parameters unchanged, a lower m would necessarily return higher viscosity at temperatures above Tg (e.g., at eruptive temperature); thus, disregarding for a moment the effects of nanocrystallization described above, it is important to ascertain whether or not melt fragility should depend on water concentration. To do so, we evaluate the relationship between m and water content for our Stromboli basalt within the framework of Adam and Gibbs (1965) theory that predicts a positive correlation between m and the configurational heat capacity (\({C}_{p}^{conf}\)) of the melt (e.g., Bouhifd et al. 2013, 2006; Di Genova et al. 2014b; Robert et al., 2012; Smedskjaer et al. 2011). For glass-forming melts, \({C}_{p}^{conf}\) at Tg can be expressed as follows:

$$\begin{array}{c}{C}_{p}^{conf}\left({T}_{g}\right)={C}_{pl}-{C}_{pg}\left({T}_{g}\right)\end{array}$$
(10)

where \({C}_{pl}\) is the heat capacity of the relaxed liquid, and \({C}_{pg}\left({T}_{g}\right)\) is the heat capacity of the glass at Tg, which is extrapolated using the expression after Maier and Kelley (1932):

$$\begin{array}{c}{C}_{pg}\left(T\right)=a+bT-c{T}^{-2}\end{array}$$
(11)

Using our DSC rate-matching data (i.e., second upscans), we derived \({C}_{p}^{conf}\) of four samples with different water content following Bouhifd et al. (2013) (Supplementary Material Fig. 3). Our results show that \({C}_{p}^{conf}\) does not vary significantly with water content, as \({C}_{p}^{conf}\left({T}_{g}\right)\) dry is equal to 0.38 J g−1 K−1, while it is equal to 0.37 J g−1 K−1 at 2.87 ± 0.05 H2O wt% (Supplementary Material Fig. 3). After conversion from mass to mol, \({C}_{p}^{conf}\left({T}_{g}\right)\cong 23\pm 1 \mathrm{J }{\mathrm{mol }}^{-1}{\mathrm{K}}^{-1}\) (under the assumption of 50% of the total iron as FeO); our values exhibit moreover very good agreement with the literature (Robert et al. 2014). We therefore conclude that the addition of water should not be expected to significantly change the melt fragility of Stromboli liquid, as suggested by (i) BLS data (Table 3), (ii) the low variation of the DSC-derived m when using only nanolite-free measurements (Fig. 6), and iii) the prediction of the F-DSC-derived hydrous viscosity (Fig. 9) using the anhydrous m = 40.7 ± 0.7. Thus, the well-constrained fragility of the anhydrous melt (Fig. 5) can be used to parameterize the melt viscosity as a function of temperature and water content. This conclusion substantiates in a new viscosity model of Stromboli basalt as a function of temperature and water content η(T, H2O) (Fig. 8) based on the MYEGA parametrization (Eq. 5), where Tg is described according to Eq. 8 (Fig. 7 for fitting parameters) and m is fixed and equal to 40.7 ± 0.7 (Fig. 5). A viscosity calculator is provided in the Supplementary Material. We stress that our experimental data can also provide insight into the possible origin of the decrease in m with increasing water content in previous empirical models (e.g., Giordano et al. 2009, 2008): we have shown that unavoidable nanocrystallization during viscosity measurements of hydrous samples leads to viscosity values that are significantly higher than the crystal-free melt trend (Fig. 6), leading to a seemingly lower (and physically implausible) melt fragility. This lower fragility would be unsuitable to describe nanolite-free experimental data acquired at higher temperatures by F-DSC, as identifiable in Figs. 6 and 9 (at η = 108.32 Pa). This aspect becomes clearer when comparing predicted versus measured hydrous viscosity using previous models (Fig. 6 in Supplementary Material). For example, the Giordano et al. (2008) model either predicts the viscosity of nanolite-bearing samples or overestimates the (virtually) crystal-free viscosity of hydrous samples measured within this work.

Fig. 8
figure 8

Viscosity of Stromboli basalt as a function of water content (wt%) and temperature (℃)

Full size image
Fig. 9
figure 9

Viscosity results of nanolite-free Stromboli samples and literature viscosity data from Misiti et al. (2009). Dashed lines represent the viscosity predictions of our model for 0, 0.91, 1.52, 2.91 and 4.16 H2O wt%

Full size image

Figure 9 shows the comparison between our nanolite-free viscosity measurements, our model predictions, and the viscosity data reported by Misiti et al. (2009). The hydrous viscosity data obtained from melts that did not experience relevant nanocrystallization after either C-DSC (S_0.91, 1010.32 <  < 1012 Pa s) or F-DSC (S_4.31, η = 108.32 Pa s) measurements are accurately predicted by our model. These data were not used to train our model, so its prediction capability is remarkable and demonstrates that the combination of Tg from C-DSC and m from BLS enables the accurate derivation of the anhydrous and hydrous viscosity (Cassetta et al. 2021).

Concerning the comparison with literature data from Misiti et al. (2009), we observed that, for a given water content, our model positively predicts the hydrous viscosity around 1012 Pa s but then predicts lower viscosity with increasing temperature (Fig. 9). For example, at relatively low water content (H2O = 1.52 wt%), we successfully predict viscosity data from Misiti et al. (2009) between 1011.18 Pa s (534.85 ℃) and 1010.58 Pa s (549.85 ℃) (Fig. 9); however, at 574.85 ℃, our model predicts a viscosity of η= 109.56 Pa s, slightly lower than the 109.76 Pa s reported by Misiti et al. (2009). At higher water content (H2O = 2.91 wt%), Misiti et al. (2009) measured η = 1011.1 Pa s (474.85 ℃), while our prediction is 1010.94 Pa s. At 499.85 and 524.85 ℃ Misiti et al. (2009) measured respectively 1010.22 and 109.92 Pa s, where our model predicts significantly lower viscosity values (109.77 and 108.77 Pa s, respectively). We also compared our model predictions with the high-temperature falling-sphere-derived viscosity reported by Misiti et al. (2009). In general, our model predicts significantly lower viscosity at high temperatures. For instance, at H2O = 1.52 wt%, they reported viscosities of 101.38, 101.2 and 100.84 Pa s at 1200, 1250 and 1300 ℃ respectively. For the same water content, our model predicts viscosities of 100.70, 100.47 and 100.27 Pa s, respectively. At 2.91 H2O wt%, our model successfully reproduced the η = 100.23 Pa s at 1200 ℃ reported by Misiti et al. (2009); however, their data subsequently display a physically paradoxical increase in viscosity with increasing temperature, from 100.23 Pa s (1200 ℃) to 100.6 Pa s (1250 ℃). A similar behaviour is observed at 4.16 H2O wt% in Misiti et al. (2009), where viscosity increased from 100.61 to 100.98 Pa s when temperature increased from 1100 to 1150 ℃. As such, we conclude that falling-sphere measurements entail unavoidable experimental challenges that may seriously affect their reliability, whereas our experimental approach intrinsically circumvents such limitations.

Figure 10a shows the comparison between our model and two global viscosity models of volcanic melts (Giordano et al. 2008; Langhammer et al. 2022). We considered the Giordano et al. (2008) model (GRD) because it is the most used viscosity model in the literature, and the Langhammer et al. (2022) model (ANN), which is the most recent viscosity model and the first one based on artificial neural networks. We input the chemical composition of our Stromboli melt (Supplementary Material Table 1) and assumed a Fe3+/Fe2+ ratio of 0.5. In general, while the ANN performs more similarly to our parameterization than GRD, the two viscosity models predict excessively high viscosities with increasing temperature. This is also the case if we compare our results with other viscosity models, such as the global model of Hui and Zhang (2007) and the Giordano et al. (2009), specifically targeted on Stromboli melt (Supplementary Material Fig. 4).

Fig. 10
figure 10

a Comparison of our model with two viscosity models for Stromboli basalt from 0 wt% (left border) to 5 wt% H2O content (right border): Giordano et al. 2008 (GRD) and Langhammer et al. 2021 (ANN). The vertical red line marks the pre-eruptive temperature of Stromboli basalt (T = 1150 ℃; Giordano et al. 2009; La Spina et al. 2015). b Comparison of predicted viscosity as a function of water content at the pre-eruptive temperature (T = 1150 ℃)

Full size image

For the anhydrous melt (left border in Fig. 10a), our model shows similar behaviour in comparison to both GRD and ANN literature models. This result is consistent with the observation that the anhydrous Stromboli melt is not prone to nanocrystallization during viscosity measurements, preventing experimental artifacts whatever the methodology applied. Nevertheless, for water content higher than ~ 0.8 wt%, our model predicts lower viscosities (Fig. 10). For example, at pre-eruptive conditions of 1150 ℃ and 3.67 wt% H2O (Giordano et al. 2009; La Spina et al. 2015; Andronico et al. 2021), our model predicts a viscosity of 100.15 Pa s, in contrast to the 100.91 and 100.54 Pa s predicted by GRD and ANN respectively, i.e. 5.7–2.5 times lower than previous studies. We note that our model diverges from GRD when the water content increases above ~ 0.8 wt%. We argue that this behaviour is controlled by the ease of nanocrystallization of hydrous melts during viscosity measurements: for example, while the sample S_0.91 did not experience relevant crystallization during viscosity measurements (Fig. 3a and Fig. 6), we observed nanocrystallization when the water content is greater than 1.25 wt%, as suggested by Raman spectra (Fig. 3). Thus, we conclude that the excessively high viscosity predicted by the empirical models (Fig. 10) results from the (erroneously) assumed decrease in m with increasing water content, which we have shown to be related to the crystallization of nanolites and water loss during hydrous viscosity measurements. Parallelly, the ANN model predicts an unsteady decrease in viscosity between 0.5 and 1.5 H2O wt% (Fig. 10b), which mirrors the respective dependence of m on H2O (Supplementary Material Fig. 5). Because the ANN model does not make any conceptual assumptions concerning the dependence of melt fragility on water content (Langhammer et al. 2022), our study suggests that more high-quality hydrous viscosity data, combined with Brillouin spectroscopy and heat capacity data, are required to accurately constrain the variations of melt fragility with water concentrations, and thereby model the viscosity of hydrous volcanic melts by an artificial neural network approach.

Implications for Stromboli magma dynamics

Our observations suggest that the viscosity of Stromboli melt at pre-eruptive conditions is lower than identified so far (Giordano et al. 2009, 2008; Hui and Zhang 2007; Misiti et al. 2009). This aspect is critical when modelling the change in viscosity during magma ascent upon decompression, as we rely on viscosity models to define the rate of melt phase viscosity increase due to water exsolution. Such a rate is key in controlling the thermodynamic equilibrium or disequilibrium in magmas during ascent, and therefore, degassing and crystallization dynamics (Mangan and Sisson 2000; La Spina et al. 2016; Polacci et al. 2018; Arzilli et al. 2019; Kolzenburg et al. 2019). Notably, our model predicts a very large increase in melt viscosity upon water exsolution at a constant temperature of 1150 ℃ (Fig. 10), as we calculated η = 100.15 Pa s, at H2O = 3.67 wt%, and η = 102.56 Pa s at anhydrous conditions, which difference is 9 times greater compared to GRD model predictions, respectively η = 100.91 and 102.56 Pa s.

Considering a simple ascent rate model that neglects the shear-rate dependence of viscosity (Sparks et al. 2006; Kokandakar et al. 2018), and following Misiti et al. (2009), the ascent velocity of a bubble-free Stromboli basalt (T = 1150 ℃ and H2O = 3.67 wt%) with a crystal content of 10 vol% through a 4 m wide dike is 41 m s−1 using our viscosity model ~ 30% greater with respect to the previous estimation by Misiti et al. (2009). Although this result is significantly higher than estimates of 1.5–3 m s−1 from bubble number density (BND) data of experimental samples and erupted materials (Pichavant et al. 2013; Le Gall and Pichavant 2016b, a), pre-explosion ground deformation analyses suggest ascent rates of 10–15 m s−1 for the 2019 Stromboli paroxysms, when the fragmentation occurs at the vent and η = 102 Pa s, and up to our estimate of 35 m s−1 if the fragmentation depth is fixed deeper, at 150 m below the vent, as inferred from the time delay between the thermal and acoustic onsets for the 15 March 2007 paroxysm (Ripepe and Harris 2008; Ripepe et al. 2021b).

In general, the lower melt viscosity revealed by our study promotes a more efficient decoupling between the magma and the gas phase (La Spina et al. 2017a; Valdivia et al. 2022), and decreases the minimum bubble diameter required for bubble segregation (Sparks 2003). This effect, in addition to the constant evolution of the permeable pathways in low-viscosity fluids, diminishes the accuracy of permeability-dependant estimations coming from pyroclastic vesicle textures (La Spina et al. 2017b). On the other hand, a lower magma viscosity produces higher estimations of ascent rates (Sparks et al. 2006; Kokandakar et al. 2018; La Spina et al. 2020), affecting the calculation of the Reynolds number, and increasing the likelihood of having a turbulent flow regime (Melnik and Sparks 2006).

Paroxysmal events at Stromboli volcano have been attributed to the rapid ascent of a low-porphyritic volatile-rich magma from a 7–10 km depth reservoir that interacts with a high-porphyritic crystal-rich and denser magma mush at shallower depths of 2–3 km (Andronico et al. 2021; Métrich et al. 2021; Ripepe et al. 2021b), being responsible for the most dangerous outcomes that occur unexpectedly (Bertagnini et al. 2003; Le Gall and Pichavant 2016a; Andronico et al. 2021; Mattia et al. 2021). Our results further support that the volatile-rich basalt rises rapidly and in a turbulent regime. Additionally, if we consider lower viscosity, the depth estimations for the onset of gas expansion used in ground deformation analyses should increase (Ripepe et al. 2021b), possibly matching the crystal-rich magma mush depth. If that is the case, as the volatile-rich gas-magma mix rises, the limited expansion of the gas phase, which is controlled by the interaction with a more viscous and denser crystal-rich magma, might generate enough overpressure to fragment the magma and produce a paroxysmal event. This effect would be also enhanced by the formation of nanolites during ascent as their presence reduce the required oversaturation for bubbles to form through heterogeneous nucleation at higher depths. Therefore, it is imperative to undertake further investigations to fully grasp the extensive implications arising from our viscosity predictions. This critical endeavour will not only enhance numerical modelling but also advance our comprehension of magma dynamics and outgassing processes in compositions akin to Stromboli basalt.

Conclusions

In this work, we measured the viscosity of anhydrous and hydrous Stromboli basalt. We accomplished full characterization of the Stromboli melt viscosity as a function of temperature and water content by combining conventional and flash differential scanning calorimetry with Raman, FTIR, and Brillouin spectroscopy. We showed that while the anhydrous Stromboli basalt is not prone to crystallization during viscosity measurements, the hydrous melt is prone to nanocrystallization of Fe-Ti-oxides when the water content is higher than 1 wt%.

As a consequence, the viscosity of Stromboli magma under eruptive conditions is 2 to 5 times lower than what previous empirical models predict. Our findings are crucial for advancing our understanding of the dynamics of Stromboli volcano. The observed reduction in pure melt viscosity can explain the rapid ascent of magma during paroxysmal events, which are often accompanied by short-lived geophysical signals.