Abstract
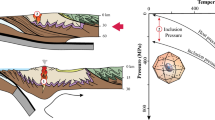
Determining pressure and temperature variations between high-pressure/low-temperature (HP–LT) eclogite blocks is crucial for constraining end-member exhumation models; however, it has historically been challenging to constrain eclogite pressures due to the high variance associated with this bulk-rock composition. In this work, we utilize quartz-in-garnet elastic barometry to constrain formation pressures of eclogites from the northern (Junction School, Ring Mountain, Jenner Beach) and southern Franciscan Complex (Santa Catalina Island). Multiple eclogite blocks from Jenner Beach are analyzed, and a single eclogite from the other localities. By comparing garnet growth conditions from within a single outcrop and between distinct outcrops, we evaluate the local and regional spatial distribution of P conditions recorded by eclogites. We compare the mean, median, and max pressures between different garnet zones and eclogites. Pressures sometimes exhibit systematic changes across garnet zones; however, some eclogites exhibit no systematic pressure variations across garnet zones. Pressures from northern Franciscan eclogites range from \(\sim \)1.4–1.8 GPa, at an estimated temperature of 500 \(^{\circ }\)C; pressures from the Catalina eclogite range from \(\sim \)1.2–1.5 GPa, at an estimated temperature of 650 \(^{\circ }\)C. Mean and maximum pressures of different eclogites from the northern Franciscan exhibit negligible differences (< 0.1 GPa). The results are inconsistent with models that propose exhumation of metamorphic blocks from different structural levels, and suggest that now exposed HP–LT eclogites from the northern Franciscan Complex may represent rocks that were coherently underplated, and exhumed from similar structural levels.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
High pressure–low temperature (HP–LT) rocks provide insight into the thermal (e.g., Penniston-Dorland et al. 2015), mechanical (e.g., Agard et al. 2018), fluid (e.g., Collins et al. 2015), and temporal (e.g., Baldwin et al. 2004) evolution of subduction zones. The Franciscan Complex of California represents an exhumed accretionary complex that preserves exceptional HP–LT rocks that are well-known for their block-and-matrix relationship, with high-grade blocks embedded within metasediments or an ultramafic matrix (serpentinites, chlorite, talc, actinolite). These rocks have been used to understand: (a) the evolution of the Franciscan complex (e.g., Wakabayashi 2015), (b) the formation conditions of blueschists and eclogites (e.g., Tsujimori et al. 2006; Page et al. 2007; Ukar et al. 2012), (c) interactions among multiple deep subduction zone processes (e.g., Viete et al. 2018), and (d) the mechanisms responsible for exhumation of HP–LT rocks (e.g., Cloos 1982; Platt 1986; Horodyskyj et al. 2009). Determining P–T conditions of high-grade blocks is fundamental for understanding these subduction zone processes, but constraining the formation pressures of blocks such as eclogites has historically been challenging due to a lack of suitable barometers. Eclogites present a thermobarometric challenge owing to the high number of components and the low number of phases (omphacite + garnet ± rutile ± quartz) present in their bulk composition (i.e., high variance, Essene 1989). Furthermore, most thermobarometers that are suitable for eclogites are more appropriate as thermometers (e.g., garnet–pyroxene thermobarometry). Owing to the lack of suitable eclogite barometers, the reported maximum and mean formation pressures of eclogites from within the same locality, and across the broader Franciscan Complex, have significantly varied.
Elastic thermobarometry is a rapidly developing technique that can be a suitable alternative to conventional thermobarometry. The seminal studies that used the elastic properties of minerals to constrain the conditions at which a host entraps an inclusion (solid) were published in the 1960’s and 70’s (Rosenfeld and Chase 1961; Rosenfeld 1969; Adams et al. 1975a, b; Cohen and Rosenfeld 1979). The application of elastic thermobarometry has recently increased largely due to the simple applicability of using Raman spectroscopy systems to constrain residual pressures recorded by inclusions (e.g., Enami et al. 2007). The residual pressure is combined with elastic modeling of the inclusion–host pair to constrain the conditions of host growth (e.g., Adams et al. 1975a, b; Rosenfeld and Chase 1961; Rosenfeld 1969; Cohen and Rosenfeld 1979; Angel et al. 2015). Recent work shows that the quartz-inclusions-in-garnet (qtz-in-grt) elastic barometer is ideally suited for constraining pressures of eclogites because it is insensitive to compositional constraints (e.g., Zhong et al. 2020b; Cisneros and Befus 2020), and exhibits minimal temperature dependence (e.g., Guiraud and Powell 2006; Ashley et al. 2014; Kohn 2014). Furthermore, experiments that grow garnet around quartz at known laboratory conditions have shown that the qtz-in-grt barometer records accurate pressures (± 0.2 GPa, Thomas and Spear 2018; Bonazzi et al. 2019), and garnet flow laws (i.e., Wang and Ji 1999) predict that viscous relaxation only affects the barometer at temperatures \(\ge \) 650 \(^{\circ }\)C over short timescales (Zhong et al. 2020b). Recent studies have also shown that pressure constraints from quartz-in-garnet barometry can be coupled with chemical zoning of garnet to better understand the tectonic history of metamorphic rocks (e.g., Taguchi et al. 2019; Bayet et al. 2020; Groß et al. 2020; Cisneros et al. 2021; Schwarzenbach et al. 2021).
In this work, we compare pressures recorded by spatially and temporally variant eclogite blocks from the Franciscan Complex in California. We focus on eclogites, because previous studies suggest that they preserve the maximum pressure conditions reached by the Franciscan Complex. We use qtz-in-grt barometry to constrain quartz inclusion entrapment pressures (pressure at which garnet grows around quartz inclusions, \(P_\mathrm{trap}\)) of eclogites from the northern (Jenner Beach, Ring Mountain, and Junction School) and southern Franciscan Complex (Santa Catalina Island). By comparing garnet growth conditions within and between distinct outcrops, we evaluate the local and regional spatial distribution of pressure conditions recorded by eclogites. We use these results to address spatio-temporal variations of peak pressures recorded by eclogites, compare our results with conventional thermobarometry, and discuss implications for exhumation of high-grade blocks from the Franciscan Complex.
Geologic background of the Franciscan complex
Geologic history of the Franciscan complex
The Franciscan accretionary complex records subduction of the east-dipping Farallon plate beneath western North American (e.g., Wakabayashi 1992; Raymond 2019). The Franciscan complex is overlain by the Coast Range Ophiolite (CRO), which forms the basement to the Great Valley Sequence forearc sediments. To the east of the Franciscan, the Sierra–Klamath–Salinia terranes are composed of magmatic arc and metamorphic basement with overlying sediments that comprise most of central-east California. Protolith age constraints suggest the CRO formed between \(\sim \)172–162 Ma (e.g., Shervais et al. 2005; Hopson et al. 2008), and the oldest reported ages of metamorphism from Franciscan high-grade blocks, i.e., blocks with significantly higher metamorphic grade (blueschist, eclogite, and amphibolites facies) relative to the surrounding matrix, are \(\sim \)176 Ma (mean U-Pb age of metamorphic zircon inclusions in garnet, Mulcahy et al. 2018). However, metamorphic zircon U-Pb ages from high-grade blocks are primarily younger (\(\sim \)166–157 Ma), and \(\sim \)180 Ma ages (U–Pb zircon core) have been related to protolith basalt crystallization (Rutte et al. 2020). The similar age of metamorphism of Franciscan high-grade blocks and formation of CRO magmatic and sedimentary rocks, suggests that subduction of the Franciscan complex occurred simultaneously with CRO formation (Anczkiewicz et al. 2004), or that initiation of subduction of the Franciscan occurred slightly before CRO formation (Mulcahy et al. 2018). CRO serpentinite geochemistry suggests a supra-subduction zone origin (Barnes et al. 2013), and may support coeval formation of the CRO with Franciscan subduction initiation. By contrast, younger K-Ar and \(^{40}\)Ar/\(^{39}\)Ar ages (155–145 Ma) from high-grade blocks from the Franciscan have also been used to suggest that subduction–initiation postdates CRO formation (e.g., Cloos 1985; Ukar et al. 2012). Debate over the timing of Franciscan subduction–initiation and CRO formation has led to competing hypotheses over the tectonic evolution of western North America (e.g., Stern and Bloomer 1992; Godfrey and Klemperer 1998; Hopson et al. 2008).
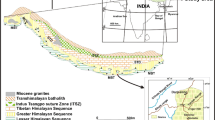
(a) Geologic map of California that shows the location of the Franciscan Complex (divided into the Eastern, Central, and Coastal belts), relative to the Sierra–Klamath–Salinia Terranes, Great Valley Group, and Coast Range Ophiolite. (b) The San Francisco Bay area that includes the Ring Mountain outcrop, and (c) Junction School are further highlighted. (d) Schematic cross section of the San Franciscan Bay area, within the Central Belt of the Franciscan Complex. Main geologic map is modified from Cooper et al. (2011), and detailed geologic maps are modified from Wakabayashi (1992) (Bay area) and Page et al. (2007) (Junction School).The cross section is modified from Wakabayashi (1990)
The Franciscan Complex is exposed over \(\sim \)1800 km along the Western margin of California (Wakabayashi 1992, 2015). The northern Franciscan complex is divided into three subunits: the Coastal, Eastern, and Central belts (Ernst 1975, Fig. 1). The Coastal belt has been described as a coherent terrane composed of Paleogene age protolith rocks that reached low-grade zeolite facies (Bachman 1982). The Central belt is described as a “melange”, primarily characterized by high-grade blocks that were metamorphosed between 172–147 Ma (e.g., Anczkiewicz et al. 2004; Mulcahy et al. 2018), and now lie within a Jurassic–Cretaceous (Coleman and Lanphere 1971) shaley matrix that reached prehnite-pumpellyite facies conditions (Terabayashi and Maruyama 1998), or an ultramafic matrix (Wakabayashi et al. 2010). The Eastern belt has been described as a coherent blueschist facies terrane composed of late-Jurassic to early Cretaceous protolith rocks (Isozaki and Blake 1994), that records P–T conditions of \(\sim \)215–365 \(^{\circ }\)C and \(\sim \)0.78–1.1 GPa at \(\sim \)123–110 Ma (e.g., Bröcker and Day 1995; Dumitru et al. 2010; Schmidt and Platt 2020). The younging trend of protolith ages from the Eastern to Coastal belts is generally agreed upon; however, the relationship amongst high-grade blocks from the central belt remains debated. The southern Franciscan Complex (exposed on Santa Catalina Island, Fig. 2) is primarily composed of a series of internally coherent slices (uniformly deformed, cohesive packages that did not form block-matrix structures) with metamorphic grade ranging from lawsonite blueschist to amphibolite facies. The coherent slices consist of metagraywacke, metachert, and mafic igneous protoliths, and individual slices preserve a single metamorphic grade. The amphibolite facies rocks reached peak temperatures of 640–750 \(^{\circ }\)C (e.g., Platt 1976; Sorensen 1988; Harvey et al. 2021a; Grove and Bebout 1995) at \(\sim \)115 Ma (Mattinson 1986; Anczkiewicz et al. 2004), recording a warmer geothermal gradient in comparison to the northern Franciscan Complex.
(a) Geologic map of Santa Catalina island. (b) Simplified cross section of the Catalina Schist based on Platt (1975). Tectonic blocks are mainly amphibolite facies garnet hornblendites, with some eclogites. Sample PG10 is inferred to have been a tectonic block along the blueschist–greenschist thrust, but was found as a float block below the thrust. Basemap is from the USGS 3D Elevation Program; figure is modified from Harvey et al. (2021b)
Timing, pressure, and temperature constraints of high-grade blocks
High-grade blocks from the Central belt in the northern Franciscan Complex include amphibolites, eclogites, and blueschists (e.g., Coleman and Lanphere 1971). The geologic relationship between blocks of different metamorphic grade has remained enigmatic, but Lu–Hf ages from garnet suggest that amphibolites record the oldest ages (\(\sim \)169–163 Ma), and eclogites (\(\sim \)158 Ma) and blueschists (\(\sim \)147 Ma) record younger ages (Anczkiewicz et al. 2004; Cooper et al. 2011). The observation that the ages correlate with different metamorphic facies has been interpreted to reflect progressive cooling of the western North America subduction zone through time such that the eclogites and blueschists represent original amphibolites brought to lower temperature–higher pressure conditions along a counter-clockwise P–T path, or that eclogites and blueschists are separate crustal slices that formed after amphibolites (e.g., Oh and Liou 1990; Wakabayashi 1992; Krogh et al. 1994; Anczkiewicz et al. 2004; Tsujimori et al. 2006). By contrast, recent U–Pb zircon ages from a single sample have been interpreted to record eclogite facies conditions at \(\sim \)176 Ma, and amphibolite facies conditions at \(\sim \)160 Ma (Mulcahy et al. 2018). Hence it is possible that different blocks from the Franciscan followed different P–T paths (clockwise vs counter-clockwise loops, Mulcahy et al. 2018).
Estimates of P–T conditions of eclogite HP–LT blocks (northern Franciscan) are highly variable, and vary within a single locality and between localities. Massonne (1995) used garnet–omphacite–phengite thermobarometry to estimate maximum conditions of \(\sim \)3.1 GPa and 563 \(^{\circ }\)C from garnet cores and mantles from the Junction School eclogite, and \(\sim \)2.6 GPa and 640 \(^{\circ }\)C from garnet rims from Ring Mountain (Fig. 1). Max P estimates from Massonne (1995) (Junction School) are within the coesite stability field; but coesite has not been found in rocks from the Franciscan Complex. Other studies have estimated lower maximum eclogite pressures (i.e., Ernst 1988; Wakabayashi 1990; Krogh et al. 1994; Tsujimori et al. 2006; Page et al. 2007; Cooper et al. 2011), that widely range from up to \(\sim \)1.3 GPa (Jenner Beach, Cooper et al. 2011) up to \(\sim \)2.6 GPa (Ring Mountain garnet rims, Tsujimori et al. 2006). We note that some studies (e.g., Wakabayashi 1990) constrain pressures based on the jadeite content of omphacite, and may reflect minimum pressures that can be consistent with higher pressure estimates. The pressure estimate by Cooper et al. (2011) is based on the presence of albite in equilibrium with omphacite, and is a maximum pressure. Maximum temperature conditions exhibit a narrower range, from \(\sim \)520 \(^{\circ }\)C (Page et al. 2007) to 640 \(^{\circ }\)C (Wakabayashi 1990; Massonne 1995).
The southern Franciscan exposed on Santa Catalina Island consists of several tectonic slices (metabasites, ultramafics, and metasediments) of different metamorphic grades, including lawsonite blueschist, epidote blueschist, albite–epidote amphibolite, and amphibolite facies rocks. These slices appear in a systematic structural sequence, with the oldest, hottest rocks at the top, and the youngest, coldest rocks at the bottom. The highest grade rocks at the top of the structural sequence are associated with ultramafic rocks, including a serpentinite-matrix melange with tectonic blocks of high-grade rocks. Partly amphibolitized eclogite occurs in the serpentinite-matrix melange, and as tectonic blocks along the thrust contact between the higher grade rocks and the underlying lawsonite blueschists. The high-grade rocks on Catalina have been interpreted to record a transition to a warmer geothermal gradient (Platt 1976), in support of timing constraints that suggest these rocks have a distinctly different history relative to the northern Franciscan Complex (e.g., Grove and Bebout 1995; Anczkiewicz et al. 2004). In contrast to data from northern California, high-grade rocks on Santa Catalina Island have yielded a garnet Lu–Hf age of 114.5 ± 0.8 Ma (Anczkiewicz et al. 2004), a mean Sm-Nd age of garnets from amphibolite facies blocks of 111.2 ± 1.1 Ma (Harvey et al. 2021b), U-Pb isochrons (titanite-garnet-hornblende-clinopyroxene) of 112 and 114 Ma (Mattinson 1986), and a U–Pb zircon age of 115.1 ± 2.5 Ma (Page et al. 2019). These ages may indicate younger subduction initiation in southern California, or underthrusting of the accretionary complex beneath the former magmatic arc (Grove et al. 2008).
Maximum P conditions from blueschists and amphibolites are estimated to be in the range \(\sim \)0.8–1.6 GPa (Sorensen and Barton 1987; Grove and Bebout 1995; Penniston-Dorland et al. 2018; Harvey et al. 2021a), but no previous P constraints exist for any eclogites from Catalina. Sorensen and Barton (1987) estimated P–T conditions from migmatite blocks within the serpentinite-matrix melange, to be \(\sim \)0.8–1.1 GPa and \(\sim \)640–750 \(^{\circ }\)C. Grove and Bebout (1995) used schematic stability fields to constrain peak P conditions within amphibolite facies rocks of \(\sim \)1.2 GPa and \(\sim \)700 \(^{\circ }\)C. Penniston-Dorland et al. (2018) and Harvey et al. (2021a) used zirconium-in-rutile thermometry and quartz-in-garnet barometry to estimate peak conditions of \(\sim \)1.6 GPa and \(\sim \)575 \(^{\circ }\)C from a blueschist facies block and \(\sim \)1.4 GPa and \(\sim \)650–745 \(^{\circ }\)C from amphibolite facies blocks; however, the determined temperatures for the blueschist block are above those of typical blueschist facies conditions.
The goal of this work is to compare formation pressures of eclogites constrained from qtz-in-grt barometry, with previous pressure constraints from the Franciscan Complex. The large variation of reported formation pressures of eclogites (northern Franciscan) from previous studies may indicate (1) that eclogite blocks are sourced from different depths, or (2) that different thermobarometry techniques and calibrations have resulted in the reported variations in pressure. Our approach is to examine mean and peak pressure variations between eclogite blocks from the same and different localities using a single technique (qtz-in-grt barometry). The results allow us to place new constraints on formation pressures of eclogites from the Franciscan Complex, and to evaluate whether the eclogite blocks have been sourced from a range of different subduction depths versus a single source depth, with implications for the eclogite entrainment process.
Sample localities and descriptions
We focus on eclogite blocks that are found within the Central belt of the northern Franciscan (Junction School, Ring Mountain, and Jenner Beach), and a single eclogite from Catalina Island. The sample localities, primary mineralogy, and previous age constraints for these rocks are given in Table 1. Thin section scans of all samples are provided in the Supplementary Material.
The Junction School locality preserves isolated high-grade blocks interpreted to be embedded in a serpentinite or low-grade greywacke matrix (Page et al. 2007). Sample PG26B was collected from the largest block, located 5 km SW of Healdsburg, California, near Mill Creek Road, on private property. The eclogite is primarily composed of clinopyroxene + garnet + rutile, but exhibits strong blueschist facies retrogression as indicated by late-stage glaucophane, white mica, and chlorite growth within and adjacent to a deformed vein, and late-stage overgrowths of titanite on rutile. Contact relationships with the surrounding rocks are not preserved.
The Ring Mountain locality on the Tiburon peninsula preserves a large number of separated high-grade blocks (garnet hornblendites and eclogites, with a blueschist facies overprint) up to several tens of meters in diameter, interpreted to be embedded in serpentinite, low-grade greywacke, and shale (e.g., Wakabayashi 1990, 1992; Tsujimori et al. 2006; Errico et al. 2013). Sample PG22A is from nearby the block named TIBB by Wakabayashi (1990). Wakabayashi (1992) refers to these rocks as the Tiburon melange, which forms the structurally highest thrust sheet in the Franciscan, lying directly beneath the Coast Range ophiolite (Fig. 1d). Sample PG22A is from a prominent block of nearly pristine eclogites \(\sim \)400 m north of the block named TIBB by Wakabayashi (1990). TIBB is a garnet hornblendite, with layers and patches of eclogite, and a variable blueschist facies overprint. The timing relationship between eclogite and garnet hornblendite metamorphism is debated: Wakabayashi (1992) inferred that the eclogite facies metamorphism occurred later, whereas Tsujimori et al. (2006) considered the two assemblages to have formed coevally. Samples from the TIBB block were dated by Anczkiewicz et al. (2004) and Rutte et al. (2020), and thermobarometric estimates were obtained by Tsujimori et al. (2006) and Cooper et al. (2011). Garnet from the garnet hornblendite gave a Lu-Hf age of 153.4 ± 0.8 Ma (Anczkiewicz et al. 2004), hornblende gave an Ar-Ar age of 159.19 ± 0.81 Ma (Rutte et al. 2020), and U-Pb ages from zircon cores and rims suggest crystallization over the period of 166–157 Ma (Rutte et al. 2020). Sample PG22A is primarily composed of clinopyroxene + garnet + rutile, but exhibits variable degrees of retrogression as indicated by glaucophane replacement of clinopyroxene, garnet chloritization, and late-stage white mica and titanite growth. The serpentinite matrix surrounding these blocks is locally exposed, and has a fragmental character consistent with a detrital origin (Wakabayashi 2012).
The Jenner beach locality consists of a large number of loose blocks of glaucophane-bearing eclogite and garnet-glaucophane schist at the base of the cliff. These are thought to have been derived from one or more blocks several hundreds of meters in extent embedded in serpentinite in the hillside above (Raymond 2017). The high-grade blocks often preserve actinolite rinds. Five eclogites from four different eclogite blocks were analyzed. Two samples (JEN11-2B and JEN11-2D) come from the same eclogite block. Two eclogites from this outcrop are near pristine, and are primarily composed of clinopyroxene + garnet (PG31B, JEN11-2B). Sample JEN11-2B shows variable degrees of retrogression recorded by glaucophane + chlorite replacement of clinopyroxene and garnet, respectively. Three eclogites (JEN11-1C, JEN11-3C, JEN11-2D) preserve significant volumetric proportions of epidote, and exhibit variable degrees of retrogression that is evidenced by glaucophane replacement of clinopyroxene and chloritization of garnet. A Lu-Hf garnet age of 157.9 ± 0.7 Ma was obtained from sample PG31B by Anczkiewicz et al. (2004), and a garnet-hornblendite from Jenner gave an inverse Ar isochron on hornblende of 158.1 ± 1.6 Ma (Rutte et al. 2020).
Eclogite on Santa Catalina Island is very rare—the main occurrences are layers and patches of garnet–clinopyroxenite within garnet hornblendite blocks (cm to \(\sim \)100 m) situated in zones of ultramafic melange. The clinopyroxene in these rocks is around 10–22 \(\%\) jadeite + acmite, which is lower than in most eclogites, reflecting the low sodium content in these tectonic blocks (Sorensen and Barton 1987). Sample PG10 was found as a float block in Bullrush Canyon, on the south side of the island. The canyon exposes blueschist facies rocks, but the block was likely derived from a zone of mélange carrying high-grade blocks exposed in the walls of the canyon, which separates the lawsonite blueschist facies rocks from overlying albite–epidote amphibolite rocks along what Platt (1976) called the Blueschist-Greenschist thrust (Fig. 2b). This interpretation is supported both by similarities in petrology to eclogitic layers in garnet hornblendite blocks within the melange, and the close similarity in radiometric age. PG10 is primarily composed of clinopyroxene + garnet + titanite. The clinopyroxene is \(\sim \)10 \(\%\) jadeite + acmite. Late-stage hornblende statically overgrows clinopyroxene + titanite grains, green-brown amphiboles are also found as inclusions in garnets.
Methods
Electron microprobe analyses and electron imaging
Electron probe X-ray mapping was carried-out at ETH Zürich using a JEOL JXA-8230 Electron Probe Microanalyzer (EPMA). Garnets were analyzed for Al, Ca, Mn, Fe, and Mg on TAP, PETJ, LIFL, LIFH, and TAPH crystals, respectively. Si was stoichiometrically calculated. Standardization was carried out using synthetic forsterite (Al, Ca), synthetic pyrolusite (Mn), synthetic fayalite (Fe), and synthetic forsterite (Mg). A mean atomic number background correction was applied. All analyses used a 15 keV accelerating voltage. Beam current, dwell times, and step sizes varied between garnet analyses (Supplementary Table S1). Mole fractions of garnet end members were calculated with CalcImage (Probe for EPMA). EPMA X-ray maps were not collected for all garnets that were analyzed by using qtz-in-barometry. We collected X-ray maps of one or two garnets from each analyzed section, and used these as representative X-ray maps that we link to zonation that is evident in Back Scattered Electron (BSE) images of other analyzed garnets. Fe and Mg zonation is evident in BSE images.
An electron backscatter diffraction (EBSD) map was collected around quartz inclusions within a garnet (Garnet 1 of sample PG10 from Santa Catalina Island). The sample was polished by standard methods, and a final step of mechanical–chemical polishing using an alkaline solution of colloidal silica on a neoprene substrate was performed for 5 minutes. EBSD data were collected at ScopeM (ETH Zürich) on a FEI Quanta 200F FEG scanning electron microscope (SEM) with EDAX analytics. SEM parameters included a 20 kV accelerating voltage, 8 nA beam current, 17 mm working distance, and a 100 nm stepsize (under low-vacuum conditions).
Raman measurements and data reduction
Raman spectroscopy measurements were carried out at ETH Zürich using a DILOR LabRAM Raman system, with a 300 mm focal length spectrometer. We used a 532 nm laser, an 1800 grooves mm\(^{-1}\) grating, a 100x objective with a 0.9 NA, a 200–400 \(\mu \)m confocal aperture, and a 200–300 \(\mu \)m slit width. A laser power of 2–7 mW was used at the sample surface. The diffraction grating was centered at \(\sim \)850 cm\(^{-1}\) for all analyses. The spectrometer was calibrated with the Rayleigh scattered line of the laser and the 520.5 cm\(^{-1}\) band of a Si wafer. The diffraction grating center position was fixed (never moved) during the session after the initial spectral calibration.
Raman spectroscopy measurements were conducted on \(\sim 80\,\, \upmu \hbox {m}\) and \(\sim 150\,\, \upmu \hbox {m}\) petrographic thin sections. Measured quartz inclusions were a minimum of 3 times their radial distance from fractures, the garnet exterior, and other inclusions to avoid non-elastic stress modifications (Campomenosi et al. 2018; Zhong et al. 2020b), and no geometric corrections were applied (Mazzucchelli et al. 2018). All Raman spectra were reduced with a Bose–Einstein temperature-dependent population factor (Kuzmany 2009). All Raman bands were fit by using PeakFit v4.12 from SYSTAT Software Inc. Voigt and Pearson IV functions were used to fit the quartz 128 cm\(^{-1}\) and 206 cm\(^{-1}\), and 464 cm\(^{-1}\) bands, respectively; a Voigt function was used to fit garnet bands. Raman bands of quartz and garnet were fit simultaneously, and a linear background subtraction was applied during peak fitting.
Inclusion and entrapment pressure calculations
Encapsulated inclusions preserve strain that causes the peak position of their Raman active vibrational modes to be shifted to higher or lower wavenumbers relative to minerals that are unstrained (fully exposed, Fig. 3). We calculated the Raman shift(s) of inclusions (\(\omega _\mathrm{inc}\)) relative to Raman shift(s) of a strain-free (never an inclusion), gem quality Herkimer quartz standard (\(\omega _\mathrm{ref}\)) at ambient temperature (\(\varDelta \omega \) = \(\omega _\mathrm{inc}\)–\(\omega _\mathrm{ref}\)). Herkimer quartz was analyzed prior to and after quartz inclusion analyses, and a time-dependent linear drift correction was applied to \(\omega _\mathrm{inc}\) based on the drift shown by Herkimer quartz analyses that bracketed inclusion analyses. The mean drift between Herkimer quartz analyses was 0.26, 0.40, and 0.26 cm\(^{-1}\) for the 128 cm\(^{-1}\), 206 cm\(^{-1}\), and 464 cm\(^{-1}\) bands, respectively. Instrument uncertainty was determined by calculating the \(\varDelta \omega \) of repeat measurements on the same quartz inclusions on different days. Reproducibility of \(\varDelta \omega \) for the 128 cm\(^{-1}\), 206 cm\(^{-1}\), and 464 cm\(^{-1}\) quartz bands was 0.13 cm\(^{-1}\), 0.31 cm\(^{-1}\), and 0.02 cm\(^{-1}\), respectively (Supplementary Table S4).
We calculated residual inclusion pressures (\(P_\mathrm{inc}\)) in two ways for comparison: (1) \(P_\mathrm{inc}\) was calculated using pressure-dependent Raman shift(s) (P-\(\varDelta \omega \)) of the quartz 128 cm\(^{-1}\), 206 cm\(^{-1}\), and 464 cm\(^{-1}\) bands, that were calibrated via hydrostatic diamond anvil cell experiments (Schmidt and Ziemann 2000). (2) \(P_\mathrm{inc}\) was calculated via a mean stress [\(P_\mathrm{inc}\) = (\(\sigma _1\) + \(\sigma _2\) + \(\sigma _3\))/3], that was calculated from quartz strains (\(\epsilon _1\), \(\epsilon _2\), and \(\epsilon _3\)) that were determined from the \(\varDelta \omega \) of the 128 cm\(^{-1}\), 206 cm\(^{-1}\), and 464 cm\(^{-1}\) quartz bands using Strainman (Murri et al. 2018, 2019; Angel et al. 2019); a weighted fit was applied based on the \(\varDelta \omega \) error associated with each quartz Raman band. Calculated strains were converted to a mean stress using the relationship \(\sigma _i\) = c\(_{ij}\epsilon _{j}\), where \(\sigma _i\), c\(_{ij}\), and \(\epsilon _j\), are the stress, elastic moduli, and strain matrices, respectively. We used the \(\alpha \)-quartz trigonal symmetry constraints of Nye (1985) and quartz elastic constants of Wang et al. (2015). The instrumental uncertainty was propagated with individual peak fit errors to calculate \(\varDelta \omega \). \(\varDelta \omega \) errors and errors of coefficients in hydrostatic calibrations were propagated to calculate \(P_\mathrm{inc}\) errors (Supplementary Tables S4, S5).
Molar volume and elastic modeling calculations were carried-out using a MATLAB program (Solid Inclusion Calculator) described in Cisneros and Befus (2020); reproducibility of calculations are validated against EoSFit-Pinc (Angel et al. 2017b) in Cisneros and Befus (2020). Molar volumes of almandine, spessartine, and pyrope, were calculated using thermodynamic properties from Holland and Powell (2011). Grossular molar volumes were calculated using the Milani et al. (2017) thermodynamic properties. Quartz molar volumes were calculated by using the curved-boundary approach and thermodynamic properties from Angel et al. (2017a). Shear moduli for garnet end-members were derived from the following references: almandine and pyrope (Wang and Ji 2001), spessartine (Bass 1995), and grossular (Isaak et al. 1992). Entrapment pressures (\(P_\mathrm{trap}\)) were calculated using the non-linear elastic model of Guiraud and Powell (2006), with an updated solution given in Angel et al. (2017b); however, we note that the Guiraud and Powell (2006) and Angel et al. (2017b) elastic models only differ in their strain definition, and produce \(P_\mathrm{trap}\) differences that vary by \(\le \) 0.1 \(\%\) (Zhong et al. 2020a). All thermodynamic properties and associated EoS’ that were used for molar volume calculations are given in Supplementary Table S2.
We used a constant garnet composition for all \(P_\mathrm{trap}\) calculations, that closely approximates the mean composition of analyzed garnets (Supplementary Table S5, X\(_\mathrm{almandine}\) = 0.6; X\(_\mathrm{grossular}\) = 0.3; X\(_\mathrm{pyrope}\) = 0.07; X\(_\mathrm{spessartine}\) = 0.03). To account for garnet compositions, we implemented linear mixing of molar volumes and shear moduli (at modelled P and T conditions); the Solid Inclusion Calculator program permits linear mixing of mineral end members to account for solid-solutions. Almandine-pyrope garnet solid solutions exhibit ideal molar volume behavior (Milani et al. 2015). Almandine-grossular garnet solid solutions exhibit slight non-ideal molar volume behavior (Cressey et al. 1978), and pyrope-grossular solid solutions exhibit greater non-ideal behavior (Geiger 2000), thus our linear approximation may introduce additional errors in our final \(P_\mathrm{trap}\) calculations. However, the difference in molar volume between pure garnet end-members far exceeds the difference between ideal and non-ideal molar volume estimations, and not accounting for mixing introduces greater uncertainties. Nonetheless, most garnets in this study are primarily almandine garnets (\(\sim \)60 %), and accounting for solid-solutions changes the final the \(P_\mathrm{trap}\) by < 0.1 GPa (Supplementary Table S5).
To calculate \(P_\mathrm{trap}\), we assumed entrapment temperatures (\(T_\mathrm{trap}\)) of 500 \(^{\circ }\)C (Northern Franciscan) and 650 \(^{\circ }\)C (Catalina) for all inclusions from different garnet zones. The \(T_\mathrm{trap}\) (500 \(^{\circ }\)C) of Northern Franciscan eclogites is based on estimated garnet growth temperatures (at max P) from previous studies (Wakabayashi 1992; Krogh et al. 1994; Massonne 1995; Ravna and Terry 2004; Page et al. 2007; Cooper et al. 2011); previous studies show a large range of garnet growth pressures, but a more restricted temperature range. The assumed \(T_\mathrm{trap}\) (650 \(^{\circ }\)C) for the Catalina eclogite is also based on garnet growth temperatures from previous studies (Harvey et al. 2021a). \(T_\mathrm{trap}\) has a minimal influence on \(P_\mathrm{trap}\) (\(\sim \)0.1 GPa 100 \(^{\circ }\)C\(^{-1}\), e.g., Cisneros and Befus 2020); the assumed \(T_\mathrm{trap}\) does not sufficiently change \(P_\mathrm{trap}\) to influence our interpretations; however, as quartz approaches the alpha-beta transition at higher temperatures, \(P_\mathrm{trap}\) becomes more sensitive to changes in \(T_\mathrm{trap}\).
Lu–Hf dating
Lu–Hf dating was carried out on eclogite PG10 from Santa Catalina Island. Sample preparation, sulphuric acid leaching, sample digestion, and analytical procedures follow Anczkiewicz et al. (2004), and were carried out at the Department of Geology, Royal Holloway University of London. Mineral separates included two garnet fractions and clinopyroxene. Age calculations were carried out using Isoplot v. 4.15 (Ludwig 2001) and were cross-checked with IsoplotR (Vermeesch 2018). Additional information on PG10 garnet chemistry is provided in Supplementary Table S6 and Supplementary Figure S1, and Lu–Hf data are provided in Table 2.
Results
Garnet chemical zonation
Garnet X-ray maps were collected for 1–2 garnets from each eclogite sample. The oxide sums (wt %) from garnet X-ray maps total 100–102 %. X-ray intensity maps suggest that sharp chemical transitions occur in garnets, and they exhibit up to three distinct zones (i.e., core, inner rim, and outer rim). For garnets without x-ray maps, we used BSE images to evaluate their chemical zonations. Zoning evident in BSE images closely correlates with mole fraction almandine (X\(_\mathrm{alm}\), Fe); higher Z regions (brighter) correspond to higher X\(_\mathrm{alm}\). We used BSE images to spatially identify where sharp X\(_\mathrm{alm}\) changes occur, and to assign inclusions to specific garnet zones. When three distinct zones were evident, quartz inclusions were assigned to the appropriate garnet zone (core, inner rim, or outer rim). When only two distinct zones were evident, quartz inclusions were assigned to a garnet core or rim.
Junction School
PG26B (core and rim): Garnets from Junction School preserve an inclusion-rich core and inclusion-poor rim in plane light (Supplementary Fig. S1). X-ray maps reveal two distinct garnet zones (core and rim); chemical changes correlate well with inclusion-rich and -poor regions. Mole fraction spessartine (X\(_\mathrm{sps}\), Mn) and pyrope (X\(_\mathrm{prp}\), Mg) gradually decrease and increase from core-to-rim, respectively. X\(_\mathrm{alm}\) and mole fraction grossular (X\(_\mathrm{grs}\), Ca) are nearly constant within the garnet core (Fig. 4). A decrease in X\(_\mathrm{alm}\) and increase in X\(_\mathrm{prp}\) marks the garnet core-rim boundary. Garnet zoning evident in BSE images closely tracks X\(_\mathrm{alm}\) and X\(_\mathrm{prp}\) zoning.
X-ray maps of garnets from a Junction School (PG26B) and Ring Mountain (PG22A) eclogite. Pixels that are within the imposed end-member concentration range are colored. Blue and white dashed lines indicate the core–inner rim and outer rim–inner rim boundaries, respectively. Garnets from PG26B only contained a core-rim boundary (white dashed line). Circles (core) and squares (inner rim) indicate the location of measured quartz inclusions, and \(P_\mathrm{inc}\) data is given in MPa
Ring Mountain
PG22A (core, inner rim, and outer rim): Garnets from Ring Mountain preserve inclusion-rich and -poor cores and rims, respectively (Supplementary Fig. S1). X-ray maps and BSE images reveal three distinct garnet zones (core, inner rim, and outer rim); chemical changes correlate well with inclusion-rich and -poor areas. Garnets show decreasing X\(_\mathrm{sps}\), constant X\(_\mathrm{grs}\) and X\(_\mathrm{prp}\), and increasing X\(_\mathrm{alm}\) from core-to-inner rim (Fig. 4). X\(_\mathrm{sps}\) and X\(_\mathrm{grs}\) decrease, and X\(_\mathrm{prp}\) and X\(_\mathrm{alm}\) increase at the core-inner rim boundary. The inner-outer rim boundary is marked by a sharp increase in X\(_\mathrm{sps}\) and X\(_\mathrm{prp}\), and decrease in X\(_\mathrm{alm}\). Garnet zoning evident in BSE images closely tracks X\(_\mathrm{alm}\) and inverse X\(_\mathrm{prp}\) zoning.
Jenner: epidote-free eclogites
Garnets from epidote-free eclogites preserve an inclusion-rich core and inclusion-poor rim (Supplementary Fig. S1). X-ray intensity maps reveal more complicated zonation that transitions from gradual element zonation near the garnet core, to sharper and sometimes oscillatory zonation near the garnet rim; however, inclusion-rich and -poor regions correlate well with chemical transitions seen in x-ray maps. Furthermore, variations in absolute elemental abundances and zoning patterns exist between garnets from different eclogite blocks (Supplementary Fig. S1). Garnets in epidote-free eclogites exhibit three distinct zones in x-ray maps (core, inner rim, and outer rim).
PG31B (core, inner rim, and outer rim): Garnet 4 shows a continuous decrease in X\(_\mathrm{sps}\) and X\(_\mathrm{grs}\), and increase in X\(_\mathrm{alm}\) and X\(_\mathrm{prp}\) from core-to-inner rim (Fig. 5, Supplementary Fig. S1). Sharp increases in X\(_\mathrm{sps}\) and X\(_\mathrm{prp}\) mark the garnet inner rim. The garnet inner rim exhibits sharp chemical oscillation of all elements. The inner-to-outer rim transition of garnet 4 exhibits a sharp increase in X\(_\mathrm{sps}\) and X\(_\mathrm{grs}\). Zoning in BSE images closely tracks X\(_\mathrm{alm}\) zonation.
X-ray map of garnets from Jenner Beach eclogites. Pixels that are within the imposed end-member concentration range are colored. Blue and white dashed lines indicate the core-inner rim and outer rim-inner rim boundaries, respectively. Circles (core), squares (inner rim), and stars (outer rim) indicate the location of measured quartz inclusions, and \(P_\mathrm{inc}\) data are given in MPa. In these examples, only garnet 1 (JEN11-1C) contained suitable quartz inclusions in the outer rim
JEN11-2B (core, inner rim, and outer rim): Garnets 1 and 6 exhibit minimal compositional change from core-to-inner rim; however, X\(_\mathrm{sps}\) exhibits a gradual decrease from core-to-inner rim (Fig. 5, Supplementary Fig. S1). An increase in X\(_\mathrm{grs}\) and X\(_\mathrm{sps}\), and a decrease in X\(_\mathrm{alm}\) and X\(_\mathrm{prp}\) marks the core-to-inner rim transition. The inner–outer rim boundary exhibits a sharp increase in X\(_\mathrm{sps}\) and X\(_\mathrm{prp}\) (decrease in X\(_\mathrm{grs}\) and X\(_\mathrm{alm}\)). Zoning in BSE images closely tracks X\(_\mathrm{alm}\) zonation; however, the inner–outer rim boundary is not clear in BSE images nor x-ray maps (X\(_\mathrm{alm}\) zonation).
Jenner: epidote-bearing eclogites
Garnets from epidote-bearing eclogites (Jenner beach) preserve an inclusion-rich core and an inclusion-poor rim (Supplementary Fig. S1). Different garnets from separate eclogite blocks exhibit similar absolute element abundances and zoning patterns.
JEN11-1C (core, inner rim, and outer rim): Garnet 1 exhibits decreasing X\(_\mathrm{sps}\) and X\(_\mathrm{grs}\) and increasing X\(_\mathrm{alm}\) and X\(_\mathrm{prp}\) from core-to-inner rim (Fig. 5, Supplementary Fig. S1). A decrease in X\(_\mathrm{alm}\) and increase in X\(_\mathrm{grs}\) marks the core-inner rim transition. A sharp decrease in X\(_\mathrm{alm}\) and increase in X\(_\mathrm{grs}\) marks the inner-outer rim transition. The core, inner rim, and outer rim transitions are evident in BSE images. Zoning in BSE images closely tracks X\(_\mathrm{alm}\) zonation.
JEN11-3C (core, inner rim, and outer rim): Garnet 2 shows decreasing X\(_\mathrm{grs}\) and X\(_\mathrm{sps}\), and increasing X\(_\mathrm{alm}\) and X\(_\mathrm{prp}\) from core-to-inner rim (Fig. 5, Supplementary Fig. S1). X\(_\mathrm{alm}\), X\(_\mathrm{grs}\), X\(_\mathrm{prp}\) and X\(_\mathrm{sps}\) are nearly constant across the garnet inner rim. A sharp decrease in X\(_\mathrm{alm}\) and increase in X\(_\mathrm{prp}\) marks the garnet inner–outer rim boundary. Garnet zoning evident in BSE images closely tracks X\(_\mathrm{alm}\).
JEN11-2D (core, inner rim, and outer rim): Garnet 1 shows a similar zonation pattern as that seen in Garnet 2 from JEN11-3C (Fig. 5, Supplementary Fig. S1). Garnet zoning in BSE images closely tracks X\(_\mathrm{alm}\).
Catalina
PG10 (core, inner rim, and outer rim): Garnets preserve an inclusion-rich core and inclusion-poor rim (Supplementary Fig. S1). X\(_\mathrm{sps}\) and X\(_\mathrm{grs}\) decrease, X\(_\mathrm{prp}\) increases, and X\(_\mathrm{alm}\) is nearly constant from the core-to-inner rim (Fig. 6). A sharp increase in X\(_\mathrm{prp}\) and decrease in X\(_\mathrm{alm}\) marks the core-inner rim boundary. Garnet rims exhibit an decrease and increase in X\(_\mathrm{alm}\) and X\(_\mathrm{grs}\), respectively. Garnet 1 and 2 exhibit textural evidence of inner rim resorption, and growth of a new garnet outer rim. Garnet zoning evident in BSE images closely tracks X\(_\mathrm{alm}\) zoning.
X-ray map of a garnet from a Santa Catalina Island eclogite. Pixels that are within the imposed end-member concentration range are colored. Blue and white dashed lines indicate the core–inner rim and outer rim–inner rim boundaries, respectively. Garnets from PG26B only contained a core-rim boundary (white dashed line). Circles (core) and squares (inner rim) indicate the location of measured quartz inclusions, and \(P_\mathrm{inc}\) data is given in MPa
Quartz-in-garnet barometry pressures
Herein, we report inclusion pressures (\(P_\mathrm{inc}\)) calculated by accounting for quartz anisotropy at ambient temperature (strains); \(P_\mathrm{inc}\) values calculated from hydrostatic calibrations (quartz 128, 206 and 464 cm\(^{-1}\) bands) are given in Supplementary Table S5. \(P_\mathrm{inc}\) calculated from strains and hydrostatic calibrations results in different values (Fig. 7); however, \(P_\mathrm{inc}\) calculated from strains and the quartz 464 cm\(^{-1}\) band generally results in a \(P_\mathrm{trap}\) that differs by \(\le \) 0.1 GPa (Supplementary Table S5). Pressures calculated from strains generally result in the highest \(P_\mathrm{inc}\) values (Fig. 7). There are disagreements regarding the methodology that produces the most accurate residual \(P_\mathrm{inc}\): hydrostatic calibrations versus strains determined from a Grüneisen tensor (mean stress). Thomas and Spear (2018) tested if \(P_\mathrm{inc}\) calculated from hydrostatic calibrations and a 1-D isotropic elastic model (Guiraud and Powell 2006), reproduce known experimental conditions of garnet growth (0.8–3.0 GPa). The authors found that the hydrostatic calibrations (464 cm\(^{-1}\) band) and 1-D isotropic elastic model reproduce experimental conditions of garnet growth by ± 0.1–0.2 GPa. Bonazzi et al. (2019) measured quartz-inclusions-in-garnet from the same experiments (2.5 and 3.0 GPa), and compared \(P_\mathrm{inc}\) calculated using hydrostatic calibrations and a mean stress (calculated from three strain components). The mean stress and a 1-D isotropic elastic model (Angel et al. 2017b) were used to calculate \(P_\mathrm{trap}\); however, we note that the Guiraud and Powell (2006) and Angel et al. (2017b) elastic models only differ in their strain definition, and produce \(P_\mathrm{trap}\) differences that vary by \(\le \) 0.1 \(\%\) (Zhong et al. 2020a). Bonazzi et al. (2019) found that for 2.5 GPa experiments, hydrostatic calibrations and the mean stress (and a 1-D isotropic elastic model) reproduce experimental conditions by ± 0.1–0.2 GPa. However, for the 3.0 GPa experiments, only the mean stress and 1-D isotropic model reproduces experimental conditions by ± 0.1–0.2 GPa. Therefore, we report \(P_\mathrm{inc}\) calculated from strains (mean stress), but note that a comparison of \(P_\mathrm{inc}\) calculated by using both approaches may be warranted for lower pressure experiments.
Comparison of \(P_\mathrm{inc}\) calculated from hydrostatic calibrations (P\(^{128}_\mathrm{inc}\), P\(^{206}_\mathrm{inc}\), P\(^{464}_\mathrm{inc}\)) and from strains (P\(^{strains}_\mathrm{inc}\)). (a) P\(^{464}_\mathrm{inc}\) vs P\(^{128}_\mathrm{inc}\), (b) P\(^{464}_\mathrm{inc}\) vs P\(^{206}_\mathrm{inc}\), and (c) P\(^{464}_\mathrm{inc}\) vs P\(^{strains}_\mathrm{inc}\). The 1:1 line is dashed (hydrostatic stress). P\(^{strains}_\mathrm{inc}\) is generally greater than P\(^{464}_\mathrm{inc}\). Quartz inclusions from the Catalina eclogite (PG10) record lower \(P_\mathrm{inc}\) values relative to northern Franciscan eclogites
We used chemical zoning (X-ray maps) and BSE images to sort inclusions into three groups (core, inner rim and outer rim), depending on the location of measured inclusions relative to chemical zonation. All garnets preserve a core and rim; seven eclogites have garnets that exhibit clear inner rims (Figs. 4, 5, 6; Supplementary Fig. S1). In some samples, inclusions within garnet cores, inner rim, and outer rims show systematic differences in \(P_\mathrm{inc}\) and subsequent \(P_\mathrm{trap}\) (Fig. 4, 5, 6,7, 8). Generally, the absolute mean \(P_\mathrm{inc}\) (and subsequent \(P_\mathrm{trap}\)) calculated from garnet inner rims and outer rims is greater than \(P_\mathrm{inc}\) calculated from garnet cores (Figs. 4, 5, 6, 8). Garnets from eclogite JEN11-1C (Jenner Beach), record a \(P_\mathrm{inc}\) increase from core-to-inner rim, but decrease at the garnet outer rim. Catalina garnets also record differences in the absolute \(P_\mathrm{inc}\) from different garnet zones (Figs. 6, 7, 8). Due to the close spacing of qtz-in-grt isomekes (large changes in \(P_\mathrm{inc}\) cause small changes in \(P_\mathrm{trap}\)), \(P_\mathrm{inc}\) differences are further reduced in subsequent \(P_\mathrm{trap}\) calculations (Cisneros and Befus 2020).
To better compare the \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) between different eclogites, we compare the mean \(P_\mathrm{inc}\) (and subsequent \(P_\mathrm{trap}\)) and whisker plots of qtz-in-grt barometry results (Fig. 8). The mean \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) of samples was calculated from inclusions within individual garnet zones (i.e., core, inner rim and outer rim, Fig. 8). The garnet core mean \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) (northern Francsican eclogites) range from 594–731 MPa and 1.42–1.67 GPa (Table 1; Figs. 7, 8). The core median and maximum \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) range from 584–743 MPa and 1.40–1.69 GPa, and 662–818 MPa and 1.54–1.82 GPa, respectively (Table 1; Fig. 7, 8). The garnet inner rim mean \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) (northern Francsican eclogites) range from 678–729 MPa and 1.57–1.66 GPa. Single inclusions within garnet inner rims record the highest (JEN11-1C) and lowest (JEN11-2D) \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) values (high: 783 MPa and 1.76 GPa; low: 605 MPa and 1.44 GPa). The inner rim median and maximum \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) range from 696–760 MPa and 1.60–1.72 GPa, and 711–837 MPa and 1.63–1.87 GPa, respectively; the single inclusion within a garnet inner rim (JEN11-2D) records the lowest maximum \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) (605 MPa and 1.44 GPa). Inclusions within the garnet outer rim from sample PG26B (Junction School) record the highest mean \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) values (810 MPa and 1.81 GPa); a single inclusion from JEN11-1C (rim) records the lowest \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) values (574 MPa and 1.39 GPa). Whisker plots suggest that 3 northern Franciscan eclogites have inclusion analyses that are statistical outliers (max \(P_\mathrm{trap}\) inclusions); however, no issues were observed with these specific inclusions (e.g., close to other inclusions, close to surface or fractures, anomalous grain shapes); therefore, the pressures calculated from these inclusions were not discarded. The mean, median, and maximum \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) of the Catalina eclogite (garnet core) are 380 MPa, 375 MPa, and 419 MPa, and 1.27 GPa, 1.26 GPa, and 1.33 GPa, respectively (Table 1; Fig. 7, 8). A single inclusion from a garnet inner rim records a \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) of 548 MPa and 1.53 GPa, respectively.
\(P_\mathrm{trap}\) (calculated from P\(^{strains}_\mathrm{inc}\)) values from northern Franciscan and Santa Catalina Island eclogites. (a) Whisker plots and (b) mean \(P_\mathrm{trap}\) from inclusions in different garnet zones are shown for comparison. (a) If less than 3 quartz inclusions were measured within a garnet zone, no whisker plot was created; (b) if only one inclusion existed within a garnet zone (not a mean value), the analysis is indicated by n = 1. \(T_\mathrm{trap}\) = 500 \(^{\circ }\)C for calculations from the northern Franciscan; \(T_\mathrm{trap}\) = 650 \(^{\circ }\)C for calculations from Catalina. (b) Circles, squares, and stars, represent \(P_\mathrm{trap}\) values calculated from inclusions in the garnet core, inner rim, and outer rim, respectively. Dashed lines represent the mean \(P_\mathrm{trap}\) for a northern Franciscan sub-population (e.g., mean \(P_\mathrm{trap}\) from all inclusions in garnet core)
Epidote-free eclogites from the northern Franciscan record similar garnet core growth conditions (mean and median \(P_\mathrm{trap}\), Figs. 4, 5, 6, 8). The absolute mean and median \(P_\mathrm{trap}\) (garnet core) of epidote-bearing eclogites tends to be lower, but the mean \(P_\mathrm{trap}\) is within error (1\(\sigma \)) of the epidote-free eclogites (Fig. 8). Garnet inner rim growth conditions are generally higher from epidote-free eclogites; however, an inclusion from sample JEN11-1C (epidote bearing) records a high garnet inner rim \(P_\mathrm{trap}\) (n = 1) that exceeds that of most other epidote-free eclogites. In general, the mean, median, and max \(P_\mathrm{trap}\) between epidote-free and epidote-bearing eclogites overlap. A notable exception is epidote-bearing sample JEN11-2D. Inclusions within the garnet core and inner rim record similar conditions as other eclogite samples, but the maximum \(P_\mathrm{trap}\), is statistically lower (2\(\sigma \) errors do not overlap) than that of other samples.
Northern Franciscan and Catalina eclogites record differences in min and max \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) values. \(P_\mathrm{inc}\) values from northern Franciscan eclogites range from 531 to 837 MPa; \(P_\mathrm{inc}\) values from a Catalina eclogite range from 342 to 548 MPa (Fig. 7, Table 1). The max \(P_\mathrm{inc}\) from the garnet core is 419 MPa (Catalina).
Lu–Hf age of eclogite PG10 (Santa Catalina Island)
We present a new Lu–Hf age based on a 3-point isochron (two garnet and clinopyroxene separates) from eclogite PG10 (Table 2, Fig. 9). This gives an age of garnet growth of 115.8 ± 0.6 Ma (MSWD = 1.13), which is within error of the garnet Lu-Hf age of 114.5 ± 0.8 Ma (Anczkiewicz et al. 2004) from a garnet hornblendite layer in coherent migmatitic gneiss in the high-grade unit on Catalina.
Discussion
Garnet zonation and pressures from northern Franciscan eclogites
Eclogites from the northern Franciscan generally preserve chemical zonation that defines a garnet core, inner rim, and outer rim; some garnets do not preserve a clear inner rim [PG26B (Junction School)]. The decrease in Mn and increase in Mg from core to inner rim/outer rim (observed in all garnets) is indicative of prograde garnet growth. Similar zoning has been described in garnets from Junction School (Page et al. 2007) and Ring Mountain eclogites (Tsujimori et al. 2006; Viete et al. 2018). A sharp Mn increase at garnet rims has been attributed to garnet resorption and re-growth (Page et al. 2007), and chemical oscillations have been attributed to pore-fluid pressure variations during seismic cycles (Viete et al. 2018). In most garnets from northern Franciscan eclogites, we observe minimal textural evidence for garnet resorption; however, this does not preclude garnet resorption in more retrogressed areas, and Mn redistribution to adjacent garnets. We interpret Mn decreases from core-to-inner rim/outer rim to indicate that many garnets record a simple prograde (increasing temperature) growth history from core-to-rim, that can be attributed to increasing P and T during subduction, or underplating and attachment to the upper plate, wherein temperatures can increase but pressures are near isobaric (e.g., Yamato et al. 2007; Dragovic et al. 2012; Penniston-Dorland et al. 2015).
Most samples show no systematic \(P_\mathrm{inc}\) variations across garnets [i.e., mean \(P_\mathrm{inc}\) values from different zones (± 1\(\sigma \)) overlap], suggesting the garnets grew under near isobaric conditions; however, quartz inclusions within different garnet zones record small pressure differences in some samples (Fig. 4 - 6, 8). The constant \(P_\mathrm{inc}\) from different garnet zones suggests that inclusions were entrapped on an elastic isomeke (constant \(P_\mathrm{inc}\) line). If \(T_\mathrm{trap}\) was constant between garnet zones, this would produce no changes in \(P_\mathrm{trap}\) and would suggest rapid garnet growth. If \(T_\mathrm{trap}\) did increase during garnet growth, \(P_\mathrm{trap}\) would also increase (\(\sim \)0.1 GPa 100 \(^{\circ }\)C\(^{-1}\)). If \(T_\mathrm{trap}\) significantly varies between initial garnet growth (e.g., 450 \(^{\circ }\)C) and late garnet growth (e.g., 600 \(^{\circ }\)C), \(P_\mathrm{trap}\) would increase by \(\sim \)0.15 GPa. In garnets in which \(P_\mathrm{inc}\) differences occur, pressures generally increase from garnet core-to-inner rim (or outer rim), and the average magnitude of this increase is \(\sim \)0.2–0.3 GPa (\(P_\mathrm{trap}\)). Sample JEN11-1C (Jenner Beach) is the only sample to exhibit decreasing \(P_\mathrm{inc}\) at the garnet outer rim (associated with a sharp decrease in X\(_\mathrm{alm}\)); however, only one suitable inclusion was found within the garnet inner rim. If garnet growth is interpreted to have occurred during subduction, the small pressure differences between garnet rims of 0.2–0.3 GPa would equate to rapid garnet growth over \(\sim \)0.2–2 m.y., assuming a subduction rate of 2–10 cm yr\(^{-1}\), a slab dip of 15–25\(^{\circ }\) (Dumitru 1991), and a 30 MPa km\(^{-1}\) pressure gradient. Rapid garnet growth under near isobaric conditions has been recorded in other subduction zones (e.g., Hellenic arc: Dragovic et al. 2012, 2015), and may reflect growth under moderate convergence rates or pulses of growth associated with internally-derived fluid fluxes. The near-isobaric conditions recorded in the garnet could also support slower garnet growth if it occurred after the eclogites were underplated and attached to the warmer upper plate. Alternatively, isobaric garnet growth could represent overstepping of the garnet isograd (Wolfe and Spear 2018; Spear et al. 2014; Spear and Wolfe 2020). The reason for which some eclogites do or do not preserve garnet \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) zonations is unclear. This is possibly related to differences in eclogite bulk compositions and its effect on garnet nucleation and growth conditions. The difference may also be related to the location of eclogite rocks after being subducted and underplated, wherein garnet in eclogite blocks initially grew garnet during subduction, but blocks that were juxtaposed with warm upper mantle initiated a second stage of protracted garnet growth.
Secondary effects can influence quartz-in-garnet barometry, and potentially minimize pressure differences between different garnet zones. These include, for example: (1) inclusion–host anisotropy (e.g., Murri et al. 2018; Angel et al. 2019), (2) non-spherical inclusion shape effects (Mazzucchelli et al. 2018), (3) relaxation (or compression) adjacent to fractures or the surface (e.g., Tait 1992; Zhang 1998), (4) tensile strain limits (Cisneros and Befus 2020), and (5) non-elastic viscous creep (e.g., Zhukov and Korsakov 2015; Zhong et al. 2020b). Our interpretation is that none of these processes affect our qtz-in-grt barometry results for the following reasons: (1) accounting for quartz anisotropy generally changes the final \(P_\mathrm{trap}\) by \(\le \) 0.1 GPa (relative to \(P_\mathrm{inc}\) calculated from the 464 cm\(^{-1}\) band), and garnet should impose a minimal anisotropic effect, (2 and 3) inclusions were near spherical, and 3x the radial distance away from the host exterior, fractures, or other inclusions, 4) all inclusions exist under compression (thus strain limits are not relevant), and 5) the max T reached by eclogites from the northern Franciscan has been estimated to be \(\sim \)650 \(^{\circ }\)C (Massonne 1995), though most studies suggest that max T is \(\le \) 600 \(^{\circ }\)C (Krogh et al. 1994; Ravna and Terry 2004; Tsujimori et al. 2006; Page et al. 2007; Cooper et al. 2011; Viete et al. 2018). At T \(\le \) 650 \(^{\circ }\)C, garnet flow laws (Ji and Martignole 1994; Wang and Ji 1999) predict that viscous creep is negligible over geologic timescales (Zhong et al. 2018, 2020b). Viscous relaxation may be more important for Catalina samples (max T \(\ge \) 650 \(^{\circ }\)C), and pressure variations at high temperatures may instead be due to varying degrees of non-elastic relaxation (Zhong et al. 2018, 2020b; Moulas et al. 2020).
The qtz-in-grt barometer has closely spaced isomekes (constant \(P_\mathrm{inc}\) lines). Small and large isomeke spacing produces small and large \(P_\mathrm{trap}\) variations, respectively. Due to the closely-spaced isomekes of the qtz-in-grt barometer, \(P_\mathrm{inc}\) variations are reduced in subsequent \(P_\mathrm{trap}\) calculations (% difference, Cisneros and Befus 2020). The similar mean, median, and max \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) of eclogites from different northern Franciscan localities suggests that they formed at similar depths (Figs. 4–8). A sampling bias of inclusions in specific garnet zones (e.g., inclusion-rich cores) skews our mean \(P_\mathrm{trap}\) results; however, the similar max \(P_\mathrm{trap}\) suggests that eclogites do preserve similar maximum \(P_\mathrm{trap}\) values (depths). A notable exception is sample JEN11-2D (Jenner Beach); the max \(P_\mathrm{trap}\) is significantly lower than that recorded by other eclogites. The difference in \(P_\mathrm{trap}\) may be due to this eclogite having reached shallower max depths, but we find it difficult to state this with certainty for three primary reasons: (1) this is an epidote-bearing eclogite, and the absolute \(P_\mathrm{trap}\) values from epidote-bearing eclogites seem to suggest that these rocks initiate garnet growth at slightly different P conditions (max \(P_\mathrm{trap}\) still similar, Fig. 8), (2) the garnet rim may capture max P conditions (similar to JEN11-3C, Fig. 8); however, no suitable quartz inclusions were found within the garnet rim, and (3) sample JEN11-2D is from the same eclogite block as JEN11-2B, and we find significantly different max P conditions from the same block, difficult to reconcile.
Garnet zonation and pressures from a Catalina eclogite
Garnets from Catalina record complex chemical zonation, and \(P_\mathrm{inc}\) and \(P_\mathrm{trap}\) differences between the core and inner rim (Fig. 6,8). We relate the decrease in Mn and increase in \(P_\mathrm{inc}\) from core-to-inner rim, to garnet growth during subduction. X-ray maps and BSE images reveal textural evidence for garnet resorption (PG10: Garnet 1 and 2), and formation of a new garnet outer rim that exhibits a sharp increase in X\(_{grs}\). We do not have qtz-in-grt barometry constraints for the pressure conditions during outer rim growth (no suitable quartz inclusions). Nonetheless, our results differ from previous qtz-in-grt barometry results from Santa Catalina island that show no difference in \(P_\mathrm{inc}\) from different garnet zones (Harvey et al. 2021a). However, their analyses were carried-out on amphibolites and blueschists (not eclogites), and are not accompanied by compositional information of garnets. The results from this study suggest that spatial information of garnet zoning may sometimes be needed to accurately interpret qtz-in-grt barometry results. To date, we are not aware of any eclogite P–T data that exists from Santa Catalina island; however, our mean (core) and max (rim) \(P_\mathrm{trap}\) results (1.27 and 1.53 GPa, Table 1), are in good agreement with previous P constraints on amphibolite facies rocks from Catalina (Sorensen and Barton 1987; Sorensen 1988; Grove and Bebout 1995; Harvey et al. 2021a). At high temperatures, \(P_\mathrm{trap}\) becomes more sensitive to \(T_\mathrm{trap}\); assuming a \(T_\mathrm{trap}\) of 750 \(^{\circ }\)C would result in mean (core) and max (rim) \(P_\mathrm{trap}\) values of 1.44 and 1.69 GPa, respectively. The max (rim) \(P_\mathrm{trap}\) conditions calculated at \(T_\mathrm{trap}\) = 650 \(^{\circ }\)C (1.53 GPa) remain higher than the mean (core) \(P_\mathrm{trap}\) results calculated at 750 \(^{\circ }\)C (1.44 GPa), suggesting that the core and rim may record real differences in growth conditions.
The maximum temperatures from previous studies (Catalina: \(\sim \)650–750 \(^{\circ }\)C), and the textural evidence of hornblende statically overprinting clinopyroxene (PG10, this study), suggests that rocks from Catalina reached high enough temperatures such that some intracyrstalline plasticity in garnet is possible at geologic strain rates based on existing flow laws (Wang and Ji 1999), or thermally induced shape changes of quartz may affect qtz-in-grt barometry results (Cesare et al. 2021). We observe no macro-scale textural evidence for dislocation activity in garnet (based on micrographs); and an EBSD map of Garnet 1 (PG10, Supplementary Figure S2) shows no evidence for micro-scale intracrystalline plasticity adjacent to formerly pressurized inclusions where differential stresses between the inclusion and host are highest (Dabrowski et al. 2015; Zhong et al. 2020b; Moulas et al. 2020). However, we cannot rule out that quartz underwent shape changes that are imposed by the host morphology (Cesare et al. 2021). The good agreement between \(P_\mathrm{trap}\) results from this study and previous P constraints also suggests that viscous creep of garnet and quartz shape changes were negligible. The following possibilities could explain the minimal evidence for intracrystalline plasticity: (1) garnet flow laws predict weakening of garnet at temperatures that are too low (Ji and Martignole 1994; Wang and Ji 1999), or (2) the lack of viscous relaxation may indicate that exhumation (or cooling) of Franciscan eclogites occurred over a time interval much shorter than the Maxwell relaxation time of the garnet.
Comparison with previous eclogite P–T constraints
Qtz-in-grt barometry results from the northern Franciscan Complex reveal some differences recorded by different eclogites. Notably, the lack-of or presence of \(P_\mathrm{trap}\) variations across garnets, that correspond to chemical zonation. The variation and trend (increase) of \(P_\mathrm{trap}\) from garnet core-to-inner rim (or outer rim) is in agreement with previous studies that suggest garnet cores record the lowest pressures, and garnet inner rims/outer rims record higher pressures (Massonne 1995; Tsujimori et al. 2006; Page et al. 2007). The \(P_\mathrm{trap}\) decrease at the garnet rim of sample JEN11-1C (Jenner Beach), is in agreement with previous studies that documented retrograde garnet growth during decreasing P–T conditions (e.g., Massonne 1995; Page et al. 2007).
Eclogite P–T paths, mean, and max pressures vary widely between previous studies (northern Franciscan, Fig. 10). Absolute mean and max \(P_\mathrm{trap}\) from this study (\(\sim \)1.5–1.8 GPa) best agree with the results of Page et al. (2007), Cooper et al. (2011), and Viete et al. (2018) (Fig. 10). Our results significantly disagree (> 0.5 GPa difference) with previous studies that suggest higher (Massonne 1995; Tsujimori et al. 2006) or lower (Ernst 1988; Wakabayashi 1990) formation pressures of eclogites. Several possibilities can explain the disagreement between our results and those from previous studies.
Eclogite formation conditions from this study (\(P_\mathrm{trap}\)), and reference P–T conditions. \(P_\mathrm{trap}\) values from individual eclogites are shown as whisker plots (core, inner rim, and outer rim combined). \(P_\mathrm{trap}\) values from the northern Franciscan were calculated at \(T_\mathrm{trap}\) = 500 \(^{\circ }\)C, but are slightly offset on the x-axis (temperature) for visual clarity. \(P_\mathrm{trap}\) values from Santa Catalina Island were calculated at \(T_\mathrm{trap}\) = 650 \(^{\circ }\)C
Multiple studies have used garnet-white mica-pyroxene (grt-wm-px) thermobarometry to constrain formation conditions of Franciscan eclogites (Massonne 1995; Tsujimori et al. 2006; Page et al. 2007), but resultant P–T conditions significantly differ (Fig. 8). Previous studies have used the Waters and Martin (1993) [Junction School: Page et al. (2007)], Ravna and Terry (2004) [Jenner Beach: Ravna and Terry (2004); Ring Mountain: Tsujimori et al. (2006); Junction School: Page et al. (2007)], and the Massonne (1995) [Ring Mountain, Junction School: Massonne (1995)] calibrations. Page et al. (2007) compared P–T conditions calculated using the Ravna and Terry (2004) and Waters and Martin (1993) grt-wm-px calibrations (Jenner Beach eclogites). P–T conditions calculated using the Ravna and Terry (2004) calibration are higher than those calculated using the Waters and Martin (1993) calibration with an empirical correction (Wain et al. 2000). The authors determined that calculations based on the Waters and Martin (1993) calibration best agree with independent mineral equilibria P–T constraints. P–T conditions calculated using the Massonne (1995) calibration exceed all other reference P–T conditions, and some results suggest that Junction School eclogites reached the coesite stability field; however, no coesite has been found in Franciscan eclogites (to the best of our knowledge).
Contrasting results from previous grt-wm-px thermobarometry can be attributed to four possible scenarios: (1) the use of different grt-wm-px calibrations, (2) inaccuracies associated with the underlying thermodynamic data of the grt-wm-px thermobarometer, (3) the use of minerals that do not record chemical equilibrium, or (4) true P–T heterogeneity between eclogites from different outcrops. Page et al. (2007) show how using different grt-wm-px calibrations for the same mineral chemistry, can drastically affect P–T results; however, the same grt-wm-px calibration (Ravna and Terry 2004) is used for eclogites from Ring Mountain and Jenner Beach, and different P–T results were obtained (Tsujimori et al. 2006; Page et al. 2007), suggesting true P–T heterogeneity recorded by eclogites from different outcrops. The benefit of this study is that we use a single barometer for similar rock types (eclogites), and this barometer has a minimal temperature (and compositional) dependence. Results from this study (similar \(P_\mathrm{trap}\) conditions for eclogites from all outcrops), suggest that variations between grt-wm-px calibrations, or disequilibria associated with minerals (grt-wm-px) analyzed for thermobarometry calculations, are what led to the drastically different P–T estimates in the published literature, rather than true P–T condition variations.
The mean and max \(P_\mathrm{trap}\) determined from the Catalina eclogite is in good agreement with previous P–T constraints. Harvey et al. (2021a) used qtz-in-grt barometry and Zr-in-rutile thermometry on blueschists and amphibolites from Catalina, and calculated P–T conditions between 1.16–1.65 GPa and 580–735 \(^{\circ }\)C (no systematic core-rim variations). Other studies on rocks from the amphibolite facies units on Catalina document a wide P–T range between \(\sim \)0.8–1.2 GPa and \(\sim \)640–750 \(^{\circ }\)C (Sorensen and Barton 1987; Grove and Bebout 1995; Penniston-Dorland et al. 2018). Qtz-in-grt barometry results from rocks of different metamorphic facies indicate that rocks from Catalina reached similar peak pressures. Harvey et al. (2021a) found a pressure range of \(\sim \)1.3–1.4 GPa from amphibolite facies blocks within the serpentinite-matrix melange and a larger pressure range for blocks from the epidote amphibolite facies (\(\sim \)1.2–1.4 GPa) and lawsonite-blueschist facies units (\(\sim \)1.6 GPa). The authors interpret pressure differences to indicate mixing of blocks from different depths; but we note that minor differences in bulk compositions can affect garnet growth conditions (e.g., epidote-bearing eclogites in this study). Given the pressure range documented from a single eclogite in this study (core-rim: \(\sim \)1.3–1.5 GPa) and pressure precision from quartz inclusions from different garnet zones (\(\sim \)0.1–0.2 GPa), we suggest that small pressure differences between different blocks from Catalina can be explained by minor differences in bulk composition, or incomplete characterization of inclusion pressures from different garnet zones.
Evolution of the Franciscan Complex and implications for exhumation models
Our results suggest that different eclogites from the northern Franciscan Complex record a similar pressure evolution and reached similar depths, and are in agreement with previous results that suggest the northern Franciscan Complex did not reach the coesite stability field. Furthermore, our results are consistent with the southern Franciscan Complex exposed on Santa Catalina island recording lower max P conditions. The most striking result of this study is the similar \(P_\mathrm{trap}\) recorded by different eclogites from the northern Franciscan Complex. Previous results on eclogites from the northern Franciscan (Fig. 10), suggested that different eclogite blocks reached significantly different depths.
Three primary models have been proposed to explain exhumation of high-grade blocks (e.g., eclogites) from the northern Franciscan, that exist within a lower pressure matrix (such as in the central belt): (1) high-grade blocks were exhumed along with coherent blueschists by underplating and extension in the rear of the accretionary wedge (Platt 1986). The blocks were then emplaced within a sedimentary matrix by erosion and mass-wasting in the inner trench wall, and subsequently re-subducted to produce the present-day relationships (Platt 2015). (2) Return flow of subducted mud-matrix melange driven by the closure of the subduction channel at depth removed and exhumed the high-grade blocks from depth (i.e., Cloos 1982). (3) High-grade blocks rise within a buoyant serpentinite matrix (e.g., Horodyskyj et al. 2009). A comparison of mean and max \(P_\mathrm{trap}\) conditions from different eclogites, cannot differentiate between these models; but the results from this study (similar max and mean pressures), better support a model that does not incorporate sourcing of eclogite blocks from different depths. ‘Melange’-style mixing may be best recorded by the incorporation of blocks of different grades, within a shaley or ultramafic matrix; but our results are inconsistent with the idea that different eclogite blocks reached different depths, and instead suggest that pressure differences result from different grt-wm-px calibrations, or minerals chosen for thermobarometry. Previous studies from other field areas that employ quartz-in-garnet barometry have proposed similar geologic histories. Bayet et al. (2020) studied interlayered mafic and metapelite rocks across the Southern Tianshan metamorphic belt. The authors also found consistent peak pressures from quartz-in-garnet barometry (mean P \(\approx \) 2.5 GPa), and suggest that this supports coherent subduction and exhumation of a single coherent crustal section. Groß et al. (2020) found similar peak pressures (\(\sim \)2.0 GPa) between metasediments from within the Modereck and Glockner nappes (central Tauern Window), and propose a model that involves crustal-scale sheath folding of different nappes near peak metamorphic conditions.
The P–T conditions estimated here (\(\sim \)1.5–1.8 GPa, estimated at \(T_\mathrm{trap}\) = 500 \(^{\circ }\)C), suggest that these are low-temperature eclogites that formed in a thermal gradient of \(\sim \)8–11 \(^{\circ }\)C km\(^{-1}\) (assuming 30 MPa km\(^{-1}\)), and the similar pressures between eclogites and their recorded thermal gradient may have implications for the recovery process of HP–LT rocks from subduction zones. Agard et al. (2018) note that exhumed subduction zone rocks are commonly recovered from discrete depths between \(\sim \)25–33 km, \(\sim \)55–60 km, and \(\sim \)80 km with punctuated recovery; but the compiled data is statistically dispersed between these depth ranges. Several models have been proposed for exhuming rocks from similar depths at \(\sim \)55–60 km.
Exhumation of low-temperature blueschists and eclogites has been thought to occur coherently, wherein detachment and exhumation of coherent slices from the subducting plate is triggered due to the step-down of the plate interface that roots into décollement horizons and/or localizes along a serpentinized crust/mantle boundary in the subducting plate (Vogt and Gerya 2014; Ruh et al. 2015; Agard et al. 2018; Tewksbury-Christle et al. 2021). Agard et al. (2016) propose that during subduction infancy, warm thermal gradients produce shallow detachment and underplating of subducting material due to small viscosity contrasts between subducting material and the serpentinized upper mantle (increased interplate coupling). Ruh et al. (2015) and Agard et al. (2018) propose that once steady-state thermal gradients are achieved, detachment of subducting crust requires a weak horizon, such as serpentinized mantle between subducting oceanic crust and mantle. Numerical models indicate that the detachment of slices occurs when the shear stresses in the subducting crust overcome the mechanical yield strength, and the dominant shear zone “steps-down” into upper mantle. The depth of detachment and underplating is strongly temperature dependent, wherein cooler thermal gradients (deeper serpentinite dehydration) produce deeper underplating, and hotter thermal gradients (shallower serpentinite dehydration) produce shallower underplating. Interestingly, this may also be consistent with mafic rocks from the northern Franciscan Complex, where older rocks (amphibolites, \(\sim \)169–163 Ma) record lower pressures (shallower underplating), and younger rocks (eclogites, \(\sim \)158–153 Ma) record higher pressures (deeper underplating) as the subduction zone matures and cools. At later times, sediments are underplated and exhumed, complicating this comparison due to the greater buoyancy of sediments. Rutte et al. (2020) propose a single exhumation event for high-grade blocks of the Franciscan Complex based on amphibolite and phengite Ar-Ar dating, perhaps consistent with a coherent underplating and exhumation model.
Buoyancy forces, and the strength and/or thickness of a basal shear zone (zone separating material that can be underplated and the subducting plate) can cause the detached material to be further subducted or underplated (Bialas et al. 2011). Eclogites from the northern Franciscan Complex are commonly found in close proximity to serpentinites, a rock-type that can form a weak basal shear zone, and lead to detachment and return flow of coherent slices of material. Previous studies from the Condrey Mountain show that strain localization within a weak serpentine basal shear zone, can lead to underplating/return flow (Tewksbury-Christle et al. 2021); however the buoyant return flow was driven by sediments. On the contrary, denser underplated eclogites would oppose return flow. At high enough temperatures, the viscosity reduction of eclogites attached to the downgoing plate could reduce the viscosity contrast between subducting rocks and the upper plate, such that it leads to increased interplate coupling and facilitates detachment and underplating of eclogites. Later subduction and underplating of lower density sediments beneath previously underplated oceanic material, could produce the final buoyancy-driven exhumation of the underplated oceanic material by coherently carrying the eclogites upward.
Conclusions
This work highlights the advantage of using qtz-in-grt barometry on a single rock type (eclogites) to compare pressures between HP–LT blocks. Our results allow us to determine robust pressure estimates for a rock-type that has historically presented challenges. Combining residual inclusion pressures with detailed spatial characterization of garnet zonation, shows that the qtz-in-grt barometer can preserve pressure variations that are related to protracted garnet growth. This work further highlights the importance of coupling qtz-in-grt barometry with spatial information of garnet zonation, to accurately interpret results from garnets that exhibit large pressure variations.
Mean and max entrapment pressures from northern Franciscan eclogites best agree with low-pressure estimates from the Franciscan Complex, and significantly disagree with previous high-pressure estimates that approach or reach the coesite stability field (e.g., Massonne 1995; Tsujimori et al. 2006). Pressures from a Santa Catalina Island eclogite agree with most reference pressure constraints from high-grade rocks on the island. Mean and max entrapment pressures exhibit minimal differences between eclogites, and best support exhumation models that propose exhumation of high-grade blocks from similar structural depths, rather than ‘melange-style’ mixing and exhumation of eclogites from variable depths. The similar depths recorded by eclogite blocks may also have implications for the recovery process of high-grade rocks, perhaps indicating the detachment of coherent mafic slices due to weak serpentinite-bearing basal shear zones. The pressure and age evolution of northern Franciscan blocks would be in agreement with numerical modeling results that document the effect of serpentinized upper mantle on crustal detachment, that shows that shallower detachment and underplating of oceanic material would be expected when the subduction zone is hotter (e.g., older, shallower amphibolites), and deeper detachment and underplating would be expected when the subduction zone cools (e.g., younger, deeper eclogites) due to differences in depths of serpentine dehydration.
References
Adams H, Cohen LH, Rosenfeld JL (1975) Solid inclusion piezothermometry I: comparison dilatometry. Am Miner 60:574–583
Adams H, Cohen LH, Rosenfeld JL (1975) Solid inclusion piezothermometry II: geometric basis, calibration for the association quartz-garnet, and application to some pelitic schists. Am Miner 60:584–598
Agard P, Yamato P, Soret M, Prigent C, Guillot S, Plunder A, Dubacq B, Chauvet A, Monié P (2016) Plate interface rheological switches during subduction infancy: Control on slab penetration and metamorphic sole formation. Earth and Planetary Science Letters 451:208–220, https://doi.org/10.1016/j.epsl.2016.06.054, https://www.sciencedirect.com/science/article/pii/S0012821X16303478
Agard P, Plunder A, Angiboust S, Bonnet G, Ruh J (2018) The subduction plate interface: rock record and mechanical coupling (from long to short timescales). Lithos 320–321:537–566, https://doi.org/10.1016/j.lithos.2018.09.029, http://www.sciencedirect.com/science/article/pii/S0024493718303566
Anczkiewicz R, Platt JP, Thirlwall MF, Wakabayashi J (2004) Franciscan subduction off to a slow start: evidence from high-precision Lu-Hf garnet ages on high grade-blocks. Earth and Planetary Science Letters 225(1):147–161, https://doi.org/10.1016/j.epsl.2004.06.003, http://www.sciencedirect.com/science/article/pii/S0012821X04003796
Angel RJ, Nimis P, Mazzucchelli ML, Alvaro M, Nestola F (2015) How large are departures from lithostatic pressure? Constraints from host-inclusion elasticity. J Metamorph Geol 33(8):801–813. https://doi.org/10.1111/jmg.12138
Angel RJ, Alvaro M, Miletich R, Nestola F (2017) A simple and generalised P-T-V EoS for continuous phase transitions, implemented in EosFit and applied to quartz. Contrib Miner Petrol 172(5):29. https://doi.org/10.1007/s00410-017-1349-x
Angel RJ, Mazzucchelli ML, Alvaro M, Nestola F (2017) EosFit-Pinc: A simple GUI for host-inclusion elastic thermobarometry. American Mineralogist 102(9):1957–1960, https://doi.org/10.2138/am-2017-6190, https://search.proquest.com/docview/1940599109/abstract/D77CD94E26414FADPQ/1
Angel RJ, Murri M, Mihailova B, Alvaro M (2019) Stress, strain and Raman shifts. Zeitschrift für Kristallographie - Crystalline Materials 234(2):129–140, https://doi.org/10.1515/zkri-2018-2112, https://www.degruyter.com/view/j/zkri.2019.234.issue-2/zkri-2018-2112/zkri-2018-2112.xml
Ashley KT, Caddick MJ, Steele-MacInnis MJ, Bodnar RJ, Dragovic B (2014) Geothermobarometric history of subduction recorded by quartz inclusions in garnet. Geochem Geophys Geosyst 15(2):350–360. https://doi.org/10.1002/2013GC005106
Bachman SB (1982) The Coastal Belt of the Franciscan: youngest phase of northern California subduction. Geological Society, London, Special Publications 10(1):401–417, https://doi.org/10.1144/GSL.SP.1982.010.01.27, https://sp.lyellcollection.org/content/10/1/401, publisher: Geological Society of London Section: California
Baldwin SL, Monteleone BD, Webb LE, Fitzgerald PG, Grove M, June Hill E (2004) Pliocene eclogite exhumation at plate tectonic rates in eastern Papua New Guinea. Nature 431(7006):263–267, https://doi.org/10.1038/nature02846, https://www.nature.com/articles/nature02846, number: 7006 Publisher: Nature Publishing Group
Barnes JD, Eldam R, Lee CTA, Errico JC, Loewy S, Cisneros M (2013) Petrogenesis of serpentinites from the Franciscan Complex, western California, USA. Lithos 178:143–157, https://doi.org/10.1016/j.lithos.2012.12.018, http://www.sciencedirect.com/science/article/pii/S0024493713000029
Bass JD (1995) Elastic properties of minerals, melts, and glasses. Handbook of Physical Constants pp 45–63, publisher: AGU Washington, D. C
Bayet L, Agard P, John T, Menneken M, Tan Z, Gao J (2020) Tectonic evolution of the Tianshan Akeyazi metamorphic complex (NW China). Lithos 354–355:105273, https://doi.org/10.1016/j.lithos.2019.105273, https://www.sciencedirect.com/science/article/pii/S0024493719304335
Bialas RW, Funiciello F, Faccenna C (2011) Subduction and exhumation of continental crust: insights from laboratory models. Geophys J Int 184(1):43–64. https://doi.org/10.1111/j.1365-246X.2010.04824.x
Bonazzi M, Tumiati S, Thomas J, Angel RJ, Alvaro M (2019) Assessment of the reliability of elastic geobarometry with quartz inclusions. Lithos 350–351:105201, https://doi.org/10.1016/j.lithos.2019.105201, http://www.sciencedirect.com/science/article/pii/S0024493719303603
Bröcker M, Day HW (1995) Low-grade blueschist facies metamorphism of metagreywackes, Franciscan Complex, northern California. J Metamorph Geol 13(1):61–78. https://doi.org/10.1111/j.1525-1314.1995.tb00205.x
Campomenosi N, Mazzucchelli ML, Mihailova B, Scambelluri M, Angel RJ, Nestola F, Reali A, Alvaro M (2018) How geometry and anisotropy affect residual strain in host-inclusion systems: Coupling experimental and numerical approaches. American Mineralogist 103(12):2032–2035, https://doi.org/10.2138/am-2018-6700CCBY, https://www.degruyter.com/view/j/ammin.2018.103.issue-12/am-2018-6700CCBY/am-2018-6700CCBY.xml
Cesare B, Parisatto M, Mancini L, Peruzzo L, Franceschi M, Tacchetto T, Reddy S, Spiess R, Nestola F, Marone F (2021) Mineral inclusions are not immutable: Evidence of post-entrapment thermally-induced shape change of quartz in garnet. Earth and Planetary Science Letters 555:116708, https://doi.org/10.1016/j.epsl.2020.116708, https://www.sciencedirect.com/science/article/pii/S0012821X2030652X
Cisneros M, Befus KS (2020) Applications and Limitations of Elastic Thermobarometry: Insights From Elastic Modeling of Inclusion-Host Pairs and Example Case Studies. Geochem Geophys Geosyst 21(10):e2020GC009231. https://doi.org/10.1029/2020GC009231
Cisneros M, Barnes JD, Behr WM, Kotowski AJ, Stockli DF, Soukis K (2021) Insights from elastic thermobarometry into exhumation of high-pressure metamorphic rocks from Syros. Greece. Solid Earth 12(6):1335–1355, https://doi.org/10.5194/se-12-1335-2021, https://se.copernicus.org/articles/12/1335/2021/, publisher: Copernicus GmbH
Cloos M (1982) Flow melanges: Numerical modeling and geologic constraints on their origin in the Franciscan subduction complex. California. GSA Bulletin 93(4):330–345, https://doi.org/10.1130/0016-7606(1982)93<330:FMNMAG>2.0.CO;2, https://pubs.geoscienceworld.org/gsa/gsabulletin/article/93/4/330/202762/flow-melanges-numerical-modeling-and-geologic
Cloos M (1985) Thermal evolution of convergent plate margins: Thermal modeling and reevaluation of isotopic AR-ages for Blueschists in the Franciscan Complex of California. Tectonics 4(5):421–433. https://doi.org/10.1029/TC004i005p00421
Cohen LH, Rosenfeld JL (1979) Diamond: Depth of Crystallization Inferred from Compressed Included Garnet. J Geol 87(3):333–340. https://doi.org/10.1086/628422
Coleman RG, Lanphere MA (1971) Distribution and Age of High-Grade Blueschists, Associated Eclogites, and Amphibolites from Oregon and California. GSA Bulletin 82(9):2397–2412, https://doi.org/10.1130/0016-7606(1971)82[2397:DAAOHB]2.0.CO;2, https://pubs.geoscienceworld.org/gsa/gsabulletin/article/82/9/2397/7272/Distribution-and-Age-of-High-Grade-Blueschists, publisher: GeoScienceWorld
Collins NC, Bebout GE, Angiboust S, Agard P, Scambelluri M, Crispini L, John T (2015) Subduction zone metamorphic pathway for deep carbon cycling: II. Evidence from HP/UHP metabasaltic rocks and ophicarbonates. Chemical Geology 412:132–150, https://doi.org/10.1016/j.chemgeo.2015.06.012, http://www.sciencedirect.com/science/article/pii/S0009254115002995
Cooper FJ, Platt JP, Anczkiewicz R (2011) Constraints on early Franciscan subduction rates from 2-D thermal modeling. Earth and Planetary Science Letters 312(1):69–79, https://doi.org/10.1016/j.epsl.2011.09.051, http://www.sciencedirect.com/science/article/pii/S0012821X11005711
Cressey G, Schmid R, Wood BJ (1978) Thermodynamic properties of almandine-grossular garnet solid solutions. Contrib Miner Petrol 67(4):397–404. https://doi.org/10.1007/BF00383299
Dabrowski M, Powell R, Podladchikov Y (2015) Viscous relaxation of grain-scale pressure variations. J Metamorph Geol 33(8):859–868. https://doi.org/10.1111/jmg.12142
Dragovic B, Samanta LM, Baxter EF, Selverstone J (2012) Using garnet to constrain the duration and rate of water-releasing metamorphic reactions during subduction: An example from Sifnos, Greece. Chemical Geology 314–317:9–22, https://doi.org/10.1016/j.chemgeo.2012.04.016, http://linkinghub.elsevier.com/retrieve/pii/S0009254112001829
Dragovic B, Baxter EF, Caddick MJ (2015) Pulsed dehydration and garnet growth during subduction revealed by zoned garnet geochronology and thermodynamic modeling, Sifnos, Greece. Earth and Planetary Science Letters 413:111–122, https://doi.org/10.1016/j.epsl.2014.12.024, http://www.sciencedirect.com/science/article/pii/S0012821X14007857
Dumitru TA (1991) Effects of subduction parameters on geothermal gradients in forearcs, with an application to Franciscan Subduction in California. J Geophys Res Solid Earth 96(B1):621–641. https://doi.org/10.1029/90JB01913
Dumitru TA, Wakabayashi J, Wright JE, Wooden JL (2010) Early Cretaceous transition from nonaccretionary behavior to strongly accretionary behavior within the Franciscan subduction complex. Tectonics 29(5), iSBN: 0278-7407 Publisher: Wiley Online Library
Enami M, Nishiyama T, Mouri T (2007) Laser Raman microspectrometry of metamorphic quartz: A simple method for comparison of metamorphic pressures. American Mineralogist 92(8–9):1303–1315, https://doi.org/10.2138/am.2007.2438, https://pubs.geoscienceworld.org/msa/ammin/article/92/8-9/1303/134496/laser-raman-microspectrometry-of-metamorphic
Ernst WG (1975) Systematics of large-scale tectonics and age progressions in Alpine and Circum-Pacific blueschist belts. Tectonophysics 26(3):229–246, https://doi.org/10.1016/0040-1951(75)90092-X, https://www.sciencedirect.com/science/article/pii/004019517590092X
Ernst WG (1988) Tectonic history of subduction zones inferred from retrograde blueschist P-T paths. Geology 16(12):1081–1084, https://doi.org/10.1130/0091-7613(1988)016<1081:THOSZI>2.3.CO;2, https://pubs.geoscienceworld.org/gsa/geology/article/16/12/1081/204628/tectonic-history-of-subduction-zones-inferred-from
Errico JC, Barnes JD, Strickland A, Valley JW (2013) Oxygen isotope zoning in garnets from Franciscan eclogite blocks: evidence for rock-buffered fluid interaction in the mantle wedge. Contrib Miner Petrol 166(4):1161–1176. https://doi.org/10.1007/s00410-013-0915-0
Essene EJ (1989) The current status of thermobarometry in metamorphic rocks. Geological Society, London, Special Publications 43(1):1–44, https://doi.org/10.1144/GSL.SP.1989.043.01.02, https://sp.lyellcollection.org/content/43/1/1, publisher: Geological Society of London
Geiger CA (2000) Volumes of mixing in aluminosilicate garnets: Solid solution and strain behavior. American Mineralogist 85(7–8):893–897, https://doi.org/10.2138/am-2000-0702, https://pubs.geoscienceworld.org/msa/ammin/article/85/7-8/893/133677/Volumes-of-mixing-in-aluminosilicate-garnets-Solid, publisher: GeoScienceWorld
Godfrey NJ, Klemperer SL (1998) Ophiolitic basement to a forearc basin and implications for continental growth: The Coast Range/Great Valley ophiolite. California. Tectonics 17(4):558–570. https://doi.org/10.1029/98TC01536
Grove M, Bebout GE (1995) Cretaceous tectonic evolution of coastal southern California: Insights from the Catalina Schist. Tectonics 14(6):1290–1308. https://doi.org/10.1029/95TC01931
Grove M, Bebout G, Jacobson C, Barth A, Kimbrough D, King R, Zou H, Lovera O, Mahoney J, Gehrels G (2008) The Catalina Schist: Evidence for middle Cretaceous subduction erosion of southwestern North America. In: Special Paper of the Geological Society of America, vol 436, Geological Society of America, pp 335–361, https://doi.org/10.1130/2008.2436(15), journal Abbreviation: Special Paper of the Geological Society of America
Groß P, Handy MR, John T, Pestal G, Pleuger J (2020) Crustal-Scale Sheath Folding at HP Conditions in an Exhumed Alpine Subduction Zone (Tauern Window, Eastern Alps). Tectonics 39(2):e2019TC005942. https://doi.org/10.1029/2019TC005942
Guiraud M, Powell R (2006) P-V-T relationships and mineral equilibria in inclusions in minerals. Earth and Planetary Science Letters 244(3):683–694, https://doi.org/10.1016/j.epsl.2006.02.021, http://www.sciencedirect.com/science/article/pii/S0012821X06001592
Harvey KM, Penniston-Dorland SC, Kohn MJ, Piccoli PM (2021) Assessing P-T variability in mélange blocks from the Catalina Schist: Is there differential movement at the subduction interface? J Metamorph Geol 39(3):271–295. https://doi.org/10.1111/jmg.12571
Harvey KM, Walker S, Starr PG, Penniston-Dorland SC, Kohn MJ, Baxter EF (2021b) A Mélange of Subduction Ages: Constraints on the Timescale of Shear Zone Development and Underplating at the Subduction Interface, Catalina Schist (CA, USA). Geochem Geophys Geosyst 22(9):e2021GC009790. https://doi.org/10.1029/2021GC009790
Holland T, Powell R (2011) An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J Metamorph Geol 29(3):333–383. https://doi.org/10.1111/j.1525-1314.2010.00923.x
Hopson CA, Mattinson JM, Pessagno EA, Luyendyk BP, Wright JE, Shervais JW (2008) California Coast Range ophiolite: composite middle and late Jurassic oceanic lithosphere. SPECIAL PAPERS-GEOLOGICAL SOCIETY OF AMERICA 438:1, iSBN: 0072-1077 Publisher: Boulder, Colo.; Geological Society of America; 1999
Horodyskyj U, Lee CTA, Luffi P (2009) Geochemical evidence for exhumation of eclogite via serpentinite channels in ocean-continent subduction zonesGeochemical signatures of Franciscan eclogite exhumation. Geosphere 5(5):426–438, https://doi.org/10.1130/GES00502.1, https://pubs.geoscienceworld.org/gsa/geosphere/article/5/5/426/31236/Geochemical-evidence-for-exhumation-of-eclogite, publisher: GeoScienceWorld
Isaak DG, Anderson OL, Oda H (1992) High-temperature thermal expansion and elasticity of calcium-rich garnets. Phys Chem Miner 19(2):106–120. https://doi.org/10.1007/BF00198608
Isozaki Y, Blake MC (1994) Biostratigraphic Constraints on Formation and Timing of Accretion in a Subduction Complex: An Example from the Franciscan Complex of Northern California. The Journal of Geology 102(3):283–296, https://doi.org/10.1086/629671, publisher: The University of Chicago Press
Ji S, Martignole J (1994) Ductility of garnet as an indicator of extremely high temperature deformation. Journal of Structural Geology 16(7):985–996, https://doi.org/10.1016/0191-8141(94)90080-9, http://www.sciencedirect.com/science/article/pii/0191814194900809
Kohn MJ (2014) “Thermoba-Raman-try”: Calibration of spectroscopic barometers and thermometers for mineral inclusions. Earth and Planetary Science Letters 388:187–196, https://doi.org/10.1016/j.epsl.2013.11.054, http://www.sciencedirect.com/science/article/pii/S0012821X1300695X
Krogh EJ, Oh CW, Liou JC (1994) Polyphase and anticlockwise P-T evolution for Franciscan eclogites and blueschists from Jenner, California, USA. J Metamorph Geol 12(2):121–134. https://doi.org/10.1111/j.1525-1314.1994.tb00008.x
Kuzmany H (2009) Solid-state spectroscopy: an introduction. Springer Science & Business Media
Ludwig KR (2001) Isoplot/Ex version 2.49 : A geochronology toolkit for Microsoft Excel. Berkeley Geochronology Center Special Publication 55, https://ci.nii.ac.jp/naid/10011476874/
Massonne HJ (1995) Experimental and petrogenetic study of UHPM. Ultrahigh Pressure Metamorphism pp 33–95, https://ci.nii.ac.jp/naid/10027123230/, publisher: Cambridge University Press
Mattinson JM (1986) Geochronology of high-pressure–low-temperature Franciscan metabasites: A new approach using the U-Pb system. In: Blueschists and eclogites, vol 164, Geological Society of America, pp 95–105
Mazzucchelli ML, Burnley P, Angel RJ, Morganti S, Domeneghetti MC, Nestola F, Alvaro M (2018) Elastic geothermobarometry: Corrections for the geometry of the host-inclusion system. Geology 46(3):231–234, https://doi.org/10.1130/G39807.1, https://pubs.geoscienceworld.org/gsa/geology/article/46/3/231/526077/elastic-geothermobarometry-corrections-for-the
Milani S, Nestola F, Alvaro M, Pasqual D, Mazzucchelli ML, Domeneghetti MC, Geiger CA (2015) Diamond-garnet geobarometry: The role of garnet compressibility and expansivity. Lithos 227:140–147, https://doi.org/10.1016/j.lithos.2015.03.017, http://www.sciencedirect.com/science/article/pii/S0024493715001097
Milani S, Angel RJ, Scandolo L, Mazzucchelli ML, Ballaran TB, Klemme S, Domeneghetti MC, Miletich R, Scheidl KS, Derzsi M, Tokár K, Prencipe M, Alvaro M, Nestola F (2017) Thermo-elastic behavior of grossular garnet at high pressures and temperatures. American Mineralogist 102(4):851–859, https://doi.org/10.2138/am-2017-5855, https://pubs.geoscienceworld.org/ammin/article/102/4/851/298077/Thermo-elastic-behavior-of-grossular-garnet-at, publisher: GeoScienceWorld
Moulas E, Kostopoulos D, Podladchikov Y, Chatzitheodoridis E, Schenker FL, Zingerman KM, Pomonis P, Tajčmanová L (2020) Calculating pressure with elastic geobarometry: A comparison of different elastic solutions with application to a calc-silicate gneiss from the Rhodope Metamorphic Province. Lithos 378–379:105803, https://doi.org/10.1016/j.lithos.2020.105803, https://www.sciencedirect.com/science/article/pii/S0024493720304400
Mulcahy SR, Starnes JK, Day HW, Coble MA, Vervoort JD (2018) Early Onset of Franciscan Subduction. Tectonics 37(5):1194–1209. https://doi.org/10.1029/2017TC004753
Murri M, Mazzucchelli ML, Campomenosi N, Korsakov AV, Prencipe M, Mihailova BD, Scambelluri M, Angel RJ, Alvaro M (2018) Raman elastic geobarometry for anisotropic mineral inclusions. American Mineralogist 103(11):1869–1872, https://doi.org/10.2138/am-2018-6625CCBY, https://www.degruyter.com/view/j/ammin.2018.103.issue-11/am-2018-6625CCBY/am-2018-6625CCBY.xml
Murri M, Alvaro M, Angel RJ, Prencipe M, Mihailova BD (2019) The effects of non-hydrostatic stress on the structure and properties of alpha-quartz. Phys Chem Miner 46:487–499. https://doi.org/10.1007/s00269-018-01018-6
Nye JF (1985) Physical properties of crystals: their representation by tensors and matrices. Oxford University Press, Oxford
Oh CW, Liou JG (1990) Metamorphic evolution of two different eclogites in the Franciscan Complex, California, U.S.A. Lithos 25(1):41–53, https://doi.org/10.1016/0024-4937(90)90005-L, https://www.sciencedirect.com/science/article/pii/002449379090005L
Page FZ, Armstrong LS, Essene EJ, Mukasa SB (2007) Prograde and retrograde history of the Junction School eclogite, California, and an evaluation of garnet-phengite-clinopyroxene thermobarometry. Contrib Miner Petrol 153(5):533–555. https://doi.org/10.1007/s00410-006-0161-9
Page FZ, Cameron EM, Flood CM, Dobbins JW, Spicuzza MJ, Kitajima K, Strickland A, Ushikubo T, Mattinson CG, Valley JW (2019) Extreme oxygen isotope zoning in garnet and zircon from a metachert block in mélange reveals metasomatism at the peak of subduction metamorphism. Geology 47(7):655–658. https://doi.org/10.1130/G46135.1
Penniston-Dorland SC, Kohn MJ, Manning CE (2015) The global range of subduction zone thermal structures from exhumed blueschists and eclogites: Rocks are hotter than models. Earth and Planetary Science Letters 428:243–254, https://doi.org/10.1016/j.epsl.2015.07.031, http://www.sciencedirect.com/science/article/pii/S0012821X15004665
Penniston-Dorland SC, Kohn MJ, Piccoli PM (2018) A mélange of subduction temperatures: Evidence from Zr-in-rutile thermometry for strengthening of the subduction interface. Earth and Planetary Science Letters 482:525–535, https://doi.org/10.1016/j.epsl.2017.11.005, http://www.sciencedirect.com/science/article/pii/S0012821X17306416
Platt JP (1975) Metamorphic and deformational processes in the Franciscan Complex, California: Some insights from the Catalina Schist terrane. GSA Bull 86(10):1337–1347. https://doi.org/10.1130/0016-7606(1975)861337:MADPIT2.0.CO;2
Platt JP (1976) The petrology, structure and geologic history of the Catalina Schist terrane, southern California. University of California Press, California
Platt JP (1986) Dynamics of orogenic wedges and the uplift of high-pressure metamorphic rocks. GSA Bulletin 97(9):1037–1053, https://doi.org/10.1130/0016-7606(1986)971037:DOOWAT2.0.CO;2, https://pubs.geoscienceworld.org/gsa/gsabulletin/article/97/9/1037/203199/Dynamics-of-orogenic-wedges-and-the-uplift-of-high, publisher: GeoScienceWorld
Platt JP (2015) Origin of Franciscan blueschist-bearing melange at San Simeon, central California coast. Int Geol Rev 57(5–8):843–853. https://doi.org/10.1080/00206814.2014.902756
Ravna EJK, Terry MP (2004) Geothermobarometry of UHP and HP eclogites and schists - an evaluation of equilibria among garnet-clinopyroxene-kyanite-phengite-coesite/quartz. J Metamorph Geol 22(6):579–592. https://doi.org/10.1111/j.1525-1314.2004.00534.x
Raymond LA (2017) A metasomatic setting, the Russian River Arch, and gravitational emplacement in the history of eclogites at the classic eclogite locality of Jenner, California, USA. International Geology Review 59(5–6):577–598. https://doi.org/10.1080/00206814.2016.1213143, publisher: Taylor & Francis
Raymond LA (2019) Origin of Mélanges of the Franciscan Complex, Diablo Range and Northern California: An Analysis and Review. Geosciences 9(8):338, https://doi.org/10.3390/geosciences9080338, https://www.mdpi.com/2076-3263/9/8/338
Rosenfeld JL (1969) Stress effects around quartz inclusions in almandine and the piezothermometry of coexisting aluminum silicates. American Journal of Science 267(3):317–351, https://doi.org/10.2475/ajs.267.3.317, http://www.ajsonline.org/content/267/3/317
Rosenfeld JL, Chase AB (1961) Pressure and temperature of crystallization from elastic effects around solid inclusions in minerals? American Journal of Science 259(7):519–541, https://doi.org/10.2475/ajs.259.7.519, http://www.ajsonline.org/content/259/7/519
Ruh JB, Pourhiet LL, Agard P, Burov E, Gerya T (2015) Tectonic slicing of subducting oceanic crust along plate interfaces: Numerical modeling. Geochem Geophys Geosyst 16(10):3505–3531. https://doi.org/10.1002/2015GC005998
Rutte D, Garber J, Kylander-Clark A, Renne PR (2020) An Exhumation Pulse From the Nascent Franciscan Subduction Zone (California, USA). Tectonics 39(10):e2020TC006305. https://doi.org/10.1029/2020TC006305
Scherer E, Münker C, Mezger K (2001) Calibration of the Lutetium-Hafnium Clock. Science 293(5530):683–687, https://doi.org/10.1126/science.1061372, publisher: American Association for the Advancement of Science
Schmidt C, Ziemann MA (2000) In-situ Raman spectroscopy of quartz: A pressure sensor for hydrothermal diamond-anvil cell experiments at elevated temperatures. American Mineralogist 85(11–12):1725–1734, https://doi.org/10.2138/am-2000-11-1216, https://pubs.geoscienceworld.org/msa/ammin/article/85/11-12/1725/133600/in-situ-raman-spectroscopy-of-quartz-a-pressure
Schmidt WL, Platt JP (2020) Metamorphic temperatures and pressures across the eastern franciscan: implications for underplating and exhumation. Lithosphere. https://doi.org/10.2113/2020/8853351
Schwarzenbach EM, Zhong X, Caddick MJ, Schmalholz SM, Menneken M, Hecht L, John T (2021) On exhumation velocities of high-pressure units based on insights from chemical zoning in garnet (Tianshan, NW China). Earth and Planetary Science Letters 570:117065, https://doi.org/10.1016/j.epsl.2021.117065, https://www.sciencedirect.com/science/article/pii/S0012821X21003204
Shervais JW, Murchey BL, Kimbrough DL, Renne PR, Hanan B (2005) Radioisotopic and biostratigraphic age relations in the Coast Range Ophiolite, northern California: Implications for the tectonic evolution of the Western Cordillera. GSA Bulletin 117(5–6):633–653, https://doi.org/10.1130/B25443.1, https://pubs.geoscienceworld.org/gsa/gsabulletin/article/117/5-6/633/2167/Radioisotopic-and-biostratigraphic-age-relations, publisher: GeoScienceWorld
Sorensen SS (1988) Petrology of amphibolite-facies mafic and ultramafic rocks from the Catalina Schist, southern California: metasomatism and migmatization in a subduction zone metamorphic setting. J Metamorph Geol 6(4):405–435. https://doi.org/10.1111/j.1525-1314.1988.tb00431.x
Sorensen SS, Barton MD (1987) Metasomatism and partial melting in a subduction complex Catalina Schist, southern California. Geology 15(2):115–118, https://doi.org/10.1130/0091-7613(1987)15115:MAPMIA2.0.CO;2, https://pubs.geoscienceworld.org/gsa/geology/article-abstract/15/2/115/204339/Metasomatism-and-partial-melting-in-a-subduction, publisher: GeoScienceWorld
Spear FS, Wolfe OM (2020) Revaluation of “equilibrium” P-T paths from zoned garnet in light of quartz inclusion in garnet (QuiG) barometry. Lithos 372–373:105650, https://doi.org/10.1016/j.lithos.2020.105650, https://www.sciencedirect.com/science/article/pii/S0024493720302875
Spear FS, Thomas JB, Hallett BW (2014) Overstepping the garnet isograd: a comparison of QuiG barometry and thermodynamic modeling. Contrib Miner Petrol 168(3):1059. https://doi.org/10.1007/s00410-014-1059-6
Stern RJ, Bloomer SH (1992) Subduction zone infancy: Examples from the Eocene Izu-Bonin-Mariana and Jurassic California arcs. GSA Bulletin 104(12):1621–1636, https://doi.org/10.1130/0016-7606(1992)1041621:SZIEFT2.3.CO;2, https://pubs.geoscienceworld.org/gsa/gsabulletin/article/104/12/1621/182637/Subduction-zone-infancy-Examples-from-the-Eocene, publisher: GeoScienceWorld
Taguchi T, Enami M, Kouketsu Y (2019) Metamorphic record of the Asemi-gawa eclogite unit in the Sanbagawa belt, southwest Japan: Constraints from inclusions study in garnet porphyroblasts. J Metamorph Geol 37(2):181–201. https://doi.org/10.1111/jmg.12456
Tait S (1992) Selective preservation of melt inclusions in igneous phenocrysts. Am Miner 77(1–2):146–155
Terabayashi M, Maruyama S (1998) Large pressure gap between the Coastal and Central Franciscan belts, northern and central California. Tectonophysics 285(1):87–101, https://doi.org/10.1016/S0040-1951(97)00194-7, http://www.sciencedirect.com/science/article/pii/S0040195197001947
Tewksbury-Christle CM, Behr WM, Helper MA (2021) Tracking Deep Sediment Underplating in a Fossil Subduction Margin: Implications for Interface Rheology and Mass and Volatile Recycling. Geochemistry, Geophysics, Geosystems : G(3) 22(3), https://doi.org/10.1029/2020GC009463, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7988558/
Thomas JB, Spear FS (2018) Experimental study of quartz inclusions in garnet at pressures up to 3.0 GPa: evaluating validity of the quartz-in-garnet inclusion elastic thermobarometer. Contrib Miner Petrol 173(5):42. https://doi.org/10.1007/s00410-018-1469-y
Tsujimori T, Matsumoto K, Wakabayashi J, Liou JG (2006) Franciscan eclogite revisited: Reevaluation of the P-T evolution of tectonic blocks from Tiburon Peninsula, California, U.S.A. Mineral Petrol 88(1):243. https://doi.org/10.1007/s00710-006-0157-1
Ukar E, Cloos M, Vasconcelos P (2012) First 40Ar-39Ar Ages from Low-T Mafic Blueschist Blocks in a Franciscan Mélange near San Simeon: Implications for Initiation of Subduction. J Geol 120(5):543–556. https://doi.org/10.1086/666745
Vermeesch P (2018) IsoplotR: A free and open toolbox for geochronology. Geoscience Frontiers 9(5):1479–1493, https://doi.org/10.1016/j.gsf.2018.04.001, https://www.sciencedirect.com/science/article/pii/S1674987118300835
Viete DR, Hacker BR, Allen MB, Seward GGE, Tobin MJ, Kelley CS, Cinque G, Duckworth AR (2018) Metamorphic records of multiple seismic cycles during subduction. Science Advances 4(3):eaaq0234, https://doi.org/10.1126/sciadv.aaq0234, http://advances.sciencemag.org/content/4/3/eaaq0234
Vogt K, Gerya T (2014) Deep plate serpentinization triggers skinning of subducting slabs. Geology 42(8):723–726, https://doi.org/10.1130/G35565.1, https://pubs.geoscienceworld.org/gsa/geology/article-abstract/42/8/723/131678/Deep-plate-serpentinization-triggers-skinning-of, publisher: GeoScienceWorld
Wain A, Waters D, Jephcoat A, Olijynk H (2000) The high-pressure to ultrahigh-pressure eclogite transition in the Western Gneiss Region, Norway. European Journal of Mineralogy 12(3):667–687, https://okayama.pure.elsevier.com/en/publications/the-high-pressure-to-ultrahigh-pressure-eclogite-transition-in-th
Wakabayashi J (1990) Counterclockwise P-T-t Paths from Amphibolites, Franciscan Complex, California: Relics from the Early Stages of Subduction Zone Metamorphism. J Geol 98(5):657–680. https://doi.org/10.1086/629432
Wakabayashi J (1992) Nappes, Tectonics of Oblique Plate Convergence, and Metamorphic Evolution Related to 140 Million Years of Continuous Subduction, Franciscan Complex. J Geol 100(1):19–40. https://doi.org/10.1086/629569
Wakabayashi J (2012) Subducted sedimentary serpentinite mélanges: Record of multiple burial-exhumation cycles and subduction erosion. Tectonophysics 568–569:230–247, https://doi.org/10.1016/j.tecto.2011.11.006, https://www.sciencedirect.com/science/article/pii/S0040195111004628
Wakabayashi J (2015) Anatomy of a subduction complex: architecture of the Franciscan Complex, California, at multiple length and time scales. Int Geol Rev 57(5–8):669–746. https://doi.org/10.1080/00206814.2014.998728
Wakabayashi J, Ghatak A, Basu AR (2010) Suprasubduction-zone ophiolite generation, emplacement, and initiation of subduction: A perspective from geochemistry, metamorphism, geochronology, and regional geology. GSA Bull 122(9–10):1548–1568. https://doi.org/10.1130/B30017.1
Wang J, Mao Z, Jiang F, Duffy TS (2015) Elasticity of single-crystal quartz to 10 GPa. Phys Chem Miner 42(3):203–212. https://doi.org/10.1007/s00269-014-0711-z
Wang Z, Ji S (1999) Deformation of silicate garnets; brittle-ductile transition and its geological implications. The Canadian Mineralogist 37(2):525–541, https://pubs.geoscienceworld.org/canmin/article-abstract/37/2/525/13176/Deformation-of-silicate-garnets-brittle-ductile, publisher: GeoScienceWorld
Wang Z, Ji S (2001) Elasticity of six polycrystalline silicate garnets at pressure up to 3.0 GPa. American Mineralogist 86(10):1209–1218, https://doi.org/10.2138/am-2001-1009, https://pubs.geoscienceworld.org/ammin/article/86/10/1209/133798/Elasticity-of-six-polycrystalline-silicate-garnets, publisher: GeoScienceWorld
Waters D, Martin H (1993) Geobarometry in phengite-bearing eclogites. Terra Abstracts 5(1):410–411
Wolfe OM, Spear FS (2018) Determining the amount of overstepping required to nucleate garnet during Barrovian regional metamorphism, Connecticut Valley Synclinorium. J Metamorph Geol 36(1):79–94. https://doi.org/10.1111/jmg.12284
Yamato P, Agard P, Goffé B, Andrade VD, Vidal O, Jolivet L (2007) New, high-precision P-T estimates for Oman blueschists: implications for obduction, nappe stacking and exhumation processes. J Metamorph Geol 25(6):657–682. https://doi.org/10.1111/j.1525-1314.2007.00722.x
Zhang Y (1998) Mechanical and phase equilibria in inclusion-host systems. Earth and Planetary Science Letters 157(3):209–222, https://doi.org/10.1016/S0012-821X(98)00036-3, http://www.sciencedirect.com/science/article/pii/S0012821X98000363
Zhong X, Moulas E, Tajčmanová L (2018) Tiny timekeepers witnessing high-rate exhumation processes. Scientific Reports 8(1):2234, https://doi.org/10.1038/s41598-018-20291-7, https://www.nature.com/articles/s41598-018-20291-7, number: 1 Publisher: Nature Publishing Group
Zhong X, Dabrowski M, Powell R, Jamtveit B (2020a) “EosFit-Pinc: A simple GUI for host-inclusion elastic thermobarometry’’ by Angel et al. (2017)–Discussion. Am Miner 105(10):1585–1586. https://doi.org/10.2138/am-2020-7267
Zhong X, Moulas E, Tajčmanová L (2020) Post-entrapment modification of residual inclusion pressure and its implications for Raman elastic thermobarometry. Solid Earth 11(1):223–240, https://doi.org/10.5194/se-11-223-2020, https://www.solid-earth.net/11/223/2020/se-11-223-2020-discussion.html
Zhukov VP, Korsakov AV (2015) Evolution of host-inclusion systems: a visco-elastic model. J Metamorph Geol 33(8):815–828. https://doi.org/10.1111/jmg.12149
Acknowledgements
We thank Jaime Barnes for sharing eclogite samples from the northern Franciscan Complex (Jenner Beach), Julien Allez for assistance on the electron microprobe at ETH Zürich, Luiz Morales for assistance on the SEM and with EBSD measurements at ETH Hönggerberg, and the Structural Geology and Tectonics Group at ETH Zürich for helpful discussions. This work was supported by ETH Zürich Career SEED Grant SEED-11 19-2 awarded to M. Cisneros. We acknowledge support of the Scientific Center for Optical and Electron Microscopy (ScopeM) of the ETH Zürich. We thank Xin Zhong, Zeb Page, and an anonymous reviewer for constructive comments that greatly helped improve the quality of this manuscript. We thank Timm John for editorial handling.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Timm John.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cisneros, M., Behr, W.M., Platt, J.P. et al. Quartz-in-garnet barometry constraints on formation pressures of eclogites from the Franciscan Complex, California. Contrib Mineral Petrol 177, 12 (2022). https://doi.org/10.1007/s00410-021-01876-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00410-021-01876-4