Abstract
Four voluminous ignimbrites (150–500 km3) erupted in rapid succession at 27 Ma in the central San Juan caldera cluster, Colorado. To reconstruct the timescales and thermal evolution of these magma reservoirs, we used zircon ID-TIMS U–Pb geochronology, zircon LA-ICP-MS geochemistry, thermal modeling, and zircon age and crystallization modeling. Zircon geochronology reveals dispersed zircon age spectra in all ignimbrites, with decreasing age dispersion through time that we term a ‘chimney sweeping’ event. Zircon whole-grain age modeling suggests that 2σ zircon age spans represent approximately one-quarter of total zircon crystallization timescales due to the averaging effect of whole-grain, individual zircon ages, resulting in zircon crystallization timescales of 0.8–2.7 m.y. Thermal and zircon crystallization modeling combined with Ti-in-zircon temperatures indicates that magma reservoirs were built over millions of years at relatively low magmatic vertical accretion rates (VARs) of 2–5 × 10–3 m y−1 (2–5 × 10–6 km3 y−1 km−2), and we suggest that such low VARs were characteristic of the assembly of the greater San Juan magmatic body. Though we cannot unequivocally discern between dispersed zircon age spectra caused by inheritance (xenocrystic or antecrystic) versus prolonged crystallization from the same magma reservoir (autocrystic), our findings suggest that long-term magma input at relatively low VARs produced thermally mature upper crustal magma reservoirs resulting in protracted zircon crystallization timescales. Compiling all U–Pb ID-TIMS zircon ages of large ignimbrites, we interpret the longer timescales of subduction-related ignimbrites as a result of longer term, lower flux magmatism, and the shorter timescales of Snake River Plain ignimbrites as a result of shorter term, higher flux magmatism.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Large caldera-forming eruptions in close temporal and spatial proximity, known as ignimbrite flare-ups, are one of the most spectacular expressions of silicic magmatism on Earth. Large eruptions can have devastating effects on society and cause global climate perturbations (e.g., Self 2006; Newhall et al. 2018), which could be exacerbated by multiple eruptions in a short time interval (Guillet et al. 2020). Thus, determining the magmatic timescales and rates responsible for such clusters of large eruptions is critical to identifying active systems with the potential to feed these events and mitigating the impact of these eruptions.
Ignimbrite flare-ups occur around the world mainly at subduction-related settings, but also in non-subduction settings such as the Snake River Plain and the Afro-Arabian volcanic field (e.g., Christiansen 2001; Peate et al. 2005). They consist of temporally and spatially associated, large-volume ignimbrites (> 10 km3) with total erupted volumes in the 103 s to 104 s of km3 (e.g., Gravley et al. 2016). These events are typically considered to be the result of dramatic, transient increases in magmatic input and associated with major tectonic changes (e.g., de Silva and Gosnold 2007; Lipman 2007; Schöpa and Annen 2013; Gravley et al. 2016; Kern et al. 2016; De Silva and Kay 2018). Timescales of magma assembly between 103 and 105 s of years based on zircon geochronology (e.g., Wotzlaw et al. 2015; Kern et al. 2016) are consistent with this model. Such high fluxes and short timescales for ignimbrites are often juxtaposed to those of plutons, leading to debates about the relationship between plutons and ignimbrites (Coleman et al. 2004; de Silva and Gosnold 2007; Lipman 2007; Annen 2009; Tappa et al. 2011; Mills and Coleman 2013; Frazer et al. 2014; Lipman and Bachmann 2015; Eddy et al. 2016; Gaynor et al. 2019a). However, recent studies show that timescales required for the assembly of large volumes of eruptible magma in the crust can be on the order of millions of years at relatively low rates of magma input (e.g., Kaiser et al. 2017; Karakas et al. 2017; Szymanowski et al. 2019). Such prolonged periods of magma accumulation can be better reconciled with the assembly of large magma reservoirs in the mid to upper crust. In fact, mechanical calculations suggest that the rapid addition of magma into the crust can result in the repeated pressurization of upper crustal reservoirs, favoring frequent small eruptions instead of the accumulation of a large volume of eruptible magma (Jellinek and DePaolo 2003; Caricchi et al. 2014a).
Here, we discuss potential ways to distinguish ignimbrite flare-ups caused by dramatic increases of magma input versus those caused by prolonged maturation of the magmatic system. We determine the rates, timescales, and thermal evolution for one of the most rapid ignimbrite flare-ups in the world, the last four eruptions of the central San Juan Caldera cluster, Colorado, using zircon geochronology and geochemistry, synthetic zircon age modeling, and thermal and zircon crystallization modeling.
Geologic setting
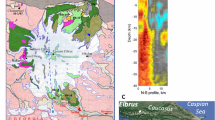
The San Juan Mountains are part of the Southern Rocky Mountain volcanic field in southern Colorado (Fig. 1). The beginning of mid-Cenozoic volcanism in this region coincides approximately with the tectonic transition from the Sevier–Laramide Orogeny to the extensional environment that formed the Basin and Range province in the western U.S. (Humphreys et al. 2003; Rosera et al. 2021). Volcanism in the San Juan Mountains began in the late Eocene (35 Ma) with the eruption of the Conejos Formation, approximately 25,000 km3 of mostly basaltic andesite to dacite lavas (Fig. 1; Lipman et al. 1970; Lipman 1975; Colucci et al. 1991). Concurrently with continued emplacement of intermediate-composition lavas, 24 caldera-forming eruptions released around 15,000 km3 of material between approximately 33.9 Ma and 22.9 Ma, with the 9 ignimbrites from the central San Juan caldera cluster making up 8,650 km3 of this total in < 2 million years (m.y.; Fig. 1; 28.9–27 Ma; Lipman 2006, 2012; Lipman and McIntosh 2008). The last four ignimbrites of the central cluster were the most rapid and intense series of eruptions during this flare-up, erupting approximately 1400 km3 of material in rapid succession (i.e., overlapping 40Ar/39Ar sanidine ages; Lipman and McIntosh, 2008). These four ignimbrites, ordered from oldest to youngest, are the subject of this study: the 150 km3 zoned Rat Creek Tuff, 250 km3 dacitic Cebolla Creek Tuff, 500 km3 zoned Nelson Mountain Tuff, and 500 km3 dacitic Snowshoe Mountain Tuff, erupted at approximately 27 Ma (Lipman and McIntosh 2008).
Geologic map of the central San Juan caldera cluster, Colorado. Deposits in yellow (this study) are the last four ignimbrites (Rat Creek Tuff, Cebolla Creek Tuff, Nelson Mountain Tuff, and Snowshoe Mountain Tuff), and those in green are the first five ignimbrites in the eruptive sequence (Mason Park Tuff, Fish Canyon Tuff, Carpenter Ridge Tuff, Blue Creek Tuff, and Wason Park Tuff). The Conejos Formation volcanics are shown in purple. 40Ar/39Ar eruption ages (Ma) for caldera-related ignimbrites are in parentheses (McIntosh and Chapin 2004; Lipman and McIntosh 2008; Lipman 2012). All 40Ar/39Ar eruption ages were recalculated using the most recent Fish Canyon Tuff sanidine age (28.201 Ma; Kuiper et al. 2008), except for the North Pass caldera (*). Sample localities: 1—Powderhorn Park Trail; 2—Cathedral; 3—Los Pinos Creek Graben; 4—Stone Cellar; 5—Point Bennett; 8—Nelson Mountain; 9—Wheeler Geologic Monument; 10—Northwest Snowshoe Mountain; 11—South Snowshoe Mountain; 12—Cattle Mountain
The overlapping Rat Creek Tuff, Cebolla Creek Tuff, and Nelson Mountain Tuff calderas constitute the nested San Luis caldera complex in the northwest portion of the greater La Garita caldera, which formed by the eruption of the Fish Canyon Tuff (Fig. 1; Lipman 2000, 2006). The Rat Creek Tuff is zoned from weakly welded, crystal-poor rhyolite upward to densely welded crystal-rich dacite. The Cebolla Creek Tuff, a crystal-rich, unzoned mafic dacite, follows the Rat Creek Tuff stratigraphically and is weakly to moderately welded. The Nelson Mountain Tuff follows the Cebolla Creek stratigraphically and is a zoned ignimbrite consisting of crystal-poor rhyolite that grades upward into densely welded crystal-rich dacite. Lipman and McIntosh (2008) inferred that the Cochetopa Park caldera, 25 km northeast of the San Luis caldera complex, subsided passively during the Nelson Mountain Tuff eruption as magma drained towards the Nelson Mountain Tuff caldera through a southwest-trending dike system (Fig. 1).
In the central portion of the La Garita caldera and to the south of the San Luis caldera complex, the eruption of the Snowshoe Mountain Tuff formed the Creede caldera (Fig. 1; Lipman 2000, 2006). The Snowshoe Mountain Tuff, the final ignimbrite of the central San Juan sequence, is a crystal-rich dacite. It consists of a thick intracaldera deposit of densely welded tuff exposed as a resurgent dome (geographic Snowshoe Mountain) and weakly welded, poorly preserved outflow tuff (Fig. 1; Lipman 2000, 2006).
Methods
Zircons from nine samples were analyzed. We analyzed two samples from each of the Rat Creek Tuff, Nelson Mountain Tuff and Snowshoe Mountain Tuff, and three samples from the Cebolla Creek Tuff. Whole-rock samples were crushed using a hydraulic press, and zircons were extracted using standard density (water table; methylene iodide heavy liquid) and magnetic (Frantz Isodynamic Separator) separation techniques. Prior to U–Pb geochronology and laser ablation geochemical analyses, cathodoluminescence (CL) images of zircons were acquired on scanning electron microscopes, either a CamScan MV2300 at the University of Lausanne (10 kV) or a JEOL JSM7001F at the University of Geneva (15 kV). Detailed sample information and CL images of zircons are in the Supplementary Material (Table S1; Figs. S1–S4). All whole-rock samples were geochemically characterized in Curry et al. (2021).
U–Pb CA-ID-TIMS zircon geochronology
Chemical abrasion-isotope dilution-thermal ionization mass spectrometry (CA-ID-TIMS) analyses were performed at the University of Geneva in labs optimized for high-sensitivity U–Pb geochronology. To remove inclusions and volumes with radiation damage susceptible to Pb loss, zircons were thermally annealed and chemically abraded (Mattinson 2005; Widmann et al. 2019). Zircons were thermally annealed at 900 °C for 48 h and then hand-picked under a binocular microscope. Some zircons were then individually loaded into 200 µL microcapsules with a 3:1 mixture of HF:7 N HNO3, put into a Parr bomb, and heated for 12–18 h at 210 °C for chemical abrasion. Alternatively, some zircons were chemically abraded in bulk using 3-mL Savillex beakers with the same chemical mixture and heating schedule. Next, zircons were fluxed in 6 N HCl overnight at 80 °C, washed four times in clean 7 N HNO3, and again loaded into 200 µL microcapsules with a 3:1 mixture of HF:7 N HNO3. Zircons were then spiked with EARTHTIME 205Pb–233U–235U tracer solution (ET535; Condon et al. 2015; McLean et al. 2015) before dissolution at 210 °C for 48 h in a Parr bomb. Dissolved zircons were subsequently converted to chloride form and loaded onto columns filled with pre-cleaned anion exchange resin for U and Pb isolation (Krogh 1973). U–Pb samples were loaded onto single outgassed Re filaments with a Si-Gel emitter. Measurements of U and Pb were conducted on an IsotopX Phoenix TIMS. Measurements of Pb were performed on an axial Daly photomultiplier system in ion-counting mode. Uranium was measured as an oxide, using either faraday cups (1012 Ohm resistance) or Daly-based ion-counting, assuming 18O/16O = 0.00205. All common Pb was assumed to be procedural blank, with a composition of: 206Pb/204Pb = 17.1 ± 0.205, 207Pb/204Pb = 15.07 ± 0.105, and 208Pb/204Pb = 36.17 ± 0.253. Mass fractionation of U was corrected using an isotopic ratio of 233U/235U = 0.995062 (± 0.0054% 1σ) in the ET535 tracer, and a natural 238U/235U ratio of 137.818 ± 0.045 (2σ; Hiess et al. 2012), as outlined in McLean et al. (2015). Fractionation of Pb was corrected using 0.19%/amu based on repeat measurements of SRM 981. All U–Pb data were processed using Tripoli and Redux U–Pb software (Bowring et al. 2011; McLean et al. 2011). All ID-TIMS 206Pb/238U ages were corrected for initial Th disequilibrium using previously published whole-rock Th/U ratios for these samples (Table S1; Curry et al. 2021).
LA-ICP-MS zircon geochemistry
We determined zircon trace element contents using laser ablation, inductively coupled plasma mass spectrometry (LA-ICP-MS) with an ASI RESOlution ablation system combined with a sector field, Thermo Fisher Scientific Element XR spectrometer at the University of Lausanne. Analyses were performed with a 24–30 µm spot size, 10 Hz repetition rate, 3 J/cm2 on-sample energy density, 30 s of ablation time, and 90 s of background between each point. We used NIST 610 as the primary standard. We reduced the data using SILLS (Guillong et al. 2008), with the empirical SiO2 content of zircon (31.57%) as the internal standard.
Zircon crystallization temperatures were calculated using the Ti-in-zircon thermometer of Ferry and Watson (2007) using aTiO2 = 0.75 and aSiO2 = 1 for all ignimbrites except the Cebolla Creek Tuff. Since the Cebolla Creek Tuff lacks quartz, we used MELTS to estimate aSiO2 (Gualda and Ghiorso 2015), which yielded a value of aSiO2 = 0.9. Given the uncertainty of aSiO2 in all four ignimbrites, we calculated reasonable upper and lower bounds on Ti-in-zircon temperatures using aSiO2 values of 0.55 (which increases T by about 30 °C) and 0.9 (which decreases T by about 20 °C; Fig. S5). These values represent plausible minimum and maximum aSiO2 values using Hayden and Watson (2007), MELTS (Ghiorso and Gualda 2013; Gualda and Ghiorso 2015), and temperatures and pressures from Curry et al. (2021).
Thermal and zircon crystallization modeling
Thermal modeling and associated zircon crystallization modeling were performed to characterize the thermal evolution of the magmatic system and the resulting zircon record. We used a thermal modeling approach similar to Caricchi et al. (2014b, 2016), implementing a finite-element method to solve the heat conduction-advection equation. We modeled the thermal evolution of the crust with an initial geothermal gradient of 20° C/km undergoing intrusion of 900 °C magmatic sills with an 18 km radius during intervals of 1 and 5 m.y. Sills were intruded into the core of the reservoir at a constant depth of 20 km, which results in the advection of previously injected material towards the top and bottom of the injection region. Previous thermal modeling studies showed that variations of the modality of magma injection, geometry of the magmatic system, and convection (not modeled in this study) played a minor role on the long-term thermal evolution of magmatic systems (Carrigan 1988; Annen et al. 2006, 2015; Caricchi et al. 2014b; Karakas et al. 2017; Weber et al. 2020; Lukács et al. 2021), which is the core target of this study.
Magma was injected at VARs of 5 × 10–3 m y−1 and 2 × 10–3 m y−1 for 5 m.y., which translate into volumetric magma flux rates of 5 × 10–6 km3 y−1 km−2 and 2 × 10–6 km3 y−1 km−2 using the final volumes and the area of the modeled injection region. Magma was also injected at a VAR of 1 × 10–2 m y−1 for 1 m.y., which translates into a volumetric magma flux rate of 1 × 10–5 km3 y−1 km−2. The fastest VAR of 1 × 10–2 m y−1 is equivalent to 1 × 10–2 km3 y−1, and the slowest is equivalent to 2 × 10–3 km3 y−1. This range is consistent with flux estimates associated with large eruptions (e.g., Fig. 4c of Caricchi et al. 2014b) and is within the range of values employed in other modeling studies that have focused on large silicic magma reservoirs (e.g., Annen 2009; Schöpa and Annen 2013). The thermal model includes passive tracers recording the temperature evolution through time, and each tracer represents the time–temperature evolution for a hand-sized parcel of magma. The fraction of zircon crystallizing as a function temperature is defined using the non-linear model of Tierney et al. (2016), in which the rate of zircon crystallization decreases with decreasing temperature from zircon saturation to solidus (Fig. S7a–b). We assumed that zircon crystallization starts at the zircon saturation temperature (810 °C) and stops at the solidus temperature (700 °C). We chose 810 °C for zircon saturation based on calculated zircon saturation temperatures for the four ignimbrites in this study using the method of Boehnke et al. (2013; see Fig. S6). We chose 700 °C as the solidus temperature based on experimental studies (Caricchi and Blundy 2015; Marxer and Ulmer 2019). We consider “measurable” zircons (i.e., those that would be found in erupted products) to be zircons in those tracers at temperatures higher than the solidus temperature (700 °C) at the moment of eruption. The number of measurable zircons at each time step is calculated by summing the measurable zircons of each tracer (Fig. S7c, d). This definition of “measurable” implies that all zircons that have cooled and remained below 700 °C at the time of eruption will not contribute to the final distribution of zircon ages and chemistry. On the other hand, zircons in tracers that cooled below 700° C and were reheated above this temperature before eruption do contribute to the final distribution of zircon ages and chemistry (Fig. S7c, d). We do not account for potential zircon resorption during reheating (e.g., Bindeman and Melnik 2016). However, if the volume of injected magma is significantly smaller than the volume of resident super-solidus magma, the thermal effect is local and does not affect all zircon throughout the modeled reservoir crystallizing in a specific time interval (i.e., does not affect the calculated distribution of zircon crystallization ages). To assess the effect of the temperatures of zircon saturation and solidus on modeling results, we ran models with different zircon saturation (775° C and 850° C) and solidus (650° C) temperatures. The influence of these parameters is relatively limited and does not affect our conclusions (e.g., Fig. S8).
Results
U–Pb CA-ID-TIMS zircon geochronology
In total, 98 zircons were dated from these 9 samples with both concordant (n = 92) and normally discordant (n = 6) results (Fig. 2; Table 1). Zircons from all four ignimbrites have both oscillatory and sector zoning, melt inclusions, minor apatite inclusions, and some complex cores (Fig. 3, S1–S4). All ages are Th-corrected 206Pb/238U ages, unless otherwise noted. For comparison to recalculated 40Ar/39Ar sanidine ages (Supplementary Information S1; Table S2), 206Pb/238U zircon ages are reported in the text with an uncertainty combining analytical, tracer calibration, and decay constant uncertainties (“Z” column of Table S3). Full uncertainty information (± X/Y/Z) is in Table S3.
Summary of zircon geochronology from the central San Juan caldera cluster with recalculated 40Ar/39Ar geochronology (Bachmann et al. 2007; Lipman and McIntosh 2008; Wotzlaw et al. 2013). Colored and black vertical bars are individual ID-TIMS U–Pb (Th-corrected) zircon ages with 2σ uncertainty. Horizontal gray rectangles for samples 20AC16 and 36AC16 are weighted mean ages with 2σ uncertainty. Age ranges (Δt) are in m.y. Gray vertical bars are 40Ar/39Ar sanidine ages recalculated from Lipman and McIntosh (2008) using the most recent Fish Canyon Tuff sanidine age of 28.201 ± 0.046 Ma (Kuiper et al. 2008). Each gray bar represents the 2σ uncertainty range of the weighted means of samples in that eruption. Gray circles are recalculated 40Ar/39Ar (not sanidine). See Supplementary Table S2 and Supplementary Information S1 for 40Ar/39Ar recalculation information. Kernel density estimate curves are plotted to the right using all zircon U–Pb ages from each ignimbrite and the average 2σ error as the bandwidth. Only concordant zircon ages shown here. Plotted uncertainties included analytical, spike calibration (for U–Pb only), and decay constant uncertainties (Table S3)
Rat Creek Tuff
Most zircon ages of the zoned Rat Creek Tuff are significantly older than its 40Ar/39Ar sanidine ages (27.08 Ma), with only two zircon ages overlapping the 40Ar/39Ar ages (Fig. 2). Zircons in the Rat Creek Tuff are typically smaller than the other ignimbrites of this study (Fig. 3d, S4). A nonwelded, rhyolitic sample of the Rat Creek Tuff (11AC16) yielded ten concordant zircons with ages between 29.04 ± 0.05 Ma and 27.39 ± 0.04 Ma. One zircon from sample 11AC16 is normally discordant with a 206Pb/238U age of 88.94 Ma and a 207Pb/206Pb age of approximately 1400 Ma. Seven zircons from a welded, dacitic sample of the Rat Creek Tuff (09AC16) yielded concordant ages ranging from 28.57 ± 0.06 Ma to 27.26 ± 0.32 Ma. One zircon from sample 09AC16 is normally discordant with a 206Pb/238U age of 31.37 Ma and a 207Pb/206Pb age of approximately 1600 Ma.
Cebolla Creek Tuff
The majority of zircon ages from three welded samples of the dacitic Cebolla Creek Tuff overlap with 40Ar/39Ar sanidine ages of the stratigraphically bounding Rat Creek Tuff and Nelson Mountain Tuff (Fig. 2). Sample 36AC16 yielded ten concordant zircons with ages ranging from 27.83 ± 0.07 Ma to 27.11 ± 0.10 Ma, and the eight youngest overlap between 27.29 ± 0.22 Ma and 27.11 ± 0.10 Ma. Eleven zircons from sample 08AC16 are concordant with ages between 28.87 ± 0.32 Ma and 26.89 ± 0.22 Ma, and the eight youngest have a narrower range between 27.26 ± 0.07 and 26.89 ± 0.22 Ma. One zircon from sample 08AC16 is normally discordant with a 206Pb/238U age of 665.48 Ma and a 207Pb/206Pb age of around 1400 Ma. Sample 06AC16 produced eight concordant zircons with ages ranging from 28.84 ± 0.32 Ma to 27.18 ± 0.27 Ma, with a main population between 27.69 ± 0.09 Ma and 27.18 ± 0.27 Ma. One zircon from sample 06AC16 is normally discordant with a 206Pb/238U age of 29.82 Ma and a 207Pb/206Pb age of approximately 150 Ma.
Nelson Mountain Tuff
Most zircon ages from two welded samples of the zoned Nelson Mountain Tuff overlap its 40Ar/39Ar sanidine ages (27.08 Ma; Fig. 2). Eleven zircons of the rhyolitic sample 28AC16 are concordant with ages ranging from 31.29 ± 0.14 Ma to 27.03 ± 0.13 Ma, with the youngest eight overlapping between 27.46 ± 0.11 Ma and 27.03 ± 0.13 Ma. Sample 28AC16 yielded one normally discordant zircon with a 206Pb/238U age of 27.66 Ma and a 207Pb/206Pb age of around 290 Ma. Silicic dacite sample 03AC16 yielded 12 concordant zircons with ages between 28.01 ± 0.07 Ma and 26.99 ± 0.15 Ma, and the 9 youngest are between 27.33 ± 0.08 Ma and 26.99 ± 0.15 Ma. One normally discordant zircon from sample 03AC16 yielded a 206Pb/238U age of 35.89 Ma and a 207Pb/206Pb age of about 160 Ma.
Snowshoe Mountain Tuff
Most zircon ages from two welded samples of the Snowshoe Mountain Tuff cluster tightly and overlap its 40Ar/39Ar sanidine ages (27.05 Ma; Fig. 2). All 11 zircons of sample 20AC16 are concordant with ages ranging from 27.35 ± 0.22 Ma to 27.06 ± 0.22 Ma. All 12 zircons of sample 19AC16 are concordant with ages between 27.88 ± 0.09 Ma and 26.96 ± 0.35 Ma, with all except the oldest between 27.37 ± 0.13 Ma and 26.96 ± 0.35 Ma.
Zircon geochemistry
Zircon Ti content ranges from 2 to 26 ppm, with dominant Ti modes at 4–7 ppm for each ignimbrite (Fig. 4). The dacitic Rat Creek Tuff has another dominant mode at approximately 21 ppm Ti, and the Snowshoe Mountain Tuff has another significant peak at 13 ppm Ti. These Ti contents translate into temperatures ranging from 650 to 875 °C. Zircon U content and Yb/Dy correlate to Ti content in an L-shaped pattern with higher values occurring at lower Ti (Fig. 4a–b), and zircon Zr/Hf ratios have a positive correlation with Ti content (Fig. 4c). Zircon U content ranges from 20 to 1340 ppm, with an interquartile range (IQR) of 114–279 ppm. Zircon Yb/Dy values range from 2 to 9, with an IQR of 3.5–4.3. Zircon Zr/Hf ratios range from 35 to 65, with an IQR of 43–49 (Fig. 4). Zircon Zr/Hf values fall on two distinct trends, with higher or lower Zr/Hf, which converge at around 9 ppm Ti and an approximate Zr/Hf value of 47. The trend with higher Zr/Hf is dominated by zircons from dacitic Rat Creek Tuff samples (Fig. 4). Zircon LA-ICP-MS data are in Table S4.
Trace elements U (ppm; a), Yb/Dy (b), and Zr/Hf (c) versus Ti (ppm) and Ti-in-zircon temperature (°C), calculated using the Ti-in-zircon thermometer of Ferry and Watson (2007). Kernel density estimate curves are shown opposite each respective axis, using bandwidths of 1 ppm (Ti), 35 ppm (U), 0.5 (Yb/Dy), and 2 (Zr/Hf). Legend in (a) is applicable to (b, c)
Thermal and zircon crystallization modeling
Modeling results show distinct thermal evolutions through time for each investigated VAR (Fig. 5). For the following, we consider only tracers that are within zircon saturation at 1 m.y. after the onset of magma input for the model with the highest VAR and at 5 m.y. for the other models. The fastest VAR (1 × 10–2 m y−1) results in an IQR of average temperatures of 772–782 °C, and average temperatures are almost completely between 750 °C and 800 °C (Fig. 5a). For the intermediate VAR (5 × 10–3 m y−1) model, average temperatures have an IQR of 731–752 °C, and outliers below 700 °C are present (Fig. 5b). The slowest VAR model (2 × 10–3 m y−1) has average temperatures with an IQR of 745–781 °C, with significant outliers extending down to 600 °C (Fig. 5c). The VAR also affects the variation of the average temperature. In the fastest VAR model (1 × 10–2 m y−1), the average temperature spends the entire 1 m.y. of history within zircon saturation, and the average temperature is consistently decreasing throughout this time. The slower VAR models (5 × 10–3 m y−1 and 2 × 10–3 m y−1) require approximately 1–1.5 m.y. of thermal priming for the average temperature to rise above solidus into the zircon saturation window (Fig. 5b–c). In contrast to the fastest model, the average temperature of models with lower VARs tends to increase over time and reach relatively constant values (Fig. 5b–c).
Temperature–time evolution of thermal models using VARs of 1 × 10–2 m y−1 (a), 5 × 10–3 m y−1 (b), and 2 × 10–3 m y−1 (c). Only modeling tracers (gray lines) that are within zircon saturation after 1 m.y. (a) or 5 m.y. (b, c) are shown. The orange line is the average temperature at each time step, with the 1σ range around this temperature in black. Ti-in-zircon temperatures are shown on the right axis. Boxplots of average temperatures of each model shown at right
Combining this thermal evolution with zircon crystallization modeling provides additional information. The length of time spent within zircon saturation, which is directly related to the VAR, provides the total possible age spread of erupted zircons (Figs. 5, 6). At the highest investigated VAR (1 × 10–2 m y−1), zircon crystallization starts immediately after the onset of magma injection, and zircon remains available to be erupted until the end of the simulation (i.e., 1 m.y.; Figs. 5a, 6a). For the intermediate VAR (5 × 10–3 m y−1), zircons crystallized during the first 1 m.y. from the onset of magma input remain in the solidified portion of the magmatic system (Figs. 5b, 6a). For the slowest VAR (2 × 10–3 m y−1), this delay increases to about 1.5 m.y. (Figs. 5c, 6a).
a Normalized fraction of measurable zircon ages, meaning those zircons contained in eruptible magma, through model time. This plot shows the delay in zircon appearance in erupted products in the two slower models (VARs 5 × 10–3 m y−1 and 2 × 10–3 m y−1 b Duration of zircon crystallization (m.y.) versus total magmatic duration (m.y.) showing the degree to which the duration of zircon crystallization will underestimate the total magmatic duration
Discussion
Interpretation of zircon crystallization ages
Zircon pretreatment by thermal annealing and chemical abrasion, combined with modern data reduction techniques (Mattinson 2005; Bowring et al. 2011; McLean et al. 2011; Widmann et al. 2019), yield high-precision ages that can have a range outside of analytical precision, such as those in this study (Fig. 2). Numerous recent studies show dispersions of zircon ages in both plutonic and volcanic environments (e.g., Coleman et al. 2004; Bachmann et al. 2007; Schaltegger et al. 2009; Schoene et al. 2012; Wotzlaw et al. 2013, 2015; Rivera et al. 2014, 2016; Singer et al. 2014; Broderick et al. 2015; Samperton et al. 2015; van Zalinge et al. 2016; Colón et al. 2018), leading to revisions of the interpretation of U–Pb zircon geochronology of magmatic bodies (e.g., Schaltegger and Davies, 2017) and their relation to economic mineralization events (e.g., Tapster et al. 2016; Gaynor et al. 2019b; Large et al. 2020; Rosera et al. 2021). Here, we add to this discussion, providing an interpretation of U–Pb zircon ages for a magmatic system that produced one of the world’s most rapid and voluminous ignimbrite flare-ups.
Most zircon ages in this study form a main cluster near the 40Ar/39Ar sanidine ages for the eruptive sequence with a minor older tail in the age spectra, and Rat Creek Tuff samples have more complex age spectra (Fig. 2). Here, we use the notation Δtm to denote the age range of the main group of zircons in each sample’s age spectrum, and following the notation of Samperton et al. (2015), we use the notation Δth to denote the age difference of all zircons in a given hand sample. For samples containing normally distributed zircon ages, we report the weighted mean and 2σ uncertainty. Snowshoe Mountain Tuff samples have the most coherent zircon age spectra with only one older zircon analyzed between the two samples. For sample 19AC16, this single older zircon extends the Δth to 0.92 ± 0.36 m.y., and the 11 grains in the main cluster define a Δtm of 0.41 ± 0.37 m.y. All zircons from sample 20AC16 are coeval within uncertainty, and the weighted mean is 27.192 ± 0.039 Ma (mean standard of weighted deviates [MSWD] = 1.9; Fig. 2).
The other three ignimbrites have more complicated zircon age spectra, with significantly more dispersion and older ages. The main group of zircon ages of sample 03AC16 of the Nelson Mountain Tuff ranges from 27.33 ± 0.09 Ma to 26.99 ± 0.15 Ma (Δtm = 0.34 ± 0.17 m.y.), and all zircon ages of this sample yield a Δth of 1.02 ± 0.17 m.y. (Fig. 2). The younger, main age cluster of sample 28AC16 ranges from 27.46 ± 0.11 Ma to 27.03 ± 0.13 Ma (Δtm = 0.43 ± 0.17 m.y.). The oldest concordant zircon age of this study is from sample 28AC16 (31.29 ± 0.14 Ma), and several ages occur between that age and the near-eruption age group of 28AC16. These older ages result in a Δth of 4.26 ± 0.19 m.y. for sample 28AC16, and excluding the oldest age yields a Δt of 1.28 ± 0.18 m.y. The main zircon age clusters of the Cebolla Creek Tuff range from 27.69 ± 0.09 Ma to 27.18 ± 0.27 Ma for sample 06AC16 (Δtm = 0.51 ± 0.28 m.y.) and 27.26 ± 0.07 Ma to 26.89 ± 0.22 Ma for sample 08AC16 (Δtm = 0.37 ± 0.23 m.y.). The weighted mean for the youngest 8 zircons of sample 36AC16 is 27.173 ± 0.053 Ma (MSWD = 0.69; Fig. 2). Older zircons of the Cebolla Creek Tuff result in a Δth of 1.66 ± 0.42 m.y. (06AC16), 1.98 ± 0.39 m.y. (08AC16), and 0.72 ± 0.12 m.y. (36AC16).
The Rat Creek Tuff has the most complex and dispersed zircon spectra of the samples analyzed, with only two zircon ages overlapping its 40Ar/39Ar sanidine ages (Fig. 2). We interpret the main group of zircons in sample 09AC16 as the ages ranging from 27.93 ± 0.22 Ma to 27.26 ± 0.32 Ma (Δtm = 0.67 ± 0.39 m.y.), and the Δth of 09AC16 is 1.31 ± 0.33 m.y. The zircon age spectrum of sample 11AC16 has a main population between 28.85 ± 0.06 Ma and 28.18 ± 0.20 Ma (Δtm = 0.86 ± 0.21 m.y.), over 1 m.y. prior to the Rat Creek Tuff 40Ar/39Ar sanidine ages, and a younger zircon at 27.39 ± 0.04 Ma (Fig. 2). Sample 11AC16 has a Δth of 1.65 ± 0.06 m.y.
Besides sample 20AC16 and the main cluster (youngest 8 zircons) of sample 36AC16, no other main clusters of zircons produce statistically meaningful weighted mean ages with a low MSWD (Fig. 2). Because of their zircon age spectra, samples 20AC16 and 36AC16 could represent zircon crystallization timescales equal to ± their 2σ error, which is 0.08 m.y. in 20AC16 and 0.11 in 36AC16 (Fig. 2). However, the other samples in each ignimbrite (Snowshoe Mountain Tuff and Cebolla Creek Tuff) have main clusters of zircons that show dispersion outside of uncertainty estimates. For samples with a dispersed zircon age spectrum, we take the age range of the main cluster of zircon ages (Δtm) as a conservative starting point for the duration of magma input to build the magma reservoir that produced that ignimbrite.
A spread of zircon ages outside of analytical uncertainty requires a geologic explanation. Scenarios explaining zircon age dispersion include: (1) unmitigated Pb loss, (2) acquisition from surrounding country rock that is significantly older (xenocrysts), (3) acquisition of older zircons from previous magmatic episodes or pulses (antecrysts), and (4) continuous and prolonged crystallization in the same magma reservoir (autocrysts). Unmitigated Pb loss after thermal annealing and chemical abrasion has been demonstrated previously (Ovtcharova et al. 2015; Gaynor et al. 2019b; Rosera et al. 2021), but there is little to no evidence for unmitigated Pb loss in this study because the youngest zircon ages are not younger than the 40Ar/39Ar sanidine ages for this eruptive sequence (Fig. 2). Concerning potentially xenocrystic material, our zircon geochronology dataset notably contains normally discordant, xenocrystic zircon ages in every ignimbrite except the Snowshoe Mountain Tuff (Table 1). These discordant zircons have Precambrian (1400–1600 Ma) to Permian (290 Ma) to Jurassic (150–160 Ma) 207Pb/206Pb ages, and we interpret these zircons as products of inheritance from crustal basement rock, which contains Precambrian to Eocene material (Lipman 2006, 2012). The ages of four normally discordant analyses have 206Pb/238U ages between 27.66 Ma and 35.89 Ma, with the other two having much older 206Pb/238U ages. Based on this, it is possible that some of the older, concordant zircons contain xenocrystic and/or antecrystic inheritance (Fig. 2). Complex cores in CL images of some Cebolla Creek Tuff and Rat Creek Tuff zircons also provide evidence for inheritance, although the nature of these cores as xenocrystic versus antecrystic is hard to discern without accurate and precise in situ dating (Fig. 3c–d). However, xenocrystic material, if present in the concordant analyses in this study, does not comprise the entire grain based on the age distributions in Fig. 2 and the geologic history of the area. Volcanic activity in the San Juan Mountains started at 35 Ma (Lipman et al. 1970; Lipman 1975, 2000; Colucci et al. 1991; Parker et al. 2005), so a concordant zircon composed of entirely xenocrystic material would need to predate this timeframe. As such, we rule out an interpretation in which the dispersion in concordant ages (Fig. 2) is caused by wholly xenocrystic zircons.
One interesting feature of our ID-TIMS dataset is the increasingly suppressed age variability (i.e., decreased age dispersion) with each progressive eruption (Fig. 2), which we describe here as a ‘chimney sweeping’ effect. The initial ignimbrite in the sequence, the Rat Creek Tuff, yields the most pronounced zircon age dispersion, and the final ignimbrite, the Snowshoe Mountain Tuff, yields the zircon age spectrum with the least amount of dispersion (Fig. 2). Whether the dispersion itself is caused by xeno/antecrystic inheritance or simply progressive, autocrystic crystallization, the act of clearing out the magmatic plumbing system, or the ‘chimney sweeping,’ is a process that leads to the gradual disappearance of older zircons from the Rat Creek Tuff to the Snowshoe Mountain Tuff.
To understand the contribution of xenocrystic, antecrystic, and autocrystic zircon components to the age dispersion in this study, a better understanding of magma accumulation rates and timescales, and the resulting zircon crystallization timescales, is necessary. Interpreting the older zircon ages in each eruption as caused by inheritance (whether it be antecrystic or xenocrystic) implies discontinuous, punctuated magmatic pulses over shorter timescales to produce the main zircon age clusters, with xeno/antecrysts captured from previous magmatic episodes/reservoirs. In this interpretation, older ages are simply a mix of these separated magma pulses. A purely autocrystic interpretation for both younger and older zircons implies protracted magma input into the crust generating a large thermal anomaly containing super-solidus magma in which zircons crystallize over longer periods of time. In this scenario, while zircons might not have grown from the same individual magma batch, they grew from the same region occupied (partly or entirely) by super-solidus magma.
Timescales and thermal evolution of magma reservoirs in the central San Juan caldera cluster
To attempt to distinguish between an inheritance versus autocrystic interpretation of the zircon age dispersion in this study, we consider the volcanic history of the San Juan Mountains, synthetic whole-grain zircon age modeling, thermal and zircon crystallization modeling, and zircon chemistry. The traditional interpretation of protracted zircon age spectra is that the older zircon ages outside of the main clusters (Δtm) contain some type or degree of inheritance, whether it be an antecrystic or xenocrystic component (e.g., Wotzlaw et al. 2014; Deering et al. 2016; Colón et al. 2018). In this interpretation, Δtm is the total duration of magma accumulation before an eruption and magma input or flux is faster as a result of this shorter timeframe. The alternative hypothesis is that older zircons in each ignimbrite are autocrystic, resulting from protracted magmatism for the total duration of Δth for each ignimbrite, or at least Δt > Δtm. Importantly, estimates of magma flux associated with large eruptions are different for these two end-member scenarios, with significantly higher fluxes associated with the first model (de Silva et al. 2006; Annen 2009; Gelman et al. 2013; Eddy et al. 2016; Glazner and Sadler 2016).
The volcanic history of the central San Juan caldera cluster lends evidence to the antecrystic interpretation. The San Juan Mountains hosted volcanic activity for approximately 12 m.y., beginning with the eruption of 25,000 km3 of dominantly basaltic andesite–dacite lavas (Conejos Formation) between approximately 35 to 29 Ma and followed by 24 caldera-forming eruptions totaling 15,000 km3 between 34 and 23 Ma (Fig. 1; Lipman et al. 1970, 2015; Lipman 1975, 2006, 2007, 2012; Colucci et al. 1991; McIntosh and Chapin 2004; Parker et al. 2005; Lipman and McIntosh 2008). In particular, the five large ignimbrite eruptions in the central San Juan caldera cluster prior to the four studied here likely left a significant volume of unerupted magma in the crust (Martí et al. 2008). Based on 40Ar/39Ar geochronology of the previous ignimbrites within the central San Juan caldera cluster, there are significant overlaps between previous eruptive events and the zircon geochronology of the final four tuffs (Fig. 2). Many of the older Rat Creek Tuff zircon ages correlate well with the timing of Fish Canyon Tuff or the timing of the Masonic Park Tuff. Zircon ages of the Cebolla Creek Tuff older than 28 Ma also correlate with those two older ignimbrites, and Cebolla Creek zircon ages between 28 Ma and 27.5 Ma overlap with the timeframe of the Carpenter Ridge Tuff, Blue Creek Tuff, and Wason Park Tuff (Fig. 2). Similar observations can be made for the older zircons in the Nelson Mountain Tuff and Snowshoe Mountain Tuff. This coincident timing seems to argue for an antecrystic interpretation for the older zircons in each ignimbrite. However, temporal coincidence of ID-TIMS ages with previous eruptions does not necessarily mean that magmatism was either continuous or discontinuous, so this does not rule out the possibility of an autocrystic interpretation for older zircon ages.
Further insight can be gained by exploring the nature of an ID-TIMS zircon age, which is an average age of an entire zircon that can be formed with many different age zones. Previous studies, to varying degrees, have modeled this (Samperton et al. 2015; Rivera et al. 2016), and here we present a new model of synthetic whole-grain zircon ages to better understand the total duration of zircon crystallization encapsulated in an ID-TIMS age and subsequent age spectrum. Younger, outer portions of a zircon are more voluminous than older, inner portions, as can be visualized by considering the cubic relationship between volume and radius of an idealized spherical zircon. Assuming a constant growth rate with several growth increments and constant U content, a whole-grain zircon age will be more heavily weighted towards the younger ages in the outer portions of the zircon. In this simple case, the older, inner portions of a zircon will be less influential in a whole-grain age, and the age will be weighted towards its youngest age.
To estimate the total duration of zircon crystallization necessary to produce the Δtm intervals of ID-TIMS ages in this study, we modeled the whole-grain age distribution of a set of synthetic zircons. We generated 200 zircons as cubes with two pyramids on each end in which the length of the cube was equal to the height of the pyramids (Fig. S9a). Zircons ranged in size from 100 to 500 µm in total c-axis length and contained 3–10 age zones. The zircon lengths, number of age zones within each zircon, and thickness of age zones were generated as a uniform distribution by random sampling within their respective ranges (Fig. S9b–d), and we simulated zircon crystallization durations of 0.2–4 m.y. Each zircon has the same rim age of 0.01 m.y. before eruption and a variable core age depending on the number of zones to simulate zircon nucleation throughout magmatic history. Moving inward from the rim, zones increase in age by (agemax–agerim)/(nmax–1), in which nmax is the maximum number of zones (10), agemax is the total duration of zircon crystallization for that model run, and agerim is the age of the zircon rim (0.01 m.y. before eruption). Thus, zircons with 10 zones record the entire period of crystallization, whereas zircons with the minimum number of zones (3) record the shortest period of zircon crystallization. For each zircon, a whole-grain (e.g., ID-TIMS) age was calculated using age contributions weighted for volume and U content of each zone, since these are the main factors controlling the relative contributions of each age domain in whole-grain zircon geochronology. For zircons in this study with multiple LA-ICP-MS spots, most profiles of U content remain fairly constant, with the exception of the Nelson Mountain Tuff, which shows a number of profiles with decreasing U content towards the rim (Fig. 7). To assess the role of U content, we modeled linear changes of U by 50% from core to rim because most profiles in Fig. 7 show less than 50% change in U content. To model end-member zircon zone configurations observed in CL images of zircons in this study (Figs. 3, S1), we modeled zircons with a random distribution of zone thicknesses, zones becoming thinner towards the rim, and zones becoming thicker towards the rims. We note that our model does not incorporate the effect of chemical abrasion during the CA-ID-TIMS process. The model is included as an R code in the Supplementary Material (Code S1).
For optimal comparison of natural and synthetic zircon populations, we calculated the 2σ age span (m.y.) for each ignimbrite and modeled age distribution (Fig. 8). For natural zircon populations, only zircons included in the Δtm of each sample (Fig. 2) were used for the 2σ age span of the ignimbrite as a conservative estimate for the duration of zircon crystallization in the magma released by each eruption. No ages from sample 11AC16 were used in the 2σ age span for the Rat Creek Tuff because most are significantly older than the eruption age, and therefore, not part of the ‘main’ zircon age cluster for the Rat Creek as a whole.
Two sigma (2σ) age span of synthetic whole-grain zircon ages versus the total duration of modeled zircon crystallization. Each point represents a single model run with a unique zircon zone thickness configuration (increasing to rim, decreasing to rim, or random) and U content (increasing by 50%, decreasing by 50%, or constant to rim). The 2σ age spans of ID-TIMS zircon ages of natural ignimbrites are shown as horizontal lines for comparison
This synthetic zircon age modeling helps address the impact of different zone thicknesses and U content of zircons on the final distribution of zircon ages obtained by ID-TIMS. The effect of zircon U content on modeled ages is not as dramatic as in the modeling of Rivera et al. (2016) that found the high-U cores of Mesa Falls Tuff zircons (> 2000 ppm U) overwhelmed the signal of the more-voluminous, lower U rimward areas (300–500 ppm U). Zircons in this study do not have such dramatic shifts in U content (Fig. 7). The zircon zone thickness, on the other hand, significantly affects the estimated total duration of zircon crystallization, with thicker rims yielding smaller age spans and thinner rims producing larger age spans (Fig. 8). This suggests that in the case of the zircons in this study, with typically less than 50% change in U content from core to rim, the volume of each age zone is more important for the final age than U content (Fig. 8).
According to these calculations, the shorter zircon age spans of natural data in this study, the Snowshoe Mountain Tuff and Nelson Mountain Tuff, record total zircon crystallization durations of approximately 0.8–1 m.y. (Fig. 8). The zircon age span of the Cebolla Creek Tuff necessitates a total duration of approximately 1.5 m.y., and that of the Rat Creek Tuff requires approximately 2.7 m.y. of total zircon crystallization. This modeling suggests that whole-grain averaging of a zircon age may cause significant underestimation of the total duration of zircon crystallization seen in a distribution of ID-TIMS zircon ages. Importantly, such underestimations lead to overestimations of flux calculations, as pointed out by Glazner and Sadler (2016), and our model shows that this effect could be even larger than that estimated by Glazner and Sadler (2016). Since this model is predicated on an autocrystic nature of the crystallizing zircon (i.e., does not explicitly incorporate inheritance), it can only suggest the possibility that an autocrystic nature of zircons could explain the significant age dispersion seen in Fig. 2. It cannot rule out inheritance (antecrystic or xenocrystic) as a cause of the age dispersion seen in Fig. 2.
Comparing zircon geochemistry and thermal modeling also provides valuable insights into the hypothesis of protracted zircon crystallization timescales. Two general observations are important: the time–temperature variation and the temperature distribution for each VAR. First, the consistently decreasing nature of the average temperature of the fastest VAR model contrasts with the increasing average temperature of the slower VARs (Fig. 5). All ignimbrites have a significant number of higher Ti content analyses near the rims (Fig. 7), indicating that some parts of these magma reservoirs were at higher temperatures during their last stages of zircon crystallization. This contradicts the trend predicted for the highest simulated VAR. Second, magma reservoirs formed by a relatively high VAR (1 × 10–2 m y−1) are dominated by temperatures higher than 750 °C (Fig. 9). The prominence of zircon temperatures in this study below 750 °C suggests that the reservoirs that fed these four eruptions were assembled at VARs lower than 1 × 10–2 m y−1 (Fig. 9). Zircon temperatures of the Nelson Mountain Tuff and Cebolla Creek Tuff have IQRs similar to that of the intermediate VAR model (5 × 10–3 m y−1), with most or all of the IQR below 750 °C. Zircon temperatures of the Snowshoe Mountain Tuff have an IQR most similar to that of the slowest VAR (2 × 10–3 m y−1). Zircon temperatures of the dacitic Rat Creek Tuff are the only ones with an IQR completely above 750 °C (Fig. 9). The Rat Creek Tuff presents an interesting system in which the rhyolitic portions are generally older and colder, and the dacitic portions are hotter and younger (Figs. 2, 9). The hotter zircon temperatures in the dacitic Rat Creek Tuff are likely due to late-stage influx of hotter, more mafic magma, as hypothesized by previous studies (Sliwinski et al. 2019; Curry et al. 2021), but it could also be due in part to other factors such as a higher zircon saturation temperature (Fig. S6).
Zircon Ti data exist for two other ignimbrites in the central San Juan caldera cluster, the Masonic Park Tuff and Fish Canyon Tuff (Sliwinski et al. 2017). Using aTiO2 = 0.75 and aSiO2 = 1, similar to most of the ignimbrites in this study, we calculated Ti-in-zircon temperatures for these zircons for comparison (Fig. S5f). Resulting temperatures are lower than all four ignimbrites of this study: the IQR of the Fish Canyon Tuff zircon temperatures is 664–706 °C, and that of the Masonic Park Tuff is 678–717 °C. These low temperatures could be a result of the small amount of data (n = 40,43), resulting in a nonrepresentative temperature distribution, or that the aTiO2 value used was too high. Using a lower aTiO2 (i.e., 0.55) would increase the temperatures by about 20–30 °C, which still puts these temperature distributions dominantly < 750 °C. This implies that the low VARs of 2–5 × 10–3 m y−1 are common throughout the larger, overall magmatic system encompassing the central San Juan caldera cluster.
Our zircon geochronology and geochemistry data in combination with thermal and zircon modeling suggest that the protracted injection of magma into the crust at relatively low rates of magma input led to the assembly of the San Juan magmatic body, which fed a series of large ignimbrites. Estimates of eruptible magma production from thermal modeling suggest that the fastest VAR (1 × 10–2 m y−1) could produce the necessary volume of magma for the ignimbrites in this study in relatively short timescales, < < 1 m.y. (Fig. 10), and this is consistent with the minimum timescales considered in this study, those of Δtm of each ignimbrite (Fig. 2). However, the fastest VAR does not produce the necessary combination of (1) the timescales estimated by synthetic zircon age modeling necessary for zircon crystallization (0.8–2.7 m.y.) and (2) the lower zircon crystallization temperatures (< 750 °C) prevalent in all ignimbrites (Figs. 8, 9). This means, with lower VARs, magma reservoirs may have started building via magmatic intrusion up to 1 m.y. before zircon crystallization. In this case, the total duration of magmatism ranges between 1.8 m.y. (Snowshoe Mountain Tuff) and 3.7 m.y. (Rat Creek Tuff). However, the extensive volcanic history of the area argues for the possibility that thermal priming of the crust occurred prior to these four ignimbrites, which would negate the necessity for this 1 m.y. period priming period. In either case, based on thermal modeling and Ti-in-zircon temperatures, we argue for protracted, low magmatic fluxes of 2–5 × 10–3 m y−1 VAR to form not only these four magma reservoirs, but also the greater central San Juan magmatic body.
Total injected magma volume compared to eruptible volume showing the accumulation rates of eruptible magma for each VAR in this study. Horizontal lines show total erupted volumes of large ignimbrites for the entire San Juan Mountains (15,000 km3), the central San Juan caldera cluster (8,650 km3), and the four eruptions of this study (1,400 km3)
This thermal modeling also shows that a zircon age spectrum consisting of a main cluster of near-eruption ages with some slightly older ages is to be expected in magmatic systems best described by the thermal models presented here. One aspect of the thermal and zircon modeling results is that the relative fraction of measurable (i.e., eruptible) zircon ages available in the magmatic system increases during the model (i.e., with decreasing zircon age; Fig. 6a). For example, the amount of zircon in the last million years of magma injection history (i.e., 4–5 m.y. after injection starts) is much higher than in the first million years after zircon starts to appear in the erupted material (i.e., 0.9–1.15 m.y. after injection starts; Fig. 6a). Thus, even with a protracted, low VAR of magma input, it is statistically much more likely to sample zircons from the near-eruption timeframe. The progressive accumulation of eruptible magma crystallizing zircon increases the probability of sampling zircon with an age close to eruption age and tends to produce age dispersion that is only a portion of the total duration of zircon crystallization.
With regard to the distinction between inheritance-caused and autocrystic-caused zircon age dispersion, posed at the beginning of this section, our findings can neither confirm nor disprove each hypothesis. Our thermal modeling results cannot be used to unequivocally distinguish between an autocrystic- versus antecrystic/inheritance-based interpretation of zircon age dispersion, but they do suggest that protracted zircon crystallization in a crustal thermal anomaly, or a magma reservoir, is unavoidable if magma is injected in the crust for prolonged periods of time. In addition, thermal models in this study and previous studies (e.g., Karakas et al. 2017; Biggs and Annen 2019) both result in evolution towards a unique thermal anomaly in the crust with temperature evolution controlled by rate of magma supply. This is interesting because this study injected magma into the same location, whereas previous studies injected magma into random locations in the crust. Therefore, changing the mode of magma injection location does not affect the long-term thermal evolution, and this suggests that our conclusions would be similar using a different modality of magma injection.
In terms of zircon crystallization throughout such magma reservoirs, traditional definitions dictate that a zircon crystallized in an injected portion of magma that is separate from a later portion of magma is an antecryst, whereas zircon crystallized from the same physical batch of magma is an autocryst (Miller et al. 2007). However, autocrysts and antecrysts are not as clear-cut in this geologic setting because of the complexity of temporal and spatial associations of individual magma injections. Individual magma batches, or injections, into the overall magma reservoir in this geologic setting share and contribute to the overall thermal anomaly of the magma reservoir, even if they are separated by potentially large distances or long times. In a geologic setting with such long-lived volcanism and magmatism, an autocryst is better described as a zircon crystallizing from the same thermal anomaly instead of the same specific magma batch. Whether or not an individual batch of magma was separated physically or temporally, which helps define traditional antecrysts and autocrysts, is not as important as the fact that the individual magma batches contribute to and benefit from the overall crustal thermal anomaly, which is the most important aspect of a magma reservoir. We favor a model in which zircons crystallized over prolonged periods of time within a large magmatic plumbing system possibly containing melt-rich regions dispersed in a crystal-rich magmatic mush occupying the same thermal anomaly within the crust.
This discussion also sheds light on the chimney sweeping effect described previously. Decreasing dispersion of zircon ages from older to younger eruptions (Fig. 2) could be due to either (1) a lack of older zircon material available in the magma reservoirs of the younger eruptions compared to those of the older eruptions or (2) the younger eruptions did not sample available older zircon material as effectively as the older eruptions. The first scenario implies that the magma reservoirs of the younger eruptions were built in a shorter timeframe than the older eruptions, which in this case also means a faster magmatic flux due to the larger size of younger eruptions over the shorter timeframe. However, zircon geochemistry and thermal modeling argue for similarly low magmatic fluxes (VARs of 2–5 × 10–3 m y−1) for all four ignimbrites and the San Juan magmatic body at large. Even though VARs in this study are long-term averages and VAR variations are likely in nature, a large VAR increase from the Rat Creek Tuff (150 km3) to the Snowshoe Mountain Tuff (500 km3) that would be able to produce the large amount of eruptible magma necessary for the Snowshoe Mountain Tuff in the necessary timeframe (Δtm = 0.41 ± 0.37 m.y.) would produce a distinct thermal evolution and zircon geochemical signal that we do not see in this study. The second scenario could be explained by the rapid sequence of these ignimbrite eruptions based on overlapping 40Ar/39Ar sanidine ages (Fig. 2). In this scenario, the eruptions occurred in such quick succession that younger eruptions were unable to effectively sample older zircon material that is statistically harder to sample (Fig. 6a). Based on the low magmatic fluxes found here for the San Juan magma body, we propose that the second scenario is a more likely cause for the chimney sweeping effect.
Zircon crystallization timescales in large ignimbrites
In this section, we compare zircon crystallization ages of all large ignimbrites with U–Pb ID-TIMS data to explore the evolution of large silicic magmas across different geodynamic settings. To ensure a robust comparison between ignimbrites and with modeling results, we calculated the 2σ age span of ID-TIMS ages using the main population of zircon ages, as we did above for the ignimbrites in this study (Fig. 11; Table S5). Outliers, or ages outside of the main population of data, were not used to calculate the 2σ age span. Zircon ID-TIMS 2σ age spans range from 0.009 m.y. (Bishop Tuff) to 0.65 m.y. (Rat Creek Tuff; Fig. 11). All ignimbrites from the Snake River Plain with ID-TIMS zircon ages except the Castleford Crossing Ignimbrite have 2σ age spans < 0.1 m.y. (Rivera et al. 2014, 2016; Singer et al. 2014; Wotzlaw et al. 2014, 2015; Colón et al. 2018), and the majority of all other ignimbrites (except 4) have 2σ age spans > 0.1 m.y. (Fig. 11). Ignimbrites in this study are among the longest recorded zircon age spans in the literature, and they form a negative slope in Fig. 11 due to the chimney sweeping effect that lowers the 2σ age spans of the younger Snowshoe Mountain Tuff and Nelson Mountain Tuff. Compiled ID-TIMS zircon age spans range between 0.009 m.y. (Bishop Tuff) and 0.24 m.y. (Kneeling Nun Tuff), and the Cebolla Creek Tuff and Rat Creek Tuff extend this to 0.35 m.y. and 0.65 m.y., respectively (Fig. 11).
Zircon U–Pb ID-TIMS age span (2σ) versus ignimbrite volume for all large ignimbrites with ID-TIMS data in the literature. Western U.S. ignimbrites (*) include all those in the western U.S. besides the Snake River Plain and Southern Rocky Mountain Volcanic Field ignimbrites. Lines connect different studies of the same ignimbrite. BCT—Badger Creek Tuff; BT—Bishop Tuff; CCI—Castleford Crossing Ignimbrite; CCT—Cebolla Creek Tuff; CI—Cardones Ignimbrite; FCT—Fish Canyon Tuff; HRT—Huckleberry Ridge Tuff; KNT—Kneeling Nun Tuff; KPT—Kos Plateau Tuff; KT—Kilgore Tuff; LCT—Lava Creek Tuff; MFT—Mesa Falls Tuff; NMT—Nelson Mountain Tuff; OI—Oxaya Ignimbrite; RCT—Rat Creek Tuff; RhyCT—Rhyolite Canyon Tuff; SMT—Snowshoe Mountain Tuff; SRMVF—Southern Rocky Mountain volcanic field (Schmitz and Bowring 2001; Bachmann et al. 2007; Crowley et al. 2007; Tappa et al. 2011; Wotzlaw et al. 2013, 2014, 2015; Mills and Coleman 2013; Guillong et al. 2014; Rivera et al. 2014, 2016; Singer et al. 2014; van Zalinge et al. 2016; Deering et al. 2016; Colón et al. 2018; Szymanowski et al. 2019). See Supplementary Material (Table S5) for zircon age data compilation
The geodynamic setting of each ignimbrite is important in understanding differences in zircon age spans. Ignimbrites related to the hot spot magmatism of the Snake River Plain include the Castleford Crossing Ignimbrite, Kilgore Tuff, Huckleberry Ridge Tuff, Mesa Falls Tuff, and Lava Creek Tuff (Rivera et al. 2014, 2016; Singer et al. 2014; Wotzlaw et al. 2014, 2015; Colón et al. 2018). Ignimbrites related to traditional arc magmatism include the Oxaya Ignimbrite and Cardones Ignimbrite from the central Andes (van Zalinge et al. 2016), and the Kos Plateau Tuff from the Aegean arc (Guillong et al. 2014; Fig. 11). The 0.76 Ma Bishop Tuff, on the other hand, occurred in an extensional regime on the western edge of the Basin and Range province (Crowley et al. 2007; Hildreth and Wilson 2007). Ignimbrites in the Southern Rocky Mountain volcanic field (Fish Canyon Tuff, Badger Creek Tuff, Amalia Tuff, this study), in addition to the Rhyolite Canyon Tuff in Arizona and Kneeling Nun Tuff in New Mexico, have more complicated geodynamic settings (Schmitz and Bowring 2001; Bachmann et al. 2007; Tappa et al. 2011; Mills and Coleman 2013; Wotzlaw et al. 2013; Deering et al. 2016; Szymanowski et al. 2019). The Eocene–Oligocene geodynamic setting of the western U.S. includes the transition from the Sevier–Laramide Orogeny to the extensional environments of the Basin and Range province and the Rio Grande rift (Humphreys 1995; Humphreys et al. 2003). Magmatism during this transition is typically thought to be caused by hydration of lithospheric mantle during low-angle subduction followed by influx of hotter mantle during slab foundering or steepening (Dickinson and Snyder 1978; Farmer et al. 2008). While subduction likely played some role in the generation of these magmas, though not typical arc magmatism, the relative timing of ignimbrite to onset of extension is not always clear (Best et al. 2016; Ricketts et al. 2016; Abbey and Niemi 2020; Rosera et al. 2021).
The most notable distinction in this data compilation is the shorter 2σ age spans of Snake River Plain ignimbrites compared to most other ignimbrites (Fig. 11). The shorter zircon age spans of hot spot ignimbrites are commonly interpreted by previous studies to represent brief pre-eruption magmatic histories (Rivera et al. 2014; Wotzlaw et al. 2015; Loewen and Bindeman 2016; Colón et al. 2018). Within the Snake River Plain, Colón et al. (2018) observed that central Snake River Plain ignimbrites (e.g., Twin Falls volcanic center, Castleford Crossing Ignimbrite) have larger zircon age ranges than the Heise (Kilgore Tuff) and Yellowstone (Huckleberry Ridge Tuff, Mesa Falls Tuff, Lava Creek Tuff) volcanic centers (Rivera et al. 2014, 2016; Singer et al. 2014; Wotzlaw et al. 2014, 2015), and we observe the same (Fig. 11). Colón et al. (2018) interpreted this difference to be caused by the higher frequency of eruptions (i.e., short repose intervals) and more structural complexity in the central Snake River Plain, making antecrystic zircons more readily available.
Petrologically, drier magmas in the hotspot-related Snake River Plain erupt at higher temperatures compared to colder and wetter subduction-related magmas (e.g., Christiansen 2005). Magmas with more water also crystallize over a larger temperature range than those with less water (Melekhova et al. 2013; Caricchi and Blundy 2015; Hartung et al. 2019), particularly from liquidus to crystallinities of rheological lockup (e.g., 50–60% crystals; Marsh 1981). Combined, this gives wetter magmas a larger interval within which to record zircon crystallization compared to drier magmas, which manifests as smaller 2σ zircon age spans for the Snake River Plain magmas compared to subduction-related magmas. Thus, this difference between Snake River Plain zircon 2σ age spans and those of other ignimbrites can be accounted for considering magma chemistry, especially water content.
Several ignimbrites from outside the Snake River Plain have zircon 2σ age spans < 0.1 m.y., including the Badger Creek Tuff, Amalia Tuff, Kos Plateau Tuff, and Bishop Tuff (Fig. 11). This could be the result of magma generation in different geodynamic settings or undersampling. In terms of geodynamic setting, the 0.76 Ma Bishop Tuff occurred in an extensional regime (Riley et al. 2012), and this may have been the case for the 25.5 Ma Amalia Tuff based on thermochronology (Ricketts et al. 2016; Abbey and Niemi 2020). The Kos Plateau Tuff and Badger Creek Tuff, on the other hand, were subduction-related ignimbrites. The number of zircon dates for each ignimbrite is also important because, as mentioned above, it is statistically easier to sample a zircon closer to the eruption age (Fig. 6a), so studies with a smaller number of ID-TIMS ages are more likely to underestimate the 2σ age span. Studies of ignimbrites with comparably few ID-TIMS ages include the Kos Plateau Tuff (n = 7; Guillong et al. 2014), the Badger Creek Tuff (n = 5; Mills and Coleman 2013), and the Amalia Tuff (n = 4; Tappa et al. 2011). Therefore, while some potentially reflect undersampling of the zircon age spectra (e.g., Kos Plateau Tuff, Badger Creek Tuff, and Amalia Tuff), the Bishop Tuff is fairly well sampled (n = 19; Crowley et al. 2007). This suggests that some aspects of magma generation during extension may be associated with shorter zircon crystallization timescales, similar to the Snake River Plain.
Age modeling suggests that total durations of zircon crystallization may be four times higher than 2σ zircon age ranges (Fig. 8). At lower 2σ age spans (< 0.1 m.y.), age modeling is less clear, and we conservatively estimate that these small age ranges either represent the full zircon crystallization timeframe, or at least underestimate it less than larger age spans (Fig. 8). Based on this, 2σ zircon age spans of most subduction-related ignimbrites (> 0.1 m.y.) could represent much longer timescales of zircon crystallization, whereas those of extension-related ignimbrites and most Snake River Plain ignimbrites (< 0.1 m.y.) have less or no underestimation of zircon crystallization timescales. In addition, studies have shown that some Snake River Plain zircons have quite high-U content (Rivera et al. 2016; Troch et al. 2018) in their core, which would have the additional effect of decreasing the amount of underestimation by giving larger weight to older age zones. This difference could also be related to the difference in water content and eruption temperature of hotter, drier hot spot magmas compared to colder, wetter subduction-related magmas, as discussed earlier. Based on observations in this study, the longer zircon timescales of most subduction-related ignimbrites could be indicative of protracted magma input at relatively low VARs, whereas the shorter age spans of most Snake River Plain ignimbrites could be caused by shorter term, higher flux magma input.
Conclusions
New zircon ID-TIMS geochronology and LA-ICP-MS geochemistry for the last four ignimbrites in the central San Juan caldera cluster combined with thermal modeling, zircon crystallization modeling, and synthetic age modeling provide evidence for a new model for magmatism related to the construction of one of the world’s most voluminous and rapid ignimbrite flare-ups. The age dispersion seen in Fig. 2 could be the result of inheritance (antecrystic or xenocrystic) or simply autocrystic zircon crystallization, and our findings cannot unequivocally confirm or disprove each hypothesis. We interpret the geochronologic signal in Fig. 2 as the expression of a long-lived magmatic system with zircon crystallization occurring during magma input at relatively low VARs, and we observe for the first time a chimney sweeping effect of decreasing age dispersion with each progressive eruption (Fig. 2), which is likely a result of the rapid succession of the eruptions. We estimate the dominant VARs that built the magma reservoirs responsible for these four ignimbrites, and possibly the overall magmatic system below the central San Juan caldera cluster, to be 2–5 × 10–3 m y−1. This protracted, low magma input model contrasts with other models of high magmatic fluxes over shorter timescales responsible for ignimbrites. This means that higher magma fluxes are not always necessary to produce the large amount of eruptible magma in the upper crust needed for an ignimbrite flare-up. Expanding our study to a wider compilation of ID-TIMS U–Pb zircon geochronology for large ignimbrites throughout the world, we show that subduction-related ignimbrites typically have longer 2σ zircon age spans than those in the Snake River Plain. We interpret this as suggesting that most subduction-related ignimbrites require lower magma fluxes over longer timescales, whereas most ignimbrites of the hot spot-related Snake River Plain are built by higher flux magma input over shorter timescales.
Availability of data and material
All data are included in the Supplementary Material.
Code availability
The code for the synthetic zircon age model is provided in the Supplementary Material.
References
Abbey AL, Niemi NA (2020) Perspectives on continental rifting processes from spatiotemporal patterns of faulting and magmatism in the Rio Grande Rift, USA. Tectonics. https://doi.org/10.1029/2019TC005635
Annen C (2009) From plutons to magma chambers: Thermal constraints on the accumulation of eruptible silicic magma in the upper crust. Earth Planet Sci Lett 284:409–416. https://doi.org/10.1016/j.epsl.2009.05.006
Annen C, Blundy JD, Sparks RSJ (2006) The genesis of intermediate and silicic magmas in deep crustal hot zones. J Petrol 47:505–539. https://doi.org/10.1093/petrology/egi084
Annen C, Blundy JD, Leuthold J, Sparks RSJ (2015) Construction and evolution of igneous bodies: Towards an integrated perspective of crustal magmatism. Lithos 206–221
Bachmann O, Oberli F, Dungan MA et al (2007) 40Ar/39Ar and U–Pb dating of the Fish Canyon magmatic system, San Juan Volcanic field, Colorado: Evidence for an extended crystallization history. Chem Geol 236:134–166. https://doi.org/10.1016/j.chemgeo.2006.09.005
Best MG, Christiansen EH, de Silva S, Lipman PW (2016) Slab-rollback ignimbrite flareups in the southern Great Basin and other Cenozoic American arcs: A distinct style of arc volcanism. Geosphere 12:1097–1135. https://doi.org/10.1130/GES01285.1
Biggs J, Annen C (2019) The lateral growth and coalesence of magma systems. Philos Trans R Soc A Math Phys Eng Sci. https://doi.org/10.1098/rsta.2018.0005
Bindeman IN, Melnik OE (2016) Zircon survival, rebirth and recycling during crustal melting, magma crystallization, and mixing based on numerical modelling. J Petrol 57:437–460. https://doi.org/10.1093/petrology/egw013
Boehnke P, Watson EB, Trail D et al (2013) Zircon saturation re-revisited. Chem Geol 351:324–334. https://doi.org/10.1016/j.chemgeo.2013.05.028
Bowring JF, McLean NM, Bowring SA (2011) Engineering cyber infrastructure for U-Pb geochronology: Tripoli and U-Pb_Redux. Geochemistry, Geophys Geosystems. https://doi.org/10.1029/2010GC003479
Broderick C, Wotzlaw JF, Frick DA et al (2015) Linking the thermal evolution and emplacement history of an upper-crustal pluton to its lower-crustal roots using zircon geochronology and geochemistry (southern Adamello batholith, N. Italy). Contrib Mineral Petrol 170:1–17. https://doi.org/10.1007/s00410-015-1184-x
Caricchi L, Blundy J (2015) Experimental petrology of monotonous intermediate magmas. Geol Soc London Spec Publ 422:105–130. https://doi.org/10.1144/sp422.9
Caricchi L, Annen C, Blundy J et al (2014a) Frequency and magnitude of volcanic eruptions controlled by magma injection and buoyancy. Nat Geosci 7:126–130. https://doi.org/10.1038/ngeo2041
Caricchi L, Simpson G, Schaltegger U (2014b) Zircons reveal magma fluxes in the Earth’s crust. Nature 511:457–461. https://doi.org/10.1038/nature13532
Caricchi L, Simpson G, Schaltegger U (2016) Estimates of volume and magma input in crustal magmatic systems from zircon geochronology: the effect of modeling assumptions and system variables. Front Earth Sci. https://doi.org/10.3389/feart.2016.00048
Carrigan CR (1988) Biot number and thermos bottle effect: implications for magma- chamber convection. Geology 16:771–774. https://doi.org/10.1130/0091-7613(1988)016%3c0771:BNATBE%3e2.3.CO;2
Christiansen EH (2005) Contrasting processes in silicic magma chambers: Evidence from very large volume ignimbrites. Geol Mag 142:669–681. https://doi.org/10.1017/S0016756805001445
Christiansen RL (2001) The Quaternary and Pliocene Yellowstone Plateau Volcanic Field of Wyoming, Idaho, and Montana. United States Geol Surv Prof Pap 729-G:145
Coleman DS, Gray W, Glazner AF (2004) Rethinking the emplacement and evolution of zoned plutons: Geochronologic evidence for incremental assembly of the Tuolumne Intrusive Suite, California. Geology 32:433–436. https://doi.org/10.1130/G20220.1
Colón DP, Bindeman IN, Wotzlaw J-F et al (2018) Origins and evolution of rhyolitic magmas in the central Snake River Plain: insights from coupled high-precision geochronology, oxygen isotope, and hafnium isotope analyses of zircon. Contrib Mineral Petrol 173:11. https://doi.org/10.1007/s00410-017-1437-y
Colucci MT, Dungan MA, Ferguson KM (1991) Precaldera lavas of the Southeast San Juan volcanic field: parent magmas and crustal interactions. J Geophys Res 96:413–434
Condon DJ, Schoene B, McLean NM et al (2015) Metrology and traceability of U–Pb isotope dilution geochronology (EARTHTIME Tracer Calibration Part I). Geochim Cosmochim Acta 164:464–480. https://doi.org/10.1016/j.gca.2015.05.026
Crowley JL, Schoene B, Bowring SA (2007) U-Pb dating of zircon in the Bishop Tuff at the millennial scale. Geology 35:1123–1126. https://doi.org/10.1130/G24017A.1
Curry A, Caricchi L, Lipman PW (2021) Magmatic evolution of zoned and unzoned ignimbrites: evidence for a complex crustal architecture feeding four rapid-sequence, caldera-forming eruptions in the San Juan Mountains, Colorado. J Petrol 62:1–37
de Silva SL, Gosnold WD (2007) Episodic construction of batholiths: Insights from the spatiotemporal development of an ignimbrite flare-up. J Volcanol Geotherm Res 167:320–335. https://doi.org/10.1016/j.jvolgeores.2007.07.015
de Silva S, Zandt G, Trumbull R et al (2006) Large ignimbrite eruptions and volcano-tectonic depressions in the Central Andes: A thermomechanical perspective. Geol Soc Spec Publ 269:47–63. https://doi.org/10.1144/GSL.SP.2006.269.01.04
De Silva SL, Kay SM (2018) Turning up the heat: High-flux magmatism in the Central Andes. Elements 14:245–250. https://doi.org/10.2138/gselements.14.4.245
Deering CD, Keller B, Schoene B et al (2016) Zircon record of the plutonic-volcanic connection and protracted rhyolite melt evolution. Geology 44:267–270. https://doi.org/10.1130/G37539.1
Dickinson WR, Snyder WS (1978) Plate tectonics of the Laramide orogeny. Geol Soc Am Mem 151:355–366. https://doi.org/10.1130/mem151-p355
Eddy MP, Bowring SA, Miller RB, Tepper JH (2016) Rapid assembly and crystallization of a fossil large-volume silicic magma chamber. Geology 44:331–334. https://doi.org/10.1130/G37631.1
Farmer GL, Bailley T, Elkins-Tanton LT (2008) Mantle source volumes and the origin of the mid-Tertiary ignimbrite flare-up in the southern Rocky Mountains, western U.S. Lithos 102:279–294. https://doi.org/10.1016/j.lithos.2007.08.014
Ferry JM, Watson EB (2007) New thermodynamic models and revised calibrations for the Ti-in-zircon and Zr-in-rutile thermometers. Contrib Mineral Petrol 154:429–437. https://doi.org/10.1007/s00410-007-0201-0
Frazer RE, Coleman DS, Mills RD (2014) Zircon U-Pb geochronology of the Mount Givens Granodiorite: Implications for the genesis of large volumes of eruptible magma. J Geophys Res Solid Earth 119:2907–2924. https://doi.org/10.1002/2013JB010716.Received
Gaynor SP, Coleman DS, Rosera JM, Tappa MJ (2019a) Geochronology of a Bouguer Gravity Low. J Geophys Res Solid Earth 124:2457–2468. https://doi.org/10.1029/2018JB015923
Gaynor SP, Rosera JM, Coleman DS (2019b) Intrusive history of the Oligocene Questa porphyry molybdenum deposit, New Mexico. Geosphere 15:548–575. https://doi.org/10.1130/GES01675.1
Gelman SE, Gutiérrez FJ, Bachmann O (2013) On the longevity of large upper crustal silicic magma reservoirs. Geology 41:759–762. https://doi.org/10.1130/G34241.1
Ghiorso MS, Gualda GAR (2013) A method for estimating the activity of titania in magmatic liquids from the compositions of coexisting rhombohedral and cubic iron-titanium oxides. Contrib Mineral Petrol 165:73–81. https://doi.org/10.1007/s00410-012-0792-y
Glazner AF, Sadler PM (2016) Estimating the duration of geologic intervals from a small number of age determinations: A challenge common to petrology and paleobiology. Geochem Geophys Geosyst 17:4892–4898. https://doi.org/10.1002/2016GC006542
Gravley DM, Deering CD, Leonard GS, Rowland JV (2016) Ignimbrite flare-ups and their drivers: A New Zealand perspective. Earth Sci Rev 162:65–82. https://doi.org/10.1016/j.earscirev.2016.09.007
Gualda GAR, Ghiorso MS (2015) MELTS_Excel: A Microsoft Excel-based MELTS interface for research and teaching of magma properties and evolution. Geochem Geophys Geosyst 16:315–324. https://doi.org/10.1002/2014GC005545
Guillet S, Corona C, Ludlow F et al (2020) Climatic and societal impacts of a “forgotten” cluster of volcanic eruptions in 1108–1110 CE. Sci Rep 10:6715. https://doi.org/10.1038/s41598-020-63339-3
Guillong M, Meier DL, Allan MM et al (2008) SILLS: A MATLAB-based program for the reduction of laser ablation ICP-MS data of homogeneous materials and inclusions. Mineral Assoc Canada Short Course Ser 40:328–333
Guillong M, Von Quadt A, Sakata S et al (2014) LA-ICP-MS Pb-U dating of young zircons from the Kos-Nisyros volcanic centre, SE Aegean arc. J Anal at Spectrom 29:963–970. https://doi.org/10.1039/c4ja00009a
Hartung E, Weber G, Caricchi L (2019) The role of H 2 O on the extraction of melt from crystallising magmas. Earth Planet Sci Lett 508:85–96. https://doi.org/10.1016/j.epsl.2018.12.010
Hayden LA, Watson EB (2007) Rutile saturation in hydrous siliceous melts and its bearing on Ti-thermometry of quartz and zircon. Earth Planet Sci Lett 258:561–568. https://doi.org/10.1016/j.epsl.2007.04.020
Hiess J, Condon DJ, McLean N, Noble SR (2012) 238U/235U Systematics in Terrestrial Uranium-Bearing Minerals. Science (80-) 335:1610–1614. https://doi.org/10.1126/science.1229223
Hildreth W, Wilson CJN (2007) Compositional Zoning of the Bishop Tuff. J Petrol 48:951–999. https://doi.org/10.1093/petrology/egm007
Humphreys ED (1995) Post-laramide removal of the Farallon slab, western United States. Geology 23:987–990. https://doi.org/10.1130/0091-7613(1995)023%3c0987:PLROTF%3e2.3.CO;2
Humphreys E, Hessler E, Dueker K et al (2003) How Laramide-age hydration of North American lithosphere by the Farallon slab controlled subsequent activity in the Western United States. Int Geol Rev 45:575–595. https://doi.org/10.2747/0020-6814.45.7.575
Jellinek AM, DePaolo DJ (2003) A model for the origin of large silicic magma chambers: Precursors of caldera-forming eruptions. Bull Volcanol 65:363–381. https://doi.org/10.1007/s00445-003-0277-y
Kaiser JF, de Silva S, Schmitt AK et al (2017) Million-year melt–presence in monotonous intermediate magma for a volcanic–plutonic assemblage in the Central Andes: Contrasting histories of crystal-rich and crystal-poor super-sized silicic magmas. Earth Planet Sci Lett 493:262–266. https://doi.org/10.1016/j.epsl.2018.04.033
Karakas O, Degruyter W, Bachmann O, Dufek J (2017) Lifetime and size of shallow magma bodies controlled by crustal-scale magmatism. Nat Geosci. https://doi.org/10.1038/ngeo2959
Kern JM, de Silva SL, Schmitt AK et al (2016) Geochronological imaging of an episodically constructed subvolcanic batholith: U-Pb in zircon chronochemistry of the Altiplano-Puna Volcanic Complex of the Central Andes. Geosphere 12:1054–1077. https://doi.org/10.1130/GES01258.1
Krogh TE (1973) A low-contamination method for hydrothermal decomposition of zircon and extraction of U and Pb for isotopic age determinations. Geochim Cosmochim Acta 37:485–494
Kuiper KF, Deino A, Hilgen FJ et al (2008) Synchronizing rock clocks of earth history. Science (80-) 320:500–504. https://doi.org/10.1126/science.1154339
Large SJE, Wotzlaw J-F, Guillong M et al (2020) Resolving the timescales of magmatic and hydrothermal processes associated with porphyry deposit formation using zircon U–Pb petrochronology. Geochronology 2:209–230. https://doi.org/10.5194/gchron-2-209-2020
Lipman PW (1975) Evolution of the Platoro caldera complex and related volcanic rocks, southeastern Colorado. USGS Prof Pap 852:1–128
Lipman PW (2000) Central San Juan caldera cluster: regional volcanic framework. Geol Soc Am Spec Pap 346:9–68. https://doi.org/10.1130/0-8137-2346-9.9
Lipman PW (2007) Incremental assembly and prolonged consolidation of Cordilleran magma chambers: Evidence from the Southern Rocky Mountain volcanic field. Geosphere 3:42–70. https://doi.org/10.1130/GES00061.1
Lipman PW (2012) Geologic Map of the Cochetopa Park and North Pass Calderas, Northeastern San Juan Mountains, Colorado. USGS Sci Investig Map 3123:48. https://doi.org/10.3133/sim3123
Lipman PW, Bachmann O (2015) Ignimbrites to batholiths: Integrating perspectives from geological, geophysical, and geochronological data. Geosphere 11:705–743. https://doi.org/10.1130/GES01091.1
Lipman PW, McIntosh WC (2008) Eruptive and noneruptive calderas, northeastern San Juan Mountains, Colorado: Where did the ignimbrites come from? Geol Soc Am Bull 120:771–795. https://doi.org/10.1130/B26330.1
Lipman PW, Steven TA, Mehnert HH (1970) Volcanic history of the San Juan Mountains, Colorado, as indicated by potassium-argon dating. Geol Soc Am Bull 81:2329–2352. https://doi.org/10.1130/0016-7606(1970)81
Lipman PW, Zimmerer MJ, McIntosh WC (2015) An ignimbrite caldera from the bottom up: Exhumed floor and fill of the resurgent Bonanza caldera, Southern Rocky Mountain volcanic field, Colorado. Geosphere 11:1902–1947. https://doi.org/10.1130/GES01184.1
Lipman PW (2006) Geologic Map of the Central San Juan Caldera Cluster, Southwestern Colorado. USGS Geol Investig Ser I–2799:34
Loewen MW, Bindeman IN (2016) Oxygen isotope thermometry reveals high magmatic temperatures and short residence times in Yellowstone and other hot-dry rhyolites compared to cold-wet systems. Am Mineral 101:1222–1227. https://doi.org/10.2138/am-2016-5591
Lukács R, Caricchi L, Schmitt AK et al (2021) Zircon geochronology suggests a long-living and active magmatic system beneath the Ciomadul volcanic dome field (eastern-central Europe). Earth Planet Sci Lett 565:116965. https://doi.org/10.1016/j.epsl.2021.116965
Marsh BD (1981) Mineralogy and Petrology On the Crystallinity , Probability of Occurrence , and Rheology of Lava and Magma. 85–98
Martí J, Geyer A, Folch A, Gottsmann J (2008) Chapter 6 A Review on Collapse Caldera Modelling. Dev Volcanol 10:233–283. https://doi.org/10.1016/S1871-644X(07)00006-X
Marxer F, Ulmer P (2019) Crystallisation and zircon saturation of calc-alkaline tonalite from the Adamello Batholith at upper crustal conditions: an experimental study. Contrib Mineral Petrol 174:1–29. https://doi.org/10.1007/s00410-019-1619-x
Mattinson JM (2005) Zircon U–Pb chemical abrasion (“CA-TIMS”) method: Combined annealing and multi-step partial dissolution analysis for improved precision and accuracy of zircon ages. Chem Geol 220:47–66. https://doi.org/10.1016/j.chemgeo.2005.03.011
McIntosh WC, Chapin CE (2004) Geochronology of the central Colorado volcanic field. New Mex Bur Geol Miner Resour Bull 160:205–237
McLean NM, Bowring JF, Bowring SA (2011) An algorithm for U-Pb isotope dilution data reduction and uncertainty propagation. Geochem Geophys Geosyst. https://doi.org/10.1029/2010GC003478
McLean NM, Condon DJ, Schoene B, Bowring SA (2015) Evaluating uncertainties in the calibration of isotopic reference materials and multi-element isotopic tracers (EARTHTIME Tracer Calibration Part II). Geochim Cosmochim Acta 164:481–501. https://doi.org/10.1016/j.gca.2015.02.040
Melekhova E, Annen C, Blundy J (2013) Compositional gaps in igneous rock suites controlled by magma system heat and water content. Nat Geosci 6:385–390. https://doi.org/10.1038/ngeo1781
Miller JS, Matzel JEP, Miller CF et al (2007) Zircon growth and recycling during the assembly of large, composite arc plutons. J Volcanol Geotherm Res 167:282–299. https://doi.org/10.1016/j.jvolgeores.2007.04.019
Mills RD, Coleman DS (2013) Temporal and chemical connections between plutons and ignimbrites from the Mount Princeton magmatic center. Contrib Mineral Petrol 165:961–980. https://doi.org/10.1007/s00410-012-0843-4
Newhall C, Self S, Robock A (2018) Anticipating future Volcanic Explosivity Index (VEI) 7 eruptions and their chilling impacts. Geosphere 14:572–603. https://doi.org/10.1130/GES01513.1
Ovtcharova M, Goudemand N, Hammer Ø et al (2015) Developing a strategy for accurate definition of a geological boundary through radio-isotopic and biochronological dating: The Early-Middle Triassic boundary (South China). Earth-Sci Rev 146:65–76. https://doi.org/10.1016/j.earscirev.2015.03.006
Parker DF, Ghosh A, Price CW et al (2005) Origin of rhyolite by crustal melting and the nature of parental magmas in the Oligocene Conejos Formation, San Juan Mountains, Colorado, USA. J Volcanol Geotherm Res 139:185–210. https://doi.org/10.1016/j.jvolgeores.2004.08.015
Peate IU, Baker JA, Al-Kadasi M et al (2005) Volcanic stratigraphy of large-volume silicic pyroclastic eruptions during Oligocene Afro-Arabian flood volcanism in Yemen. Bull Volcanol 68:135–156. https://doi.org/10.1007/s00445-005-0428-4
Ricketts JW, Kelley SA, Karlstrom KE et al (2016) Synchronous opening of the Rio Grande rift along its entire length at 25–10 Ma supported by apatite (U-Th)/He and fission-track thermochronology, and evaluation of possible driving mechanisms. Bull Geol Soc Am 128:397–424. https://doi.org/10.1130/B31223.1
Riley P, Tikoff B, Hildreth W (2012) Transtensional deformation and structural control of contiguous but independent magmatic systems: Mono-Inyo Craters, Mammoth Mountain, and Long Valley Caldera, California. Geosphere 8:740–751. https://doi.org/10.1130/GES00662.1
Rivera TA, Schmitz MD, Crowley JL, Storey M (2014) Rapid magma evolution constrained by zircon petrochronology and 40Ar/39Ar sanidine ages for the Huckleberry Ridge Tuff, Yellowstone, USA. Geology 42:643–646. https://doi.org/10.1130/G35808.1
Rivera TA, Schmitz MD, Jicha BR, Crowley JL (2016) Zircon petrochronology and 40Ar/39Ar sanidine dates for the mesa falls tuff: Crystal-scale records of magmatic evolution and the short lifespan of a large yellowstone magma chamber. J Petrol 57:1677–1704. https://doi.org/10.1093/petrology/egw053
Rosera JM, Gaynor SP, Coleman DS (2021) Spatio-Temporal Shifts in Magmatism and Mineralization in Northern Colorado Beginning in the Late Eocene. Econ Geol. https://doi.org/10.5382/econgeo.4815
Samperton KM, Schoene B, Cottle JM et al (2015) Magma emplacement, differentiation and cooling in the middle crust: Integrated zircon geochronological-geochemical constraints from the Bergell Intrusion, Central Alps. Chem Geol 417:322–340. https://doi.org/10.1016/j.chemgeo.2015.10.024
Schaltegger U, Davies JHFL (2017) Petrochronology of Zircon and Baddeleyite in Igneous Rocks: Reconstructing Magmatic Processes at High Temporal Resolution. Rev Mineral Geochem 83:297–328. https://doi.org/10.2138/rmg.2017.83.10
Schaltegger U, Brack P, Ovtcharova M et al (2009) Zircon and titanite recording 1.5 million years of magma accretion, crystallization and initial cooling in a composite pluton (southern Adamello batholith, northern Italy). Earth Planet Sci Lett 286:208–218. https://doi.org/10.1016/j.epsl.2009.06.028
Schmitz MD, Bowring SA (2001) U-Pb zircon and titanite systematics of the Fish Canyon Tuff: An assessment of high-precision U-Pb geochronology and its application to young volcanic rocks. Geochim Cosmochim Acta 65:2571–2587. https://doi.org/10.1016/S0016-7037(01)00616-0
Schoene B, Schaltegger U, Brack P et al (2012) Rates of magma differentiation and emplacement in a ballooning pluton recorded by U–Pb TIMS-TEA, Adamello batholith, Italy. Earth Planet Sci Lett 355–356:162–173. https://doi.org/10.1016/j.epsl.2012.08.019
Schöpa A, Annen C (2013) The effects of magma flux variations on the formation and lifetime of large silicic magma chambers. J Geophys Res Solid Earth 118:926–942. https://doi.org/10.1002/jgrb.50127
Self S (2006) The effects and consequences of very large explosive volcanic eruptions. Philos Trans R Soc A Math Phys Eng Sci 364:2073–2097. https://doi.org/10.1098/rsta.2006.1814
Singer BS, Jicha BR, Condon DJ et al (2014) Precise ages of the Réunion event and Huckleberry Ridge excursion: Episodic clustering of geomagnetic instabilities and the dynamics of flow within the outer core. Earth Planet Sci Lett 405:25–38. https://doi.org/10.1016/j.epsl.2014.08.011
Sliwinski JT, Bachmann O, Dungan MA et al (2017) Rapid pre-eruptive thermal rejuvenation in a large silicic magma body: the case of the Masonic Park Tuff, Southern Rocky Mountain volcanic field, CO, USA. Contrib to Mineral Petrol. https://doi.org/10.1007/s00410-017-1351-3
Sliwinski J, Farsky D, Lipman PW et al (2019) Rapid magma generation or shared magmatic reservoir? petrology and geochronology of the Rat Creek and Nelson Mountain Tuffs, CO, USA. Front Earth Sci. https://doi.org/10.3389/feart.2019.00271
Szymanowski D, Ellis BS, Wotzlaw JF, Bachmann O (2019) Maturation and rejuvenation of a silicic magma reservoir: High-resolution chronology of the Kneeling Nun Tuff. Earth Planet Sci Lett 510:103–115. https://doi.org/10.1016/j.epsl.2019.01.007
Tappa MJ, Coleman DS, Mills RD, Samperton KM (2011) The plutonic record of a silicic ignimbrite from the Latir volcanic field, New Mexico. Geochem Geophys Geosyst 12:1–16. https://doi.org/10.1029/2011GC003700
Tapster S, Condon DJ, Naden J et al (2016) Rapid thermal rejuvenation of high-crystallinity magma linked to porphyry copper deposit formation; evidence from the Koloula Porphyry Prospect, Solomon Islands. Earth Planet Sci Lett 442:206–217. https://doi.org/10.1016/j.epsl.2016.02.046
Tierney CR, Schmitt AK, Lovera OM, de Silva SL (2016) Voluminous plutonism during volcanic quiescence revealed by thermochemical modeling of zircon. Geology 44:683–686. https://doi.org/10.1130/G37968.1
Troch J, Ellis BS, Schmitt AK et al (2018) The dark side of zircon: textural, age, oxygen isotopic and trace element evidence of fluid saturation in the subvolcanic reservoir of the Island Park-Mount Jackson Rhyolite, Yellowstone (USA). Contrib Mineral Petrol 173:1–17. https://doi.org/10.1007/s00410-018-1481-2
van Zalinge ME, Sparks RSJ, Cooper FJ, Condon DJ (2016) Early Miocene large-volume ignimbrites of the Oxaya Formation, Central Andes. J Geol Soc London 173:716–733. https://doi.org/10.1144/jgs2015-123
Weber G, Caricchi L, Arce JL, Schmitt AK (2020) Determining the current size and state of subvolcanic magma reservoirs. Nat Commun. https://doi.org/10.1038/s41467-020-19084-2
Widmann P, Davies JHFL, Schaltegger U (2019) Calibrating chemical abrasion: Its effects on zircon crystal structure, chemical composition and U-Pb age. Chem Geol 511:1–10. https://doi.org/10.1016/j.chemgeo.2019.02.026
Wotzlaw J-F, Schaltegger U, Frick DA et al (2013) Tracking the evolution of large-volume silicic magma reservoirs from assembly to supereruption. Geology 41:867–870. https://doi.org/10.1130/G34366.1
Wotzlaw J-F, Bindeman IN, Watts KE et al (2014) Linking rapid magma reservoir assembly and eruption trigger mechanisms at evolved yellowstone-type supervolcanoes. Geology 42:807–810. https://doi.org/10.1130/G35979.1
Wotzlaw J-F, Bindeman IN, Stern RA et al (2015) Rapid heterogeneous assembly of multiple magma reservoirs prior to Yellowstone supereruptions. Sci Rep. https://doi.org/10.1038/srep14026
Acknowledgements
We thank Jean-Marie Boccard at the University of Geneva Department of Earth Sciences for his help with preparation of zircon grain mounts. We also thank Pierre Vonlanthen and Alexey Ulianov at the University of Lausanne Institute of Earth Sciences for their help with visualization of zircon grain mounts and acquisition of zircon trace element data, respectively. We thank Clémentine Antoine for assisting in recalculating previously published 40Ar/39Ar geochronology. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 677493-FEVER).
Funding
Open access funding provided by University of Geneva. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 677493-FEVER).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
The authors consented to publication.
Additional information
Communicated by Timothy L. Grove.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Curry, A., Gaynor, S.P., Davies, J.H.F.L. et al. Timescales and thermal evolution of large silicic magma reservoirs during an ignimbrite flare-up: perspectives from zircon. Contrib Mineral Petrol 176, 103 (2021). https://doi.org/10.1007/s00410-021-01862-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00410-021-01862-w