Using the elastic properties of zircon-garnet host-inclusion pairs for thermobarometry of the ultrahigh-pressure Dora-Maira whiteschists: problems and perspectives

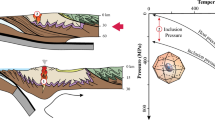
Abstract

The ultrahigh-pressure (UHP) whiteschists of the Brossasco-Isasca unit (Dora-Maira Massif, Western Alps) provide a natural laboratory in which to compare results from classical pressure (P)–temperature (T) determinations through thermodynamic modelling with the emerging field of elastic thermobarometry. Phase equilibria and chemical composition of three garnet megablasts coupled with Zr-in-rutile thermometry of inclusions constrain garnet growth within a narrow P–T range at 3–3.5 GPa and 675–720 °C. On the other hand, the zircon-in-garnet host-inclusion system combined with Zr-in-rutile thermometry would suggest inclusion entrapment conditions below 1.5 GPa and 650 °C that are inconsistent with the thermodynamic modelling and the occurrence of coesite as inclusion in the garnet rims. The observed distribution of inclusion pressures cannot be explained by either zircon metamictization, or by the presence of fluids in the inclusions. Comparison of the measured inclusion strains with numerical simulations shows that post-entrapment plastic relaxation of garnet from metamorphic peak conditions down to 0.5 GPa and 600–650 °C, on the retrograde path, best explains the measured inclusion pressures and their disagreement with the results of phase equilibria modelling. This study suggests that the zircon-garnet couple is more reliable at relatively low temperatures (< 600 °C), where entrapment conditions are well preserved but chemical equilibration might be sluggish. On the other hand, thermodynamic modelling appears to be better suited for higher temperatures where rock-scale equilibrium can be achieved more easily but the local plasticity of the host-inclusion system might prevent the preservation of the signal of peak metamorphic conditions in the stress state of inclusions. Currently, we cannot define a precise threshold temperature for resetting of inclusion pressures. However, the application of both chemical and elastic thermobarometry allows a more detailed interpretation of metamorphic P–T paths.

Introduction

Mineral inclusions provide valuable information on the history of metamorphic rocks and their pressure and temperature (P–T) paths since they can preserve direct evidence of extreme conditions experienced by a rock, such as ultrahigh-pressure (UHP) metamorphism. The pioneering contribution by Chopin (1984) documented coesite inclusions within garnet from the whiteschists of the Brossasco-Isasca unit (Dora-Maira Massif, Western Alps). After his discovery, this terrain has become a world-renowned setting for UHP metamorphism (e.g., Schertl et al. 1991; Chopin et al. 1991; Henry et al. 1993; Compagnoni and Hirajima 2001; Hermann 2003; Ferrando et al. 2009; Gauthiez-Putallaz et al. 2016; Groppo et al. 2019). Considerable efforts have been made to constrain the exact P–T conditions attained during metamorphism of the Brossasco-Isasca unit. The first pressure estimates of P > 2.8 GPa by Chopin (1984), suggested a depth of mineral formation corresponding to at least 90 km. Determining the mechanisms by which such rocks are then able to be exhumed to the Earth’s surface are still a challenge for the scientific community (e.g., Malusà et al. 2015; Schenker et al. 2015).

In the last decade, interest in mineral inclusions has risen due to the refinement of the elastic thermobarometry method: an alternative approach for obtaining metamorphic P–T estimates based on the elastic properties of host-inclusion mineral couples (e.g., Rosenfeld and Chase 1961; van der Molen and van Roermund 1986; Nasdala et al. 2003; Enami et al. 2007; Kohn 2014; Murri et al. 2018; Zhong et al. 2019; Alvaro et al. 2020; Gilio et al. 2020a). Mineral inclusions at room conditions commonly retain pressures (the so-called residual pressure, P_inc) that deviate from the external pressure because of their contrast in the elastic properties with the surrounding host. Rosenfeld and Chase (1961) were the first to suggest exploiting such residual pressures to constrain the conditions of inclusion entrapment. Since then, many studies have improved the thermo-mechanical models allowing us to achieve more accurate thermo-barometric estimates (e.g., Zhang 1998; Angel et al. 2015). The added value of elastic thermobarometry is related to (i) its independence on chemical equilibrium and (ii) its possible application to rocks lacking mineral assemblages that are sensitive to P–T changes. Moreover, further developments of this method can provide quantitative information on paleo-stress conditions during metamorphism by exploiting the intrinsic anisotropy of the host-inclusion system (e.g., Alvaro et al. 2020).

In this work, a detailed comparison of the results of classical and elastic thermobarometric methods has been carried out on garnet-bearing whiteschists from the UHP Brossasco-Isasca unit in the Dora-Maira Massif. We applied thermodynamic modelling and Zr-in-rutile inclusion geothermometry to constrain formation of three garnet megablasts and, consequently, the conditions of inclusion entrapment. Phase equilibria estimates and the zircon-in-garnet elastic thermobarometry indicate significantly different conditions for inclusion entrapment. In the first case, we obtained P–T conditions of 3–3.5 GPa and 675–720 °C while in the second case below 1.5 GPa and 600–650 °C. Several hypotheses to explain this discrepancy, including the presence of fluids, local non-hydrostatic stress during entrapment and plastic relaxation of the host-inclusion system, are evaluated and discussed. In particular, we show how the comparison between the measured strain states of our zircon inclusions and those predicted by numerical simulations for the same system can shed light on this issue.

Geological background

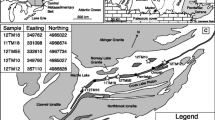
The Dora-Maira Massif is a pile of slices of Variscan continental crust involved in Alpine subduction and subsequent exhumation (e.g., Compagnoni et al. 1995). The Brossasco-Isasca coesite-bearing unit is estimated to be about 10 × 4 × 1 km in size (e.g., Compagnoni and Rolfo 2003) and is tectonically sandwiched between the lower-pressure San Chiaffredo, Rocca Solei and Pinerolo units (Fig. 1) that, according to current P–T estimates, experienced comparable peak conditions at 2–2.4 GPa and 500–520 °C (Groppo et al. 2019). The Brossaco-Isasca UHP unit itself consists of two main sub-units, the Monometamorphic and the Polymetamorphic Complexes, derived from Alpine reworking of late Variscan granitoids (now orthogneiss) and of Variscan amphibolite-facies basement (now metapelite, eclogite, marble), respectively (Compagnoni et al. 1995). Our study focuses on solid inclusions within three garnet megablasts from the whiteschists of the Monometamorphic Complex.

Fig. 1

Schematic geological map of the Brossasco-Isasca UHP unit (southern part of the Dora-Maira Massif). The two stars indicate the location of the two main outcrops of whiteschists. G stands for the “Gilba” locality while M stands for the “Martiniana” locality (after Castelli et al. 2007)

Following the initial work of Chopin (1984), mineral equilibria studies supported by experimental work constrained the peak conditions to between 3.2–3.7 GPa and 720–800 °C (Schertl et al. 1991; Sharp et al. 1993; Simon et al. 1997; Rubatto and Hermann 2001; Coggon and Holland 2002; Osborne et al. 2019), with a maximum values at about 4.3 GPa and 730 °C (Hermann 2003).

Tilton et al. (1989, 1991) first defined the age of Alpine metamorphism of the Brossasco-Isasca unit at 34–38 Ma by Sm/Nd dating on pyrope mineral separates. Later, Gebauer et al. (1997) using SHRIMP method on zircon crystals confirmed an age of UHP metamorphism at 35 Ma and obtained by zircon fission track ages of 29.9 ± 1.4 Ma. By combining, P–T estimates with in situ U–Pb titanite and zircon fission track dating Rubatto and Hermann (2001) also defined three different stages at ~ 3.5 GPa, 720 °C at 35.1 ± 0.9 Ma, 0.8–1 GPa and 600 °C at 32.9 ± 0.9 Ma, 0.4–0.5 GPa and 600–620 °C at 31.8 ± 0.6 Ma.

Sample description

The Brossasco-Isasca garnet-bearing whiteschists crop out in two main localities: (1) close to Case Ramello and Case Parigi in the Martiniana valley and (2) close to Case Tapina in the Gilba valley (Fig. 1). These rocks form lenses within the country orthogneiss of the Monometamorphic complex (e.g., Compagnoni et al. 1995) and consist mainly of quartz (former coesite), white mica, kyanite, talc and garnet; garnet crystals range in size from a few millimeters to almost 20 cm in diameter, which are usually referred to as garnet neoblasts and megablasts, respectively.

The modal abundance of garnet and quartz is highly variable, suggesting local differences in the bulk chemistry of the protolith. On this basis, two groups of whiteschists can be distinguished: SiO₂-rich and SiO₂-poor (Chopin 1984; Hermann 2003; Schertl and Schreyer 2008; Ferrando et al. 2009; Gauthiez-Putallaz et al. 2016). In the SiO₂-rich whiteschist, garnet forms millimetre-sized crystals and the surrounding rock matrix consists mainly of a large amount (> 40%) of quartz (former coesite), followed by kyanite and phengite. In the SiO₂-poor whiteschists, garnet forms very large crystals (up to 20 cm across) and the rock matrix presents a larger amount of kyanite and phengite (see also Simon et al. 1997; Simon and Chopin 2001). In these rock types, coesite occurs as an inclusion only in garnet rims and small amounts of quartz are present in the rock matrix. In this work, we focus on garnet megablasts from the SiO₂-poor whiteschists because they host numerous solid inclusions, thus appearing particularly suitable for the application of elastic thermobarometry.

Petrography and selection of solid inclusions in garnet

The solid inclusions in garnet megablasts mainly consist of kyanite, rutile, zircon, rare coesite (the latter only found at the megablast rims), biotite, chlorite, apatite and subordinate rare phases such as ellenbergerite and dumortierite (see also Chopin 1984; Schertl et al. 1991). Some minerals found as inclusions, such as biotite, are absent in the rock matrix. Among our samples, the garnet megablasts coming from the Gilba locality are generally less affected by late-stage chloritization compared to those from Martiniana and contain a larger number of rutile and zircon inclusions. Moreover, garnets from the two localities also differ in crystal shape; those from Gilba being spherical whereas idiomorphic or sub-idiomorphic garnets are found at Martiniana.

Among all of the solid inclusions hosted in the pyrope megablasts, zircon is the only one suitable for elastic thermobarometry. Rutile cannot be used because rutile inclusions do not show any residual pressure at room conditions due to the contrast in the elastic properties of rutile to those of its garnet host (Musiyechenko et al. 2020). Coesite is commonly back-reacted to quartz while kyanite is too large with respect to the host garnet and it is usually itself full of solid and fluid inclusions. Moreover, although quartz is abundant in the rock matrix, it is almost absent as single crystalline inclusions: we found only one grain, and it was exposed to the external surface of a thin section. Zircon inclusions were selected for study according to the “geometrical” requirements given by Mazzucchelli et al. (2018) and Campomenosi et al. (2018), that they should be isolated at a distance at least three times the inclusion radius or major axis from any kind of discontinuity (host surfaces, fractures) or other inclusions, and of regular inclusion shape, from approximately spherical to ellipsoidal. Only inclusions with widths (full width at half maximum FWHM) of less than 5 cm⁻¹ for their Raman peak near 1008 cm⁻¹ were measured to avoid inclusions affected by significant radiation damage (Campomenosi et al. 2020b).

Material and methods

Electron microprobe and LA-ICP-MS

Microprobe analyses were carried out with a JEOL JXA 8200 electron microprobe at the University of Milan (Earth Science Institute) using wavelength dispersive spectrometers. The electron microprobe analyses and chemical element mapping of garnet were done with an acceleration voltage of 15 kV and a beam current of 40 nA. The measurements of all elements were performed with a 30 s counting time while background-counting time was 10 s for the positive and negative part each. Natural standards used for quantification are: omphacite for Na, ilmenite for Ti, rhodonite for Mn, K-feldspar for K, olivine for Mg, grossular for Si, Ca and Al, fayalite for Fe and pure Cr metal for Cr.

The chemical compositions of partially exposed zircon and rutile inclusions as well as garnet hosts were measured by LA-ICP-MS with a Resonetics RESOlutionSE 193 nm excimer laser system equipped with an S-155 large-volume constant-geometry chamber (Laurin Technic, Australia) at the Institute of Geological Sciences, University of Bern, Switzerland. The laser system was coupled to an Agilent 7900 quadrupole ICP-MS instrument. The spot size on the zircon crystals was 20 µm while those on rutile and garnet crystals was 64 µm. Standards for garnet trace elements were GSD-1 g (primary), NIST 612 (secondary), primary and secondary standard for rutile and zircon trace elements were NIST 610, GSD-1G and NIST 612, Zircon 91,500, respectively. Stoichiometric Si was employed as an internal standard for both zircon (SiO₂: 31.6 wt%) and garnet (SiO₂: 43.9 wt%) while for rutile stoichiometric TiO₂ (99 wt%) was used. Reproducibility and accuracy were within 10% or better for all analyzed elements. The data were reduced with the freeware Iolite (Hellstrom et al. 2008; Paton et al. 2011) using the data reduction scheme for trace elements of Woodhead et al. (2007).

Phase equilibria modelling and Zr-in-rutile geothermometry

Phase equilibria modelling was carried out by means of Gibbs free energy minimization using the software Perple_X (version 6.6.8; Connolly 2005, 2009) and the thermodynamic database of Holland and Powell (2011). In agreement with previous studies (Schreyer 1988; Hermann 2003; Gauthiez-Putallaz et al. 2016), the whiteschists can be successfully modelled by the KFMASH chemical system (K₂O–FeO–MgO–Al₂O₃–SiO₂–H₂O). However, the presence of garnet megablasts within the rock complicates the choice of a representative reactive bulk chemistry. As described in Sample description, one major variable in the Dora-Maira whiteschists is the amount of bulk SiO₂. For instance, the large garnet megablasts are referred to as SiO₂-poor whiteschists (e.g., Chopin 1984; Schertl and Schreyer 2008). Therefore, a series of T-X_bulk content (wt%) and T-bulk Mg# pseudosections have been computed at different P. The final bulk chemistry we used for our modelling is: 50 wt% SiO₂, 26 wt% Al₂O₃, 1.5 wt% FeO, 16.5 wt% MgO and 6 wt% K₂O with water in excess. This bulk chemistry differs from the one of SiO₂-poor whiteschists given by Gautiez-Putallaz et al. (2016) in the Mg# that is 0.9 rather than 0.8 (see the Supplementary material for further details). Information on the activity-composition relationships for mineral solid solutions are given in the Supplementary material.

Because in our samples zircon is the only suitable inclusion for elastic thermobarometry, we need another independent constraint to define unique points in P–T space. To this purpose, we used the Zr concentration in rutile inclusions as a geothermometer (Tomkins et al. 2007) assuming that, after entrapment, the garnet-rutile system remained isolated from the surrounding environment.

Raman spectroscopy

Raman measurements were performed with a Horiba Jobin–Yvon T64000 triple-monochromator spectrometer operating in a subtractive mode equipped with a Symphony LN2-cooled CCD detector, 1800-gr/mm holographic gratings, an Olympus BH-41 optical microscope with a 50 × long-working distance objective and a Coherent Ar + laser at the Department of Earth Sciences of the University of Hamburg (Germany). The spectral resolution was 2 cm⁻¹. The laser power delivered to the sample was approximately 8 mW, which was sufficient to avoid overheating of the examined zircon grains (Zhong et al. 2019). The instrumental precision in the peak position determination is about 0.35 cm⁻¹. For details on Raman spectra processing and evaluation, see the Supplementary material.

Determination of residual strain and residual pressure of zircon inclusions

The independent residual strain components (i.e., ε₁ and ε₃) and residual volume strain in zircon inclusions were calculated via the Grüneisen tensor approach (e.g., Murri et al. 2018; Angel et al. 2018) using four different zircon phonon modes: the B_1g mode near 1008 cm⁻¹, the A_1g mode near 975 cm⁻¹, the E_g mode near to 357 cm⁻¹ and the A_1g mode near to 440 cm⁻¹. Grüneisen tensor coefficients for each mode are from Stangarone et al. (2019). Once the strain was determined, we defined the independent stress components and the inclusion residual pressures (i.e., the negative of the mean normal stresses) with EntraPT, an online platform for elastic thermobarometry (Mazzucchelli et al. 2021) using the zircon stiffness tensor given by Özkan et al. (1974). Residual pressures were also calculated using the hydrostatic pressure calibrations of the Raman shifts (Binvignat et al. 2018).

Results

Garnet mineral chemistry and Zr concentration in rutile inclusions

Garnet

Table 1 lists representative microprobe analyses of the three garnet megablasts (samples DM17-13, DM17-35 and DMG4-5). Samples DM17-13 from Martiniana and DMG4-5 from the Gilba locality display a chemical zonation with decreasing almandine and grossular content from core to rim and increasing pyrope from about 88 mol% to about 96 mol%. In contrast, sample DM17-35 is homogeneous in composition with constant pyrope content of about 94 mol% from core to rim. The spessartine content in the garnet megablasts is generally below 1 mol% and Mn concentration decreases from core to rim. Figure 2a shows and compares the core to rim variation of pyrope content for the three megablasts.

Table 1 Representative compositions of garnet megablasts

Fig. 2

a pyrope content, b REE patterns, c Zr vs. P concentration and d Zr concentration of rutile inclusions within the three garnet megablasts along core to rim transects (full and empty symbols represent measurements at the garnet core and rim, respectively)

The garnet DM17-13 (Martiniana locality) shows the highest HREE content variation with normalized Lu content ranging from about 1000 to 70 from core to rim, respectively (full and empty symbols, respectively, in Fig. 2b). The core of garnet DM17-13 also shows the highest concentration of REE with respect to the other two megablasts, with a difference of about one order of magnitude (Fig. 2b). In contrast, garnets DMG4-5 and DM17-35 (Gilba locality) show flatter HREE patterns at the crystal core with slight HREE depletion towards the rim (Fig. 2b).

In principle, the presence of zircon and apatite inclusions enables the use of Zr and P concentrations in garnet as indicators of P and T conditions during growth (Kohn et al. 2015; Hermann and Spandler 2008). Figure 2c shows the Zr vs. P concentration for the different domains (core and rim) of the three garnet megablasts. Sample DM17-13 shows a slight core to rim increase in Zr (full and empty grey squares, respectively), at the same P concentration, whereas samples DM17-35 and DMG4-5 show no clear compositional difference between core and rim (Fig. 2c).

Rutile inclusions in garnet

Table 2 lists the mean concentration values and relative standard deviation of Zr concentration obtained by LA-ICP-MS in rutile inclusions within the three garnet hosts. Sample DM17-13 (Martiniana) shows an average concentration of 144 ppm while samples DM17-35 and DMG4-5 (both Gilba) have 220 and 216 ppm, respectively. Multiple measurements on the largest crystals of rutile revealed no detectable chemical zoning within single grains.

Table 2 Zr concentration in rutile inclusions (LA-ICP-MS data)

Zr in rutile thermometry and pseudosection modelling of garnet growth

The intersection between the P–T lines indicated by Zr-in-rutile thermometry and the pyrope isopleths constrains the growth of the three garnet megablasts to about 3–3.5 GPa and 675–720 °C (Fig. 3b).

Fig. 3

a Pseudosection modelling of SiO₂-poor whiteschists. b Combination of Zr-in-rutile thermometer (line thickness indicates the T uncertainty) and computed isopleths of pyrope (labelled in mole fraction) in garnet (black labeled lines) to constrain the conditions of garnet growth, indicated by the three colored ellipses (DM17-13 in grey, DM17-35 in blue, DMG4-5 in orange). The garnet stability field is also color-coded by its mode as indicated in the legend. The Fe-free line represents the garnet-in phase boundary computed for a Fe-free bulk composition, to take into account possible effects of fractionation that otherwise are neglected. Note that the P–T range of garnet growth indicated by the garnet composition and the Zr content of rutile corresponds to a significant increase of the garnet mode (from 5–8% to about 45%) in agreement with the observed growth of garnet megablasts

The lower and upper T limits correspond to the differences in the average Zr concentration found in the rutile inclusions in each garnet megablast. The application of the Zr-in-rutile thermometry requires that a SiO₂ is present. Coesite was found in the garnet rim and SiO₂ saturation is achieved through the reaction of talc + kyanite to give garnet + coesite (e.g. Gauthiez-Putallaz et al. 2016). Therefore, the Zr-in-rutile temperatures for inclusions in the garnet rims are accurate and these values are reported in Fig. 5. For rutile trapped in the interior, the SiO₂ activity is below unity (but buffered by the assemblage talc-kyanite-pyrope) and these temperatures represent maximum values. We did not note a systematic change in Zr contents of rutile in different positions within the garnet megablasts (Fig. 2d), indicating that the analytical scatter is larger than the effect of SiO₂-activity below unity. The difference of Zr content in rutile between the garnets from the two different localities cannot be readily explained by differences in SiO₂-activity since no quartz/coesite occurs in any of the garnet cores and requires further investigation. It is possible that the temperatures of garnet growth in the two localities that we have studied are actually the same. Recent data on T dependence of Zr concentration within garnet by Kohn et al. (2015) would yield a similar T range of garnet growth.

Residual strain and residual pressure of zircon inclusions from Raman spectroscopy

Selected zircon inclusions were measured to cover the entire range of garnet growth as reported in Fig. 4a. All measured inclusions show the typical “rosette” birefringence of the garnet host immediately surrounding the stressed inclusions (Fig. 4b), which is the result of the local symmetry breaking of the garnet host due to the stress field developed around inclusions (e.g., Howell et al. 2010; Campomenosi et al. 2020a).

Fig. 4

a Equatorial slice of a garnet megablast (sample DM17-13, Martiniana locality), with the location of selected zircon inclusions indicated by yellow spots covering the entire range of garnet growth. b Completely buried zircon inclusion viewed under crossed (top) and plane (bottom) polarized light showing the characteristic stress-induced birefringence halo in the surrounding host. c Changes in the peak position (i.e., Δω) of the B_1g mode near 1008 cm⁻¹ of completely buried zircon inclusions entrapped within the three garnet megablasts plotted against their distance from the core of the host crystal. d Calculated residual pressure from Raman measurements as function of the position within the garnet host from the three garnet megablasts

Figure 4c shows the changes in the Raman peak position (i.e., Δω) for the zircon B_1g phonon mode near 1008 cm⁻¹ with respect to a free zircon crystal taken as reference. The residual pressures resulting from the Raman measurements are shown in Fig. 4d. Note that, within data uncertainty, there is no difference between the zircon residual pressures computed using the hydrostatic and the Grüneisen tensor approaches (Table 3). In general, the residual pressure values vary considerably from core to rim of the garnet megablasts. Sample DM17-35 shows an average value of about 0.6 GPa up to about 45 mm of distance from the crystal core and then a drop to an average value of about 0.3 GPa from 45 to 55 mm. Sample DMG4-5 displays more variation in residual pressure values, ranging from 0.75 to 0.45 GPa with a slightly decreasing trend from core to rim. On the other hand, sample DM17-13 displays a bell-shaped trend moving from core to rim with residual pressures of about 0.6 GPa at the garnet core (i.e., 10 and 20 mm), a peak value of about 0.9 GPa around 35 mm and a decreasing trend moving toward the external rim down to about 0.6–0.65 GPa (Fig. 4d).

Table 3 Residual strain and residual pressure of zircon inclusions within the three garnet megablasts

Overall, the mean residual pressure value for all of the zircon inclusions is about 0.6 GPa. If we use this mean value of P_inc combined with the Zr-in-rutile thermometry the calculated entrapment conditions would be below 1.5 GPa and 650 °C. On the other hand, if we combine the average P_inc with the pyrope isopleths the calculated entrapment conditions would be 2–2.5 GPa and above 800 °C.

Discussion

These Dora-Maira pyrope megablasts provide an excellent natural laboratory to investigate the relationship between chemical and mechanical equilibration of garnet. The large garnets allow multiple zircon inclusions to be measured from core to rim of their host and can be compared with the well-constrained P–T conditions of garnet formation. The P–T-time path of the rocks is also well constrained (e.g., Gebauer et al. 1997; Rubatto and Hermann 2001) and includes first a pressure increase to about 3.5–4 GPa, 720–750 °C followed by near isothermal decompression to 0.5 GPa, 600–650 °C resulting in significant differences in the garnet-zircon isomekes between entrapment and the later metamorphic evolution. This provides the opportunity to thoroughly assess to what extent the entrapment conditions are preserved, which might be difficult to detect in systems with a smaller drop in pressure. In the following, we will first compare the results from chemical and elastic thermobarometry. Then the observed strain data are compared to predictions from numerical models. Finally, possible factors are discussed to explain the discrepancy between results from chemical and elastic thermobarometry.

Combining chemical and elastic thermobarometry

Chemical homogenization during the metamorphic thermal peak is negligible for big crystals (e.g., Spear and Peacock 1989) such as the pyrope megablasts from the Dora-Maira whiteschists. Therefore, the zonation in major and trace elements of garnet, combined with the pseudosection modelling, suggest garnet growth in a relatively small prograde interval of P–T conditions within the coesite stability field.

Figure 5a shows the results of phase equilibria modelling of the garnet stability together with Zr-in rutile thermometry and the entrapment isomekes for the range of zircon residual pressures (in GPa) that we measured. The entrapment isomeke for a given P_inc represents possible conditions of inclusion entrapment or elastic re-equilibration (e.g., Angel et al. 2015; Ferrero and Angel 2018). From Fig. 5a, the slopes of zircon-in-garnet isomekes and Zr-in-rutile isopleths allow us to define the garnet growth in terms of P–T conditions for inclusion entrapment independently from the garnet composition. However, for entrapment at the conditions determined by the thermodynamic modelling, the expected range of zircon inclusion residual pressure should be between 0.4 and 0.3 GPa. But only a few inclusions along the rims of garnet samples DM17-35 and DMG4-5 exhibit such pressures. On the other hand, most inclusion residual pressures are between 0.55 and 0.65 GPa (green band in Fig. 5b) with a weighted mean of 0.6 GPa. These values, in combination with the Zr-in-rutile thermometry, would correspond to entrapment conditions far below the stability fields of both garnet and coesite. This is not consistent with the petrographic observations. Moreover, from Fig. 5a we can rule out the possibility of garnet-forming reaction overstepping as a possible explanation of residual pressure changes. Indeed, for a prograde garnet growth, as in this case of study, the pressure in the inclusions would be lower than expected. Therefore, the deviation of most measured P_inc values from those expected for the P–T conditions of entrapment needs to be evaluated in a different way.

Fig. 5

a Garnet and Zr-in-rutile isopleths (from Fig. 3b) compared with calculated zircon-in-garnet isomekes labelled by the P_inc (given in GPa) of zircon inclusions expected in the recovered samples. b Data points are the measured zircon inclusion residual pressures (from Fig. 4d, Table 3) with their weighted mean indicated by the green band labelled ‘W.M.’. The yellow band indicates the P_inc calculated for zircon inclusions entrapped at the P–T conditions shown in a, assuming hydrostatic stress conditions during entrapment and purely elastic behavior during the subsequent metamorphic history and exhumation

Combining residual strain from Raman spectroscopic measurements and residual strain from selected numerical models

In addition to giving the residual inclusion pressures, the Raman measurements also give their residual strains, expressed in terms of their independent components ε₃ and ε₁. These can be compared to calculations of the strain in zircon inclusions via numerical simulations (e.g., Mazzucchelli et al. 2019). Figure 6a shows the contour map of deviatoric strain (i.e., ε₃–ε₁) computed for zircon inclusions in garnet at room P and T as function of metamorphic entrapment conditions (i.e., P_trap and T_trap). Note that such a contour map is obtained assuming (i) a purely elastic behavior of the host-inclusion system; (ii) a hydrostatic stress conditions at the moment of entrapment and (iii) a spherical shape of the inclusion (see Mazzucchelli et al. 2019). Here, the range of zircon-in-garnet isomekes, of interest for these garnet megablasts, and the Dora-Maira P–T path (Rubatto and Hermann 2001) are superimposed for reference. The green ellipse in Fig. 6a indicates the conditions of garnet growth on the prograde path as suggested by chemical thermobarometry (3–3.5 GPa and 675–720 °C), while the blue ellipse in Fig. 6a represents the intersection of the known P–T path with the isomeke corresponding to the mean residual inclusion pressure of 0.6 GPa, at about 575–600 °C and 0.5 GPa along the retrograde evolution of the UHP unit.

Fig. 6

a Contour map of the calculated deviatoric strain (ε₃ − ε₁) expected at room conditions for zircon inclusions within garnet as a function of inclusion entrapment conditions. Calculations assume a spherical shape of the inclusion, a hydrostatic stress during entrapment and a purely elastic behavior of the host–inclusion system (Mazzucchelli et al. 2019). Colour scale for the contours is given at the top of the diagram. Yellow solid lines represent the zircon-in-garnet entrapment isomekes for the range of measured inclusion residual pressures. The green and the blue ellipses represent respectively the conditions of inclusion entrapment according to the pseudosection modelling and the conditions of entrapment according to the intersection between the average entrapment isomeke and the P–T path of Rubatto and Hermann (2001) (solid black arrow). b–d display the zircon inclusion strains ε₃ and ε₁ within the three garnet megablasts calculated via the Grüneisen tensor approach from Raman measurements. The green and blue ellipses represent the modelled strain states of zircon inclusions in garnet for the corresponding P, T conditions in a. The size of confidence ellipses refers to 1σ. Black dashed lines represent the conditions of equal volume strain (i.e., isochores), they are labeled with the corresponding residual pressure given in GPa

In Fig. 6b–d, the strains measured by Raman in the zircon inclusions (samples DM17-13, DMG4-5 and DM17-35, respectively) are plotted in ε₃ vs. ε₁ diagrams.

The residual-independent strain components expected for zircons trapped during garnet growth on the prograde path (green ellipse) are significantly different from those measured in the inclusions (red dots in Fig. 6b–d). Instead, the blue ellipse in Fig. 6b–d corresponding to the strain conditions expected from the “average isomeke” (i.e., P_inc = 0.6 GPa), is closer to those measured in our zircon inclusions than the green one. Indeed, most of the measured strains, within the data uncertainties, lie close to the lines of isotropic strain and hydrostatic stress conditions (blue and green solid lines respectively in Fig. 6b–d). Note that this is true even for the few zircon inclusions showing residual pressures consistent with the entrapment conditions during the prograde path (i.e., with P_inc = 0.3–0.4 GPa). These data clearly suggest that other processes than simple entrapment at the inferred conditions have to be considered to explain the evolution of the Dora-Maira host-inclusion systems.

Possible factors influencing zircon residual pressure

Fluid phase at the host inclusion boundary

The presence of a fluid film at the host-inclusion boundary will strongly affect both the residual pressure and the strain state of the inclusion (e.g., Nimis et al. 2016). Fluids cannot support shear stresses, and therefore a zircon inclusion surrounded by fluid would exhibit strains (Fig. 6) corresponding to hydrostatic stress. In general, the second effect of water or other fluid phases is to reduce the effective bulk modulus of the composite inclusion with respect to a single-crystal inclusion, thus resulting in an increase in its measured residual pressure. Furthermore, if there was a fluid phase present, this would be expected to result in the incorporation of OH groups into the crystal structures of both the zircon and the host garnet. The presence of OH groups in the crystal structure of nominally anhydrous minerals also affects their elastic properties (e.g., Fan et al. 2017) and thus the measured residual inclusion pressure. FTIR spectroscopy measurements and maps on four inclusions showing higher residual pressure, and their surrounding host garnet, showed that no detectable fluid occurs around the inclusions (see Supplementary materials). There is up to ⁓70 ppm of intra-crystalline OH groups present in the garnet (approximately 0.001 a.p.f.u. H in the tetrahedral site), but no detectable OH groups in the zircon inclusions. FTIR maps also reveal that the OH group content in garnet is not related to the presence of the inclusions but it is uniform across the crystal. This level of H substitution into the garnet structure would not have any significant effect on the equation of state of the garnet (Fan et al. 2017). Hence fluid is not responsible for the anomalously high inclusion pressures, nor their strain state.

Undetectable level of radiation damage in zircon inclusions

The anomalous increase in inclusion residual pressure could also be due to very low degrees of structural defects due to radiation damage. For example, post-entrapment radiation damage that would cause a free zircon crystal to expand by 0.2% would increase the inclusion pressure by ~ 0.3 GPa. However, such a low degree of radiation damage cannot be detected by Raman since the corresponding change in the Raman peak width (in terms of FWHM) would be within the instrumental spectral resolution. However, charge-contrast (CC) imaging coupled with LA-ICP-MS analysis, on exposed inclusions in the same garnet hosts, has shown that most zircon grains do not have any radiation damage (Campomenosi et al. 2020b) and therefore radiation damage cannot explain the large number of inclusions with pressures of > 0.6 GPa or more (Fig. 5b).

Local deviatoric stress conditions during entrapment

As described in Combining residual strain from Raman spectroscopic measurements and residual strain from selected numerical models, a major assumption of the analysis of strains in inclusions (e.g., Fig. 6a) is that the inclusion entrapment occurred under hydrostatic stress conditions (Mazzucchelli et al. 2019). Consequently, the observed divergence of measured strain values from the predicted ones (Fig. 6b–d) might be related to deviations from hydrostatic stress around the inclusions at the time of entrapment. Henry et al. (1993) described the presence of internal S-shaped foliation within the rims of some garnet megablasts that would potentially suggest crystal growth in a stress field. However, no inclusion foliations have been observed in the studied samples. Moreover, garnet formation in these rocks is driven by dehydration reactions producing about 10 vol% of water (Gauthiez-Putallaz et al. 2016); within such a fluid-rich environment, the development of local deviatoric stress appears to be unlikely. Indeed, for interconnected pore fluids, deviatoric stresses disappear because the rock cannot support shear stress components. On the other hand, if fluids were not interconnected, the mechanism of pressure solution would probably have operated to reduce the deviatoric stresses. In addition, the presence of fluid decreases the amount of stress necessary to develop dislocation creep in crystals (Xu et al. 2013) that, once again, would reduce deviatoric stresses in the garnets. In addition, since our inclusions are randomly oriented within the host, the presence of a local deviatoric stress field at the time of entrapment should scatter the inclusion strains along a single isochore corresponding to a unique volume strain rather than forming a cluster corresponding to isotropic strain or hydrostatic stress conditions. Indeed, under the same amount of deviatoric stress, for inclusions unable to change their orientation according to the stress field, the independent components of the strains would change in absolute values as a function of the crystallographic orientation of the inclusion (Gilio et al. 2020b) keeping the volume strain constant (i.e., lying along one single isochore). Therefore, local deviatoric stress conditions cannot properly explain the strain state of our inclusions.

Post-entrapment plastic relaxation

The measured strains in all of the inclusions deviate from the strains expected for purely elastic behavior after entrapment and approximate those expected if the inclusions were under hydrostatic stress. The clustering of measured inclusion strains near isotropic conditions can be attributed to post-entrapment recovery of the deviatoric components that should be present if the behavior of the host-inclusion system was merely elastic and retained a stress and strain state that reflected only the original conditions of entrapment (green ellipses in Fig. 6). In this regard, the other process that can explain the deviations of our results from the numerical predictions is a post-entrapment plastic relaxation of the host-inclusion system (e.g., Carstens 1971).

As described above, the peak metamorphic conditions at 730–750 °C and ~ 4 GPa are followed by a large P drop and slight cooling to about 0.5 GPa and 600–650 °C within a time of about 3 Ma. The results of Zhong et al. (2020) suggest that partial or complete plastic relaxation of inclusion stresses can occur by viscous creep in the garnet for T above 650 °C within a range of time of 1 Ma. At lower temperatures, and certainly below 600 °C, the rate of viscous creep becomes so slow as to have negligible effects on inclusion pressures. Therefore, plastic relaxation of the host-inclusion system during exhumation to about 0.5 GPa and 600–650 °C would explain both the higher inclusion residual pressures (Fig. 5) and the tendency of all of our measured inclusions to exhibit strains and stresses that are closer to isotropic than expected for purely elastic behavior of the host-inclusion system (Fig. 6). In addition, zircon inclusions entrapped within some small pyrope garnet neoblasts (< 2 mm in size) in the SiO₂-rich whiteschists present similar features in terms of inclusion residual pressures and independent strain components (Supplementary materials). This is evidence in favor of the plastic-relaxation hypothesis. However, it is still difficult to understand why some P_inc values are significantly higher than 0.6 GPa, and why some zircon inclusions in the rims of the garnet megablasts retain the inclusion pressures (but not the strain state) indicative of original entrapment on the prograde path (Fig. 5b).

Previous studies using zircon-in-garnet host-inclusion thermobarometry, from higher-temperature geological settings (e.g., Zhong et al. 2019; Gilio et al. 2020b), reported good agreement between P–T conditions obtained by both zircon-in garnet inclusion and chemically based thermobarometric estimates. At this stage, it is not clear whether this agreement is due to the coincidence that the P–T paths of these rocks approximately follow an isomeke during exhumation (i.e., Zhong et al. 2019) or whether there are still unknown factors that can influence the elastic behavior of the garnet-zircon couple. Further studies are required to better understand these issues.

Conclusions

The reliability of chemical and elastic thermobarometry has been assessed in a detailed study from the well-known Dora-Maira UHP unit. Three garnet megablasts have been investigated in detail by combining major and trace element zoning of garnet and Zr trace element content in rutile inclusions to constrain the metamorphic conditions of garnet growth and, consequently, inclusion entrapment. Pseudosection modelling of garnet isopleths and Zr-in-rutile-inclusion thermometry suggest garnet formation at about 3–3.5 GPa and 675–720 °C. On the other hand, the elastic method returns zircon entrapment conditions within garnet at inconsistent P and T if the Zr-in-rutile thermometer or the garnet isopleths are combined with the zircon-in-garnet isomekes. In addition, the analyses of the residual strain components of zircon inclusions indicates, for most of them, an approximately isotropic strain state at room conditions that disagrees with the prediction of deviatoric strain expected from numerical models if the entrapment occurred at the conditions inferred from phase equilibria modelling.

The process that best explains our results is a plastic relaxation of the host garnet via dislocation creep (e.g., Zhong et al. 2020) that appears to operate in pyrope-rich garnets down to temperatures of about 600 °C. This interpretation of our data suggests that plastic relaxation in the garnet immediately adjacent to each inclusion is much faster than grain-scale chemical homogenization due to intra-crystalline diffusion, which is not expected to occur at such T conditions and similar timescales (Caddick et al. 2010). As a consequence, zircon-in-garnet thermo-barometry might be more successful for lower temperature metamorphism, where viscous relaxation is negligible and P–T estimation by classic equilibrium thermodynamics can be hampered by incomplete chemical equilibration at the rock scale (Lanari and Hermann 2021). Therefore, because of their complementary nature, the combination of chemical and elastic based thermobarometric estimates is a valuable tool to better characterize and gain detailed information from complex metamorphic paths covering a large evolution-T range where both plastic flow (at high T) and sluggish chemical diffusion (at low T) can be expected.