Abstract
Forty-one diamonds sourced from the Juina-5 kimberlite pipe in Southern Brazil, which contain optically identifiable inclusions, have been studied using an integrated approach. The diamonds contain <20 ppm nitrogen (N) that is fully aggregated as B centres. Internal structures in several diamonds revealed using cathodoluminescence (CL) are unlike those normally observed in lithospheric samples. The majority of the diamonds are composed of isotopically light carbon, and the collection has a unimodal distribution heavily skewed towards δ13C ~ −25 ‰. Individual diamonds can display large carbon isotope heterogeneity of up to ~15 ‰ and predominantly have isotopically lighter cores displaying blue CL, and heavier rims with green CL. The light carbon isotopic compositions are interpreted as evidence of diamond growth from abiotic organic carbon added to the oceanic crust during hydrothermal alteration. The bulk isotopic composition of the oceanic crust, carbonates plus organics, is equal to the composition of mantle carbon (−5 ‰), and we suggest that recycling/mixing of subducted material will replenish this reservoir over geological time. Several exposed, syngenetic inclusions have bulk compositions consistent with former eclogitic magnesium silicate perovskite, calcium silicate perovskite and NAL or CF phases that have re-equilibrated during their exhumation to the surface. There are multiple occurrences of majoritic garnet with pyroxene exsolution, coesite with and without kyanite exsolution, clinopyroxene, Fe or Fe-carbide and sulphide minerals alongside single occurrences of olivine and ferropericlase. As a group, the inclusions have eclogitic affinity and provide evidence for diamond formation at pressures extending to Earth’s deep transition zone and possibly the lower mantle. It is observed that the major element composition of inclusions and isotopic compositions of host Juina-5 diamonds are not correlated. The diamond and inclusion compositions are intimately related to subducted material and record a polybaric growth history across a depth interval stretching from the lower mantle to the base of the lithosphere. It is suggested that the interaction of slab-derived melts and mantle material combined with subsequent upward transport in channelised networks or a buoyant diapir explains the formation of Juina-5 diamonds. We conclude that these samples, despite originating at great mantle depths, do not provide direct information about the ambient mantle, instead, providing a snapshot of the Earth’s deep carbon cycle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Diamond is thought of as a rare mineral that usually forms in the lithospheric mantle between depths of 140 and 220 km. However, a small proportion (<5 %) of diamonds studied worldwide originated at much greater depths (Stachel 2001; Stachel et al. 2005), with some containing inclusions indicating their transport from up to 800 km depth (Harte 2010). These diamonds are of great geological importance, providing the only direct samples of the sub-lithospheric mantle, and they allow us to test models of the processes we believe are occurring in Earth’s deep interior.
Diamonds that originated in the asthenospheric upper mantle were first recognised by the occurrence of majoritic garnet in samples from the Monastery mine, South Africa (Moore and Gurney 1985). In the years following this original discovery examples of majorite as diamond-hosted inclusions have vastly increased, becoming both numerous and geographically widespread. Multiple samples have been identified in the Monastery (Moore and Gurney 1985; Moore et al. 1991) and Jagersfontein kimberlites of South Africa (Deines et al. 1991), Kankan in Guinea (Stachel et al. 2000a), alluvial deposits and kimberlites from the Juina district in Brazil (Wilding 1990; Harte 1992; Hutchinson 1997; Walter et al. 2008; Bulanova et al. 2010) alongside additional one-off finds in Russia (Sobolev 1977), Tanzania (Stachel et al. 1998), Canada (Davies et al. 2004) and other South African sources (Gurney et al. 1985). This population of majoritic garnets is dominated by samples with an eclogitic or pyroxenitic signature (indicated by low Cr2O3 and high CaO), an observation potentially explained by the majority of upper mantle diamond formation occurring within subducting assemblages (Stachel 2001).
The first suggestion that diamonds are also exhumed from the Earth’s lower mantle was made by Scott-Smith et al. (1984), who identified two ferropericlase inclusions and a single inclusion of enstatite in three separate diamonds from kimberlites near Orroorro in Australia. Similar observations were also made by Gurney in South African diamonds (unpublished, data in Scott-Smith et al. 1984). The lack of evidence that the inclusions were previously in chemical equilibrium with each other prevented the definitive identification of a lower mantle origin. It was the discovery of diamonds containing coexisting, but non-touching, inclusions of ferropericlase, MgSiO3 and CaSiO3 (Harte et al. 1999) that provided convincing evidence that some diamonds are exhumed from the lower mantle. As with majorite-bearing samples, the number of possible lower mantle diamond occurrences has grown since the initial discoveries, and examples are now recognised in South Africa (Moore et al. 1986), Guinea (Stachel et al. 2000b, 2002), Canada (Davies et al. 2004; Tappert et al. 2005), Australia (Tappert et al. 2009a, b) and Brazil, both from Machado river (Bulanova et al. 2008) and the Juina region (see below). However, in contrast to majorite-bearing diamonds, the number of definitively lower mantle diamonds remains small and most of the diamonds are associated with peridotitic material (Harte 2010; Kaminsky 2012).
Diamonds from multiple sources in the Juina region (Brazil), including both kimberlite pipes and alluvial deposits, have been extensively studied (Harte et al. 1999; Kaminsky et al. 2009, 2001; Hutchison et al. 2001; Hayman et al. 2005; Brenker et al. 2007; Walter et al. 2008, 2011; Bulanova et al. 2010; Araujo et al. 2013; Zedgenizov et al. 2014) as they commonly have been found to contain mineral inclusions of sub-lithospheric origin. In fact, more than half of all recognised lower mantle diamonds are from Juina sources (Harte 2010), which makes Juina a unique geological locality. Studies of alluvial Juina diamonds (Harte et al. 1999; Kaminsky et al. 2001; Hutchison et al. 2001; Hayman et al. 2005; Brenker et al. 2007) have revealed mineral inclusion assemblages associated with peridotitic material whilst the diamonds generally carry a “mantle-like” carbon isotope signature (i.e. δ13C ~ −5 ‰). Conversely, diamonds from the kimberlitic sources in the region (the Pandrea pipes, Aripuana-1, Collier-4 and Juina-5) have revealed superdeep inclusions that do not carry a clear mantle signature, but instead are related to a variety of high-pressure eclogitic, sedimentary and also peridotitic lithologies (Walter et al. 2008, 2011; Kaminsky et al. 2009; Bulanova et al. 2010; Zedgenizov et al. 2014).
In a recent study, Walter et al. (2011) presented data on six diamonds from the Juina-5 collection studied here in more detail. These samples were found to host composite mineral inclusions interpreted to have formed within the transition zone and/or lower mantle. What distinguished these inclusions from those in most previous studies was the recognition of lower mantle minerals associated with subducted oceanic crust, including former iron- and alumina-rich eclogitic magnesium silicate perovskite, calcium silicon–titanium perovskite and the very first natural examples of NAL-phase and CF-phase minerals. Prior to this, only a handful of diamonds had ever been discovered that contained mafic inclusions of possible lower mantle origin (Harte et al. 1999; Hayman et al. 2005; Bulanova et al. 2010).
We have investigated forty-one diamonds containing optically identifiable mineral inclusions from the Juina-5 kimberlite pipe. We will present: 234 carbon isotopic analyses of host diamonds measured by SIMS; detailed major element compositions of 35 mineral inclusions measured by EMPA and identification of additional coesite and sulphide inclusions that weren't chemically analysed; cathodoluminescence images that reveal original diamond growth structures; Raman spectroscopic data that confirm the current mineral structure of several studied inclusions; and FTIR measurements that provide the nitrogen contents of a subset of the diamonds. During the study of these samples, the trace element composition of the mineral inclusions was also determined using SIMS; however, these data and modelling thereof will be presented elsewhere (Thomson et al. in prep). Using the information presented in this paper, we construct a model that explains the genesis of the Juina-5 samples in the sub-lithospheric mantle from subducted material.
Sample description
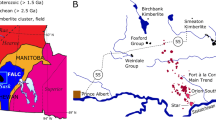
The Juina kimberlites are one of many NW–SE trending expressions of alkaline magmatism present in Brazil previously associated with the passage of the Trindade plume beneath the South American lithosphere (Gibson et al. 1995) during the Cretaceous period and have eruption ages of 92–95 Ma (Heaman et al. 1998). However, a recent study suggests that the location of this alkaline magmatism is outside the region of plume influence, whilst kimberlite compositions appear to have no link with the Trindade plume (Guarino et al. 2013). Alternatively, they may have been emplaced along pre-existing weaknesses in the South American lithosphere that were exploited during the formation of sedimentary basins associated with the opening of the Atlantic Ocean (Riccomini et al. 2005). The kimberlites are situated in Western Brazil, intruding into the granitoid gneisses of the Proterozoic Rio Negro–Juruena Mobile Belt, which itself was accreted onto the Amazon craton during the Proterozoic Eon as part of an island arc setting (Tassinari et al. 2000). The location of the Juina-5 pipe, the source of diamonds in this study, within this belt of alkaline magmatism is shown in Fig. 1.
Simplified geological map showing the location of the Juina region in south-west Brazil with the location of the Juina-5 kimberlite pipe, and previously studied Collier-4 kimberlite pipe, in the enlarged panel (after Araujo et al. 2013)
Diamonds selected for polishing range from <1 to ~3 mm in their longest dimension, are light brown or white in colour and are a mixture of octahedral, macle, docdecahedral or transitional forms. Most of the diamonds are frosted, coated with graphitic material or heavily etched with trigons. They are often highly resorbed, aggregates of multiple nuclei, or broken fragments of originally much larger diamonds. This combination of complex morphological features makes identification of the diamonds’ crystallographic axes for orientation during polishing non-trivial and also prevents polishing in certain directions. Many of the diamonds also contain cracks, both small internal features and some that extend throughout the diamond crystals to their external surfaces. Most of the diamonds studied contain abundant small inclusions. The combination of all these features makes these samples rather opaque to transmitted light, and there are usually few clear paths through the diamonds to allow inclusion identification with optical or spectroscopic methods prior to polishing.
All mineral inclusions reported are thought to be primary and either syngenetic or protogenetic with diamond growth as they have the imposed shape of negative diamond inclusions and are located away from any cracks connected with diamond surfaces. They are often associated with local internal cracks sometimes highlighted by dark material that is assumed to be graphite, which likely formed due to inclusion expansion during exhumation. Diamonds were polished on dodecahedral, cubic or slightly inclined to octahedral lattice planes using a jeweller’s polishing wheel at the University of Bristol until one or more mineral inclusions were partially exposed at the sample surface. Any remnant pressure contained by the inclusion/diamond pairs is released, sometimes causing local cracks to propagate from the inclusion during the polishing procedure. This approach provides a flat surface allowing the growth features of the surrounding diamond to be investigated using luminescence techniques and the isotopic composition of the diamonds to be measured using secondary ion mass spectrometry (SIMS). The exposed inclusions only represent a small fraction of the total number of inclusions in each diamond; most of the samples have many more inclusions that remain unstudied. Finally, Raman spectroscopy was employed (where possible) to determine the current crystal structure of retrograde mineralogical assemblies that result from re-equilibration of primary, high-pressure mineral inclusions, and FTIR spectroscopy was used to determine the nitrogen content and speciation of the host diamonds.
Analytical methods
CL, SEM and EMPA analysis
The cathodoluminescence (CL) response of the polished samples was recorded using a monochrome CL detector attached to a Hitachi S-3500 N scanning electron microscope (SEM) at the University of Bristol. An accelerating voltage between 5 and 15 kV and a beam current of ~5 nA were used. The CL response of diamonds is controlled by the concentration of various defects incorporated into the diamond lattice during growth, thus providing vital information about each sample’s growth history. Diamonds were also later photographed under an optical CL microscope at the University of Edinburgh (20 kv and 12 nA), allowing the true colours of CL response in the Juina-5 diamonds to be recorded.
Mineral inclusions were identified using the EDAX Genesis energy-dispersive spectrometer attached to the SEM in Bristol and imaged in backscatter electron mode (BSE). Subsequently, the major element compositions of silicate inclusions were determined by electron microprobe analysis (EMPA) and also performed at the University of Bristol using a Cameca SX100. Operating conditions were either 15 kV and 10 nA or 20 kV and 10 nA with calibration of counts for all elements achieved using a combination of silicate, oxide and metal standard materials. A beam size of ~1 µm was used for analysing single-phase mineral inclusions and individual components of composite inclusions. The bulk composition of composite inclusions was measured using a defocussed electron beam of variable size, up to ~30 µm, such that the entire inclusion was enclosed in the analysis beam. When using a defocussed beam, EMPA totals are always lower than 100 %, due to overlap of the electron beam with the diamond host, and therefore have been renormalised. An additional method of estimating bulk compositions using an image analysis technique, whereby the compositions of component phases were added in the proportions revealed by BSE images, was used for inclusions too large for defocussed beam analysis. Estimating inclusion bulk compositions of diamond inclusions in this way has previously been employed in a number of studies (Harte and Cayzer 2007; Walter et al. 2008, 2011; Bulanova et al. 2010). However, they are not ideal because (1) there is an implied assumption that the modal mineralogy of the two-dimensional section is representative of the whole three-dimensional inclusion and (2) the conversion of X-ray count rates into chemical compositions makes assumptions that are not strictly valid. However, they are by far the best of all commonly available techniques for analysing samples of this rarity and complexity. As the inclusions are so small, the penetration depth of the electrons and the depth from which X-rays can escape are significant compared with the size of the inclusions, mitigating problem (1) to some extent. Other reasons to have confidence in our bulk inclusion compositions include the observations that both methods of analysis provide similar results for a given inclusion, that measured compositions of different inclusions of each type are fairly consistent and that all results correspond closely to the compositions of synthetic, homogeneous phases from high-pressure experiments.
Secondary ionisation mass spectrometry analyses
The carbon isotopic composition of host diamonds was measured using the Cameca IMS-1270 instrument at the Edinburgh Ion Microprobe Facility (EIMF). The diamonds were pressed into indium mounts and gold coated to create a flat and conductive surface for analysis. A primary beam of 133Cs+ ions at 6 nA was used to extract carbon isotopes at 10 kV, which were counted using dual Faraday cups. Beam size at the surface was approximately 15–20 µm. Each analysis involved a pre-sputtering time of 40 s followed by 10 counting cycles lasting a total of 40 s. To correct for instrumental mass fractionation, counts were normalised to a synthetic diamond standard (either SYNAL or SYNAT, both of δ13C −23.92 ‰ PDB) that was mounted in the same indium mount as unknowns. Standard analyses were conducted 5–10 times every 50–60 min throughout analysis sessions to monitor instrumental drift. All observed drift was <±1 ‰ (δ13C) per day and was removed using linear or quadratic functions. Analysis precision is estimated using repeated standard measurements at δ13C ± 0.22 ‰ PDB over all 3 days of analysis from 151 standard measurements. Full details of standard analyses are presented alongside all measurements in the supplementary tables. Carbon isotope analyses were combined with CL imagery to allow the variation of isotopic composition with diamond growth to be evaluated.
Raman spectroscopy
After the gold coating was removed from samples, Raman spectroscopy was used to verify the crystal structure of exposed inclusions. This information can confirm complete pressure release during polishing and be used in future studies that investigate the retrograde phase transformations that occur during inclusion exhumation. Analyses were made with a Thermo Scientific DXR Raman microscope using a 532-nm laser operating at 3–8 mW and a 50 × LWD lens. This was successful except in some cases where inclusions had already undergone trace element analysis using SIMS (Thomson et al. in prep) and no undamaged material remained.
FTIR spectroscopy
Fourier transform infrared spectroscopy (FTIR) was used to assess the nitrogen content and speciation in the Juina-5 diamonds. Preliminary work (in 2009) on 57 unpolished Juina-5 diamonds was performed using a SpectraTech infrared microscope coupled to a Nicolet Nexus Fourier transform infrared spectrometer at the University of Bristol. It was particularly difficult to obtain good quality spectra for these samples because of the presence of abundant cracks and inclusions and the presence of a partial graphite coat covering much of the sample surface. The detection limits on these analyses were therefore likely to be greater than 20 ppm nitrogen. Subsequently, as described above, many of the diamonds were polished to expose inclusions and became more suitable for FTIR analysis. Furthermore, an improved FTIR system, a Thermo iN10MX, was installed at the University of Bristol. Therefore, a selection of the Juina-5 diamonds was re-analysed using a 100 µm aperture, 128 scans and 2 cm−1 spectral resolution. For these spectra, the detection limit for N is <5 ppm. Even for samples with exposed inclusions and using the superior instrument, it was still not possible to obtain spectra for all samples. It was not possible to produce the double polished plates that would have been ideal for FTIR because (1) it is difficult to polish specific directions in these diamonds with complex internal morphologies, and (2) this process would have caused the loss of valuable inclusions.
Results
Internal diamond morphology
Monochrome CL imagery collected from the Juina-5 diamonds demonstrates that several diamonds display weak but distinctive octahedral zonation. This growth habit is accompanied by evidence of slight resorption in the occurrence of alternating light and dark bands orientated perpendicular to growth direction and the rounded corners of internal octahedral growth zones (Bulanova, 1995), features most obvious in Fig. 2b, e. Concentric octahedral growth zones are not entirely continuous and often vary in width (Fig. 2d, e). Some of these zoned samples have nuclei, usually not optically visible, around which the remaining diamond has formed (Fig. 2b, d). These cores are small (<500 µm) and have euhedral shapes that are clearly defined from the surrounding diamond by sharp boundaries and different responses in CL. For example, diamond Ju5-115 (Fig. 2d) possesses a core with sectorial structure, defining a cubo-octahedral habit, with a much brighter CL response than the surrounding diamond. The diamond surrounding this core has octahedral growth, which is complicated by plastic deformation and dislocated diamond blocks. In contrast, a large number of the Juina-5 diamonds possess no evidence of octahedral zonation and, instead, are irregular and display blocky structures (e.g. Fig. 2a, c, f). Evidence of the severe stresses that these diamonds have undergone during solid-state transport in the mantle is also preserved in the CL. Some diamonds are only small fragments of originally much larger crystals; the zonation in Ju5-104 (Fig. 2c) shows that it is now only a fragment of the peripheral part of the original diamond. Other samples have textures akin to breccias, with patchy CL caused by stress and are macles (twinned crystals). These features are typical for sub-lithospheric diamonds (Hutchison 1997; Gaspar et al. 1998; Hayman et al. 2005; Kaminsky et al. 2001; Bulanova et al. 2010) and can often be used to distinguish them from their lithospheric counterparts. In common with many sub-lithospheric diamonds, the Juina-5 samples have been affected by plastic deformation and the development of cracks and intensive selective etching after growth was complete (evidence of plastic deformation is clearly visible in Fig. 2f).
CL images of six Juina-5 diamonds with the carbon isotopic analyses locations (marked with white dots) and δ13C compositions: a irregular diamond with curved growth zones (Ju5-21); b octahedral zonation with rounded (dissolved) corners in the elongated diamond with plastic deformation (Ju5-52); c a peripheral fragment of broken octahedron (Ju5-104) and d octahedral crystal with sectorial cubo-octahedral core growth structure, followed by octahedral zonation (Ju5-115); e blocky octahedral core followed by regular octahedral zonation with rounded resorbed corners and uneven colours of CL inside of the single zones (Ju5-71); and f macled octahedron with blocky irregular internal structure and plastic deformation (Ju5-83)
Alongside the variety of internal structures, the variation in CL response colour has also been documented. All samples are a deep blue colour throughout their core regions (supplementary Figure 1), which is usually explained by the presence of N3-aggregated nitrogen centres (Bruce et al. 2011). The rims of many samples have a bright green CL colour. An explanation for this green response is unknown; however, a similar CL colour was observed in type IaAB and IaB Rio Soriso diamonds (Hayman et al. 2005). Some samples also display a third CL colour, a very intense light blue colour.
Carbon isotope composition
The carbon isotope composition of thirty-five diamonds was measured at two or more locations within each diamond; a total of 234 analyses were performed. Diamonds with distinctive zonation from core to rim, identified using CL images, were analysed using more detailed traverses to reveal the variation of isotopic composition throughout diamond growth.
The average and the range of carbon isotopic composition observed in each diamond is reported in Table 1, and a full list of all analyses is presented in supplementary Table 1. Care should be taken when directly comparing these carbon isotopic measurements with previous studies especially where only a single value for each diamond was achieved by combustion analysis (see Mikhail et al. 2014b). Isotopic compositions range from −28.4 to −3.6 ‰ (rel. to PDB) across all the individual spot analyses (Fig. 3), encompassing the majority of the worldwide diamond population (~+5 to −40 ‰, Cartigny 2005) and similar to the ranges observed from other kimberlite sources in the Juina region (Kaminsky et al. 2009; Bulanova et al. 2010, Araujo et al. 2013). The majority of the Juina-5 diamonds are δ13C-depleted when compared with mantle carbon value (−5 ‰). Only three diamonds have mantle compositions (−5 ± 3 ‰) whilst twenty-seven samples have compositions lighter than −20 ‰. Five diamonds could be described as having an intermediate composition.
A plot of all the carbon isotope analyses completed as part of this study. The histogram shows the number of measurements taken in each isotopic bracket, with the ‘normal mantle’ range (Cartigny 2005) marked as a grey bar at −5 ‰. The bar chart shows the range of carbon isotope compositions measured within each individual diamond (grey bars). The black vertical ticks within these bars mark the compositions of the individual analyses. The letters ‘C’ and ‘R’ positioned at either end of some grey bars define the direction of isotopic evolution from the core to rim of that diamond, where this is possible
It is observed that many individual diamonds show large δ13C variation from core to rim, with differences of 0.2–14.9 ‰ between measurements within a single sample (Figs. 2, 3). The significance of these variations will be discussed below.
Nitrogen content and speciation
Preliminary FTIR work conducted on the SpectraTech instrument in 2009 concluded that all of the diamonds further studied here had undetectable nitrogen contents and were classified as type II. The new analyses conducted using the Thermo iN10MX found that all measured samples contained a small quantity of nitrogen that was below detection limits of the older system.
The five samples studied were found to possess between 6.5 ± 3 and 17.5 ± 3 ppm total nitrogen entirely aggregated to the B form. This content was estimated from the size of the 1,331 cm−1 B peak relative to the adjacent portion of the baseline. There was no apparent contribution from A-aggregated nitrogen. No platelet peak was observed in any samples. Therefore, the Juina-5 diamonds are fully aggregated IaB diamonds, or if the definition of type II is taken as <20 ppm total nitrogen, they would be classified as type II diamonds.
An estimate of the minimum mantle residence temperature is made using the measured nitrogen contents and aggregation states. In our calculation, we assume that the mantle residence time is ~10 million years, based on the age of a calcium perovskite inclusion in a diamond from the nearby Collier-4 kimberlite and its associated eruption age (Bulanova et al. 2010). We estimate that there could be up to 5 % A-aggregated nitrogen present without detection. Employing these values in the calculation provides a minimum temperature estimate for diamond storage of 1,534 °C for 6.5 ppm nitrogen and 1,495 °C for 17.5 ppm nitrogen (using Taylor et al., 1990). These minimum temperature estimates drop to 1,446 and 1,411 °C, respectively, if a storage time of 100 Ma is used instead of 10 Ma. These high temperatures are consistent with the complete platelet degradation that is observed.
Mineral inclusion compositions
Exposed mineral inclusions range in size from 5 to 50 µm in their longest dimension and are a mixture of single-phase minerals and composite inclusions (see BSE images in Fig. 4). All inclusions reported are assumed to be primary, i.e. they formed prior to or during diamond growth. The composite inclusions are interpreted as the remnants of what were originally high-pressure mineral phases that have unmixed during uplift in the mantle (Walter et al. 2008, 2011; Bulanova et al. 2010). Thus, the measurement of the bulk compositions of all inclusions is critical to the interpretation of where and how the Juina-5 diamonds formed.
Greyscale backscatter electron images of a subset of the inclusions analysed in this study. Component phases are labelled with their mineralogy: sp spinel, opx orthopyroxene, TAPP tetragonal almandine pyrope phase; ky kyanite, coes coesite, kal kalsilite, MgPv magnesium perovskite, maj majorite, cpx clinopyroxene, neph nepheline, sul sulphide. The white bar in each image is a 10-µm scale bar. a MgPv in Ju5-117, b former stishovite in Ju5-90, c former NAL phase in Ju5-42, d CaSiO3 with ZrO2 exsolution in Ju5-52, e Ca(Si,Ti)O3 in Ju5-82, f MgPv in Ju5-31, g majorite in Ju5-32, h former NAL phase in Ju5-84, i three adjacent unmixed calcium perovskite inclusions in Ju5-115, j MgPv in Ju5-102, k majorite in Ju5-83 and l cpx surrounded by Fe/Fe-carbide microinclusions in Ju5-71
The exposed mineral inclusions are described in the following sections, with the samples grouped according to their chemistry and composite/single-phase nature. Table 1 documents which inclusions have been exposed in which diamond so a comparison of diamond and inclusion features can be made. Chemical compositions of inclusions are provided in Tables 2, 3, 4, 5 and 6. BSE images of some inclusions are shown in Fig. 4. It is worth reiterating that the documented inclusions do not account for all the inclusions within each diamond; in many samples, there are several more inclusions that remain unstudied.
Magnesium- and iron-rich composite silicate inclusions
Six silicate mineral inclusions that are rich in magnesium and iron have been identified in five Juina-5 diamonds. Four of the inclusions are composed of well-defined coexisting mineral phases, large enough to allow individual analysis (e.g. Fig. 4a, j). In all four cases, the coexisting phases are a combination of at least one mineral with pyroxene or TAPP stoichiometry (similar to that in Bulanova et al. 2010) and grains of spinel and/or ilmenite. Raman spectra of two of these inclusions (Ju5-102 and Ju5-117a) confirmed the presence of a TAPP-structured component (the Raman spectra of a TAPP grain from São Luiz was used as comparison; Nestola et al. in prep). Alongside, the TAPP component in Ju5-117a orthopyroxene was also identified using Raman, as in inclusions Ju5-43 and Ju5-47 (Walter et al. 2011), and multiple microinclusions (<2 µm) of magnesite were observed in the diamond surrounding inclusion Ju5-117a (Fig. 5).
In the two remaining inclusions, it was not possible to analyse the separate phases by EMPA as they are too small; thus, only a large defocussed beam was used to achieve a bulk composition for the entire inclusion. Summarising the results, the six inclusions have similar bulk compositions with magnesium numbers of between 43 and 66 mol%, high titanium contents (~4–7 wt% TiO2) and essentially no calcium or alkalis (Table 2). These six similar inclusions are thought to represent former eclogitic magnesium silicate perovskites (MgPv) that have been exhumed from within the lower mantle and undergone retrograde reactions (after Walter et al. 2011). It can be seen that their compositions are very similar to experimental eclogitic MgPvs (see Table 2; Fig. 6). The bulk compositions of the inclusions are also similar to those of garnet minerals; however, as they contain no calcium and, except possibly Ju5-47, possess no majorite component, it appears unlikely that they represent the retrograde products of garnet. Thus, the preferred hypothesis (as proposed by Walter et al. 2011) is that the inclusions correspond to the retrograde reaction products of magnesium silicate perovskite exhumed from the lower mantle.
Ternary diagram plotting the compositions of the seven magnesium-rich inclusions reported in Table 2 each shown as a pair of closed or open circles connected with a tie line. The end nearest to the Fe3+ apex calculates the elemental composition assuming 100 % of the measured iron is ferric (Fe3+), whilst the other end calculates the composition assuming all iron is ferrous (Fe2+). The true composition of each inclusion will lie somewhere on the tie line between the two end members. Also plotted are the fields of experimental magnesium perovskites in both peridotitic and eclogitic systems and also calculated as 100 % ferric and ferrous iron, respectively (labelled grey fields). The two possible substitution vectors that could occur in magnesium silicate perovskite minerals are plotted as arrows, the grey field between defines the possible limits of magnesium perovskite stability
The analysed totals of these inclusions, when converted to elemental concentrations per oxygen atom, have noticeable cation excesses for a perovskite structure. This could result from the oxygen vacancy substitution mechanism, experimentally shown to occur in Fe3+-bearing perovskite (Hummer and Fei 2012). These high cation totals make it impossible to estimate the ferric and ferrous iron contents of the inclusions using a cation assignment mechanism. Experiments, and other diamond-hosted MgPv samples, suggest that a large proportion of the total iron contents in these inclusions will be in the form of ferric iron (>50 wt%, McCammon et al. 1997; Frost and McCammon 2008). However, as an accurate assessment of this ratio is not possible, the composition of the inclusions in Fig. 6 is plotted as two end members, both 100 % ferric and 100 % ferrous iron, joined with tie lines. The true compositions of each inclusion must lie between these end members. It can be seen that all six inclusions have bulk compositions that straddle the fields of experimental magnesium perovskite.
Alumina- and alkali-rich composite inclusions
Eight composite inclusions with aluminium and alkali-rich bulk compositions have been exposed and analysed in the Juina-5 collection. All consist of a binary mixture of an exsolved spinel mineral (containing the Mg and Fe components) coexisting with nepheline, kalsilite and/or clinopyroxene (containing the alkali and silica components; see Fig. 4c, h). All eight inclusions are very small (<10 µm in their longest dimension). The presence of nepheline and clinopyroxene alongside spinel was confirmed by Raman spectroscopy in diamonds Ju5-89 and Ju5-20, respectively (Walter et al. 2011). Unfortunately, SIMS analysis extensively damaged all exposed inclusions preventing the identification of component mineral phases in the remaining samples using Raman. Their compositions are reported in Table 3 and plotted in Fig. 7. An estimate of Fe3+ content has been achieved using either cation assignment or charge balance and is incorporated in Table 3.
Part of a ternary diagram displaying the compositions of the alkali-rich composite inclusions (Table 3) thought to originally be high-pressure minerals. Open circles are assigned as CF phase, closed circles as NAL phase based on the potassium content of the inclusions. The limits of CF- and NAL-phase compositions observed in experiments on natural systems are shown as light and dark regions, respectively (Irifune and Ringwood 1993; Kesson et al. 1994; Miyajima et al. 2001; Hirose and Fei 2002; Litasov and Ohtani 2004, 2005; Hirose et al. 2005; Ricolleau et al. 2008). The inset compares these stability fields and inclusion compositions with the extent of NAL and CF solid solutions in the system NaAlSiO4–MgAl2O4 at 25 GPa (Imada et al. 2011). The ideal composition of NAL is marked as a white star
All eight inclusions are interpreted to represent former NAL- or CF-phase minerals exhumed from the transition zone or lower mantle (as in Walter et al. 2011), but distinguishing between the two original phases on the basis of inclusion bulk chemistry is not trivial. NAL phase is generally described as having a structure based on a stoichiometry close to AB2[Al,Si]6O12 (Gasparik et al. 2000; Kojitani et al. 2011) where alkalis and calcium partition onto the A site. CF phase has a similar stoichiometry of A3[Al,Si]6O12, where A can be occupied by univalent or divalent cations (Ono et al. 2009; Kato et al. 2013). Thus, compositions such as NaMg2Al5SiO12 can exist in either NAL or CF structures depending on pressure and temperature (Imada et al. 2011). The details of phase equilibria involving the two phases are not fully understood, but identification of the stable phases in experiments on basaltic compositions, and systematic studies of phase relations in simple systems give some clues as to the likely compositional ranges in shallow lower mantle. Firstly, in experiments on natural basaltic compositions containing potassium, CF has very low K concentrations and NAL has higher K concentrations. Thus, our primary criterion for distinguishing the two phases is that CF has <0.1 wt% K and NAL has >0.1 wt% K. Using this criterion, NAL inclusions are shown as solid symbols and CF are open symbols in Fig. 7. Data in Kato et al. (2013) provide a qualitative explanation for K concentrations of the two phases. They show that in the system NaMg2Al4.8Si1.15O12–KMg2Al4.8Si1.15O12 at 2,400 K, between approximately 30 and 50 GPa, there is a range of bulk compositions where K-free CF and K-bearing NAL coexist. Furthermore for bulk compositions with greater than 10 mol% of the K end member component, only NAL would be stable at pressures up to 60 GPa. The second criterion used to distinguish CF from NAL involves the (Na + K + Ca)/(Mg + Fe) ratio of each inclusion. In Fig. 7, the inclusions’ compositions are compared with fields for CF and NAL minerals from experiments on basaltic and haplobasaltic compositions. Even though we have discriminated on the basis of K concentration, most of the inclusions we classified as NAL fall close to the NAL field on this projection; Ju5-20, classified as CF, falls within the CF field. Ju5-105, classified as CF, falls away from either field. This is most probably because the measured composition of the exposed plane is not representative of the bulk inclusions (see “Analytical methods”). It should be also noted (see the inset in Fig. 7) that the NAL field and most of the inclusions fall close to the ideal NAL composition with a ratio of 1:2:6 for (Na + K):(Mg + Fe):(Si + Al). They are also close to the composition of NAL in the system NaAlSiO4–MgAl2O4 (Imada et al. 2011). The compositions of CF and NAL at 25 GPa from the Imada et al. (2011) study are also shown in the inset. There is an offset between compositions of the Ju5 inclusions and the phase relations in the simple system studied by Imada et al. (2011) (presumably related to the effect of other solid solutions on the phase equilibria), but comparison of the two systems suggests that the gap between the composition of Ju5-20 CF and the most alkali-rich NAL inclusions could represent the extent of the 2 phase field, and the whole range in NAL inclusion compositions could represent solid solution within the one phase NAL field.
Calcium-, silicon- and titanium-rich composite inclusions
Calcium-rich inclusions with a perovskite stoichiometry (ABO3) have been exposed in four diamonds (eight inclusions in total). Their compositions are reported in Table 4 and plotted in Fig. 8. Four of these inclusions appear to be almost pure CaSiO3 minerals, whereas the other four are composite CaSi- and CaTi-rich inclusions similar to those previously reported in Brenker et al. (2005, 2007), Hayman et al. (2005), Walter et al. (2008) and Bulanova et al. (2010) as retrograde products of transition zone or lower mantle minerals. In two of the inclusions exposed during our study, there are also observable phases rich in Zr within the inclusions (Ju5-52 and Ju5-115(b); see Fig. 4d, i). Raman spectroscopy has identified that these inclusions are a mixture of walstromite-structured CaSiO3 (Ju5-52(b), Ju5-82, Ju5-115(b) and Ju5-115(c)) and perovskite-structured CaTiO3 (Ju5-82 and Ju5-115(b)). The Zr-rich portion of Ju5-115(b) has a Raman spectra that remains unassigned to any mineral structure, but it is chemically almost 100 % ZrO2 and thought to be baddeleyite.
Ternary diagram, adapted from Walter et al. (2008) and Armstrong et al. (2012) showing the perovskite-phase relations in the system CMST. The grey field represents the miscibility gap between calcium and magnesium perovskite at 30 GPa; any bulk composition lying in this field, i.e. peridotite (black star) or eclogite (white star), will contain two perovskite phases with compositions lying on the edge of this field (e.g. small white symbols). The dashed line shows the effect of pressure on the miscibility gap. The compositions of calcium perovskite inclusions observed (this study) are plotted as grey circles and inverted triangles. Majorite inclusions are plotted as grey squares. The black circle and square joined with a tie line are the compositions of experimental phases coexisting with a carbonated melt at transition zone pressure (Walter et al. 2008)
Exsolved majoritic garnet inclusions
Majoritic garnets have been exposed in two diamonds. Both consist of a majorite core with an exsolved Na-rich pyroxene rim (both phases confirmed using Raman). These are in textural equilibrium with no fine-scale exsolution, similar to those observed by Harte and Cayzer (2007). Their compositions are reported in Table 5 and are plotted in relation to the calcium perovskite inclusions in Fig. 8. Both inclusions have ~1.1 wt% Na2O and low Cr2O3 (<0.2 wt%) and so are classified as eclogitic or pyroxenitic according to the scheme of Grütter et al. (2004).
SiO2 inclusions
Nine SiO2 inclusions have been exposed in the Juina-5 diamonds investigated in this study. Raman spectroscopy has been used to confirm that the inclusions currently have the coesite structure. Two of the inclusions have visible exsolution of kyanite from the SiO2 component on the exposed surface (Ju5-43 and Ju5-90), although that in Ju5-43 is too small for EMPA analysis. It is experimentally known that stishovite can have a significant aluminium component (e.g. Pawley et al. 1993). Therefore, we conclude that these two, and possibly all nine, coesite minerals represent the retrograde products of exhumed stishovite.
Other silicate inclusions
Aside from the inclusions already described, three pyroxene minerals, a garnet, an olivine and two unassigned composite inclusions (CAS + kyanite and spinel + orthopyroxene), have been exposed. Their compositions are reported in Table 6. The three pyroxene minerals have varying compositions; however, a high sodium content in two of them might suggest that they originate from a basaltic protolith. The olivine inclusion has a magnesium number of 90 mol%, which is normal for a mantle olivine mineral. The significance of the CAS plus kyanite inclusion is unknown, but it is noted that CAS phase is observed on eclogitic and sediment experiments at transition zone pressures (Litasov and Ohtani 2010; Grassi and Schmidt 2011). Another composite inclusion in Ju5-13 diamond (opx + spinel) might be a non-representative section of a further retrograde magnesium silicate perovskite mineral. The compositions of the mineral phases currently exposed in Ju5-13 are very similar to those in the other MgPv inclusions.
Iron, ferropericlase and sulphide inclusions
There are also two diamonds with native iron (or iron carbide) inclusions as well as a single inclusion of ferropericlase (Mg# = 83 %; Table 6) exposed. The ferropericlase contains ~1 wt% Na2O, a feature commonly observed in diamond-hosted inclusions of this type (Brey et al. 2004).
Eight iron sulphide inclusions have been exposed in the Juina-5 collection and identified using SEM techniques. EDS analysis suggests that these all have a FeS2 stoichiometry and therefore are of eclogitic affinity (Yefimova et al. 1983).
Discussion
Insights into the nature of diamond growth
The octahedral zonation preserved in many of the Juina-5 samples, especially in the core regions, demonstrates that these samples grew by a mechanism similar to that of lithospheric diamonds. This zonation structure is created by tangential (layer by layer) growth from a fluid or melt with very low degrees of carbon supersaturation (Sunagawa 1984; Bulanova 1995) that allows even growth on all crystal faces. Growth rates in this regime are slow, with the delivery of carbon unimpeded to the growing crystal, possibly in a surrounding fluid.
In sharp contrast with these ‘normal’ samples are those that fundamentally differ from lithospheric diamonds, containing irregular internal structures, evidence of growth during deformation, breakages and abundant twinning. All of these features are likely to have occurred simultaneous with growth and indicate that the diamonds formed from fluids or melts with high degrees of supersaturation in space-restricted environments and at faster growth rates than commonly experienced by lithospheric samples. The externally distorted, elongated shapes and dominance of macles in the Juina-5 diamonds serve as further evidence of rapid growth on selective crystal faces caused by a space-restricted regime and pulsating carbon-rich fluids. The internal structures of octahedrally zoned diamonds record a history of alternating incremental growth and resorption events with their alternating CL bands and rounded corners as described above. These CL features may also be diagnostic of growth from multiple pulses of infiltrating fluid (as in Smart et al. 2011). We can begin to test this hypothesis by studying the correlation between carbon isotope analyses and the changes observed in CL response; if, indeed, changes in CL represent influxes of new fluids, we would expect sharp changes to occur across these boundaries.
The CL image of Ju5-52 (Fig. 2b) reveals an inner core region with rounded resorbed edges that are surrounded by typically zoned diamond. The central core zone has an isotopic composition lying between −25.3 and −23.2 ‰. There is a well-defined compositional difference between this core zone and the surrounding diamond, which is isotopically heavier (−21.5 to −20.5 ‰). This sharp compositional discontinuity is much larger than the analytical uncertainty (~0.2 ‰) and provides strong evidence to support the interpretation based on CL features; an original core underwent resorption and was overgrown by diamond crystallising from a distinct new pulse of carbon-bearing fluid. If the isotopic evolution of the core region from its centre towards the diamond rims is studied in more detail, it is possible to discern further evidence for diamond growth for multiple pulses of fluid. It is known that if diamond grows from a single batch of fluid, it will evolve continuously in a single direction, depending on its redox state, as carbon is removed from the fluid (Deines 1980; Smart et al. 2011). The isotopic composition of Ju5-52 does not evolve continuously towards heavier or lighter values across either of the two fine-scale traverses of its core region (Fig. 2b). Rather the isotopic composition fluctuates between slightly heavier and lighter values, but enough that these variations cannot simply be within analytical uncertainties. Therefore, diamond Ju5-52 preserves evidence for a core region grown from either multiple small pulses of distinct fluid or a larger batch of fluid that was repeatedly replenished by pulses of chemically discrete fluids.
There is evidence for similar behaviour in other diamonds of the Juina-5 collection. Ju5-115 (shown in Fig. 2d) also displays isotopic variation towards heavier and lighter values across a core to rim traverse. Some of these variations are coincident with distinct changes in CL response. Using the same reasoning as above, it is concluded that these features are evidence of growth from multiple pulses of distinct fluids. However, Ju5-115 also displays sharp changes in CL response, from the bright cubo-octahedral core region into surrounding growth, which is not associated with any change in isotopic composition. Diamond Ju5-71 (Fig. 2e) is a third example displaying similar features that are diagnostic of growth from multiple fluids. There are further diamonds in the collection that display these features, and we suggest that the majority of the Juina-5 diamonds formed from chemically changing fluids during multiple growth events.
Whilst several of the diamonds display fine-scale isotopic oscillations of both positive and negative sense along traverses perpendicular to growth directions, a general trend has been identified whereby the core of each diamond is isotopically lighter than the rim material (see Fig. 3). This is coupled with the observation of a change from dark blue CL colour in the core of samples to green response at the rims (supplementary material). This evolution from light to heavy isotopic composition echoes the observations made by Bulanova et al. (2010) and Zedgenizov et al. (2014) in superdeep diamonds from Collier-4 and São Luiz, respectively. This general feature of superdeep diamonds could be result of progressively increased mixing of slab and mantle carbon as diamond growth continues.
Additionally, we are able to place some constraint on the fO2 of diamond growth from the observation of magnesite inclusions surrounding Ju5-117 (a), which was also observed in São Luiz diamonds (Zedgenizov et al. 2014). Stagno et al. (2011) experimentally determined that the equilibrium between MgCO3 and diamond is located between one and two log units above the IW buffer across mantle pressures. This oxygen fugacity is also consistent with diamond growth during mixing of ambient mantle and oxidised slab materials, see below.
Subducted source of isotopically light carbon
Many studies of natural diamonds have used carbon and nitrogen isotopic compositions to determine the source of diamond-forming material and to model the type of the processes involved in diamond formation (Boyd et al. 1987; Cartigny et al. 1998; Mikhail et al. 2013; Palot et al. 2012; Thomassot et al. 2007). It is widely believed that the mantle has a relatively uniform carbon isotopic composition of δ13C = −5 ‰, a composition reflected in the worldwide diamond population (Cartigny 2005). Diamonds with an isotopic composition that varies from this value resulted from sampling either a primordial or recycled reservoir in the mantle or isotopically fractionated mantle carbon.
It is apparent that Juina-5 diamonds do not reflect a mantle carbon reservoir of −5 ‰, unlike the global distribution of peridotitic diamond samples (Cartigny 2005). There have been several previous studies of diamonds where similarly isotopically light diamonds have been identified (Cartigny et al. 1998; Stachel 2001; Bulanova et al. 2010; Smart et al. 2011; Walter et al. 2011; Schulze et al. 2013). However, a single unified explanation for the wide range of carbon isotopic compositions seen in non-peridotitic diamonds remains contentious.
One explanation for the origin of diamonds with a light carbon isotopic composition is that they sample a primordial reservoir (e.g. Thomassot et al. 2007; Palot et al. 2012). As mantle convection should be an efficient mixing mechanism (Kellogg 1992) and carbon residence time in the mantle is estimated to be significantly <4 Ga (Dasgupta and Hirschmann 2010), preservation of a primordial reservoir is hard to explain. One potential location for the storage and preservation of an ancient isotopic reservoir might be in the deepest parts of the mantle (e.g. the D`` layer). However, there is little evidence that suggests that Juina-5 samples or other isotopically depleted diamonds are related to material from such great depths. Therefore, we do not favour primordial carbon isotope heterogeneities as a suitable mechanism for explaining the light carbon isotopic composition of the Juina-5 diamonds.
A second mechanism explaining the generation of isotopically light diamonds is the isotopic fractionation of mantle carbon. Isotopic fractionation of carbon could occur during many mantle processes, e.g. melting of subducted material, crystallisation of low-degree melts and the reduction of carbonate to diamond or graphite. However, experimental studies of isotopic fractionations are limited to ~4 ‰ in between carbon species in closed systems at 1,000 °C (Bottinga 1969; Deines 1980). A recent study of isotopic fraction between iron carbide and diamond in natural samples observed a fractionation of 7.2 ‰ (Mikhail et al. 2014a), however, in the wrong sense to explain light diamond formation from mantle material. Increasing temperature would reduce fractionation, and the effects of pressure remain mostly unconstrained. Open-system processes are perhaps more realistic reflections of natural processes and provide the potential for much larger isotopic fractionations to occur. Smart et al. (2011) considered two situations where Rayleigh-type fractionation may cause large isotopic fractionation during diamond formation by using numerical modelling: (1) fractionation during direct diamond precipitation from a fluid/melt and (2) fractionation related to the source fluid/melt prior to diamond formation (model of Cartigny et al. 2001). They concluded in both scenarios that only minute quantities of isotopically light carbon could be produced if fractionating from mantle material. Thus, isotopic fractionation, based on current knowledge, is not our favoured mechanism to explain the composition of isotopically light diamonds.
The third explanation, that recently appears to have become more widely accepted, is that isotopically light diamonds are formed from recycled material (Sobolev and Sobolev 1980; Bulanova et al. 2010; Smart et al. 2011; Schulze et al. 2013; Ickert et al. 2013). It is known that many sediments possess the correct isotopic characteristics to account for the δ13C compositions observed in diamonds; marine carbonates have δ13C ~ 0 ‰, and organic carbon-rich sediments have δ13C ~ −25 ‰ (Schidlowski 2001; Eigenbrode and Freeman 2006). However, it is not entirely clear whether sedimentary materials can survive sub-arc processes (i.e. dehydration and potential melting at depths <150 km), and whether they will be lost due to gravitational instability during initial subduction. We therefore explore a source of carbon trapped deeper within subducting assemblages and hence less likely to be removed during subduction.
The distribution of carbon-bearing compounds through the oceanic crust is controlled by hydrothermal alteration at the mid-ocean ridge and subsequent interaction with seawater and sedimentary material. The resulting distribution of carbon in the oceanic crust can be determined by studying drill cores retrieved from sections of the ocean-floor.
ODP hole 1256D makes the perfect case study to investigate the speciation and isotopic composition of material added during hydrothermal alteration at the ridge axis. The drill core is located on the eastern flank of the East Pacific Rise and provides a 1,500-m section of 15-million-year-old (i.e. young) oceanic crust belonging to the Cocos plate (Teagle et al. 2006). The carbon inventory of this section is dominated by abiotic organic carbon species (elemental carbon and hydrocarbon chains) over wide depth intervals in concentrations ranging up to ~2,500 ppm (Shilobreeva et al. 2011). This organic carbon cargo is attributed to the interaction of volcanic gasses with hydrothermal fluids and is isotopically light, with δ13C ranging from −30.4 to −10.9 ‰ (average~−26 ‰).
ODP hole 801C penetrates ~400 m into much older (~170 Ma) crustal material of the Pigafetta basin in the Western Pacific (Lancelot et al. 1990). The carbon observed throughout this drill core is strongly dominated by carbonate minerals with a heavy isotopic composition, δ13C of 0–3 ‰ (Alt and Teagle 2003). This material was mostly in downward penetrating veins created during reaction of crust with seawater; therefore, it is only present in the upper sections (~200 m) of crust.
The resulting distribution of carbon in the crust as it reaches a subduction environment will be a bimodal mixture of abiotic organic carbon from hydrothermal alteration and inorganic carbonate from seawater interaction. The crust also has a layered structure, in terms of carbon component, as the inorganic carbonate (heavy) is only present near the crust–water interface, whereas the organic component (light) is present throughout the slab (see Shilobreeva et al. 2011 Fig. 6 for an illustration of the process of carbon addition to the oceanic crust). Interestingly, the average carbon isotope composition of the subducting crustal assemblage is ~−5 ‰ (mass balance calculation of Shilobreeva et al. 2011). Considering estimates of the mantle residence time of carbon (Dasgupta and Hirschmann 2010), it is conceivable that the mantle composition of −5 ‰ reflects the bulk mixing of recycled carbon into the mantle over geological time.
The organic carbon component of the ocean crust provides a source of isotopically light carbon that could explain the source of light carbon observed in the Juina-5 diamonds. As this component is present throughout the oceanic crust, it will not experience the same high temperatures as the sedimentary package and slab surface during subduction, therefore, potentially making it a much more suitable source for generating isotopically light, superdeep diamonds. We acknowledge that it is surprising that crustal isotopic signatures could be preserved in diamonds exhumed from >500 km depth; however, this is currently the most satisfactory explanation.
Eclogitic protolith and formation from a melt
As identified by Walter et al. (2011), the mineral inclusions observed in the Juina-5 diamonds have compositions that are strongly linked to an eclogitic protolith. The magnesium silicate perovskite inclusions are enriched in aluminium, titanium and iron, but depleted in chromium, very similar to those observed in experiments on basaltic bulk compositions. The majoritic garnet inclusions also have eclogitic compositions, with high sodium and calcium contents whilst being deficient in chromium. Two Juina-5 clinopyroxenes also have elevated sodium contents that are indicative of eclogitic material at high pressure (Kiseeva et al. 2013). NAL and CF phases are not stable minerals in peridotite but are known to be important components of eclogite at deep transition zone or lower mantle conditions (Ricolleau et al. 2010; Holland et al. 2013). The widespread occurrence of SiO2 inclusions also suggests that the Juina-5 diamonds formed in a silica-rich protolith. Comparison of the mineral assemblage observed in these diamonds with the experimentally defined eclogitic phase diagram (Figure 5 in Ricolleau et al. 2010) shows that we have observed all the minerals expected in a basaltic rock exhumed from high pressure. The only non-eclogitic inclusions identified in the studied collection are two peridotitic minerals, an olivine and ferropericlase inclusion, that were identified in a single diamond.
The composition of the calcium silicate perovskite inclusions can provide more specific information about the formation environment of the Juina-5 mineral inclusions. Experiments have demonstrated that subsolidus calcium silicate perovskite minerals at pressures above 20 GPa (both titanium-bearing and titanium-free types) that are in equilibrium with a magnesium-rich phase always have a detectable magnesium component (Walter et al. 2008; Armstrong et al. 2012). As the quantity of titanium in the system increases, the miscibility gap between MgSiO3 and CaSiO3 shrinks, which leads to a larger magnesium content in calcium perovskite minerals (Armstrong et al. 2012). These two results are illustrated in the pseudo-ternary-phase diagram in Fig. 8. The calcium silicate perovskite inclusions observed in this study have no measurable magnesium component. Accordingly, they cannot have originally been subsolidus phases in any lower mantle assemblage saturated in magnesium perovskite (see Fig. 8). Walter et al. (2008) experimentally demonstrated that these mineral inclusions are, instead, more likely to represent crystals formed from a carbonate melt alongside majorite. By plotting the composition of the two Juina-5 majorite inclusions on Fig. 8, it is shown that they are very similar to the experimental phases produced by Walter et al. (2008). Coupled with knowledge of the high trace element contents of similar mineral inclusions in Collier-4 diamonds (Walter et al. 2008), and of these inclusions (Thomson et al. in prep), this strongly suggests that the calcium perovskite and majorite mineral inclusions observed in the Juina-5 diamonds are products of equilibration with a low-degree melt.
Depth of individual inclusion formation
The depth of diamond formation can be inferred to be the same as the depths at which the mineral inclusions they contain are stable phases in the mantle. We have made an attempt to place minimum and maximum constraints on the depth interval for the diamond formation by considering the pressure of the mineral inclusions stability.
Magnesium silicate perovskite is a lower mantle mineral, only becoming stable after the breakdown of garnet or olivine polymorphs at around 660 km depth. Depending on the chemical system under investigation, the minimum pressure at which magnesium perovskite becomes stable varies. In the Mg2SiO4 system, perovskite becomes stable (alongside periclase) at 22–23 GPa (Fei et al. 2004), whereas it is stable at ~20 GPa in the MgSiO3 system (Hirose et al. 2001). The minimum pressure of its stability increases to 23–25 GPa with the addition of aluminium (MgSiO3–Al2O3 system; Kubo and Akaogi 2000). Therefore, the minimum formation depth of diamonds containing eclogitic magnesium perovskite inclusions is likely to be within the uppermost part of the lower mantle. The maximum depth of magnesium perovskite stability is controlled by the location of the transition into the post-perovskite phase; this occurs at depths approaching the core–mantle boundary (CMB; Murakami et al. 2004).
The composition of the calcium perovskite inclusions can be simplified into the CaSiO3–CaTiO3 binary system, which was experimentally studied by Kubo et al. (1997). They demonstrated that the minimum pressure of CaSiO3 perovskite stability is ~12 GPa, whereas titanium-bearing Ca(Si,Ti)O3 is stable to pressures as low as ~9 GPa. This implies that the Juina-5 calcium perovskite mineral inclusions must have been exhumed from at least 270–350 km. The lack of magnesium component, as already discussed, suggests that the minerals were originally formed in the transition zone or deep upper mantle, despite calcium perovskite being a stable phase to the CMB.
Experimental work has also been conducted on the stability of NAL and CF phases in the binary systems NaAlSiO4–MgAl2O4 (Ono et al. 2009) and CaAl2O4–MgAl2O4 (Akaogi et al. 1999). Whilst both phases are stable as part of a lower mantle eclogite assemblage, it has been shown that NAL phase (also called hexagonal phase) is stable at pressures of 13.5 GPa (~400 km), whilst CF phase is stable at 17 GPa (~510 km) depending on composition. The more complex compositions of the natural minerals, instead of those in experimental studies, will alter the limits of stability fields. It is therefore concluded that these inclusions represent either transition zone or lower mantle minerals.
The formation pressures of the two majoritic garnet inclusions have been calculated using the geobarometer of Collerson et al. (2010). Pressures for the bulk composition of each inclusion are calculated as 15.2 ± 1.4 and 12.9 ± 1.4 GPa, suggesting original growth at depths equivalent to the shallowest parts of the transition zone.
The SiO2 inclusions are all coesite structured and two of the observed examples contain an exsolved kyanite mineral. This observation suggests that inclusions possess a significant aluminium component, a feature only possible if they represent the retrograde products of inclusions that were originally stishovite minerals. Whether all the SiO2 inclusions were originally stishovite is unclear, but the two inclusions with observable kyanite have a formation depth in the sub-lithospheric mantle.
Other inclusions from the studied Juina-5 diamonds are either low-pressure phases or stable across extremely wide depth intervals. For example, the clinopyroxene inclusions are stable at pressures <~13–15 GPa and remain stable to surface pressures. Ferropericlase is most often thought of as a lower mantle mineral; however, it is stable throughout the mantle depth interval with its stability depending critically on bulk composition.
The abundance of inclusions that must have formed at sub-lithospheric pressures (a total of 27 mineral inclusions) provides undeniable evidence that many of the Juina-5 diamonds of this study began their existence at sub-lithospheric depths, in some cases within the lower mantle. However, the realisation that not all inclusions can have formed at the same depth coupled with the evidence of diamond growth from several distinct fluids suggests that the Juina-5 samples have formed throughout multiple growth episodes from several fluid fluxes of changing composition whilst en route to the surface.
A conceptual model of Juina-5 diamond formation
We present two models for the growth and exhumation of the Juina-5 diamonds that collate and account for all the observations throughout this study. Recycled material is the source of carbon for diamond growth in both models, and they differ only in their proposed geometries and exhumation mechanisms. We highlight that the observations in this study do not directly constrain these exhumation mechanisms, but rather the two models provide possible ways of transporting the diamonds from great depths in the Earth to the surface. Illustrative cartoons of both models are drawn in Fig. 9. A third possible mechanism allowing upward transit of the Juina diamonds would involve transport of material in a passing mantle plume; however, as recent work suggests that the alkaline volcanism at Juina is not related to any known palaeo-hotspot and this model has been described elsewhere (e.g. Bulanova et al. 2010), we do not dwell on this possibility here.
Illustrative cartoon of the model we envisage to explain formation of the Juina-5 diamonds. Top right shows organic carbon is added to the crust in the mid-ocean ridge environment (δ13C ~ −25 ‰, Shilobreeva et al. 2011) followed by subsequent carbon addition by seawater interaction (δ13C ~ −0 ‰, Alt and Teagle 2003). Subduction carries this carbonated assembly past sub-arc depths until stagnation and thermalisation occurs in the transition zone. This causes the melting of the carbonated component and resultant diamond formation by ‘redox-freezing’ during melt infiltration. Continued pulses of melt percolate further away from the slab source in a channelised melt system, carrying and enlarging existing whilst also nucleating new diamonds. During this process, diamonds may break or stall in carbonated horizons in the mantle. Exhumation of diamond-bearing material may also occur by some passive upwelling, the return flow from subduction, but does not require a mantle plume to be present. Eventually, the diamonds are carried to the surface by kimberlitic volcanism
Subduction of crustal material is responsible for providing the return flow of volatile species to the mantle from the Earth’s surface environment (Hilton et al. 2002; Dasgupta and Hirschmann 2010; Kendrick et al. 2013). Experiments have demonstrated that hydrous materials undergo deserpentinisation and melting at sub-arc depths (2–6 GPa) causing the loss of the majority of the water stored in subducted material (e.g. Rupke et al. 2004; Kessel et al. 2005; Klimm et al. 2008). In contrast, it appears that the same lithologies are able to retain a significant carbon component at similar conditions (Kerrick and Connolly 2001; Connolly 2005; Poli et al. 2009). Therefore, the subducting slab’s composition can be approximated as a mixture of water-poor carbonated eclogite and peridotite at depths beyond approximately 100–150 km. After this dehydration, the solidus of subducting lithologies is expected to rise, such that further melting may not be expected until the slab reaches the base of the upper mantle (e.g. Hammouda 2003; Dasgupta et al. 2004, 2006; Litasov and Ohtani 2010; Rohrbach and Schmidt, 2011). At pressures of the transition zone, and approaching the upper/lower mantle boundary, the experimentally determined melting curves of carbonated peridotite (Ghosh et al. 2009; Rohrbach and Schmidt 2011) and eclogite (Kiseeva et al. 2013) become flat or possibly have a negative slope (Thomson et al. 2014), and slab melting is expected to occur somewhere in the deep mantle. Seismic observations show that slabs often stagnate in the transition zone (Fukao et al. 2009), and in this case, it is likely that melting of subducting assemblages occurs as the slab heats up in the deep transition zone or upper lower mantle.
The low-degree melts of carbonated assemblages produced at high pressures are expected to be carbonatitic or carbonate rich (Brey et al. 2008; Rohrbach and Schmidt 2011). If such melts are highly mobile (Hammouda and Laporte 2000), they will rapidly percolate through the subducting assemblage to the surface of the slab and react with surrounding mantle peridotite. Due to the increased incorporation of ferric iron in mantle silicates with pressure and associated disproportionation of iron, the deep transition zone and lower mantle are thought to be reducing, possibly buffered at an oxygen fugacity close to or below the iron wüstite buffer (IW) (Frost and McCammon 2008; Stagno et al. 2013; Rohrbach and Schmidt 2011). At this oxygen fugacity, carbonates (and carbonate melts) are unstable, with carbon becoming reduced to diamond (Stagno and Frost 2010; Stagno et al. 2011; Rohrbach and Schmidt 2011). This reduction-based diamond formation mechanism was termed ‘redox-freezing’ by Rohrbach and Schmidt (2011). Any region of ambient mantle can continue to reduce carbonate until its entire free metal content has been oxidised, and when this occurs, carbonatite melts have the ability to infiltrate further into the ambient mantle assemblage. We propose that the diamonds and their inclusions crystallised together by this type of mechanism.
Our proposed models suggest that this type of redox–infiltration reaction could occur in two contrasting geometries. In model A (Fig. 9a), we suggest that multiple pulses of carbonatite melt are produced as various regions of the subducting material undergo the onset of melting. Each melt pulse, due to its high mobility, rapidly percolates into the peridotitic mantle. It is suggested that multiple fluxes of fluid leaving the slab result in the formation of channels or high-porosity pathways throughout the surrounding mantle. Over time, this channel network will grow sufficiently to allow the rapid percolation of melt large distances from the slab, similar to those observed in exhumed shallow subduction sections (Sleep 1988; Zack and John 2007). This channelisation process could occur by a reactive infiltration instability (RII)-type mechanism (e.g. Steefel and Lasaga 1990; Spiegelman et al. 2001) whereby high-porosity channels form as a feedback to the corrosive dissolution by a melt phase. Alternatively, Connolly and Podladchikov (2007) showed that similar channel networks form as a result of compactive stresses. Once pathways have been created, any melt entering the region will preferentially travel by the high-porosity path, as opposed to undertaking porous flow. The ability for melts to quickly travel far from their slab source with minimal mantle interaction is a key to explaining the presence of inclusions formed across large depth ranges. It is possible that repeated melt pulses passing through this channelised network could transport the diamonds as xenocrysts to shallower levels, as required by their retrograde, composite inclusion mineralogy.
Alternatively model B (Fig. 9b) suggests that upward transport is achieved by the formation of a diapir of buoyant slab material. This could either be a carbonatite diapir if slab-derived melts are able to pool at the slab–mantle interface or could be composed of a mixture of low-degree slab melts, slab and overlying mantle material sourced from the slab/mantle interface region. In the case of a carbonatite diapir as time passes, the volume of the melt pool increases until it becomes gravitationally buoyant compared with the overlying mantle; at which time, it can diapirically rise through the overlying mantle. In the situation of a mixed composition diapir, it is likely the stranded slab/mantle/melt package will require a period of heating before it becomes buoyant with respect to the overlying mantle. In either case during the journey to the surface, the carbonate-bearing diapir’s surface will experience inward penetrating reduction by reaction with the surrounding metal-saturated mantle. Diamonds could form across a wide depth range from ~660 km until iron is no longer stable in the mantle (~250–180 km). En route individual diamonds might experience multiple redox-freezing and melting regimes as they variably interact with the carbonate inside and mantle outside the diapiric plume. This model is conceptually similar to one suggested by Litasov et al. ( 2013), and numerical modelling of a similar wet plume has previously been presented by Richard and Iwamori (2010).
Both illustrative models not only allow for diamond formation during the interaction of subducted and mantle material but also provide an environment where the growth features can be created and a transport mechanism to move the diamonds from the deep mantle towards the surface that allows for inclusion exsolution and re-equilibration.
Concluding remarks
Superdeep diamonds, like the Juina-5 samples studied here, provide a valuable opportunity to study sub-lithospheric material that has been exhumed from transition zone and/or lower mantle depths. It is apparent, at least in this study, that diamonds and their inclusions do not represent fragments of ambient “normal” mantle. Instead, the major element chemistry of the mineral inclusion assemblage is strongly linked to basaltic material and crystallisation from a carbonated melt whilst the diamonds themselves are also linked to subducted materials by their light isotopic compositions. Internal growth structures of the Juina-5 diamonds are unlike those commonly observed in lithospheric diamonds and suggest that these samples have undergone high stresses both during and after formation. As we suggest these diamonds formed during by a ‘redox-freezing’-type reaction as slab-derived melts infiltrate and metasomatise the ambient mantle, it is possible that superdeep diamonds provide us with a snapshot of the deep volatile cycle. They, therefore, do not tell us about the state of the ambient mantle and caution should be exerted when using samples like these to draw conclusions about bulk properties of the deep Earth.
References
Akaogi M, Hamada Y, Suzuki T, Kobayashi M, Okada M (1999) High pressure transitions in the system MgAl2O4–CaAl2O4: a new hexagonal aluminous phase with implication for the lower mantle. Phys Earth Planet Inter 115:67–77. doi:10.1016/S0031-9201(99)00076-X
Alt JC, Teagle DAH (2003) Hydrothermal alteration of upper oceanic crust formed at a fast-spreading ridge: mineral, chemical, and isotopic evidence from ODP Site 801. Chem Geol 201:191–211. doi:10.1016/S0009-2541(03)00201-8
Araujo DP, Gaspar JC, Bulanova GP, Smith CB, Kohn SC, Walter MJ, Hauri EH (2013) Juina diamonds from kimberlites and alluvials: a comparison of morphology, spectral characteristics and carbon isotope composition. In: Pearson DG, Grütter HS, Harris JW et al. (eds) Proceedings of 10th international kimberlite conference. Springer, India, pp 255–269. doi:10.1007/978-81-322-1170-9_16
Armstrong LS, Walter MJ, Tuff JR, Lord OT, Lennie AR, Kleppe AK, Clark SM (2012) Perovskite phase relations in the system CaO–MgO–TiO2–SiO2 and implications for deep mantle lithologies. J Petrol 53:611–635. doi:10.1093/Petrology/Egr073
Bottinga Y (1969) Carbon isotope fractionation between graphite diamond and carbon dioxide. Earth Planet Sci Lett 5(5):301–307
Boyd S, Mattey D, Pillinger C, Milledge H, Mendelssohn M, Seal M (1987) Multiple growth events during diamond genesis: an integrated study of carbon and nitrogen isotopes and nitrogen aggregation state in coated stones. Earth Planet Sci Lett 86(2):341–353
Brenker FE, Vincze L, Vekemans B, Nasdala L, Stachel T, Vollmer C, Kersten M, Somogyi A, Adams F, Joswig W, Harris JW (2005) Detection of a Ca-rich lithology in the Earth’s deep (>300 km) convecting mantle. Earth Planet Sci Lett 236(3–4):579–587. doi:10.1016/J.Epsl.2005.05.021
Brenker FE, Vollmer C, Vincze L, Vekemans B, Szymanski A, Janssens K, Szaloki I, Nasdala L, Joswig W, Kaminsky F (2007) Carbonates from the lower part of transition zone or even the lower mantle. Earth Planet Sci Lett 260(1–2):1–9. doi:10.1016/J.Epsl.2007.02.038
Brey GP, Bulatov V, Girnis A, Harris JW, Stachel T (2004) Ferropericlase—a lower mantle phase in the upper mantle. Lithos 77(1–4):655–663. doi:10.1016/J.Lithos.2004.03.013
Brey GP, Bulatov VK, Girnis AV, Lahaye Y (2008) Experimental melting of carbonated peridotite at 610 GPa. J Petrol 49(4):797–821. doi:10.1093/Petrology/Egn002
Bruce LF, Kopylova MG, Long M, Ryder J, Dobrzhinetskaya LF (2011) Luminescence of diamonds from metamorphic rocks. Am Mineral 96(1):14–22. doi:10.2138/Am.2011.3467
Bulanova GP (1995) The formation of diamond. J Geochem Explor 53(1–3):1–23. doi:10.1016/0375-6742(94)00016-5
Bulanova G, Smith C, Kohn S, Walter M, Gobbo L, Kearns S Machado River, Brazil—a newly recognised ultradeep diamond occurrence. In: 9th International Kimberlite Conference. Extended Abstract, 2008. vol 9IKC-A, p 00233
Bulanova GP, Walter MJ, Smith CB, Kohn SC, Armstrong LS, Blundy J, Gobbo L (2010) Mineral inclusions in sublithospheric diamonds from Collier 4 kimberlite pipe, Juina, Brazil: subducted protoliths, carbonated melts and primary kimberlite magmatism. Contrib Mineral Petr 160(4):489–510. doi:10.1007/S00410-010-0490-6
Cartigny P (2005) Stable isotopes and the origin of diamond. Elements 1(2):79–84. doi:10.2113/Gselements.1.2.79
Cartigny P, Harris JW, Javoy M (1998) Eclogitic diamond formation at Jwaneng: no room for a recycled component. Science 280(5368):1421–1424. doi:10.1126/Science.280.5368.1421
Cartigny P, Harris JW, Javoy M (2001) Diamond genesis, mantle fractionations and mantle nitrogen content: a study of delta C-13-N concentrations in diamonds. Earth Planet Sci Lett 185(1–2):85–98. doi:10.1016/S0012-821x(00)00357-5
Collerson KD, Williams Q, Kamber BS, Omori S, Arai H, Ohtani E (2010) Majoritic garnet: a new approach to pressure estimation of shock events in meteorites and the encapsulation of sub-lithospheric inclusions in diamond. Geochim Cosmochim Acta 74(20):5939–5957. doi:10.1016/J.Gca.2010.07.005
Connolly JAD (2005) Computation of phase equilibria by linear programming: a tool for geodynamic modeling and its application to subduction zone decarbonation. Earth Planet Sc Lett 236(1–2):524–541. doi:10.1016/j.epsl.2005.04.033
Connolly JAD, Podladchikov YY (2007) Decompaction weakening and channeling instability in ductile porous media: implications for asthenospheric melt segregation. J Geophys Res 112:B10. doi:10.1029/2005jb004213
Dasgupta R, Hirschmann MM (2010) The deep carbon cycle and melting in Earth’s interior. Earth Planet Sci Lett 298(1–2):1–13. doi:10.1016/J.Epsl.2010.06.039
Dasgupta R, Hirschmann MM, Withers AC (2004) Deep global cycling of carbon constrained by the solidus of anhydrous, carbonated eclogite under upper mantle conditions. Earth Planet Sci Lett 227(1–2):73–85. doi:10.1016/J.Epsl.2004.08.004
Dasgupta R, Hirschmann MM, Stalker K (2006) Immiscible transition from carbonate-rich to silicate-rich melts in the 3 GPa melting interval of eclogite plus CO2 and genesis of silica-undersaturated ocean island lavas. J Petrol 47(4):647–671. doi:10.1093/Petrology.Egi088
Davies RA, Griffin WL, O’Reilly SY, McCandless TE (2004) Inclusions in diamonds from the K14 and K10 kimberlites, Buffalo Hills, Alberta, Canada: diamond growth in a plume? Lithos 77(1–4):99–111. doi:10.1016/J.Lithos.04.008
Deines P (1980) The carbon isotopic composition of diamonds—relationship to diamond shape, color, occurrence and vapor composition. Geochim Cosmochim Acta 44(7):943–961. doi:10.1016/0016-7037(80)90284-7
Deines P, Harris JW, Gurney JJ (1991) The carbon isotopic composition and nitrogen-content of lithospheric and asthenospheric diamonds from the Jagersfontein and Koffiefontein Kimberlite, South-Africa. Geochim Cosmochim Acta 55(9):2615–2625. doi:10.1016/0016-7037(91)90377-H
Eigenbrode JL, Freeman KH (2006) Late Archean rise of aerobic microbial ecosystems. Proc Natl Acad Sci USA 103(43):15759–15764. doi:10.1073/Pnas.0607540103
Fei Y, Van Orman J, Li J, van Westrenen W, Sanloup C, Minarik W, Hirose K, Komabayashi T, Walter M, Funakoshi K (2004) Experimentally determined postspinel transformation boundary in Mg2SiO4 using MgO as an internal pressure standard and its geophysical implications. J Geophys Res 109(B2):B02305. doi:10.1029/2003jb002562
Frost DJ, McCammon CA (2008) The redox state of Earth’s mantle. Annu Rev Earth Planet Sci 36:389–420. doi:10.1146/Annurev.Earth.36.031207.124322
Fukao Y, Obayashi M, Nakakuki T, Grp DSP (2009) Stagnant Slab: a review. Annu Rev Earth Planet Sci 37:19–46. doi:10.1146/Annurev.Earth.36.031207.124224
Gaspar J, Teixeira N, Steele I (1988) Cathodoluminescence of Juina diamonds. In: Extended abstracts 7th international Kimberlite conference, Cape Town, pp 242–244
Gasparik T, Tripathi A, Parise JB (2000) Structure of a new Al-rich phase, [K, Na]0.9[Mg, Fe]2[Mg, Fe, Al, Si]6O12, synthesized at 24 GPa. Am Min 85:613–618
Ghosh S, Ohtani E, Litasov KD, Terasaki H (2009) Solidus of carbonated peridotite from 10 to 20 GPa and origin of magnesiocarbonatite melt in the Earth’s deep mantle. Chem Geol 262(1–2):17–28. doi:10.1016/J.Chemgeo.2008.12.030
Gibson SA, Thompson RN, Leonardos OH, Dickin AP, Mitchell JG (1995) The late cretaceous impact of the Trindade mantle plume—evidence from large-volume, mafic, potassic magmatism in Se Brazil. J Petrol 36(1):189–229
Grassi D, Schmidt MW (2011) The melting of carbonated pelites from 70 to 700 km depth. J Petrol 52(4):765–789. doi:10.1093/Petrology/Egr002
Grütter HS, Gurney JJ, Menzies AH, Winter F (2004) An updated classification scheme for mantle-derived garnet, for use by diamond explorers. Lithos 77:841–857
Guarino V, Wu F-Y, Lustrino M, Melluso L, Brotzu P, Gomes CdB, Ruberti E, Tassinari CCG, Svisero DP (2013) U-Pb ages, Sr–Nd- isotope geochemistry, and petrogenesis of kimberlites, kamafugites and phlogopite-picrites of the Alto Paranaíba Igneous Province, Brazil. Chem Geol 353:65–82
Gurney JJ, Harris JW, Rickard RS, Moore RO (1985) Inclusions in Premier mine diamonds. S Afr J Geol 88:301–310
Hammouda T (2003) High-pressure melting of carbonated eclogite and experimental constraints on carbon recycling and storage in the mantle. Earth Planet Sci Lett 214(1–2):357–368. doi:10.1016/S0012-821x(03)00361-3
Hammouda T, Laporte D (2000) Ultrafast mantle impregnation by carbonatite melts. Geology 28(3):283–285. doi:10.1130/0091-7613(2000)28<283:Umibcm>2.0.Co;2
Harte B (1992) Trace element characteristics of deep-seated eclogite parageneses—an ion microprobe study of inclusions in diamonds. In: V.M. Goldschmidt Conference, 1992. pp A–48
Harte B (2010) Diamond formation in the deep mantle: the record of mineral inclusions and their distribution in relation to mantle dehydration zones. Mineral Mag 74(2):189–215. doi:10.1180/Minmag.2010.074.2.189
Harte B, Cayzer N (2007) Decompression and unmixing of crystals included in diamonds from the mantle transition zone. Phys Chem Miner 34(9):647–656. doi:10.1007/S00269-007-0178-2
Harte B, Harris J, Hutchison M, Watt G, Wilding M (1999) Lower mantle mineral associations in diamonds from Sao Luiz, Brazil. Mantle Petrology: Field Observations and High Pressure Experimentation: A Tribute to Francis R(Joe) Boyd, The Geochemical Society, Houston, Geochem Soc Spec Publ 6:125–153
Hayman PC, Kopylova MG, Kaminsky FV (2005) Lower mantle diamonds from Rio Soriso (Juina area, Mato Grosso, Brazil). Contrib Mineral Petr 149(4):430–445. doi:10.1007/S00410-005-0657-8
Heaman L, Teixeira N, Gobbo L, Gaspar J (1998) U-Pb mantle zircon ages for kimberlites from the Juina and Paranatinga provinces, Brazil. VIIth International Kimberlite Conference. Extended abstracts, Cape Town, pp 322–324
Hilton DR, Fischer TP, Marty B (2002) Noble gases and volatile recycling at subduction zones. Noble Gases Geochem Cosmochem 47:319–370. doi:10.2138/Rmg.2002.47.9
Hirose K, Fei Y (2002) Subsolidus and melting phase relations of basaltic composition in the uppermost lower mantle. Geochim Cosmochim Acta 66(12):2099–2108
Hirose K, Komabayashi T, Murakami M, Funakoshi K (2001) In situ measurements of the majorite-akimotoite-perovskite phase transition boundaries in MgSiO3. Geophys Res Lett 28(23):4351–4354. doi:10.1029/2001gl013549
Hirose K, Takafuji N, Sata N, Ohishi Y (2005) Phase transition and density of subducted MORB crust in the lower mantle. Earth Planet Sci Lett 237(1):239–251
Holland TJ, Hudson NF, Powell R, Harte B (2013) New thermodynamic models and calculated phase equilibria in NCFMAS for basic and ultrabasic compositions through the transition zone into the uppermost lower mantle. J Petrol 54(9):1901–1920. doi:10.1093/Petrology/Egt035
Hummer DR, Fei YW (2012) Synthesis and crystal chemistry of Fe3+-bearing (Mg, Fe3+)(Si, Fe3+)O3 perovskite. Am Mineral 97(11–12):1915–1921. doi:10.2138/Am.2012.4144
Hutchinson MT (1997) Constitution of the deep transition zone and lower mantle shown by diamonds and their inclusions. PhD Thesis, University of Edinburgh
Hutchison M, Hursthouse M, Light M (2001) Mineral inclusions in diamonds: associations and chemical distinctions around the 670-km discontinuity. Contrib Mineral Petr 142(1):119–126
Ickert RB, Stachel T, Stern RA, Harris JW (2013) Diamond from recycled crustal carbon documented by coupled δ18O–δ13C measurements of diamonds and their inclusions. Earth Planet Sci Lett 364:85–97. doi:10.1016/J.Epsl.2013.01.008
Imada S, Hirose K, Ohishi Y (2011) Stabilities of NAL and Ca-ferrite-type phases on the join NaAlSiO4-MgAl2O4 at high pressure. Phys Chem Minerals 38:557–560
Irifune T, Ringwood AE (1993) Phase transformations in subducted oceanic crust and buoyancy relationships at depths of 600–800 km in the mantle. Earth Planet Sci Lett 117:101–110
Kaminsky F (2012) Mineralogy of the lower mantle A review of ‘super-deep’ mineral inclusions in diamond. Earth Sci Rev 110(1):127–147. doi:10.1016/J.Earscirev.2011.10.005
Kaminsky FV, Zakharchenko OD, Davies R, Griffin WL, Khachatryan-Blinova GK, Shiryaev AA (2001) Superdeep diamonds from the Juina area, Mato Grosso State. Brazil. Contrib Mineral Petr 140(6):734–753
Kaminsky FV, Khachatryan GK, Andreazza P, Araujo D, Griffin WL (2009) Super-deep diamonds from kimberlites in the Juina area, Mato Grosso State, Brazil. Lithos 112:833–842. doi:10.1016/J.Lithos.2009.03.036
Kato C, Hirose K, Komabayashi T, Ozawa H, Ohishi Y (2013) NAL phase in K-rich portions of the lower mantle. Geophys Res Let 40:5085–5088
Kellogg LH (1992) Mixing in the Mantle. Annu Rev Earth Planet Sci 20:365–388
Kendrick MA, Honda M, Pettke T, Scambelluri M, Phillips D, Giuliani A (2013) Subduction zone fluxes of halogens and noble gases in seafloor and forearc serpentinites. Earth Planet Sci Lett 365:86–96. doi:10.1016/J.Epsl.01.006
Kerrick DM, Connolly JAD (2001) Metamorphic devolatilization of subducted oceanic metabasalts: implications for seismicity, arc magmatism and volatile recycling. Earth Planet Sci Lett 189(1–2):19–29. doi:10.1016/S0012-821x(01)00347-8
Kessel R, Schmidt MW, Ulmer P, Pettke T (2005) Trace element signature of subduction-zone fluids, melts and supercritical liquids at 120–180 km depth. Nature 437(7059):724–727. doi:10.1038/Nature03971
Kesson SE, Gerald JF, Shelley JMG (1994) Mineral chemistry and density of subducted basaltic crust at lower-mantle pressures. Nature 372:767–769
Kiseeva ES, Litasov KD, Yaxley GM, Ohtani E, Kamenetsky VS (2013) Melting and phase relations of carbonated eclogite at 9–21 GPa and the petrogenesis of alkali-rich melts in the deep mantle. J Petrol 54(8):1555–1583. doi:10.1093/Petrology/Egt023
Klimm K, Blundy JD, Green TH (2008) Trace element partitioning and accessory phase saturation during H2O-saturated melting of basalt with implications for subduction zone chemical fluxes. J Petrol 49(3):523–553. doi:10.1093/Petrology/Egn001
Kojitani H, Iwabuchi T, Kobayashi M, Miura H, Akaogi M (2011) Structure refinement of high-pressure hexagonal aluminous phases K1.00Mg2.00Al4.80Si1.15O12 and Na1.04Mg1.88Al4.64Si1.32O12. Am Mineral 96(9):1248–1253. doi:10.2138/Am.2011.3638
Kubo A, Akaogi M (2000) Post-garnet transitions in the system Mg4Si4O12-Mg3Al2Si3O12 up to 28 GPa: phase relations of garnet, ilmenite and perovskite. Phys Earth Planet Int 121(1–2):85–102. doi:10.1016/S0031-9201(00)00162-X
Kubo A, Suzuki T, Akaogi M (1997) High pressure phase equilibria in the system CaTiO3–CaSiO3: stability of perovskite solid solutions. Phys Chem Miner 24(7):488–494. doi:10.1007/S002690050063
Lancelot Y, Larson R, Fisher A, Staff Scientist L, Rabinowitz PD, Meyer AW, Garrison LE (1990) Ocean Drilling Program, Leg 129 Preliminary Report: Old Pacific Crust. Program, Texas A & M University
Litasov KD, Ohtani E (2004) Relationship between Al-bearing phases NAL and CF in the lower mantle. Geol Geofiz 45(11):1313–1325
Litasov KD, Ohtani E (2005) Phase relations in hydrous MORB at 18–28GPa: implications for heterogeneity of the lower mantle. Phys Earth Planet Int 150(4):239–263
Litasov K, Ohtani E (2010) The solidus of carbonated eclogite in the system CaO–Al2O3–MgO–SiO2–Na2O–CO2 to 32 GPa and carbonatite liquid in the deep mantle. Earth Planet Sci Lett 295(1–2):115–126. doi:10.1016/J.Epsl.2010.03.030
Litasov KD, Shatskiy A, Ohtani E, Yaxley GM (2013) Solidus of alkaline carbonatite in the deep mantle. Geology 41(1):79–82. doi:10.1130/G33488.1
McCammon C, Hutchison M, Harris J (1997) Ferric iron content of mineral inclusions in diamonds from Sao Luiz: a view into the lower mantle. Science 278(5337):434–436. doi:10.1126/Science.278.5337.434
Mikhail S, Dobosi G, Verchovsky AB, Kurat G, Jones AP (2013) Peridotitic and websteritic diamondites provide new information regarding mantle melting and metasomatism induced through the subduction of crustal volatiles. Geochim Cosmochim Ac 107:1–11. doi:10.1016/J.Gca.2012.12.036
Mikhail S, Guillermier C, Franchi IA, Beard AD, Crispin K, Verchovsky AB, Jones AP, Milledge HJ (2014a) Empirical evidence for the fractionation of carbon isotopes between diamond and iron carbide from the Earth’s mantle. Geochem Geophys Geosyst. doi:10.1002/2013GC005138
Mikhail A, Verchovsky AB, Howell D, Hutchison MT, Southwark R, Thomson AR, Warburton P, Jones AP, Milledge HJ (2014b) Constraining the internal variability of the stable isotopes of carbon and nitrogen within mantle diamonds. Chem Geol 366:14–23
Miyajima N, Yagi T, Hirose K, Kondo T, Fujino K, Miura H (2001) Potential host phase of aluminum and potassium in the Earth’s lower mantle. Am Min 86(5–6):740–746
Moore RO, Gurney JJ (1985) Pyroxene solid-solution in garnets included in diamond. Nature 318(6046):553–555. doi:10.1038/318553a0
Moore R, Otter M, Rickard R, Harris J, Gurney J (1986) The occurrence of moissanite and ferro-periclase as inclusions in diamond. In: 4th International Kimberlite Conference, Perth, Extended Abstracts; Abstr. Geol. Soc. Australia. pp 409–411
Moore RO, Gurney JJ, Griffin WL, Shimizu N (1991) Ultra-high pressure garnet inclusions in Monastery diamonds—trace-element abundance patterns and conditions of origin. Eur J Mineral 3(2):213–230
Murakami M, Hirose K, Kawamura K, Sata N, Ohishi Y (2004) Post-perovskite phase transition in MgSiO3. Science 304(5672):855–858
Ono A, Akaogi M, Kojitani H, Yamashita K, Kobayashi M (2009) High-pressure phase relations and thermodynamic properties of hexagonal aluminous phase and calcium-ferrite phase in the systems NaAlSiO4–MgAl2O4 and CaAl2O4–MgAl2O4. Phys Earth Planet Int 174(1–4):39–49. doi:10.1016/J.Pepi.2008.07.028
Palot M, Cartigny P, Harris JW, Kaminsky FV, Stachel T (2012) Evidence for deep mantle convection and primordial heterogeneity from nitrogen and carbon stable isotopes in diamond. Earth Planet Sci Lett 357:179–193. doi:10.1016/J.Epsl.09.015
Pawley AR, Mcmillan PF, Holloway JR (1993) Hydrogen in stishovite, with implications for mantle water-content. Science 261(5124):1024–1026. doi:10.1126/Science.261.5124.1024
Poli S, Franzolin E, Fumagalli P, Crottini A (2009) The transport of carbon and hydrogen in subducted oceanic crust: an experimental study to 5 GPa. Earth Planet Sci Lett 278(3–4):350–360. doi:10.1016/J.Epsl.2008.12.022
Riccomini C, Velázquez VF, Gomes CB (2005) Tectonic controls of the Mesozoic and Cenozoic alkaline magmatism in central-southeastern Brazilian Platform. In: Gomes (ed) Mesozoic to Cenozoic alkaline magmatism in central-southeastern Brazilian Platform. Edusp, pp 31–55
Richard GC, Iwamori H (2010) Stagnant slab, wet plumes and Cenozoic volcanism in East Asia. Phys Earth Planet Int 183(1–2):280–287. doi:10.1016/j.pepi.2010.02.009
Ricolleau A, Fiquet G, Addad A, Menguy N, Vanni C, Perrillat JP, Daniel I, Cardon H, Guignot N (2008) Analytical transmission electron microscopy study of a natural MORB sample assemblage transformed at high pressure and high temperature. Am Min 93(1):144–153
Ricolleau A, Perrillat JP, Fiquet G, Daniel I, Matas J, Addad A, Menguy N, Cardon H, Mezouar M, Guignot N (2010) Phase relations and equation of state of a natural MORB: implications for the density profile of subducted oceanic crust in the Earth’s lower mantle. J Geophys Res 115:B08202. doi:10.1029/2009jb006709
Rohrbach A, Schmidt MW (2011) Redox freezing and melting in the Earth’s deep mantle resulting from carbon-iron redox coupling. Nature 472(7342):209–212. doi:10.1038/Nature09899
Rupke LH, Morgan JP, Hort M, Connolly JAD (2004) Serpentine and the subduction zone water cycle. Earth Planet Sci Lett 223(1–2):17–34. doi:10.1016/J.Epsl.2004.04.018
Schidlowski M (2001) Carbon isotopes as biogeochemical recorders of life over 3.8 Ga of Earth history: evolution of a concept. Precambrian Res 106(1–2):117–134. doi:10.1016/S0301-9268(00)00128-5
Schulze DJ, Harte B, Page FZ, Valley JW, Channer DMD, Jaques AL, Facility EIM (2013) Anticorrelation between low δ13C of eclogitic diamonds and high δ18O of their coesite and garnet inclusions requires a subduction origin. Geology 41(4):455–458. doi:10.1130/G33839.1
Scott-Smith B, Danchin R, Harris J, Stracke K (1984) Kimberlites near Orroroo, South Australia. Kimberlites I Kimberlites Related rocks: 121–142
Shilobreeva S, Martinez I, Busigny V, Agrinier P, Laverne C (2011) Insights into C and H storage in the altered oceanic crust: results from ODP/IODP Hole 1256D. Geochim Cosmochim Ac 75(9):2237–2255. doi:10.1016/J.Gca.2010.11.027
Sleep NH (1988) Tapping of melt by veins and dikes. J Geophys Res Solid 93(B9):10255–10272. doi:10.1029/Jb093ib09p10255
Smart KA, Chacko T, Stachel T, Muehlenbachs K, Stern RA, Heaman LM (2011) Diamond growth from oxidized carbon sources beneath the Northern Slave Craton, Canada: a δ13C–N study of eclogite-hosted diamonds from the Jericho kimberlite. Geochim Cosmochim Ac 75(20):6027–6047. doi:10.1016/J.Gca.2011.07.028
Sobolev NV (1977) Deep-Seated Inclusions in Kimberlites and the Problem of the Composition of the Upper Mantle (trans: Edition TfR). AGU, Washington. doi:10.1029/SP011
Sobolev V, Sobolev N (1980) New proof on very deep subsidence of eclogitized crustal rocks. Dokl Akad Nauk Sssr+ 250(3):683–685
Spiegelman M, Kelemen PB, Aharonov E (2001) Causes and consequences of flow organization during melt transport: the reaction infiltration instability in compactible media. J Geophys Res 106(B2):2061–2077. doi:10.1029/2000jb900240
Stachel T (2001) Diamonds from the asthenosphere and the transition zone. Eur J Mineral 13(5):883–892. doi:10.1127/0935-1221/2001/0013/0883
Stachel T, Harris JW, Brey GP (1998) Rare and unusual mineral inclusions in diamonds from Mwadui, Tanzania. Contrib Mineral Petr 132(1):34–47. doi:10.1007/S004100050403
Stachel T, Brey GP, Harris JW (2000a) Kankan diamonds (Guinea) I: from the lithosphere down to the transition zone. Contrib Mineral Petr 140(1):1–15. doi:10.1007/S004100000173
Stachel T, Harris JW, Brey GP, Joswig W (2000b) Kankan diamonds (Guinea) II: lower mantle inclusion parageneses. Contrib Mineral Petr 140(1):16–27. doi:10.1007/S004100000174
Stachel T, Harris JW, Aulbach S, Deines P (2002) Kankan diamonds (Guinea) III: δ13C and nitrogen characteristics of deep diamonds. Contrib Mineral Petr 142(4):465–475
Stachel T, Brey GP, Harris JW (2005) Inclusions in sublithospheric diamonds: glimpses of deep Earth. Elements 1(2):73–78. doi:10.2113/Gselements.1.2.73
Stagno V, Frost DJ (2010) Carbon speciation in the asthenosphere: experimental measurements of the redox conditions at which carbonate-bearing melts coexist with graphite or diamond in peridotite assemblages. Earth Planet Sci Lett 300(1–2):72–84. doi:10.1016/J.Epsl.2010.09.038
Stagno V, Tange Y, Miyajima N, McCammon CA, Irifune T, Frost DJ (2011) The stability of magnesite in the transition zone and the lower mantle as function of oxygen fugacity. Geophys Res Lett 38:L19309. doi:10.1029/2011gl049560
Stagno V, Ojwang DO, McCammon CA, Frost DJ (2013) The oxidation state of the mantle and the extraction of carbon from Earth’s interior. Nature 493 (7430):84–+. doi: 10.1038/Nature11679
Steefel CI, Lasaga AC (1990) Evolution of dissolution patterns—permeability change due to coupled flow and reaction. Acs Sym Ser 416:212–225
Sunagawa I (1984) Morphology of natural and synthetic diamond crystals. In: Sunagawa I (ed) Materials Science of the Earth’s Interior. Terrapub, Tokyo, pp 303–331
Tappert R, Stachel T, Harris JW, Shimizu N, Brey GP (2005) Mineral inclusions in diamonds from the Panda kimberlite, Slave Province, Canada. Eur J Mineral 17(3):423–440. doi:10.1127/0935-1221/2005/0017-0423
Tappert R, Foden J, Stachel T, Muehlenbachs K, Tappert M, Wills K (2009a) Deep mantle diamonds from South Australia: a record of Pacific subduction at the Gondwanan margin. Geology 37(1):43–46. doi:10.1130/G25055a.1
Tappert R, Foden J, Stachel T, Muehlenbachs K, Tappert M, Wills K (2009b) The diamonds of South Australia. Lithos 112:806–821. doi:10.1016/J.Lithos.2009.04.029
Tassinari CCG, Bettencourt JS, Geraldes MC, Macambira MJB, Lafon JM (2000) The Amazonian craton. In: Cordani UG, Milani EJ, Thomaz Filho A, Campos DA (eds) Tectonic evolution of South America. Geological Society, pp 41–96
Taylor WR, Jaques AL, Ridd M (1990) Nitrogen-defect aggregation characteristics of some Australasian diamonds: time-temperature constraints on the source regions of pipe and alluvial diamonds. Am Mineral 75:1290–1310
Teagle DAH, Alt JC, Umino S, Miyashita S, Banerjee NR, Wilson DS, Expedition 309/312 Scientists (2006) Superfast spreading rate crust 2 and 3. In: In Proc. Integrated Ocean Drill. Program, 309/312. p 50. doi:10.2204/iodp.proc.309312.2006
Thomassot E, Cartigny P, Harris JW, Viljoen KSF (2007) Methane-related diamond crystallization in the Earth’s mantle: stable isotope evidences from a single diamond-bearing xenolith. Earth Planet Sci Lett 257(3–4):362–371. doi:10.1016/J.Epsl.02.020
Thomson AR, Walter MJ, Lord OT, Kohn SC (2014) Experimental determination of melting in the systems Enstatite–Magnesite and Magnesite–Calcite from 15–80 GPa. Am Mineral 99:1544–1554. doi:10.2138/am.2014.4735
Walter MJ, Bulanova GP, Armstrong LS, Keshav S, Blundy JD, Gudfinnsson G, Lord OT, Lennie AR, Clark SM, Smith CB, Gobbo L (2008) Primary carbonatite melt from deeply subducted oceanic crust. Nature 454(7204):U622–U630. doi:10.1038/Nature07132
Walter MJ, Kohn SC, Araujo D, Bulanova GP, Smith CB, Gaillou E, Wang J, Steele A, Shirey SB (2011) Deep mantle cycling of oceanic crust: evidence from diamonds and their mineral inclusions. Science 334(6052):54–57. doi:10.1126/Science.1209300
Wilding MC (1990) PhD Thesis, University of Edinburgh
Yefimova ES, Sobolev NV, Pospelova LN (1983) Inclusions of sulfides in diamonds and their paragenesis (in Russian). Zap Vses Mineral va CXII:300-309
Zack T, John T (2007) An evaluation of reactive fluid flow and trace element mobility in subducting slabs. Chem Geol 239(3–4):199–216. doi:10.1016/J.Chemgeo.10.020
Zedgenizov DA, Kagi H, Shatsky VA, Ragozin AL (2014) Local variations of carbon isotope composition in diamonds from São-Luis (Brazil): evidence for heterogenous carbon reservoir in sublithospheric mantle. Chem Geol 363:114–124. doi:10.1016/j.chemgeo.2013.10.033
Acknowledgements
This work was supported by the Natural Environmental Research Council grant awarded to ART at Bristol (Grant Number NE/J500033/1). We would like to thank Thermo Scientific for the loan of the DXR Raman microscope that was used during this study. We would also like to thank Stuart Kearns for assistance with EMPA analyses. We thank Max Schmidt for his role as Associate Editor and Greg Yaxley and Vincenzo Stagno for their constructive reviews.
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
Communicated by O. Müntener.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Thomson, A.R., Kohn, S.C., Bulanova, G.P. et al. Origin of sub-lithospheric diamonds from the Juina-5 kimberlite (Brazil): constraints from carbon isotopes and inclusion compositions. Contrib Mineral Petrol 168, 1081 (2014). https://doi.org/10.1007/s00410-014-1081-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00410-014-1081-8