Felix Klein’s early contributions to anschauliche Geometrie

Abstract

Between 1873 and 1876, Felix Klein published a series of papers that he later placed under the rubric anschauliche Geometrie in the second volume of his collected works (1922). The present study attempts not only to follow the course of this work, but also to place it in a larger historical context. Methodologically, Klein’s approach had roots in Poncelet’s principle of continuity, though the more immediate influences on him came from his teachers, Plücker and Clebsch. In the 1860s, Clebsch reworked some of the central ideas in Riemann’s theory of Abelian functions to obtain complicated results for systems of algebraic curves, most published earlier by Hesse and Steiner. These findings played a major role in enumerative geometry, whereas Plücker’s work had a strongly qualitative character that imbued Klein’s early studies. A leitmotif in these works can be seen in the interplay between real curves and surfaces as reflected by their transformational properties. During the early 1870s, Klein and Zeuthen began to explore the possibility of deriving all possible forms for real cubic surfaces as well as quartic curves. They did so using continuity methods reminiscent of Poncelet’s earlier approach. Both authors also relied on visual arguments, which Klein would later advance under the banner of intuitive geometry (anschauliche Geometrie).

1 Introduction

Felix Klein used the term anschauliche Geometrie as the heading for various works he put together in the second volume of his Collected Works (Klein 1921–1923, 2: 3–253), many of them written during the years 1873–1876. He dedicated this section of volume 2 to David Hilbert, who had shortly before offered a lecture course under the same title in Göttingen. Hilbert taught this special course four times during the 1920s, and he eventually asked Stefan Cohn-Vossen to write up these lectures for publication in Anschauliche Geometrie (Hilbert and Cohn-Vossen 1932). Comparing that text with Klein’s earlier lectures on higher geometry (Klein 1893/1907) or the revised edition, Vorlesungen über die höhere Geometrie (Klein 1926) prepared by Wilhelm Blaschke shortly after Klein’s death in 1925, one finds many of the same topics. On the other hand, Hilbert made no mention of the several other topics discussed below, with the single exception of cubic surfaces (Hilbert and Cohn-Vossen 1932, 140–151). Klein’s several papers from the mid-1870s represent his most original contributions to a new deformation theory for algebraic curves and surfaces. Clearly, Hilbert found those more esoteric themes too difficult for the broad audience he had in mind in his lectures. Yet the fact remains that among Klein’s many notable works, those discussed in the present study have only rarely received attention in the historical literature, despite the circumstance that Klein’s mathematical reputation has long been linked with his visual style as a geometer.

Klein has often been remembered as a leading promoter of Riemannian ideas, in particular through his own geometric approach to complex analysis, which began in earnest in the late 1870s. He combined this work with new methods in the theory of transformation groups, a topic he made famous in his “Erlangen Program” (Klein 1872). The works described here by contrast—studies published immediately afterward during the years 1873–1876—owe almost nothing to the main ideas in Klein’s “Erlangen Program.” Nor do they reflect a strong and direct influence coming from Riemann. Seen against Klein’s own interests in projective algebraic geometry, Riemann’s published work certainly had less relevance for him than those of his mentors, Plücker and Clebsch, whose ideas and methods permeate Klein’s early forays into anschauliche Geometrie.

Only months before he died unexpectedly in November 1872 at age 39, Alfred Clebsch paved the way for Klein’s appointment to a professorship in Erlangen (Tobies 2021, 123–137). During the next 2 years, Klein had very little chance to interact with other mathematicians, though he did attract a small group of industrious students. His isolated situation changed in 1874, when he succeeded in bringing Paul Gordan to Erlangen. Gordan had been Clebsch’s closest collaborator during the mid-1860s when both worked together in Giessen. Clebsch had himself been a student of Otto Hesse, whose final academic station was the Munich Institute of Technology, where he taught up until his death in 1874. Afterward, Klein gained Hesse’s professorship, soon afterward joined by Alexander Brill, another protégé of Alfred Clebsch. The papers discussed below were, thus, written during Klein’s formative years from 1873 to 1876 when he taught in Erlangen and Munich.

These various appointments reveal that the Clebsch network continued to play a major role in German mathematics long after the master’s death. Among Clebsch’s many pupils, Max Noether stands out as the leading exponent of the Clebschian tradition in algebraic geometry. Noether joined Gordan in 1875, when the latter assumed Klein’s chair in Erlangen. Both became fixtures of this smaller provincial university, where they remained throughout their careers. In later years, Noether grew somewhat disdainful of Klein’s attempts to dabble with problems in algebraic geometry that could not be attacked by straightforward heuristic arguments (Rowe 2021).

Throughout his youth, Klein worked with and promoted intuitive methods that others often found inadequate. One such method was Poncelet’s principle of continuity (Poncelet 1822, xiii–xiv; sections 135–140).¹ Thus, in a letter to Max Noether from 15 April 1870, written shortly after a sojourn of some months in Berlin, Klein offered these reflections in connection with a paper by Ernest de Jonquières that dealt with problems in enumerative geometry (de Jonquières 1866). Here, he commented:

These investigations are not considered stringent in Berlin mathematical circles. I think this is wrong. The principle of continuity, as far as it comes into consideration, can quite well, it seems to me, be proved. But one need not restrict oneself to the viewpoint (Anschauung), as is usually done in my opinion without any reasonable justification, that considers only real constants.²

In 1872–73, Klein began to explore the possibility of deriving all types of cubic surfaces (Klein 1873). He did so using continuity arguments, reminiscent of Poncelet’s methods, together with local deformations that removed singularities one point at a time. A few years later, in studies devoted to real algebraic curves in the plane, Klein adopted deformations that enabled him to remove all of the singularities at once. His approach was highly visual, a style Klein would later advance under the banner of intuitive geometry (anschauliche Geometrie). Klein typically argued on the basis of special concrete cases, often employing pictures to depict geometrical relationships. With regard to methods for reducing singularities of algebraic curves, Noether and others were already using birational transformations for this purpose. Klein’s more intuitive approach to singularities was based on his idiosyncratic understanding of topological transformations, as briefly described in his Erlangen Program (Klein 1921–1923, 1: 482). For analysis situs, he took these to be the group of (real) infinitesimal point-transformations combined with real collineations, which act on the region at infinity. This reflects the extent to which his approach was rooted in projective geometry, here extended to allow for locally continuous mappings.

Before taking up Klein’s early papers related to anschauliche Geometrie, Sects. 2 and 3 lay out the general context of mathematical interests that motivated this work. In Sect. 2, Trends in Algebraic Geometry, 1840–1870, the accent falls on general background information involving the invariants of curves and their singularities. The latter topic was famously connected with Klein’s teacher, Julius Plücker, who found the dual formulas connecting point and line singularities for algebraic curves. In Sect. 3, a brief prelude to the later discussion of deformations of quartic curves leads over to Klein’s refinement of Plücker’s formulas. This involved distinguishing between real and imaginary singularities, a standard motif in nearly all of Klein’s work from the mid-1870s. Here, as in other places, the text breaks with a strictly chronological presentation to bring out important mathematical developments.

With this as background, Sect. 4 goes on to discuss the quite distinct ways in which Plücker and Clebsch influenced the young Felix Klein during his formative years. Plücker’s intuitive geometrical style as well as his interest in producing models to illustrate various types of surfaces clearly carried over in shaping Klein’s approach to anschauliche Geometrie. In the case of Clebsch, the influence of Riemannian ideas played a major role, though in a more mediated fashion.

Section 5 begins with the brief collaboration between Clebsch and Klein involving two different models for cubic surfaces. Their respective interests at that time diverged, in fact, so that when Clebsch died soon thereafter his original algebraic motivation was quickly forgotten. Klein, on the other hand, took up the challenging problem of classifying the various types of real cubic surfaces by means of careful deformation processes, which enabled him to remove singular points systematically (Klein 1873). Although he left this topic for others to pursue, his efforts in this direction lived on, thanks in part to the impressive collection of plaster models designed by Carl Rodenberg, as these provided a vivid idea of how this theory actually worked (Fischer 1986, I: 13–31). Section 6 continues with the discussion of Klein’s paper on cubic surfaces (Klein 1873), while describing its relevance for curve theory. As Klein well knew, the 27 lines on cubic surfaces are intimately related to the 28 bitangents of quartic curves, a fact that the Swiss geometer Carl Geiser elegantly showed in Geiser (1869). Geiser’s work inspired H.G. Zeuthen to classify the various types of real quartic curves (Zeuthen 1874, 1875), two studies that Klein, in turn, could build on afterward.

Section 7 begins a detailed presentation of key elements that guided Klein’s work on anschauliche Geometrie, focusing on his new interpretation of Riemann surfaces. These surfaces employed a special visual feature, namely, with them one could easily distinguish between real and imaginary points and lines. Klein used such projective Riemann surfaces, firstly, to gain a complete picture of the real and imaginary points on a (low-degree) algebraic curve. Second, he employed them to carry out deformations of an algebraic curve, thereby connecting the genus of the surface with the presence or absence of singularities. As this work illustrates, Klein’s mathematical style was purposefully discursive, and he often preferred to illustrate his ideas via examples rather than by presenting general arguments. The fact that some of his favorite notions seem odd or idiosyncratic makes them all the more interesting to think about today.

Following the fairly long discussion in Sect. 7, Sect. 8 on configurations and tangency relations turns backwards to describe some classical results obtained by Hesse and Clebsch on systems of algebraic curves. By taking advantage of new methods and results in invariant theory and complex analysis, Clebsch was able to recast Hesse’s findings from the 1840s and 50s and place these in a clearer light. This work served as the background for Klein’s studies on different types of quartic curves and the systems of real conic and cubic curves tangent to them, the main topic in Sect. 9. Klein continued to utilize projective Riemann surfaces in “On the Form of Abelian Integrals for Fourth-Degree Curves” (Klein 1876c), his most ambitious paper from this period. In some ways, this study already anticipates the approach to Riemann surfaces that Klein set forth in his booklet On Riemann’s Theory of Algebraic Functions and their Integrals (Klein 1882). The paper ends with tables identifying the imaginary parts of the periodicity modules for the five types of real nonsingular quartics under investigation. From these, Klein could draw conclusions as to how many of the systems of tangent curves derived by Clebsch (1864c) (presented in Sect. 8) corresponded to real curves, i.e., those whose equations have real coefficients. Klein’s later use of Riemannian ideas in complex analysis was far more influential than these earlier papers, which used projective Riemann surfaces as visual aids in algebraic geometry. Nevertheless, the physical ideas discussed at the outset of Sect. 9 carried over to his later theory of Riemann surfaces, best known from his booklet (Klein 1882).

Section 10 takes up Heinrich Weber’s correspondence with Richard Dedekind in connection with the publication of the first edition of Riemann’s Werke in 1876. Their letters suggest that contemporary knowledge of Riemann’s investigations of the bitangents to quartic curves was very fragmentary before that date. This section may be read as a first attempt to gauge the extent to which Klein seriously engaged with Riemann’s works in the mid-1870s. Here, I also raise some questions concerning the contemporary reception of Riemann’s theory of Abelian functions insofar as that theory related to algebraic geometry. In addressing these matters, I take up some events surrounding Weber’s activities during the time he worked on Riemann’s Werke.

The final Sect. 11 recapitulates some key points, while arguing that the essential influences underlying Klein’s works on algebraic geometry during the mid-1870s came from his two teachers, Plücker and Clebsch. These influences are perhaps most apparent in the discussion of Klein’s work on singular curves in Sect. 3 and in his refinement of Clebsch’s results on tangent systems, discussed at the close of Sect. 9. To be sure, Klein’s papers on anschauliche Geometrie represent only one important aspect of his early work. Nevertheless, it is noteworthy that they were written in the immediate wake of his famous Erlangen Program (Klein 1872), which contains almost nothing related to them. Although the results Klein presented in these papers were largely of didactic importance, the novel methods he employed have considerable historical interest. Written decades before any of the requisite topological techniques were available, these works provide many insights into problems that could only be tackled with blunt tools and much intuition. Klein enjoyed the good fortune of living to see how, shortly before the outbreak of the Great War, Hermann Weyl transformed his intuitive ideas on Riemann surfaces into a rigorous abstract mathematical concept (Weyl 1913).

Throughout this essay, I have taken pains to avoid using later sources or interpretations whenever possible. A standard source that could hardly be neglected, though, is the second volume of Klein’s Gesammelte Mathematische Abhandlungen (Klein 1921–1923), which contains reprints of nearly all the papers discussed below. Nevertheless, many of those reprinted papers were edited by Klein and his assistants almost 50 years later, and some of the changes they made were consequential. Thankfully, the internet makes it easy to access the original journal articles, which are the basis for my analyses. On the other hand, I have usually reproduced the drawings made for volume 2 of his collected works, since these are technically superior to the originals.

2 Trends in algebraic geometry, 1840–1870

2.1 Heuristic tools

Like most commentators, Klein regarded Jean-Victor Poncelet as the decisive figure who inaugurated a kind of renaissance of synthetic geometry with the publication of his Traité des propriétes projectives des figures (Poncelet 1822).³ Prior to this, classical synthetic geometry had steadily lost ground to analytic geometry, a trend that began with Descartes, who polemicized very effectively against the methods of the ancients. Klein’s first mentor, Julius Plücker, was a leading proponent of analytic methods, whereas Berlin’s Jakob Steiner favored a synthetic style.⁴ Both knew one another personally, probably already in the early 1820 s, when they were both studying in Heidelberg. Later, when they were together in Berlin, they developed a deep mutual antipathy that undoubtedly reenforced the presumption that the differences in their methodological orientation were the root cause for this.⁵

Fig. 1

Pascal’s hexagon theorem

This view can easily lead to an exaggerated picture of the gulf separating these two central figures. For while it is true that Steiner’s followers shunned the use of analytic tools, the master himself was happy to consult with leading analysts, in particular C.G.J. Jacobi and Karl Weierstrass, who were eager to find new ways of attacking subtle geometrical problems. The old rivalry between Plücker and Steiner was, for Klein, entirely passé. In the first of the seven notes he appended to the text of his Erlangen Program, he discounted the traditional distinction between synthetic and analytic projective geometry entirely (Klein 1921–1923, 1: 490–491). Indeed, all his life, Klein regarded this particular methodological boundary as artificial and those who respected it, whether from the one side or the other, as engaged in a largely sterile and ultimately futile endeavor.

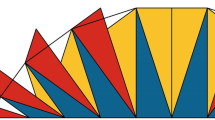
From the time of Poncelet and Joseph Diez Gergonne, geometers had puzzled over problems associated with the principle of duality, which treated points and lines as dual objects in the plane. A famous example was Pascal’s theorem, which states that for any hexagon inscribed in a conic section its extended opposite sides will meet in three points that lie on a line (Fig. 1). Here, the conic curve is viewed as a point locus, whereas the dual curve will be a conic enveloped by its tangent lines. The corresponding dual statement, found only in 1810 by Charles Julien Brianchon, is known today as Brianchon’s theorem (Fig. 2). This states that when six lines circumscribe a conic curve, the lines joining the three pairs of opposite vertices will pass through a single point.

Fig. 2

Brianchon’s dual theorem

Another famous case involving Steiner and Jacobi concerned Poncelet’s closure theorem (Fig. 3), also known as Poncelet’s porism (Poncelet 1822, sections 565–567).⁶ This states that if an n-gon is inscribed in a given conic C and also circumscribes another conic $C'$, then for any point $P \in C$ there is an n-gon with vertex P which is inscribed in C and circumscribed around $C'$. Steiner had known this earlier for the case of two disjoint circles, and after learning that Poncelet had proved the result for conics he suggested this as a suitable problem for Jacobi, who famously solved it using elliptic functions (Bos 1987, 313–321). This achievement represents one of the earliest examples in which a geometrical theorem was recast in the language of complex analysis. As we shall see, Clebsch proved to be a central figure in this type of enterprise.

Fig. 3

Poncelet’s closure theorem

Classical algebraic geometry dealt almost exclusively with curves and surfaces given by real equations. Over the course of the nineteenth century, however, mathematicians grew more and more accustomed to admitting imaginary points and lines that arose from such equations. They could then exploit the full force of the fundamental theorem of algebra, which so interpreted asserts that a curve given by an nth-degree polynomial equation with real coefficients, $y=f_n(x)$, will intersect the line $y=0$ in n points, taking multiplicities into account. Moreover, the roots of the equation will appear in conjugate pairs: $x= a\pm bi$.

These familiar algebraic facts point directly to key properties of real algebraic curves, the loci of homogeneous real algebraic equations treated as geometric objects in $P^2(\mathbb {C})$, the complex projective plane. By Bézout’s theorem, if $C_m$ and $C_n$ are given by equations with real coefficients of degree m and n, respectively, then $C_m \cap C_n$ consists of $m \cdot n$ points, counted with multiplicity, and the imaginary points will appear in pairs whose coordinates are complex conjugates. No one doubted this, though nothing like a rigorous proof for these claims existed at the time. One should also add, these statements pertain to irreducible curves. More precisely, if $C_m \cap C_n$ has more than mn points, then there are infinitely many and the curves are reducible. One typically neglected such degeneracies, however; an equation $f_4= f_2 \cdot f_2' =0$ was not viewed as a quartic curve but simply as the union of two conics. Similarly, for surfaces $F_m$ and $F_n$: their intersection $F_m \cap F_n$ will be a real space curve $C_{mn}$ of degree mn. These results became standard heuristic tools in algebraic geometry, although many geometers struggled to find intuitively clear explanations for how one could visualize imaginary objects.

As emphasized by Bottazzini and Gray, Riemann’s novel approach to complex analysis—including his appeal to Riemann surfaces, which cannot be embedded in $\mathbb {R}^3$—greatly exacerbated these difficulties (Bottazzini and Gray 2013, 331–334). They noted further that Alfred Clebsch was the first to bring out the fertility of Riemann’s ideas for algebraic geometry in “On the Application of Abelian Functions in Geometry” (Clebsch 1864c), a study that paved the way for several papers by Klein to be discussed below. Klein drew on many different sources in his early work, though some of his papers reflected a strong visual style almost entirely absent in the publications of Clebsch and Riemann.

As a student of Otto Hesse in Königsberg, Alfred Clebsch developed a strong affinity for the kinds of analytic methods Hesse had used in his studies of algebraic curves and surfaces. Many of their properties had been uncovered earlier by Plücker and Steiner, but Hesse’s approach was far more powerful and elegant. By the time Clebsch arrived in Giessen in 1863, he had immersed himself in the symbolic methods Siegfried Aronhold had begun to introduce in invariant theory (Parshall 1989). As pointed out in an insightful section of the multi-authored obituary article for Clebsch (Brill 1873, 199)— surely written by his boyhood friend Carl Neumann with whom Clebsch had co-founded Mathematische Annalen in 1868—this phase in his career, from 1863 to 1868, coincided with Clebsch’s fruitful collaboration with Paul Gordan (Clebsch and Gordan 1866). After Klein brought Gordan to Erlangen in 1874, they too began working together closely. Immediately after Plücker’s death in 1868, Clebsch came to exert a strong influence on Klein, though his pupil later took pains to distance himself from the legacy of his second mentor.⁷

Although Plücker was an analytic geometer, he never sought to subordinate intuitive geometric conceptions to modern formalisms, which he in fact used rather sparingly. One of the keys to Plücker’s working methods was his ability to exploit an abbreviated notation so as to “read into an equation” or to make cunning use of a parameter in it (the Plückerian $\mu$) (Klein 1926–27, 1: 122–123). As an example of the first, he found a way to write the equation of a general quartic curve so that four of its 28 double tangents pop out of the equation immediately. He wrote this in the special form:

$$\begin{aligned} \Omega ^2-\mu \, pqrs=0, \end{aligned}$$

where $\Omega =0$ represents a conic, $p=0, q=0, r=0, s=0$ are four lines, and $\mu$ is a free parameter. Plücker’s argument was based on counting coefficients: he showed that this form had 14 parameters in agreement with the number for a general quartic equation. Writing the quartic in this form, he could immediately deduce that the lines $p=0, q=0, r=0, s=0$ are double tangents, since their two intersection points with the conic $\Omega =0$ are counted twice. Thus, for these four bitangents, all eight points of tangency lie on a conic. Plücker then jumped to the erroneous conclusion that this result applied for all 28 bitangents, namely that one could find for any two of them another pair so that these four took the above form.⁸

Plücker’s celebrated proof of Pascal’s theorem provides a splendid example of how he exploited the Plückerian $\mu$ (Klein 1926–27, 1: 122). Instead of starting with six points on a conic $C_2$, he considered two triples of lines p, q, r and $p',q',r'$ for which six of their nine points of intersection lie on a $C_2$, whereas the other three are $p\cap p'= P, \,\, q\cap q'= Q, \,\, r\cap r'= R$. He then formed the net of cubic curves $C_{\mu }: pqr-\mu \, p'q'r'=0$ covering the plane. Since all of these $C_{\mu }$ pass through the same six points on $C_2$ as well as $\{P,Q,R\}$, if we take any seventh point on the conic, then this will determine a value of $\mu$ corresponding to a curve in $C_{\mu }$ passing through seven points on $C_2$. But by Bézout’s Theorem, this can only happen when the cubic contains all the points of the conic, hence for this particular cubic $C_{\mu } = C_2 \cup \ell$, where $\ell$ is the the Pascal line containing $\{P,Q,R\}$. Voila.

These few examples are suggestive of Plücker’s methods as an analytic geometer. Such rather intuitive techniques differed sharply from those developed afterward by analytic geometers such as Otto Hesse and Alfred Clebsch, both of whom developed and systematically exploited determinants and other invariant-theoretic methods in their work.

Felix Klein’s own style was influenced by both of these directions, though he was fundamentally an intuitive geometer who sought to take advantage of the modern analytic methods that had radically reshaped geometrical research after Plücker’s time. Long before then, Plücker made a particularly important discovery that enabled him to unravel one of the old mysteries connected with duality. In 1839, he found the so-called Plücker formulas (Plücker 1839), which describe how the point and tangential singularities of a given curve are related to its reciprocal, the associated dual curve (Gray 2011, 165–168). For curves of degree two (conic sections) this problem does not arise, since the maximum number of tangents to a curve from a generic point, called the class k of the curve, agrees with its order n, the maximum number of points that meet a generic line, namely two. Applying duality, which interchanges points and lines, produces a curve with order k and class n, so applying it twice should produce the original curve, which it does if $n=k=2$. Clearly this breaks down, however, for higher curves (degree $n>2$), as $k= n(n-1)$ when no singularities are present.

Plücker was able to salvage the duality principle by noting that a nonsingular curve of degree 3 or higher, viewed as a point locus, always has simple tangential singularities (inflection or double tangents). He found that for a curve of degree n, there are $w=3n(n-2)$ inflection tangents, whereas for a curve with d double points and r cusps this number reduces to

$$\begin{aligned} w=3n(n-2)-6d-8r.\end{aligned}$$

Similarly, the degree of the dual curve $C^*$ will be affected by the point singularities of the curve C. Plücker allowed only the simplest singularities—double points and cusps—which suffice for curves of degree less than five; these point singularities correspond to double tangents and inflection tangents for class curves. Based on these, he was able to establish the following dual formulas, where t denotes the number of double tangents:

$$\begin{aligned} k= & {} n(n-1)-2d -3r, \qquad w = 3n(n-2)- 6d -8r,\\ n= & {} k(k-1)-2t -3w, \qquad r = 3k(k-2)- 6t -8w. \end{aligned}$$

Since point singularities arise as special cases for curves of order $n \ge 3$, Plücker conceived of their acquisition as part of a dynamic process. He, thus, spoke of a double point as “absorbing” six inflection tangents, whereas a cusp absorbed eight (and dually for class curves).

From these formulas, Plücker could also derive the number of bitangents,⁹ namely

$$\begin{aligned} t= \frac{1}{2}n(n-2)(n^2-9). \end{aligned}$$

It follows that the number of double tangents for a nonsingular quartic curve is 28.¹⁰ The 28 bitangents to quartic curves later gave rise to a substantial literature, which included two oft-cited works by Steiner (1855) and Aronhold (1864).

The Plücker formulas clearly remain valid when a curve is transformed to its dual, as the point singularities then pass over into tangential singularities and vice versa. Since their presence lowers the order and the class of the curve by exactly the same amount, duality is fully preserved. One sees, in particular, that a nonsingular cubic curve will have $w = 3\cdot 3(3-2)=9$ inflection lines, though only three of these can be real. Somewhat later, geometers uncovered another invariant, which they placed alongside the Plücker formulas:

$$\begin{aligned} p= \frac{1}{2}(n-1)(n-2)- d - r. \end{aligned}$$

Clebsch called this the genus (Geschlecht) of the curve, and in 1866 he and Paul Gordan proved it was a birational invariant (Clebsch and Gordan 1866, 15). Riemann had earlier recognized the importance of this invariant in the context of geometric function theory, and Klein struggled to gain an intuitive understanding of its significance in his early work.¹¹ Cayley called p the deficiency of an algebraic curve $C_n$, an allusion to the maximum number of double points possible (Cayley 1865, 2). Thus, for a nonsingular quartic, for which $p=3$, allowing $d =3$ double points leads the deficiency to vanish. Here again, following Plücker, geometers might speak of double points (or cusps) absorbing part of the deficiency or genus. If a quartic $C_4$ has $d =4$, it can no longer absorb them, and so the curve reduces to two conics: $C_4 = C_2 \cup C_2'$. Riemann gave this invariant an entirely different twist by connecting p with the number of independent Abelian integrals of the first kind that can live on a given Riemann surface, a number he connected with the topology of the surface. At the same time, he used this means to discuss complex integration for algebraic functions. Such a function can be represented by a surface, say with m leaves and w branch points, in which case

$$\begin{aligned} p= w/2 -m +1, \end{aligned}$$

(Riemann 1857, 104). Clebsch wanted to avoid using complex analysis, and he later found a way to define p without it.

Although the Plücker formulas pertain to points and lines with complex coordinates, one could easily recognize their relevance for the main object of interest, namely the points on and tangents to a curve in the real projective plane ($P^2(\mathbb {R})$). The genus of an algebraic curve, on the other hand, appeared to have little or no connection with that portion of the curve that one could actually see. Klein would later write that he felt a deep urge to resolve this conundrum, which he experienced as a “truly tormenting problem.”¹² Part of the answer he found to that problem drew on ideas about duality that he had learned from Plücker, who emphasized that the geometer should study objects based on any suitable space element rather than feeling constrained to regard points as the fundamental entities. In the same spirit, Plücker impressed on Klein the importance of studying class curves, which arise as envelopes of lines. Thus, instead of viewing a curve C of degree n as a locus of points, one could examine its dual curve $C^* \subset P^2(\mathbb {R})$ as a class curve with $k=n$. This image of the real curve then served as a kind of skeletal framework around which Klein could attach the imaginary part to obtain the full complex curve or what he would later call a new type of (projective) Riemann surface (see Sect. 7).

Naturally, this object was never meant to displace the conventional Riemann surfaces employed in complex analysis. Klein only mimicked the properties of these geometrical objects without attempting to do more than provide insights for the theory of real algebraic curves. Since the imaginary points (s, z) that satisfy such an equation $F(s,z)=0$ appear as conjugate pairs, Klein imagined each of these as lying on different leaves of the surface. One can appreciate the motivation behind this new image of a Riemann surface by reflecting on long-standing interests in the properties of real algebraic curves, which brings to mind Isaac Newton’s elaborate studies on cubic curves (Guicciardini 2009, 109–136). Moreover, the dearth of studies devoted to real curves after 1900 should not deflect attention from the fact that many questions in this classical field, including Hilbert’s sixteenth Paris problem (Hilbert 1900, 317), still remain open. Many mathematicians have long recognized that algebraic geometry over the field of real numbers is a very difficult subject.

In modern terms, one associates an algebraic curve with a compact Riemann surface and vice versa. Klein’s projective Riemann surfaces had the same property; in many cases they were also without branch points. His idea started by noting that the topological genus for a nonsingular curve agreed with $p= \frac{1}{2}(n-1)(n-2)$. He then used qualitative arguments to show how the presence of double points and cusps lowered the genus in accordance with the formula $p= \frac{1}{2}(n-1)(n-2)- d - r$. Thus, by means of pictures, he hoped to provide a convincing argument that could account for the deeper meaning of Clebsch’s formula (see Sect. 7). As I shall argue here, Klein’s new types of Riemann surfaces owed rather little to Riemann and much to Plücker and Clebsch. One can fairly say that Klein sought not only to refine certain results from their works—in particular, Plücker (1839), Clebsch (1864a, 1864c)—but also to make those findings visually transparent.

2.2 International connections

In this connection, it should also be emphasized that Plücker, Clebsch, and Klein all cultivated numerous contacts with geometers outside Germany.¹³ Indeed, so did several others, as projective algebraic geometry took on an international character over the course of the nineteenth century. Plücker’s work, in particular, circulated among leading mathematicians in Paris as well as in Great Britain. Regarding the latter, the Irish theologian George Salmon collaborated with the highly prolific Arthur Cayley on algebraic curves and surfaces. Knowledge of their achievements soon spread to the continent, largely thanks to Wilhelm Fiedler’s numerous German translations and elaborations of Salmon’s assorted textbooks, including Salmon (1848, 1852). The various editions of Salmon-Fiedler served as one of the major conduits transmitting a suggestive new style in geometry to the German-speaking world, whose practitioners soon returned the favor. By the 1870s, Cayley and J.J. Sylvester, who together pioneered British invariant theory, saw their work enriched and transformed by leading German algebraists, one of whom was Alfred Clebsch (Parshall 1989).

Salmon and Cayley were the first to discover that cubic surfaces contain a special configuration composed of 27 lines, all of which can be real in some cases (Cayley 1849). This breakthrough soon led to numerous investigations of the properties of that configuration and its implications for the geometrical structures found on general cubics. By the mid-1860s, projective algebraic geometry was moving into a new phase characterized by more systematic investigations. The Swiss geometer Ludwig Schläfli made an important advance in the classification of cubic surfaces by studying their singularities and the reality of their lines (Schläfli 1863). His work was followed by a related investigation undertaken by Cayley (1869), who also attempted to construct a model for the configuration of 27 lines. At the instigation of Clebsch, Christian Wiener produced the first successful model of a cubic surface showing all 27 lines on it (Fig. 4). Soon thereafter, Clebsch and Klein began working together in Göttingen to produce other models of cubics, including Clebsch’s diagonal surface (Fig. 11, see Sect. 5).

Fig. 4

Christian Wiener’s model of a cubic surface, models collection of Tübingen University; (Seidl et al. 2018, 186)

These various developments in higher geometry went hand in hand with counting problems, which eventually led to the sub-discipline known as enumerative geometry. Like the field of geometry itself, its leading practitioners came from across Europe and included Michel Chasles (France), H.G. Zeuthen (Denmark), and Hermann Schubert (Germany). Their methods were largely heuristic in nature. Thus, Chasles developed what came to be called the Chasles characteristic, which he used to ascertain the number of conics satisfying given algebraic conditions (Michel 2020). In the 1880s, this principle was closely analyzed and refined by Georges Halphen, but his findings later came under sharp attack from Eduard Study, whose criticisms sparked a heated international debate (Hartwich 2006). By 1890, several geometers had come to recognize the need for rigorizing enumerative techniques, in particular those of Schubert’s calculus. Thus, Hilbert was merely adding his voice to this chorus when in 1900 he announced his 15th Paris problem, which called for a stringent grounding of Schubert’s methods (Hilbert 1900, 316),¹⁴

Klein’s interest in Riemann’s work was initially filtered through the publications of his second mentor, Alfred Clebsch, who was among the first to exploit Riemannian ideas in algebraic geometry, including the notoriously complicated realm of enumerative geometry. After mid-century, the mathematical world witnessed a veritable explosion of new results regarding the number of systems of conics or cubics with special tangency relations to a given quartic curve, etc. Such findings had classical roots if one hearkens back to the famous problem of Apollonius calling for the construction of a circle tangent to three given circles, where one can easily see that this might involve as many as $2^3=8$ cases. Enumerative geometry, though, had nothing to do with explicit constructions; one inquired simply as to the number of cases possible. Steiner was an incredible virtuoso in this realm, though he left his contemporaries in the dark as to how he found many of his results, as Hesse duly noted in Hesse (1863).

Such problems held great appeal for Clebsch, who saw himself as an intellectual descendent of Plücker (Clebsch 1871a). Clebsch clearly appreciated Plücker’s talents as an intuitive thinker, both in geometry as well as in physics. In a memorial address in his honor, Clebsch explicitly drew that parallel in claiming: “Just as the pleasure in form in a higher sense is what makes the geometer, so it was the source of his [Plücker’s] physical investigations.” (Clebsch 1871a, 6).¹⁵ One finds very little in Riemann’s works that reflects a similar interest. Riemann was a notoriously difficult author, and since he died young his contemporaries faced a major challenge in attempting to grapple with his novel ideas. Clebsch was one of the first to do so, but it seems likely that Riemann felt he had only scratched the surface. Shortly before Riemann’s death, Enrico Betti commented in a letter to Felice Cassorati that so far as geometry was concerned, Riemann thought that “Clebsch still had a long way to go” (Bottazzini and Gray 2013, 331).

It may be appropriate here to cite the words of Clebsch himself, who had this to say about two distinctly different research orientations among mathematicians:

Research may start from definite problems whose importance it recognizes and whose solution is sought more or less directly by all forces. But equally legitimate is the other method of research which only selects the field of its activity and, contrary to the first method, freely seeks for problems which are capable of solution. Different individuals will hold different views as to the relative value of these two methods. If the first method leads to greater penetration, it is also easily exposed to the danger of sterility. To the second method we owe the acquisition of large and new fields, in which the details of many things remain to be determined and explored by the first method. (Brill 1873, 201)

The author who cited this passage rightly pointed out that Clebsch belonged to the second of these two types of researchers.

3 Klein’s refinement of Plücker’s formulas

3.1 Zeuthen’s classification of quartic curves

In Zeuthen (1874), the Danish geometer Hieronymus Georg Zeuthen gave the first comprehensive classification of real plane curves of degree four. A simple way to derive two basic types of quartics involves starting with the equations for two real conics that meet in four real points (Klein 1921–1923, 2: 110–111). Let $f_2=a^2x^2+b^2y^2-1= 0, \,\, g_2=b^2x^2+a^2y^2-1= 0$. Together, these conics serve as a skeletal frame for a quartic with the equation $f_2 \cdot g_2 = \epsilon \ne 0$, where $\epsilon$ is a small number.

Fig. 5

Two standard real quartic curves: the outer component of the “belt curve” on the left has four real double tangents, whereas all 28 bitangents of the curve on the right are real

If $\epsilon >0$ then the curve has two components, like the one on the left in Fig. 5. Here, the points on $C_4$ lie either outside or inside both conics. The type on the right arises simply by reversing the sign of $\epsilon$, so that the equation becomes $f_2 \cdot g_2 = \epsilon <0$; the curve then appears in the four sectors that lie outside one conic and inside the other. Virtually all studies of the various types of real algebraic curves in the plane utilized such deformations starting with a degenerate curve.¹⁶

The two standard types shown in Fig. 5 play an important role in Zeuthen’s theory. For the first, he called the outer branch a quadrifolium because it has four double tangents (see Fig. 6 from Zeuthen (1874)). For the second type, Zeuthen presented it alongside another curve (Fig. 7), as the quadrifolium of curve 1 touches the four unifolia of curve 2 in eight points. These are the points of contact for four internal double tangents, which play a key role in Zeuthen’s classification scheme. The remaining 24 tangents are all real and appear in fours by taking the six pairs of unifolia.

Fig. 6

An annular quartic with a quadrifolium and an internal oval: Zeuthen’s type I.1

Fig. 7

Curve 1 (type I.2) is a quadrilateral quartic consisting of a quadrifolium and two external ovals. Curve 2 (type I.3) is a trilateral quartic composed of four unifolia

Zeuthen’s overall classification involved 13 main types of quartics, broken down into 36 forms altogether (Zeuthen 1874, 419–420). He established their existence by using a slightly different version of Plücker’s form for a 1-parameter family of quartic curves:

$$\begin{aligned} k\Omega ^2 + pqrs=0, \end{aligned}$$

where $\Omega =0$ is a conic and $p=0,\,\, q=0,\,\, r=0,\,\, s=0$ are four double tangents to the curve. After this, Zeuthen allowed the parameter k to vary continuously as he described the various types of curves that arose. This qualitative discussion based on continuity was, of course, undertaken in precisely the same spirit as Klein’s treatment of the manifold of all real cubic surfaces.

Zeuthen noted at the outset that if $k=0$, then the $C_4$ degenerates to the case of a quadrilateral with 6 double points. For small values of k, the curve will be of type I.2 (the darker curve in Fig. 7), a quadrifolium with two external ovals. As k grows larger, the ovals will shrink until they eventually become isolated double points before disappearing altogether; these parts of the curve have then become imaginary. A curve of type I.1 (Fig. 6) can now emerge from an isolated point in the interior of the quadrifolium, etc.

In the course of his classification of quartic curves, Zeuthen made a fundamental distinction between bitangents touching a single component of the curve (bitangents of the first kind) and those touching two different components (the second kind). In Fig. 7 two of the four bitangents of the first kind can be seen. When such a curve evolves into a different type, however, Zeuthen observed that the double tangent can disappear (becoming an imaginary bitangent). When this happens, the unifolium passes into an oval, which means that two real inflection points disappear as well.

3.2 Klein on singularities of real algebraic curves

Zeuthen’s insight into the connection between imaginary double tangents and inflection points on quartic curves awoke Klein’s curiosity. He asked himself why this relationship should be restricted to quartics, as Zeuthen seemed to suggest. It turned out, as Klein showed in Klein (1876b), that Zeuthen’s finding was valid for any real algebraic curve. The case of four unifolia (curve 2 in Fig. 7) is instructive in several respects. First, it illustrates Harnack’s theorem, which states that an algebraic curve can have at most $p+1$ real components (Harnack 1876). Since a nonsingular quartic has genus $p=3$, it can have at most four. Furthermore, as Zeuthen observed, since each double tangent of the first kind encloses two inflection points, this special quartic realizes the maximum number of real inflection points for a quartic, namely eight. Altogether a nonsingular quartic has 24, and in the general case a $C_n$ has $w= 3n(n-2)$ inflection points.

In Klein (1876b) Klein proved that for a nonsingular $C_n$ with $w'$ real inflection tangents and $t''$ isolated double tangents

$$\begin{aligned} w' + 2 t'' = n(n-2). \end{aligned}$$

Thus, when no isolated bitangents are present, the number of real inflection points will be one third of the total, in agreement with the case just considered. Klein interpreted this formula as asserting that whenever a real bitangent becomes isolated (whether as a real or imaginary line) it reduces the number of real inflection points by two. Klein proved this result before considering the case of curves with simple singularities, double points and cusps, which are the only types that enter into the Plücker formulas. Here, he considered a curve of order n and class k with $r'$ real cusps and $d''$ isolated double points, and then showed that

$$\begin{aligned} n+ w' + 2 t'' = k + r' + 2d''. \end{aligned}$$

He noted that if these $d''$ are the only point singularities, then following Plücker one has $k= n(n-1) -2d''$, in which case $n+ w' + 2 t'' = n(n-1)-2d'' + 2d''$, which leads back to $w' + 2 t'' = n(n-2).$

Klein began his proof by showing that for nonsingular curves $w' + 2 t''$ was a constant. He then considered special cases of curves of even and then odd degree to confirm the result. In the case of a curve of order $n= 2\mu$, Klein took a family of congruent concentric ellipses, arranged symmetrically about the origin. Each ellipse then intersects every other in four points, so that there are

$$\begin{aligned} 4 \frac{\mu (\mu -1)}{2}= \frac{n(n-2)}{2} \end{aligned}$$

double points altogether. The total number of bitangents is then $t= \frac{1}{2}n(n-2)(n^2-9)$, and in this case all are real and none are isolated. Klein noted that there are three types:

• 1) $n(n-2)/2$ are bitangents to pairs of ellipses;

• 2) $n(n-2)(n-4)/2$ pass through an intersection point of two ellipses and touch a third (these count twice);

• 3) $n(n-2)(n^2-2n-2)/8$ which join pairs of intersection points of ellipses (these counted 4 times).

Next Klein desingularizes this curve by the same method discussed above, noting that the dissolution of each of the $\frac{n(n-2)}{2}$ double points produces two real inflection points, showing that

$$\begin{aligned} w' = n(n-2). \end{aligned}$$

He then presented a simple argument to conclude that the number of real isolated double tangents $t''=0$ throughout this deformation process (Klein 1921–1923, 2: 85), thereby proving the general result. For a curve of odd degree $n=2\mu +3$ he used a similar idea with $\mu$ ellipses that meet a specially chosen cubic curve in six points.

To handle simple singularities, Klein considered the effect on $w'$ and $t''$ of small deformations that remove them. He noted three cases, the first two of which had been discussed earlier by Plücker: (1) every real (non-isolated) double point and every real cusp absorbs two of the $w'$ real inflection tangents; (2) isolated real double points do not affect $w'$; (3) the real line connecting two conjugate imaginary double points absorbs two of the $t''$ real isolated double tangents, whereas the real line connecting two conjugate imaginary cusps absorbs three. Drawing on these transformation rules, and breaking down the double points and cusps ($d'$ real non-isolated, $d''$ real isolated, $d'''$ imaginary) and cusps ($r'$ real, $r''$ imaginary), Klein could generalize the above formula to read:

$$\begin{aligned} w' + 2 t'' = n(n-2) - 2d' - 2r' -2 d''' -3r''. \end{aligned}$$

Together with the Plücker formula

$$\begin{aligned} k= n(n-1) -2(d' + d'' + d''') - 3(r' + r''), \end{aligned}$$

this leads to the elegant result connecting the order and class:

$$\begin{aligned} n+ w' + 2 t'' = k + r' + 2d''. \end{aligned}$$

Klein ended this paper with a brief discussion of curves with complex coefficients. His principal findings, however, concerned real curves and, in effect, presented a refinement of the classical results presented decades earlier by Plücker. Unlike many other contemporary algebraic geometers, Klein paid little attention to the difficult problems that arise when studying curves with higher singularities. Cayley had already set forth a bold approach to these in 1866 (Cayley 1866), where he claimed that one could effectively simplify the structure of any singular point by reducing it to Plücker’s singularities. Alexander Brill then took up this challenge in 1880 (Brill 1880), a lengthy paper in which he utilized Puiseux series to analyze the local structure of singular points (on this method, see Brieskorn and Knörrer (1986, 512–535)). In his paper, Brill mentioned Klein’s results only in passing, while emphasizing that his own work provided a rigorous analytic method for what it means to deform a singularity (Brill 1880, 631). Seen from the perspective of mainstream interests in algebraic geometry during the 1870s, it seems fair to say that Klein’s research aimed to explore some attractive rivulets that others mostly ignored.

4 Plücker and Clebsch as key influences

4.1 Plücker’s geometrical models

Plücker’s strong interest in the visual side of geometry can readily be seen from the exotic-looking models he designed as tools for his research in line geometry. These illustrate the various shapes of special quartic surfaces enveloped by families of lines that belong to a complex of the second degree (Fig. 8 is one such example) (Klein 1874c). These models were usually made from a heavy metal, such as zinc or lead, and for around 50 years after Plücker’s death, one could still see them on display in Germany and elsewhere abroad. In 1866, Plücker took some with him to Nottingham. There at a scientific conference he spoke about the properties of these so-called complex surfaces. Arthur Cayley, Thomas Archer Hirst, Olaus Henrici, and other leading British mathematicians soon took an interest in them, as they were certainly among the more interesting geometrical objects of their day (Cayley 1871).

Plücker realized that the 3-parameter family of lines in a quadratic line complex was far too complicated to be studied globally. His models, thus, aimed to provide a picture of the local structure of such a complex by fixing a line $\ell$ in space. If $K_2$ is a quadratic complex, then Plücker calculated the 2-parameter subfamily of lines in $K_2$ that intersected $\ell$. These form a congruence of lines, which envelopes a caustic surface, the object to be modeled. Because Plücker’s calculations involved complex coordinates, he needed to differentiate carefully between real and imaginary structures, while also taking degenerate cases into account.

Fig. 8

A Plücker model from Munich Technical University, Photo courtesy of Gerd Fischer

Plücker’s complex surfaces turned out to be closely related to Kummer surfaces (Klein 1874b; Hudson 1905), which originally arose in the context of geometrical optics (Rowe 2019, 2022).¹⁷ Indeed, Kummer surfaces represent a natural generalization of the wave surface, first introduced by Augustin Fresnel to explain double refraction in biaxial crystals (Rowe 2013). In 1870, when he was collaborating with Sophus Lie, Klein made good use of a geometrical model to explore the asymptotic curves on a Kummer surface (Rowe 2023, 178–184). Three years later, after studying a model of Clebsch’s diagonal surface (see Fig. 11), he published a qualitative picture of the family of asymptotic curves on it (Fig. 9).

Fig. 9

Klein’s drawing of asymptotic curves on the diagonal surface in Klein (1921–1923, 2: 39)

Klein was probably the first to recognize the importance of Kummer surfaces and related quartics for the classification of quadratic line complexes. Rather than working out this theory in detail, however, he assigned that task to his Erlangen doctoral student, Adolf Weiler, whose dissertation was later published in 1874 (Weiler 1874). By the late 1880 s, this became his dominant approach to research, as he began to orchestrate large-scale projects carried out by others, one of whom, Robert Fricke, became his nephew.

4.2 Clebsch and the birth of modern algebraic geometry

During the early 1860s, Clebsch had come to realize the importance of Riemann’s monumental study of Abelian functions (Riemann 1857) and Abel’s Theorem as tools for deriving deep results in algebraic geometry. Igor Shafarevich later called Clebsch’s lengthy study (Clebsch 1864c) the “birth cry” of modern algebraic geometry (Shafarevich 1983, 136). Shafarevich remarked further that Clebsch’s long-term reputation may have suffered not only due to his early death—he succumbed to an attack of diphtheria in November 1872 at the age of 39—but also because his influence spread through the work of his many students, among whom Klein would become the most prominent.

If we resist the strong temptation to view this chapter in the emergence of algebraic geometry retrospectively, then the question arises as to the place occupied by Riemann and his followers within the course of these developments. Clearly, Riemann’s influence was vast, and yet among the many responses to his work listed by Bottazzini and Gray (2013, 311–312), nearly all had far more relevance for complex analysis than for algebraic geometry. A key aspect to consider in this connection concerns Riemann’s investigations on the bitangents to quartic curves, one version of which appeared posthumously in Riemann (1876).¹⁸ That publication came from a manuscript compiled by Gustav Roch in 1862, when he attended a lecture course taught by Riemann.

Although we cannot exclude the possibility that Clebsch had known about Riemann’s work on this topic, there appears to be no extant evidence for supporting this claim. Assuming that Clebsch’s knowledge of Riemann’s theory of Abelian functions was limited to Riemann (1857), one can hardly consider Clebsch’s study (Clebsch 1864c) as anything less than an impressive creative achievement that made Riemann’s work accessible to algebraic geometers for the first time. Unfortunately, however, the historical circumstances are drenched in complications that obscure the processes of reception and development, which will be described briefly in Sect. 10.

A key figure for understanding Riemann’s interests in this direction was Gustav Roch. In 1866, the year of Riemann’s death, Roch also published a detailed study of the bitangents to a quartic curve based on theorems and formulas derived by Riemann. In that paper, Roch alluded to the latter’s lecture course, noting that Riemann had showed how one can forgo the use of $\theta$-functions in obtaining the same results (Roch 1866, 97). What he meant by that remark, however, remains unclear. Roch’s own paper from 1866 appears to be the first place in which Riemann’s notion of characteristics of $\theta$-functions appeared in print (Roch 1866, 101).¹⁹

Had Roch lived longer, he would likely have clarified various questions relating to Riemann’s interest in algebraic curves. Roch’s paper from 1866—which also drew on Roch (1866), his far more famous paper from 1 year earlier, which turned the Riemann inequality into a meaningful equality: the Riemann–Roch theorem—is filled with precise references to Riemann’s famous study of Abelian functions from 1857 (Riemann 1857) but without a single direct reference to Clebsch’s publications. Roch instead began by alluding to the many related results on algebraic curves published by Hesse and Steiner in volume 49 (1855) of Crelle (Hesse 1855a, b; Steiner 1855). Only later did he mention Clebsch’s work in passing (Roch 1866, 108), stating in effect that Riemann’s theory of $\theta$-functions leads directly to the principal tool utilized by Clebsch in his work on algebraic curves, namely the addition theorem for Abelian integrals. Roch’s apparent animus against Clebsch may well have come in response to remarks the latter penned at the outset of his groundbreaking study (Clebsch 1864c, 189–190), which placed this work firmly in the soil of Jacobi’s methods as opposed to those of Riemann.

These personal attitudes aside, the main question I wish to raise here concerns what Klein may have known about Riemann’s work during the period he wrote the papers described below. Since he penned these prior to the appearance of Riemann’s Werke in 1876—and even Klein (1877), his own study of the bitangents to quartics based on $\theta$-characteristics, made no mention of Riemann—he almost surely had never seen Roch’s posthumously published manuscript based on Riemann’s lectures. Whatever Klein did know about Riemann’s theory of Abelian functions, we can be sure this was strongly filtered through Clebsch, including the latter’s (Clebsch 1864c) as well as the monograph he and Paul Gordan published in 1866 (Clebsch and Gordan 1866). Klein was also aware of an important monograph by Heinrich Weber that appeared in 1876 (Weber 1876). We will pick up this discussion again in Sect. 10.

4.3 Klein’s early interest in geometric Galois theory

The algebraic side of Clebsch’s influence on Klein can readily be seen in the latter’s first paper on geometric Galois theory (Klein 1871), in which he noted their personal discussions relating to Clebsch’s paper on quintic equations (Clebsch 1871c).²⁰ At the outset, Klein referred directly to Camille Jordan’s Traité (Jordan 1870), which deals with several special equations derived from configurations in algebraic geometry (Brechenmacher 2011). Here Klein’s basic idea was to replace the n! permutations of the roots of an nth-degree equation by n! linear transformations of n elements (points, lines, planes) in $R_{n-2}$ (Heller 2022, 434–435). He viewed the image of these as a general Galois resolvent, from which he derived special resolvents, whose elements were multiples of certain subsets of these. Klein illustrated his method first for the case $n=4$ by taking a complete quadrilateral Q, thus four lines in general position in the plane, intersected by a fifth line $\ell$. This will, in general, lead to a group of $4!=24$ lines, unless $\ell$ happens to pass through a vertex of $V \in Q$, in which case the lines pass in pairs through V and the group reduces to one of order 12. If, on the other hand, $\ell$ passes through two vertices $V_1, V_2 \in Q$, then the group reduces to the three diagonal lines.

With this simple example as motivation, Klein then took up Sylvester’s pentahedron, the key structure underlying the lines and points on Clebsch’s diagonal surface. Its five planes, given by five linear equations

$$\begin{aligned} p=0, \qquad q=0, \qquad r=0, \qquad s=0, \qquad t=0, \end{aligned}$$

can be used to represent resolvents of quintic equations by means of $5!= 120$ planes in space. Klein emphasized, however, that the same considerations apply to any covariant of the pentahedron, in particular the 27 lines of the diagonal cubic surface studied by Clebsch, which satisfies the homogeneous equations:

$$\begin{aligned} p+q+r+s+t=0, \qquad \qquad p^3+q^3+r^3+s^3+t^3=0. \end{aligned}$$

Clebsch showed that these lines fall into two groups of 15 and 12, whose resolvents have multiplicity 8 and 10, respectively.²¹

With regard to ternary forms, Klein took the famous case of Hesse’s inflection-point configuration for plane cubic curves. He first observed that the cubic $C_3$ and its nine inflection points remain invariant under 18 linear transformations. These, however, permute certain groups of the inflection points which correspond to an equation of degree nine. Klein indicated how the corresponding resolvents can be found by first parameterizing the curve by an elliptic function and exploiting its periods, an idea first developed by Clebsch (1864a); see further Lê (2018). The nine inflection tangents form six triangles, each of which remains invariant under three of the 18 linear maps that fix $C_3$. A resolvent of degree 24 corresponds to the triangles, which requires solving an equation of degree four to determine the six groups of triangles and then the solution of the equation for the nine inflection points themselves. The problem essentially reduces to the division of an elliptic function by nine, as discussed by Jordan (1870). Klein’s interest in geometric Galois theory peaked soon after he published his well-known Ikosaeder book (Klein 1884). During the summer semester of 1886, his first in Göttingen, he taught a 4-h lecture course on this topic; its contents and goals are described in detail in Heller (2023). As might be expected, one of his principal examples was the equation for the nine inflection points of a cubic curve (Heller 2023, 36–37), as shown in Fig. 10. Hesse’s derivation of this famous configuration is discussed in 7.2.

Fig. 10

Klein’s drawing of the 9 points and 12 lines forming the inflection-point configuration (Heller 2023, 37)

As a more novel application, Klein ended with a treatment of the general equation of degree six. Here, he represented its six roots by six fundamental mutually apolar linear complexes,

$$\begin{aligned} x_1=0, \quad x_2=0, \quad \dots \quad x_6=0, \end{aligned}$$

i.e., complexes that lie pairwise in involution with each other.²² The $6!=720$ linear transformations of these six complexes correspond to 360 collineations and 360 reciprocal spatial mappings by which 720 lines, 360 points and 360 planes represent an image of the general resolvent for an equation of degree six. Klein then proceeded to sketch the other resolvents that arise by considering subfamilies of lines determined by belonging to 2, 3, or 4 of the $x_i$. Taking any two of them, one gets a 2-parameter congruence of lines with two directrices, which are the lines common to the other four complexes. This yields $6 \cdot 5/2 = 15$ pairs of directrices corresponding to a resolvent of degree 15. Furthermore, these 30 lines belong to 15 tetrahedra, which determine another resolvent of degree 15. One can also take five tetrahedra that contain all 30 lines and this can be done is six ways, so these groups of five tetrahedra correspond to a resolvent of degree six. Taking any three of the complexes, these determine a set of generators for a hyperboloid, whereby the other set of generators belong to the other three complexes. There are ten such hyperboloids, since $6 \cdot 5 \cdot 4/ \,\, 3 \cdot 2 \cdot 1 = 10$, and so we get a resolvent of degree 10.

Geometrical configurations play a prominent role in line geometry, providing problems that held much allure for Klein and his students in the future. Klein’s initial approach to Galois theory placed it in a geometric context, but in this paper he did not otherwise develop any new methods for solving the equations under investigation. We are also struck by the fact that he made no direct appeal to group theory; indeed, Klein did not so much as even invoke the language of group theory. His aim was merely to set forth a geometric image for the root substitutions of an algebraic equation by means of linear transformations of space (Klein 1871, 269). Later, starting around 1875, Galois theory would re-emerge as a focal point for Klein’s research thanks to a fruitful collaboration he developed with Clebsch’s long-standing protégé Paul Gordan (Gray 2019).

In the next section, we turn to Klein’s first important contribution to intuitive algebraic geometry: his deformation theory for real cubic surfaces.

5 Clebsch and Klein on cubic surfaces

5.1 Schläfli’s double-six and Clebsch’s diagonal surface

On 30 March 1872, Klein wrote to his older friend Otto Stolz in Innsbruck about his new findings in the theory of cubic surfaces $F_3$:

I have recently been working on a completely new project that I believe I can complete. The task is to derive the forms of the $F_3$. Depending on the reality of the straight lines, I arrive, like Schlaefli, at 5 types; but I show that these 5 types can also be defined by their connectivity in Riemann’s sense, the surfaces are fourfold, three-, two-, one-, zerofold connected. This would bring algebra and analysis situs together, which gives me great pleasure. I am particularly pleased that I can show how all possible forms of an $F_3$ are exhausted. I want to work this out.²³

Indeed, Klein did manage to work this out in a lengthy paper completed in June 1873 (Klein 1873). By the time this paper appeared, however, Schläfli had published a short paper (Schläfli 1872), in which he presented essentially the same connectivity results for the five types of cubic surfaces as those Klein announced in his letter to Stolz. At the close of his paper, Klein addressed the main differences between his projective approach and Schläfli’s treatment, which was based on Riemannian principles (Klein 1873, 577–581) (see the discussion at the end of this section) (Fig. 11).

Klein’s study marks the first attempt to establish a deformation theory for real cubic surfaces, a problem at the heart of his general interest in methods related to anschauliche Geometrie. As we shall see, the results Klein obtained were closely linked with concurrent findings of Zeuthen, who gave a new and complete classification of real quartic curves in the plane. Before turning to Klein’s paper directly, we first take account of the intellectual context that led to his interest in this topic.

Fig. 11

Clebsch’s diagonal surface. Model by Oliver Labs

In 1872, Clebsch and Klein had begun to explore a number of avenues opened by recent progress in the theory of cubic surfaces. Their work depended heavily on the celebrated discoveries made roughly a decade earlier by Schläfli, who showed that real cubics could be classified into five different types. His approach was based on a careful study of the 27 lines on a cubic surface, which he derived from a special configuration of 12 lines in space, today known as Schläfli’s double-six (Schläfli 1858). This can be denoted in matrix form as

$$\begin{aligned} \left[ {\begin{array}{cccccc} a_1 &{} a_2 &{} a_3 &{} a_4 &{} a_5 &{} a_6\\ b_1 &{} b_2 &{} b_3 &{} b_4 &{} b_5 &{} b_6\\ \end{array} } \right] , \end{aligned}$$

where the $a_i$ as well as the $b_i$ are mutually skew, whereas $a_i$ meets every $b_j$ and vice versa, except when $i = j$.

One can construct such a double-six by starting with any line $a_1$ and choosing four mutually skew lines $b_2, b_3, b_4, b_5$ that meet $a_1$. These four lines then uniquely determine a fifth line $a_6$ skew to $a_1$ and which also meets the four lines $b_2, b_3, b_4, b_5$. One can now choose a line $b_6$ that meets $a_1$ and lies in general position with respect to the four lines $b_2, b_3, b_4, b_5$. This means that $b_6$ is skew to these lines, so that any quadruple formed by taking $b_6$ and any three of the other lines cannot lie on a ruled surface. Now there will be exactly one line $a_5$ skew to $a_1$ that meets the four lines $b_2, b_3, b_4, b_6$. Analogously, we can find mutually skew lines $a_4, a_3, a_2$ that meet the corresponding four lines from the group of five $b_2, b_3, b_4, b_5, b_6$. Finally, since $b_6$ meets the lines in the quadruple $a_5, a_4, a_3, a_2$, but also $a_1$, one can show that there is a unique line $b_1$ that meets the same quadruple, but with $a_6$ rather than $a_1$, which completes the construction.

The remaining 15 of the 27 lines arise from such a double-six simply by taking pairs of indices i, j. Since for $i \ne j$ the four lines determine two planes, $E_{ij}= a_i \cap b_j$ and $E_{ji}= a_j \cap b_i$, these pairs of planes determine 15 additional lines. The double-six forms a $(12_5, 30_2)$ configuration, i.e., five points lie on each of its twelve lines and two lines pass through each of its thirty points. Likewise, the 27 lines form a $(27_{10}, 135_2)$ configuration, which contains 36 different double-sixes of lines.

One can now easily recognize how this construction leads to the 27 lines on a cubic surface by counting constants and making use of Bézout’s theorem. In the commonly employed language of classical algebraic geometers, one referred to the space of all cubic surfaces $F_3$ as a 19-dimensional manifold (either real or complex, depending on the coefficients utilized), and wrote $\infty ^{19}$ to indicate the number of parameters required. An arbitrary line $\ell$ then meets an $F_3$ in three points, except in exceptional situations. If $\ell \cap F_3$ contains four points, then by Bézout’s theorem, $\ell \subset F_3$. Returning to the construction above, take any four points on $a_1$ and three points each on $b_2, b_3, b_4, b_5, b_6$, so long as these points avoid the 30 incidence points of the double-six. These 19 points will then lie on an $F_3$ that contains $a_1$, and since $a_1$ meets the other fours lines, $F_3$ must also contain $b_2, b_3, b_4, b_5, b_6$. But for the same reason $F_3$ has to contain all 12 lines of the double-six, and hence the other 15 lines determined by its pairs of planes (Hilbert and Cohn-Vossen 1932, 146–148).

The 15 tangent planes passing through those lines cut out a triangle of lines on the surface. In special cases, these planes can even cut out three lines on the surface that pass through a single point called Eckardt points (Eckardt 1876). The special cubic Clebsch dubbed the diagonal surface has ten Eckardt points. He apparently came upon it in connection with his studies on quintic equations. In Clebsch (1871b) Clebsch noted that the English mathematician George Jerrard had found a resolvent of a class of quintic equations of class 30.²⁴ This corresponded to a space curve $C_6$ of degree six, which Clebsch showed was the complete intersection of surfaces of degree 2 and 3, thus $C_6= F_2 \cap F_3$, where the cubic $F_3$ is the diagonal surface, which is unique up its 120 automorphisms; see further Lê (2017).

In Lê (2015) François Lê described how Clebsch’s interest in “geometrical equations” inspired Camille Jordan to explore this topic. Jordan acknowledged this by writing:

Another fruitful research path has been opened up to analysts by M. Hesse’s famous memoirs on the inflection points of the curves of third order. The problems of analytic Geometry give indeed many other remarkable equations of which the properties, studied by the most illustrious geometers and especially by Mssrs. Cayley, Clebsch, Hesse, Kummer, Salmon, Steiner, are now well known and allow easy application of the methods of Galois. [...] Thanks to the liberal communications of M. Clebsch, we have been able to tackle the geometrical problems of Book III, Chapter III. (Jordan 1870, vi–viii)

As noted above, the structure of the diagonal surface depends on five planes that form a pentahedron. Clebsch gave this surface its name because 15 of its 27 lines appear in threes in each of the five planes of the pentahedron: they are the three diagonals determined by the complete quadrilateral cut out by the other four planes. These 15 lines meet in groups of three in the 10 vertices of the pentahedron, which are Eckardt points, accounting for the highly symmetric form of the diagonal surface. Its remaining 12 lines form a Schläfli double-six. In this first paper, Clebsch indicated the desirability of having a physical model that illustrated its properties (Clebsch 1871b, 342).

As it happened, the Swiss geometer Adolf Weiler was studying under Clebsch at the same time Klein was teaching in Göttingen as a Privatdozent while collaborating with his second mentor. In August 1872, Clebsch presented Weiler’s model of the diagonal surface to the Göttingen Scientific Society. At the same meeting, Klein presented a model of a cubic surface with four singular nodes, which was built by the physicist Friedrich Neesen. Already on this occasion, Klein claimed that one could begin with any surface of this type and obtain every other type of cubic by systematically desingularizing such a cubic with four nodes, the maximum number possible (Clebsch and Klein 1872, 404). The following June, Klein submitted his fairly lengthy paper to Mathematische Annalen in which he attempted to prove this claim (Klein 1873).

5.2 Klein’s deformations of cubic surfaces

Klein’s original inspiration for removing singular points on cubic surfaces came from curve theory (Klein 1873, 551), though the situation when handling plane curves is far simpler. In the case of cubic curves, one can easily follow such a deformation process by starting with the standard equation

$$\begin{aligned} y^2 = (x-e_1)(x-e_2)(x-e_3), \end{aligned}$$

where $e_1< e_2 <e_3$. This curve, shown on the left in Fig. 12 is nonsingular, so $p=1$, and it has two components. The curve on the right with a single component is also nonsingular, but one can only reach it from the curve on the left by passing through a singular cubic.

Fig. 12

Two types of nonsingular cubic curves in standard form

Fig. 13

Three types of singular cubic curves

This can happen in one of two ways, as illustrated in Fig. 13. Taking $e_3=0$ and gradually shrinking the oval on the left until $e_1 = e_2$, we obtain a cubic with isolated double point, as shown on the right. To desingularize this curve, we imagine this double point dissolving into two conjugate imaginary points, thereby producing a curve that looks like the one on the right in Fig. 12. A slightly lengthier process can be seen from the two other curves in Fig. 13. Again letting $e_3=0$, but holding $e_1$ fixed while $e_2$ gradually moves toward $e_3$, we get a cubic with ordinary double point when $e_2 = e_3$. Shrinking the loop until $e_1= e_2 = e_3$, we get a cubic with a cusp at the origin. The equation then reads $y^2=x^3$, a curve known as Neile’s parabola. To desingularize it means breaking the cusp up into three points, two being conjugate imaginary and the remaining one is then the regular point at the origin.

These types of singularities are easily handled, whereas a cubic surface can have more complicated types. The simplest are conical points, but a cubic surface can also have biplanar singularities, if the cone degenerates into two intersecting planes, and if the planes coincide, uniplanar singular points. Klein therefore needed to convince himself that one could remove any type of singular point without introducing new ones. For this purpose, he used two types of deformations: the first by joining (denoted +) and the second by separating (denoted –).

Klein’s starting point was a special cubic that Adolf Weiler modeled for him. Its four singular points form the vertices of a convex tetrahedral shaped piece at the center of Fig. 14. Three of these singular points are visible in the triangular front face of the tetrahedron, as are its three edges. Only the front edge of the top face is visible, but one can see the extended portions of the other two lines that form its edges, which meet at the invisible fourth vertex point. These four singular points are thus joined by six edges, which counted in fours represent 24 of the 27 lines on the surface. The remaining three are located in a plane just below the tetrahedron. Carrying out the two types of deformations on a single vertex produces two types of cubics with three singular points, and repeating this process leads to three types with two singularities, four types with one, and finally five types with none. All but the fifth type (– – – –), which consists of two components, are connected surfaces.

Fig. 14

Model of a cubic surface with four singular points. From Klein (1873, 2: 15)

Having worked his way up to the nonsingular cubics, Klein next considered the global situation in the space of all cubic surfaces. He claimed, following the method of continuity, that one could pass from any given cubic surface to any other by varying the coefficients in their equations. What he meant, though, was that one could show, in principle, that this was always possible. He thus began by counting constants, which as noted above reveals that the manifold of all cubics has dimension 19. The same, thus, holds for generic cubics, namely those without singularities.²⁵ Furthermore, each additional singularity reduces the dimension by one. Thus, by carrying out these local deformations, Klein had begun in a manifold $\infty ^{15}$, moving up by one dimension each time a singular point was removed. He realized that this was a special situation, valid only for cubic surfaces, and that the space of all quartics could not be handled similarly.²⁶

Klein’s basic idea was sound, though his attempt to prove that this method enabled him to move with complete control in this space of all cubics left many loose ends. If we compare the original text in §6 and §7 with the corresponding sections in the revision made nearly 50 years later (Klein 1921–1923, 2: 23–25) and Appendix I (Klein 1921–1923, 2: 44–56), it is apparent that Klein’s original proof overlooked several delicate points. Even so, this revised text was hardly the last word on the classification of real cubic surfaces, which remained a difficult challenge through most of the twentieth century.²⁷

Klein was quite vague about when two cubics can be regarded as equivalent. A sticking point involved surfaces that were mirror images, a problem he tried to resolve, but later he decided to junk his argument in favor of another (see the emended text in §6 of Klein (1921–1923, 2: 23)). In effect, he took a topological view of the situation, allowing any continuous variation of the defining constants for cubics, so long as these did not affect the singularity structure. The $\infty ^{19}$ of nonsingular cubics was thus bounded by the $\infty ^{18}$ of cubics with a single singularity, and the latter thus served to separate the different types of nonsingular cubics into various components. By the same reasoning, each submanifold fell into components based on the bounding manifold of one dimension lower. Had Klein noted that the collineations of $P^3(\mathbb {R})$ form a group $G_{15}$ with fifteen parameters that preserve the various types of cubics, then part of his argument might have been clearer. The manifold structure would then have started with dimension 4, thus:

$$\begin{aligned} M_4 \supset M_3 \supset M_2 \supset M_1 \supset M_0. \end{aligned}$$

Klein argued that one can pass from $M_0$ to $M_1$ by forming a pencil of cubics based on two belonging to the respective submanifolds. Thus, suppose $f=0$ is a cubic with three singular points, and $f'=0$ a cubic with four, so that $f \in M_1, f' \in M_0$. Now consider the pencil $f+ \lambda f'=0$, noting that it can contain only finitely many cubics in the zero-dimensional submanifold $M_0$. Klein then said we should choose the smallest value of $\lambda$ which yields a cubic $\phi$ in $M_0$, and then carry out one of the two deformation processes on one of its singular points to arrive at $f=0$. The implication seems to be that this merely involves varying the parameter $\lambda$ until it vanishes, though Klein does not say this explicitly. In any case, it is also obvious that this argument can only be made to pass from $M_0$ to $M_1$ since it depends on knowing that the parameter has a least value for cubics in the lower dimensional submanifold.

Much of what Klein had to say in this paper concerned properties derived from the diagonal surface, which he had studied carefully by making use of Weiler’s model (Klein 1873, 568). He began by denoting 12 lines that form a double-six. As described above, these lead to 15 additional lines, which Klein placed in two groups denoted A and B. Group A consists of five sets of three lines, those contained in the five planes of the pentahedron. Group B consists of ten sets of three lines, which meet in the ten vertices of the pentahedron. Those ten points are the only places on the surface with null curvature: thus, the parabolic curve consists only of the isolated points. Elsewhere, the surface is everywhere hyperbolically curved.

Klein then turned to a general cubic with 27 real lines, noting that its properties are easily derived from those of the diagonal surface by means of small deformations. In particular, the incidence structure of the lines in the schemata A resp. B no longer hold, as a general cubic will have no Eckardt points. Instead, the triples of lines that formerly met in the ten vertices of the pentahedron will now form a triangle that circumscribes a small oval curve, one of ten parabolic curves arising from the ten vertices. The remaining differences between the diagonal surface and a general cubic with 27 real lines are few, supporting Klein’s argument that this special cubic lends itself well to an appreciation of the generic case.

In the letter Klein wrote to Otto Stolz cited above (see the beginning of Sect. 5), it is apparent that Klein originally thought of the connectivity of cubic surfaces in terms of Riemann’s results for closed orientable surfaces. Klein knew Jordan’s paper from 1866, in which he showed that any two such surfaces with the same genus p are topologically equivalent (Jordan 1866). Schläfli took this same approach in discussing the topology of nonsingular cubic surfaces in Schläfli (1872). This led to a short-lived dispute between him and Klein, who came to realize the need to modify Riemann’s topological concepts in order to make them compatible with projective objects (Klein 1874a). He thus emphasized that $P^1(\mathbb {C})$, the Riemann sphere, has a different connectivity than the projective plane, $P^2(\mathbb {R})$, as the latter is non-orientable (Scholz 1980, 163–167). In Klein’s approach, the crux of the matter for surfaces in $P^3(\mathbb {R})$ is that Jordan’s argument no longer holds. He illustrated this by noting that a hyperboloid of one sheet and a torus have the same topological connectivity, but they cannot be transformed into one another. Here, Klein described the allowable transformations as a combination of global collineations and local continuous deformations (Klein 1874a, 552). Klein’s reflections on connectivity in surface theory opened the doors to deeper topological investigations (Klein 1876a), though this line of development lies beyond the scope of the present paper. Nevertheless, connectivity had major importance for Klein’s studies of projective Riemann surfaces, as will be seen in Sect. 7.

6 Geiser and Zeuthen on quartic curves

Klein’s paper on cubic surfaces (Klein 1873) broke new ground in a number of directions, including for investigations of quartic curves. In §8 of his paper, Klein made use of an important technique by which data on an $F_3$ can be projected onto a plane. This approach was due to the Swiss geometer Carl Geiser, who used it to establish an elegant connection between cubic surfaces and the bitangents to quartic curves (Geiser 1869). Klein recognized its utility for understanding the effect of the two deformations (+ and –) when dealing with the special cubic with four conical points (recall that these form a tetrahedron T whose edges represent $4 \times 6 = 24$ of the 27 lines on the $F_3$). Klein chose a projection point $P \in F_3$ in such a way that a degenerate imaginary quartic appeared in the projection plane. This curve was the union of two conics $C_4 = C_2 \cup C_2'$ that met in four real points $P_1, P_2, P_3, P_4 \in C_2 \cap C_2'$. As Geiser had shown, the 27 lines on an $F_3$ pass over to double tangents of the quartic curve, and since 24 lines are given by the edges of T these correspond to the six lines joining the points $P_i, P_j$.

Klein then described the corresponding changes affected by the operations + and – on the vertices of T. Separating a vertex by – means that it and the real lines passing through it become imaginary. In the plane, then, one of the three points disappears and along with it $4 \times 3 = 12$ lines. For the operation +, the corresponding point blows up into a small oval curve. Repeating the operation + on all four vertices yields a quartic curve consisting of four separate ovals, which have 24 double tangents. Since these deformations in the neighborhood of T have no effect on the three remaining lines on $F_3$, Klein could claim that all 27 lines of the desingularized $F_3$ had to be real. Furthermore, this method confirmed Schläfli’s findings for cubics with singularities. As noted above, in passing to three singular points via –, one loses 12 lines, leaving 15 total. Two singular points lowers the number of real lines to 7, and for the other two cases one has 3 real lines on the surface, all in accordance with what Schläfli had shown (Klein 1873, 564–566).

During the brief period when Klein and Clebsch collaborated on cubic surfaces, a young student of Clebsch named Carl Rodenberg wrote his doctoral thesis on the relationship between pentahedra and the singularities of cubic surfaces. This turned out to be complicated, but 5 years later Rodenberg gave this topic a new twist by studying deformations of cubics with a fixed pentahedron, for which Clebsch’s diagonal surface served as a canonical case (Rodenberg 1878). Soon afterward, Rodenberg produced an impressive series of models demonstrating changes in the singularity structure in passing from type of cubic to another (see the photos in Fischer (1986, I: 13–31) and commentary in Fischer (1986, II: 10–14)).

To follow the reception of Klein’s work on the deformation of singularities on cubic surfaces, it will be useful to describe Geiser’s mapping more closely. One begins by taking a fixed point P on a given $F_3$ that lies off of the configuration of 27 lines. Then, the 6th-degree cone of tangents to the surface $K_6$ will decompose into $K_6= K_4 \cup E_P^2$, thus a 4th-degree cone and the tangent plane at P counted twice. Now take any arbitrary plane E, which leads to a quartic curve $C_4= K_4 \cap E.$ Geiser could then easily show that by projecting $F_3$ onto E from the point P, the 27 lines pass over to 27 of the 28 double tangents of $C_4$, whereas the remaining double tangent is simply given by $E_P \cap E$. For if g is one of the 27 lines of $F_3$, then the plane $E_g$ passing through P and g cuts out a conic $C_2(g) \subset F_3$ that determines two points $r,s \in C_2 \cap g$. These, in turn, yield two double lines rP and sP on $K_4$, which project to the two points of tangency $r',s'$ on the double tangent $g' \in E$ determined by $g \in F_3$. The two points of tangency of the remaining double tangent $E_P \cap E$ are determined by the asymptotic directions at P on $F_3$. Geiser further showed that the converse construction held, namely, if one started with a plane $C_4$ and took an arbitrary point P outside the plane, then one could build an $F_3$ whose 27 lines, when projected from P, pass over to 27 bitangents of the $C_4$, the remaining bitangent being determined by the tangent plane at P.

Geiser’s mapping thus signaled an intimate connection between the bitangents of quartics and the spatial configurations of 27 lines that was so crucial for Schläfli’s classification of real cubic surfaces. In passing, Geiser also noted the intense prior interest in the structure of the 28 bitangents to a $C_4$, a topic that had already been studied by Aronhold, Clebsch, Hesse, Roch, Salmon, and Steiner. The name Riemann was missing here, as his study Riemann (1876) only came to light in 1876 with the publication of the first edition of his Collected Works (Weber 1876/1892/1902) (see Sect. 10).

One of the first to react to Klein’s study of cubic surfaces was H.G. Zeuthen (see 3.1), who also studied a shorter note that Klein wrote in May 1873 for the Erlangen Scientific Society. In all likelihood, Klein sent this note to Zeuthen shortly after they met in Göttingen 1 month earlier during a mathematics conference Klein had helped organize (Tobies 2021, 120). Zeuthen surely had known Alfred Clebsch from many years before; he already published a paper in the first volume of the latter’s journal, Mathematische Annalen, which appeared in 1869. As Max Noether emphasized in his obituary article from 1921, Zeuthen published all his major mathematical papers in the Annalen (Noether 1921). During the first two decades of the twentieth century, Zeuthen secured his reputation as the era’s leading expert on enumerative geometry by publishing a lengthy survey article in the German Encyclopedia (Zeuthen 1903), followed by his definitive textbook on the subject (Zeuthen 1914). This work was firmly anchored in the French tradition of Poncelet, Chasles, and Georges Halphen, a close friend of Zeuthen’s.

In reacting to Klein’s paper (Klein 1873), Zeuthen actually picked up where Geiser had left off with the study of quartic curves and their bitangents (Zeuthen 1874). Klein had used the Geiser mapping to confirm Schläfli’s classification of cubic surfaces, but no one had given a comparable classification of real quartic curves, the task Zeuthen therefore took up. Zeuthen’s account of the Geiser mapping emphasizes how one can always inscribe a real fourth-order cone in a real cubic surface so that its vertex lies anywhere outside the 27 lines. Any plane section of the cone is, thus, a quartic curve, and since the lines on the surface project to double tangents one can study the latter by considering the incidence structure of the former, which had already been studied intensively. In his subsequent study (Zeuthen 1875), Zeuthen took up the Geiser mapping in greater detail.

In Sect. 2.1, brief mention was made of Klein’s representation of the real and imaginary points on curves given by equations with real coefficients. This new type of Riemann surface, as he called it, aimed to give a vivid picture of objects that Clebsch had described using Riemannian tools. Klein gave numerous concrete examples to illustrate the construction of what I will call projective Riemann surfaces. The drawings in the following sections are based on those found in Klein’s papers from the middle 1870s.

7 Klein’s projective Riemann surfaces

7.1 Visualizing the deformations of cubic curves

Already as a teenaged student in Bonn, Klein gained exposure to novel representations of algebraic curves through his teacher Plücker. By the 1860s, geometers had long known that one could dualize an algebraic curve to study the corresponding relationships on the class curve given by the envelope of tangents to the dual curve. Thus, a nonsingular cubic has $n=3$ and $k= 3 \cdot 2= 6$. Passing to the dual curve, its three real inflection tangents become cusps. Plücker impressed on Klein how relatively little effort had been spent in studying dualized class curves such as the one shown in Fig. 15.

Fig. 15

A curve of order 6 and class 3

One easily sees that a line can intersect the curve in as many as six points. Moreover, the six asymptotes indicate that the line at infinity also contains six points of the curve. The asymptotes are tangent lines and the curve itself has a single connected component. It seems we are looking at a curve of order $n=6$ and its three cusp points provide another hint: this curve is the dual of a nonsingular cubic, which has 3 real and 6 imaginary inflection tangents. When taking its dual, the inflection tangents pass over into cusp points.²⁸

As noted earlier, the genus p is of fundamental importance for complex curves, whereas it represents a measure of connectivity in surface theory. On a surface S of genus p one can find p disjoint closed curves such that cutting S along them produces a simply connected surface; thus, any further cut along a closed curve would disconnect it. Riemann employed a system of 2p closed curves on a surface S to define the periodicity relations satisfied by p Abelian integrals of the first kind (Weber 1876/1892/1902, 104). One can also introduce the genus of an orientable compact surface F by means of the Euler characteristic $\chi$, which gives the topological formula: $\chi = 2-2p$. Here, p counts the number of holes in the surface.

For an nth-degree nonsingular algebraic curve, Clebsch derived the formula $p= \frac{1}{2}(n-1)(n-2)$. The connection between this and the geometric interpretations seemed for some time quite opaque. Then, in 1891, Adolf Hurwitz found a simple formula for the Euler characteristic of a Riemann surface that covers a base space with known Euler characteristic. More precisely, if A is a branched covering of degree n over B, then

$$\begin{aligned} \chi (A) = n \cdot \chi (B) - r, \end{aligned}$$

where r is the number of branch points counted with multiplicity. This leads immediately to Clebsch’s formula by simply projecting a nonsingular curve $C_n$ of degree n onto the projective line $P^1(\mathbb {C})$ from a point $P \notin C_n$. Since there are no singularities, the branch points occur precisely from the $n(n-1)$ tangent lines to $C_n$ through P. Since $\chi (P^1(\mathbb {C}))=2$, Hurwitz’s theorem gives:

$$\begin{aligned} \chi (C_n) = n \cdot 2 - n(n-1), \end{aligned}$$

from which we obtain

$$\begin{aligned} 2 -2p = n \cdot 2 - n(n-1), \,\,\text{ so } \text{ that } \,\, p= \frac{1}{2}(n-1)(n-2). \end{aligned}$$

Probably, no one before Klein imagined one could connect this notion to real curves, which are merely one-dimensional parts of a 2-dimensional object when we think of a complex curve as lying in $\mathbb {C} \times \mathbb {C}$. In 1874 he found a straightforward way to build a topological object around the skeleton of a real curve when the latter was nonsingular (Klein 1874b). For cubics this meant taking the duals of the two point curves in Fig. 12 and treating these as class curves, which look like those in Fig. 16. These two new dual curves preserve the number of components (two or one) and in each case the real inflection tangents pass over into cusps. The incidence structure also dualizes: whereas before the three inflection points fell on a line, here the three cuspidal tangent lines meet in a single point. Since a nonsingular cubic has genus $p=1$, Klein needed to build a topological torus around these plane real curves. To accomplish this, he simply needed to find a way to represent the imaginary tangents at each point $P\in P^2(\mathbb {R})$.

Fig. 16

Two nonsingular curves of class 3

Klein’s approach was particularly transparent for the case of a conic, since the dual curve is itself a $C_2$ and thus equivalent to an ellipse in $P^2(\mathbb {R})$. For points outside $C_2$ the two tangents are real, whereas for P inside $C_2$ they are conjugate imaginary lines. As one moves toward the curve, whether from outside or inside it, the two tangents gradually near one another until they finally coincide as a single tangent to $C_2$, which is counted twice. Taking the curve in Fig. 16 with two real components, one readily sees that for any point outside as well as inside the two branches there will be three real tangents. In the annular region between them, however, only one real tangent can be drawn from a given point P. Since the complex class curve must have three tangents, two are obviously imaginary. To represent them, Klein imagined placing an axis through P perpendicular to the plane of the curve. As representatives for the two missing tangents he took two points $P', P''$ on this axis, both equidistant from P, but with one below and the other above the plane of the real curve. By moving P continuously throughout the annular region, while letting the distance between $P'$ and $P''$ go to zero as P approached the two branches of the curve, the leaves above and below closed together at the boundary. The resulting surface thus had the form of a torus.

One might well wonder how Klein could push such an argument through for the real curve with only one component. But keeping in mind that these constructions take place in projective space, where nothing can literally wander off to infinity, it is easy to see that the resulting surface must be closed. Klein likened it with a hyperboloid of one sheet, which in projective 3-space is a closed surface with the connectivity of a torus, thus with $p=1$.

7.2 Hesse’s inflection-point configuration for cubic curves

As noted above, Alfred Clebsch drew inspiration for much of his work in algebraic geometry from earlier studies undertaken by Otto Hesse. In 1844, Hesse published his famous work on the inflection-point configuration for nonsingular cubic curves (Hesse 1844a, b).²⁹ Some early results for real points had already been found in the eighteenth century. Independently of one another, Jean Paul de Gua de Malves and Colin Maclaurin showed that when a line passes through two inflection points on a cubic curve it will also pass through a third (Pascal 1910, 384) (Kohn and Gino 1908, 475). Maclaurin also deduced that a cubic could have at most three real inflection points, and so these always lie on a line.

In 1835, Plücker found the inflection points of a given curve C by intersecting it with an associated curve $C'$ (Plücker 1835). Plücker’s $C'$ was not, however, a covariant curve, since its definition depended on the coordinate system chosen. Hesse, on the other hand, took advantage of the technical advances made using determinants to produce such a covariant curve H(C), now called the Hessian, which cuts out precisely those points which yield inflection tangents to a given curve C. Unlike ordinary tangents, which have twofold contact with a curve, an inflection tangent has threefold contact. Not surprisingly, H(C) is thus defined by a determinant that introduces the second derivatives of the equation defining C.

If this equation is given in homogeneous coordinates by $f(x_0, x_1,x_2) = 0$, then the equation of H(C) is:

$$\begin{aligned} {\text {det}} \left( \frac{\partial ^2 f}{\partial x_i \partial x_j} \right) =0. \end{aligned}$$

For a curve $C_m$ of order m, $H(C_m)$ has order $3(m-2)$, so by Bézout’s theorem $C_m$ can have at most $3m(m-2)$ inflection points. In particular, the Hessian curve of a nonsingular cubic is again a cubic, which means that in general the number of inflection points will be $C \cap H(C)= 3 \times 3=9$. Hesse further showed that these 9 points lie in fours on 12 lines in the projective complex plane, forming a $\left( 9_4, 12_3\right)$ configuration (see Fig. 10).

In fact, Hesse’s findings imply that the nine inflection points determined by $C \cap H(C)$ do not lie in general position, since these two cubics are only two among a pencil of cubics all sharing the same inflection-point configuration. One can write the equation for this pencil of cubics $C_{\lambda }$ using a complex parameter $\lambda$, where $\lambda ^ 3 + 27 \ne 0$:

$$\begin{aligned} x^3+y^3+z^3+ \lambda xyz=0, \end{aligned}$$

which J.J. Sylvester called a syzygetic pencil. The Hessian curve $H(C_{\lambda })$ is, thus, given by:

$$\begin{aligned} D_\lambda =\begin{vmatrix}6x&\quad \lambda z&\quad \lambda y\\ \lambda z&\quad 6y&\quad \lambda x \\ \lambda y&\quad \lambda x&\quad 6 z\end{vmatrix} = -6\lambda ^2(x^3 + y^3 +z^3)+ (216+2\lambda ^3)xyz=0. \end{aligned}$$

This can then be written in the simplified form:

$$\begin{aligned} \alpha (x^3 + y^3 +z^3)+\beta xyz =0. \end{aligned}$$

$H(C_{\lambda })$, thus, belongs to the pencil of cubics $C_{\lambda }$ (set $\lambda = \frac{\beta }{\alpha }$), which accounts for why this is a syzygetic pencil: all its curves share the same 9 inflection points. The singular curves of this system are those for which either $\alpha =0$ or $\lambda ^ 3 + 27 = 0$. When $\alpha =0$ one obtains $xyz=0$, the three lines $x=0$, $y=0$ and $z=0$ of the coordinate triangle. The three roots of $\lambda ^ 3 + 27 = 0$ are $\lambda = -3, -3 \omega$ or $-3 \omega ^2$, where $\omega$ and $\omega ^2$ are the imaginary cube roots of unity. In these three cases, the cubic decomposes into three lines:

$$\begin{aligned}{} & {} \lambda =-3: (x+y+z) (x+\omega y +\omega ^2 z) (x+\omega ^2 y+\omega z)=0,\\{} & {} \lambda =-3 \omega : (x+y+\omega z) (x+\omega y + z) (x+\omega ^2 y+\omega ^2 z)=0,\\{} & {} \lambda =-3 \omega ^2: (x+y+\omega ^2 z) (x+\omega y + \omega z) (x+\omega ^2 y+ z)=0. \end{aligned}$$

Together, these form the 12 lines of the Hessian configuration, 4 of which are real and the other 8 imaginary. Since any two curves of the pencil meet in the 9 inflection points, one can find them by letting $\lambda = 0, \,\,\infty$:

$$\begin{aligned} \left\{ \begin{array}{ll} xyz=0 ~~~ \qquad \quad \,\,\text{ for }\,\, ~~~ \alpha =0, \\ x^3 + y^3 +z^3 =0 ~~~ \,\,\text{ for }\,\, ~~~ \beta =0. \end{array}\right. \end{aligned}$$

The coordinates of the nine points of intersection are then:

$$\begin{aligned} \begin{array}{ccc} (0, 1, -1) &{}\; (1, 0, -1) &{}\; (-1, 1, 0) \\ (0, \omega ^2, -1) &{} \;(\omega , 0, -1) &{}\; (-1, \omega , 0) \\ (0, \omega , -1) &{}\; (\omega ^2, 0, -1) &{} \;(-1, \omega ^2, 0). \end{array} \end{aligned}$$

Since the coordinates of these nine points are independent of $\lambda$, these are the inflection points for any curve in the Hessian pencil. The 12 lines of the configuration fall into 4 sets of 3 lines forming 4 triangles. Hesse discovered these four triangles and proved that each contains all 9 inflection points. The existence of these four triangles reduces the degree of the equation for these 9 points, as Jordan showed in his Traité (Jordan (1870, 302); see also Lê (2015, 329–330)). In the first section of chapter 3, entitled “Equation de M. Hesse,” Jordan observed that the configuration of inflection points on a cubic coincides with the points and lines of the affine plane over the field of 3 elements (Jordan 1870, 302).

Felix Klein emphasized the importance of this algebraic aspect in his obituary article for Hesse:

Hesse seized on the problem of the algebraic determination of the nine inflection points. Because one can sort out four triangles with twelve lines on which the points lie three by three, the solution of the equation of the ninth degree depends on an equation of the fourth degree. It was a first remarkable example that geometry gave to the theory of equations .... (Klein 1875, 48)

7.3 Clebsch and the parameterization of cubic curves

In Clebsch (1864a), Clebsch showed that the Hesse configuration can easily be derived by means of an elliptic integral. Here, we illustrate his general approach by deriving a few basic results for a nonsingular cubic $C_3$ with $p=1$. Its points are parameterized by an elliptic integral (u), which Clebsch employs along with the converse of Abel’s theorem. The latter entails that when a certain sum of definite integrals vanish for a certain set of 3m points on the curve $C_3$, then these points are cut out by a curve $C_m$. Here, we can neglect the lower endpoints by integrating from a single fixed point $y\in C_3$, so the definite integrals require only the upper endpoint and are written $(u)^{P_i}$.

The following argument, inspired by Clebsch (1864b), was presented by Henry Seely White in Klein’s seminar (Parshall and Rowe 1994, 224–227). Let a line $\ell$ cut three points $P_1, P_2, P_3$ on $C_3$ and for each $P_i$ pass a line $\ell _i$ through it cutting out two additional points. White then showed that the six new points $P_4, \dots P_9$ must lie on a conic. From the four lines $\ell$ and $\ell _i$, we have

$$\begin{aligned}{} & {} (u)^{P_1} + (u)^{P_2} + (u)^{P_3} = (u)^{P_1} + (u)^{P_4} + (u)^{P_5} \\{} & {} \quad = (u)^{P_2} + (u)^{P_6} + (u)^{P_7} = (u)^{P_3} + (u)^{P_8} + (u)^{P_9} =0. \end{aligned}$$

Adding the last three sums and subtracting the first yields

$$\begin{aligned} (u)^{P_4} + (u)^{P_5} + (u)^{P_6} + (u)^{P_7} + (u)^{P_8} + (u)^{P_9} =0, \end{aligned}$$

which is the condition for six points to lie on a conic.

This condition should actually be formulated to reflect the fact that elliptic functions are doubly periodic. So if these periods are $\omega _1, \omega _2$, the equality above should read $\equiv 0 \,\,(\text{ mod }\,\,\Omega )$, where $\Omega = \{m\omega _1 + n\omega _2 | m, n \in \mathbb {Z}\}$. From here, it is easy to formulate the condition for a conic to be tangent to a cubic curve at three points. We need only write $P_4 =P_5, P_6 =P_7, P_8 =P_9$, and the equation above becomes

$$\begin{aligned} 2((u)^{P_4} + (u)^{P_6} + (u)^{P_8}) \equiv 0\,\,(\text{ mod }\,\,\Omega ) \end{aligned}$$

or equivalently

$$\begin{aligned} (u)^{P_4} + (u)^{P_6} + (u)^{P_8} \equiv \,\,\frac{i\omega _1 + j\omega _2}{2}(\text{ mod }\,\,\Omega ), \end{aligned}$$

for $i,j\in \{0,1\}.$ This leads to the four characteristics (0, 0), (1, 0), (0, 1), (1, 1), where (0, 0) is the degenerate case of a double line. The other cases represent three distinct systems of conics tangent to a cubic at three points, as Hesse had shown long before.

The case of an elliptic curve does not require Riemann’s theory, of course, so Clebsch found what he needed in Jacobi’s work. His paper (Clebsch 1864a) nevertheless makes for difficult reading because he took a rather complicated approach to obtaining u. Once in hand, though, it was easy for him to derive Hesse’s inflection-point configuration. An inflection tangent to a $C_3$ is a line $\ell _P$ that has threefold contact at $P= C_3 \cap \ell _P$. This corresponds to the condition

$$\begin{aligned} 3(u)^{P} \equiv 0\,\,(\text{ mod }\,\,\Omega ) \end{aligned}$$

or

$$\begin{aligned} (u)^{P} \equiv \frac{m_1 \omega _1 + m_2 \omega _2}{3} \,\,(\text{ mod }\,\,\Omega ), \end{aligned}$$

for $m_1, m_2 \in \{0,1,2\}.$ Clebsch wrote these nine points schematically as

$$\begin{aligned} \begin{array}{ccc} 0,0 &{}\quad 0,1 &{}\quad 0,2 \\ 1,0 &{}\quad 1,1 &{}\quad 1,2 \\ 2,0 &{}\quad 2,1 &{}\quad 2,2. \end{array} \end{aligned}$$

The twelve lines then appear as the rows and columns together with the pairs of triples one would obtain from the corresponding determinant (Clebsch 1864a, 111–112). These four triples of lines yield Hesse’s four triangles containing all nine inflection points. Note that the sums of the integrals for the three inflection points on any of the twelve lines vanishes.

Clebsch showed how such curves can be parameterized by elliptic functions, which he utilized to illuminate Hesse’s inflection-point configuration for cubic curves (Clebsch 1864a). In this same spirit, Klein introduced a similar parameterization of the projective Riemann surface constructed from a real cubic with two components. In modern language, he thereby endowed it with a complex structure as each point acquires a value $u+iv$, defined modulo the two periods $\omega$ and $i\omega '$. Translating Clebsch’s analytical approach for point coordinates into line coordinates, Klein could assert that three tangents $u_1+iv_1, u_2+iv_2, u_3+iv_3$ will intersect in a point when

$$\begin{aligned}{} & {} u_1+ u_2+ u_3 \equiv 0 \,\,(\text{ mod } \,\, \omega ), \\{} & {} v_1+ v_2+ v_3 \equiv 0 \,\,(\text{ mod } \,\, \omega '). \end{aligned}$$

Fig. 17

Klein’s representation of the inflection-point configuration on a nonsingular cubic curve

The inner branch of the real curve, thus, takes on values $0 \le u < \omega$, whereas the outer branch runs through the same range with values $u + i\omega '/2$. The three real cusps, which correspond to the three real inflections points on the original cubic, are $u=0, \omega /3, 2\omega /3$, so the three cuspidal tangents meet in a point. The remaining six, which are imaginary, lie on the meridian curves that pass through the real cusps: $0+iv, \,\,\omega /3 +iv, \,\,2\omega /3 +iv$, where $0 \le v < \omega '$. These six arise by dividing the period $\omega '$ by 3:

$$\begin{aligned} i\omega '/3,\,\, 2i\omega '/3, \,\,\omega /3 + i\omega '/3, \,\,\omega /3 +2i\omega '/3, \,\,2\omega /3 + i\omega '/3, \,\,2\omega /3 +2i\omega '/3. \end{aligned}$$

Klein gave few details about the elliptic integral u, referring readers to Clebsch’s paper (Clebsch 1864a, 105). A short time later, Klein’s student Axel Harnack published on this topic using Jacobi’s theory in Harnack (1875). As Klein later noted (Klein 1921–1923, 2: 98), these earlier parameterizations of elliptic curves led to many complications, which Weierstrass overcame by introducing the $\sigma$ and $\wp$ functions.³⁰

Fig. 18

Transition between the two types of nonsingular cubic class curves via a double tangent singularity

The next step was the crucial one in Klein’s whole approach, which aimed to give an overview of the various possible types of curves that can be visualized in this way. He now needed to show by means of continuous deformations that the genus of the curve would be reduced when singularities appear, in line with Clebsch’s formula $p= \frac{1}{2}(n-1)(n-2)- d - r$, where d and r are the number of double points and cusps, respectively. Since projective Riemann surfaces employ class curves, the appropriate singularities are given by t and w, the number of double tangents and inflection tangents. At this stage, Klein’s arguments are all “proofs by pictures,” as in Fig. 18. One can easily see that all of these amount to topological proofs that rest on methods akin to the “principle of continuity.” Klein dealt with a multitude of examples, most of which are shown in the remainder of this section. Readers who prefer not to delve into all these special cases, can get the general idea from looking at Figs. 17, 18 and 19 and then jump ahead to Sects. 8 and 9. The type of continuity arguments Klein employed in these simplest examples illustrates well his overall procedure.

Klein starts on the left in Fig. 18 with the standard torus model, which is then steadily deformed at the bottom until the two cusps are crushed out and a double tangent emerges. This line, being one-dimensional, has no effect on the genus of the surface, as Klein here implies. The deformation thus leads to a complex curve with the same structure as a topological sphere, hence $p=0$, as expected. Notice further that the new double tangent reduced the number of inflection points to three, only one of which is real (represented by the cusp). Passing through this transitional state, Klein thickens up the double line, which reintroduces the two missing cusps. The corresponding surface now has genus $p=1$ again, but its real curve contains only a single component, corresponding to a projective Riemann surface for the curve on the right in Fig. 16.

Fig. 19

Transition between the two types of nonsingular cubic class curves via an isolated double tangent

With Fig. 19, Klein illustrated how an isolated double tangent can emerge by deforming the surface, starting from a torus shape. On the left we see that same type of surface where the outer curve has “passed through infinity,” as geometers used to say. By identifying opposite points an isolated double tangent emerges, though topologically this is a closed curve as before (all lines in $P^2(\mathbb {R})$ are closed). In this case, Klein made no attempt to argue that the genus of this transitional surface was $p=0$, appealing instead to the case above (Klein 1874b, 563).³¹ When the double tangent disappears by becoming imaginary, the surface will be of the same type as the third one in the case considered above (Fig. 18).

Fig. 20

Transition between singular cubic class curves passing from an isolated double tangent to an inflection tangent to an ordinary double tangent

As for the situation when the real class curve takes on an inflection tangent, Klein drew the suggestive pictures in Fig. 20. On the left, we see two real cusps approaching an isolated double tangent, thus a deformation of the situation depicted in the middle of Fig. 19. As they merge into the double tangent, these cusps disappear just as the line becomes an inflection tangent. In the third picture, the inflection point has split into two real points of tangency and the line is now a real double tangent, the same situation as shown in the middle picture of Fig. 18. Later, in Klein (1876d), Klein returned to this picture in order to refine his approach to connectivity, as in the meantime he had uncovered a parallel refinement of Plücker’s formulas (see Sect. 3).

Fig. 21

The dual curve for a cubic with an isolated double point

Klein closed this gallery of pictures by discussing the projective Riemann surface associated with a cubic curve that has an isolated double point (the third type shown in Fig. 13). Here, the class curve has $k= 3 \cdot 2 - 2 \cdot 1= 4$, so it is singular. In fact, from Fig. 21 one can see that it has three real inflection tangents. This accords with the Plücker formula for its dual, namely $n= k(k-1)-2t-3w= 4 \cdot 3 -2 \cdot 0 - 3 \cdot 3 = 12- 9 = 3.$

Fig. 22

The isolated double point is a branch point of the surface

One can easily see that for points in the three regions opposite the sides of the interior triangle one can draw exactly two tangents to the curve, so the other two are imaginary. We, thus, require two leaves in those regions, whereas passing over the asymptotes of the curve into the triangle there should be four leaves, but no more since the curve is of class four. One can take account of this by treating the isolated point in the interior of the triangle as a branch point. Doing so leads to the relations pictured in Fig. 22, which show how pairs of the leaves from the bounding regions combine, each contributing two, so that the interior of the triangle will be covered by four leaves throughout.

7.4 Visualizing deformations of quartic curves

Fig. 23

Quartics with three components and only one for better quality, please produce smaller images for these two figures

Although in principle similar to the case of cubics, the construction of projective Riemann surfaces for quartic curves leads to many new complications, beginning with the fact that the nonsingular quartic has genus $p=3$. Klein treated several cases in his major paper “On the Form of Abelian Integrals for Fourth-Degree Curves” (Klein 1876c). As a first step, he drew on Zeuthen’s classification, transforming the point curves by duality into their corresponding class curves. He considered five principal types of quartics, two of which appear in Fig. 5. The other three are pictured in Figs. 23 and 24.

Fig. 24

A quartic with two components, one a unifolium

Klein mainly focused on the dual class curves associated with the two standard quartics shown in Fig. 5. He derived these in a similar way, namely by starting with two conic class curves. The four double points go over to four double tangents, and since this exceeds the deficiency $p=3$ the curve must be reducible. This situation is, thus, closely related to the familiar one discussed above, in which one deforms a quartic from the union of two point conics (see Fig. 5).

Fig. 25

Four double tangents are the singularities for a pair of conics. Their inner segments lead to the dual of a belt curve

To construct the dual of the belt curve, Klein took the inner segments of the four bitangents (Fig. 25 on the right), which are counted twice. He next deformed the curve by splitting off one part on these segments to form an oval outer curve, the dual of the inner oval of the belt curve. This leaves the other part to join the inner curve, dualizing the quadrifolium, and indeed its four bitangents. which bound pairs of inflection points, pass over to four double points with pairs of cusps attached to each (Fig. 26).

Fig. 26

The dual of a belt curve

Fig. 27

A nonsingular curve of class 4, left, and the deformed curve with a double tangent

The corresponding projective Riemann surface is formed within the region bounded by the belt curve; its leaves are numbered in the picture on the left in Fig. 27. In the process of dissolving one of the loops with two cusps and a double point a double tangent emerges. The genus of the Riemann surface thus drops from $p=3$ to $p=2$, and similarly for the curves shown in Fig. 28.

Fig. 28

These class quartics have $t=2, 3$ double tangents, so their genus is $p=1$, resp. $p=0$

To construct the other dual class curve, Klein took the eight outer segments of the four bitangents to the two conics (Fig. 29). These split off to form four small loops on four components that pass to infinity on pairs of asymptotes.

Fig. 29

Two class conics with the outer segments of the four bitangents

These are the duals of the four unifolia with four bitangents of the first kind that enclose pairs of inflection points, which now appear as pairs of cusps enclosed in a loop with a double point. Notice that each component curve crosses the other three components six times, producing another 24 double points. These correspond to the 24 + 4 = 28 bitangents of the point quartic.

Fig. 30

The dual of a quartic with four unifolia

To construct the projective Riemann surface around this curve, pictured in Fig. 31, note that the sector where the two conics cross will have four leaves. The regions immediately surrounding it have two, but unlike the projective Riemann surface for the belt curve (shown schematically on the left in Fig. 27) these pairs of leaves extend through infinity in the directions of pairs of adjacent tangents (the indices $t_{ij}$ are explained in Sect. 9). These opposite pieces then join to form the four parts of the surface labeled in the picture. Note that four regions in Fig. 30 separate pairs of adjacent tangents. Since four real tangents can be drawn to the curve from points in these regions, they correspond to the darkened space surrounding the surface in Fig. 31. One can easily see that this is a genus $p=3$ surface by observing that its central core with one pair of $t_{ij}$ is a topological ball to which three handles have been attached.

Fig. 31

The projective Riemann surface built on the curve in Fig. 30

Klein only discussed how to build projective Riemann surfaces for quartic curves very briefly in his first paper from 1874 (Klein 1874b). Thus, when he presented pictures of the singular quartics (see Figs. 27 and 28), he merely noted how the presence of a new double tangent lowered the genus by one. The only hint he offered, though, regarding the topology of these surfaces came from the example that followed: a singular class quartic with three real inflection tangents (Figs. 21 and 22). This curve has an isolated double point in the interior of the central triangle, where a branch point emerges on the surface. Something similar occurs during the deformation processes for removing a pairs of cusps, which lead to the curves in Figs. 27 and 28. Two years later, in Klein (1876c), Klein explained the process of removing point singularities by deforming the class curves on a projective Riemann surface. The typical situation beforehand is shown in Fig. 32.

Fig. 32

The local structure of the leaves near a pair of cusps

Fig. 33

Removing the cusps by pulling together a loop introduces a branch point

As noted above, dissolving the double point and pair of cusps has the effect of adding a double tangent, a singularity for the class curve. But it also produces a branch point on the surface, as illustrated in Fig. 33. Pulling a loop around the cusps leads, in fact, to a double branch point, a structure Klein later discussed in Klein (1876d). Without entering into further details, one can see from this discussion that investigations into the topology of Klein’s projective Riemann surfaces led very quickly to complications. An important special case illustrating these difficulties was published by Klein’s American student Mellen W. Haskell in (1890). This begins with the dual class curve for the real part of the famous Klein quartic and proceeds to construct the projective surface around its skeletal frame; see the pictures in Rowe (2018, 115–118).

Initially at least, Klein suggested that understanding the connectivity of these projective objects involved little more than employing the definitions and methods Riemann had introduced for conventional surfaces. Klein addressed these matters in (Klein 1874a), a short paper published directly before (Klein 1874b). Two years later, however, he felt compelled to revisit the problem of connectivity, a move prompted by his own reflections on the relationship between real and imaginary singularities on algebraic curves. The initial impulse to explore this terrain came from studying Zeuthen’s earlier investigations on the forms of real quartic curves (see 3.1). Klein related Zeuthen’s results to earlier work of Clebsch, which was inspired by findings of Hesse that Clebsch rederived using analytical methods introduced by Riemann. The following section briefly sets out this background before discussing Klein’s new approach in Sect. 9.

8 Hesse and Clebsch: configurations and tangency relations in algebraic geometry

8.1 Clebsch on applications of Abel’s theorem in algebraic geometry

In a paper from 1848, Hesse derived several properties for the three systems of conics tangent to a given cubic curve at three points. If such a conic is given touching a $C_3$ at P, Q, R, then one can easily construct other conics belonging to the same system simply by passing any conic $C_2$ through P, Q, R. Then $C_2 \cap C_3$ will determine three other points $P',Q',R'$ at which another conic in the system will be tangent to the cubic curve (Hesse 1848, [167]).

This was merely a special case of the general theory developed by Hesse in two papers from 1855 (Hesse 1855a, b). Thus, in the case of a quartic curves, an analogous result holds, namely if a conic is tangent to a $C_4$ at points P, Q, R, T, passing a conic through these yields four points $P',Q',R',T'$ which determine another conic in the same system, and for any two conics in the same system all eight points lie on a conic (Hesse 1855b, 303). The same method also applies for cubic curves touching a $C_4$ at six points $P_i, \,\, i= 1, \dots 6$, then by taking any $C_3$ that passes through these $P_i$ it will determine six other points $P_i' \in C_3 \cap C_4$, and these constitute points of tangency for another cubic in the same system. Furthermore, taking any two such cubics, the twelve points will all lie on a cubic curve (Hesse 1855b, 293).

Hesse and Steiner both determined an immense number of related results, in particular with respect to various groups of bitangents to a quartic curve. To study this configuration Hesse began with a net of quadric surfaces, a 2-parameter system generated by three quadrics that meet in 8 points. This net contains a 1-parameter system of quadric cones whose vertices line on a 6th-degree space curve of genus 3. This sextic can be mapped birationally to a plane quartic. Moreover, the lines joining pairs of the 8 base points are chords of the sextic that meet it in two points. They, thus, map to bitangents of the quartic, which provided Hesse with a notation for all 28 bitangents simply by taking pairs of numbers from the set $\{1, 2, \dots 8\}$.

Steiner noted that to every system of conics tangent to a quartic at four points there belong six pairs of bitangents. Thus there are $28 \cdot 27/12 = 63$ systems of such conics. Altogether, there are 20,475 quadruples of bitangents, only 315 of these can enter in Plücker’s form $\Omega ^2-\mu \, pqrs=0$ where all eight points of contact lie on a conic. Salmon produced a table showing all 315 cases (Salmon 1852, 198). Many of Steiner’s results were given without any proof, and some he even set forth as open problems. Hesse’s algebraic methods were far more transparent, but his calculations were often unwieldy and he left many details for the reader to work out or contemplate. Complex analysis offered powerful new transcendental methods that made it possible to attack recalcitrant problems in algebraic geometry from a new perspective.

Clebsch took on the challenge of applying Riemann’s theory of Abelian integrals and their functions, though his introductory remarks in Clebsch (1864c) clearly revealed that he remained a partisan of Jacobi’s analytical methods. To adapt Riemann’s theory to projective algebraic geometry, Clebsch needed to homogenize the equations in the Riemannian formalism. As a first step he replaced the algebraic relation $F(s,z)=0$ by a homogeneous polynomial $f(x_1, x_2, x_3)=0$ of degree n.³² Clebsch viewed $f=0$ as defining a ground curve $C_n \subset P^2(\mathbb {C})$ with double points and cusps as its only singularities. In Riemann’s theory, $F(s,z)=0$ is associated with p linearly independent integrals of the first kind

$$\begin{aligned} \int \frac{\phi (s,z)\textrm{d}z}{\frac{\partial F}{\partial s}}, \end{aligned}$$

with $\phi$ a polynomial of degree $n-2$ in s and $m-2$ in z that vanishes when $F= \frac{\partial F}{\partial s}= \frac{\partial F}{\partial z}=0.$ If r is the number of such points, then Riemann showed that p is invariant under a rational mapping between $F(s,z)=0$ and $F_1(s,z)=0$, where here $p= (n-1)(m-1)-r$ (Weber 1876/1892/1902, 118–119).

In Clebsch’s formulation, these p Abelian integrals can be written:

$$\begin{aligned} \int \phi _k \,\,\textrm{d}\tilde{w}, \quad k = i, \dots , p, \end{aligned}$$

where the $\phi _k$ are homogeneous polynomials of degree $n-3$ that vanish at the singular points of $C_n$ and

$$\begin{aligned} \textrm{d}\tilde{w} = \frac{x_k\, \textrm{d}x_l-x_l \,\textrm{d}x_k}{\frac{\partial f}{\partial x_m}}, \end{aligned}$$

is an expression independent of the permutations of k, l, m. The corresponding definite integrals can be written

$$\begin{aligned} (u_k)_y^x = \int _y^x \phi _k \,\,\textrm{d}\tilde{w}, \quad k = i, \dots , p. \end{aligned}$$

This leads to Clebsch’s version of Abel’s theorem: Let $C_m$ and $C_m'$ cut out mn pairs of points on $C_n$, then

$$\begin{aligned} \sum _{i=1}^{mn}(u_1)_{y_i}^{x_i}= \sum _{i=1}^{mn}(u_2)_{y_i}^{x_i}= \dots = \sum _{i=1}^{mn}(u_p)_{y_i}^{x_i}= 0. \end{aligned}$$

More importantly, Clebsch proved the converse, namely that the vanishing of these p sums implies that the mn pairs of points lie on two curves of order m (Clebsch 1864c, 197–198).³³

The values of the p integrals $(u_k)_y^x$ depend on the paths of integration, so that for fixed limits of integration one obtains: $(u_k)_y^x + A_k$, where the $A_k$ constitute a system of the form

$$\begin{aligned} A_k = m_k i\pi + a_{k1}q_1+ a_{k2}q_2+ \dots + a_{kp}q_p, \qquad k= 1,2, \dots p. \end{aligned}$$

Here, the $a_{ij}$ depend only on $C_n$, whereas $m_i, \,q_i \in \mathbb {Z}.$ Suppose, for example, we want to identify the 64 systems of cubic curves tangent to a nonsingular quartic at six points (Clebsch 1864c, 211). Let these six points be $P_1, P_2, \dots P_6$, then this leads to the three conditions:

$$\begin{aligned} (u_k)^{P_1}+(u_k)^{P_2}+ \dots (u_k)^{P_6} \equiv \frac{A_k}{2}, \qquad k= 1,2,3, \end{aligned}$$

where the $A_k$ vary depending on $m_i$ and $q_i$, $i= 1,2,3$. Since the sums of the six integrals are given modulo 2, there are $2^6= 64$ different possible systems that solve this problem.

Hesse had dealt with the same question in Hesse (1855b), where he showed that these 64 systems of tangential cubics to a $C_4$ fall into two subsystems, depending on whether the six points $P_1, P_2, \dots P_6$ lie on a conic $C_2$. This occurs in 28 cases, and Hesse could then show that the other two points $\{P_7, P_8\} \subset C_4 \cap C_2$ lie on a bitangent to the quartic. Clebsch showed that this followed immediately from the fact that the bitangents to quartics correspond to the condition $\sum m_i\cdot q_i \equiv 1 \,\,(\text{ mod }\,\,2),$ which occurs in 28 cases, whereas $\sum m_i\cdot q_i \equiv 0 \,\,(\text{ mod }\,\,2)$ in 36 cases. Thus, taking the equations above together with the conditions for a bitangent, namely

$$\begin{aligned} (u_k)^{P_7}+(u_k)^{P_8} \equiv \frac{A_k}{2} \end{aligned}$$

leads to

$$\begin{aligned} (u_k)^{P_1}+(u_k)^{P_2}+ \dots (u_k)^{P_6}+ (u_k)^{P_7}+(u_k)^{P_8} \equiv 0 \qquad k= 1,2,3, \end{aligned}$$

which shows these eight points lie on a conic.

Clebsch also dealt with the characteristics of double tangents, though he did not employ that terminology as such. He handled this topic in connection with Hesse’s results on the 63 systems of conics tangent to a quartic at four points (Clebsch 1864c, 209–210). In Clebsch’s notation, these are given by

$$\begin{aligned} (m_1, m_2, m_3; q_1, q_2, q_3), \end{aligned}$$

where $m_i, q_i \in \{0,1\}$ and (0, 0, 0; 0, 0, 0) is excluded. These conics degenerate into pairs of lines exactly when $\sum m_i\cdot q_i \equiv 1 \,\,(\text{ mod }\,\,2),$ and Clebsch listed these 28 cases explicitly. Klein gave a more detailed treatment of this configuration of lines for a special type of quartic curve for which all the bitangents are real lines (Klein 1877) (see the discussion relating to Fig. 47).

This paper was a sequel to Klein (1876c), which closed with new results that went beyond the findings Clebsch presented in connection with Riemann’s theory of Abelian functions. These concerned four different tangency relations with respect to a given nonsingular quartic curve $C_4$:

• 1) the 63 systems of conics tangent to a $C_4$ at four points;

• 2) the 64 systems of cubics tangent to a $C_4$ at six points;

• 3) the 728 systems of cubics with threefold contact at four points of a $C_4$;

• 4) the 4096 systems of cubics with fourfold contact at three points of a $C_4$ (Clebsch 1864c, 295).

These four findings, to be sure, were not new discoveries; moreover, they were, of course, purely enumerative results. In fact, the cases 3) and 4) can be treated just like the other two as a combinatorial result for systems of Abelian integrals with $p=3$. Clebsch made this clear by noting that requiring r-fold contact to a curve of genus p leads, in general, to the problem of inverting 2p integrals that assume r different values, which yields $r^{2p}$ solutions. In the case of $p=3$, we have for 3) $3^6 -1= 728,$ whereas for 4) $4^6=4096$, all possibilities being admissible.

9 Klein’s visualization of integral curves on Riemann surfaces

9.1 Physical inspirations

In “On the Form of Abelian Integrals for Fourth-Degree Curves” (Klein 1876c), Klein found a way to connect Clebsch’s findings with his projective Riemann surfaces. At the same time, for five different types of quartic class curves, he was able to determine the number of tangent systems of conics and cubics that were real. The numbers he derived drew not only on Clebsch’s analytical approach but also on a novel method for constructing a new type of Riemann surface with properties that reflected the Gestalt of a real curve. Klein published his results in Klein (1876c), but he reserved the special case of 1) involving degenerate conics, thus pairs of lines that touch a quartic in four points, for a subsequent study (Klein 1877). He began as before with the degenerate case of two conics. Once he had parameterized these by means of logarithmic integrals, he introduced small deformations to obtain nonsingular quartics without disturbing the structure of the integral curves on the projective Riemann surface. Klein’s arguments mixed fairly simple analysis with a good deal of geometric intuition. This work, thus, involved visualizing integral curves on the corresponding projective Riemann surfaces along with their periodicity modules.

Klein’s early work on projective Riemann surfaces was later overshadowed by his influential booklet Über Riemanns Theorie der algebraischen Functionen und ihrer Integrale (Klein 1882). In this text, Klein famously appealed to physical ideas, in particular potential theory and electrical or hydrodynamical principles, to motivate the construction of complex-valued functions on a closed surface. Far less well known, however, is the fact that he had already alluded to this possibility back in the mid-1870 s in connection with projective Riemann surfaces. Indeed, his motivation in Klein (1876c) was quite similar, namely to gain a visual grasp of the complex structure on a Riemann surface of genus p, as in the present case of nonsingular quartics with $p=3$.

For this purpose, Klein wrote $f(x+iy) = P+ iQ$, where f is the integral of an algebraic function. In conventional complex analysis, the corresponding integral curves $P=C$ and $Q=C'$ arise from the Cauchy-Riemann partial differential equations in the complex plane. Klein’s main innovation involved transporting those methods to an arbitrary closed surface S of known genus so that the functions could be identified directly with such systems of curves. These ideas were first elaborated in Klein (1882), where he considered the “flows” on S determined by two conjugate harmonic functions $P=C$ and $Q=C'$. These systems cover S and at most points they cross each other at right angles. The exceptional points are zeroes of the function $f(x+iy)$ as well as the “sources” and “sinks” for the flow, which correspond to pole points.

In Klein (1876c), Klein displayed these curve systems on the projective Riemann surfaces built on real curves of the fourth class. He began, though, with the general observation that one can view $P=C$ as equipotential curves, which correspond to a stationary flow represented by $Q=C'$. If then $Q=C'+ dC'$ is a nearby curve, these two curves together form a canal. Assuming this narrow canal contains no singular points, Klein concluded that a nearby curve will be closed whenever a given $Q=C'$ is closed. In this manner, he obtained a general result regarding the properties of integral curves on closed Riemann surfaces. After dealing with various preliminary matters, Klein returned to discuss some special cases of such curve systems.

Fig. 34

Integral curves on an ellipse

The simplest of these involves a single conic $C_2$, shown as the ellipse in Fig. 34. Its projective Riemann surface has the form of an ellipsoid $F_2$, where its two leaves join together along $C_2$. Klein used a logarithmic integral to parameterize $F_2$, essentially following the lead of Clebsch. Thus, he wrote $f(u)=0$ for the equation of $C_2$ in line coordinates $u= (u_1, u_2, u_3)$ and put the integral in the form³⁴

$$\begin{aligned} \int \frac{\begin{vmatrix} c_1&u_1&du_1 \\ c_2&u_2&du_2 \\ c_3&u_3&du_3 \end{vmatrix}}{(\alpha _1\,u_1+\alpha _2\,u_2+\alpha _3\,u_3)\left( c_1\frac{\partial f}{\partial u_1}+ c_2\frac{\partial f}{\partial u_2}+c_3\frac{\partial f}{\partial u_3}\right) } = \int \frac{|cu\textrm{d}u|}{u_{\alpha } \sum \,c_if_i}. \end{aligned}$$

The point $u_{\alpha }=0$ outside the ellipse serves as the origin, through which the two tangents determine points at $\pm \infty$ on the curve. Klein wrote $U_1=U_2=0$ for the coordinates of the points of tangency and $U_3=u_{\alpha }=0$ for the origin, so the equation $f(u)=0$ in point coordinates appeared as

$$\begin{aligned} F= U_1U_2 - U_3^2=0, \end{aligned}$$

and the integral took the form

$$\begin{aligned} \int \frac{|CU\textrm{d}U|}{U_3 \sum \,C_i\,F_i}. \end{aligned}$$

Klein set $C_1=C_2=0$ to obtain the result:

$$\begin{aligned} \frac{1}{2} \,\text{ log } \,\, \frac{U_1}{U_2}+K = P + iQ. \end{aligned}$$

Thus, the integral is everywhere finite except at the two points of tangency on the curve, $U_1=0$ and $U_2=0$. He then showed that the integral curves $P=C$ and $Q=C'$ corresponded, in the first case, to lines through the origin $U_3=0$ and, in the second, to conics that touch the $C_2$ at the two points at infinity $U_1=U_2=0$, as shown in Fig. 34.

Note that this picture gives only a view of the top of the ellipsoid, but exactly the same types of curves appear on the bottom. Here the straight lines on $P=C$ cross the segment connecting $U_1=0$ and $U_2=0$ at points with imaginary parameter $i\pi /2$. The points on the curve itself have either a real parameter x or an imaginary one of the form $x+i \pi$, a fact that Klein exploited at the end of his analysis. He next extended these considerations to the case of a degenerate quartic in the form of two ellipses.

9.2 Parameterizing a degenerate quartic

Fig. 35

The sectors on a pair of conics

Fig. 36

Parameterization of a pair of conics

Klein took these two curves together in symmetrical form so that their equations in line coordinates read:

$$\begin{aligned} \psi = a^2u^2 +b^2v^2 - w^2=0, \qquad \chi = b^2u^2 +a^2v^2 - w^2=0, \end{aligned}$$

and then gave the equation for the quartic as $\phi = \psi \cdot \chi =0.$ Its four double tangents touch this degenerate quartic in eight points that divide the curve into sectors (see Fig. 35). He labeled these $S_1, \dots S_4$, each consisting of a pair of disjoint arcs bounded by two points of tangency. He designated the four bitangents $t_{13}, t_{14}, t_{23}, t_{24},$ where $t_{ik}$ touches the curve in points that separate $S_i$ from $S_k$. Following the procedure described above for a single integral that parameterizes an ellipse, Klein now introduced four logarithmic integrals, taking the four crossing points of the bitangents as origins for pencils of lines restricted to the region between the two respective bitangents. Each of these four integrals $I_1, I_2, I_3, I_4$ induces a parameterization yielding real values from $-\infty , +\infty$ for a sector $S_i$ and where all other points on the curve have values of the form $x+i\pi$ (see Fig. 36).

Taking care to adjust the lower limit of integration, the sum to any $x \in \phi$ or its interior is

$$\begin{aligned} I_1^x + I_2^x + I_3^x + I_4^x = \,\,\text{ const. }\,\, \equiv \pi i \,\,\text{ mod }\,\,2\pi i. \end{aligned}$$

Klein gave a table showing the sectors on the curve where parameter value for the four integrals was imaginary:

$$\begin{aligned} {\begin{array}{ccccc} &{}\quad S_1 &{}\quad S_2 &{}\quad S_3&{}\quad S_4 \\ \hline I_1 &{}\quad 0 &{}\quad \pi i &{}\quad \pi i&{}\quad \pi i \\ I_2 &{}\quad \pi i &{}\quad 0 &{}\quad \pi i &{}\quad \pi i \\ I_3 &{}\quad \pi i &{}\quad \pi i &{}\quad 0 &{}\quad \pi i \\ I_4 &{}\quad \pi i &{}\quad \pi i &{}\quad \pi i &{}\quad 0\\ \end{array} } \end{aligned}$$

As he explained later, points whose imaginary parameter is $\pi i$ will appear in pairs, so in sum they yield the value $2\pi i \equiv 0$. This was a key point in his argument when he turned to identifying the systems of real curves tangent to a given quartic. We can already anticipate another main aspect in Klein’s approach by recalling his simple technique for deforming a pair of conics into a nearby quartic curve (see Fig. 5). In keeping with the principle of continuity, Klein first wanted to develop the machinery needed to study the integral curves on the degenerate projective Riemann surface—thus a pair of ellipsoids—before dissolving the singularities on the underlying class curve and following the resulting integral curves on the desingularized surface. In this sense, his strategy was entirely analogous to the one he followed earlier in connection with cubic surfaces (see Sect. 5).

Fig. 37

Meridian curves on the two ellipsoids

To proceed further, Klein introduced a system of meridian curves within the interior of the two ellipses, starting with $\psi =0$ (see Fig. 37). These carry over to meridian curves on the ellipsoids of the corresponding Riemann surface. He obtained six paths on each ellipse, corresponding to pairs of sectors on the boundary curve. Klein labeled these $b_{ik}$ to designate a path running from $S_i$ to $S_k$. He then used the path relations

$$\begin{aligned} b_{12} = b_{13} - b_{23}= - b_{14} + b_{24} \qquad b_{34} = b_{13} + b_{14}= - b_{23} + b_{34} \end{aligned}$$

to confirm that each of the four integrals $I_1, \dots I_4$ assumes the values $0, \pm 2\pi i$ along each of the six paths.

9.3 The curves of types I and V

Among the five types of class curves Klein dealt with in this study, he only focused on types I and V, shown in Figs. 30 and 26, both of which have symmetric shapes. One of Klein’s students produced the schematic picture of a genus 3 projective Riemann surface associated with a type I curve shown in Fig. 31.

Fig. 38

Meridian curves on the surface of the belt curve

Klein then transferred these relations over to the case of the Riemann surface arising from the dual of the belt curve (see Fig. 38). Since his goal was to explore the real curves associated with a nonsingular quartic, he took a system of $p=3$ cross-cuts, along which he fixed the periods for a system of three normal integrals $\mathfrak {I}_k, k= 1,2, 3$ following Clebsch and Gordan (1866). These take standard values on the three cross-cuts, namely:

$$\begin{aligned} {\begin{array}{ccc} 2\pi i &{} 0 &{} 0 \\ 0&{} 2 \pi i &{} 0 \\ 0 &{} 0 &{} 2\pi i\\ \end{array} } \end{aligned}$$

and these were precisely what Klein had found for the three integrals $I_1, I_2, I_3$ when calculated along the three independent paths $b_{14}, b_{24}, b_{34}$. From this, he concluded that he could extend the above three normal integrals to a system of four that will carry over for all six paths on the projective Riemann surface of a nearby quartic curve, such as shown in Fig. 38.

Klein summarized the results in a table that gave the imaginary contributions $\beta _{jk}i$ for the four integrals along these six curves:

$$\begin{aligned} {\begin{array}{ccccccc} &{}\quad b_{23} &{}\quad b_{13} &{}\quad b_{12} &{}\quad b_{14} &{}\quad b_{24} &{}\quad b_{34} \\ \hline \mathfrak {I}_1 &{}\quad 0 &{}\quad -2 \pi i &{}\quad -2\pi i&{}\quad + 2\pi i &{}\quad 0 &{}\quad 0\\ \mathfrak {I}_2 &{}\quad -2\pi i &{}\quad 0 &{}\quad +2\pi i &{}\quad 0 &{}\quad +2\pi i &{}\quad 0\\ \mathfrak {I}_3 &{}\quad +2\pi i &{}\quad +2\pi i &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad +2\pi i\\ \mathfrak {I}_4 &{}\quad 0&{}\quad 0 &{}\quad 0 &{} \quad -2\pi i &{}\quad -2\pi i &{}\quad -2\pi i\\ \end{array} } \end{aligned}$$

Fig. 39

Integral curves for a degenerate quartic

To describe the integral curves on the projective Riemann surfaces for the curves of types I and V, Klein first began with the simpler case of the degenerate quartic (Fig. 39). Referring back to his initial remarks about the role of singularities, he noted that this case has none because the integral $\mathfrak {I_3}$ is finite everywhere. The four points on the two conics where the tangents through the origin touch the curves can be viewed as representing places where the potential and velocity of the flow vanish. On the surface the curves $P=C$ pass from the top to the bottom and return. They are, thus, closed and cross those in $Q=C'$ at right angles. A schematic picture of the corresponding curves on the Riemann surface of a belt curve (type V) is shown in Fig. 40.

Fig. 40

Integral curves for the surface in Fig. 38

Klein provided more details to explain how one should imagine the integral curves on the surface for a type I curve as the analogs of those in the degenerate case. He illustrated these in Figs. 41 and 42 in relation to the integral $\mathfrak {I_3}$.

Fig. 41

Integral curves for the surface in Fig. 31

Fig. 42

Conjugate curves for the surface in Fig. 31

Note how in Fig. 41, the curves $P=C$ on the two tangential parts $t_{13}$ and $t_{23}$ are closed meridians, whereas those marked $t_{14}$ and $t_{24}$ run through the length of these canals before returning to form closed curves. Klein described how one can view the four meridian curves $b_{13}, b_{14}, b_{23}, b_{24}$ as belonging to the system $P=C$. The curves $t_{14}$ and $t_{24}$ meet in the origin, which divides them into two parts of equal but opposite sign. Integrating along these, one thus gets no contribution.

Klein next introduced three more cross-cuts to supplement the three $b_{14}, b_{24}, b_{34}$ introduced with the three normal integrals $\mathfrak {I}_k, k= 1,2, 3$ to obtain a so-called canonical system. He denoted these by $A_i,\,\, i=1,2,3$, which are closed non-separating curves on the surface that meet only one of the $b_{k4}$. Klein constructed these $A_i$ as one of three types depending on the form of the class quartic among the types $I, \dots V$.

Fig. 43

Starting point for the construction of an $A_3$ curve

His starting point in each case was one of the four integrals Klein employed with the degenerate quartic $\phi =0$ consisting of two ellipses. For $I_3$ we have the two sectors $S_3$ and the double tangents t13 and t23 (see Fig. 43).

Fig. 44

Constructing the first type of $A_3$ curve

A corresponding $A_3$ curve arises, just as described earlier, by splitting apart the double tangents. Two cusps then emerge above the new curve near the former location of the points of tangency. Below the curve we get the familiar pair of cusps with double point that pass into two asymptotes, thus ordinary tangents touching the curve at infinity (see Fig. 44). Clearly, this fits the process of deforming $\phi$ into a type I quartic class curve, which produces the same type of curve $A_i$ for any $I_i$. Along this type of $A_i$ a real integral takes on real values.

Fig. 45

Constructing the second type of $A_3$ curve

The second type of $A_3$ curve breaks off one of the double tangents as above, but reverses the direction of the other leaving a gap on the other side (see Fig. 45). To connect those pieces Klein proposes inserting half of a meridian curve, in the picture this is the segment $b_{13}/2$. Except for this piece, the integral $\mathfrak {I}_3$ will be real along $A_3$, so the imaginary part of the full integral will be $2\pi i/2 = \pi i$.

Fig. 46

Constructing the third type of $A_3$ curve

If both sides reverse direction when $\phi =0$ is deformed, then two half-meridians are needed to connect the gaps on both sides, as illustrated in Fig. 46. Integrating over this type of $A_3$ introduces an imaginary periodicity of $(\beta _{13}+\beta _{23})i/2$.

These various types of cross-cuts $A_i$ come into play when examining the deformation processes for each type of integral $I_i$ corresponding to the five types of class quartics. Klein noted that types I and V are the simplest to handle in view of their symmetries, and in fact he only summarized the relevant results for types II, III, IV in a table. The periodicity module for type I contains no imaginary contribution from the integrals $\mathfrak {I}_k, \, k= 1,2,3$ along the curves $A_i$, whereas type II with three components has for $A_2$ a contribution of $-\pi i$. The curve with two components (type III) produces the same imaginary value for the curves $A_1$ and $A_2$. Type IV has just one real component and all three $A_i$ yield imaginary values. The same is true for the belt curve, type V, for which all three curves are of the type pictured in Fig. 46.

9.4 Refining the findings of Hesse and Clebsch

With these data in hand, Klein was prepared to attack the problem raised earlier (see the close of Sect. 8). Among the many different tangency results Clebsch derived during the early 1860 s, four were based on a given nonsingular quartic curve $C_4$. Such a curve admits

1) 63 systems of tangent conics;

2) 64 systems of tangent cubics;

3) 728 systems of cubics with threefold contact; and

4) 4096 systems of cubics with fourfold contact.

Klein proposed to determine how many of these various systems correspond to real curves—meaning curves whose equations have real coefficients—for each of the five types of quartics he investigated. To answer this, he only needed to make use of the methods Clebsch had exploited in his classic paper (Clebsch 1864c).

The Abelian integrals that arise with these four problems are calculated with respect to the canonical system consisting of $b_{14}, b_{24}, b_{34}$ together with the curves $A_1, A_2,, A_3$ for the five types of projective Riemann surfaces associated with the real class curves $I, \dots V$. The values these integrals can assume along these six curves are determined by the degree of contact r and the combinations for $m_i, q_i$ that enter as multiples in the periodicity modules. Thus, if the integral $\mathfrak {I}_k$ takes on the values $\beta _{ik}$ on the curves $b_{14}, b_{24}, b_{34}$ and $a_{ik}$ on $A_1, A_2,, A_3$, then the $m_i, q_i \in \{0, 1, \dots r-1\}$ and for each $k= 1,2,3$ the different possibilities for the periods are

$$\begin{aligned} \frac{1}{r}(m_1 \beta _{1k} + m_2 \beta _{2k} +m_3 \beta _{3k} + q_1 a_{1k}+ q_2a_{2k} +q_3a_{3k}). \end{aligned}$$

Clebsch had emphasized that these $r^{2p}$ systems are discrete, so one cannot transition continuously from one to another (Clebsch 1864c, 201). With respect to the four enumerative problems above, for 1) and 2) $r=2$, whereas for 3) and 4), $r=3$ and $r=4$, respectively. Klein showed that the Jacobi inversion problem associated with the sums of these integrals will lead to a real curve only when the imaginary part of these sums modulo $2\pi i$ equals either zero or $\pi i$. More precisely, if for 4n points $x_1, x_2, \dots x_{4n}$ on a nonsingular $C_4$ the sums for $k=1,2,3$ are

$$\begin{aligned} \mathfrak {I}_k^{x_1} + \mathfrak {I}_k^{x_2} + \dots + \mathfrak {I}_k^{x_4n} =v_k, \end{aligned}$$

then these 4n points will lie on a real curve of degree n if and only if the imaginary parts of the $v_k$ modulo $2\pi i$ equal either zero or $\pi i$.

For this reason, Klein was only concerned with the imaginary parts of the periodicity modules, which vary for each of the five curve types. Thus, for type I, since the $a_{ik}$ are all real, the $q_i$ can be chosen freely. The $\beta _{ik}= 2\pi i, i=k$ and otherwise vanish, so summarizing for case I we have

$$\begin{aligned} \mathfrak {I}_1 = 2m_1 \pi i; \,\, \mathfrak {I}_2 = 2m_2 \pi i; \,\, \mathfrak {I}_3 = 2m_3 \pi i. \end{aligned}$$

The imaginary values in cases II and III are a bit more complicated, and those in IV and V more so still. When $r=2$, the $m_i, q_i$ can be freely chosen for type I, so we get $2^6= 64$, indicating that all the curve systems for problems 1) and 2) are real. When $r=3$, on the other hand, $m_1=m_2=m_3=0$ and the $q_i$ can vary freely, leading to $3^3=27$ real systems. Finally, for $r=4$ the $m_i \in \{0, 2\}$ and the $q_i$ can take on any of the four values 0, 1, 2, 3, so we have $2^3\cdot 4^3 =512$ real systems.

In the case of the belt curve (type V), the imaginary parts of the three integrals are:

$$\begin{aligned} \mathfrak {I}_1 = (2m_1-q_3) \pi i; \,\, \mathfrak {I}_2 = (2m_2-q_3) \pi i; \,\, \mathfrak {I}_3 = (2m_3-q_1-q_2+2q_3) \pi i. \end{aligned}$$

For $r=2$, the first two integrals require that $q_3=0$, whereas $m_1, m_2$ can assume either 0 or 1, so there are four possibilities. The third integral requires $q_1=q_2$, and $m_3$ can be freely chosen, so there are $4 \cdot 4 = 16$ real systems. For $r=3$ there are three possible choices, so $3^3= 27$ altogether. Klein compiled a table listing the number of real cases for the five types of curves:

$$\begin{aligned} {\begin{array}{ccccccc} &{}\quad I &{}\quad II &{}\quad III &{}\quad IV &{}\quad V &{}\quad r^6\\ \hline r=2 &{}\quad 64 &{}\quad 32 &{}\quad 16 &{}\quad 8 &{}\quad 16 &{}\quad 64\\ r=3 &{}\quad 27 &{}\quad 27 &{}\quad 27 &{}\quad 27 &{} \quad 27 &{}\quad 729\\ r=4 &{}\quad 512 &{}\quad 256 &{}\quad 128 &{}\quad 64 &{}\quad 128 &{}\quad 4096\\ \end{array} } \end{aligned}$$

He then summarized this analysis, while taking the exceptional cases for $r=2,3$ into account. Thus, for the five types of quartics I, II, III, IV, V, the number of real cases among the 63 systems of tangent conics is, respectively, 63, 31, 15, 7, 15. This is just one less than the numbers for the 64 systems of tangent cubics. Among the 728 systems of cubics in threefold contact with the quartic, only 26 are real, a result that applies in all five cases. Finally, for the 4096 systems of cubics with fourfold contact, the table shows that the real curves arise in 512 cases for type I but only 64 in case IV.

9.5 Klein on the characteristics of the 28 bitangents

In closing this section, let me depart from this kind of thick description of Klein’s work to comment briefly on his paper treating the 28 bitangents to quartic curves (Klein 1877), a topic already discussed in several earlier parts of this essay. This was written as a sequel to the paper described above (Klein 1876c). To place this work chronologically, Klein submitted the first manuscript in April 1876, whereas the second was already completed in August of the same year. The topic made for a natural sequel, but Klein handled it very differently than he did in discussing non-degenerate tangent curves to quartics in Klein (1876c). There he employed class curves and qualitative arguments based on projective Riemann surfaces, which led to different results depending on the type of real quartic in question. In Klein (1877), on the other hand, he dealt only with one type of real quartic in point coordinates, utilizing the standard Plücker form

$$\begin{aligned} \Omega ^2-\mu \, pqrs=0, \end{aligned}$$

mentioned already in Sect. 4.

Especially curious, though, were Klein’s introductory remarks, where he emphasized that his earlier study had made no use of “so-called $\theta$-characteristics,” whereas these were critically important for a systematic investigation of bitangents to quartics. As with his other papers discussed above, Klein’s goal was to make the combinatorial representation of bitangents by means of characteristics visually comprehensible. This meant displaying all 28 double tangents to a quartic with four real components, as shown in the closing diagram given in Fig. 47. These results clearly drew on the work of others, though it is difficult to trace the lines of influence; Riemann’s role was indirect, since his contributions to this topic had yet to appear in print.

Fig. 47

Characteristics for the 28 bitangents

Like other authors from this time, Klein gave very few references to the literature, but he did mention the monograph by Clebsch and Gordan (1866), which may have been an important source.³⁵ In a footnote, Klein also listed Clebsch-Lindemann (Clebsch 1876) as well as Heinrich Weber’s monograph (Weber 1876). Strikingly absent was any mention of Roch’s paper (Roch 1866), which underscored the importance of Riemann’s $\theta$-characteristics for the study of bitangents to quartics. Surely Klein knew of it, so why did he decide not to cite it? And why the vague expression “so-called $\theta$-characteristics”? During these early years, Klein had little patience for carefully reading journal articles and other mathematical literature, preferring instead to pick up information and clues by talking with other mathematicians. One can easily imagine that such circumstances might account for some of the idiosyncrasies in this particular contribution to anschauliche Geometrie.

In Sect. 4, I raised some questions regarding the importance of Riemann’s work for algebraic geometry in the period considered here. On a general level there can be no question that the long-term impact of Riemann’s ideas was huge, but my concern here has been to assess how Klein came to develop the ideas that led to his papers on anschauliche Geometrie. These contain barely any mention of Riemann’s works, whereas Klein put some of Clebsch’s publications on prominent display. In the following section, I briefly consider concurrent events that shed some light on the mysteries surrounding Riemann’s influence on Clebsch and Klein.

10 On the prehistory of the publication of Riemann’s Werke

Only 7 months before his death in November 1872, Alfred Clebsch sought to promote the theory of Abelian functions for the case $p=3$. As Vice-Rector of Göttingen Universty, he saw to it that the philosophical faculty proposed this problem for the Benecke Prize, posing it as a challenge to the entire German mathematical community. Unfortunately, Clebsch was no longer alive when Heinrich Weber submitted his winning manuscript, later published by the Berlin Academy in 1876 (Weber 1876). Weber’s study offered only a partial solution to the problem posed, but it nevertheless gave a nearly exhaustive analysis of the various cases pertaining to the bitangents of a quartic curve. Clearly, Weber drew on Riemann’s initial work, but he cited it only sparingly; more surprising still, he made no reference whatsoever to Roch’s 1866 study.³⁶ Weber’s monograph was studied by Klein, however, and he evidently also recommended it to at least one of his students.³⁷

What Clebsch may have known about Riemann’s unpublished investigations and their importance for algebraic geometry seems to be shrouded in mystery, a difficulty that will surely remain unsolved unless new archival sources turn up that can shed light on what Clebsch knew from others, in particular from Gustav Roch. An inquiry into these matters could add a new dimension to studies on the reception of Riemannian ideas, for we know that Clebsch had spent the last months of his life deeply engaged in the study of Riemann’s work. An account of this can be found in correspondence between Richard Dedekind and Heinrich Weber, recently edited by Katrin Scheel (2014). The present section draws on this work, which brought to light some of the behind-the-scenes activity leading up to the publication of Riemann’s Werke in 1876 (Weber 1876/1892/1902).

Not long after he won the Benecke Prize, Weber received a long letter from Dedekind, dated 1 November 1874 (Scheel 2014, 43–46). In it, Dedekind recalled events relating to various works and assorted documents given to him originally by Riemann’s widow shortly after her husband’s death in 1866. Dedekind thought three of the manuscripts—among them Riemann’s famous Habilitationsvortrag (Riemann 1868/1876)—needed virtually no editing, so he arranged for their immediate publication.³⁸ He then went to work on the remaining material, hoping to salvage as much as possible.

In the years afterward, Dedekind invested a good deal of time and energy editing these other manuscripts from Riemann’s papers. Before he could submit them, however, he learned in early 1872 from Clebsch of a plan to publish Riemann’s collected works, including manuscripts from his estate. Dedekind agreed to support this project, leaving Clebsch, who had assumed Riemann’s former chair in 1868, to do the lion’s share of the work. As Dedekind reported to Weber, Clebsch pursued this undertaking with great fervor up until his sudden death in November 1872. By that time, Clebsch had delivered a paginated text containing 23 works, to which he had planned to add three short supplementary papers.³⁹ Having summarized this prehistory, Dedekind asked Weber whether he would agree to take over the editorship at this stage.

Weber wrote back already on 5 November from Zurich, promising to do whatever he could to bring this worthy project to completion. Only a few weeks later, he reported to Dedekind that he was now oriented with regard to the unpublished papers in Riemann’s estate. He was particularly keen to restore Riemann’s work on the bitangents to quartic curves, for which he found only unordered pages of diverse calculations in a hopelessly chaotic state. Luckily, due to his intimate familiarity with this topic, demonstrated in Weber (1876), plus the fact that he possessed corresponding lecture notes prepared by Gustav Roch, he “already recognized the essential core (das Wesentliche) of his very beautiful and important investigation for the Abelian functions” (Scheel 2014, 52). Surely hoping for Dedekind’s approval, he added that no one would probably take issue with Weber’s planned use of Roch’s Vorlesungsheft.

This matter came up more than once in the correspondence, but it seems Weber was never able to elicit a reaction from Dedekind, a famously reticent personality. Clearly, Weber had a major stake in preparing this topic for the edition, but as months went on he developed serious doubts about the feasibility of this plan. In March 1875, he wrote Dedekind:

...regarding the investigations on double tangents, I have become doubtful again about whether it is appropriate to take these up. Among [Riemann’s] papers, one finds only formulas, and I must take a great deal from [Roch’s] Heft to deliver something comprehensible, which requires going into some lengthier elaborations (Scheel 2014, 65).

Finally, in a letter from 8 July 1875 (Scheel 2014, 70–72), Weber asked for Dedekind’s opinion as to whether two topics in Roch’s lecture notes could be published in Riemann’s Werke. If Dedekind ever replied, no evidence of this survives, though ultimately these were published as numbers XXIX and XXX in (Weber 1876/1892/1902). In the Vorrede to the 1876 edition, Weber mentioned that these texts were based on Roch’s Vorlesungsheft, which presumably no longer exists.

Given the fact that Gustav Roch had passed away already a decade earlier, one naturally wonders how Weber ever acquired access to his manuscript based on Riemann’s lectures. A likely reconstruction of these events can be construed from one of Weber’s letters to Dedekind, which mentions that he had obtained this document from Hermann Amandus Schwarz, who was then his colleague at the ETH in Zurich (Scheel 2014, 71). One can only speculate as to how Schwarz had acquired Roch’s lecture notes, but this probably occurred shortly after Roch’s death in Venice on 21 November 1866 (exactly 4 months after Riemann had died in Italy). Roch had recently been promoted to an associate professorship in Halle before he succumbed to tuberculosis. Soon afterward, the Prussian ministry appointed his successor, namely H.A. Schwarz, who later took a very avid interest in the publication of Riemann’s Werke.

Assuming Roch had hopes of returning to Halle after his sojourn in Italy, one can easily imagine that he had left many of his personal belongings behind, including those of a scientific nature. Schwarz may have inquired about Roch’s estate or he could have been solicited to investigate whether it contained documents of potential value. In any event, it would appear likely that Roch’s notes on Riemann’s lectures came into Schwarz’s possession during this period in the latter’s career. In fact, he only remained a short time in Halle, as by 1870 he had received a professorship at the ETH in Zurich, where he was joined by Heinrich Weber (Frei and Stammbach 1994, 41). They both remained in Zurich until 1875, when Weber left to assume Friedrich Richelot’s professorship in Köngisberg, whereas Schwarz went to Göttingen, where he took the chair formerly occupied by Riemann and Clebsch. This placed Schwarz in an ideal position to monitor progress on the Riemann edition, as his neighbor on Weender Chausee was none other than Elise Riemann, widow of the famous mathematician (see his letters to Weber from 1875 to 1876 in Scheel (2014, 360–378)).

Weber was, thus, in Köngisberg when he put the last touches on the first edition of Riemann’s Werke. In February 1876, he mentioned to Dedekind that President Kappeler from the ETH had written him with an urgent plea that he return to Zurich, but after consulting with his wife they decided he should decline the offer. Dedekind found this a good decision, but also an amusing situation, wishing ironically that the Swiss might offer both of them positions in Zurich (Scheel 2014, 116).

11 Concluding remarks

The works by Klein described above have been neglected almost entirely by historians of mathematics, partly no doubt because they reflect a stage of naive exploration that even Klein himself no longer pursued after about 1877. This is not to say, however, that he attached little importance to these ideas from his youth. During the remainder of his career, he promoted projective Riemann surfaces and related methods in anschauliche Geometrie in his lecture courses and seminars, especially those he taught up until around 1900.⁴⁰ Klein’s impact as a teacher, however, while broad and inspirational, had far less influence on the stylistic level. Moreover, his approach was that of a generalist during an era when specialization began to dominate mathematical research. As Eric Temple Bell aptly noted in 1945:

...few of Klein’s contemporaries were willing to assimilate his singular personal methods. ...Klein’s mathematics demanded too much knowledge of too many things for mastery in a reasonable time, and in addition it frequently presupposed a facility in spacial [sic] linguistics beyond the capacities of most mathematicians. (Bell 1945, 511–512)

In my attempt to contextualize Klein’s contributions in the arena of anschauliche Geometrie, the working methods of two geometers stand out as especially important: his first mentor, Julius Plücker, and the Danish geometer H.G. Zeuthen.⁴¹ Like Klein, both promoted the use of continuity arguments in algebraic geometry. In fact, one might even say that Zeuthen’s book (Zeuthen 1914) tried to affirm Klein’s claim back in 1870, when he wrote to Max Noether that “the principle of continuity ...can quite well ...be proved.” What Klein meant by that, though, remains unclear, as he continued to use this and other heuristic principles without showing much concern for their justification. Years later, he recalled a conversation with Weierstrass, who told him that Riemann had voiced a similar lack of concern about using Dirichlet’s principle to establish the existence of complex functions satisfying certain fixed conditions. As Klein remembered Weierstrass’s account, Riemann fully acknowledged that this principle was not mathematically rigorous, but he nevertheless insisted that the existence results he based on it were sound (Klein 1926–27, 1: 264).

Klein’s interests in geometrical models dated already from the mid-1860s, when he studied under Plücker in Bonn. After completing the second-part of Plücker’s Neue Geometrie des Raumes, Klein sent a copy to Luigi Cremona along with a short letter. In it, he called Cremona’s attention to the final part, which contained an appendix on complex surfaces:

Apart from the theory of complexes, this section seems to me to be interesting in so far as it treats a manifold family of surfaces in such a way that the different forms that occur are made evident. It seems always to me, and this I take to be the sense of the method employed by Plücker, who had models made of the surfaces discussed here—that in the case of geometric problems, it is important not only to express the relationships between the structures treated by means of propositions, but also by an immediate intuition (Anschauung) of these structures (Israel et al. 1994, 55).

Even though Schläfli had succeeded in classifying real cubic surfaces, Klein wanted to grasp what that classification meant intuitively and qualitatively. He conceived of the collection of all cubics as a 19-dimensional manifold and imagined wandering through the entire manifold by way of small deformations that systematically removed singularities. His starting point for this was a special type of surface due to Cayley, a cubic with four singularities. Despite numerous gaps and technical deficiencies, algebraic geometers today regard this work as standing at the threshold of modern deformation theory.

The other two principal influences on Klein’s early work came through Riemann and Clebsch, but their importance had far more to do with substantive mathematical matters than with methods. Klein sought to go beyond or refine several of Clebsch’s findings in order to determine precisely how many of those enumerative results pertained to real solutions. Thus, at this early stage, Klein’s interest in Riemann surfaces had mainly to do with a novel way of using these to picture how the real and imaginary parts of a complex curve can be visualized in 3-space. He used this approach to shed new light on tangency relations for plane algebraic curves, but already in the case of genus $p=3$ this line of inquiry seemed to raise just as many new difficulties as it solved old ones.

In looking back on these investigations, Klein thought they owed too much to Clebsch’s influence, which he believed had deflected him from the “true Riemann” (Klein 1921–1923, 2: 5). Here he was alluding to his many papers on complex analysis, but especially the new interpretation of Riemann surfaces that he sketched in his monograph Über Riemanns Theorie der algebraischen Functionen und ihrer Integrale (Klein 1882). Aside from a section on symmetric Riemann surfaces, Klein’s presentation in this booklet departed entirely from the approach in his earlier papers. Even when he dealt with symmetric Riemann surfaces, he derived the portion of the Riemann surface S corresponding to the points on a real curve from a special property, namely these constitute the fixed points under a conformal mapping of S of order two. The fact that this leads to an equation with real coefficients is, thus, merely a consequence of a geometric property (Klein 1921–1923, 3: 566–567).

This shift in Klein’s thinking played a vital role in subsequent developments, though it would take another 30 years before Hermann Weyl could draw on a wealth of new ideas needed to shore up Klein’s fundamental conception. During the intervening years, Klein’s approach to Riemann surfaces in the context of complex functions met with a mixed reception. Carl Neumann, author of the first monograph on Riemann surfaces (Neumann 1865), apparently found Klein’s booklet superficial and unimpressive (Tobies 2021, 254). The publication of Weyl’s classic monograph Die Idee der Riemannschen Fläche (Weyl 1913), however, went a long way toward promoting the ideas in Klein’s older booklet (Klein 1882), which was appreciated long afterward (Springer 2001, 1–41). Weyl’s preface certainly paid due homage to Klein’s general views:

Here and there, one encounters the view that the Riemann surface is nothing more than an “image,” a (one admits: very useful, very suggestive) means of visualizing and illustrating many-valued functions. This view is altogether mistaken. The Riemann surface is an indispensable substantive component of the theory and its very foundation. It ...must certainly be regarded as the prius, as the mother soil out of which the functions can grow and flourish in the first place. It must be admitted, however, that Riemann himself has somewhat obscured this true relationship of the functions to the Riemann surface through the form of his presentation ...as he did not make use of the more general ideas (only later developed with transparent clarity by Klein) .... And yet there can be no doubt that it is only in Klein’s conception that Riemann’s basic ideas come to full fruition in their natural simplicity and in their living, penetrating power. The present work is based on this conviction.⁴²

In their broad study of the rise of complex analysis in the nineteenth century up until its consolidation as a discipline in the twentieth, Bottazzini and Gray fittingly end with a historical survey of the textbook literature (Bottazzini and Gray 2013, 691–760). The monographs by Klein and Weyl, two classics in the early literature on Riemann surfaces, were written with a different purpose in mind and with a select audience as well. In Weyl’s case, he even implied that his own booklet was meant to inspire more than merely to teach:

...the idea of the Riemannian surface requires, if we want to do justice to the rigorous demands of modernity, a plentitude of abstract and subtle concepts and reflections. But by sharpening this view a bit one can easily recognize that this whole complicated logical web (in which the beginner may get tangled up) is not what really matters: it is only the net by which we lift up the idea proper, which by its very nature is simple and grand and divine, from the $\tau o \pi o\varsigma$ $\alpha \tau o \pi o\varsigma$, as Plato says—like a pearl from the sea—to the surface of our world of reason.

Yet to grasp the core within this tissue of delicate and meticulous concepts—that, which accounts for the life, the true substance and inner value of the theory—for that a book (and even a teacher) can only provide scanty indications; here everyone has to wrestle himself afresh to gain understanding (Weyl 1913, iv).⁴³