Abstract
In this series of papers I attempt to provide an answer to the question how the Babylonian scholars arrived at their mathematical theory of planetary motion. Papers I and II were devoted to system A theory of the outer planets and of the planet Venus. In this third and last paper I will study system A theory of the planet Mercury. Our knowledge of the Babylonian theory of Mercury is at present based on twelve Ephemerides and seven Procedure Texts. Three computational systems of Mercury are known, all of system A. System A1 is represented by nine Ephemerides covering the years 190 BC to 100 BC and system A2 by two Ephemerides covering the years 310 to 290 BC. System A3 is known from a Procedure Text and from Text M, an Ephemeris of the last evening visibility of Mercury for the years 424 to 403 BC. From an analysis of the Babylonian observations of Mercury preserved in the Astronomical Diaries and Planetary Texts we find: (1) that dates on which Mercury reaches its stationary points are not recorded, (2) that Normal Star observations on or near dates of first and last appearance of Mercury are rare (about once every twenty observations), and (3) that about one out of every seven pairs of first and last appearances is recorded as “omitted” when Mercury remains invisible due to a combination of the low inclination of its orbit to the horizon and the attenuation by atmospheric extinction. To be able to study the way in which the Babylonian scholars constructed their system A models of Mercury from the available observational material I have created a database of synthetic observations by computing the dates and zodiacal longitudes of all first and last appearances and of all stationary points of Mercury in Babylon between 450 and 50 BC. Of the data required for the construction of an ephemeris synodic time intervals Δt can be directly derived from observed dates but zodiacal longitudes and synodic arcs Δλ must be determined in some other way. Because for Mercury positions with respect to Normal Stars can only rarely be determined at its first or last appearance I propose that the Babylonian scholars used the relation Δλ = Δt −3;39,40, which follows from the period relations, to compute synodic arcs of Mercury from the observed synodic time intervals. An additional difficulty in the construction of System A step functions is that most amplitudes are larger than the associated zone lengths so that in the computation of the longitudes of the synodic phases of Mercury quite often two zone boundaries are crossed. This complication makes it difficult to understand how the Babylonian scholars managed to construct System A models for Mercury that fitted the observations so well because it requires an excessive amount of computational effort to find the best possible step function in a complicated trial and error fitting process with four or five free parameters. To circumvent this difficulty I propose that the Babylonian scholars used an alternative more direct method to fit System A-type models to the observational data of Mercury. This alternative method is based on the fact that after three synodic intervals Mercury returns to a position in the sky which is on average only 17.4° less in longitude. Using reduced amplitudes of about 14°–25° but keeping the same zone boundaries, the computation of what I will call 3-synarc system A models of Mercury is significantly simplified. A full ephemeris of a synodic phase of Mercury can then be composed by combining three columns of longitudes computed with 3-synarc step functions, each column starting with a longitude of Mercury one synodic event apart. Confirmation that this method was indeed used by the Babylonian astronomers comes from Text M (BM 36551+), a very early ephemeris of the last appearances in the evening of Mercury from 424 to 403 BC, computed in three columns according to System A3. Based on an analysis of Text M I suggest that around 400 BC the initial approach in system A modelling of Mercury may have been directed towards choosing “nice” sexagesimal numbers for the amplitudes of the system A step functions while in the later final models, dating from around 300 BC onwards, more emphasis was put on selecting numerical values for the amplitudes such that they were related by simple ratios. The fact that different ephemeris periods were used for each of the four synodic phases of Mercury in the later models may be related to the selection of a best fitting set of System A step function amplitudes for each synodic phase.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this series of papers I study the astronomical concepts, the inventions and the innovations underlying the development of Babylonian planetary theory. The central question to be answered is: “How did the Babylonian astronomersFootnote 1 proceed from observation to theory?” Trying to provide an answer to this question is a real challenge because no texts are preserved in which the Babylonian scholars tell us how this was done. What we do have are observational texts, the so-called Astronomical Diaries and Planetary Texts (Sachs and Hunger 1988, 1989, 1996; Hunger, Sachs and Steele 2001, also referred to as ADART I–III and V) and the finished theoretical products, the lunar and planetary ephemeridesFootnote 2 published by Neugebauer (1955) in his Astronomical Cuneiform Texts (henceforth referred to as ACT). The Procedure Texts in which the Babylonian scholars left us instructions how to compute the ephemerides are not of much help because they contain little additional information (Ossendrijver 2012). The preserved Astronomical Diaries and Planetary Texts provide a (strongly fragmented) continuous record of standardized naked–eye astronomical observations covering a period of about six centuries from about 650 to 50 BC, the preserved ephemerides cover a period of about three centuries from about 310 to 50 BC.
The development of Babylonian planetary theory must have been a gradual stepwise process that may have taken more than a century. Since a zodiacal coordinate system is a prerequisite for a theoretical description of planetary motion and since we know that the 360° Babylonian zodiac was introduced sometime during the fifth-century BC, this development probably took place during the fifth- and fourth-century BC preceding the appearance of the earliest preserved ephemeris (for the planet Mercury) for the years 309–289 BC (ACT No. 300). This timeframe is consistent with the discovery of early system A–type schemes for Venus (424 BC ± 8 yrs), Mercury (424–403 BC), Saturn (390–331 BC) and Mars (355–342 BC).Footnote 3 Elsewhere I have suggested (de Jong 2017) that the oldest elements of Babylonian lunar theory may date from the late sixth/early fifth-century BC so that the development of lunar system A theory probably preceded planetary theory. In papers I and II of this series (de Jong 2019a, b) I have discussed the development of Babylonian system A theories of the planets Saturn, Jupiter and Mars and of the planet Venus. In this third paper I will treat the system A theory of Mercury.
Our knowledge of the Babylonian theory of Mercury is at present based on twelve ephemerides and seven Procedure Texts (Ossendrijver 2012, 68–75). Three computational systems of Mercury are known, all of system A. In a system A planetary theory the variation of the synodic arc with position in the zodiac is approximated by a step function such that the zodiac is divided in a number of zones with different constant values of the synodic arc. System A1 is represented by nine ephemerides ACT No. 300–305, ACT No. 303a,b and BM 48147 (Aaboe 1977) and system A2 is represented by two ephemerides ACT No. 300a,b. The ephemerides of system A1 originate from Uruk and Babylon and cover a period of about 90 years, from about 190 BC to 100 BC. They are all connectable by introducing shifts of a few days in time or a few degrees in longitude. The two ephemerides of system A2 both originate from Babylon and cover about 20 years from 310 to 290 BC.
System A3 was discovered by Neugebauer based on the computational procedures in ACT No. 816. This Procedure Text does not carry a date but its scribe, Bel- appla-idin is known to have lived around 320 BC (Britton and Walker 1991). Thirty-five years after the publication of ACT Aaboe et al. (1991) published Text M, an ephemeris of the last evening visibility of Mercury which turned out to have been computed according to system A3 for the years 424–403 BC. This makes system A3 the earliest known planetary system of mathematical astronomy. As we shall see below the special arrangement of this early ephemeris in three columns plays a central role in the development of the system A modelling of Mercury.
The ephemerides of Mercury list dates and positions of Mercury at its four first and last appearances: MF, ML, EF and EL.Footnote 4 The stations are ignored for good reasons as we shall see later. In the system A1 ephemerides MF and EF are primary phenomena while ML and EL are derived using a separate algorithm (ACT, 293–294). In system A2 the situation is reversed, ML and EL are computed and MF and EF are derived (ACT, 296–298). In our study below we will only consider the primary system A models.Footnote 5
Using the large number of planetary observations systematically recorded in the Astronomical Diaries over centuries the Babylonian astronomers eventually recognized certain periodicities in the motion of the planets (Hunger and Pingree 1999, 203–205). These periods are given in a number of different texts. One of these texts, tablet BM 41004, contains periods for all five planets (Neugebauer and Sachs 1967; Brack-Bernsen and Hunger 2005/6). For Mercury this tablet lists three periods after which it returns to the same position in the sky (Normal Star) on the same date in the lunar calendar as follows:
“The passings of Mercury by the Normal Stars. In 13 years, it lacks 3 days to your year. In 46 years, it lacks 1 day to your year. Thirdly: in 125 years, you see the (same) day for the day.”
The 13-year and the 46-year periods could have been directly extracted from the observational material but the 125-year period was probably constructed because in 125 (= 3 × 46 – 13) years the differences in the day decrements of the 13- and 46-year periods cancel so that after 125 years the return of Mercury to the same position in the sky on the same lunar date is indeed exact. According to the colophon of tablet BM 41004 it was copied from an older original by the scribe Iddin BelFootnote 6 who flourished in Babylon in the early third-century BC, so that the planetary periods were known at the time that the Babylonian planetary theories were developed. The 46-year period of Mercury was later extensively used in the so-called Goal-year Texts (Gray and Steele 2008).
In the upper section of Table 1 I list the observed lengths of different Babylonian periods for Mercury in years, the number of synodic events (EL, MF, ML or EF) that Mercury experiences during each of these periods and the number of full sky passages of Mercury during each of these periods. The number of full sky passages of Mercury equals the number of years because Mercury, as an inner planet, is dragged along by the Sun while it moves through the sky as seen from the Earth. For the 13-year and the 46-year periods the number of synodic phenomena is found by counting in the observational record. For the 125-year period it is found from the relation 3 × 145 − 46 = 394, parallel to the way in which the length of that period was constructed.
For the development of their planetary theories the Babylonian scholars defined long ephemeris periods of several hundred years (for the outer planets, see paper I) up to over one thousand years (for Venus, see paper II), which they constructed from linear combinations of the observed periods. For Mercury they went even so far as to define different ephemeris periods for each of the four synodic phases. The reason for this will become clear when we study the planetary theory for Mercury in more detail below. In the second section of Table 1 I list the periods and the derived parameters for each synodic phase separately. They are constructed by linear combination of the observed quantities in the upper section of Table 1. In the third section of Table 1 I list the basic parameters of the Babylonian theory of Mercury which are directly derived from the period relations.
The calculation of the synodic period Δt, the average increase in time between two successive first or last appearances of Mercury, makes use of the length of the solar year of 12;22,08 lunar monthsFootnote 7 or 6,11;04 tithis, resulting in 117;43,15 tithis or 115;52,44 days.Footnote 8 The length of the synodic arc, i.e. the average increase in longitude of Mercury between two successive first or last appearances, equals Δλ = 114;12,36°. Both values differ by less than 0;00,04 between the four synodic phases, corresponding to a relative accuracy of 10−5. Compared to modern astronomical values both quantities are accurate to better than 10−4.
It is important to realize that the mean synodic period of a planet, the average time interval after which it experiences its next similar synodic phenomenon, is the same for all synodic phenomena (first/last appearances and stations). This is due to the fact that each synodic phenomenon of a planet is characterized by a specific value of its solar elongation, the angular distance of the planet to the Sun as seen from the Earth.Footnote 9
A key concept in Babylonian planetary theory is that the synodic period can be computed from the synodic arc, and vice–versa, by using the difference c = Δt–Δλ, derived from the period relation. For Mercury we find c = 3;30,39 (see Table 1, Sect. 3). That this number was indeed used by the Babylonian scribes to compute the dates in their ephemerides is clearly stated in Procedure Text ACT No. 801 where we read: “add to it 3;30,39,4,20Footnote 10 and predict the dates”.
In principle we now could compute a zero–order average Babylonian ephemeris for the first or last appearances of Mercury, starting with an observed initial position λ0 at t0 by progressing the longitude of Mercury in steps of Δλ = 114;12,36° and the time in time steps of Δt = 117;43,15 tithis, such that after n steps we have λn = λ0 + n. Δλ, and tn = t0 + n. Δt. This would lead to an extremely inaccurate ephemeris because in reality the synodic arc varies between 90° and 150° and the synodic time step varies between 3 and 5 lunar months. This is the reason why the Babylonian scholars modelled the motion of Mercury by a step function with different amplitudes (synodic arcs) in different zones of the zodiac.
An important limitation in all theoretical work on Babylonian planetary theory is that at first and last appearance of a planet its position (relative to one of the Normal Stars) is usually impossible to establish by direct observation because when the planet is observed for the first time at dawn or for the last time at dusk close to the horizon, the sky is so bright that no nearby stars are visible. Only in the quite exceptional case that one of the few Normal Stars that is brighter than the planet itself happens to be sufficiently nearby can it be done. In papers I and II it was shown that for the outer planets and for the planet Venus this difficulty was overcome by the Babylonian astronomers by using observations of the planets at its two other synodic phases: the stationary points in their orbits. At the stations the outer planets can be observed during about 6 h of dark night and for Venus there is about 1 h of dark night available in the early morning before dawn and in the early evening after dusk. However, this does not work for the planet Mercury because it reaches its stationary points a few days before or after its last appearance in the evening and its first appearance in the morning.Footnote 11 How the Babylonian scholars solved this problem will be discussed further on in this paper.
2 The planet Mercury and its Babylonian observations
Our Solar System contains ten planets of which five can be observed with the naked eye: Saturn, Jupiter, Mars, Venus and Mercury. Since the planets move against the background of fixed stars in the sky they have intrigued mankind from time immemorial, inspiring religious awe and arousing intellectual curiosity. Their motion was often imagined as driven by divine power and in many ancient cultures the planets were associated with the gods themselves. Modern scholars are often inclined to consider their ancient colleagues and predecessors as early scientists but it is important to keep in mind that these magical notions and ideas may have been prominent in the minds of the scholarly priests who observed the Babylonian skies, recorded the observations in the Astronomical Diaries and computed the ephemerides in which future positions of the planets were predicted (see de Jong 2016, 298–299; Rochberg 2016).
Three of the five visible planets, the so-called outer planets Saturn, Jupiter and Mars, revolve around the Sun in orbits that are situated outside the Earth orbit. The two remaining planets Venus and Mercury, the so-called inner planets, have orbital radii which are smaller than that of the Earth so that they revolve around the Sun within the Earth orbit. Of these two Mercury is the one which is closest to the Sun. As seen from the Earth, the angular distance of Mercury to the Sun is always less than 27° and of Venus less than 48°. Because of their proximity to the Sun inner planets are observed as morning star before sunrise near the eastern horizon or as evening star after sunset near the western horizon depending on which side of the Sun they are located. Another consequence of this orbital configuration is that inner planets experience a first and a last appearance both as morning and as evening star.
Since naked eye observations of first and last appearances of stars and planets form the basis of Babylonian astronomy it is of importance to understand how those observations were carried out and what difficulties the observers may have encountered. To this end I briefly discuss the observation of the first and last appearance of stars located in the zodiac. Since the planets move through the zodiac their appearance and disappearance is similar in many respects to that of stars that form part of the signs of the zodiac.Footnote 12
Due to the rotation of the earth stars rise in the east (in the morning) and set in the west (in the evening). They are only visible at night when the Sun is below the horizon. As the Sun moves through the ecliptic (its path on the sky against the background of stars) in the course of 1 year, stars experience a period of invisibility when the Sun is too close. The first day that a star becomes visible again at dawn near the eastern horizon about half an hour before sunrise, having been invisible for about 4 to 8 weeks (depending on its brightness), is called the date of its first appearance (also called heliacal rising or first visibility). On that day the star remains visible for about 5 to 10 min before it disappears in the brightening morning sky. As the Sun moves on from day to day the star appears near the horizon earlier each night thereby extending its period of visibility from night to night until it is visible during most of the night when it stands opposite the Sun. Eventually the Sun starts catching up with it from behind so that the nightly period of visibility decreases again until finally the day of its last appearance (also called heliacal setting or last visibility) is reached. On that date the star appears for the last time for about 5 to 10 min at dusk just after sunset near the western horizon. The cycle of first appearance, nightly visibility and last appearance repeats every year. Because the star is faint with respect to the bright twilight sky background and only visible for a short time at its first and last appearance its observation is difficult and quite dependent on atmospheric conditions and on the eyesight of the observer. To appreciate the excitement of expecting and then indeed observing the first appearance of a star in the morning sky and the gnawing uncertainty of perhaps having missed it in the slowly darkening evening sky I recommend any student of Babylonian astronomy to once spend a few mornings and evenings carrying out such observations himself.
Mercury is the fastest moving planet, orbiting the Sun in about 88 days. Its orbit has a large inclination to the ecliptic of about 7° which as seen from the Earth leads to ecliptic latitudes in the range ± 3°. Since the orbit of Mercury is situated within the Earth orbit Mercury experiences two conjunctions with the Sun, the outer conjunction at a distance of about 1.5 AUFootnote 13 on the far side of its orbit as seen from the Earth, and the inner conjunction at 0.5 AU on the near side of its orbit. At inner conjunction Mercury moves retrograde (backwards with respect to the stellar background) with a velocity of about −0.5° per day and at outer conjunction it moves prograde (in the same direction as the Sun) with a velocity of about 1.5° per day.
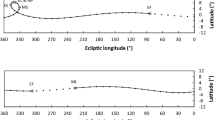
To illustrate the difficulties that confronted the Babylonian scholars in their attempt to model the motion of the planet Mercury I shown in Fig. 1 its path in the sky during 12 months, from 17 March 412 BC to 9 March 411 BC when Mercury made exactly one full passage through the ecliptic. The upper panel in Fig. 1 shows the real path of Mercury while in the lower panel the latitude scale has been blown up by a factor 7.5 to more clearly exhibit the positions of the first and last appearances of Mercury (grey dots) and its stations (black squares). Notice the large variations in ecliptic latitude of Mercury in the region of the sky where it reverses its motion.
The apparent motion of the planet Mercury from 17 March 412 BC to 9 March 411 BC when Mercury completed one full circle of 360° in the sky in just over three synodic cycles. The upper panel shows the actual path of Mercury while in the lower panel the latitude scale is blown up by a factor 7.5 to more clearly indicate the positions of Mercury at its first and last appearances (grey dots) and at its stationary points (black squares). Mercury is invisible due to the proximity of the Sun during large parts of its orbit (dashed lines), from its last appearance in the evening (EL) to its first appearance in the morning (MF) and from its last appearance in the morning (ML) to its first appearance in the evening (EF)
The path of Mercury in Fig. 1 can be understood by realizing that while the Sun steadily moves through the ecliptic in 1 year (counterclockwise from right to left in Fig. 1) it drags Mercury along while Mercury completes four (small) orbits around the Sun in the meantime (also moving counterclockwise). The combined motion of the two is such that on average after one synodic period of about 115 days (about 117 tithis, see Table 1) Mercury is again at the same elongation from the Sun (MF → MF, ML → ML, etc.). Since Mercury moves faster than the Sun the combined motion of the two results in a backward (retrograde) motion of Mercury during about 20 days around inner conjunction during each synodic period.
During one passage through the ecliptic Mercury completes a little more than three synodic periods, experiencing twelve first and last appearances and six standstills at its stations (see Fig. 1). Due to its proximity to the Sun Mercury is invisible about half of the time, indicated by dashed lines in the figure.Footnote 14 Also notice in Fig. 1 the large variations in the lengths of the synodic arc going from one synodic phase to the next similar one (MF → MF, MS → MS, ML → ML, etc.). The largest variation from 99° to 142° occurs for EF (with a corresponding variation in the synodic period of 105 to 138 days).
Figure 1 also illustrates the close coincidence of the evening stations of Mercury with the last appearances in the evening (EL) and its morning stations with the first appearances in the morning (MF). The first and the third evening station (ES) exactly coincide with EL and the second one falls 4 days later (when Mercury is no longer visible), while the first morning station (MS) falls 14 days before MF (when Mercury is not yet visible) and the other two fall 1 and 4 days after MF, respectively.
The synodic phenomena of the planets, sometimes also referred to as the synodic phases, were extensively observed by the Babylonian astronomers and the dates on which the planets first appeared, reached their stationary points and finally disappeared were systematically recorded in the Astronomical Diaries. The Babylonian scholars also compiled lists of observations of the synodic phenomena for each planet separately, covering many tens of years. The data in these Planetary Texts (ADART V) were extracted from the observational data routinely recorded in the Astronomical Diaries.
The Planetary Texts for Mercury list dates in the Babylonian lunar calendar of its first and last appearance and for each first or last appearance the zodiacal sign in which it stood and occasionally a nearby Normal Star is recorded. Interspersed between the observations of first and last appearances are dates of Normal Star passages of Mercury and the observed distances to the Normal Stars on those dates.
Observations of the stations of Mercury were not recorded in the Diaries and Planetary Texts, presumably because – as we have seen above – they occurred so close to its first appearance in the morning (MF) or its last appearance in the evening (EL) that their dates could not be determined.Footnote 15
A representative example of a Planetary Text for Mercury is No. 59 (BM 36600+, ADART V, 199) which lists observations for at least the years 398 to 388 BC. For the first 8 months of year 16 of Artaxerxes II (389/388 BC) the text gives:
“Month I, on the 13th or 14th, last appearance in the east in the end of Pisces; I did not watch. From its first to its last appearance it was very small.
Month II, the 18th, first appearance in the west in the beginning of Gemini; it was bright (and) high, (ideal) first appearance on the 14th.
Month III, the 3rd, first part of the night, Mercury was 2 cubits 8 fingers below β Geminorum.
Month IV, the 1st, last appearance in the west in Cancer. The 27th, first appearance in the east in the beginning of Cancer; it was bright (and) high, (ideal) first appearance on the 25th.
Month V, the 16th, last appearance in the beginning of Leo.
Month VI2, the 5th, first appearance in the west, omitted. The 15th, last appearance in the west, omitted.
Month VII, the 13th, first appearance in the east, 2 2/3 cubits [behind α] Librae; it was bright (and) high, (ideal) first appearance on the 8th.
Month VIII, the 4th, last part of the night, it was 1 cubit 20 fingers behind [the hea]d? of Scorpius. The 7th, it was 1 ½ cubits behind α Scorpii.”
Thus during this period of 8 months four first and four last appearances of Mercury are observed, at one first appearance Mercury is near a Normal Star and one first and one last appearance is “omitted”. Finally there are three Normal Star passages observed during these 8 months. I discuss Normal Star observations near first and last appearances and “omitted” phases in more detail below.
2.1 Normal star observations near first and last appearances of Mercury
The observation of the Normal Star α Librae 2 2/3 cubits (in reality 4°) in front of Mercury at its first appearance near the eastern horizon in Babylon in the morning of the 13th day of month VII in year 16 of Artaxerxes II (30 October 389 BC) is a rare event. Of the roughly one hundred preserved first and last appearances of Mercury listed in Planetary Text No. 59, only seven are associated (on the same day or within a few days) with a Normal Star observation. In another Planetary Text No. 65 (BM 36648+, ADART V, 246), covering the years 362 to 343 BC, we find that in three out of about one hundred twenty preserved observations of first and last appearances of Mercury a nearby Normal Star is mentioned. So it seems that on average only in one out of about twenty observations of first or last appearances of Mercury a nearby Normal Star is visible. This implies that the probability to observe a Normal Star near Mercury in a series of observations of first or last appearances of the same kind equals about 1/80. I conclude that the zodiacal longitude of Mercury at its first or last appearance usually cannot be determined from observations of nearby Normal Stars. The approximate positions of planets in zodiacal signs given in the text may have been estimated by extrapolating from earlier nights when Normal Stars were visible near Mercury on its path through the ecliptic.
The difficulty to determine the position of Mercury at its first and last appearance also exists for the other planets (see papers I and II). For Mars and Saturn the situation is similar to Mercury because they have about the same magnitude at their first and last appearances. For Venus and Jupiter the situation is worse because those two planets are brighter than even the brightest Normal Stars so that at their first or last appearance no nearby Normal Stars are ever visible.Footnote 16 Because of this observational obstacle the Babylonian scholars had to look for other ways to determine the positions of the planets as input for the construction of their planetary models.
2.2 Omitted phases of Mercury
In the excerpt from the Planetary Text No. 59 quoted above the text mentions in month VI2 of year 16 of Artaxerxes II on the 5th day an “omitted” first appearance in the west (EF) and on the 15th day an “omitted” last appearance in the west (EL) of Mercury. Later in that same text there are more records of omitted phasesFootnote 17 of Mercury, both in the west (evening) and in the east (morning). Omitted phases of Mercury are routinely reported in the Diaries and they are also encountered in Almanacs and Normal Star Almanacs, in Goal-Year Texts, and in the computed ephemerides. The earliest preserved record of an omitted first and last appearance of Mercury is found in Planetary Text No. 59, 1 year before the passage quoted above, in month VII of year 15 of Artaxerxes II (390 BC). It is obvious that the omitted phases come in pairs because once a first appearance is not observed a last appearance does not occur.
Omitted first and last appearances of Mercury are not a rare event. From the two hundred and twenty preserved observations of first and last appearances of Mercury in the Planetary Texts No. 59 and No. 65, sixteen pairs are omitted so that roughly one out of every seven pairs of first and last appearances is omitted.
Astronomically, the occurrence of omitted first and last appearances is caused by the combination of two effects: a small inclination to the horizon of the orbit of Mercury (the ecliptic) and attenuation by atmospheric extinction. Since Mercury is at an angular distance of about 18° on either side of the Sun at its first and last appearance (see note 8) it may never rise high enough above the horizon before sunrise or after sunset to become visible. This happens in the spring (April–June) in the morning and in the fall (September–October) in the evening because then the orbit of Mercury has its smallest inclination of about 35° to the horizon.Footnote 18 So morning appearances are omitted in the spring and evening appearances in the fall. In the ephemerides this was formulated by the Babylonian scholars in the form of the following algorithm: first and last appearances in the morning are omitted (DIB) when the longitude of Mercury is between 10° Aries and 20° Taurus, and in the evening when the longitude of Mercury is between 0° Libra and 5° Scorpio (ACT, 288).
Since atmospheric extinction may vary from day to day it can happen that around its date of first or last visibility a star or a planet may be visible one day but invisible the next day, and vice versa. This introduces a certain asymmetry in the visibility probability: first appearances may occur a few days earlier than expected and last appearances a few days later due to atmospheric variability. I have discussed this effect for observations of the planet Venus elsewhere (de Jong 2012).
The variability of the atmospheric extinction may also effect the omission of first and last appearances of Mercury because omission requires the same prohibitive atmospheric conditions during a number of consecutive days. There are a few interesting examples of this recorded in the Astronomical Diaries and Planetary Texts. For instance, in the first line of the passage quoted above from Planetary Text No. 59 we read that in month I of year 16 of Artaxerxes II (April 389 BC) on the 13th or 14th day the last appearance in the east of Mercury in Pisces was expected and that it had been very faint (and apparently difficult to observe) ever since its first appearance in Aquarius on the 28th of the preceding month. So here we have a case where the observation of Mercury might have been close to being omitted but where the atmosphere was sufficiently clear, at least on some days during this fortnight, that Mercury was visible. Although an omitted observation is not expected when Mercury is in Pisces this observational record shows that the situation is close. That also follows from its short period of visibility of 14 days.
Indeed a short period of visibility is a characteristic of the omitted phases of Mercury. Of the sixteen pairs of omitted first and last appearances of Mercury in the Planetary Texts No. 59 and No. 65 there are seven with preserved expected dates for both first and last appearance. The average visibility interval for these 7 pairs is 14 ± 2 days.
By comparing the dates of the omitted first and last appearances in a number of Planetary Texts and preserved Diaries I have found that the early estimates of these dates from the first half of the fourth-century BC propagate through later texts by the application of the 46-year Mercury period.Footnote 19 Starting out with the twenty-one omitted phases between 195 BC and 180 BC listed in the Planetary Text A3456 (Hunger 1988) I looked for omitted phases of Mercury in other Planetary Texts and Diaries at one or more 46-year intervals forward and backward in time. This search resulted in nine sequences of omitted phases connected by 46-year periods in a timespan of three centuries, from 379 to 95 BC. Four of these sequences cover four 46-year periods or 184 years. For instance, the dates of the omitted first and last appearances in the west of Mercury (VII, 7 and VII, 21) in year 29 of Artaxerxes II (376 BC) are exactly repeated 184 years later in SE 120 (192 BC). There are a few more examples in this data set where the dates are also exactly repeated, but in several other cases the dates differ by up to a few days.
There is one interesting case – a possibility I suggested above – where Mercury was observed while its observation was expected to be omitted. In Diary No. −321 (year 2 of Philip Arrhidaeus) we find the following record (ADART I, 227):
“Month VI…. The 8th… Mercury’s first appearance in the east (error for: west) in Virgo (error for: Libra); it was small, sunset to setting of Mercury: 11°.”
From the unusually large number of errors in the text one gets the impression that the observer is surprised and confused by this unexpected observation on day 8 of month VI. Maybe this is the only day that Mercury was observed which would explain why the last appearance in the west is not recorded. Three 46-year periods later in month VI of SE 128 (184 BC) we find that the first appearance in the west of Mercury is omitted on day 1 of month VI and that 10 days later its last appearance is omitted on day 11 of month VI.
On the other hand I found in the Diaries also an explicit observation of an omission which shows that the Babylonian astronomers were still looking for Mercury even when the chances of observing it were small. In the Diary No. −232 (SE 79) we find the following observational record (ADART II, 105):
“Month VIII… The 9th, Mercury’s first appearance in the east in Sagittarius; I did not watch…. The 14th, Mercury’s last appearance in the west in Sagittarius; from its first to its last appearance, when I watched, I did not see it.”
So I conclude that somewhere around 400 BC the Babylonian astronomers started to include the omitted phases of Mercury in their regular observational reports while they had been aware of the invisibility of the first and last appearances of Mercury at certain times of the year for a long time. I suspect that the reason to start including the omitted phases in the observational record has to do with the need to properly count all synodic phases for the correct formulation of period relations (as discussed earlier) which form the basis of the construction of the system A models of Mercury (see Table 1). This is consistent with the adopted time frame for the development of Babylonian planetary theory between about 450 and 300 BC.
3 A more detailed look at the Babylonian observational database
To be able to study the way in which the Babylonian scholars constructed their system A models of Mercury from the available observational material I have created a database of synthetic observations by computing the dates and zodiacal longitudes of all first and last appearances and of all stationary points of Mercury in Babylon between 450 and 50 BC. The computations are based on modern astronomical theory and on the physical visibility criterion that I used in previous studies of first and last appearances of stars and planets (see de Jong 2012 and references therein). The computations were carried out for two values of the atmospheric extinction: the average value in Babylon of 0.27 magnitudes per air mass and a value of 0.20 magnitudes per air mass,Footnote 20 representing a clear night.
The synthetic database consists of lists of dates of the first and last appearances of Mercury and of its stations in the Babylonian lunar calendar and of the zodiacal longitudesFootnote 21 of Mercury on those dates in the Babylonian fixed sidereal zodiac similar to what we find in the Babylonian Planetary Texts with two important differences: (1) the longitudes of Mercury in the synthetic database are given to a fraction of a degree while the Planetary Texts usually only give the zodiacal sign and occasionally an association with a nearby Normal Star, and (2) the Planetary Texts do not include dates and longitudes of the stations. From the synthetic data we may construct the synodic time interval and the synodic arc (the longitude interval) for Mercury from one synodic phenomenon to the next similar one.
To be able to construct an ephemeris for a synodic phenomenon of a planet the Babylonian scholars needed the length of the synodic arc that had to be added to the longitude of the planet at that synodic phase to obtain the longitude at the next similar synodic phase. These synodic arcs vary with position of the planet in the zodiac because the angular velocity varies with position in its orbit.Footnote 22 They also needed synodic time intervals to compute the successive dates of that particular synodic phenomena. The synodic time intervals also vary with position. As discussed above, the Babylonian scholars computed synodic time intervals (in tithis) from synodic arcs (in degrees), or vice versa, by adding or subtracting a constant number c. There we showed that for Mercury c = 3;39,30 (see Table 1).
From the large synthetic database of observations of the synodic phenomena of Mercury I have selected a subset covering the last three decades of the fifth century BC for a more detailed study. In 30 years Mercury completes about 125 revolutions around the Sun and about 95 synodic periods resulting in a database which is comparable in size to the collections of planetary observations found in Babylonian Planetary Texts. In Fig. 2 I have plotted, for all first and last appearances of Mercury between 430 and 400 BC, the synodic arcs that must be added to the longitude of Mercury to obtain the longitude at its next first or last appearance. These synodic arcs are computed from the synthetic observational data and they are graphical representations of the data required for the construction of system A models of the first and last appearances of Mercury. Black dots represent the synodic arcs for a clear atmosphere with an atmospheric extinction of k = 0.20 magnitudes per air massFootnote 23 and open circles represent the synodic arcs for the average atmosphere in Babylon with k = 0.27.
The variation of the synodic arc of Mercury at its last appearance in the evening (EL), its first appearance in the morning (MF), its last appearances in the morning (ML) and its first appearance in the evening (EF) as a function of its zodiacal longitude. Black dots represent values derived from synthetic observations of Mercury in Babylon between 430 and 400 BC for a clear atmosphere characterized by an atmospheric extinction k = 0.20 magnitudes per air mass and open circles represent data for an atmosphere with k = 0.27 magnitudes per air mass. Notice that for the nominal atmosphere in Babylon (k = 0.27) the data show gaps due to “omitted” observations
The most striking feature of Fig. 2 is the occurrence of omitted phases which show up in the data (open circles) for the average atmosphere in Babylon (k = 0.27) while for the clear sky case (k = 0.20, black dots) no omitted phases occur. Omitted visibility phases cause two gaps in the data because when an appearance is passed over the synodic arc has no begin point and the previous one has no end point. A detailed comparison with observations shows that the synthetic data for k = 0.27 are quite successful in predicting the observed omitted phases,Footnote 24 confirming that an extinction of this magnitude provides a good approximation to the average atmospheric conditions in Babylon.
Notice also in Fig. 2 the differences in the shapes and the amplitudes of the variation of the synodic arcs with zodiacal longitude between the different synodic phases. These differences are caused by the interplay of three factors: (1) the variation in the brightness of Mercury (its visual magnitude), (2) the variation of the inclination of the orbit of Mercury to the horizon, and (3) the magnitude of the atmospheric extinction; the same three factors that determine whether a visibility phase is omitted.
A more detailed inspection of the first and last appearances of Mercury in the synthetic data base shows that for the case of a nominal atmosphere (k = 0.27) in Babylon 12 out of 97 evening visibilities are omitted and 15 out of 97 morning visibilities, in good agreement with the observed fraction of about one in seven derived earlier. On the other hand we have seen that for clear skies with k ≤ 0.20 all first and last appearances of Mercury can be observed. Adopting a skewed Gaussian probability distribution with a dispersion of 0.05 for values k ≤ 0.27 and a dispersion of 0.07 for k > 0.27 we find that during 7% of all nights the atmospheric extinction is smaller or equal than 0.20 magnitudes per air mass. This implies that during the visibility window of omitted phases of about 2 weeks there is one night that Mercury might be just visible for 5 or 10 min so that the chances to observe Mercury during an omitted visibility phase are very small indeed.
To avoid the complications introduced by omitted phases as much as possible I will in general use synthetic data computed for k = 0.20 when comparing the Babylonian system A models of Mercury with observations.Footnote 25 This approach is justified by inspection of Fig. 2 which illustrates that the variation of the synodic arc of Mercury as a function of its zodiacal longitude is virtually identical for the two atmospheres within the accuracy of Babylonian observational astronomy. The relative large differences near the beginning and the end of the omitted longitude zones are artifacts of the calculation caused by the extreme sensitivity of the synthetic data to changes in the atmospheric extinction when Mercury is at the verge of (in)visibility. In reality these runaway effects are suppressed by variations in the atmospheric extinction from day to day which causes the dates of the first and last appearances of Mercury to be dominated by the occasional night with clear skies. This effect narrows the omission zones in Fig. 2 and it diminishes the deviations between the two curves near the beginning and the end of the omission zones.
In Fig. 3 I show the synodic arcs Δλ (black dots) and the synodic time intervals Δt (open squares) of the first and last appearances of Mercury as a function of zodiacal position for k = 0.20. These data clearly show that the relation Δt–Δλ = 3;30,39 derived from the period relations in Table 1 for the difference between the average synodic period and the average synodic arc of Mercury, provides a rather poor approximation to astronomical reality, since the actual values of Δt − Δλ may vary between +15 and −7. In practice it turns out that applying the Babylonian algorithm to compute synodic time intervals by adding 3;30,39 to the synodic arcs results in predicted dates of the synodic phenomena of Mercury that are on average correct to within ± 6 days.Footnote 26
The variation of the synodic arcs (black dots) and of the synodic time intervals (open squares) of Mercury at its last appearance in the evening (EL), its first appearance in the morning (MF), its last appearances in the morning (ML) and its first appearance in the evening (EF) as a function of its zodiacal longitude. These data are derived from synthetic observations of Mercury in Babylon between 430 and 400 BC for a clear atmosphere characterized by an atmospheric extinction k = 0.20 magnitudes per air mass
It is important to realize that of the observational data in Figs. 2 and 3, synodic time intervals can be directly derived from observed dates while zodiacal longitudes of Mercury and synodic arcs must be determined in some other way. In papers I and II we have seen that for Saturn, Jupiter, Mars and Venus this difficulty was overcome by using observations of these planets at their stationary points, where longitudes can be determined from the measurement of distances to nearby Normal Stars. However, as pointed out in Sect. 2.1, this is not possible for Mercury because the dates at which Mercury reaches its stationary points coincide within a few days with the dates at which it experiences its last appearance in the evening or its first appearance in the morning and because positions of Mercury with respect to Normal Stars can only rarely be determined at its first or last appearance.
4 The Babylonian System A models of Mercury
That the Babylonian astronomers were nevertheless successful in determining the variation of the synodic arc with position in the zodiac for Mercury is unambiguously proven by their theoretical modelling of this quantity. To illustrate this I show in Fig. 4 the “observed” variation of the synodic arc for the first and last appearances of Mercury (dots and open circles) together with the Babylonian model values (full-drawn lines) computed from the generic System A step functions (dashed lines). The system A1 and A2 step function parameters for the four different synodic phases (see ACT, 296–298) are collected in Table 1 in the section System A step functions.
The observed variation of the synodic arcs of Mercury at its first and last appearances (black dots and open circles) compared to the Babylonian System A1 and A2 model curves (solid lines) and the generating step functions (dashed lines). Parameters of the System A step functions are taken from Table 1. The model curves are computed from the step function parameters using the well-known Babylonian algorithms (see Ossendrijver 2012, 48–49, and Appendix C)
Each of these four step functions has three different amplitudes, distributed over three zodiacal zones in the System A1 models (for MF and EF) or over four zones in the System A2 models (for EL and ML). The values of the amplitudes w(i) and the begin values of the zones λ(i) are listed for each model. The length of each zone then simply follows from the relation z(i) = λ(i + 1)–λ(i). Also indicated in Table 1 are the ratios w(i + 1)/w(i) of the successive amplitudes used in the computation of the longitudes of the next synodic phase (EL → EL, MF → MF, etc.). To keep these computations manageable the amplitudes were chosen in such a way by the Babylonian scholars that their ratios were easy to handle in the sexagesimal number system (see Table 1). In addition, the zone lengths and the amplitudes must satisfy the zone sum rule
and the period relation
That these relations are indeed satisfied for each System A model of Mercury can be easily verified by inserting values of the parameters given in Table 1. These relations reduce the number of free parameters of each model by two, so that the System A1 models of Mercury are fully defined by choosing values for three amplitudes and one zone length, and the System A2 models by choosing three amplitudes and two zone lengths.Footnote 27
The ephemerides computed by the Babylonian scholars based on their System A models turn out to be rather accurate given the simplicity of the method. This is demonstrated in Table 2 where I show the results of a comparison with synthetic observational data (for an atmospheric extinction of 0.20 magnitudes per airmass) for five preserved Mercury ephemerides published in ACT. In column (v) of Table 2 I have listed the mean difference between computed and observed longitudes and its standard deviation for each synodic phase in the various ephemerides.Footnote 28 The magnitude of the standard deviations is a measure of the quality of fit with which the System A model fits the observations while the mean difference reflects the absolute accuracy of the ephemeris. This absolute accuracy is determined by the choice of the initial longitude of the ephemeris, i.e. the accuracy of the Normal Star observation(s) on which it is based. Notice that the early Mercury ephemerides (system A2) are more accurate than the later ones (system A1), both in the quality of fit as in their absolute accuracy.
Two of the ephemerides, ACT 300 and ACT 301, contain computed longitudes of Mercury for the same synodic event, its first appearance in the morning (MF). The data in Table 2 show that the absolute accuracy of the two ephemerides differs by 1.3°, probably due to a different choice of the initial value of the ephemeris (related to different Normal Star observations). Neugebauer (ACT, 318) points out that this difference may be related to the fact that ACT 300 comes from Uruk and ACT 301 from Babylon.
The data displayed in Fig. 4 and in Table 1 show that the synodic arc of Mercury varies between about 90° and 150° and that nine of the fourteen amplitudes of the four System A step functions are larger than the associated zone lengths so that in the computation of the longitudes of the synodic phases of Mercury quite often two zone boundaries are crossed. Although the Babylonian algorithm to compute longitudes of Mercury at its first and last appearances is in itself straightforward, a crossing of two zone boundaries seriously complicates the calculations (Ossendrijver 2012, 527) and it causes the model curves to deviate strongly from the generating step functions (see Fig. 4). This complication makes it difficult to understand how the Babylonian scholars managed to construct System A models for Mercury that fitted the observations so well because it requires an excessive amount of computational effort to find the best possible generating step function in a complicated trial and error fitting process with four (System A1 models) or five (System A2 models) free parameters.
To circumvent this difficulty, I propose that the Babylonian scholars used an alternative more direct method to fit System A-type models to the observational data of Mercury. This alternative is based on a suggestion by Neugebauer (ACT, 289–297) who noticed that the computation of the Mercury ephemerides simplifies considerably if the longitudes of the synodic phases are computed in steps of three synodic events. Since on average three synodic arcs span 3 × 114.2° = 342.6°, the longitudes of every third synodic event decrease on average by 360° – 342.6° = 17.4°. Neugebauer showed that by scaling the amplitudes of the step functions by a factor (3∆λ − 360°)/∆λ (see Table 1) but keeping the same zone boundaries, the computation of what I will call 3-synarc system A models of Mercury is indeed significantly simplified. A full ephemeris of a synodic phase of Mercury can then be composed by combining three columns of longitudes computed with 3-synarc step functions, each column starting with a longitude of Mercury one synodic event apart.
Evidence that this method was indeed used by the Babylonian scholars comes from Procedure Text ACT No. 816 where in Sect. 1 algorithms are given to compute the decrease in longitude of Mercury at its the last appearance in the evening (EL) “year by year” according to a 3-synarc System A model called System A3 by Neugebauer (ACT, 425). Confirmation that this method was indeed used by the Babylonian astronomers was published by Aaboe et al. (1991) who discovered a very early ephemeris of the last appearance in the evening (EL) of Mercury (Text M) computed in three columns according to System A3 (their Table 11; see Fig. 6). I will have opportunity to come back to this text later in this paper.
This method of composing a Mercury ephemeris from longitudes computed in three columns has the great advantage that the (negative) amplitudes of the scaled step functions are so small that never more than one zone boundary is crossed in the computation of the longitude of the next third synodic event. This is illustrated in Fig. 5 where I show the generating step function of the System A1 model (upper panel) for successive first appearances in the morning (MF) of Mercury and of the scaled 3-synarc System A1 model (lower panel) for every third first appearance in the morning. It is also immediately clear from Fig. 5 that fitting system A models to longitude differences between every third first appearance in the morning of Mercury is a quite straightforward process because the System A model curve (solid line) deviates only little from the generating System A step function (dashed line).
The translation of Text M and the layout of the different fragments from which the text was reconstructed by Aaboe et al. (1991). Notice the regnal year numbers in columns II and III which enabled the dating of the period covered by the computed longitudes of Mercury. [Courtesy of the American Philosophical Society]
So the essence of my proposal is that the Babylonian scholars first determined System A parameters for the synodic phases of Mercury by fitting step functions to observed longitude decrements three synodic events apart and then scaled those models up to the System A models that we know from ACT in which longitudes of successive occurrences of the synodic phases of Mercury are computed. Below I will investigate how the Babylonian scholars may have constructed the System A models of the first and last appearances of Mercury in this way from observational data available to them in the Astronomical Diaries.
The main stumbling block in fitting step functions to observed synodic arcs is that longitudes of Mercury cannot be directly determined from observations because, as discussed in Sect. 2.2, at its first and last appearances nearby Normal Stars are generally too faint to be visible. The only possibility to circumvent this problem then seems to use time intervals and convert those to longitude intervals using the relation Δλ = Δt – c, which follows from the Babylonian period relations. This was originally proposed by Swerdlow (1998, 1999) who suggested that this approach was used for the construction of all Babylonian planetary theories. This idea was strongly opposed by Britton (1998). In my earlier papers in this series (de Jong 2019a,b) I have shown that for Venus, Mars, Jupiter and Saturn the System A models appear to be based on positions of the planets determined with respect to nearby Normal Stars when they were at their stationary points. However, for Mercury it seems that Swerdlow’s original proposal is the only way in which longitude intervals can be determined.
As we have seen above after every third occurrence of a first or last appearance Mercury returns to a position in the zodiac which falls on average short by only 17° with respect to its previous position. According to the period relations of Mercury (see Table 1) its synodic period equals about 118 tithis so that on average each next third first or last appearance of Mercury occurs 354 tithis later, i.e. one year of 12 lunar months later minus 6 days. This makes it easy to find dates of every third first or last appearances of Mercury in lists of observations of Mercury over several decades compiled in Planetary Texts. An excerpt of such a Planetary Text of Mercury was discussed in Sect. 2.1.
Once a list of dates of first or last appearances of Mercury a little less than one year apart is compiled, time intervals ∆t in tithis can be determined by counting the differences in months and in days between dates. Using the relation ∆λ = ∆t – 3;39,40 which directly results from the period relations of Mercury (see Table 1) the Babylonian scholars could then have computed the longitude difference between positions of Mercury three appearances apart by subtracting 3 x 3;39,40 = 10;59 from the time intervals. This would have resulted in a list of successive longitude intervals between every third first or last appearance of Mercury. If the Planetary Text from which the observations of Mercury were extracted would have covered a period of thirty years this would have resulted in about 90 longitude intervals. Since on average a nearby Normal Star will be visible about once in about 80 observed appearances (see Sect. 2.1) a suitable Normal Star observation could have been picked to provide an initial longitude from which a list of 90 successive third occurrences could have been constructed with zodiacal longitudes of Mercury and associated longitude intervals (synodic arcs).
This is exactly what I have done using data from the synthetic database of Mercury observations from 430–400 BC discussed in Sect. 2. The results are graphically presented in Fig. 7 for each of the first and last appearances of Mercury together with the System A step functions of the 3-synarc models of Mercury in Table 1 and the resulting model curves. Solid squares in Fig. 7 represent data points constructed from synthetic observations for an atmospheric extinction of 0.20 magnitudes per airmass (all first and last appearances observed) and open squares represent data points for the nominal atmosphere in Babylon with an extinction of 0.27 (some first or last appearances omitted). Notice the runaway behaviour of the computed synodic arcs near the beginning and the end of the zodiacal zone where omitted phases occur caused by the extreme sensitivity to atmospheric extinction. Also indicated in Fig. 7 between the dashed vertical lines are the zodiacal zones where the Babylonian scholars indicated in the Mercury ephemerides that synodic phases would be omitted (by the logogram DIB). These omission zones run from 198° to 240° for EL, from 10° to 50° for MF, from 24° and 65° for ML, and from 180° to 215° for EF (see ACT, 288).
Graphical representation of the variation of the longitude differences between positions of Mercury three synodic arcs apart as a function of zodiacal longitude constructed from synodic time intervals as described in the text for all four first and last appearances together with the System A step functions of the 3-synarc models of Mercury (dashed lines) and the resulting model curves (solid lines). Black squares represent data points constructed from synthetic observations for an atmospheric extinction of 0.20 (all first and last appearances observed) and open squares represent data points for the nominal atmosphere in Babylon with an extinction of 0.27 (some first or last appearances omitted). Also indicated between the thin dashed vertical lines are the zodiacal zones where the Babylonian scholars indicated in the Mercury ephemerides that synodic phases would be omitted
While the Babylonian scholars worked with lists of longitudes and associated longitude intervals the graphical representations in Fig. 7 illustrate that they succeeded in developing System A-type models that provided good fits to the constructed data points of the longitude intervals between every third first or last appearance of Mercury. Notice that the models fit best if the data points in the omitted gaps are not included. The fitting process is straightforward because the model curves only deviate little from the generating step functions for the 3-synarc models. It is further simplified by the fact that the 3-synarc data experience only one omitted phase gap while the data in Fig. 4 for the regular synodic arcs show two gaps for reasons explained there. The fact that the second maximum around 300° in the EL model seems to be shifted from around 240° to 300° may be attributed to the fact that the maximum occurs in the omitted gap between 200° and 260°.
If we accept that the parameters of the Babylonian System A models of the first and last appearances of Mercury may indeed have been constructed in this way, or in ways which follow a similar line of reasoning, the question arises if anything more can be said about the way in which numerical values were selected for the model parameters.
Earlier in this Section I have shown that the System A models of Mercury are fully defined by selecting four free parameters. The System A2 models which seem to require selecting five parameters, in actual fact also need only four parameters because two of the four amplitudes are identical and its associated zone can be arbitrarily split in two pieces, resulting in two zones with two identical amplitudes. Since the amplitudes all have nice ratios in the sexagesimal number system (2/3, 3/4, 4/5, 5/6, 8/9 and 9/10; see Table 1) it seems most appropriate to first select the numerical value of one amplitude, then select the other two amplitudes such that all three amplitudes have nice ratios and finally select the length of one zone (for instance the one belonging to the maximum amplitude). The lengths of the other two zones than follow from the zone sum rule (1) and the period relation (2) discussed above. It is obvious that the trial and error process to come up with a model that provides an adequate fit to the observational data requires a substantial amount of computation but – by doing it myself – I have verified that the process converges and that the computational effort is manageable.
There are indications that the selection of the maximum amplitude was indeed the first step in the parameter selection process. In the bottom section of Table 1 I have listed values of the first amplitude which appears to have been chosen because they are simple fractions (1/2, 1/3 and 1/6) of the scaled down number of sky passages in one ephemeris period of 33 (EL), 129 (MF), 59 (ML) and 73 (EF) listed in the bottom section of Table 1. By choosing amplitude values that are simple fractions of these numbers the period relation (2) becomes numerically rather easy to manage which drastically simplifies the selection of possible zone lengths. I recommend the reader to carry out some of these computations by hand for him- or herself to experience how simple they become in this way.
One can carry this approach even one step further by realizing that the choice of the ephemeris period for each synodic phase separately directly translates into the numerical value of the first amplitude choice. It is straightforward to show that adding or subtracting Mercury periods of 46 or 125 years to or from the defining ephemeris period in the second section of Table 1 increases or reduces the scaled down number of sky passages in the scaling factors in Sect. 5 of Table 1 by ± 7 and ± 19. For instance, increasing the ephemeris period of the last appearance in the evening (EL) of Mercury by 46 years to 125 + 3 x 46 = 263 years (compare Sect. 2 of Table 1) the scaling factor (3Δλ − 360°)/Δλ would have been changed to −40/263 and the first amplitude choice of the 3-synarc model would have become −40/2 = − 20;00. So if the first amplitude chosen did not fit the data sufficiently well, the ephemeris period could have been enlarged or reduced by a suitable number of 46 or 125 years to come up with a first amplitude value that fitted the data better. This may be the reason why each of the synodic phases of Mercury is characterized by a different ephemeris period.
5 Text M: an early System A ephemeris of Mercury
In a paper resulting from a collaboration between Asger Aaboe and Abraham Sachs that started 20 years earlier, Aaboe et al. (1991) discussed seven pre-Seleucid tablets that contained early astronomical texts. One of these, Text M, turned out to be an early Mercury ephemeris, written on the obverse of a tablet of which in total five pieces have been preserved: BM 36651, BM 37032, BM 37053, BM 36791 and BM 37162 (see Fig. 6 for Aaboe’s reconstruction). All fragments are part of the 80–6–17 collection of tablets in the British Museum.Footnote 29 Aaboe et al. were able to date the ephemeris by using the regnal years which are preserved in the upper part of column II and in the lower part of column III to the reigns of Darius II and Artaxerxes II. Text M is the earliest preserved Babylonian planetary ephemeris containing computed positions of the planet Mercury at its last appearance in the evening for the years 424 to 403 BC.
The longitudes of Mercury in Text M (see Fig. 6) are listed in three columns about 115° apart and they are decreasing in each column line by line with amounts between 16° and 20°, exactly as one would expect for an ephemeris of a synodic phase of the planet Mercury computed in the way described in the previous Section. So here we have direct evidence that the Babylonian astronomers indeed computed Mercury ephemerides in the way proposed. Even before analysing this ephemeris in more detail I note that the computation probably started in the lower left-hand corner of the text where we find Mercury at 3;30° Leo, the only entry in the table with a “nice” sexagesimal number, so that the computation apparently was carried out upwards in column I with positive increments in each computational step. The choice of this initial position was probably based on the observation of the last appearance in the evening of Mercury on 2 July 403 BC when Mercury was 1½ cubits below the Normal Star LUGAL (α Leonis) and both were visible for about 15 min around 19:50 h Local Time in Babylon.Footnote 30
In spite of the fact that Text M is a very early ephemeris it turns out to be a rather accurate one. From a comparison of the longitudes in the text with longitudes of the last appearances in the evening of Mercury taken from the synthetic observational database for the years 424 to 403 BC I find a mean difference of −0.6° ± 2.0°. This is slightly more accurate than ACT 300a (see Table 2), an Mercury EL ephemeris computed for dates about 120 years later.
Aaboe et al. (1991) discovered that the longitudes of Mercury in Text M were computed according to procedures known from Procedure Text ACT No. 816. Neugebauer (ACT, 425; HAMA, 468) showed that these procedures belong to a System A model of Mercury called System A3. The parameters defining System A3 are listed in column (2) of Table 3 in the section System A step functions. Since Text M gives longitudes of Mercury at its last appearance in the evening at intervals of three appearances in three columns, the longitudes in each column are computed using the parameters of the scaled down 3-synarc step functions in column (2) of Table 3.
A closer look at Text M shows that the longitudes of Mercury are indeed computed according to the algorithm in Sect. 1 of Procedure Text ACT No. 816, but, as noted by Aaboe et al. (1991; see also HAMA, 470), it also shows that according to this algorithm the boundary between the zones with amplitudes −20;00° and −16;00° is located at longitude 20;37,30° Cancer rather than at 20° Cancer, the value expected for system A3 (see Table 3). The reason for this change of zone boundary is obscure. It is certainly not due to a scribal error, as proposed by Neugebauer (ACT, 426), because the algorithm is consistently applied in all three columns of Text M.Footnote 31
As suggested above the computation of Text M was probably started in the lower left-hand corner with the initial longitude of 3;30° Leo, based on the observation of Mercury at its last appearance in the evening of 2 July 403 BC. The scribe may then first have computed the other longitudes in column I of Text M going upward (backward in time) by applying positive values of the amplitudes of the 3-synarc step function in Table 3. Then, from the longitude of 24;04,10° Leo in the upper left-hand corner, he could have computed the longitudes of Mercury in the top line of Text M using the full System A3 step function parameters in Table 3. Since the 20° Cancer boundary is not crossed in this computation the longitudes in the top line of the text are insensitive to changes in this zone boundary. Starting with these values as initial longitudes for columns II and III he then could have computed the longitudes going downward (forward in time) in each of these two columns by exactly applying the procedures in Sect. 1 of ACT No. 816. The additional computational effort caused by this change of zone boundary is minimal because it affects only one step in the computation in each column. It also has little effect on the numerical values of the longitudes of Mercury because it can be shown that the maximum differences due to this boundary change are 0;7,54,36,33,45°, negligible small compared to the typical accuracy of the Mercury ephemerides of several degrees (see Table 2).
If we accept the observation of Mercury near α Leo in July 403 BC as a terminus post quem for Text M we may conclude that already around 400 BC or shortly afterwards the Babylonian scholars had developed the full sophisticated apparatus of System A planetary theory, even for the planet Mercury for which the observational data had to be massaged to come up with longitude intervals.
In Table 3 I have also listed for comparison in column (3) the period relations and the parameters of the System A2 model for the last appearance in the evening of Mercury discussed in the previous Section. A comparison of the 3-synarc parameters of the System A3 and A2 models shows several interesting differences which may be related to changes in the Babylonian approach to theory building over time. The ephemeris period of system A3 is again constructed from a linear combination of the well-known shorter observed periods of Mercury. However, in the choice of the parameters of the 3-synarc models there seems to have been more emphasis on nice numbers for the amplitudes than for the amplitude ratios.
To illustrate this I show in Fig. 8 the System A3 and A2 step functions and the resulting model curves in separate panels together with the observational data constructed from observed dates in the synthetic database as explained earlier. If we discard data points at longitudes between about 180° and 270° where synthetic observations are extremely sensitive to extinction and/or where they are omitted, the more simple early System A3 model seems to provide a slightly better fit to the data points. It seems plausible to assume that for system A3 an amplitude of −20;00° and a length of the associated zone of 80° were first chosen to fit the bump in the data (see Fig. 8) and that then as the next step an amplitude value of −16;00° (4/5 of −20;00°) was chosen to fit part of the remaining data points. It turns out that the sum rule (1) and the period relation (2) formulated in Sect. 4 above then allow only three solutions in which the two remaining zone lengths have integer values and in which the third amplitude has a “nice” sexagesimal number (see Table 4, columns (4)–(6), numbers in italic script). Of these three possible solutions the one chosen by the Babylonian scholars, w(3) = − 16;52.30° and z(3) = 240°, provides the best fit to the data points when the unreliable and omitted data (between 180° and 270°) are left out.
System A3 and A2 step functions (dashed lines) and the resulting model curves (solid lines) in two separate panels together with the observational data for the last appearance in the evening (EL) taken from the left upper panel of Fig. 7
This choice of the parameters defining System A3 suggests that in the early models of Mercury indeed whole number values for the amplitudes (−20;00° and −16;00°) received more attention than simple ratios of the amplitudes (4/5, 135/128 and 32/27). In the later models of Mercury a technique appears to have been developed where numerical values for the first amplitudes were chosen by manipulating the period relation as suggested in Sect. 4 above and that the choice of the subsequent amplitudes was driven by the requirement of nice values for the amplitude ratios. This might explain why the primary models for the four different synodic phases of Mercury are characterized by different ephemeris periods.
It is further worth noticing that, contrary to several of the later ephemerides of Mercury, none of the entries in Text M are marked as “omitted” (by the logogram DIB). In Sect. 2.2 where I discussed the omitted phases of Mercury we have seen that the Babylonian astronomers had been aware of the omitted phases of Mercury for centuries before they started recording them in the Astronomical Diaries from around 390 BC onwards, consistent with a date for the composition of Text M around 400 BC.
Finally, I suggest that Text M may have been computed to function as a template table for the computation of longitudes of Mercury at its last appearance in the evening (like the Venus tablet ACT 1050; see de Jong 2019b) since each column covers just over one zodiacal cycle of 360°. It may also have been used to check the model on which it is based against previous observations of Mercury near Normal Stars.
6 Concluding remarks
The results of my study of Mercury ephemerides fits in quite nicely with what we know about the development of system A planetary theory during the late fifth and fourth century BC. Early attempts of system A theory formation are known for Venus (BM 36301 column II, containing data for 424 BC ± 8 years; Neugebauer and Sachs 1967; Britton and Walker 1991), Mercury (Text M, containing data for 424–403 BC; Aaboe et al. 1991; this paper), Saturn (BM 45726, containing data for 390–331 BC; Steele and de Jong, forthcoming) and Mars (BM 36301 column I, containing data for 355–342 BC; Neugebauer and Sachs 1967; de Jong unpublished).
I have shown here that the system A theory for Mercury was probably based on fitting models to observations of the synodic phases of Mercury three synodic intervals apart, resulting in what I have called 3-synarc models which could be scaled up to the regular System A models by multiplying the amplitudes with scaling factors derived from the period relations (see Tables 1 and 3). Based on an analysis of Text M, the earliest preserved Mercury ephemeris, I have suggested that around 400 BC the initial approach in system A modelling may have been directed towards choosing “nice” sexagesimal numbers for the amplitudes of the system A step functions while in the later final models, dating from around 300 BC onwards, more emphasis was put on selecting numerical values for the amplitudes such that they were related by simple ratios.
Notes
I will refer to Babylonian astronomers, scholars, or scribes to describe the class of priests or temple functionaries who in the late Babylonian period became known as tupšarrū Enūma Anu Enlil (Robson 2019, 133) and whose tasks were (among other things) to observe the night sky, to write Astronomical Diaries, to compose Almanacs and Normal Star Almanacs and to compute lunar and planetary ephemerides.
Following Neugebauer (ACT, 1) I will use the term ephemeris for texts which contain "lists of positions of the sun, the moon and the planets computed for regular time intervals".
For references see the concluding remarks in Sect. 6.
In this paper I will use the acronyms MF (first appearance in the morning), MS (morning station), ML (last appearance in the morning), EF (first appearance in the evening), ES (evening station) and EL (last appearance in the evening) proposed by Ossendrijver (2012, 56–58) for the different synodic phenomena of inner planets. In the older literature one often encounters the Greek capital letters Γ, Φ, Σ, Ξ, Ψ and Ω that were introduced by Neugebauer (ACT, 280; see also HAMA, 386) to represent the "characteristic phenomena" of the inner planets.
It may be worth mentioning here that three to five centuries later in Greek papyri and Demotic ostraca Systems A1 and A2 were used together in ephemerides and procedure texts of Mercury (Jones 1999; Ossendrijver and Winkler 2018). It is quite well possible that the Babylonians also used Systems A1 and A2 together in one and the same ephemeris of Mercury but without textual confirmation this remains at present a speculation.
Apparently the Babylonian scholars used the length of the solar year of 12;22,08 lunar months derived in their lunar system A theory (see de Jong 2017) also for the planetary theories.
One tithi is defined as 1/30 of a lunar month. By introducing the lunar month and the tithi as units of time all computations of time intervals simplify considerably because it avoids having to keep track whether a lunar month consists of 29 or 30 days. A year length of 12;22,08 lunar months corresponds to 371;04 × 29.530,589/30 = 365.261 days, 0.005 days longer than the modern value of the sidereal year (the time it takes the Sun to return to the same Normal Star).
In present day astronomy the synodic period is defined as the time it takes for a planet to move from one conjunction with the Sun to the next one. At conjunction the solar elongation of a planet, the angle between the Sun and the planet as seen from Earth, is by definition equal to zero. Each of the synodic phenomena of a planet is characterized by a specific value of the solar elongation. For Mercury we find solar elongations of −17° ± 4° at MF and MS, −14° ± 5° at ML, 13° ± 4° at EF and 18° ± 4° at ES and EL.
In the computations of the dates in the Mercury ephemerides this number is usually rounded off to 3; 30, 39.
This also explains why no observations of the stations of Mercury are recorded in the Astronomical Diaries.
Like zodiacal stars the outer planets Saturn, Jupiter and Mars experience a first appearance (in the morning) and a last appearance (in the evening), while the inner planets Venus and Mercury experience first and last appearances in the morning and in the evening.
One AU (Astronomical Unit) is defined as the mean distance between the Earth and the Sun, averaged over its orbit.
There is however one undated fragment of a Planetary Text (No. 84) which lists stations of Mercury. This suggests that the Babylonian scholars may have been aware of the fact that Mercury was stationary near its last appearance in the evening and its first appearance in the morning.
The visibility of Normal Stars near planets at their first and last appearance is an interesting astrophysical problem. It depends on the brightness of the planet, of the Normal Star and of the sky background and on the angular distance of the star to the planet. However, a more detailed study of this problem is outside the scope of this paper.
The texts use the logogram DIB for etēqu, meaning literally "pass by".
It is interesting to note that already in the seventh-century BC Mesopotamian astronomers were aware of the fact that the first and last appearances of Mercury are sometimes difficult or even impossible to observe. In a letter of the court astronomers Balasî and Nabû-aḫḫe-erība to the Assyrian king Esarhaddon of 25 March 669 BC (Letter # 53, Parpola 1970) we read: “As regards the planet Mercury about which the king our lord wrote to us: I have heard it can be seen in Babylon, he who wrote to the king may really have observed it. His eye must have fallen on it. We ourselves have kept watch but we have not observed it. One day it might be too early, the other day it may lie flat in the horizon. Our eyes should indeed have fallen on it.”
The 46-year period of Mercury is quite accurate, falling short by only one day in the lunar calendar after 46 years.
One air mass is defined as the amount of atmospheric material along the line of sight to a star or planet at zenith. At an altitude of about 5° above the horizon (zenith distance 85°) where Mercury experiences its first and last appearances the atmospheric material along the line of sight to Mercury amounts to 1/cos(85°) = 11.5 air masses. For a visual extinction of 0.27 magnitudes per air mass which characterizes the average atmosphere in Babylon this corresponds to an extinction along the line of sight of 3.1 magnitudes causing an attenuation of the brightness of Mercury by a factor of 17.
Ecliptic longitudes of Mercury in the database are converted to longitudes in the Babylonian fixed zodiac by using the relation (see Huber 1958) λbab = λecl + 4°28' − (T + 100)/71.6, where T is the Julian astronomical year (e.g. 423 BC = − 422).
We know now that this variation of the angular velocity of a planet in the sky is due to the eccentricity of its elliptic orbit around the Sun but for the Babylonians this was just an empirical fact.
For economy of space I will omit the units of the atmospheric extinction k [magnitudes per air mass] in the remainder of this paper.
For example in Planetary Text No. 65 seven out of the eight observed omitted visibility phases of Mercury are correctly predicted by the k = 0.27 synthetic data.
This results in observational data that are not disturbed by discontinuities due to the occurrence of omitted phases, similar to what was done by the Babylonian astronomers who included expected dates and zodiacal positions of Mercury at its omitted phases in the observational records.
Apparently the Babylonian scholars were well aware that Δt–Δλ could deviate appreciably from its average value of 3;30 because in ephemeris ACT 300a dates are computed for the last appearances in the evening and in the morning of Mercury (System A2) by applying values of Δt–Δλ which vary between 0 and 9. Unfortunately the data are insufficient to be able to derive the algorithm used to compute these values (ACT, 298).
Of the four amplitudes defining the system A2 models of Mercury two are identical.
For this comparison all computational errors in longitude in the texts were corrected (see ACT 316–321).
Early collections of tablets in the British Museum were often indicated by the dates that the shipment of tablets was received by the Museum. The 80-6-17 collection of tablets was shipped by Hormuzd Rassam, who was organizing excavations in Iraq on behalf of the Museum from February 1879 to July 1882. It consisted in total of 1862 tablets and fragments excavated in Babylon (Clancier 2009, 191). Unfortunately, the exact provenance of the tablets in this collection is unknown. In view of the astronomical nature of a large fraction of the tablets in this collection (at least 15%) they probably come from archives associated with the Esagila temple or from private archives of scholars employed by the temple.
In Sect. 2.1 I showed that the observation of a visible nearby Normal Star at the last appearance of Mercury is a rare event with a probability of about 1/80.
A possible, but admittedly speculative, reason behind this numerically inconsistent and surprising change in the value of the zone boundary may be related to scribal secrecy. We know that secrecy and exclusivity of heavenly knowledge was a serious matter for the Babylonian scribal elite who considered themselves the keepers of cuneiform culture under foreign Achaemenid rule (Rochberg 2004, 212–219). With this in mind one might understand that one of the zone boundaries of model A3 was slightly changed with little effect on the computational effort and on the numerical results but masking the specific period relation on which the parameters of model A3 were based.
References
Aaboe, A. 1977, A Computed Cuneiform Text for Mercury from Babylon: BM 48147. In Prismata: Naturwissenschaftliche Studien. Festschrift für Willy Hartner, Y. Maeyama and W.G. Saltzer eds., 1–8 Wiesbaden: Franz Steiner.
Aaboe, A., Britton, J.P., Henderson, J.A., Neugebauer, O. and Sachs, A.J. 1991, Saros Cycle Dates and Related Babylonian Astronomical Texts, Trans. Am. Phil. Soc. 81, part 6.
Brack–Bernsen, L., and H. Hunger. 2005. On the Atypical Astronomical Cuneiform Text E. Archiv für Orientforschung 51: 96–107.
Britton, J.P. 1998. Planetary Theory in Babylon. Journal for the History of Astronomy 29: 381–385.
Britton, J.P., and C.B.F. Walker. 1991. A 4th Century Babylonian Model for Venus: BM 33552. Centaurus 34: 97–118.
Clancier, P. 2009, Les Bibliothèques en Babylonie dans la Deuxième Moitié du Ier Millénaire av. J.-C., Münster: Ugarit Verlag.
Gray, J.M.K., and J.M. Steele. 2008. Studies on Babylonian Goal-Year Astronomy I. A Comparison between Planetary Data in Goal-Year Texts, Almanacs and Normal Star Almanacs. Archive for the History of Exact Sciences 62: 553–600.
Huber, P. 1958. Über den Nullpunkt der babylonischen Ekliptik. Centaurus 5: 192–208.
Hunger, H. 1988, A 3456: eine Sammlung von Merkurbeobachtungen. In A Scientific Humanist, Studies in the Memory of Abraham Sachs, E. Leichty, M. deJong Ellis & P. Gerardi eds., 201–223 Philadelphia.
Hunger, H. and Pingree, D. 1999, Astral Sciences in Mesopotamia, Leiden.
Hunger, H., Sachs, A.J. and Steele, J.M. 2001, Astronomical Diaries and Related Texts from Babylonia, Vol. V: Lunar and Planetary Texts, Vienna (ADART V).
Jones, A. 1999, Astronomical Papyri from Oxyrhynchus, Philadelphia.
de Jong, T. 2012. Babylonian Observations of Venus: Arcus Visionis, Atmospheric Extinction and Observational Practice. Journal for the History of Astronomy 43: 391–409.
de Jong, T. 2016, Babylonian Astronomy 1880–1950: The Players and the Field. In A Mathematician’s Journeys: Otto Neugebauer and Modern Transformations of Ancient Science, A. Jones, Chr. Proust and J.M. Steele eds., 265–302, New York.
de Jong, T. 2017, On the Origin of the Lunar and Solar periods in Babylonian Lunar Theory, in Studies on the Ancient Exact Sciences in Honour of Lis Brack–Bernsen, J.M. Steele and M. Ossendrijver eds., 105–126, Berlin.
de Jong, T. 2019a. A Study of Babylonian Planetary Theory I. The Outer Planets. Archive for History of Exact Sciences 73: 1–37.
de Jong, T. 2019b. A Study of Babylonian Planetary Theory II. The Planet Venus. Archive for History of Exact Sciences 73: 309–333.
Neugebauer, O. 1955, Astronomical Cuneiform Texts (3 Vols.), London (ACT).
Neugebauer, O. 1975, A History of Ancient Mathematical Astronomy (3 Vols.), Berlin (HAMA).
Neugebauer, O., and A.J. Sachs. 1967. Some Atypical Astronomical Cuneiform Texts. Journal of Cuneiform Studies 21: 183–217.
Oelsner, J. 2000, Von Iqıšâ und einigen anderen spätgeborenen Babyloniern. In Studi sul Vicino Oriente Antico dedicati alla memoria di Luigi Cagni, S. Graziani ed., 797–814, Napoli.
Ossendrijver, M. 2012. Babylonian Mathematical Astronomy: Procedure Texts. Berlin: Springer.
Ossendrijver, M. and Winkler, A. 2018, Chaldeans on the Nile: Two Egyptian Astronomical Procedure Texts with Babylonian Systems A1 and A2 for Mercury. In Scaffolding of Our Thoughts, Essays on Assyriology and History of Science in Honor of Francesca Rochberg, C.J. Crisostomo, E.A. Escobar, T. Tanaka and N. Veldhuis eds., Leiden.
Parpola, S. 1970. Letters from Assyrian Scholars to the Kings Esarhaddon and Assurbaniplal, Part I: Texts. Germany: Kevelaer/Neukirchen-Vluyn.
Reiner, E. and Pingree, D. 1975, The Venus Tablet of Ammisaduqa. In Bibliotheca Mesopotamica vol. II, part 1. Undena Publications, Malibu.
Robson, E. 2019, Who Wrote the Babylonian Astronomical Diaries?, In Keeping Watch in Babylon. The Astronomical Diaries in Context, J. Haubold, J. Steele and K. Stevens eds., Leiden.
Rochberg, Francesca. 2016. Before Nature. Chicago: Cuneiform Knowledge and the History of Science.
Sachs, A.J. and Hunger, H. 1988, 1989, 1996, Astronomical Diaries and Related Texts from Babylonia,Vols. I, II and III, Vienna (ADART I–III).
Swerdlow, N.M. 1998. The Babylonian Theory of the Planets. Princeton: Princeton University Press.
Swerdlow, N.M. 1999. Acronychal Risings in Babylonian Planetary Theory. Archive for History of Exact Sciences 54: 49–65.
Acknowledgements
I would like to thank Alexander Jones, Mathieu Ossendrijver and John Steele for a number of stimulating discussions, interesting suggestions and advice. Part of this study was carried out during a visit to the Department of Egyptology and Assyriology of Brown University in the fall of 2019. I would like to thank the Leidsch Kerkhoven-Bosscha Fonds for financial support, the Department of Egyptology and Assyriology of Brown University for its hospitality and the staff and students of the Department for making my stay in Providence pleasant and productive.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
Communicated by Alexander Jones.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
de Jong, T. A study of Babylonian planetary theory III. The planet Mercury. Arch. Hist. Exact Sci. 75, 491–522 (2021). https://doi.org/10.1007/s00407-020-00269-6
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-020-00269-6