Abstract
In this study I attempt to provide an answer to the question how the Babylonian scholars arrived at their mathematical theory of planetary motion. Although no texts are preserved in which the Babylonians tell us how they did it, from the surviving Astronomical Diaries we have a fairly complete picture of the nature of the observational material on which the scholars must have based their theory and from which they must have derived the values of the defining parameters. Limiting the discussion to system A theory of the outer planets Saturn, Jupiter and Mars, I will argue that the development of Babylonian planetary theory was a gradual process of more than a century, starting sometime in the fifth century BC and finally resulting in the appearance of the first full-fledged astronomical ephemeris around 300 BC. The process of theory formation involved the derivation of long “exact” periods by linear combination of “Goal–Year” periods, the invention of a 360° zodiac, the discovery of the variable motion of the planets and the development of the numerical method to model this as a step function. Longitudes of the planets in the Babylonian zodiac could be determined by the scholars with an accuracy of 1° to 2° from observations of angular distances to Normal Stars with known positions. However, since the sky is too bright at first and last appearances of the planets and at acronychal rising for nearby stars to be visible, accurate longitudes as input for theoretical work could only be determined when the planets were near the stationary points in their orbits. In this study I show that the Babylonian scholars indeed based their system A modeling of the outer planets on planetary longitudes near stations, that their system A models of Saturn and Jupiter provided satisfactory results for all synodic phenomena, that they realized that their system A model of Mars did not produce satisfactory results for the second station so that separate numerical schemes were constructed to predict the positions of Mars at second station from the model at first station, and finally that their system A model for Mars provided quite poor predictions of the longitude of Mars at first and last appearances over large stretches of the zodiac. I further discuss ways in which the parameters of the system A models may have been derived from observations of the outer planets. By analyzing contemporaneous ephemerides from Uruk of four synodic phenomena of Jupiter from the second century BC, I finally illustrate how the Babylonian scholars may have used observations of Normal Star passages of planets to choose the initial conditions for their ephemerides.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this study I will investigate the astronomical concepts, inventions and innovations underlying the development of Babylonian planetary theory. The central question to be answered is: “How did the Babylonian astronomers proceed from observation to theory?” Trying to provide an answer to this question is a real challenge because no texts are preserved in which the Babylonian scholars tell us how this was done. What we do have are observational texts, the so-called Astronomical Diaries and Excerpt Texts (Sachs and Hunger 1988, 1989, 1996; Hunger et al. 2001; henceforth referred to as the Diaries or ADRT I–III and V) and the finished theoretical products, the lunar and planetary ephemerides published in Astronomical Cuneiform Texts (Neugebauer 1955, henceforth ACT). The preserved Diaries provide a (strongly fragmented) continuous record of standardized naked-eye astronomical observations covering a period of about six centuries from about 650–50 BC, and the preserved ephemerides cover a period of about three centuries from about 310–50 BC.
I believe that the development of Babylonian planetary theory must have been a gradual stepwise process that may have taken more than a century. Since a zodiacal coordinate system is a prerequisite for a theoretical description of planetary motion and since we know that the 360° Babylonian zodiac must have been introduced sometime during the fifth century BC, this development probably took place during the fifth and fourth centuries BC preceding the appearance of the oldest preserved ephemeris (of the planet Mercury) for the years 309–289 BC (ACT No. 300). This timeframe is consistent with the discovery of an early system A type scheme to compute longitudes of the last appearance of the planet Mercury (Aaboe et al. 1991, text M) that can be dated to around 400 BC. In a previous paper I have suggested (de Jong 2017) that the oldest elements of Babylonian lunar theory may date from the late sixth/early fifth century BC, so that the development of lunar system A theory probably preceded planetary theory. In this paper I will discuss the development of Babylonian system A theory and the selection of the model parameters for the case of the outer planets Saturn, Jupiter and Mars. The steps that I have been able to identify in the development of Babylonian planetary theory are summarized in Sect. 9.
To illustrate the difficulties that confronted the Babylonian scholars in their attempt to model the motion of the outer planets I show in Fig. 1 a schematic representation of the apparent motion of Saturn during three successive synodic periods, each period lasting about 380 days. Notice that Saturn moves from right to left in the figure and from west to east in the sky. During one synodic period, while Saturn moves from one first appearanceFootnote 1 (FA) to the next one, it reaches its first stationary point (S1) after about 4 months, then reverses its motion to move backward (retrograde), passes its position opposite the SunFootnote 2 (AR) after about two months, continues its retrograde motion for another two months until it reaches its second stationary point (S2) and resumes its forward (prograde) motion for about four months until the day of its disappearanceFootnote 3 in the western evening twilight sky (LA) after which it becomes invisible because it is overtaken by the much faster moving Sun. After a period of invisibility of about 1 month, due to the proximity of the Sun, Saturn reappears in the eastern morning twilight sky at its next first appearance (FA) which marks the end of this synodic period and the beginning of the next one. Typical angular distances traversed by Saturn going from one synodic phenomenon to the next can be easily read off in Fig. 1.

[Adapted from Aaboe 2001]
Schematic representation of the apparent motion of Saturn during three successive synodic periods, each period lasting about 380 days. Saturn moves from right to left in the figure and from west to east in the sky. During one synodic period Saturn moves, for instance, from one first appearance (FA) to the next one, or from one first station (S1) to the next one. During part of its orbit, from the first stationary point (S1) to the second stationary point (S2), Saturn moves backward in the sky (retrograde motion) as seen from the Earth
The synodic phenomena, sometimes also referred to as synodic phases, of the planets were extensively observed by the Babylonian astronomers, and the dates on which the planets first appeared, reached their stationary points, rose acronychally and finally disappeared were systematically recorded in the Diaries. It is important to realize that the mean synodic period of a planet, the average time interval after which it returns to its next similar synodic phenomenon, is the same for all synodic phenomena. This is due to the fact that each synodic phenomenon of a planet is characterized by a specific value of its solar elongation, the angular distance of the planet to the Sun as seen from the Earth.Footnote 4
Babylonian planetary theory must have been developed by using observed dates at which the planets reach their synodic phenomena and by using observed zodiacal positions of the planets on those dates. The accuracy of the theory depends on the refinement or crudeness of the mathematical technique employed and on the accuracy of the parameters entering the mathematical model. In this paper I will study the development of Babylonian planetary theory of system A which employs simple step functions to model the variable velocity of the outer planets in different sections of their orbit around the Sun. Given the limited accuracy of this model to represent the actual variability of planetary motion, the final accuracy of the Babylonian model calculations is determined by the accuracy of the parameters characterizing the model. These parameters must somehow have been determined from the observed dates and the observed planetary positions at the synodic phases recorded in the Diaries.
For first and last appearances the observed dates have an accuracy of a few days because they depend on variations in the atmospheric conditions (weather), and for the stations the accuracy of the observed dates is about one week because the outer planets move very slowly when they reverse motion (less than 0.1° per day). Positions of planets can be determined with an accuracy of about 1°–2° when they are observed with respect to one of the thirty-odd Normal Stars (Jones 2004). Since the Normal Stars are rather unevenly distributed over the 360° zodiac there are regions in the sky where it may be quite difficult to determine accurate positions of planets. The situation is even worse at first and last appearances of planets because nearby Normal Stars are invisible during twilight conditions shortly before sunrise and shortly after sunset. Thus, accurate positions of planets at their synodic phenomena can only be determined for the stations. On the other hand, dates are more accurately observed for first and last appearances. As we shall see Babylonian planetary theory optimizes these strengths and weaknesses by choosing a formulation in which simple transformation between time and position is an essential element.
In my presentation and analysis of Babylonian planetary theory I have tried to stay as close as possible to the Babylonian texts and mindset and to refrain from using equations and presenting too much numerical detail. Although the Babylonian mindset is a somewhat imaginary notion, we may safely assume that it includes a profound knowledge of the intricacies of planetary motion acquired by observing the sky from night-to-night and by studying texts in which these observations were recorded month after month during centuries.
Apart from a number of procedure texts,Footnote 5 in which prescriptions are given how to perform the calculations, and some auxiliary texts, which were used to facilitate the calculations, the Babylonian scholars have not left us any texts with a description or an indication of how they arrived at their system A models of planetary motion. Neither do we have any information how they determined the parameters defining the model for each planet separately. The Almanacs and Normal Star Almanacs which contain predictions of synodic phenomena and Normal Star passages of planets are not of much help because these predictions are made on the basis of the so-called Goal–Year method (see below). Thus, to bridge the gap between the raw observations and the sophisticated models one is forced to speculate. This is an uncomfortable but not an unusual position for any scientist and even a fairly common position for the interpreter of cuneiform astronomical texts.
Studies of Babylonian planetary theory have in general been primarily directed toward unraveling and understanding the arithmetical methods used by the Babylonian scholars to compute and predict planetary positions. Following the pioneering studies of the Jesuit pater Franz Xaver Kugler in the early twentieth century (for references see HAMA, 1182) this became the life work of Otto Neugebauer (ACT and HAMA). Over the past century only few attempts have been published to try to answer the more fundamental question that I am addressing in this study “How did the Babylonian astronomers proceed from observation to theory?”
In an interesting paper Aaboe (1980) suggested that using the observational data recorded in the Diaries the Babylonian scholars could have counted the number of synodic phenomena in each sign of the zodiac over long periods of time and combining this information with the period relations might have selected values of the synodic arcs in different zones of the zodiac such that their ratios are convenient for computation in the sexagesimal number system. He illustrated his proposal for the case of the planet Mars. While this approach may have assisted the Babylonian scholars in finding convenient values for the ratios of the synodic arcs in different zones his proposal is not sufficient specific to see how this could explain all aspects of the parametrization of the system A models in Babylonian planetary theory.
A completely different point of view was taken by Swerdlow (1998) who proposed that Babylonian planetary theory was developed by exclusively using the observed dates of synodic phenomena of the planets, predominantly their first and last appearances. He argued that this is the only way in which the Babylonian scholars could have done it because the information of the positions of the planets in the Diaries was insufficient for this purpose. He suggested that the Babylonian planetary theory could have been derived by using the Babylonian period relations to construct planetary position intervals from the measurement of time intervals. His proposal was strongly opposed by Britton (1998) who pointed out that the Diaries clearly show that the Babylonian astronomers were routinely measuring planetary positions with respect to Normal Stars and thus could well have based their planetary theories directly on the observed positions of planets in the Babylonian zodiac. The results of my study confirm Britton’s point of view.
2 Planetary periods
The fundamental concept in Babylonian astronomical theory is the periodicity of lunar and planetary phenomena. For the Moon the Babylonian astronomers discovered the 18-year (Saros) periodicity in the occurrence of lunar eclipses and for the planets they found periods in solar years for the recurrence of synodic phenomena. Given the length and the accuracy of these periods their determination must have been based on at least about one hundred years of observing.
These so-called Goal–Year periods were applied to predict dates of the synodic phenomena of the planets and of the passing of planets by the Normal Stars found in Almanacs and Normal Star Almanacs (Hunger and Sachs 2014, ADRT VII). This was done by using observations from the past as recorded in the Diaries and Excerpt Texts and transforming these to the future by applying the Goal–Year periods. The Goal–Year periods for Saturn are 59 years, for Jupiter 71 and 83 years and for Mars 47 and 79 years. Early texts in which planetary periods are explicitly given are BM 45728 (Britton 2002) and BM 41004 (text E, section 3, Neugebauer and Sachs 1967; for a more recent discussion see Brack-Bernsen and Hunger 2006). In these texts other periods are listed in addition to the Goal–Year periods: 30 and 147 years for Saturn, 12 years for Jupiter, and 32 and 126 years for Mars.
Since these periods are derived from the observational criterion that a specific synodic phenomenon recurs after a whole number of years approximately on the same date in the Babylonian lunar calendar they may be constructed as a common multiple of the number of days in the synodic period, in the lunar month and in the solar year. Therefore, none of these periods is exact with errors from a few days to a few weeks. Apparently, these errors were observationally determined by the Babylonian scholars and applied in their predictions (Gray and Steele 2008).
The “exact” periods underlying the computation of the ephemerides of the outer planets are considerably longer than the Goal–Year periods, varying from 265 years for Saturn, 284 years for Mars to 427 years for Jupiter. It is generally accepted that these theoretical periods were constructed by linear combination of shorter observed periods. Neugebauer (1975, 391 and 441) suggests that the period of Jupiter is constructed from 6 × 12 + 5 × 71 = 427 years, of Mars from 47 + 3 × 79 = 284 years (HAMA, 426), while for Saturn we may have 2 × 59 + 147 = 265 years.
The way in which the Babylonian scholars could have derived these longer periods from the observations available to them may be illustrated by studying a synthetic database of observations of first and last appearances of Jupiter made in Babylon between 500 and 300 BC.Footnote 6 Parameters that can be derived from the synthetic observations of Jupiter are collected in Table 1. As mentioned above three periods of Jupiter are attested: 12 years, 71 years and 83 years, the latter two also known from Goal–Year Texts. In column (iii) of Table 1 I show for each period the average time interval between dates of the first/last appearance of Jupiter one period apart and its standard deviation, measured in synodic months and days.Footnote 7 For each period the total number of pairs of observations from which these averages are computed is listed in column (ii). Time intervals are converted to solar years in column (iv) by dividing the numbers in column (iii) by 12;22,08, the number of synodic months in the Babylonian solar year according to system A lunar theory. Rounding off the results to the observational accuracy of one day we end up with periods of 12 years + 5 days, 71 years − 6 days and 83 years − 1 day.Footnote 8 It then follows that the adopted “exact” period of Jupiter of 427 years can be constructed by linear combination of these three periods such that the corrections in days cancel (427 = 1 × 12 + 5 × 83 = 2 × 12 + 1 × 71 + 4 × 83 = 3 × 12 + 2 × 71 + 3 × 83 = 4 × 12 + 3 × 71 + 2 × 83 = 5 × 12 + 4 × 71 + 83 = 6 × 12 + 5 × 71).
3 The 360° zodiac
To obtain a quantitative measure of the average progression on the sky of a planet between two successive similar synodic phases a theoretical coordinate system along the ecliptic is a prerequisite. Exactly when the concept of a 360° zodiac was introduced in Babylonian astronomy is uncertain, but it must precede or at the latest be contemporary with the development of the lunar and planetary theories. That the division of the ecliptic in 12 signs of 30° may have been done in analogy to the division of the calendar year in 12 × 30 (theoretical) days has been suggested by several authors (cf. Brack-Bernsen and Hunger 1999). Hunger and Pingree (1999, 224–225) argue from the existing textual material that lunar system A theory was developed by a gradual process of continuous refinement in the fifth and fourth centuries BC, implying that the 360° zodiac may have been invented sometime during the fifth century BC.Footnote 9
The earliest text (BM 36599+) in which a 360° zodiac is attested dates from after about 450 BC. In this text positions of the Sun are computed in degrees within zodiacal signs for 475–457 BC according to a system A type algorithm (Aaboe and Sachs 1969). The earliest references to zodiacal signs probably appear in the Diary of 454 BC, but one should bear in mind that the terminology is occasionally ambiguous in differentiating between zodiacal constellations and signs in Diaries from the fifth century BC (Rochberg 2004, 130–131). Thus, the textual evidence suggests that the concept of a 360° zodiac was introduced somewhere in the second half of the fifth century BC, predating by more than one century the material collected in ACT.Footnote 10
4 The basic elements of Babylonian planetary theory
In this section I will discuss the basic elements and the arithmetical methods used by the Babylonian scholars to develop their remarkable simple and surprisingly accurate system A theory of planetary motion as we know it from the planetary tabular texts in ACT. The parameters characterizing the system A theories of the three outer planets are collected in Table 2 (adapted from HAMA, 423). For the sake of brevity I will illustrate the principles and the method for the case of Jupiter and, for the time being, limit the discussion to first appearances only.Footnote 11
4.1 The mean increase in longitude between two successive first appearances of Jupiter (synodic arc)
We know (see Table 2) that the Babylonian astronomers derived from their observational database that in 427 years Jupiter makes 36 passages through the 360° zodiac and that during that time it experiences 391 first appearances.Footnote 12 We do not have a “procedure” text in which this is stated explicitly, but it can be reconstructed from the (fragments) of procedure texts and ephemerides of Jupiter that have survived. For Saturn we do have such a text from Uruk (A 3418 = ACT No. 802) where we read in Section 4:
Concerning Saturn. 4,25 (265) years corresponds to 4,16 (256) first appearances and to 9 rotationsFootnote 13 and to 54,0 (3240) degrees.
Since after 391 synodic periods Jupiter has complete 36 sidereal rotations we may write 36 × 360° = 391 × \( \overline{\Delta \lambda } \), so that the mean synodic arc of Jupiter, i.e., the average increase in longitude of Jupiter between two successive first appearances, equals \( \overline{\Delta \lambda } \) = 33;08,45°.Footnote 14 This number is attested in section 2 of the procedure text BM 34221 + (= ACT No. 812).
4.2 The mean time interval between two successive first appearances of Jupiter (synodic period)
The synodic time interval is defined as the time measured in lunar months and days (or tithis) between two successive first appearances of Jupiter. The period relation for Jupiter (see Table 2) where 391 synodic time intervals equal 427 sidereal years results in a mean synodic period of 427 × 365.2564/391 = 398.89 days, remarkably accurate compared to the modern value of 398.88 days. Formulating the period relation for Jupiter in Babylonian terms we have 391 × (360 + \( \overline{\Delta t} \)) = 427 × 12;22,08 × 30, where \( \overline{\Delta t} \) is the mean synodic time step, the excess time in tithis of the synodic period over the length of the Babylonian year of 12 lunar months (of 30 tithis each), and where we have used the system A value for the length of the Babylonian sidereal year of 12;22,08 months. According to Aaboe and Sachs (1969) this value was apparently already known in the first half of the fifth century BC and was probably derived from the Saros (223 lunar months = 18 revolutions of the Sun + 10;30°; see also de Jong 2017). We then find \( \overline{\Delta t} \) = 45;13,53 tithis. This number is not explicitly referred to in Babylonian procedure texts, but the difference \( \overline{\Delta t} \) − \( \overline{\Delta \lambda } \) = 12;05,08 is.Footnote 15
4.3 The relation between the synodic period and the synodic arc
To understand the way in which the Babylonians looked at the relation between \( \overline{\Delta t} \), the mean synodic time step, and \( \overline{\Delta \lambda } \), the mean synodic arc, we quote Neugebauer’s translation of Sect. 2 of the Jupiter procedure text BM 34221 + (ACT No. 812):
[Alternate (method): 33;8,]45, the mean value of the longitudes, multiply by 0;1,50,40, and (you obtain) [1;1,8,8,]20. Add to it 11;04, and (you obtain) 12;5,8,8,20. Put it down for the gabariFootnote 16 of (one) year
Now 11;04 is the difference in days (tithis) between the length of the sidereal year (12;22,08 lunar months) and a nominal Babylonian calendar year of 12 lunar months. The Babylonian astronomers apparently (correctly) assumed that at each successive first appearance Jupiter has the same elongation, i.e., the same distance to the Sun (the sun distance principle; see van der Waerden 1974, 256). Then one synodic period equals the time the Sun needs to complete one sidereal rotation + 33;08,45° so that the mean synodic time step equalsFootnote 17
These relations elucidate the meaning of the Babylonian parameters, and the derivation implies that 1;01,50,40 is the time in tithis needed for the Sun to travel 1°. Thus, rather than deriving \( \overline{\Delta t} \) from an equation involving the full 427-year period the Babylonians derived it for one synodic period.
The parameter 11;04 + 1;01,08 = 12;05,08 (parameter c in Neugebauer’s notation, HAMA, 423) plays a central role in computing the dates in system A theory of Jupiter and is usually rounded off to 12;05,10 (see column (viii) of Table 2).
In principle, we now could compute an ephemeris for the first appearances of Jupiter starting with an observed initial position λ0 at t0 by progressing the longitude of Jupiter in steps of \( \overline{\Delta \lambda } \) = 33;08,45 and the time in time steps of 12 lunar months + \( \overline{\Delta t} \) = 45;13,53 tithis, such that after n steps we have λn = λ0 + n. \( \overline{\Delta \lambda } \), and tn = t0 + 12n lunar months + n. \( \overline{\Delta t} \). This would result in a quite crude ephemeris in which the differences between computed and actual positions of Jupiter can become quite large, up to about 20°. Of course, this large inaccuracy is caused by not taking account of the non-uniform orbital motion of Jupiter and the Sun (related to the orbital eccentricities of the Earth and Jupiter). Although no evidence exists that the Babylonian astronomers ever constructed such a zero-order ephemeris for Jupiter we know that they did so for Venus. The ephemeris ACT No. 400 lists dates and positions of the first appearance of the planet Venus as evening star for the years SE 111 to 135 (− 200/− 199 to − 176/− 175 BC) calculated according to this simple algorithm (Venus system A0).
Including the parameters of Jupiter, discussed above, I have listed the basic Babylonian parameters defining the mean orbital motion (the “exact” period, the corresponding number of synodic periods Π, the number of sidereal rotations, the number of synodic waves Z) and the derived mean synodic intervals (\( \overline{\Delta t} \), \( \overline{\Delta \lambda } \) and their difference c) for the outer planets in the first eight columns of Table 2.
4.4 Incorporating the variable orbital velocity of the planets into the theory
This leads us to the next step in the ingenious process of building up the full Babylonian system A theory of planetary motion: taking care of the combined variability in the orbital motion of the planet and the Sun. Here again the Babylonian astronomers could fall back on their large observational database: the Astronomical Diaries. We know that long lists of dates of first appearance and disappearance, of Normal Star passages and of the reaching of their stationary points of the planets covering many tens of years were routinely extracted in the so-called Excerpt Texts (ADRT V) from the material in the Diaries.Footnote 18
A representative example of such a list is preserved in BM 34750 + (ADRT V, nr. 60) which originally contained dates for all synodic phenomena of Jupiter from the year 18 of Artaxerxes II (387/386 BC) to year 13 of Artaxerxes III (346/345 BC). For the first and last appearances of Jupiter only the dates and sometimes the zodiacal signs are listed,Footnote 19 but for the stationary points angular distances to the nearest Normal Star are given as well (see also Jones 2004, 521–526). In view of the constant difference c = Δt − \( \Delta \lambda \) (see above) the variability in the orbital motion of Jupiter shows up as a variation both in the synodic time interval and in the synodic arc, but is most easily detected in time because the amplitude of the variation is largest for the synodic time intervals. Even from a fairly superficial inspection of such lists it is obvious that the synodic time interval of Jupiter is not constant, but varies in magnitude. A somewhat more detailed analysis shows that the amplitude of the variation is about ± 4 days around a mean value of about 44 days (plus 12 lunar months) and that the magnitude of the variation changes from month to month during the year.
To be able to perform the same kind of analysis as the Babylonian scholars I have created a synthetic observational database by computing the dates of all first and last appearances and of the stationary points of Saturn, Jupiter and Mars in Babylon during the fourth century BC as well as the zodiacal longitudes of the planets at their first and last appearances and their stationary points. These computations were done using modern astronomical parameters and applying the physical visibility criterion that I used in previous studies of first and last appearances of stars and planets (see de Jong 2012 and references therein), adopting a nominal atmosphere in Babylon characterized by a visual extinction of 0.27 magnitudes per air mass.
These calculations result in lists of dates of first appearances, first stations, second stations and last appearances in the Babylonian lunar calendar and planetary longitudes in the Babylonian fixed sidereal zodiac similar to what we find in the Babylonian excerpt texts with the one important difference that the planetary positions in the synthetic database are given to a fraction of a degree, while the excerpt texts usually only give the zodiacal sign or an association with one of the Normal Stars. From the synthetic data we may construct the time interval and the increase in longitude for each planet from one synodic phenomenon to the next similar one.
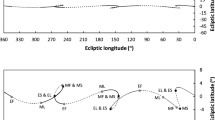
A graphical representation of such data for the three outer planets is shown in Fig. 2 where the filled dots represent the synodic time intervals (in days) and the open dots the synodic arcs (in degrees) from one first appearance to the next one during the fourth century BC. Notice that the time intervals and the synodic arcs vary exactly in phase with each other and that the difference between the two curves is roughly constant and about equal to the parameter c in column (viii) of Table 2 (which was derived for the average planetary motion). Also notice the fairly small variations in the synodic time intervals and the synodic arcs for Saturn and Jupiter compared to the much larger variations in the data for Mars.
Synodic time intervals and synodic arcs from one first appearance to the next one for the planets Saturn, Jupiter and Mars during the fourth century BC. The lengths of the synodic arcs (open circles) for Saturn (lower two curves in upper panel) and Jupiter (upper two curves in upper panel) are as shown in the figure, but for Mars (lower panel) they are in excess of one zodiacal passage of 360°. The synodic time intervals (filled circles) are measured in days in excess of 12 lunar months for Saturn and Jupiter and in excess of 24 lunar months for Mars. Notice the similarity in the pattern of the variations in the synodic time and longitude intervals and their roughly constant difference (the parameter c in Table 2)
The data in Fig. 2 nicely illustrate the astronomical meaning of the Babylonian parameters in Table 2. Saturn experiences 97 synodic phenomena (first appearances) per century moving three times through the 360° zodiac producing three synodic waves, Jupiter experiences 91 synodic phenomena distributed over eight waves and Mars 46 phenomena over six waves, consistent with the numbers in columns (i)–(v) of Table 2 scaled down to one century.Footnote 20
From the preserved ephemerides and procedure texts we know how the variable motion of the planets was incorporated in the theory: extremely elegant, numerically simple and without accumulation of numerical errors. However, we have no idea how the Babylonian scholars arrived at the parameters in columns (x)–(xii) of Table 2 used in their system A models for each planet individually. This is all the more puzzling since the lack of positional information of the planets at their first and last appearances in the Babylonian observational database seems a serious impediment to the construction of an accurate algorithm to predict the value of the synodic arc. In this paper I propose that this difficulty was overcome by first constructing a model of the variation of the synodic arc for one of the stationary points from the observed planetary positions with respect to Normal Stars and then using this same longitude model for first and last appearances.
The key concept in the Babylonian approach is the realization that variations in the synodic periods can be predicted from the synodic arcs, and vice versa, by using the average difference c = \( \overline{\Delta t} \) − \( \overline{\Delta \lambda } \) (column (viii) in Table 2), derived from the period relations. In this way, the observed variability in time can be used to derive the variability in longitude, and vice versa.Footnote 21 How excellently this concept reproduces astronomical reality is illustrated in Table 3 where I list the mean values and their standard deviations of the synodic time steps Δt (in tithis), of the synodic arcs Δλ (in degrees of arc) and of their observed differences (c = Δt − Δλ), derived from one century of synthetic observations (400–300 BC) of the main synodic phenomena of the outer planets. For comparison I also list for each of these quantities the adopted Babylonian mean values (see Table 2). The agreement between the real and the adopted values of all three quantities is striking, and the observational accuracy of the parameter c is more than sufficient for Saturn and Jupiter (about 1° or 1 day) and acceptable for Mars (about 4° or 4 days) to be used for the conversion of synodic time intervals into synodic arcs, and vice versa. The purpose of Table 3 is not to suggest that the values of the parameter c were derived in this way, but to show that the adopted values of c, based on the period relations, indeed provide values that are eminently suitable to convert synodic time intervals into synodic arcs, and vice versa.
Illustrating the further development of the theory again for the case of Jupiter we find from the data in Fig. 2 and in Table 3 that the synodic time interval Δt has a mean value of about 45 tithis with a spread of about ± 3–4 days and that the variation of the synodic arc equals \( \overline{\Delta \lambda } \) = 33° ± 2–3°. The next step in the modeling of Jupiter is then to invent a way to handle different speeds (synodic arcs) of Jupiter along its orbit. This is exactly what the Babylonian astronomers did in system A by introducing a step function with two different synodic arcs: w(1) = 30° and w(2) = 36° in different zones of the zodiac (see column (xii) of Table 2). The numbers 30 and 36 are in agreement with the observed range of values for the synodic arc, and they are well suited for computations in the sexagesimal number system. This numerical convenience is a dominant feature in the parameterization of all Babylonian planetary theories. The rationale for this is to simplify numerical interpolation as will be explained below.
It is important to realize that by choosing the values for the two different speeds (synodic arcs) of the step functions for Jupiter and Saturn one at the same time fixes the length of the sectors of the zodiac over which the fast speed and over which the slow speed applies because the average speed over one revolution of Jupiter must be conserved. Let α(1) be the zodiacal zone over which the slow speed w(1) = 30° applies (slow zone) and α(2) the zone over which the high speed w(2) = 36° applies (fast zone). Then the number of synodic steps on the slow zone equals α(1)/w(1) and on the fast zone α(2)/w(2). We further know that on average in 36 sidereal rotations of Jupiter there are 391 synodic steps (see Table 2) or in one revolution 391/36 = 10;51,40 steps. Then combining the condition α(1) + α(2) = 360° with the equality α(1)/w(1) + α(2)/w(2) = 10;51,40, where w(1) = 30° and w(2) = 36°, we find for the slow zone α(1) = 155° and for the fast zone α(2) = 205° (see column (x) of Table 2). In a similar way we find from the two different speeds of Saturn, w(1) = 11;43,07,30° and w(2) = 14;03,45°,Footnote 22 a slow zone of 200° and a fast zone of 160°, only 5° different from those of Jupiter. In the case of Mars with a sixfold step function the procedure seems to have been inverted: first defining six zodiacal zones of 60° and then trying to find six speeds (synodic arcs) with simple ratios (see column (xii) of Table 2) such that the number of synodic steps per sidereal rotation equals 133/18 = 7;23,20. It is almost miraculous that such a set can be found and that indeed (see columns (x) and (xii) of Table 2) 60/40 + 60/60 + 60/90 + 60/67;30 + 60/45 + 60/30 = 7;23,20.
From the ephemerides of Jupiter we know that in the system A theory of Jupiter the Babylonian astronomers prescribe to use the small synodic arc of 30° from 25° Gemini to 0° Sagittarius (over 155°) and the large synodic arc of 36° from 0° Sagittarius to 25° Gemini (over 205°). This implies that the slow and fast arcs are centered in the Babylonian zodiac on the axis 12;30° Virgo–Pisces (see column (xi) of Table 2). I will come back to the way in which the Babylonian scholars may have determined the amplitudes and the boundary points of the step functions of their system A models in Sect. 7.
I finally briefly outline the computational procedure by which the variable velocity algorithm was implemented in practice. When the initial position of Jupiter in the Babylonian zodiac was such that the synodic arc of 30° or 36° fell completely within the slow or fast zone, the increment was simply added to that position to obtain the longitude at the next similar synodic phenomenon. Whenever the boundaries of the slow or fast zones were exceeded when adding the synodic arc the increments in longitude were adjusted by interpolation. That part of the increment that exceeded 0° Sagittarius had to be multiplied by 0;12 (= (36 − 30)/30) and added to 30°, and the part that exceeded 25° Gemini had to be multiplied by 0;10 (= (36 − 30)/36) and subtracted from 36° to obtain the correct increment. Once the magnitude of the synodic arc Δλ was determined in this way, the magnitude of the synodic time interval Δt was determined by adding 12;05,10 (the parameter c in column (viii) of Table 2) to the computed synodic arc. The date of the next similar synodic phenomenon was then found by adding 12 synodic months + Δt to the previous date in the Babylonian calendar. In this way one proceeds from one date to the next, to the next, etc., until after 391 steps (and 427 years) one returns exactly to the initial position, because strict periodicity is ensured in the theory and no accumulation of numerical errors occurs.
Fragments of this computational procedure for Jupiter are preserved in tablet BM 34081 + (ACT No. 813) where we read in section 2, lines 8 and 9.
From one appearance to the next appearance. From 25 Gem to 0 Sag you add 30. From 0 Sag to 25 Gem you add 36.,
and in tablet BM 34221 + (= ACT No. 812) section 9, lines 3 and 4:
Multiply by 0;12 and add; you will get the fast arc.
4.5 The computation of planetary positions from day to day
The full system A theory of Jupiter is completed by giving numerical schemes for interpolation between the dates of the different computed synodic phases of Jupiter (first appearance to first station to acronychal rising to second station to disappearance to first appearance, etc.). In this way, the Babylonian astronomers succeeded in predicting the positions of Jupiter from day to day throughout the year. This aspect of system A theory will not be discussed here because it is outside the scope of this paper. The interested reader is referred to HAMA (447–454) and Ossendrijver (2011, 92–95) for more information on this topic.
5 A closer look at the observational basis of system A planetary theory
Based on the analysis of the preserved planetary ephemerides we have a fairly detailed understanding of the way in which the Babylonian scholars calculated the positions of the outer planets at the various synodic phenomena and the dates on which these phenomena took place (for a recent discussion see Ossendrijver 2011, 55–68). But in spite of the fact that we know the algorithms and the parameters used in their calculations we still have a limited understanding of how these algorithms were invented and of the way in which the parameters were obtained from the observational database as preserved in the Diaries. It is the purpose of this section to present an attempt to elucidate these aspects of Babylonian theory formation.
This attempt must necessarily be based on a close inspection and a more detailed analysis of the observational data available to the Babylonian scholars in the Diaries (ADRT, Vols. I–III) and the Excerpt Texts (ADRT, Vol. V) in which observations of the synodic phenomena of all planets covering a long time span of order 50 to 100 years were collected. In Figs. 3, 4 and 5 I present graphical representations of such data for the planets Saturn, Jupiter and Mars, constructed from the synthetic observational database of synodic phenomena of these planets generated for Babylon in the fourth century BC. These data were used previously to compose Fig. 2 and to compute the data in Table 3.
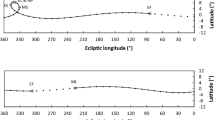
Variation of the synodic arc at first appearance, first station, second station and last appearance of Saturn as a function of Babylonian zodiacal longitude. Dots represent values derived from synthetic observations of Saturn in the fourth century BC. Also shown is the Babylonian system A model step function for the synodic arc (thin line marked by squares) and the interpolated model (thick line)
Same as Fig. 3 for Jupiter
Same as Fig. 3 for Mars. Between two successive appearances and/or stationary points Mars has moved once through the ecliptic in addition to the synodic arc. The Babylonian system A model (thin line marked by squares) for Mars uses six steps to represent the large variations in the value of the synodic arc. The interpolated model (thick line) provides a good fit to the observations at first station, but rather poor fits at second station and at first and last appearances
The four panels in Figs. 3, 4 and 5 show the synodic arc Δλ (black dots) that must be added to the zodiacal longitudeFootnote 23λ of a planet at one of its synodic phenomena to find the longitude at the next similar synodic phenomenon for first and last appearances and for first and second stations of that planet. The figures show that about one century of observations is amply sufficient to fully sample the variation of the synodic arc and that at least about 50 years of observations is required to be able to model the variation. Although the data displayed in Figs. 3, 4 and 5 were computed for the fourth century BC they are representative for the period 500–100 BC since the orbital parameters of Saturn, Jupiter and Mars only change vary slowly.
Also shown in Figs. 3, 4 and 5 are the step functions of the Babylonian system A models (thin lines) based on the parameters in columns (x)–(xii) of Table 2. The step functions are defined by the parameters α(i) and λcentr(i), the length and the central zodiacal position of the slow and fast parts of the step function, and by w(i), the amplitudes on the slow and fast parts of the step function. The thick lines in Figs. 3, 4 and 5 represent the interpolated values of the system A models. These values were taken from the ephemerides for each planet that I computed for all synodic phenomena between 400 and 300 BC using the Babylonian parameters in Table 2.
For the computation of the Babylonian ephemerides I chose initial conditions (planetary longitude and date) such that the mean difference between computed and observed values of all observations during the fourth century BC was zero, both for the longitudes and for the dates. The algorithms used for the computation of the Babylonian ephemerides were checked by reproducing the known system A ephemerides of the outer planetsFootnote 24 (ACT, 335–343). The computation of the ephemerides of Jupiter and Saturn is relatively simple and straightforward because at most one zonal boundary is transgressed in the computation of successive similar synodic phenomena. The computation of the ephemeris of Mars is slightly more complicated because up to two zonal boundaries may be transgressed going from one synodic phenomenon to the next similar one (see Ossendrijver 2011, appendix C). This shows up in the panels of Fig. 5 for Mars where the interpolated values (thick lines) deviate much more from the generating step function than in Figs. 3 and 4 for Saturn and Jupiter.
One thing that immediately catches the eye upon inspection of Figs. 3, 4 and 5 is that the amplitudes of the variation in the synodic arcs differ appreciably for the three outer planets. For Saturn the synodic arc varies from about 11° to 14.5°, for Jupiter from 30° to 37°, and for Mars from 33° to 78° at the stations, and from 30° to 110° at first and last appearances. This large difference in the variation of the synodic arc is related to the different values of the orbital eccentricities of the planets, ranging from 4.9% for Jupiter to 5.7% for Saturn, to 9.4% for Mars, and to the different distances of the planets to the Earth, ranging from 1.5 ± 1 astronomical unitsFootnote 25 for Mars, to 5.2 ± 1 A.U. for Jupiter, to 9.5 ± 1 A.U. for Saturn. However, other effects may also play an important role, in particular for Mars, as will be discussed later on this section.
While the Babylonian system A models generally fit the data points at first station in Figs. 3, 4 and 5 quite well,Footnote 26 the models are clearly not unique. On the other hand, there is not much room for numerical maneuvering because the step function amplitudes and their ratios must behave nicely in sexagesimal arithmetic and the division of the zodiac in two or more (Mars) zones is directly related to the choice of the amplitudes, and vice versa. For instance, if we would have adopted a slightly different amplitude for the step function of Jupiter in the fast zone, say 35° rather than 36°, while keeping the amplitude of 30° in the slow zone, the period relations would have led to a slow zone of 120;50° and a fast zone of 239;10°Footnote 27 and would thus have resulted in a more asymmetric step function and a poorer fit to the data points of Jupiter in Fig. 4. Similarly, once six zodiacal zones of 60° are adopted for the step function of Mars it is difficult to come up with another set of amplitudes with nice number ratios (see column (xii) of Table 2), still fitting the data points in the bottom panels of Fig. 5. I will come back to the manner in which the parameters of the system A models of the outer planets may have been derived from the observations in Sect. 7.
Because Mars is a special case in several respects, I first discuss the system A modeling of the synodic phenomena of Saturn and Jupiter. From an inspection of Figs. 3 and 4 it is clear that the models of Saturn and Jupiter provide quite a good fit to the observations for all four synodic phenomena. The model values of the synodic arc never differ more than at most 2° from the astronomically correct ones. This is confirmed by the data in Table 4 where I have listed the maximum and minimum values and the standard deviations of the differences in position (δλ) and in time (δt) between the computed ephemerides and the observations averaged over all observations in the fourth century BC.Footnote 28 These data show that the Babylonian system A models provide an excellent fit to observational reality, with planetary longitudes of Saturn and Jupiter predicted with an accuracy of about 1° and dates predicted with an accuracy of a few days. The accuracy with which the dates are predicted drowns in the observational errors because at first and last appearances the variation in atmospheric extinction from day to day (weather) creates an uncertainty margin of order ± 3 days and the accuracy with which the dates of stationarity of a planet can be determined is of order ± 7 days due to the fact that planets do not noticeably move for several days when they reverse their motion from prograde to retrograde, and vice versa.
The fact that planets at the stationary points in their orbits hardly move also explains why the observational data for the two stations in the bottom panels of Figs. 3 and 4 vary so smoothly. At first and last appearances the variation in the data is slightly more bumpy because Saturn and Jupiter then move about 0;08° and 0;14° per day so that the observational discretization in days starts showing up. Finally, it is worth noting that for Saturn and Jupiter the Babylonian scholars used one and the same step function to model all synodic phenomena (see Ossendrijver 2011, 90 and 107).
Turning to the results of the system A modeling of the motion of Mars displayed in Fig. 5, we find that the Babylonian models provide a good fit to the variation of the synodic arc with zodiacal longitude at first station, a poor fit at second station and very poor fits at first and last appearances.Footnote 29 This behavior is also reflected in the numbers in column (vi) of Table 4 where I have listed the maximum and minimum values and the standard deviations of the differences in position (δλ) between the computed ephemerides and the observations of Mars averaged over all observations in the fourth century BC. At first station the system A ephemeris of Mars is accurate to within 2°, but it is off on average by about 8° at the other synodic phases and it may even lag behind in extreme cases by more than 20°.
The fact that the system A model of Mars is so much better for first station than for the other synodic phenomena strongly suggests that it was based on observations of the position of Mars at first station. Here we have for the first time a clear indication—if not strong evidence—that the Babylonian scholars based their system A models on observations of the planets with respect to Normal Stars near the stations.
This suggestion is confirmed by a more detailed analysis of the system A model of Mars. It has long been known that the system A step function model of Mars was used by the Babylonian scholars for three primary synodic phenomenaFootnote 30 only, first and last appearances and first station. The longitudes for the other two phenomena (acronychal rising and second station) were obtained by subtracting (retrograde motion) separately computed longitude intervals from the system A longitudes for first station. Several schemes are known to compute those longitude intervals (see Ossendrijver 2011, 85). Here I use scheme S, discovered by Neugebauer (ACT, 305–306) and later confirmed by Aaboe and Sachs (1966) in their reanalysis of ACT No. 504. The results are displayed in Fig. 6 (upper panel) where I show the variation of the synodic arc at second station computed by applying scheme S to the longitudes at first station. This secondary model (solid line) provides a much better fit to the observations of Mars at its second station than the system A model (dashed line).Footnote 31 The improvement in quality of fit also clearly shows up when we again compute the parameters in column (vi) of Table 4 for the second station of Mars. Instead of the large range of errors of 11.1°/− 18.0° for the system A model we now find 5.1°/− 6.4° and the standard deviation decreases from ± 8.3° to ± 2.7°, of the same order of magnitude as for the system A model of the first station of Mars in column (vi) of Table 4.
Variation of the synodic arc of Mars at its second station (upper panel) and at its first appearance (lower panel) as a function of Babylonian zodiacal longitude. In the upper panel the dots represent values of the synodic arc derived from synthetic observations of Mars in the fourth century BC. The Babylonian model for the second station of Mars (thick line) is derived from the Babylonian system A model at first station by applying scheme S (see text). For comparison the interpolated Babylonian system A model of Mars is also shown (dashed line). In the lower panel the dots represent values of the synodic arc derived from synthetic observations of Mars for an atmosphere without extinction. Also shown in the lower panel is the Babylonian system A model step function for the synodic arc of Mars (thin line marked by squares) and the interpolated system A model (thick line)
This interesting result implies two things: (i) that the Babylonians must have also observationally determined the variation of the synodic arc at the second station of Mars, and (ii) that they were aware of the fact that the variation pattern of the synodic arc with zodiacal longitude at second station is shifted backward by about 30° in zodiacal longitude compared to first station.
This large shift toward smaller longitudes of the variation pattern of the synodic arc from first to second station is caused by the combined effect of the small distance of Mars at its stations to the Earth (~ 0.5 astronomical units) and the asymmetry in the orbital geometry created by the different values of the solar elongation of Mars of about − 136° at first station and about + 136° at second station. Apparently, it was noticed by the Babylonians and even successfully modeled without understanding the astronomical origin of the effect.
Based on the similarity in orbital geometry of the outer planets we expect that Jupiter and Saturn also experience a shift toward smaller longitudes of the variation pattern of the synodic arc with zodiacal longitude from first to second station, but that the magnitude of this shift will be smaller than for Mars because Jupiter and Saturn are at much larger distances from the Earth. Using the fact that at the stationary points in their orbits Jupiter is about 10 times further away than Mars and Saturn about 20 times, one can show that the expected shifts toward smaller longitudes of the observed variation pattern from first to second station amount to about 10° for Jupiter and about 6° for Saturn. A careful inspection of the data points in the lower panels of Figs. 3 and 4 indeed confirms the existence of a shift toward smaller longitudes of this magnitude from first to second station in the observed variation pattern of the synodic arc.
Since the variations in the synodic arcs of Jupiter and Saturn are small, about ± 3.3° and ± 1.8°, respectively, a small shift toward smaller longitudes in the zodiacal longitude dependence of these variations from first to second station has only little effect on the accuracy with which the computed ephemerides of Jupiter and Saturn at their stations reproduce the observations. This is confirmed by the standard deviations for Saturn and Jupiter in columns (ii) and (iv) of Table 4 which are identical within the errors for first and second stations and in fact for all synodic phenomena. This explains why the Babylonian astronomers could use the same system A step function to successfully model all synodic phenomena of Saturn and Jupiter, or phrased differently, why for Saturn and Jupiter all synodic phenomena are primary.
The most striking aspect of the system A modeling of Mars shown in Fig. 5 is not so much the good fit to the observed variation of the synodic arc at first station in the left lower panel, but the poor fits to the observed variations of the synodic arc at first and last appearances in the upper two panels of Fig. 5. Several questions arise. What is the reason that the variation of the synodic arc at first and last appearances of Mars differs so much from that observed at the stations? Did the Babylonian astronomers notice that their system A model of Mars is such a poor representation of astronomical reality at first and last appearances? Why is the system A model so poor for the first and last appearances of Mars while it is successful for Saturn and Jupiter?
The answer to the first question is related to the physics of the visibility process. To explain the situation I discuss the case of the first appearance of Mars. At its first appearance Mars becomes visible again for the first time near the eastern horizon shortly before sunrise. Because of the presence of atmospheric extinction no planet is ever visible exactly on the horizon even when it rises in the middle of the night when the sky is pitch-dark. Mars, at its first appearance, becomes visible in the morning twilight sky of Babylon at an altitude of about 5° above the eastern horizon when the Sun is still about 10° below the horizon, in agreement with the fact that the arcus visionis of Mars (defined as the angular distance between Mars and the Sun measured perpendicular to the horizon) in Babylon equals about 15°. Since the inclination of the orbit of Mars (the ecliptic) to the horizon in Babylon varies between 80° and 34° during the year the solar elongation of Mars (the distance of Mars to the Sun measured along the ecliptic) at its first appearance may vary from − 15° to − 27°.Footnote 32 Using the fact that the Sun moves about 1°/day and Mars about 0.75°/day around its first appearance we find that the relative velocity of Mars with respect to the Sun equals about − 0.25°/day. Thus, to bridge a difference of − 12° in solar elongation we need about 48 days in which the Sun moves about 48° and Mars about 36° so that the synodic interval may be up to about 48 days longer than expected and that the synodic arc of Mars in the most extreme case may be 36° larger than expected. This most extreme case never occurs in reality, but according to the data in the left upper panel of Fig. 5 Mars gets close when it moves from a first appearance near 255° (15° Scorpio) to its next first appearance near 365° (5° Aries) over a synodic arc of about 110° that is about 30° larger than expected on the basis of the Babylonian system A model curve.
There is another more direct way to show that the unexpected large values of the synodic arc of Mars are caused by atmospheric extinction. To do so I have generated synthetic observations of first and last appearances of Mars in the fourth century BC for an artificial atmosphere in Babylon without extinction (instead of the nominal atmosphere characterized by a visual extinction of 0.27 magnitudes per air mass) and plotting the same data as in the upper panels of Fig. 5. The results are shown in the lower panel of Fig. 6 for the first appearance of Mars. We see that the Babylonian system A model for Mars would have provided an excellent fit to the observed values of the synodic arc if the atmosphere in Babylon would have been completely transparent. This may be further illustrated by again computing the differences between the Babylonian model longitudes and the observed longitudes of Mars in the fourth century BC and their standard deviation but now for the case of the clear atmosphere. The numbers in column (vi) of Table 4 for the first appearance of Mars then improve significantly: The range of differences between the predicted longitudes and the observed ones reduces from 9.5°/− 20.9° to 6.7°/− 6.4° and the standard deviation decreases from ± 8.4° to ± 3.3°, only slightly worse than for the first station of Mars (± 2.2°).
Did the Babylonian scholars ever realize that their system A model of Mars provided such a bad fit to astronomical reality at the first and last appearances of Mars? Although an unambiguous answer to this question can probably not be given, the textual material that has survived does not contain any indication that they did. On the contrary, from the preserved ephemerides it is clear that the Babylonian scholars considered the first appearance, first station and last appearance of Mars as primary phenomena.Footnote 33 However, it is quite well possible that they may have been somewhat suspicious about the validity of their model for the first and last appearances of Mars because the dates that they predicted for these phenomena were off by up to − 28 days (see column (vii) of Table 4) in some cases.
The possibility that the Babylonian astronomers were not aware of the failure of their system A model for the first and last appearances of Mars is less surprising than it may look at first sight when one bears in mind that they were unable to observationally determine longitudes of the planets at first and last appearances. This is consistent with the observations recorded in the Diaries which contain little, and if so only very crude information (zodiacal sign) on the positions of the planets at first and last appearances. This lack of positional information may be understood by realizing that at first and last appearances of the planets the Sun is about 5° to 10° below the horizon (depending on the brightness of the planet). As a consequence the sky at the horizon is so bright that very few (if any) stars will be visible so that usually no positional reference is available (see de Jong 2007 for a detailed discussion of this point for the case of bright stars).
Why are the system A models for the first and last appearances of Saturn and Jupiter so successful while they fail for Mars? The answer to this question is again related to the orbital geometry of the three outer planets (eccentricity and distance to the Earth). From the data in the synthetic observational database I find that the maximum difference in solar elongation going from one first appearance to the next one is − 3.2° for Saturn and − 4.1° for Jupiter (compared to − 11.1° for Mars). Using a daily motion of 1°/day for the Sun and around first appearance of 0.23°/day for Jupiter and of 0.13°/day for Saturn (instead of 0.75°/day for Mars) we find that these maximum differences in solar elongation correspond to increments in the synodic arc of at most 0.5° for Saturn and at most 1.4° for Jupiter (compared to 33° for Mars). Therefore, the change in the inclination of the ecliptic to the horizon from one first appearance to the next one, that in certain sections of the zodiac strongly degrades the accuracy of the system A model for the first and last appearances of Mars, has little effect for Saturn and Jupiter so that the validity of the system A models for the first and last appearances of Jupiter and Saturn is not affected.
Summarizing the main results of our analysis in this section we have shown:
-
1.
That the Babylonian scholars based their system A modeling of the outer planets on observations of planetary longitudes near the stationary points in their orbits,
-
2.
That they found that their system A models of Saturn and Jupiter provided satisfactory results for all synodic phenomena (primary phenomena),
-
3.
That they realized that their system A model of Mars did not produce satisfactory results for the second station so that separate numerical schemes were constructed to predict the positions of Mars at second station from the system A model at first station,
-
4.
That they never may have realized that their system A model for Mars provided quite poor predictions of the longitude of Mars at first and last appearances over large stretches of the zodiac.
6 Observations of planets with respect to Normal Stars at the stations
The idea that the Babylonian scholars based their planetary models on longitudes determined from angular distances of planets to Normal Stars near their stations is not new. Jones (2004, 522) in his study of Babylonian observations of planets near Normal Stars notes that “the observational records maintained by the Babylonians would in fact have provided a rather narrow basis for theoretical work dependent on longitudes because the only events of significance for the planets’ synodic cycles for which they regularly recorded distances to Normal Stars were stations.” From observations recorded in the Diaries, Excerpt Texts and Goal–Year Texts Jones was able to show that the reported distances of planets to Normal Stars near stations never exceeded 4 cubits, equivalent to about 10°, and that the accuracy with which zodiacal longitudes were determined from these observations was expected to be between 1° and 2°.Footnote 34
To illustrate the method and to allow the reader to get some feeling for the difficulties encountered in the conversion of distances to Normal Stars to planetary longitudes I list in Table 5 all observations of Mars at its first station that could have been made in the fourth century BC. The dates in column (i) and the longitude, latitude and visual magnitude of Mars in column (ii) of Table 5 were taken from the database of synthetic observations of Mars that I used earlier in this paper. The dates in column (i) are given in the Babylonian calendar.Footnote 35 Following Babylonian practice, years in which an additional 12th month is intercalated are labeled “a” and when a 6th month is intercalated they are labeled “kin-a”. In column (iii) of Table 5 I present data for the Normal Stars nearest to Mars for each stationary position.Footnote 36 The Normal Star numbers, astronomical stellar designations, zodiacal longitudes and latitudes were taken from Jones (2004) and the stellar visual magnitudes were taken from the Yale Bright Star Catalog (Hoffleit and Jaschek 1991). In the last column of Tale 5 I list distances (in longitude and latitude) of Mars to its nearest Normal Star.
Each of the observations in Table 5 corresponds to a data point in the lower left-hand panel of Fig. 5 where the observed synodic arcs from one first station of Mars to the next one are plotted. Using the data in column (ii) of Table 5 the coordinates of each data point can be computed.
Several points are worth noticing in Table 5. First, the synodic time interval between two successive first stations of Mars is large, exceeding 24 lunar months (compare the average synodic interval derived from the period relation of Mars in column (vi) of Table 2). Next, notice the fact that Mars is on average about four magnitudes brighter than the nearest Normal Star, corresponding to about a factor 40 in intensity.Footnote 37
Although Jones (2004) quotes about 150 Babylonian observations of Normal Stars near one of the outer planets at first or second station, it appears that none have survived for Mars at its first station in the fourth century BC so that the data in column (iv) of Table 2 cannot be directly compared with preserved records of actual Babylonian observations. However, we know from his study that the accuracy with which the Babylonians were able to determine distances to Normal Stars was about 1°.
The most important conclusion to be drawn from the data in Table 5 is that in 7 out of 47 cases no nearby (distance ≤ 4 cubits = 10°) Normal Star is available so that no zodiacal longitude of Mars could be determined. This occasional failure occurs for positions of Mars from Sagittarius to Pisces. However, the data in Table 5 also show that one hundred years of observing is sufficient for Mars observations to sample the full zodiac because at least one observation of Mars sufficiently close (< 10°) to a nearby Normal Star is available in all signs of the Zodiac.
7 The selection of parameters defining the system A models of the outer planets
The results of our study suggest that the Babylonian system A models of the outer planets were based on observations of the planets at first station. However, the question how the Babylonian scholars extracted the numerical values of the parameters that characterize their system A models from the observations still remains unanswered. For Saturn and Jupiter three parameters are needed to fully define a system A model: two values of the synodic arc (the amplitudes of the step function) and the direction of the axis of symmetry. Once the two amplitudes are selected the lengths of the zodiacal zones where the slow and the fast synodic arcs must be applied follow from the period relation of the planet (see Sect. 4.4). For the system A model of Mars seven parameters are needed: six values of the synodic amplitude in six zones of the zodiac of 60° each and the direction of the axis of symmetry. The model of Mars requires more parameters to be able to properly model the strongly varying synodic arc. The selection of the model parameters is technically constrained by the requirement that the ratio of the amplitudes must be simple ratios of whole numbers so that interpolation in the sexagesimal number system remains numerically manageable (see column (xiii) of Table 2).
The observational material that the Babylonian astronomers had at their disposal to determine these parameters consisted of lists of zodiacal positions with associated synodic arcs graphically represented by the left bottom panels (first station) of Figs. 3, 4 and 5. Since the system A models of both Saturn and Jupiter consist of two-zone step functions, while the model of Mars is more complicated consisting of a six-zone step function, we first investigate the parameter selection for the models of Saturn and Jupiter. From the observational data it is straightforward to estimate the ratio of the minimum to the maximum value of the synodic arcs. For Saturn we find 0.76 ± 0.10 and for Jupiter 0.82 ± 0.05, where the uncertainty margins are based on an adopted accuracy of about 1° in the observed values of the synodic arcs. So it seems that step functions with amplitude ratios of 3/4 (0.75), 4/5 (0.80) and 5/6 (0.833) for Saturn and of 4/5 and 5/6 for Jupiter would be possible choices. Once the amplitude ratio has been selected the shape of the step function is fully determined by choosing either the length of the fast (or slow) zone or the magnitude of the fast (or slow) amplitude (synodic arc). Once either of these parameters is chosen, the other one follows from the period relation (see Sect. 4.4). Since the observations indicate that the step functions should be roughly symmetrical I have computed solutions for the five possible choices of the amplitude ratios of the two planets for all integer values of the fast zodiacal zone between 140° and 220°. This numerical exercise results in only three possible solutions with (relatively) nice values of the slow and fast synodic arcs for Saturn and two for Jupiter. The four parameters (the slow and fast synodic arcs and zones) defining these different solutions are given in columns (iii) and (iv) of Table 6. Since 360°/5° = 72 is a nice number in sexagesimal arithmetic it may not come as a surprise that the lengths of the fast and slow zones in the well-behaved solutions are multiples of 5°. Notice that the boundary values of the zones listed in Table 6 are chosen such that the symmetry axes of the models are the same for all three models of Saturn and for the two models of Jupiter and identical to the symmetry axes of the Babylonian system A models.Footnote 38
Rather than trying to carry out a similar analysis for the six-zone system A model of Mars I note that the choice of the synodic amplitudes of 90°, 67;30°, 45°, 30°, 40° and 60° (ratios 4/3, 3/2, 3/2, 3/4, 2/3 and 2/3) for the six 60° zones of the zodiac for Mars is a miracle of numerical elegance that continues to baffle me.Footnote 39 It is difficult to imagine that there exist other combinations of synodic amplitudes with simple ratios that are equally successful in reproducing the observed variation of the synodic arcs.
The data in Table 6 show that the models selected by the Babylonians as their system A models for Saturn and Jupiter (parameters printed in regular script) are the ones with amplitude ratios of 5/6. One may wonder on what basis the Babylonians selected these models from the possible candidates in Table 6 if indeed they chose their models based on rational considerations rather than just numerically stumbling upon them. In an attempt to answer this question I have compared each model in Table 6 with the observational data of the Saturn, Jupiter and Mars at first station in the fourth century BC in the same way as I did before in Sect. 5 (see Table 4). To check in addition the sensitivity of the models to the choice of the symmetry axis I have also investigated how well the observational data are reproduced by system A models of the three outer planets when they are shifted (rotated) by ± 10° in the zodiac. The results of these comparisons are displayed in columns (v) and (vi) of Table 6 where I show the maximum and the minimum deviations of the models compared to the observations and the standard deviations of both the position differences in longitude and of the difference in dates. From these data we may draw the following conclusions:
-
1.
For Saturn the 4/5 amplitude ratio model would have been slightly more accurate and numerically a little more easy to handle than the 5/6 ratio model selected by the Babylonians. Rotating the model by ± 10° does not affect the accuracy of the model significantly.
-
2.
For Jupiter the 5/6 ratio model is indeed the best choice. It is also fairly insensitive to rotation by ± 10°.
-
3.
The symmetry axis of the system A model for Mars is well chosen (within ± 5°) and rather sensitive to rotation.
One question that I have not yet addressed so far is how and with what accuracy the positions of the symmetry axes of the system A models of the outer planets could have been extracted from the observations by the Babylonian scholars. Since the accuracy with which the synodic arcs are determined (from planetary positions with respect to Normal Stars) equals about 1°–2° (Jones 2004) it is clear that the best way to do this is to analyze data in regions of the zodiac where the synodic arcs experience their largest variation, i.e., near the zero points of the sine curves in the left bottom panels in the Figs. 3, 4 and 5 (the data for first stations). Using the fact that the minimum and maximum values of the synodic arcs are positioned at 90° from the zero points I find 222°–42° ± 10° for Saturn, 151°–331° ± 10° for Jupiter and 103°–283° ± 5° for Mars, where the errors are crude estimates based on an observational accuracy of 1°–2° of the data (Jones 2004). These values fall short by 8°, 11;30° and 17° compared to the symmetry axes of the Babylonian system A models given in column (xi) of Table 2. However, one should bear in mind that due to interpolation the computed minimum values of the models (the thick lines in Figs. 3, 4, 5) are shifted toward smaller longitudes by about one half of the slow synodic arc with respect to the symmetry axis of the system A models (the thin-line system A step function). Taking account of these shifts in the position of the minimum synodic arc (6° for Saturn, 15° for Jupiter and 15° for Mars according to column (xii) of Table 2) we find improved estimates of the position of the symmetry axes of the system A models of 228°–48° for Saturn, 166°–346° for Jupiter and 118°–298° for Mars. These values are sufficiently close to the Babylonian values of 230°–50° for Saturn, 162;30°–342;30° for Jupiter and 120°–300° for Mars (see column (xi) of Table 2) that they may have been obtained in the way I have sketched here.
It is worth noticing that the central positions of the minima in the step functions in the Babylonian system A models are in good agreement with modern values of the aphelion longitudes of the outer planets in the second half of the first millennium BC. For 350 BC we find for Saturn that the aphelion (largest distance to the Sun) is located at 235° in the Babylonian fixed zodiac, for Jupiter at 164° and for Mars at 121° (Simon et al. 1994, 675–676). These values only change very slowly, increasing by less than 1° per century due to secular perturbations in the solar system. Although the observations are made from Earth which itself revolves around the Sun this agreement should not surprise us because the positions in the sky where the apparent orbital velocity of the outer planets as seen from the Earth reaches its extreme values should on average coincide with the zodiacal positions where the orbital velocity in the heliocentric orbit of the planet reaches its extreme values.
It is also interesting to note that Ptolemy in the second century AD in his Almagest uses values for the longitudes of the apogee in his epicycle theories of the outer planets which are quite close to the Babylonian positions of minimal orbital velocity: for Saturn 233° compared to 230° (Babylonian), for Jupiter 161° compared to 162;30° and for Mars 115° compared to 120° (Pedersen 1974, 423–429).Footnote 40
From all this we may conclude that the limited accuracy of 1° to 2° with which the Babylonian astronomers were able to determine the positions of the planets from measurements relative to the Normal Stars was sufficient to extract the parameters that characterized their system A theories of the three outer planets.
8 The initial conditions of Babylonian planetary ephemerides
For the construction of their planetary ephemerides the Babylonian scholars must have adopted an initial date and an initial longitude for the first entry in the ephemeris. These initial conditions were probably taken from observations recorded in the Diaries by choosing an observation when the planet was close to one of the Normal Stars so that its position in the Babylonian zodiac could be determined. The way in which this was done may be illustrated by studying four contemporaneous system A ephemerides of Jupiter from Uruk: ACT No. 600, 601, 604 and 606. These ephemerides list dates and positions of four of the five synodic phenomena of Jupiter covering a period of about 80 years during the second century BC (SE 113–191). As I will show below it appears that these four ephemerides are related in the sense that their initial conditions probably derive from observations of Jupiter passing by Normal Stars in the zodiacal signs Leo and Virgo in SE 108/109.
This follows from a calculation in which each of these four ephemerides is expanded backward and forward in time to cover a period of 100 years from SE 101 to SE 200 (211/210 BC to 112/111 BC). It turns out that of all (about 95) entries in each of these ephemerides only one date has a nice integer value, while all other dates are represented by dirty fractional sexagesimal numbers and that for all four ephemerides these integer dates fall within a narrow time span of one year in SE 108/109. The integer dates and the associated positions in longitude for each Jupiter ephemeris are listed in columns (iv) and (v) of Table 7. Huber (1957, 277) who discovered this connection suggested that the dates and the associated positions of Jupiter in columns (iv) and (v) were adopted as initial conditions for the ephemerides. Thus, these four Jupiter ephemerides are related by the fact that their initial conditions are derived from one or more observations of Jupiter in SE 108/109, a few years before the first entry in three of the ephemerides.
The way in which this was done can be found from a closer inspection of the numbers in columns (vi) and (vii) of Table 7 where I list the time intervals (in tithis) and the angular distances (in degrees) between the initial dates and positions of the consecutive synodic phenomena of Jupiter in columns (vi) and (vii) going from last appearance to first station, to acronychal rising, to second station. Huber (1957) showed that these intervals are identical to the so-called pushes in time and in angular distance known from procedure texts of Jupiter for the slow arc of system A (for a recent discussion see Ossendrijver 2011, Table 3.38a, scheme A.S1). Both the angular push between last appearance and first station of Jupiter of 22°;15 and the one between first and second stations of − 10°;00 are identical to those of scheme A.S1, while the corresponding pushes in time of 2,30 tithis (i.e., 5 months of 30 tithis each) and 2,02 tithis are identical to and only 2 tithis longer than in scheme A.S1, respectively. However, although their sum of − 10°;00 is identical, the angular intervals from first station to acronychal rising of − 4°;25 and from acronychal rising to second station of − 5°;35 in Table 7 differ by − 0°;25 and + 0°;25 from the values of the pushes in scheme A.S1 (− 4°;00 and + 6°;00).
Now the question arises whether it is possible to identify the observation(s) of Jupiter on which the adopted initial conditions in the ephemerides may have been based. In the Astronomical Diary for SE 108 only observational records for month VIII are preserved. There we read that “At that time Jupiter until the middle of the month was in Leo, until the end of the month in Virgo” (ADRT II, Diary − 203, rev. lines 2–3) so that at the beginning of month IX Jupiter must have been in one of the first degrees of Virgo. This is confirmed by modern calculation where we find that on day 4 of month IX (14/15 December 204 BC) when Jupiter reached its first station it was positioned at a distance of 0°;30 past the Normal Star β Virginis (“the rear foot of the Lion”) in longitude. This distance (about equal to one lunar diameter) may have been measured by the Babylonian astronomers because Jupiter and β Vir were both visible during most of the night around that date (from about 10:30 h in the evening to sunrise the following morning).
The position of Jupiter at midnight of day 4 of month IX SE 108 was 2;28° Virgo in the Babylonian zodiac and that of β Vir was 1;58° Virgo, quite close to the adopted initial position of Jupiter of 1;45° Virgo for ephemeris ACT No. 600 in Table 7. The actual passing of Jupiter by the Normal Star β Vir twenty days earlier may well have been recorded by the Babylonian observers, but that part of the Diary is unfortunately not preserved.
The observation of Jupiter near the Normal Star β Vir at its first station in month VIII of SE 108 is by far the most suitable observation for the determination of the initial conditions of the four connected Jupiter ephemerides from Uruk. Other observations of Jupiter in SE 108/109 are less suitable. The passing of Jupiter by Normal Star α Leo occurred in month III about 2 weeks before the last visibility of Jupiter, and the passing of Jupiter by Normal Star θ Leo occurred about 2 weeks after the first visibility of Jupiter in month V. At its acronychal rising in month XI Jupiter was about 4° (about 1;40 KÚŠ) before the Normal Stars β Vir, and at its second station in month I of SE 109 it was about 4° past θ Leo. The passing of Jupiter by Normal Star ρ Leo in month IV could not be observed because both were invisible at that time.
In summary, once the initial date and the zodiacal longitude of Jupiter for the first station ephemeris ACT No. 600 had been observationally determined the initial conditions for the ephemerides of the other synodic phenomena may have been theoretically constructed by applying the pushes in time and angular distance according to the close variant of scheme A.S1 discussed above.
9 Conclusion
Since many steps are involved in the development of system A planetary theory I conclude by briefly listing the concepts used and the innovations introduced by the Babylonian astronomers in the process:
-
1.
The derivation of planetary periods from observed dates of first and last visibilities of planets over a time span of the order of at least about 100 years.
-
2.
The construction of “exact” long periods of hundreds of years by linear combination of these periods.
-
3.
The introduction of a theoretical celestial reference system of 12 signs of 30° related to the concept of theoretical months consisting of 30 days (tithis).
-
4.
The determination of the length of the sidereal year (in terms of lunar months) from observed dates of lunar eclipses (Saros).
-
5.
The computation of mean synodic longitude intervals (synodic arcs) and mean synodic time intervals (synodic periods) between successive similar synodic phenomena based on period relations.
-
6.
The relation between the synodic arc and the synodic period (the constant c) so that the synodic arc can be obtained from the synodic period, and vice versa.
-
7.
The variation in the synodic arcs as a function of zodiacal longitude from observations of planetary positions with respect to Normal Stars when the planets were stationary.
-
8.
The theoretical treatment of the variation of the synodic arcs as a step function with values for the amplitudes and the length of the “fast” and “slow” zones such that the period relations are satisfied.
-
9.
The choice of numerical values for the amplitudes of the step function such that they are close to the values derived from the observations and that both the amplitudes and the derived values of the slow/fast zones are convenient for computation in the sexagesimal number system.
-
10.
The positioning of the fast/slow zones in the zodiac centered on longitudes where the synodic arcs are observed to have a maximum/minimum.
-
11.
The computation of the variable synodic arc for any arbitrary initial position by applying interpolation algorithms to values derived from the step function.
-
12.
The computation of the associated synodic time interval by addition of the constant c to the synodic arc.
-
13.
The choice of initial conditions for an ephemeris of a planet at one of its synodic phases or for a group of connected ephemerides for all five synodic phenomena of a planet from observations of the longitude of that planet near one of the stations.
Finally, the main contribution of this study is to have shown that the Babylonian scholars based their system A models of the outer planets on longitudes determined from distances of the planets to Normal Stars observed when they were near the stations in their orbits.
Notes
In this paper I will use the acronyms FA (first appearance), S1 (first station), AR (acronychal rising), S2 (second station) and LA (last appearance) introduced by Ossendrijver (2011, 56–58). In the older literature one often encounters the Greek capital letters Γ, Φ, Θ, Ψ and Ω that were introduced by Neugebauer (ACT, 280; see also HAMA, 386) to represent the “characteristic phenomena” of the outer planets.
Since a planet is still invisible at the moment that it stands exactly opposite the Sun the phenomenon that was actually observed by the Babylonians is the so-called acronychal rising when the planet became visible again near the eastern horizon shortly after sunset. The exact observational criterion used by the Babylonians to determine the date of acronychal rising is not fully understood (see Hollywood and Steele 2004).
It is by now generally accepted that the Babylonian term ŠU (setting) in the Astronomical Diaries has to be translated as “disappearance” rather than “last appearance” (see de Jong 2012, 392–3) so that the date of ŠU is the first day at which a star or planet will be no longer visible. Because of the symmetry in the physics of the visibility process computations are carried out in this paper for dates of first and of last appearances (= date of disappearance -1). Since we will be mainly concerned with time intervals between dates of the same synodic phenomenon this difference in convention does not affect the results.
In present-day astronomy the synodic period is defined as the time it takes for a planet to move from one conjunction of the Sun to the next one. At conjunction the solar elongation of a planet is by definition equal to zero. The different synodic phenomena of a planet are characterized by different values of the solar elongation. For instance, for Saturn we find solar elongations of 342° ± 5° at FA, 251° ± 0.4° at S1, 109° ± 0.4° at S2 and 17° ± 3° at LA.
See ACT No. 800–824 and the new edition of these texts by Ossendrijver (2011).
These synthetic observations of first and last appearances of Jupiter have been generated by using the physics of the visibility process to compute first and last appearances of stars and planets (see de Jong 2012) assuming a visual extinction of 0.27 magnitudes per air mass for Babylon.
The parameters of the 71-year and the 83-year periods of Jupiter in column (iii) are identical to those derived by Gray and Steele (2008) in their study of Goal–Year astronomy when additional variations of about ± 3 days due to variable weather conditions are included.
Notice that these increments in days are exactly equal to the increments in degrees quoted in Sect. 10 of the procedure text BM 34221 + (=ACT No. 812) for the fast arc of Jupiter where we read: “For 71 years you subtract 6. For 83 years you subtract 1. … For 427 years it reaches its position” (Ossendrijver 2011, 329).
For a more recent discussion of the gradual development of system A lunar theory from the late sixth through the fourth century BC see de Jong (2017).
Britton (2010, 638–649) has recently argued that the invention of the Babylonian zodiac must be dated later. He proposes a date sometime between 409 and 398 BC, but I find his reasoning to support this dating far from convincing.
Neugebauer (1975, 423) lists five known variants of system A theory for Jupiter (A, A1, A′, A″ and A′″). Since all variants are based on the same step function approach I will limit myself in this study to the most simple (and best documented) system A.
Notice that 427 = 391 + 36.
These are the parameters for Saturn listed in Table 2.
See column (vii) of Table 2.
See columns (vi) and (vii) of Table 2.
Neugebauer (ACT, 479) suggests a meaning of this term similar to the “epact” of 11;04 tithis for the solar year (see also Ossendrijver 2011, 695).
The numbers in boldface in this derivation refer to the same numbers quoted in the procedure text ACT No. 812.
These lists also contain dates of the acronychal rising of the planets which occurs a few days before opposition to the Sun (Hollywood and Steele 2004). However, the precise observational criterion by which the date of acronychal rising was determined by the Babylonians is not clear so that observations of acronychal rising are not included in this study.
At first and last appearances of the planets the twilight sky is too bright for nearby stars to be visible.
Notice that for Mars the number of synodic waves (18 = 151 − 133) does not equal the number of sidereal rotations (151) as is the case for Saturn and Jupiter (see Table 2). This is caused by the fact that the distance between Mars and the Earth is small so that the interval between successive synodic events of Mars is so large (780 days) that Mars experiences more sidereal rotations (151) than synodic phenomena (133). Thus, while Mars experiences 47 synodic phenomena during the fourth century BC it moves 53 times through the 360° zodiac.
This concept plays a central role in the study of Babylonian planetary theory by Swerdlow (1998). Because Swerdlow concluded (p. 190) that “the methods used by the Scribes for deriving parameters from the measurement of time were motivated above all by avoiding the requirement of precise measurement of longitude for the obvious reason that they knew perfectly well that they could do no such thing” he proposed that the Babylonian planetary theories were primarily based on records of dates and measurements of time intervals. His point of view was strongly opposed by Britton (1998) in his review of Swerdlow’s work.
In spite of the fact that on first sight these numbers seem rather awkward, their ratio of 5:4 makes them fairly easy to manage in computations.
Throughout this paper longitudes in the Babylonian fixed zodiac are computed from the astronomical tropical longitudes using the relation (due to Huber 1958) λBab = λtrop + 4°28' − (T + 100)/71.6, where T is the Julian astronomical year (e.g., 484 BC = − 483).
Strictly speaking, this can only be done for Jupiter and Mars because no system A ephemeris of Saturn is preserved. However, based on the information available in the Procedure Texts, there is no doubt that the system A ephemeris of Saturn was computed in exactly the same way as that of Jupiter (Ossendrijver 2011, 106–107).
The astronomical unit is defined as the average distance of the Earth to the Sun in its orbit around the Sun.
The exception is the poor fit of the system A model of Mars at first and last appearances in the upper panels of Fig. 5. The reason for this failure will be discussed later in this section.
Based on the relations α(1)/30° + α(2)/35° = 10;51,40 and α(1) + α(2) = 360° (see Sect. 4.4 above).
As mentioned earlier for each model the initial conditions (planetary position and calendar date) were chosen such that the difference between the model values and the observed values averaged over all observations in the fourth century BC was zero. The magnitude of the standard deviation can then be used as a criterion for the quality of fit of the Babylonian models.
The fact that the Babylonian system A model of Mars provides a good fit to the observations at first station, but a very poor fit at first appearance was noticed before by Swerdlow (1999) in a paper in which he also somewhat softened his previous extreme position (Swerdlow 1998) that Babylonian planetary theory was based on measurements of time rather than of position.
The term primary synodic phenomenon was introduced by Ossendrijver (2011, 59) to indicate those synodic phenomena of the planets that were modeled by the system A step function. For Saturn and Jupiter all five synodic phenomena are primary.
The extreme values of the inclination of the ecliptic to the horizon of 80° and 34° may be derived from the geographical latitude of Babylon of 33° north and the inclination of the ecliptic to the celestial equator of 23° by the following simple relation 90° − 33° ± 23°. The corresponding extreme values of the solar elongation of Mars at its first appearance of −15° and −27° then follow from the relations −15°/sin (80°) and −15°/sin (34°), where 15° is the value of the arcus visionis of Mars.
Neugebauer (1955) lists five surviving (fragments of) Mars ephemerides of system A: ACT No. 500, 501, 501a, 501b, 502 and 503. The text ACT No. 504 only contains longitudes (and no dates) for the synodic phenomena of Mars. Aaboe and Sachs (1966) published several additional exemplars of the same “dateless computed lists of longitudes of characteristic phenomena” of Mars as presented in ACT No. 504, thereby confirming the results of the analysis of Neugebauer (1955). Ossendrijver (2011) refers to this type of texts, only containing longitudes of the five synodic phenomena of the planets and no dates, as template tables.
Julian dates are converted to dates in the Babylonian calendar using the PVN criterion for first lunar crescent visibility (see Huber 2011) which results in dates consistent with the tables of Parker and Dubberstein (1955) in the great majority of cases and if differences occur they do not exceed one day which is negligible in the present context.
In determining the nearest Normal Star I have limited myself to the canonical set of 28 Normal Stars. In his study Jones (2004) also discusses a number of less well-established Normal Stars that were used only occasionally by the Babylonian observers.
One magnitude difference in brightness corresponds to a factor of 2.5 in intensity, two magnitudes to a factor 6, four magnitudes to a factor 40 and six magnitudes to a factor 250.
In Table 6 the parameters adopted by the Babylonian scholars for their system A models are printed in regular script. The parameters of the variant models discussed here are printed in italic script.
Aaboe (1980) offers an interesting suggestion how the Babylonian scholars could have arrived at this set of parameters from observations by counting the number of synodic events per zodiacal zone over long periods of time.
I owe this interesting observation to Alexander Jones.
References
Aaboe, A. 1980. Observation and theory in Babylonian astronomy. Centaurus 24: 14–35.
Aaboe, A. 2001. Episodes from the early history of astronomy. Berlin: Springer.
Aaboe, A., and A.J. Sachs. 1966. Some dateless computed lists of longitudes of characteristic planetary phenomena from the late-Babylonian period. Journal of Cuneiform Studies 20: 1–33.
Aaboe, A., and A.J. Sachs. 1969. Two lunar texts of the achaemenid period from Babylon. Centaurus 14: 1–22.
Aaboe, A., Britton, J.P., Henderson, J.A., Neugebauer, O. and Sachs, A.J. 1991, Saros cycle dates and related Babylonian astronomical texts, Trans. Am. Phil. Soc. 81, part 6.
Brack-Bernsen, L., and H. Hunger. 1999. The Babylonian zodiac: Speculations on its invention and significance. Centaurus 41: 280–292.
Brack-Bernsen, L. and Hunger, H. 2005/6, On the atypical astronomical cuneiform text E. Archiv für Orientforschung 51, 96–107.
Britton, J.P. 1998. Planetary theory in Babylon. Journal for the History of Astronomy 29: 381–385.
Britton, J.P. 2002. Treatments of annual phenomena in cuneiform sources. In Under one sky: Astronomy and mathematics in the ancient near east, vol. 297, ed. J.M. Steele and A. Imhausen, 21–78., Alter Orient und Altes Testament Münster: Ugarit-Verlag.
Britton, J.P. 2010. Studies in Babylonian lunar theory: Part III. The introduction of the uniform zodiac. Archive for the History of Exact Sciences 64: 617–663.
de Jong, T. 2007. Astronomical dating of the rising star list in MUL.APIN. Wiener Zeitschrift für die Kunde des Morgenlandes 97: 107–120.
de Jong, T. 2012. Babylonian observations of venus: Arcus visionis, atmospheric extinction and observational practice. Journal for the History of Astronomy 43: 391–409.
de Jong, T. 2017. On the origin of the lunar and solar periods in Babylonian lunar theory. In Studies on the ancient exact sciences in honour of Lis Brack-Bernsen, ed. J.M. Steele and M. Ossendrijver, 105–126. Berlin: Springer.
Gray, J.M.K., and J.M. Steele. 2008. Studies on Babylonian goal–year astronomy I, A comparison between planetary data in goal–year texts, almanacs and normal star almanacs. Archive for the History of Exact Sciences 62: 553–600.
Hoffleit, D., and C. Jaschek. 1991. The bright star catalogue. New Haven: Yale University.
Hollywood, L., and J.M. Steele. 2004. Acronycal risings in Babylonian astronomy. Centaurus 46: 145–162.
Huber, P. 1957. Zur täglichen Bewegung des Jupiter nach babylonischen Texten. Zeitschrift für Assyriologie and vorderasiatischen Archeologie 52: 265–303.
Huber, P. 1958. Über den Nullpunkt der babylonischen Ekliptik. Centaurus 5: 192–208.
Huber, P. 2011. The astronomical basis of Egyptian chronology of the second millennium BC. Journal of Egyptian History 4: 172–227.
Hunger, H., and D. Pingree. 1999. Astral sciences in mesopotamia. Leiden: Brill.
Hunger, H., Sachs, A.J. and Steele, J.M. 2001, Astronomical Diaries and Related Texts from Babylonia, Vol. V: Lunar and Planetary Texts, Vienna (ADRT V).
Hunger, H. and Sachs, A.J. 2006, Astronomical Diaries and Related Texts from Babylonia, Vol. VI: Goal–Year Texts, Vienna (ADRT VI).
Hunger, H. and Sachs, A.J. 2014, Astronomical Diaries and Related Texts from Babylonia, Vol. VII: Almanacs and Normal Star Almanacs, Vienna (ADRT VII).
Jones, A. 2004. A study of Babylonian observations of planets near normal. Archive for History of Exact Sciences 58: 475–536.
Neugebauer, O. 1955. Astronomical cuneiform texts, vol. 3. London: ACT.
Neugebauer, O. 1975. A history of ancient mathematical astronomy, vol. 3. Berlin: HAMA.
Neugebauer, O., and A.J. Sachs. 1967. Some atypical astronomical cuneiform texts. Journal of Cuneiform Studies 21: 183–217.
Ossendrijver, M. 2011. Babylonian Mathematical Astronomy. Berlin: Procedure Texts.
Pedersen, O. 1974. A survey of the almagest. Odense: Odense University.
Rochberg, F. 2004. The heavenly writing: Divination, horoscopy, and astronomy in mesopotamian culture. Cambridge, MA: Cambridge University Press.
Roughton, N.A., J.M. Steele, and C.B.F. Walker. 2004. A late Babylonian normal and Ziqpu star text. Archive for History of Exact Sciences 58: 537–572.
Sachs, A.J. 1952. A late Babylonian star catalog. Journal of Cuneiform Studies 6: 146–150.
Sachs, A.J. and Hunger, H. 1988, 1989, 1996, Astronomical Diaries and Related Texts from Babylonia,Vols. I, II and III, Vienna (ADRT I–III).
Simon, J.L., P. Bretagnon, J. Chapront, M. Chapront-Touzé, G. Francou, and J. Laskar. 1994. Numerical expressions for precession formulae and mean elements for the Moon and planets. Astronomy & Astrophysics 282: 663–683.
Swerdlow, N.M. 1998. The Babylonian theory of the planets. Princeton, NJ: Princeton University Press.
Swerdlow, N.M. 1999. Acronychal risings in Babylonian planetary theory. Archive for History of Exact Sciences 54: 49–65.
van der Waerden, B.L. 1974. Science awakening II: The birth of astronomy. Groningen: Springer.
Acknowledgements
I would like to thank Peter Huber, Alexander Jones, Mathieu Ossendrijver and John Steele for constructive criticisms and advice.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
Communicated by Alexander Jones.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
de Jong, T. A study of Babylonian planetary theory I. The outer planets. Arch. Hist. Exact Sci. 73, 1–37 (2019). https://doi.org/10.1007/s00407-018-0216-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-018-0216-0