Elongational rheology of 2, 3 and 4 polymer stars connected by linear backbone chains

Abstract

We consider the elongational rheology of model polystyrene topologies with 2, 3 and 4 stars, which are connected by one (2-star or “Pom-Pom”), two (3-star) and three (4-star) linear backbone chains. The number of arms of each star varies from q_a = 3 to 24, the molecular weight of the arms from M_w,a = 25 kg/mol to 300 kg/mol, and the backbone chains from M_w,b = 100 kg/mol to 382 kg/mol. If the length of the arm is shorter than the length of the backbone, i.e. M_w,a < M_w,b, and despite the vastly different topologies considered, the elongational stress growth coefficient can be modeled by the Hierarchical Multi-mode Molecular Stress Function (HMMSF) model, based exclusively on the linear-viscoelastic characterization and a single nonlinear parameter, the dilution modulus. If the length of the arms of the stars is similar or longer than the length of the backbone chain (M_w,a ≥ M_w,b) connecting two stars, the impact of the backbone chain on the rheology vanishes and the elongational stress growth coefficient is dominated by the star topology showing similar features of the elongational stress growth coefficient as those of linear polymers.

Graphical Abstract

Introduction

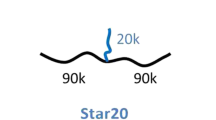
Relating molecular architecture to rheological properties is a long-standing challenge in polymer science. The understanding and modeling of the flow of homopolymer melts with branched topologies is of special interest to both fundamental research and industrial applications like film blowing, fiber spinning and foaming [Dealy and Larson 2006]. In order to induce substantial strain hardening in elongational flow, at least two branching points are needed as shown by McLeish and Larson (1998). The simplest polymer architecture with two branch points is a so-called Pom-Pom shaped molecule consisting of two stars, each with q_a arms of molecular weight ${M}_{w,a}$, connected by a backbone of molecular weight ${M}_{w,b}$ (Fig. 1).

Fig. 1

Schematic representation of the synthesized samples: 2-star-short (Pom-Pom with M_w,b = 100 kg mol⁻¹), 2-star-long (Pom-Poms with M_w,b = 220 and 300 kg mol⁻¹), 3-star, and 4-star. Grey and red lines correspond to polystyrene (PS) and polyisoprene (PI), respectively. The short post functionalized PI blocks are needed to graft the PS arms onto the backbone

Recently, Hirschberg et al. (2023a, b) showed that the elongational viscosity of 10 polystyrene Pom-Pom melts with backbone molecular weights M_w,b of 100 to 400 kg/mol, arm molecular weights of M_w,a of 9 to 50 kg/mol, and 9 to 22 arms at each of the two branch points can be described quantitatively by the Hierarchical Multi-mode Molecular Stress Function model (HMMSF), which is based on the concepts of hierarchical relaxation and dynamic dilution. Due to the high strain hardening of the Pom-Poms, elastic fracture is observed at higher strains and strain rates, which is well described by the entropic fracture criterion of Wagner et al. (2021, 2022a). In extension of the work of Hirschberg et al. (2023a, b), the objective of this article is to quantify and simulate the elongational rheology of model polystyrene topologies with 2, 3 and 4 stars. These are connected by a string consisting of one (2-star or “Pom-Pom”), two (3-star) and three (4-star) linear backbone chains, see Fig. 1. The number of arms of the stars varies from q_a = 3 to 24, the molecular weight of the arms from M_w,a = 25 kg/mol to 300 kg/mol, and the backbone chains varies from M_w,b = 100 kg/mol to 382 kg/mol. As we will show in the following, if the length of the arm is shorter than the length of the connecting backbone between the stars, i.e., M_w,a < M_w,b and despite the vastly different topologies considered, the elongational stress growth coefficient can be described by the HMMSF model, based exclusively on the linear-viscoelastic characterization and a single nonlinear parameter, the dilution modulus. If the arm length of the stars is similar or longer than the length of the backbone chain connecting two stars, the impact of the backbone chain on the rheology vanishes and the elongational stress growth coefficient is dominated by the star topology showing similar features of the elongational stress growth coefficient as linear polymers.

Materials

Polystyrene 2-, 3-, and 4-stars (Fig. 1) were synthesized in a three-step synthesis by living anionic polymerization. The backbone was synthesized by a stepwise addition of isoprene and styrene to obtain [Polyisoprene-b-Polystyrene-b-]_n-Polyisoprene copolymers followed by subsequent epoxidation of the Polyisoprene (PI) blocks [Röpert et al. (2022a)]. Living PS anions were then grafted onto the backbone, resulting in model polymer topologies with precise control over backbone length, arm length, and number of arms. It is important to emphasize that especially the stepwise synthesis of backbone and arms and the subsequent grafting onto gives full control over the molecular properties. Details of the synthesis are given in Röpert et al. (2022a, b). The molecular characteristics of the model polymers considered are summarized in Table 1.

Table 1 Molecular parameters of PS model polymers. M_w,b is the weight average molecular weight of the backbone, M_w,a the weight average molecular weight of the arms, q_a the number of arms per star, s the number of stars. Đ_b Đ_a and Đ_t are the polydispersity of backbone, arm and the total molecule

Experimental methods and linear-viscoelastic characterization

The experimental protocol for the rheological measurements in shear and elongation is reported in [Abbasi et al. 2017, 2019; Faust et al. 2023]. The small amplitude oscillatory shear (SAOS) and elongational measurements were conducted on an ARES-G2 rheometer (TA Instruments, Newcastle, USA) using a 13 mm plate-plate geometry for the SAOS shear measurements as well as an extensional viscosity fixture (EVF) for the elongational tests. The vacuum dried blends were hot-pressed at 180 °C for 10 min under vacuum. Shear rheology was measured between 130 and 220 °C, using an angular frequency range of ω = 0.1 to 100 rad/s. For all samples investigated, linear-viscoelastic master curves of storage and loss modulus, G’ and G’’, were obtained by time–temperature superposition (TTS). The plateau modulus ${G}_{N}^{0}$ is taken as the value of the storage modulus G’ at the high frequency G’ minimum of the loss tangent $\delta$. The mastercurves were fitted with about ten relaxation modes by parsimonious relaxation spectra by the IRIS software [Poh et al. 2022, Winter and Mours 2006], which are reported in the Support Information (SI). Molecular characterization, plateau modulus ${G}_{N}^{0}$, dilution modulus ${G}_{D}$, zero-shear viscosity ${\eta }_{0}$, and the Rouse time τ_R as defined below by Eqs. (7) and (8) are summarized in Table 2. The elongational tests were performed at 130 to 180 °C at Hencky strain rates of $\dot{\upvarepsilon }$= 0.003 to 10 s⁻¹ with maximum Hencky strains of ε = 4. The elongational viscosity data were time–temperature shifted to the reference temperature T_ref as given in Table 2.

Table 2 Backbone molecular weight M_w,b, backbone mass fraction ${\varphi }_{b}$, plateau modulus ${G}_{N}^{0}$, dilution modulus ${G}_{D}$, zero-shear viscosity η₀, Rouse time τ_R as determined by Eqs. (7) and (8), and reference temperature T_ref

Hierarchical molecular stress function (HMMSF) model

We summarize shortly the basic equations of the Hierarchical Multi-mode Molecular Stress Function (HMMSF) model for polydisperse linear and long-chain branched (LCB) polymer melts. The extra stress tensor of the HMMSF model is given according to Narimissa and Wagner (2016, 2019a, b),

$$\sigma \left(t\right)=\sum\limits_{i}\underset{-\infty }{\overset{t }{\int }}\frac{\partial {G}_{i}\left(t-{t}^{\prime}\right)}{\partial {t}^{\prime}}{f}_{i}^{2}\left(t,{t}^{\prime}\right){\mathbf{S}}_{DE}^{IA}\left(t,{t}^{\prime}\right){dt}^{\prime}$$

(1)

The relaxation modulus G(t) is expressed by a parsimonious spectrum of Maxwell with relaxation moduli g_i and relaxation times τ_i,

$$G\left(t\right)=\sum\limits_{i}{G}_{i}\left(t\right)=\sum\limits_{i}{g}_{i}\,exp\left(t/{\tau }_{i}\right)$$

(2)

${\mathbf{S}}_{DE}^{IA}$ is the Doi and Edwards (Doi and Edwards 1978, 1979) strain tensor assuming independent alignment (IA) of tube segments with ${\mathbf{S}}_{DE}^{IA}=5\mathbf{S}$, where S is the second order orientation tensor. The molecular stress functions f_i = f_i(t,t’) are inversely proportional to tube diameters a_i of each mode i, and are functions of both the observation time t (the time when the stress is measured) and the time t’ of creation of tube segments by diffusion. Hierarchical relaxation and dynamic dilution of tube segments are already contained in the linear-viscoelastic relaxation spectrum, and the effect of dilution by hierarchical relaxation can be extracted from the spectrum. For polydisperse linear and LCB melts, two separate dilution regimes exist during the relaxation process: The regime of permanent dilution, and the regime of dynamic dilution. The presence of oligomeric chains and un-entangled (fluctuating) chain ends leads to permanent dilution, while dynamic dilution starts as soon as the relaxation process reaches the dilution modulus ${G}_{D}\le {G}_{N}^{0}$. The dilution modulus G_D is a free parameter of the model, which is fitted to the non-linear viscoelastic experimental data, because the volume fraction of unentangled chain ends and oligomeric chains is in general not known. Dynamic dilution starts at time $t={\tau }_{D}$, when the relaxation modulus G(t) has relaxed to the value of G_D, while at times $t\le {\tau }_{D}$, the chain segments are assumed to be permanently diluted. It is important to note that dynamic dilution affects the rheology of nonlinear viscoelastic flows, as dynamic dilution needs time and its effect vanishes increasingly in faster flows. The fraction w_i of dynamically diluted polymer segments of mode i with relaxation time ${\tau }_{i}>{\tau }_{D}$ are determined by the ratio of the relaxation modulus at time $t={\tau }_{i}$ to the dilution modulus G_D,

$$\begin{array}{ll}w_i^2=\frac{G\left(t=\tau_i\right)}{G_D}=\frac1{G_D}\sum\limits_{j=1}^ng_jexp\left(-\tau_i/\tau_j\right)&\mathrm{for}\;\tau_i>\tau_D\\w_i^2=1&\mathrm{for}\;\tau_i\leq\tau_D\end{array}$$

(3)

The value of the volume fraction w_i at t = τ_i is attributed to the chain segments with relaxation time τ_i. Segments with ${\tau }_{i}<{\tau }_{D}$ are considered as permanently diluted and their volume fractions are assumed to be equal to 1. As shown by Narimissa et al. (2015), these assumptions are in agreement with the rheology of broadly distributed polymers and are largely independent of the number of Maxwell modes n used to represent the relaxation modulus G(t). Typical values of n are 8–14.

Restricting now attention to LCB polymers and extensional flows, the evolution equation for the molecular stress function f_i of each mode i is given by (Wagner and Hirschberg 2023),

$$\frac{\partial {f}_{i}}{\partial t}={f}_{i}\left(\mathbf{K}:\mathbf{S}\right)-\frac{{f}_{i}-1}{{\tau }_{i}}\left(1-{w}_{i}^{2}\right)-\frac{\left({f}_{i}^{5}-1\right)}{5{\tau }_{i}}{w}_{i}^{2}$$

(4)

with the initial conditions f_i(t = t’,t’) = 1. Affine stretch with K being the velocity gradient tensor is expressed by the first term on the right hand, while the second term takes Rouse relaxation into account. The third term limits molecular stretch due to Enhanced Relaxation of Stretch (ERS). In the case of LCB polymers with entangled side chains, stretch relaxation depends on the relaxation times ${\tau }_{i}$ and not on the Rouse time of the chain. The effect of dynamic dilution is expressed in Eq. (4) by the square of the volume fractions w_i. Dynamic dilution increases the tube diameter leading to an enhancement of stretch. In this way, stretch of segments of relaxation mode i does not only depend on the relaxation time τ_i, but also on dynamic dilution which is the larger the longer the relaxation time.

Modeling of fracture of polymers is of great importance for polymer processing. As reviewed in (Wagner et al. 2021), the research into the physical origin of fracture has been obscured for a long time by experimental issues such as inhomogeneous extensional flow. From experiments with filament stretching rheometers it is now obvious that polymeric systems can only be in one of two potential states: Polymer melts are either viscoelastic fluids, which can be deformed indefinitely, or they are viscoelastic solids, which show brittle fracture (Huang et al. 2016a; Huang and Hassager 2017). While polymer melts are liquids at low deformation rates, they transit to the state of viscoelastic solids at high Weissenberg numbers. Fracture of viscoelastic solids involves necessarily the rupture of primary, covalent bonds. As shown by Wagner et al. (2022a), fracture of polymer melts can be modeled by assuming that fracture occurs as soon as the entanglement segments corresponding to one relaxation mode fracture, i.e. when the segments of relaxation mode i reach the critical value W_c of the strain energy,

$${W}_{c}=3{kTf}_{i,c}^{2}{w}_{i}=U$$

(5)

U is the bond-dissociation energy of a single carbon–carbon bond in hydrocarbons. The strain energy of a diluted chain segment is given by $W=3{kTf}_{i}^{2}{w}_{i}$ with the stretch functions f_i obtained from Eq. (4), and the ratio of bond-dissociation energy U to thermal energy, i.e., U/3kT, is 35 and 31 at temperature of T = 130 °C and 180 °C, respectively. The entropic fracture hypothesis assumes that when the strain energy of an entanglement segment reaches the critical energy U, the total strain energy of the chain segment is concentrated on one C–C bond by thermal fluctuations, and the covalent bond ruptures. Rupture of polymer chains causes crack initiation, which is followed within a few milliseconds by brittle fracture. From Eq. (5) the critical stretch f_i,c at fracture is obtained as

$${f}_{i,c}=\sqrt{\frac{U}{3{kTw}_{i}}}$$

(6)

The fracture criterion of polymer melts is an integrated feature of the constitutive equations of the HMMSF model and has recently been verified for two low-density polyethylene melts by high speed videography (Poh et al. 2023).

In summary, the HMMSF model for LCB polymer melts in extensional flows consists of the multi-mode stress Eq. (1), the evolution equations for the molecular stresses f_i, Eq. (4), a quantification of the volume fraction of dynamically diluted chain segments according to Eq. (3) with only one free nonlinear parameter, the dilution modulus G_D, and the fracture criterion of Eq. (6). These equations represent a very concise constitutive model of the complex nonlinear steady state extensional rheology of LCB polymers based on well-defined physical assumption.

In the case of monodisperse linear polymer melts, the HMMSF model reduces to the Enhanced Relaxation of Stretch (ERS) model (Wagner and Narimissa 2021). While for LCB polymers stretch relaxation is governed by the relaxation times τ_i, stretch relaxation of linear melts depends on the Rouse stretch time τ_R of the polymer chain, which can be obtained by (Osaki et al. 1982),

$$\tau_R=\frac{12\;M\;\eta_0}{\pi^2\;\rho\;RT}\left(\frac{M_{cm}}M\right)^{2.4}$$

(7)

M is the molecular weight of the polymer, $\rho$ the density, R the gas constant and T the absolute temperature. The critical molecular weight M_cm of PS is taken as M_cm = 35 kg/mol. Alternatively, the Rouse time can be obtained from the number of entanglements z per chain and the entanglement equilibration time ${\tau }_{e}$ by (Dealy and Larson 2006).

$${\tau }_{R}= {\tau }_{e}{z}^{2}$$

(8)

The Rouse times calculated for Pom-Poms 100k-2 × 9-110k, 100k-2 × 22-110k, and 100k-2 × 14-300k by Eqs. (7) and (8) are summarized in Table 2. For Eq. (8) we used M_e = 13.5 kg/mol for PS, the entanglement equilibration time ${\tau }_{e}$ = 0.036 s⁻¹ at 140 °C and the shift factors for PS as reported by van Ruymbeke et al. (2007).

Stretch relaxation of monodisperse linear polymers occurs on the time scale of the Rouse relaxation time, which is proportional to the 2nd power of z and which for larger z is much shorter than the reptation time scaling proportional to the 3rd or 3.4th power of z. Therefore dynamic dilution can be neglected, i.e. ${w}_{i}=1$. With τ_i = τ_R, and therefore ${f}_{i}\left(t,{t}^{\prime}\right)=f\left(t,{t}^{\prime}\right)$, the HMMSF equations reduce to the constitutive equations of the ERS model with stress tensor $\sigma$,

$$\sigma \left(t\right)=\underset{-\infty }{\overset{t }{\int }}\frac{\partial G\left(t-{t}^{\prime}\right)}{\partial {t}^{\prime}}{f}^{2}\left(t,{t}^{\prime}\right){\mathbf{S}}_{DE}^{IA}\left(t,{t}^{\prime}\right){dt}^{\prime}$$

(9)

evolution equation of stretch $f\left(t,{t}{'}\right)$,

$$\frac{\partial f}{\partial t}=f\left(\mathbf{K}:\mathbf{S}\right)-\frac{{f}^{5}-1}{5{\tau }_{R}}$$

(10)

and the fracture criterion,

$${f}_{c}=\sqrt{\frac{U}{3kT}}$$

(11)

For high deformation rates and deformations, from Eq. (9) the limiting steady-state tensile stress is given by ${\sigma }_{E}=5{G}_{N}^{0}{f}^{2}$, and therefore the tensile stress ${\sigma }_{c}$ at fracture is

$${\sigma }_{c}=5{G}_{N}^{0}{f}_{c}^{2}=5{G}_{N}^{0}\frac{U}{3kT}$$

(12)

Fracture at the fracture stress ${\sigma }_{c}$ predicted by Eq. (12) has been verified by comparison to experimental fracture data of a linear PS melt with M_w = 285 kg/mol by Wagner et al. (2021).

Elongational viscosity and brittle fracture of Pom-Poms

Pom-Pom polymer macromolecules can be considered as two-star topologies connected by a backbone (Fig. 1). The mastercurves of G’ and G’’ of the Pom-Pom 300k-2 × 24-40k with a backbone of 300 kg/mol and 24 side arms, each of a molecular weight of 40 kg/mol at each of the two branch points, as well as the corresponding plot of the loss tangent $\delta$ as a function of G’ are shown in Fig. 2. We recall that we identify the plateau modulus ${G}_{N}^{0}$ with the value of the storage modulus G’ at the high frequency G’ minimum of the loss tangent δ = G’’/G’ (Table 2). After dynamic relaxation of the arms, the backbone with a weight fraction of ${\varphi }_{b}$ =0.14 (Table 2) is unentangled and relaxes by constraint Rouse relaxation creating a shallow minimum of the loss tangent $\delta$ with tan $\delta$>1 at a lower value of G’.

Fig. 2

Experimental data (symbols) of mastercurves of storage (G’) and loss (G’’) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for Pom-Pom 300 k-2 × 24-40 k. Reference temperature T = 140 °C. Lines are fit by parsimonious relaxation spectrum

Figure 3 compares the experimental data (symbols) of the time-dependant elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 300k-2 × 24-40k to predictions (lines) of the HMMSF model with a dilution modulus ${G}_{D}={G}_{N}^{0}=1.5\cdot {10}^{5}Pa$, i.e., dynamic dilution starts right at the plateau modulus ${G}_{N}^{0}$, in agreement with the results of Pom-Poms with similar high functionalities of the branch points reported by Hirschberg et al. (2023a, b). Elongational stress growth coefficient data measured at T = 130 °C (green symbols), 160 °C (red symbols), and 180 °C (pink symbols) were time–temperature shifted (TTS) to the reference temperature T of 140 °C (black symbols). Due to TTS, the range of elongation rates investigated covers more than 4 decades. Pom-Pom 300 k-2 × 24-40 k shows strong transient strain hardening with a high strain hardening factor (SHF), i.e. the maximal values of the elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ are more than 2 magnitudes larger than the linear-viscoelastic start-up viscosity ${\eta }_{E}^{0}\left(t\right)$ at the corresponding Hencky strain. Within experimental accuracy, predictions of the HMMSF model agree with the elongational data, based exclusively on the linear-viscoelastic relaxation spectrum and dilution modulus ${G}_{D}\equiv {G}_{N}^{0}$ as input. At lower strain rates a steady-state elongational viscosity is predicted, which is outside the Hencky strain range of $\varepsilon \le 4$ experimentally accessible by the EVF. Fracture is observed and predicted at the higher strain rates with maximal fracture stresses of ${\sigma }_{c}\cong 2\cdot {10}^{7}Pa$, and the Hencky strain at fracture, ${\varepsilon }_{c}$, decreases to ${\varepsilon }_{c}=3$ at the highest strain rate investigated, which is a strong indication of brittle fracture (Wagner et al. 2021, 2022a). These results agree and compliment the investigations of the elongational rheology of ten Pom-Pom systems by Hirschberg et al. (2023a, b).

Fig. 3

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 300k-2 × 24-40k. Data (symbols) measured at 130 °C (green, $\dot{\varepsilon }$=40, 12, 4 s⁻¹), 140 °C (black), 160 °C (red, $\dot{\varepsilon }$=0.26, 0.087, 0.026, 0.0087, 0.0026 s⁻¹) and 180 °C (pink, $\dot{\varepsilon }$=0.13, 0.039, 0.013, 0.0039, 0.0013, 0.00039 s⁻¹) are shifted to reference temperature of 140 °C. Lines are predictions of the HMMSF model with ${G}_{D}= {G}_{N}^{0}=1.5 {10}^{5}\mathrm{ Pa}$. The dashed black line indicates linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

While the lowest number of arms of the Pom-Poms considered by Hirschberg et al. (2023a, b) was q_a = 9, Pom-Pom 100k-2 × 5-25k has a backbone of 100 kg/mol and only 5 side arms of 25 kg/mol at each of the two branch points. As shown in Fig. 4, the low frequency G’ minimum of the loss tangent $\delta$ is less pronounced than in the case of Pom-Pom 300k-2 × 24-40k (Fig. 2) indicating less dilution of the backbone with a weight fraction of ${\varphi }_{b}$ =0.29 (Table 2). Indeed, a dilution modulus of G_D = 4^.10⁴ Pa was found to be in agreement with the elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ and the elongational stress growth ${\sigma }_{E}^{+}\left(\varepsilon \right)$ as seen in Fig. 5, which is much lower than the plateau modulus ${G}_{N}^{0}$≈ 1.8^.10⁵ Pa (Fig. 4b). In order to demonstrate the sensitivity of the value of G_D, Fig. 5a also shows predictions using G_D = 6^.10⁴ Pa and G_D = 2^.10⁴ Pa. A similar dilution modulus of G_D = 6^.10⁴ Pa was reported by Wagner et al. (2022a) for PS Pom-Pom 140k-2 × 2.5-28k with on average of 2.5 side arms per branch point investigated earlier by Nielsen et al. (2006). We note that a steady-state elongational flow is reached at strain rates of $\dot{\varepsilon }$=0.3 and 1 s⁻¹ as seen in the plot of ${\sigma }_{E}^{+}\left(\varepsilon \right)$(Fig. 5b).

Fig. 4

Experimental data (symbols) of mastercurves of storage (G’) and loss (G’’) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for Pom-Pom 100 k-2 × 5-25 k. Reference temperature T = 140 °C. Lines are fit by parsimonious relaxation spectrum

Fig. 5

(a) Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ and (b) elongational stress growth ${\sigma }_{E}^{+}\left(\varepsilon \right)$ of Pom-Pom 100k-2 × 5-25k. Data (symbols) measured at 140 °C. Continuous lines are predictions of the HMMSF model with ${G}_{D}= 4 {10}^{4}\mathrm{ Pa}$. The long-dashed black lines in (a) are predictions using G_D = 6^.10⁴ Pa and G_D = 2^.10⁴ Pa, respectively. The short-dashed black line in (a) indicates the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Another Pom-Pom with an even lower number of arms is 220 k-2 × 3-70 k with a backbone of 220 kg/mol and 3 rather long side arms of 70 kg/mol at each of the two branch points. While the backbone is entangled after relaxation of the arms, the rubbery plateau of the backbone with weight fraction of ${\varphi }_{b}$ = 0.34 (Table 2) is shifted to low frequencies (Fig. 6a). The value of G’ at the low frequency minimum of the loss tangent $\delta$ is found at G’ = 1.2 10⁴ Pa (Fig. 6 b), while the plateau modulus is ${G}_{N}^{0}$ = 1.9 10⁵ Pa. The elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ is best described by a dilution modulus of G_D = 3^.10³ Pa (Fig. 7). Again, while at lower strain rates a steady-state elongational viscosity is predicted, brittle fracture is observed and predicted at the higher strain rates with maximal fracture stresses of ${\sigma }_{c}\cong 2\cdot {10}^{7}Pa$. We may conclude that while for Pom-Poms with a large number ${q}_{a}\ge 9$ of side arms dynamic dilution starts right from the plateau modulus, a smaller number of side arms, whether short or long, leads to less dynamic dilution of the backbone chain as shown here for Pom-Poms 100k-2 × 5-25k and 220k-2 × 3-70k.

Fig. 6

Experimental data of mastercurves of storage (G’, closed symbols) and loss (G’’, open symbols) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for Pom-Pom 220k-2 × 3-70k. Reference temperature T = 140 °C. Lines are fit by parsimonious relaxation spectrum

Fig. 7

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 220k-2 × 3-70k. Data (symbols) measured at 160 °C (black symbols) and 180 °C (red symbols) and time–temperature shifted to 140 °C. Lines are predictions of the HMMSF model with G_D = 3 10³ Pa. The dashed line indicates the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Elongational viscosity of 3 and 4 stars connected by linear backbone chains

Figure 8 shows the mastercurves of G’ and G’’ and the loss ${\text{tan}}\delta$ at T = 180 °C of the 3-star 213k-3 × 11-25k and the 4-star 382k-4 × 11-27k consisting of 3 and 4 stars, each with 11 side arms connected by a linear backbone chain of molecular weight 213 kg/mol and 382 kg/mol, respectively (Fig. 1). After dynamic relaxation of the arms, the backbone remains entangled as evidenced by the lower frequency crossover of G’ and G’’ and the lower G’ at the minimum of the loss ${\text{tangent}}\delta$.

Fig. 8

Experimental data of mastercurves of storage (G’, closed symbols) and loss (G’’, open symbols) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for 3-star 213k-3 × 11-25k (a) and 4-star 382k–4 × 11-27k (b). Reference temperature T = 180 °C. Lines are fit by parsimonious relaxation spectrum

The 3-star and the 4-star polymer melts show strong transient strain hardening with strain hardening factors SHF > 120. Using a dilution modulus equal to the plateau modulus, i.e. ${G}_{D}={G}_{N}^{0}$, the data of the elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ are within experimental accuracy in general agreement with predictions of the HMMSF model, again based exclusively on the linear-viscoelastic relaxation spectra and the dilution modulus ${G}_{D}\equiv {G}_{N}^{0}$ as in the case of the Pom-Poms with high branch point functionality investigated by Hirschberg et al. (2023a, b). While at lower strain rates a steady-state elongational viscosity is predicted, brittle fracture is observed and predicted at the higher strain rates with maximal fracture stresses of ${\sigma }_{c}\cong 2\cdot {10}^{7}Pa$. At the lowest strain rate $\dot{\varepsilon }=0.1{s}^{-1}$, the experimental data for 3-star 213k-3 × 11-25k show a maximum caused by inhomogeneous deformation of the sample. We conclude that multiple stars with many side arms shorter than the connecting backbone behave similar to Pom-Poms with a high functionality of the branch points in elongational flow (Fig. 9).

Fig. 9

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of 3-star 213k-3 × 11-25k (a) and 4-star 382k-4 × 11-27k (b). Data (symbols) measured at temperature of 180 °C. Lines are predictions of the HMMSF model with G_D = ${G}_{N}^{0}$  = 1.8 10⁵ Pa for 3-star and G_D = ${G}_{N}^{0}$  = 2.8 10⁵ Pa for 4-star. The dashed lines indicate linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Transition from Pom-Pom to star/linear elongational behavior

Huang et al. (2016b) and Huang (2022) explored the elongational rheology of a symmetric 3-arm PS star and found that it reaches the same elongational steady-state viscosity in fast flows (faster than the inverse Rouse time, 1/τ_R) as a corresponding linear PS polymer melt having the same span molecular weight as the 3-arm star. This confirmed the expectation of Ianniruberto and Marrucci (2013) that entangled melts of LCB macromolecules become quasilinear by aligning the arms in strong extensional flows. Indeed, Mortensen et al. (2018, 2021) could demonstrate by small-angle neutron scattering (SANS) studies of a three-armed polystyrene star polymer that upon exposure to large elongational flow, the star polymer indeed changes its arm conformation: All three arms are oriented parallel to the flow, one arm being either in positive or negative stretching direction, while the two other arms are oriented parallel, right next to each other in the direction opposite to the first arm. Wagner et al. (2022b) confirmed that the elongational stress growth coefficient of the linear as well as the 3-arm star could be well described by the ERS model. In the following we demonstrate that Pom-Poms with length of the side arms greater than the length of the backbone are “star-type” macromolecules. The backbone connecting 2 stars has no detectable impact on the elongational stress growth coefficient.

The mastercurves of G’ and G’’ and the loss ${\text{tan}}\delta$ at T = 140 °C are shown in Fig. 10 for Pom-Pom 100 k-2 × 9-110 k with 9 side arms, and Pom-Pom 100 k-2 × 22-110 k with 22 side arms of molecular weight M_w,a of 110 kg/mol connected by a backbone of molecular weight M_w,b of 100 kg/mol. These star-like Pom-Poms show a broad plateau region with plateau modulus of ${G}_{N}^{0}$= 8.2 10⁴ Pa (Pom-Pom 100 k-2 × 9-110 k) and ${G}_{N}^{0}$= 6.1 10⁴ Pa (Pom-Pom 100 k-2 × 22-110 k), and a rather featureless terminal relaxation regime. There is no distinct effect of the backbone after dynamic dilution by the arms to weight fractions of ${\varphi }_{b}$=0.05 and 0.02 (Table 2), respectively, and a rather blurred signature of constraint Rouse relaxation at low frequencies.

Fig. 10

Experimental data (symbols) of mastercurves of storage (G’) and loss (G’’) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for Pom-Pom 100 k-2 × 9-110 k (a) and Pom-Pom 100 k-2 × 22-110 k (b). Reference temperature T = 140 °C. Lines are fit by parsimonious relaxation spectrum

Figures 11 and 12 present the experimental data (symbols) of the elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Poms 100k-2 × 9-110k and 100k-2 × 22-110k. In contrast to Pom-Pom 300 k-2 × 24-40 k with a similar number of side arms as Pom-Pom 100 k-2 × 22-110 k, but with side arms which are much shorter than the backbone, i.e., M_w,a <  < M_w,b (Fig. 3), the Pom-Poms 100k-2 × 9-110k and 100k-2 × 22-110k show only limited strain hardening. Specifically, there is no strain hardening at low elongation rates, and strain hardening only starts at elongation rates larger than the inverse of the Rouse stretch relaxation time. Except for the highest strain rate of Pom-Pom 100k-2 × 22-110k, a steady-state elongational viscosity is approached, which decreases with increasing strain rate and which is substantially below the LVE elongational viscosity ${\eta }_{E}^{0}=3{\eta }_{0}$. This type of elongational behaviour is similar to that of linear PS melts. Figures 11 and 12 also present predictions (lines) of the HMMSF model with a dilution modulus ${G}_{D}={G}_{N}^{0}$ as well as predictions of the ERS model. Using a span molecular weight of M_w,span = M_w,b + 2M_w,a = 320 kg/mol and the entanglement equilibration time according to Eq. (8), a Rouse time of ${\tau }_{R}$ = 20.2 s results for both systems. On the other hand, Osaki’s relation (7) taking also the slightly different zero-shear viscosities into account, leads to Rouse times of ${\tau }_{R}$ = 17.5 s and ${\tau }_{R}$ = 27.4 s for Pom-Pom 100k-2 × 9-110k and Pom-Pom 100k-2 × 22-110k, respectively, which we will use in the following. While the HMMSF model overpredicts the elongational stress growth coefficient and predicts brittle fracture at all strain rates investigated (Figs. 13a and 14a), the ERS model is in agreement with the experimental data at all strain rates investigated (Figs. 13b and 14b) and predicts steady-state elongational viscosities except for the highest strain rate of Pom-Pom 100k-2 × 22-110k. We conclude that if arm and backbone molecular weights are similar, M_w,a ≈ M_w,b, the impact of the backbone chain on the rheology vanishes and the elongational rheology is dominated by the star topology showing similar features of the elongational stress growth coefficient as linear polymers with a similar span molecular weight of M_w,span = M_w,b + 2M_w,a.

Fig. 11

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 100k-2 × 9-110k. Data (symbols) measured at 140 °C. Lines are predictions of (a) the HMMSF model with ${G}_{D}={G}_{N}^{0}$= 8.2 10⁴ Pa, and (b) predictions of the ERS model with ${\tau }_{R}$ = 17.5 s. The dashed lines indicate the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Fig. 12

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 100k-2 × 22-110k. Data (symbols) measured at 140 °C. Lines are predictions of (a) the HMMSF model with ${G}_{D}={G}_{N}^{0}$= 6.1 10⁴ Pa, and (b) predictions of the ERS model with ${\tau }_{R}$ = 27.4 s. The dashed lines indicate the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Fig. 13

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 100k-2 × 9-110k (black symbols) and Pom-Pom 100k-2 × 22-110k (red symbols). Lines are predictions of the ERS model. The dashed lines indicate the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Fig. 14

Experimental data (symbols) of mastercurves of storage (G’) and loss (G’’) modulus as a function of the angular frequency as well as loss ${\text{tan}}\delta$ vs. G’ for Pom-Pom 100k-2 × 14-300k. Reference temperature T = 160 °C. Lines are fit by parsimonious relaxation spectrum

It is noteworthy that the elongational stress growth coefficient is rather independent of the number of arms of the two star-like Pom-Poms (Fig. 13). Except for a small difference in the linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$, data and predictions of the ERS model are nearly the same for Pom-Pom 100k-2 × 9-110k and Pom-Pom 100k-2 × 22-110k.

An even more extreme case of a star-like Pom-Pom is the system 100k-2 × 14-300k with the 14 side arms of molecular weight M_w,a = 300 kg/mol being three times longer than the backbone with molecular weight M_w,b = 100 kg/mol. The mastercurves of G’ and G’’ and the loss ${\text{tan}}\delta$ at reference temperature T = 160 °C are shown in Fig. 14. The extended plateau region with plateau modulus of ${G}_{N}^{0}$ ≈ 1.9 10⁵ Pa transits into a broad elastic region with G’ being larger than G’’ and a crossover to the terminal regime at very low frequencies. The weight fraction of the backbone is only ${\varphi }_{b}$=0.01. The experimental data (symbols) of the elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ measured at temperatures of 140, 160 and 180 °C and time–temperature shifted (TTS) to the reference temperature of 160 °C are shown in Fig. 15. Note that due to TTS, the elongation rates investigated span a range of nearly 4 decades. Again, as in the case of Pom-Poms 100k-2 × 9-110k and 100k-2 × 22-110k, there is no strain hardening at low elongation rates, and strain hardening only starts at elongation rates $\dot{\varepsilon }>0.1{s}^{-1}$. Except for the two highest strain rates of $\dot{\varepsilon }$=180 and 54 s⁻¹, a steady-state elongational viscosity is approached, which decreases with increasing strain rate and which is orders below the LVE elongational viscosity ${\eta }_{E}^{0}=3{\eta }_{0}=5.4\cdot {10}^{9}Pas$ (Table 2). Predictions (lines) of the HMMSF model with a dilution modulus ${G}_{D}={G}_{N}^{0}$ as well as predictions of the ERS model are presented in Fig. 15. The HMMSF model overpredicts the stress growth coefficient increasingly at lower strain rates and predicts brittle fracture at all strain rates investigated. Taking the span molecular weight, i.e. M_w,span = M_w,b + 2M_w,a = 700 kg/mol, results in a Rouse time of ${\tau }_{R}$ = 331 s from Osaki’s relation (7), which is much too large compared to the experimental data. We note that Pom-Pom 100k-2 × 14-300k with the short backbone is effectively one star with 28 arms of M_w,a = 300 kg/mol, and in this case, the exponentially increased viscosity due to the high molecular weight of the arms is outside the predictive capabilities of Eq. (7). However, an effective Rouse time of ${\tau }_{R}$≈ 10 s is found to be in agreement with elongational data as shown in Fig. 15b for the ERS model, which is of the same order of magnitude as the Rouse time of ${\tau }_{R}$ ≈ 4.3 s calculated from Eq. (8) by use of the entanglement equlibration time. The longest relaxation time of the parsimoneous relaxation spectrum, ${\tau }_{i,max}$= 1.1 10⁶ s, and the Rouse time of Pom-Pom 100 k-2 × 14-300 k are separated by five orders of magnitude, and consequently, orientation and stretch of Pom-Pom 100 k-2 × 14-300 k are well separated, as discussed below. The ERS model correctly predicts the transition to a steady-state elongational viscosity within the experimentally accessible Hencky strain range of $\varepsilon \le 4$ for the lower strain rates, as well as brittle fracture at the two highest elongation rates with Hencky strains at fracture of ${\varepsilon }_{c}<3$, in agreement with experimental fracture data of a linear PS melt (Wagner et al. 2021).

Fig. 15

Elongational stress growth coefficient ${\eta }_{E}^{+}\left(t\right)$ of Pom-Pom 100k-2 × 14-300k. Data (symbols) measured at 140 °C (green), 160 °C (black), and 180 °C (red) are shifted to reference temperature of 160 °C. Lines are predictions of (a) the HMMSF model with ${G}_{D}={G}_{N}^{0}$= 1.9 10⁵ Pa, and (b) predictions of the ERS model with ${\tau }_{R}$ = 10 s. The dashed lines indicate linear-viscoelastic elongational start-up viscosity ${\eta }_{E}^{0}\left(t\right)$

Discussion and Conclusions

We considered the elongational rheology of model polystyrene topologies with 2, 3 and 4 stars connected by linear backbone chains. If the length of the arm is shorter than the length of the backbone, M_w,a < M_w,b, the elongational stress growth coefficient can be described by the HMMSF model, based exclusively on the linear-viscoelastic characterization and a single nonlinear parameter, the dilution modulus G_D, despite the vastly different topologies. The important message here is that the effect of the topology on the relaxation of arms and backbone and their interrelations are fully represented by the linear-viscoelastic relaxation spectrum. In addition to the relaxation modulus G(t), the modeling of the elongational rheology requires only consideration of hierarchical relaxation and dynamic dilution, which can be quantified by a single parameter, the dilution modulus G_D according to Eq. (3). We take G(t) from the experimental LVE characterization here, but we remark that in principle, any molecular or coarse-grained model could be employed, provided it reproduces G(t) quantitatively. For Pom-Pom 300k-2 × 24-40k with 24 arms the dilution modulus is equal to the plateau modulus,${G}_{D}={G}_{N}^{0}$, i.e. dynamic dilution starts at the plateau modulus. This is in agreement with the earlier results reported by Hirschberg et al. (2023a) for Pom-Poms with backbone molecular weights M_w,b of 100 to 400 kg/mol, arm molecular weights M_w,a of 9 to 50 kg/mol, and number of arms q_a between 9 and 22, and even for Pom-Pom/linear and Pom-Pom/star blends (Hirschberg et al. (2023b). As we show here it is also true for the 3-star 213k-3 × 11-25k and 4-star 382k-4 × 11-27k with 11 arms per star. For Pom-Poms with a smaller number of entangled arms such as Pom-Pom 100 k-2 × 5-25 k and Pom-Pom 220k-2 × 3-70k, the dilution modulus is lower than the plateau modulus, ${G}_{D}<{G}_{N}^{0}$, signifying less dynamic dilution and consequently less transient (time-dependent) strain hardening of the elongational stress growth coefficient. The value of G_D depends strongly on the functionality q_a of the branch points of the Pom-Poms. Figure 16 shows the normalized dilution modulus ${G}_{D}/{G}_{N}^{0}$ as a function of the number Nbr = 2q_a of arms for the Pom-Poms considered here and by Hirschberg et al. (2023a, b). Also reported in Fig. 16 are the values of ${G}_{D}/{G}_{N}^{0}$ for a series of PS model combs with M_w,b = 290 kg/mol, M_w,a = 44 kg/mol and with Nbr = 3 to190 branches analyzed recently by Hirschberg et al. (2024). For Nbr ≈ 20 and larger, the dilution modulus ${G}_{D}$ is found always to be identical with the plateau modulus ${G}_{N}^{0}$, while at smaller values of Nbr, the dilution modulus is significantly smaller. It seems that the number of arms is more important than their molecular weight at least within the range of $9kg/mol\le {M}_{w,a}\le 70kg/mol$ investigated, but further research will be needed before a definite conclusion can be reached.

Fig. 16

Normalized dilution modulus ${G}_{D}/{G}_{N}^{0}$ for Pom-Poms (Nbr = 2q_a) and combs. (Line is guide to the eye.)

Instead of the strain hardening factor as a measure of transient elongational strain hardening as used by Abbasi et al. (2017, 2019) and Faust et al. (2023), we present an alternative method to evaluate the strain hardening potential of polymer systems: We consider in Fig. 17 the viscosity ratio ${\eta }_{E,max}/{\eta }_{0}$, i.e. the steady-state viscosity ${\eta }_{E}$ or the maximal viscosity at break, ${\eta }_{E.max}$, normalized by the zero-shear viscosity ${\eta }_{0}$ as a function of the steady-state tensile stress ${\sigma }_{E}$ or the maximal tensile stress ${\sigma }_{E,max}={\eta }_{E,max}\dot{\varepsilon }$ in case of fracture, normalized by the plateau modulus ${G}_{N}^{0}$ (Table 2). Lines are calculated by the HMMSF or ERS model and symbols indicate the calculated values at the experimental strain rates. This representation is temperature invariant provided that the branched polymers can be considered as thermo-rheologically simple and the small effect of the different measurement temperatures on the fracture criterion can be neglected. It should also be noted that this representation is of special importance for assessing the effect of strain hardening in polymer processing, because most polymer processes are controlled by either stress or force, and not by strain rate. The plot of ${\eta }_{E,max}/{\eta }_{0}$ versus ${\sigma }_{E,max}/{G}_{N}^{0}$ has also the benefit that the LCB-type strain hardening behaviour of the 2-, 3- and 4-star polymers with M_w,a < M_w,b, which depends on the relaxation times ${\tau }_{i}$ according to the stretch evolution Eq. (4), can be directly compared to the specific elongational behaviour of the “linear-type” Pom-Poms with M_w,a > M_w,b depending on the stretch evolution Eq. (10) with the Rouse time ${\tau }_{R}$. In contrast, using Weissenberg numbers based either on relaxation times ${\tau }_{i}$ (for M_w,a < M_w,b) or Rouse time ${\tau }_{R}$ (for M_w,a > M_w,b) would lead to incompatible dimensionless strain rate measures for comparison of the elongational strain hardening behaviours.

Fig. 17

Model predictions of normalized maximal elongational viscosity ${\eta }_{E,max}/{\eta }_{0}$ as a function of the normalized maximal tensile stress ${\sigma }_{E,max}/{G}_{N}^{0}$. Lines are calculated by the HMMSF model (continuous lines) and ERS model (dashed lines). Symbols indicate the calculated values at the experimental strain rates. Contineous vertical line indicates ${\sigma }_{E,max}=5{G}_{N}^{0}$, dotted vertical line indicates ${\sigma }_{c}=170{G}_{N}^{0}$

If we take the maximum value of ${\eta }_{E,max}/{\eta }_{0}$ as a measure for the strain hardening potential, Pom-Pom 300k-2 × 24-40k shows the highest strain hardening with a maximal value of ${\eta }_{E,max}/{\eta }_{0}\approx 100$, followed by the 3-star 213k-3 × 11-25k and 4-star 382k-4 × 11-27k. In contrast, Pom-Pom 100k-2 × 5-25k and Pom-Pom 220k-2 × 3-70k with ${G}_{D}<<{G}_{N}^{0}$ show maximal values of ${\eta }_{E,max}/{\eta }_{0}\approx 10$ and ${\eta }_{E,max}/{\eta }_{0}\approx 6$, respectively. All of these five polymers with M_w,a < M_w,b are at first tensile stress thickening, while after the maximum they are stress thinning. It is interesting to note that they reach their maximal viscosity at a tensile stress between ${\sigma }_{E,max}={G}_{N}^{0}$ and ${\sigma }_{E,max}=5{G}_{N}^{0}$. According to the Doi-Edwards IA model, full alignment of chain segments in the flow direction is expected at ${\sigma }_{E}=5{G}_{N}^{0}$, which is indicated in Fig. 17 by the continuous vertical line.

If the length of the side arms of the Pom-Pom is similar or longer than the length of the backbone chain such as in the case of Pom-Poms 100k-2 × 9-110k, 100k-2 × 22-110k, and 100k-2 × 14-300k, the impact of the backbone chain on the rheology vanishes and the elongational rheology is dominated by the star topology showing similar features of the elongational stress growth coefficient as linear polymers (see schematic in Fig. 18): The elongational behavior can be characterized by an effective Rouse time ${\tau }_{R}$, and while there is still transient elongational strain hardening at strain rates larger than the inverse of the Rouse time $1/{\tau }_{R}$, the steady-state value of the elongational viscosity ${\eta }_{E}$ (or its maximal value ${\eta }_{E,max}$ in case of fracture) is lower than $3{\eta }_{0}$, i.e. these polymer systems show consistently only tensile stress thinning. This signature of linear polymers is seen in Fig. 17 when plotting ${\eta }_{E,max}/{\eta }_{0}$ as a function of normalized tensile stress ${\sigma }_{E,max}/{G}_{N}^{0}$: For Pom-Poms 100k-2 × 9-110k and 100k-2 × 22-110k, the effective Rouse relaxation time corresponds to a linear polymer with the span molecular weight of M_w,span = M_b + 2 Ma = 320 kg/mol. In this case, orientation and stretch are not well separated, but nevertheless, a small change of slope is observed at ${\sigma }_{E,max}\cong 5{G}_{N}^{0}$ when full alignment of the polymer chains in the flow direction is reached according to the Doi-Edwards IA model. However, Pom-Pom 100k-2 × 14-300k with very long arms and a span molecular weight of M_w,span = 700 kg/mol shows the expected elongational viscosity behaviour of a linear polymer with a very high molecular weight: The longest relaxation time ${\tau }_{i,max}$ and the Rouse time ${\tau }_{R}$ are separated by orders of magnitude. As shown in Fig. 17, Pom-Pom 100k-2 × 14-300k is first increasingly oriented with increasing tensile stress resulting in the strong drop of the elongational viscosity, and only at nearly full orientation of the arms at ${\sigma }_{E,max}=5{G}_{N}^{0}$ (continuous vertical line in Fig. 17) and at strain rates $\dot{\varepsilon }\ge 1/{\tau }_{R}$, chain stretching sets in, resulting in the enhanced kink of the ${\eta }_{E,max}/{\eta }_{0}$ curve.

Fig. 18

Rheological simplification of the complex Pom-Pom topology for M_w,a > M_w,b

Thus, the plot of ${\eta }_{E,max}/{\eta }_{0}$ vs. ${\sigma }_{E,max}/{G}_{N}^{0}$ allows to distinguish between the strain hardening behaviour of 2-, 3- and 4-star polymers with M_w,a < M_w,b on the one side, and that of the “linear-type” Pom-Poms with M_w,a > M_w,b on the other side. While the former show pronounced maxima of the elongational viscosity, the latter feature consistently elongational viscosity thinning with increasing tensile stress ${\sigma }_{E,max}$.

Also indicated in Fig. 17 is the fracture stress ${\sigma }_{c}$ by the dotted vertical line, which from Eq. (12) is given by ${\sigma }_{c}\cong 170{G}_{N}^{0}$ at a reference temperature of 140 °C. This is in reasonable agreement with the experimental data of the “linear-type” Pom-Poms with M_w,a > M_w,b in Figs. 11, 12 and 15, which show no fracture or only fracture at the highest elongation rates investigated, in agreement with the fracture analysis of a linear PS melt by Wagner et al. (2021). In contrast Pom-Poms as well as 3- and 4-star polymers with M_w,a < M_w,b fracture already at lower tensile stresses ${\sigma }_{E,max}$ due to the high stretch of the backbone as already shown for Pom-Poms by Hirschberg et al. (2023a), and the limiting value of ${\sigma }_{c}\cong 2\cdot {10}^{7}Pa\approx 100{G}_{N}^{0}$ reported by Hirschberg et al. is only reached at very high elongation rates.

In conclusion, polymer stars aligned on a string show a rich nonlinear elongational viscosity behaviour, which for M_w,a < M_w,b can be rationalized by considering hierarchical relaxation of the arms leading to dynamic dilution of the backbone as quantified by the Hierarchical Multi-mode Molecular Stress Function (HMMSF) model. For Pom-Poms as well as 3- and 4-stars with M_w,a < M_w,b and many arms high strain hardening is observed, which is greatly reduced when the number of branches Nbr = 2q_a is less than about 20 (Fig. 16). If the length of the arms of the stars is similar or longer than the length of the backbone chain connecting two stars, the impact of the backbone chain on the rheology vanishes and the elongational stress growth coefficient is dominated by the star topology showing similar features of the elongational stress growth coefficient as linear polymers and can be described by the Enhanced Relaxation of Stretch (ERS) model.