Introduction

Blood is a unique complex fluid as it possesses an array of rheological properties due to the dynamical behaviour of the main constituents, the red blood cells (RBCs) and their interaction with plasma proteins. Initial investigations into the behaviour of RBCs in plasma and saline solutions were conducted by Schmid-Schonbein (1969). It was observed that the morphology and dynamics of the RBCs changed with the applied shear rate. Initially, RBCs remained biconcave and exhibited tumbling motion at low shear rates, this behaviour decreased with slight increases in shear rates.

In the presence of plasma proteins (fibrinogen and globulins) at low shear rates (\(\dot{\gamma }\) < 100 s\(^{-1}\)), RBCs aggregate into a range of structures (Robertson et al. 2008). The structures which form have rod-like shapes or stacks known as rouleaux (Merrill et al. 1963), at very low shear rates, these aggregates align together to form larger three-dimensional structures. If the shear rate is increased further (\(\dot{\gamma }\) > 100 s\(^{-1}\)) these larger structures break down, and the RBCs align in the flow direction. Shape morphology and deformation dynamics of RBCs are also important factors in shear-thinning behaviour (Lanotte et al. 2016a). A combination of these interactions gives rise to the shear-thinning behaviour found in whole blood.

Although not as pronounced as other rheological properties, viscoelastic behaviour is present in whole blood (Beris et al. 2021). This arises due to the ability of aggregates to store and release energy (Chien et al. 1975; Thurston 1972). A smaller effect, the viscoelasticity in blood also exists due to the elasticity of individual RBCs at high shear rates, this is owed to the elasticity of cell membranes (Lanotte et al. 2016b). The presence of a viscoelastic time scale for both rouleaux networks, and the weakly elastic plasma (Brust et al. 2013; Varchanis et al. 2018) and individual RBCs (Horner et al. 2018), tends to complicate matters when modelling blood as a viscoelastic fluid.

This elastic (and thixotropic) behaviour has led to blood being defined as a thixo-elastic-viscoplastic material (TEVP) first described and introduced by Stoltz and Lucius (1981). Since then, several authors explored the TEVP constitutive models of blood investigating transient microstructure mechanical properties and physiological parameters (Armstrong et al. 2021b, a), while Giannokostas et al. (2020) developed the first validated TEVP model that can be applied to 0D to 3D flows.

Physiological blood flow is predominantly laminar and fully turbulent flow is uncommon, however, flow in the transitionally turbulent regime can be found, for example in the ascending aorta (Stein and Sabbah 1976). In contrast, the transition from primary to secondary flow, in which there are components of the velocity perpendicular to the main direction of the flow, is highly prevalent. The aortic arch, the artery with the strongest curvature in the arterial system, is susceptible to secondary flow structures such as Dean vortices. 3D MRI velocity measurements performed by Kilner et al. (1993) showed secondary flow patterns occurred during late systole in the upper aortic arch region with some cases of helical flow in the descending aorta, this varied between patients and on the degree of curvature. It is thought that these types of structures can affect wall shear stresses and contribute to the initiation and progression of arterial diseases such as atherosclerosis (Evegren et al. 2010; Vincent et al. 2011). Atherosclerotic plaque and lesions tend to aggregate in regions of high curvature (Caro et al. 1969; Shahcheranhi et al. 2002), and regions of low shear and oscillatory shear stresses (Cecchi et al. 2011). To reopen the lumen in severe cases, stents may be introduced and these generate secondary flow structures caused by curvature (Glenn et al. 2012). In bypass grafts, secondary flows are beneficial for mixing to prevent thrombosis and neointimal hyperplasia (Cookson et al. 2019). Flow in blood-contacting medical devices is also often turbulent, with the transition to turbulence likely influenced by blood rheology (Biswas et al. 2016; Antiga and Steinman 2009; Kelly et al. 2020). Ventricular Assist Devices (VADs) may have even stronger secondary velocity components due to the high geometric curvature and rapid rotation of the mechanical components. The fluid shear stress hot spots generated contribute to haemolysis, platelet activation, protein degradation and thrombosis (Fraser et al. 2012; Molteni et al. 2018).

This work investigates the effects of the rheological properties of blood analogues and blood with varying haematocrits in the primary and secondary flow regimes in cone-plate rheometry. The experiments were complemented by numerical modelling of the flow using two rheology models; a Newtonian and a Carreau-Yasuda model, to identify further features of secondary flow in non-Newtonian blood and to compare with experimental observations.

Experimental materials and methods

Theory

Rotational rheometry is one of the most widely used methods for understanding blood rheology. Typically, steady shear viscosity measurements using rotational rheometry are performed in what can be termed a primary flow regime. In this regime, the flow field is concentric and tangential, and it is here where the shear-thinning nature of the blood can be observed. However, when measuring fluids at higher shear rates, secondary velocity components imposed on the primary flow field can arise, resulting in a change in the flow field patterns.

The onset of the secondary flows in rheometry has been experimentally observed by an increase in relative torque, \(T_R\). This is defined as the ratio of the measured torque, T, and the torque assuming laminar/primary flow, \(T_L\). Using three different Newtonian fluids (water, n-hexane and aqueous sucrose solution), Cheng (1968) confirmed the range in which secondary flow behaviour causes changes to the torque, and consequently viscosity measurements (apparent shear-thickening). This was in line with the theoretical analysis conducted by Walters and Waters (1968).

Ellenberger and Fortuin (1985) explored the relationship further using both cone-plate and parallel plate rheometers. Experiments showed that secondary flow is not present when R* \(< 1\) for both rheometers, where R* is a modified Reynolds number, Eq. 1.

$$\begin{aligned} \text {R{*}} = \frac{\omega h^2}{\nu } \end{aligned}$$
(1)

Following Ellenberger and Fortuin (1985), we refer to this Reynolds number as a modified Reynolds number as it takes into account the fluid gap height, h, as the characteristic length, as opposed to the radius of the cone/plate. \(\omega \) is the angular velocity of the rotating component, and \(\nu \) is the kinematic viscosity of the fluid. Ellenberger and Fortuin (1985) also found two empirical relationships for the cone-plate and parallel plate to describe the relationship between \(T_R\) and R*, showing that the relative torque was a function of R*.

Further investigations of secondary flow in cone-plate flow by Sdougos et al. (1984) found the upper limit of a modified Reynolds number, \(\tilde{\textrm{R}}\), whereby secondary flow transitions into a turbulent state. For small cone angles, \(\alpha \), the surface shear stress on the cone rotating at an angular velocity, \(\omega \) is given by Eq. 2 where \(\mu \) is the viscosity of the fluid. The viscous contributions (Eq. 3) and centrifugal forces (\(\rho \omega ^2 R\)). Hence, the ratio between the centrifugal and viscous forces yields the modified Reynolds number in Eq. 4. A factor of 12 is used to enable an order of unity for the non-dimensionalised velocity components and allows a true measure of the degree of secondary flow. Readers are referred to Appendix A in Sdougos et al. (1984) for further derivation and explanation.

$$\begin{aligned} \tau = \frac{\mu \omega }{\alpha } \end{aligned}$$
(2)
$$\begin{aligned} \mu = \frac{\tau }{h} = \frac{\tau }{\alpha R} \end{aligned}$$
(3)
$$\begin{aligned} \tilde{\textrm{R}} = \frac{\omega R^{2}\alpha ^2}{12\nu } \end{aligned}$$
(4)

Indication of the secondary flow regime was verified using the \(T_R\) criteria, however using a different definition of Reynolds number \(\tilde{\textrm{R}}\), Eq. 4. The development of secondary flow is indicated to occur at \(\tilde{\textrm{R}}\) = 0.5. They additionally demonstrated through the use of a flow dye tracer that streamlines divert inwards towards the center of the cone when secondary flow begins, whereas flow is tangential and concentric in the primary flow regime. The transition to turbulence occurs at \(\tilde{\textrm{R}}\) \(\ge \) 4, with turbulence fronts beginning to form from the free surfaces and progressing to the center.

Numerical solutions of the development of secondary flows in the parallel plate viscometer initially began with the work of McCoy and Denn (1971). Using the finite difference method, the formation of a vortex was identified at the edge of the free surface. An increase in the radius-gap ratio found that the vortex changes form; however, this was not observed experimentally by Griffiths et al. (1969). Fewell and Hellums (1977) also explored the changes in torque and strain rate at varying cone angles to provide an analytical expression for the effects of secondary flow on the rate of deformation tensor.

In viscoelastic fluids, secondary flow instabilities may be found even in the absence of inertia; above a critical Deborah Number, elastic spiral instabilities can exist in cone-plate flow, as observed by Mckinley et al. (1995)

Preparation of blood analogues and whole blood

Samples of both a Newtonian and a shear-thinning blood analogue were prepared through the procedure used in Brookshier and Tarbell (1993); Walker et al. (2014). Table 1 shows the concentration of distilled water, glycerol and xanthan gum used to produce these blood analogue fluids. These fluids had rheology relevant to whole human blood at 45% haematocrit.

Table 1 The concentration of distilled water, glycerol and xanthan gum for the formulation of Newtonian and shear-thinning blood analogues
Full size table

Equine blood was obtained from a microbiological supplier (TCS Biosciences Ltd, Buckingham, UK) and pre-treated with acid-citrate-dextrose (ACD) as the anticoagulant. As described by the supplier for the equine blood, blood was collected by venepuncture into collection bags, and defibrinated by gentle mechanical agitation. Measurements of the packed cell volume (PCV) and sterility were also performed before dispatch. Experiments were conducted over a span of three days, and when the blood was not in use it was refrigerated at 4\(^{\circ }\)C, with any preparation of RBCs performed at room temperature.

Prior to experiments, the blood vials were gently agitated for homogeneity of RBCs and plasma and then treated with two prophylactic pharmaceutical compounds to prevent any bacterial and fungal growth within the samples. These were 1 mL Antibiotic-Antimycotic solution 100 × (Gibco, Fisher Scientific) and 5 mg Gentamycin (Gibco, Cascade Biologics), per 100 mL.

The PCV of the samples was measured using a Sigma 1–14 Microfuge (Sigma Centrifuges, Sigma Laborzentrifugen GmbH) with the microhaematocrit rotor. Samples were run for 5 mins at 13,000 rpm/RCF 11,903 × g. This was first used to confirm whether the correct PCV was observed, as described by suppliers, and would also indicate if lysis had occurred during transportation. Adjustment of haematocrit was achieved through centrifugal separation of the RBCs and plasma. Blood was aliquoted into 3 mL centrifuge tubes and centrifuged using a 24 fixed-angle rotor. Samples were spun at 1500 × g for 5 mins, as recommended by Baskurt et al. (2009). The RBCs were separated into separate vials, and autologous plasma was used to adjust the haematocrit. Haematocrit samples ranging from 24 to 65% were prepared, and a haematocrit test was performed to verify the PCVs. The blood samples obtained were divided into three haematocrit ranges; 24–30%, 40–50% and 60–65%. Samples of equine plasma were also aliquoted.

Steady shear and secondary flow experiments

Rheometry tests were performed using two rheometers. A TA Instruments DHR2 rheometer (TA Instruments Ltd, DE, USA) and a Bohlin Gemini 200 (Malvern Panalytical Ltd, Worcester, UK). Two types of tests were performed with both rheometers, steady shear viscosity and primary-secondary flow tests.

For blood analogue samples, steady shear tests were performed using both 40 mm\(/2^{\circ }\) (with TA Instruments rheometer) and 60 mm\(/2^{\circ }\) (with Bohlin Gemini rheometer) cone-plate geometries. Tests were performed at a fixed truncation gap height, 53µm for 40 mm\(/2^{\circ }\) and 107µm for 60 mm\(/2^{\circ }\). Tests were performed at 25\(^{\circ }\)C controlled through the Peltier plate system. A pre-shear of 20 s\(^{-1}\) was applied before each run, with a shear ramp-up test then performed 0.1s\(^{-1}\)–1000s\(^{-1}\) with three runs performed.

For whole blood samples, steady shear tests were only performed using the 60 mm\(/2^{\circ }\) cone (with Bohlin Gemini rheometer), with 107µm truncation gap height. Tests were performed at 37\(^{\circ }\)C. A pre-shear of 50 s\(^{-1}\) was applied before each run, the ramp-up test settings were the same as those for the blood analogue tests.

Secondary flow tests were performed with steady shear pre-shear settings and a ramp up of angular velocity (\(\omega \)) was performed over a range of \(0.01 \le \omega \le 100\) rad s\(^{-1}\). This is equivalent to a maximum (based upon 60 mm\(/2^{\circ }\) cone) modified Reynolds number range of \(2.75\times 10^{-4} \le {\tilde{\textrm{R}}} \le 2.75\). These tests were also performed at 25\(^{\circ }\)C for analogue fluids, and 37\(^{\circ }\)C for blood. For all steady shear and secondary flow tests performed, the mean and standard deviation of the runs were calculated.

Analysis of data

Steady shear data of shear-thinning blood analog and whole blood were fitted with the Carreau-Yasuda model, Eq. 5. The Carreau-Yasuda model describes the power law region using exponent n, and the transition region, a. The remaining constants are the zero-shear viscosity, \(\mu _0\), the infinite shear viscosity, \(\mu _\infty \), and the time constant, \(\lambda \). The fitting of the models to the experimental data was achieved using non-linear regression from the Curve Fitting Toolbox in MATLAB (MathWorks, MA, USA). R-squared values and RMSE were used as indicators for the quality of fit.

$$\begin{aligned} \mu = \mu _\infty + (\mu _0-\mu _\infty )[1+{(\lambda \dot{\gamma })}^a]^{\frac{(n-1)}{a}} \end{aligned}$$
(5)

For Newtonian fluids, \(T_R\) is the ratio between the actual torque (T) that is obtained from the rheometer and the laminar torque (\(T_L\)), Eq. 6. \(T_L\) is calculated using Eq. 7, where \(\mu _\infty \) is a constant viscosity. To determine \(T_L\) for non-Newtonian fluids, the shear rate dependent viscosity, \(\mu (\dot{\gamma })\), needs to be considered. To calculate this the modelled viscosity from Eq. 5 is combined with a form of the empirical relationship formulated by Ellenberger and Fortuin (1985), Eq. 8. This relationship captures both the primary and secondary flow effects.

$$\begin{aligned} T_R = \frac{T}{T_L} \end{aligned}$$
(6)
$$\begin{aligned} T_{L} = \frac{2\pi \mu _\infty \omega r^3}{3\alpha } \end{aligned}$$
(7)
$$\begin{aligned} T_{R} = 1 + \frac{0.309 R^{*3/2}}{50 + R^{*}} \end{aligned}$$
(8)

The apparent viscosity is the product of the actual viscosity and the relative torque. Then the apparent viscosity of a shear-thinning fluid, modelled with Carreau-Yasuda rheology, in the secondary flow regime, \(\mu _{CY}\), is given by Eq. 9. The material constants are the same for the Carreau-Yasuda model. The final term is the empirical relationship between \(T_R\) and \(\tilde{\textrm{R}}\) generalised from Ellenberger and Fortuin (1985): A and B refer to the two model constants that described the secondary flow torque behaviour. These were found by fitting the equation to the steady shear data. \(\mu _{CY}\) was then used in place of \(\mu _{\infty }\) in Eq. 7 to then find the laminar torque, \(T_{L}\).

$$\begin{aligned} \mu _{CY} \!=\!\left( \mu _\infty + (\mu _0-\mu _\infty )[1+{(\lambda \dot{\gamma })}^a]^{\frac{(n-1)}{a}} \right) \! \left( 1 + \frac{A\tilde{R}^\frac{3}{2}}{B + \tilde{R}} \right) \end{aligned}$$
(9)
Fig. 1
figure 1

Diagram of cone-plate apparatus and the fluid domain modelled. (a) Cone-plate apparatus used for shear rheometry (b) Simplified computational domain and boundaries used for numerical simulations

Full size image

Numerical methods

Governing equations

For an incompressible, Newtonian fluid, the governing Navier–Stokes equations are Eqs. 10 and 11. In these equations, \(\textbf{u}\) is the velocity vector, p is the pressure, \(\nu \) is the kinematic viscosity, \(\varvec{\uptau }\) is the viscous stress tensor and \(\textbf{f}\) are additional body forces.

$$\begin{aligned} \nabla \cdot \textbf{u} = 0 \end{aligned}$$
(10)
$$\begin{aligned} \frac{D\textbf{u}}{Dt} = \frac{\partial \textbf{u} }{\partial t} + (\textbf{u} \cdot \nabla )\textbf{u} = -\nabla \frac{p}{\rho } +\nabla \cdot \varvec{\uptau } + \textbf{f} \end{aligned}$$
(11)

For a generalised Newtonian fluid (GNF), the stress tensor can be described by Eq. 12, where the kinematic viscosity is a function of \(\dot{\gamma }\), which is the second invariant of the rate of strain tensor, \(\textbf{S}\), Eq. 14. For a Newtonian fluid, the viscosity is constant, whereas for other GNFs the functions are modelled using constitutive laws, with the mathematical forms dependent on the nature of the fluid.

$$\begin{aligned} \varvec{\uptau } = 2\rho \nu (\dot{\gamma })\textbf{S} \end{aligned}$$
(12)
$$\begin{aligned} \dot{\gamma } = \sqrt{2\mathbf {S:S}} \end{aligned}$$
(13)
$$\begin{aligned} \textbf{S} = \frac{1}{2}(\nabla U +(\nabla U)^T) \end{aligned}$$
(14)

Flow domain and numerical approach

The fluid confined between the rotating cone and the stationary plate system, as seen in Fig. 1a, was modelled from the dimensions and parameters of the experimental procedures in the “Steady shear and secondary flow experiments” section.

Due to the symmetrical nature of the flow field, a 1/8th sector of the fluid (the light grey region in Fig. 1a) was generated, as opposed to the whole flow domain. This reduced computational time and resources; allowing a more thorough investigation of primary and secondary flow regimes. This simplification of the geometry was also implemented by Lygren and Andersson (2001) for DNS simulations of cone-plate flow. A model of whole cone-plate flow was simulated at \(\tilde{\textrm{R}}\) = 12 with the relative torque compared to the simplified geometry to ensure the validity of the symmetrical simplification. The modelled computational domain consists of five boundaries, the “cone”, “plate”, “air interface”, “front” and “back”, as indicated in Fig. 1b.

A multiblocks method using hexahedral cells was used to discretize the flow domain with a grid resolution study performed on five meshes increasing both the local refinement and the number of cells for the model. The number of cells in the three principal coordinate directions, radial (r), azimuthal (\(\theta \)) and circumferential (\(\phi \)) and the dimensionless wall distance for the equivalent directions, (\(r^+\)), (\(\theta ^+\)) and (\(\phi ^+\)) are outlined in Table 2. The grid resolution study was performed at a specified modified Reynolds number \(\tilde{\textrm{R}}\) = 12. The relative torque, \(T_R\), was used to monitor grid convergence which was then compared to experimental data provided by Ellenberger and Fortuin (1985).

The governing equations for GNFs were solved using the open-source finite volume CFD code OpenFOAM v5 (Weller et al. 1998). A rotating wall velocity boundary condition was applied to the “cone” boundary at specified angular velocities, with no-slip boundary conditions applied to the stationary “plate” to give zero velocity. Rotational periodic boundary conditions were applied to the “front” and “back” boundaries for continuous flow through. On the outer “air interface”, a zero-shear stress (slip) boundary condition was applied.

Using Gaussian integration discretisation schemes, the temporal terms were discretised with a transient second-order, implicit, unbounded 2-step Adam Bashforth method with a minimum time-step of \(1\times 10^{-6}\) s. This timestepping method ensured the Courant number (Co) < 0.5 for all models. Convective and pressure terms were discretised using second-order unbounded schemes with the Pressure-Implicit Splitting of Operators (PISO) algorithm used for pressure–velocity coupling. The number of correctors for solving the pressure equation within one timestep was set to two for Newtonian, and increased to four for the shear-thinning models. Where non-orthogonality and aspect ratios were high, the pressure equation was corrected an additional two times.

Table 2 Grid resolution study was performed using five meshes for the cone-plate model
Full size table

Rheological models

Fig. 2
figure 2

Mean steady shear viscosity measurements of shear-thinning blood analogues with Carreau-Yasuda (CY) with error bars representing the standard deviation for each dataset. Experimental human blood data Shalak et al. (1980) (red diamond)

Full size image
Table 3 Carreau-Yasuda material constants and goodness of fit obtained for the shear-thinning blood analogue using different cone diameters
Full size table

Two constitutive rheology models were used in the numerical models. These were a Newtonian and a shear-thinning model described by the Carreau-Yasuda model. The model follows Eq. 5, with infinite shear rate viscosity \(\mu _{\infty } = 3.5\) mPa \(\cdot \) s, zero-shear rate viscosity \(\mu _0= 0.25\) Pa \(\cdot \) s, time constant, \(\lambda =25\) s, power law index \(n=0.25\) and transition constant \(a = 2\). These material constants were used by Cho and Kensey (1991) for studying blood flow in diseased arteries.

Analysis of data, solving and postprocessing

The computed torque on the cone was calculated by integrating the time-averaged wall shear stress (\(\overline{\tau _{r\theta }}\)) across the radius of surfaces, Eq. 15.

$$\begin{aligned} T = 2\pi r^2\int _{0}^{r} \overline{\tau _{r\theta }}~ dr \end{aligned}$$
(15)

This calculation was done as a post-processing step to find the relative torque, \(T_R\), which was computed as the ratio between actual/computed torque (T) and the laminar/primary flow torque (\(T_L\)) given by the Eq. 7.

In total, 18 simulations were performed at varying \(\tilde{\textrm{R}}\) within the primary and secondary flow regimes, with two rheological constitutive models. Simulations were carried out using HPC services Balena at the University of Bath (2.6GHz, 8 cores Intel Xeon E5-2650v2 series processors) and the GW4 Isambard Tier-2 HPC facility, a Cray XC50 system (32-core Marvell ThunderX2 processors running at 2.5 GHz series processors). Due to the potential for transient-turbulent effects at higher \(\tilde{\textrm{R}}\), all simulations were performed for more than 20 rotations, in which statistical averaging was gathered after 10 rotations for temporal flow analysis. Postprocessing was performed using Tecplot 360 EX 2017 R2 (Tecplot, WA, USA), and quantitative analysis was performed using MATLAB R2019b (MathWorks, MA, USA). Numerical data are presented using the normalised expressions, the normalised radial velocity, Eq. 16 and the normalised fluid height, Eq. 17.

$$\begin{aligned} \tilde{u_r} = \frac{u_r}{\omega r} \end{aligned}$$
(16)
$$\begin{aligned} \tilde{z} = \frac{z}{h} \end{aligned}$$
(17)

Results and discussion

Experimental results

Steady shear measurements

Steady shear viscosity measurements of the Newtonian and shear-thinning blood analogues formulated from Table 1 are shown in Fig. 2. The steady shear viscosity has very similar behaviour to human whole blood, with the shear-thinning nature of blood being replicable. The Carreau-Yasuda model fits of the shear-thinning analog are shown in Table 3 for two cone-plate geometries. In general, there is good agreement of steady shear measurements of the shear-thinning blood analogue compared to human blood at 45% haematocrit between cone radii. Compared to Shalak et al. (1980), variations in the zero-shear rate viscosity are much greater. While there was some variability at the low shear — as indicated by the standard deviation error bars — the results were in agreement with published data for human blood (Shalak et al. 1980).

Fig. 3
figure 3

Average steady shear viscosity of equine blood at 30% (black circles), 45% (black squares) and 62% (black diamond) haematocrits. Experimental measurements performed by Windberger et al. (2019) at 30% (red solid line), 50% haematocrit (red fine dashed line) and 60% (red coarse dashed line)

Full size image
Fig. 4
figure 4

Grid resolution study and comparison of the mean radial profile of the symmetry simplification. (a) Mesh sensitivity measured by the relative torque (\(T_R\)) (b) Mean radial profile of 1/8th and whole cone models

Full size image

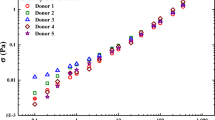
Mean steady shear viscosity measurements of equine blood at haematocrits 30%, 44% and 62% (at T = 37\(^{\circ }\)C) are shown in Fig. 3. Shear-thinning behaviour is apparent at all haematocrit levels; slight variability is noticeable between both horses and haematocrit, however, this is not significant. Measurements by Windberger et al. (2019) of equine blood across the range of haematocrit levels show reasonable agreement with the steady shear measurements at the higher haematocrit values (27% and 30%). There is very good agreement between 10 and 100 s\(^{-1}\) with a loss of agreement at values \(\le \) 10 s\(^{-1}\), resulting in higher \(\mu _0\) compared to published data. Overall a very good agreement in the average steady shear viscosity measurements of equine blood at all haematocrits across several horses can be seen when compared to published data by Windberger et al. (2019). This was also the case for the extreme haematocrit levels, 62%. In some cases, particularly at 45% haematocrit, the low shear experienced larger viscosity variations than the higher haematocrit range.

These variations can be associated with a combination of experimental errors caused by the low torque resolution of the rheometer and sample distribution of RBCs. Windberger et al. (2019) used double gap cylinders to perform these tests, which have greater accuracy at the low shear rates, compared to the cone-plate used in this study. A pre-shear was applied to the samples before each run to homogenise and resuspend the samples, in the case of sedimentation, however, the shear stress was fixed for all haematocrits. Increasing this for higher haematocrits may homogenise the suspension in the cone-plate device better, allowing a reliable low-shear measurement.

Numerical results

Numerical validation

The results obtained from the five meshes generated shown in Table 2 are plotted in Fig. 4. The relative torque (\(T_R\)) was used as the parameter to study the optimal gird resolution performed at \(\tilde{\textrm{R}}\) = 12 using the Newtonian blood rheology model. These Reynolds numbers are beyond the secondary flow regime and should indicate turbulent flow (Sdougos et al. 1984), ensuring the mesh study is beyond sufficient for the studied flows. To evaluate the mesh sensitivity, a subset of relative torque experimental data conducted by Ellenberger and Fortuin (1985) is compared.

There was a 0.175% difference between the empirical relationship and finest mesh (M5) for cone-plate DNS data. \(T_R\) at \(\tilde{\textrm{R}}\) = 12 found by Ellenberger and Fortuin (1985) was 3.74, compared to M5, the difference was slightly greater than the empirical relationship with a difference of 0.391%, with this increasing to 0.705% for M4. The absolute difference was less than 0.314% between M4 and M5, due to this slight difference, M4 was deemed the appropriate mesh density.

The influence of symmetrical simplification was examined by modelling the whole cone. For the whole cone, \(T_R\) was 3.79, whilst for 1/8th it was 3.77, a difference of 0.529%. While the mesh for 1/8th was \(1 \times 10^6\) cells, the whole cone was \(4 \times 10^6\). This simplification was significant in terms of reducing computational resources, allowing a greater number of operating points \(\tilde{\textrm{R}}\) to be solved. Figure 4b shows a comparison of the mean radial velocity profile (\(u_r\)) in the flow domain at \(\tilde{\textrm{R}}\) = 12 for the whole cone geometry and 1/8th of the geometry. The differences in the mean radial velocity profile between the simplification and the whole geometry were minimal. Slight deviations are noticeable towards the rotating cone, when \(\tilde{z} > 0.8\), with the stationary plate and core region having excellent agreement.

Fig. 5
figure 5

Mean radial velocity profiles and flow streamline angle for Newtonian and Carreau-Yasuda models. (a) Mean radial velocity profiles for Newtonian (black) and Carreau-Yasuda (grey) models. Newtonian radial profiles are difficult to see because the lines match very closely to the Carreau-Yasuda radial velocity profiles (b) Flow streamline angle for Newtonian (black) and Carreau-Yasuda (grey) models. Experimental measurements (red) by Sdougos et al. (1984)

Full size image

Secondary flow features

The mean radial velocity profiles for Newtonian and Carreau-Yasuda models are shown in Fig. 5a. These were taken from a mid-plane slice at a radial position \(r = 0.018\)m from the stationary plate surface, \(\tilde{z}\) = 0, to the cone surface, \(\tilde{z}\) = 1. As expected, in primary flow, the radial components are negligible, while increasing \(\tilde{\textrm{R}}\) produces symmetrical flow at the top surface of the cone through to the stationary side for low \(\tilde{\textrm{R}}\). Radial outflow occurs at the rotating side, whilst radial inflow is seen at the stationary plate. As \(\tilde{\textrm{R}}\) is increased into the secondary flow regime, asymmetrical flow occurs, whereby the velocity is greater towards the upper cone surface and is noticeable with a lower velocity at the bottom plate. As clearly seen from the plot, there are no significant differences between rheology models based on these profiles.

For purely laminar flow, streamlines appear to be concentric around the central axis of the cone. Figure 5b shows the angle of the flow streamlines as \(\tilde{\textrm{R}}\) from the primary flow regime through the secondary flow, and further. As expected, no significant changes to the streamline flow angle at the low Reynolds number, where the fluid flows tangentially. Comparing with Sdougos et al. (1984), we see that the largest angle observed peaks at approximately \(\tilde{\textrm{R}}\) = 1.5, with a value of −55 \(^{\circ }\). In comparison, the numerical simulation shows that a peak occurs at \(\tilde{\textrm{R}}\) = 4 with a value of −45 \(^{\circ }\) (negative sign indicates the flow streamline diverts inwards towards the cone centre). Interestingly, this is where the turbulent flow regime begins (Sdougos et al. 1984). In the numerical solutions, the velocity was monitored at a radial position equivalent to that used for dye tracer injection by Sdougos et al. (1984). The trough that appears could be indicative of another transition process.

Fig. 6
figure 6

Secondary flow features in the primary and secondary flow regimes for Newtonian (N) and Carreau-Yasuda (CY) models. (a) Radial vortex in \(r - \phi \) plane visualised by mean velocity for Newtonian (N) and Carreau-Yasuda (CY) models (b) Secondary flow streamlines in \(r - \theta \) plane visualised by mean velocity for Newtonian (N) and Carreau-Yasuda (CY) models

Full size image

For both the Newtonian and the Carreau-Yasuda numerical models, secondary flow effects are most dominant between \(\tilde{\textrm{R}}\) = 1 – 4 where the flow streamline angle at the stationary side reached the minimum angle of \(-43 ^{\circ }\) at \(\tilde{\textrm{R}}\) = 4 for both rheologies. The radial mean velocity profiles in Fig. 5a indicate a change in flow structure in the high secondary flow regime (\(\tilde{\textrm{R}}\) = 4). The low radial velocity which exists in the central region of the cone fluid domain is analogous to Batchelor flow (Poncet et al. 2005). In this type of flow, it was identified that two boundary layers begin to form, one on the rotating side and the other on the stationary side and a resulting zero-velocity core is formed. At lower \(\tilde{\textrm{R}}\), the outflow velocity and inflow radial velocity are somewhat symmetrical; however, as the central vortex breaks downs, asymmetry occurs, causing a greater radial outflow.

Figure 6a shows the development of vortical structures in the (r, \(\phi \)) plane for Newtonian and Carreau-Yasuda models. At low \(\tilde{\textrm{R}}\), a single eddy is visible, an indication of the primary flow regime. At \(\tilde{\textrm{R}}\) = 0.5, the single toroidal vortex shape begins to deform, indicating the presence of secondary flow. This vortex tends to increase in size at higher \(\tilde{\textrm{R}}\) values, \(\tilde{\textrm{R}}\) = 4. Here, the vortex elongates from the periphery and elongates inwards towards the centre. Further examination of the vortex at \(\tilde{\textrm{R}}\) = 4, shows slight perturbations of the streamlines at the outer edge (changes in inflection), indicating an apparent transition from the secondary flow field to a different flow regime.

There are also deviations from the smooth circulation motion resulting in the vortex beginning to lose shape, with inflection points developing, indicative of the transition process. The large vortex then moves towards the cone apex, with possible indication vortex breakdown as \(\tilde{\textrm{R}}\) is increased. It was suggested by Einav et al. (1994) that the formation of multiple vortices and significant changes to the radial velocity component was an indication of a transition to turbulence. However, Savins and Metzner (1970) noted that multiple vortices are present in both primary and secondary flow regimes for non-Newtonian fluids, as opposed to the single eddy present in Fig. 6a.

A visualisation of the flow streamlines, has been given in Fig. 6b. As both \(\tilde{\textrm{R}}\) and radial position increase, the streamlines at the centre of the cone begin to divert inwards, indication of secondary flow. This is particularly evident at \(\tilde{\textrm{R}}\) = 2 and \(\tilde{\textrm{R}}\) = 4. No substantial differences in the flow angle are visible when comparing Newtonian and Carreau-Yasuda models.

In this work, the interface between the fluid and air was treated using a slip boundary condition. In reality the shape of this interface and the onset of hydrodynamic instabilities will depend on capillary stresses, viscous stresses, and pressure effects. In future work, these should be accounted for using a normal stress balance.

Fig. 7
figure 7

Comparison of relative torque for the Newtonian model (solid black) and Carreau-Yasuda model (Solid grey). The empirical relationship (dashed black line) and experimental Newtonian data (red squares) by Ellenberger and Fortuin (1985). The inset figure shows the same plot on a linear scale

Full size image

Effect of GNF constitutive model on relative torque

A comparison of the relative torque as a function of the modified Reynolds number for the Newtonian and Carreau-Yasuda models is shown in Fig. 7. Differences between the rheologies can be seen between \(\tilde{\textrm{R}}\) = 0.2 – 3. The shear-thinning rheologies exhibited higher \(T_R\) in this range. Beyond \(\tilde{\textrm{R}}\) = 3, the curves begin to converge together. For the Newtonian model, the primary flow can be defined as existing when \(\tilde{\textrm{R}}\) \( \le 0.5\), beyond this \(\tilde{\textrm{R}}\), secondary flow is present. In the Carreau-Yasuda model, we note the transition occurs earlier between \(\tilde{\textrm{R}}\) = 0.2 – 0.3. The models are also compared to the empirical model developed by Ellenberger and Fortuin (1985) with similar trends in the primary and early secondary flow regimes. At \(\tilde{\textrm{R}}\) = 1, there is a divergence of the empirical model where the secondary flow becomes more dominant.

Comparison of experiments and numerical models: effect of shear-thinning rheology on relative torque

The Newtonian and shear-thinning blood analogues, shown in Fig. 8, demonstrate a similar trend in the transition to secondary flow. In particular, there is very good agreement between the Newtonian numerical model and the Newtonian blood analogue. Although the experimental data does not explore the higher secondary flow \(\tilde{\textrm{R}}\), the distinction between the primary and secondary flow regimes matches up well. The shear-thinning experimental data, however, show some differences when compared to the Carreau-Yasuda numerical results. It appears a transition to secondary flow occurs later than for the numerical model, with a higher \(T_R\) (0.3 < \(\tilde{\textrm{R}}\) < 2) meaning the transition is almost identical to that of the Newtonian fluid.

Fig. 8
figure 8

Comparison of the relative torque for numerical models and experimental blood analogues. Newtonian model (solid black line), experimental Newtonian blood analogue (black circles), Carreau-Yasuda model (solid grey line), and experimental shear-thinning blood analogue. The inset figure shows the same plot on a linear scale

Full size image

Comparison of secondary flow regime of the blood analogue fluids yields slightly higher \(T_R\) compared to the experimental and empirical relationship of Ellenberger and Fortuin (1985). This difference would not influence the secondary flow results which occur at the higher shear rates. Similarly, the numerical models slightly underpredicted \(T_R\). Newtonian blood analogue showed very good agreement with the numerical models when identifying primary flow and secondary flow regimes. On the other hand, the shear-thinning blood analogue showed slight inconsistencies concerning the start of secondary flow and the level of \(T_R\) at intermediate \(\tilde{\textrm{R}}\).

Comparison of experiments and numerical models: effect of RBC concentration on relative torque

The normalised \(T_{R}\) was averaged over all measurements taken at the haematocrits 30%, 45% and 62%. The transition from primary to secondary flow was found to occur at different \(\tilde{\textrm{R}}\) for each haematocrit (Fig. 9). The higher haematocrit range shows an earlier transition occurring at 0.03, whilst lowering the haematocrit caused the transition to occur much later. Since the shear-thinning effects have been accounted, the data is compared to both experimental blood analogues and numerical models and it can be seen that transition is different compared to both the Newtonian and shear-thinning fluids.

These results show there are differences in the transition for blood which neither numerical models or blood analogue fluids capture accurately. The experimental data of equine plasma lies much closer to the numerical models, with the transition occurring later at \(\tilde{\textrm{R}}~\) \( = 0.5\), but this is still earlier than either the numerical models or experimental blood analogue solutions. Despite plasma being considered a single-phase fluid, it has been found to have weakly viscoelastic characteristics (Brust et al. 2013; Varchanis et al. 2018; Rodrigues et al. 2022).

Fig. 9
figure 9

Comparison of the mean relative torque for experimental equine blood measurements and numericals models. Haematocrit 30% (squares), 45% (circle), 62% (triangle), plasma (diamond), Newtonian blood analogue (black circles), shear-thinning blood analogue (grey circles), Newtonian model (black circles) and Carreau-Yasuda model (solid grey line)

Full size image

Conclusion

Cone-plate flow is a standard apparatus for measuring the rheological properties of non-Newtonian fluids taken in the primary flow regime. For blood flow, secondary velocity components are important to consider as they may promote the progression of arterial diseases, and can create concentrated regions of high fluid stresses in blood-contacting devices. This paper has explored the impact of non-Newtonian blood rheology on the development of secondary flow fields in a cone-plate rheometer using experimental and numerical modelling.

Flow in a cone-plate rheometer was studied experimentally, with Newtonian and shear-thinning blood analogues, and with blood with varying haematocrits, and computationally with Newtonian and shear-thinning rheology. Secondary flow was characterised by relative torque, changes in flow angle, distortion of mean velocity profiles and by the development of a single eddy. There were no substantial differences between Newtonian and shear-thinning blood analogue rheologies in either experimental or computational studies. However, comparing equine blood with the GNF’s, showed substantial differences in relative torque in the secondary flow regime. It was found that an increase in haematocrit caused primary-secondary flow transition to occur at lower modified \(\tilde{\textrm{R}}\). This highlights that perhaps RBCs influence behaviour beyond shear-thinning rheology, and modelling the more complex rheological properties such as viscoelasticity, yield stress, thixotropic and multiphase aspects in more detail may yield more meaningful information about their behaviour in primary, secondary and turbulent flow.

These results further confirm the idea that shear-thinning is not the only important rheological property of blood, and going beyond modelling blood as a GNF might be necessary to explain and accurately predict physiological blood flows.