Study of the electroosmotic flow of a structured fluid with a new generalized rheological model

Abstract

The electroosmotic flow of a viscoelastic fluid in a capillary system was investigated analytically. The rheology of the fluid was characterized by a novel generalized exponential model equation. The charge density obeys the Boltzmann distribution, which governs the electrical double-layer field and body force generated by the applied electrical field. Mathematically, this scenario can be modeled by the Poisson-Boltzmann partial differential equation, by assuming that the zeta potential is small, i.e., less than 25 mV (Debye-Hückel approximation). Considering a pulsating electric field, the shear viscosity and the alteration in the volumetric flow were presented as a function of the material parameters through the characteristic dimensionless numbers by using an exponential-type generalized rheological model. Thixotropy, shear thinning, yield stress mechanisms, and weight concentration were analyzed through numerical results. Finally, the flow properties and rheology were predicted using experimental data reported elsewhere for worm-like micellar solution of cetyl trimethyl ammonium tosilate (CTAT). The rheological equation of state proposed in this study describes the alterations in the structure resulting from applied forces (tangential and normal). These forces induced a structural evolution (kinetic model) due to the relaxation processes caused by shear strain. It is important to mention that in electroosmotic flows, complex behavior such as (i) thixotropy, (ii) rheopexy, and (iii) shear banding flow is scarcely explained in terms of the change in the structure of the fluid under flow.

Graphical Abstract

Introduction

Electroosmotic flow (EOF) is the motion of the fluid adjacent to a charged surface due to an externally imposed electric field (Burgreen and Nakache 1964; Levine et al. 1975; Yang and Li 1997; Wang et al. 2007; Berli and Olivares 2008; Afonso et al. 2009, 2013; Ferrás et al. 2016). In EOF, the surface always carries a solution of ions, ensuring an overall charge neutrality. The primary applications of EOF include (i) microflow injection analysis, (ii) microfluidic chromatography, (iii) micro-reactors, (iv) micro-energy, and (v) microelectronic cooling systems and micro-mixing and bio-rheology (physiology of human blood) (Jendrejack et al. 2013; Stone et al. 2004; Wang et al. 2007; Berli and Olivares 2008; Ferrás et al. 2016).

In recent years, electroosmotic flow has become well-established as a micro-pumping technique used in various devices, including the well-known Lab-On-a-Chip (LOC) platforms, intravenous drug delivery systems, and biochemical reactive platforms (Dutta and Beskok 2001; Stone et al. 2004; Das and Chakraborty 2006; Chakraborty and Srivastava 2007; Mahapatra and Bandopadhyay 2020). In this context, electroosmosis is widely employed used to manipulate and control fluid flows in channels with lengths of less than a millimeter. This is achieved through the electrostatic interaction between an external constant and pulsating electric field and electric double layer (EDL) (Stone et al. 2004; Chakraborty 2005; Das and Chakraborty 2006; Chakraborty and Srivastava 2007; Rojas et al. 2019; Vargas et al. 2019; Teodoro et al. 2019). On the other hand, capillary electrophoresis is a technique in which electric fields are used to separate chemical compounds according to their electrophoretic mobility by applying an electric field to a narrow capillary, usually made of silica (Arulanandam and Li 2000; Chakraborty 2005; Das and Chakraborty 2006; Chakraborty and Srivastava 2007). In electrophoretic separations, EOF impacts the elution time of the analyses. It is projected that microfluidic devices utilizing electroosmotic flow will have great application in medical research (Stone et al. 2004). Gaining a better understanding of controlling this flow will be necessary to implement it in drug delivery systems (Stone et al. 2004; Das and Chakraborty 2006; Chakraborty 2007; Chakraborty and Srivastava 2007). Mixing fluids at the microscale is currently challenging. It is believed that successfully controlling fluids electrically will be the method which small volumes of fluid can be effectively mixed (Jendrejack et al. 2013).

Electroosmotic pumping is a crucial mechanism for the transportation and control of fluid flows. Typically, the critical parameters that determine the pumping performance are as follows: (i) the magnitude of the externally applied electrical field, (ii) the cross-sectional dimensions of the microchannel, (iii) the surface charge density of the microchannel surface, and (iv) the ion density and pH of the fluid system (Sánchez et al. 2013; Rojas et al. 2019; Vargas et al. 2019).

One method to enhance the volumetric flow rate in a microchannel is by increasing the magnitude of the applied electrical field. However, this can lead to an increase in the temperature of the fluid as a result of the Joule heating effect, which is undesirable (Sánchez et al. 2013; Rojas et al. 2019; Vargas et al. 2019). Hence, alternative mechanisms must be employed to achieve higher volumetric flow rates. With this objective, another technique for controlling fluid flow involves the utilization of oscillating forces (Rojas et al. 2019; Mederos et al. 2020). The use of time-pulsating force to enhance the volumetric flow has been applied across various scientific fields such as petroleum, oil recovery operations, blood with cholesterol, flexoelectric membranes, and more (Herrera et al. 2009, 2010; Abou-Dakka et al. 2012; Herrera-Valencia and Rey 2014, 2018; Herrera-Valencia et al. 2017). The majority of the approaches have been focused in the study of (i) ion distributions, (ii) geometry of the material, and (iii) the rheological nature of the fluid (Hayat et al. 2011; Ali et al. 2020; Mahapatra and Bandopadhyay 2020, 2021). The theoretical analysis of EOF of Newtonian and non-Newtonian fluids in microchannels (slit and capillaries) has been the subject of several mathematical and physical studies (Sánchez et al. 2013; Mederos et al. 2020;). The mathematical techniques used to solve these equations involve, among others, (i) linear ordinary and partial differential equations with different types of boundary conditions (Hayat et al. 2011); (ii) numerical methods, including finite differences, finite element, and finite volume; and (iii) regular and irregular perturbation technique is commonly employed (Rojas et al. 2019).

Rojas et al. (2013, 2019) studied the pulsatile electroosmotic flow in a microcapillary system, considering a slip boundary condition. In their work, they characterized the system using a Newtonian liquid, considering the inertial mechanisms and assuming a symmetric electrolyte and low zeta potential at the wall. Their findings show a significant increase in volumetric flow rate within microchannel when slip occurs at the wall surface and the use of hydrophobic materials emerges as a key factor for the fabrication of microchannels (Rojas et al. 2013, 2019).

Chakraborty and Srivastava (2007) studied the time periodic electroosmotic flows through nanochannels without presuming the validity of the Boltzmann distribution of ionic charges. The charge function is obtained through conservation considerations of the individual species, and their liquid is characterized by the Navier-Stokes equation (Newtonian fluid). The influence of the electric field frequency on the electroosmotic flow was studied as a function of the material parameters.

Dutta and Beskok (2021) obtained analytical solutions for the velocity distribution, mass flow rate, pressure gradient, wall stress, and vorticity in mixed electroosmotic/pressure-driven flows for a two-dimensional straight channel geometry. These solutions are applicable for cases involving small yet finite symmetric electrical double layers (EDL), which are pertinent to scenarios where the distance between the two walls of a microfluidic device is about 1–3 orders of magnitude larger than the EDL thickness.

Bio-fluids are frequently composed of long-chain molecules that induce a non-Newtonian rheological behavior characterized by variable viscosity, memory effects, normal stress effect, yield stress, and hysteresis in fluid properties (Jendrejack et al. 2013; Herrera-Valencia et al. 2019). These fluids are encountered in chips used for chemical and biological analysis or in micro-rheometers (Stone et al. 2004; Das and Chakraborty 2006; Jendrejack et al. 2013). The theoretical research on electroosmotic flows characterized by non-Newtonian fluids has been studied by numerous international research groups. Their works have been focused in the description of the mass, momentum transfer, and rheology, using various inelastic, linear, and non-linear viscoelastic constitutive equations such as (i) power law, (ii) Ellis, (iii) Maxwell, (iv) Jeffrey, (v) Burgers, (vi) Phan-Thien-Tanner (PTT), and (vii) PTTS and FENE-P models (Afonso et al. 2009, 2013; Hayat et al. 2011; Rojas et al. 2017; Ali et al. 2020).

Sánchez et al. (2013) studied the Joule effect on a purely electroosmotic flow of a non-Newtonian fluid in a slit microchannel. Mahapatra and Bandopadhyay (2020, 2021) investigated the electroosmotic pressure-driven flow over a high zeta potential modulated surface and the effect of the fluid relaxation and retardation times. Jiang et al. (2017) studied the slip and transient mechanisms of EOF. The rheology and flow were characterized by the fractional Oldroyd-B constitutive equation. In the same context, Yang et al. (2018) exanimated EOF flow of a fractional Maxwell liquid. They solve their equations using the non-linear conjugate gradient method to fit the viscoelastic parameter. The governing equations were solved through a combination of fully discrete and Legendre and spectral method for time and spatial variables.

Baños et al. (2021) studied the influence of steric and slippage effects on mass transport by using and oscillatory electroosmotic flow of power law fluids. In their research, the hydrodynamics are affected by slippage, where the slip length was used as an indicator of wall hydrophobicity. Their results suggest that the combined effects of slippage and steric promote the optimal conditions for enhancing the mass transport of species.

Thomas and Narayanan (2001) studied the mass transfer through the influence of oscillatory flow and its impact on separation of species. Medina et al. (2018) examined EOF in a microchannel with asymmetric wall zeta potential and its effects on enhancing mass transport and mixing. Peralta et al. (2020) studied the mass transfer trough a concentric-annulus microchannel driven by oscillatory electroosmotic flow of a Maxwell fluid.

Das and Chakraborty (2006) found analytical relationships for velocity, temperature, and concentration profile in electroosmotic microchannel flows of non-Newtonian bio-fluids (human blood) described by the power law model. Their research showed that when the characteristic length scale of RBC suspensions becomes significant in relation to the microchannel dimensions, a considerable augmentation in the electroosmotic transport may occur. In the regime of linear viscoelasticity, the mass transfer through a concentric-annulus microchannel driven by an oscillatory flow of a Maxwell fluid has been reported by Peralta et al. (2020). They reported that the ionic liquid was characterized by the Maxwell constitutive equation, and the Debye-Hückel approximation was employed. Their results suggest that the velocity and concentration distributions across the annular microchannel become non-uniform as the angular Reynolds number increases and depend notably on the elasticity number. It is also revealed that with a suitable combination of values of the elasticity number and gap between the two cylinders, together with the angular Reynolds number, the total mass transport rate can be increased, and the species separation can be controlled. Sadek and Pinho (2019) show analytical solution of electroosmotic oscillatory flow of multimode upper convective Maxwell (UCM) fluids. Their results may allow the quantification of the storage and loss moduli in the linear regime. This technique requires the use of smaller sample sizes than the conventional small amplitude oscillatory test. Afonso et al. (2009) provided analytical solutions for channel and pipe flows of viscoelastic fluids under the combined influence of electro-kinetic and pressure forces using two constitutive models: the Phan-Thien-Tanner model with a linear kernel for the stress coefficient function and second normal stress difference and the kinetic theory. The mean effect of these two isolated mechanisms is the introduction of an additional term in the velocity profile that simultaneously combines both forces. This term is absent in Newtonian fluids where the superposition principle applies. This extra term can contribute significantly to the total flow rate. Dhinakaran et al. (2010) studied the electroosmotic flow of a PTT fluid between parallel plates. The PTT rheological equation of state uses the Gordon-Schowalter convected derivative, resulting in a non-zero second normal stress difference in pure shear flow. To characterize the electrical double layer, a non-linear Poisson-Boltzmann equation was employed. Equations for critical shear rates and maximum electrical potential of a steady fully developed flow as function of the material properties were obtained. Afonso et al. (2013) expanded their previous study to encompass the flow of viscoelastic fluids (using the PTT model) under asymmetric zeta potential forcing, whereas de Souza Mendes (2011) examined the analysis in a microchannel flow of viscoelastic fluids by combined electroosmosis and pressure gradient mechanisms. In their research, they explored the effect of the skimming layer and the electric double layer (EDL). The derived analytical solutions are dependent of the combined effects of fluid rheology, the ration forcing strengths, the skimming layer thickness, and the relative rheology of the two fluids. In addition, some authors have explored the behavior of viscoelastic fluids and biological complex fluids in complex geometries using finite element analysis and interaction-particle-fluid, porous media in an electro-magneto hydrodynamic pulsatile flow of a Jeffrey in a constricted fluid under periodic acceleration body (Ponalagusamy and Kawahara 1989; Ponalagusamy and Kawahara 2023; Ponalagusamy and Ramakrishna 2021; Ponalagusamy and Sangeetha 2023). Most of the applications of pure and pulsatile electroosmotic flows involve fluids with complex structural when subjected to driving forces (de Souza Mendes 2011). These behaviors involve interactions within the internal structure formed by links, bonds, or entanglements which are related to the structure complexity of the system. These interactions are associated to the macroscopic properties of fluid, i.e., viscoelasticity (de Souza Mendes 2011; Castillo and Wilson 2018). Mathematical models that consider the kinetics of build-up and break down in a complex fluid structure have been used to model various complex fluids such as (i) liquid crystal dispersions; (ii) blood with low, medium, and high cholesterol levels; (iii) surfactant solutions; (iv) worm-like polymer solutions; and (v) liquid crystals (De Andrade Lima and Rey 2006; De Andrade Lima and Rey 2005). Surfactant solutions have been employed as rheological modifiers in coating process, thin films, and oil recovery operations (Castillo and Wilson 2018; de Souza Mendes 2011). On the other hand, viscoelastic surfactants are characterized by an entangled network of large surfactant-worm-like micelle structures (Zhang et al. 2021; Herrera-Valencia et al. 2017; Castillo and Wilson 2018; de Souza Mendes 2011). These structures break and reform during flow, exhibiting diverse and rich rheological behavior. The prediction of flow behavior in viscoelastic surfactants using constitutive equations has been a challenging matter (Castillo and Wilson 2018). These systems exhibit Maxwell-type behavior in small-amplitude oscillatory, shear flow, and saturation of the shear stress in steady simple shear, which leads to shear banding (Castillo and Wilson 2018). In the non-linear viscoelastic regime, elongated micellar solutions also exhibit remarkable characteristics. These include the prediction of a stress plateau in steady shear flow past a critical shear rate, accompanied by a gradual steady state (Herrera-Valencia et al. 2017). They serve a test to new constitutive equations, and this aspect motivates the present paper. This work focuses on describing the EOF using an exponential generalized thixotropic elasto-viscoplastic-banded model for structured fluids. In the literature, there are a few studies concerning the impact of structured fluids on pulsating electroosmotic flow and the flow enhancement. For example, (i) in the regimen of linear viscoelasticity, what is the role of the thermal electric forces over the relation, retardation, and geometry characteristic times? (ii) In the regimen of non-linear viscoelasticity, what is the importance of the kinetic-structural and viscoelasto-plastic mechanisms (thixotropy and Rheopexy) in the electro-rheological response? To answer these open questions, the main objectives of this original research are as follows:

• (a) To analyze the rheology and flow behavior of a structured fluid exposed to an externally applied time-pulsating electric field within a microchannel

• (b) To derive analytical expressions for shear stress, first and second normal stress difference, shear strain, axial velocity, and volumetric flow

• (c) To analyze the mechanisms of shear thinning, shear thickening, thixotropy, and yield stress through characteristic dimensionless groups associated with each mechanism

• (d) To study the effect of the surfactant concentration on dimensionless numbers and the dynamic equations, using rheometric data from an aqueous worm-like micellar solution (cetyl trimethyl ammonium tosylate)

This paper is organized as follows (Fig. 1): The “Introduction” section introduces the problem and reviews prior work. The “Governing Equations” section introduces the new generalized exponential model, discussing its mathematical and physical properties. The formulation of the problem, along with the introduction of non-dimensional variables, is presented in the “Mathematical modeling of EOF” section. The “Dimensionless theoretical equations” section proposes the solution methodology, and analytical results are detailed in the “Results” section. The final sections includes the discussion of the results, concluding remarks, and the proposed directions for future work.

Fig. 1

Flowchart depicting the organization of the paper

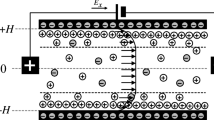
Physical description of the problem

The schematic representation of the considered geometry is shown in Fig. 2. Here, a symmetric (z:z) viscoelastic structure electrolyte in a circular microchannel with a hydrophobic surface with uniform zeta potential, ψ_a, is considered. The length of the microchannel, L, is much greater than radius r = a. The isothermal rectilinear flow is driven by pulsatile electroosmotic force; this was induced by the simultaneous effect of the EDL formed at the interface between the liquid and the microchannel surface and the sudden imposition of an external time-dependent electric field, given by:

$$\textbf{E}(t)={\textbf{E}}_0+{\textbf{E}}_1={\textbf{E}}_0\left(1+\updelta n(t)\right)$$

(1)

Fig. 2

Charge distribution at the wall when the electric field is applied in the axial direction

In Eq. (1), δ is a small perturbation parameter, and n(t) is an oscillatory function, which is a subclass of noise of the random stochastic functions. This function represents the change of the electrical field as a function of time, which can be expressed in terms of a simplest oscillatory function.

$$n(t)={a}_1+{a}_2\mathrm{Sin}\left(\upomega t\right)$$

(2)

In Eq. (2), {a₁, a₂} are the amplitudes of the oscillatory function, ω is the frequency, and t is the process time. A 2D cylindrical geometry coordinate system (r, z) is adopted, in which the origin is placed at the lower left end of the capillary geometry. Additionally, the following assumptions are made: (i) The viscosity is proportional to the number of links, bonds, or entanglements. So, the change of the viscosity is due to the construction and destruction of the microstructure. (ii) The Debye length, denoted by λ_D = (k_BT2⁻¹/2e²z²n_∞ε⁻¹)^1/2, is much smaller than r₀, i.e., L_D/r₀ <<1; here, ε, k_B, T, e, z, and n_∞ denote the dielectric permittivity of the solvent, the Boltzmann constant, the absolute temperature, the elementary charge, and the valence and bulk concentrations, respectively. (iii) The net charge density in the EDL follows the well-known Boltzmann distribution, which remains valid if the frequency of the external electric field is not very high (e.g., less than 1 MHz) (Teodoro et al. 2019; Sánchez et al. 2013).

Governing equations

Mass conservation and momentum equations

The governing equations describing the physical system include the mass balance equation without chemical reaction and the Cauchy equation (Byron Bird et al. 1987; Herrera-Valencia et al. 2017):

$$\frac{{\partial \rho }}{\partial t}+\nabla \cdot \left(\rho \textbf{v}\right)=0\kern0.5em$$

(3)

$$\frac{\partial }{\partial t}\uprho \textbf{v}=-\nabla \cdot \textbf{T}+{\uprho}_{\mathrm{e}}\textbf{E}(t)$$

(4)

$$\textbf{T}=\left(p+\uprho {\Phi}_{\mathrm{e}}\right)\textbf{I}+\uprho \left(\textbf{v}\otimes \textbf{v}\right)-\boldsymbol{\upsigma}$$

(5)

In Eq. (3), ρ is the density of the liquid, ∇ is the spatial nabla operator, v is the velocity vector, ∂/∂t time partial derivative, T is the total stress tensor, p is the scalar pressure, Φ_e is the gravitational scalar, σ is a viscoelastic stress tensor, E(t) is the input electrical field, and ρ_e is the electric charge density of the liquid.

Constitutive rheological equation

The proposed exponential model is a generalized exponential thixotropic-elasto-viscoplastic-banded model, chosen for this study due to its capacity of predicting non-Newtonian/complex behavior such as (i) shear thinning, (ii) shear thickening, (iii) yield stress, (iv) thixotropy, (iv) rheopexy, and (v) shear banding flow behavior. The exponential rheological equation of state model is defined by the following class of exponential Phan-Thien type models, which contains several particular cases exposed in the literature: (i) exponential Phan-Thien-Tanner model, (ii) Boek model, (iii) generalized PTT model with Mithas special function (Ferrás et al. 2019), and (iv) a more general constitutive equation (Ferrás et al. 2019; Ribau et al. 2021).

$$\Phi \left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\boldsymbol{\upsigma} +\frac{1}{\upvarphi_{\infty }{G}_0}\overset{\nabla }{\boldsymbol{\upsigma}}+\frac{\uplambda_{\mathrm{c}}}{\upvarphi_{\infty }{G}_0}{f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\frac{\partial }{\partial t}\overset{\nabla }{\boldsymbol{\upsigma}}=\frac{2}{\upvarphi_{\infty }}\left(\ \textbf{D}+{\uplambda}_{\mathrm{c}}{f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\frac{\partial \textbf{D}}{\partial t}\right)$$

(6)

where

$$\Phi \left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)=\mathrm{Exp}\left[\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\right]$$

(7)

Equation (6) is a constitutive rheological model for the viscoelastic stress tensor σ and the shear strain tensor D which is the symmetric part of the velocity gradient tensor ∇v; λ_c can be interpreted as a structural interdiffusion time. In Eq. (7), f_D is the relaxation function which depends on the irreversible work to break down the structure, according to

$${f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)=\mathrm{Exp}\left[\hbox{-} \upbeta tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right]$$

(8)

Equation (8) can be interpreted as activation energy for the flow. It is the energy necessary to change the system from a higher to lower structure state under flow.

$$\upbeta ={\upbeta}_0\mathrm{Exp}\left[{\uplambda}_{\mathrm{B}}{\mathrm{II}}_{\mathrm{D}}\right]$$

(9)

In Eq. (7), the material parameters are defined as follows: (i) fluidities at low and high shear rates {φ₀, φ_∞}, respectively. In Eq. (6), λ_c << λ₀ is a Jeffrey’s relaxation time, which is a measure of the retardation mechanisms. G₀ is the elastic shear modulus which is a measure of the elasticity in shear flow. The parameter β was studied by Herrera-Valencia et al. (2017, 2019) and Castillo and Wilson (2018), and it can be interpreted as the inverse of an irreversible work required to break down the fluid structure. In Eq. (9), λ_B represents the shear banding relaxation time, which causes the system to show bands with different structure and viscosity. To characterize it, rheometric experiments (start-up flow) need to be conducted. In Eq. (6), the upper-convected time derivative $\overset{\nabla }{\boldsymbol{\upsigma}}$ is a measure of the elasticity of the system during large deformations. Mathematically, it is defined by the following expression:

$$\overset{\nabla }{\boldsymbol{\upsigma}}=\frac{D}{Dt}\boldsymbol{\upsigma} -\nabla {\textbf{v}}^{\mathrm{T}}\cdot \boldsymbol{\upsigma} -\boldsymbol{\upsigma} \cdot \nabla \textbf{v}=\left(\frac{\partial }{\partial t}+\textbf{v}\cdot \nabla \right)\boldsymbol{\upsigma} -{\left(\nabla \textbf{v}\right)}^{\mathrm{T}}\cdot \boldsymbol{\upsigma} -\boldsymbol{\upsigma} \cdot \nabla \textbf{v}$$

(10)

And the time substantial derivative:

$$\frac{D}{Dt}\boldsymbol{\upsigma} =\left(\frac{\partial }{\partial t}+\textbf{v}\cdot \nabla \right)\boldsymbol{\upsigma}$$

(11)

In Eqs. (10) and (11), D is the rate of deformation, given by the following expression:

$$\textbf{D}=\frac{1}{2}\left(\nabla \textbf{v}+{\left(\nabla \textbf{v}\right)}^{\mathrm{T}}\right)$$

(12)

The second invariant of the shear rate tensor is given in terms of the double tensorial product as follows:

$${\mathrm{II}}_{\textbf{D}}=\sqrt{2 tr\left(\textbf{D}\cdot \textbf{D}\right)}$$

(13)

In micellar systems like CETAT and EHAC, a reasonable assumption is that the relaxation structure mechanisms are negligible. This allows Eq. (6) to be simplified as the following simplest analytical form:

$$\Phi \left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\boldsymbol{\upsigma} +\frac{1}{\upvarphi_{\infty }{G}_0}\overset{\nabla }{\boldsymbol{\upsigma}}=\frac{2}{\upvarphi_{\infty }}\textbf{D}$$

(14)

In the case of an inelastic fluid, the contributions of the convective derivatives are set-up or zero, and the following expression is obtained:

$$\mathrm{Exp}\left[\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\right]\boldsymbol{\upsigma} =\frac{2\textbf{D}}{\upvarphi_{\infty }}$$

(15)

Analytical expression can be obtained from the exponential equation, given by Eq. (15). At first order, we have

$$\mathrm{Exp}\left[\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\right]\cong 1+\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)$$

(16)

The second-order contribution results in

$$\mathrm{Exp}\left[\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)\right]\cong 1+\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)+\frac{1}{2!}\left({\upvarphi}_{\mathrm{r}}-1\right){f}_{\mathrm{D}}\left( tr\left(\boldsymbol{\upsigma} \cdot \textbf{D}\right)\right)$$

(17)

The second-order contributions result in a cubic equation for the shear stress and shear rate, and it can be a starting point to study flow instability such as shear banding flow. In the regime of viscoelasticity (small deformations), the rheological equation of state can be further simplified to the well-known Burgers rheological equation of state:

$$\boldsymbol{\upsigma} ={\mathrm{O}}_{\upeta}\left(\frac{\partial }{\partial t}\right)2\textbf{D}$$

(18a)

In Eq. (18a), the viscosity linear operator is defined such as

$${\mathrm{O}}_{\upeta}\left(\frac{\partial }{\partial t}\right)=\frac{\frac{1}{\upvarphi_{\infty }}+\frac{1}{G_0{\upvarphi}_{\infty }}\frac{\partial }{\partial t}}{1+\frac{1}{G_0{\upvarphi}_{\infty }}\frac{\partial }{\partial t}+\frac{\uplambda_c}{G_0{\upvarphi}_{\infty }}\frac{\partial^2}{\partial {t}^2}}$$

(18b)

Material properties (φ₀, φ_∞, G₀, β) are related to the fluid properties.

Mathematical modeling of EOF

Continuity equation

Assuming that the liquid is incompressible and the density is independent of the position and time, so the material time derivative can be expressed as

$$\frac{D\uprho \left(r,t\right)}{Dt}=0\iff \nabla \cdot \textbf{v}=0$$

(19)

Equation (19) implies that the axial velocity does not depend on the z coordinate, i.e., ∂_zv_z = 0, and assuming cylindrical symmetry leads ∂_θv_z = 0.

Axial velocity, spatial gradient tensor, and viscoelastic stress tensor

Furthermore, under isothermal conditions and with flow occurring in the z-direction, the velocity components are as follows.

$$\textbf{v}=\left(\begin{array}{c}0\\ {}0\\ {} vz\left(r,t\right)\end{array}\right)$$

(20)

The velocity gradient tensor ∇ v is given by

$$\nabla \otimes {\textbf{v}}^{\mathrm{T}}=\left(\begin{array}{c}\frac{\partial }{\partial r}\\ {}0\\ {}0\end{array}\right)\otimes \left(0\kern0.5em 0\kern0.5em vz\left(r,t\right)\right)=\frac{\partial vz\left(r,t\right)}{\partial r}\ \left(\begin{array}{ccc}0& 0& 1\\ {}0& 0& 0\\ {}0& 0& 0\end{array}\right)$$

(21)

And the shear rate tensor D can be calculated through Eq. (21)

$$2\textbf{D}=\nabla \textbf{v}+\nabla {\textbf{v}}^{\mathrm{T}}=\frac{\partial vz\left(r,t\right)}{\partial r}\ \left(\begin{array}{ccc}0& 0& 1\\ {}0& 0& 0\\ {}1& 0& 0\end{array}\right)$$

(22a)

Hence, the viscoelastic shear stress tensor σ is given by

$$\boldsymbol{\upsigma} =\left(\begin{array}{ccc}{\upsigma}_{\mathrm{rr}}& 0& {\upsigma}_{\mathrm{rz}}\\ {}0& {\upsigma}_{\uptheta \uptheta}& 0\\ {}{\upsigma}_{\mathrm{zr}}& 0& {\upsigma}_{\mathrm{zz}}\end{array}\right)$$

(22b)

Volumetric flow and flow enhancement

The volumetric flow rate can be calculated through a double integral with respect to the radial and polar coordinates, so the following equation is admitted:

$$Q(t)=\int\limits_0^{2\uppi}\int\limits_0^{\mathrm{a}} vz\left(r,t\right) rdrd\uptheta = vz\left(r=a,t\right){\uppi \mathrm{a}}^2\hbox{-} \uppi \int\limits_0^{\mathrm{a}}\frac{\partial vz\left(r,t\right)}{\partial r} rdr=\hbox{-} \uppi \int\limits_0^{\mathrm{a}}\frac{\partial vz\left(r,t\right)}{\partial r} rdr$$

(23)

In Eq. (23), a non-slip velocity condition at the wall was applied. The change in the volumetric flow rate by the effect of the pulsating electroosmotic flow is given by the pulsating electroosmotic flow enhancement, which is given by the following ratio:

$$I\left(\%\right)=\frac{\left\langle Q(t)\right\rangle -{Q}_0}{Q_0}$$

(24)

where the bracket <> is the average volumetric flow defined by the following integral:

$$\left\langle \mathrm{Q}(t)\right\rangle =\frac{1}{T}\int\limits_0^{\mathrm{T}}Q(t) dt=\frac{1}{2\uppi /\upomega}\int\limits_0^{2\uppi /\upomega}Q(t) dt$$

(25)

And Q₀ is the steady state of the volumetric flow rate. In the following section, the electrolytic function is obtained in terms of the material properties of the system.

Potential field within the electric double layer

Following Rojas et al. (2017) formalism, the flow under investigation is both steady and fully developed. The electric double layers (EDLs) are assumed to be thin, preventing interference from one wall into the other. These conditions simplify the Nernst-Planck equations governing the ionic and electric potential field ψ distributions. When a liquid comes into contact with a dielectric surface, interactions occur between the ions and the wall, leading to a spontaneous charge distribution of the fluid at the wall. The wall acquires a charge, causing the counter-ions in the fluid to be attracted to the wall while the co-ions are repelled. In Eq. (26), Φ_e represents the applied electrical field, and ψ denotes the wall potential acquired on the wall due to the contact of the complex fluid with the wall.

$${\nabla}^2\Phi e+{\nabla}^2\uppsi =\hbox{-} \frac{1}{\upvarepsilon}{\uprho}_{\mathrm{E}}(r)$$

(26)

Here, the space charge density of the mobile ions is given by

$${\uprho}_{\mathrm{E}}(r)=-2{n}_0 ze\mathrm{Sinh}\left(\frac{\uppsi (r)}{k_{\mathrm{B}}T/ ze}\right)$$

(27a)

Assuming that the electrical fields are much smaller zeψ(r)/k_BT << 1 and taking the Taylor expansion to first order (Sinh(x) ≅ x), Eq. (27a) can be simplified in the following form:

$${\uprho}_{\mathrm{E}}(r)=-2{n}_0\frac{z^2{e}^2}{k_{\mathrm{B}}T}\uppsi (r)$$

(27b)

If the applied electrical potential Φ_e satisfies the Laplace equation ∇²Φ_e = 0 and invoking this principle, the Poisson-Boltzmann equation, resulting from substitution of Eq. (27b) into Eq. (26), takes on the following simplified linear form (Mederos et al. (2020)):

$$\left\{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+\frac{\partial^2}{\partial {z}^2}+{\left(i\upalpha \right)}^2\right\}\uppsi (r)=0$$

(28a)

In Eq. (28a), the contribution of ψ(r) in the axial direction is neglected compared to the radial position (L/a << 1). Thus, the following assumption was applied: r⁻¹∂/∂r{r∂ψ(r)/∂r} >> ∂²/∂z²ψ(r).

$${(ir)}^2\frac{\partial^2\psi (r)}{\partial {(ir)}^2}+ ir\frac{{\partial \psi }(r)}{\partial ir}+{\left(i\alpha \right)}^2\psi (r)=0$$

(28b)

In Eq. (28b), α² =2n₀e²z²/(εk_BT) is the Debye-Hückel parameter, related with the thickness of the Debye layer, λ_D = 1/α (normally referred as the EDL thickness). This approximation is valid when the Debye length thickness is small but finite, i.e., for a/λ_D ∈ [10¹,10³]. Consequently, the induced potential is constrained to prevent its energy from surpassing the thermal energy in a similar way as reported by Rojas et al. (2017). Equation (28b) can be solved subjected to the following boundary condition: (i) zeta potential at the wall ψ_w = −ψ( r = a) and (ii) symmetry in the centerline, dψ/dr|_{r = 0} = 0. The general solution of Eq. (28b) is given in terms of a linear combination of the modified Bessel functions, ψ(r) = C₁I₀(αr) +C₂K₀(αr). Applying the second boundary condition, the system is not bounded at r = 0, so, for physical reasons, the constant C₂ is set up to zero. The solution of Eq. (28b) is given in terms of the modified Bessel functions:

$$\uppsi (r)=\hbox{-} {\uppsi}_{\mathrm{w}}\frac{I_0\left(\upalpha r\right)}{I_0\left(\upalpha a\right)}$$

(29)

In Eq. (29), the wall potential is given by the following expression:

$${\uppsi}_{\mathrm{w}}=\left.\hbox{-} \uppsi \left(r=a\right)\right|>0$$

(30)

Finally, the net charge density distribution Eq. (27b) reduces to ρ_E(r) = −εα²ψ(r).

$${\uprho}_{\mathrm{E}}(r)={\upvarepsilon \uppsi}_{\mathrm{w}}{\upalpha}^2\frac{I_0\left(\upalpha r\right)}{I_0\left(\upalpha a\right)}$$

(31)

Equation (31) is a measure of the bulk electronical density distribution in the system.

Dimensionless variables and groups

To facilitate the physical analysis, the following dimensionless variables were suggested for the (i) axial velocity, (ii) fluidity function, (iii) shear stress, (iv) radial coordinate, (iv) volumetric flow, and (v) time:

$${\displaystyle \begin{array}{l} vz=\frac{vz}{V_{\mathrm{HS}}};\upvarphi =\frac{\upvarphi}{\upvarphi_{\infty }};\upsigma =\frac{\upsigma_{\mathrm{zr}}}{G_0};\\ {}r=\frac{r}{a};Q=\frac{Q}{{\uppi \mathrm{a}}^2{V}_{\mathrm{HS}}};t={\upomega}_0t\end{array}}$$

(32a-f)

And in the regime of linear viscoelasticity, the scaling variables are (vi) transfer function, (vii) frequency, (viii) Betha parameter, (ix) alpha parameter, and (x) fluidity operator.

$$T\left(\upomega \right)=\frac{T\left(\upomega \right)}{\upvarphi_{\infty }};{O}_{\Phi}^{\mathrm{B}}\left(i\upomega \right)=\frac{O_{\Phi}^{\mathrm{B}}\left(i\upomega \right)}{\upvarphi_{\infty }};\upbeta =\upbeta a;\upalpha =\upalpha a;\upomega =\frac{\upomega}{\upomega_0}$$

(32h-k)

Once the dimensionless variables are substituted into the governing equations, and using the characteristic electroosmotic shear stress, velocity, and characteristic shear rate, (i) σ_E = εψ_w E₀/λ_D, (ii) V_HS = φ_∞εψ_wE₀, and (iii) ${\overset{\cdot }{\upgamma}}_{\mathrm{HS}}={V}_{\mathrm{HS}}/a$, the following dimensionless groups are obtained:

$$\upalpha =a\upalpha =\sqrt{a^2\frac{n_0{z}^2{e}^2}{\upvarepsilon {k}_{\mathrm{B}}T}}$$

(33a)

The pulsating Reynolds number is a measure of the inertia and viscous forces Rew₀, and shear thinning and thickening ratio φ_r.

$${\operatorname{Re}}_{\upomega_0}={\uprho \upomega}_0{a}^2{\upvarphi}_{\infty }$$

(33b)

Here, the fluidity ratio, which is a measure of the shear thinning and thickening mechanisms, can be expressed as follows:

$${\upvarphi}_{\mathrm{r}}=\frac{\upvarphi_0}{\upvarphi_{\infty }}$$

(33c)

And Deborah numbers were expressed as

$${\mathrm{De}}_{\uplambda}={\uplambda}_{\mathrm{c}}{\upomega}_0\;;\;{\mathrm{De}}_{\infty }=\frac{1}{G_0{\upvarphi}_{\infty }}{\upomega}_0;{\mathrm{De}}_{\mathrm{HS}}=\frac{1}{G_0{\upvarphi}_{\infty }}{\overset{\cdot }{\upgamma}}_{\mathrm{HS}};{\mathrm{De}}_{\upbeta}=\upbeta {G}_0{\overset{\cdot }{\upgamma}}_{\mathrm{HS}}$$

(33d-g)

And we can define a geometric Deborah number given by:

$${\mathrm{De}}_{\mathrm{G}}=\sqrt{{\mathrm{De}}_{\mathrm{HS}}{\mathrm{De}}_{\upbeta}}$$

(33h)

• (a) The first dimensionless number, α, deals with the competition between thermal energy (according to the equipartition theorem) and electric mechanisms.

• (b) The second dimensionless number is the oscillatory Reynolds number, Re_ω, which represents the ratio between inertial and viscous mechanisms.

• (c) The third dimensionless number, φ_r = φ₀/φ_∞, is the ratio between two fluidities at low and high shear rates, respectively. This number measures the shear thinning and thickening mechanisms based on the level of structure at low and high shear rates.

• (d) The fourth dimensionless number is the structural Deborah number, which measures the structural and oscillatory mechanisms. When De_λ = 0, the structure does not depend of time, whereas De_λ ≠ 0 implies that the structure shows a time-dependent relation, and the system shows hysteric mechanisms associated with the structure.

• (e) The fifth dimensionless number is high frequency Deborah number, De_∞ = 0, associated with low relaxation time viscoelastic oscillatory forces.

• (f) The sixth dimensionless number is the high shear rate Deborah number, De_HS = 0, associated with high viscoelastic and high shear rate, as predicted by the Helmholtz-Smoluchowski equation. When De_HS = 0, the system is inelastic, and when De_HS →∞, the system becomes elastic. The viscoelastic case corresponds to De_HS = 1.

• (g) The seventh group, De_β, is a Deborah number associated with the ratio between two energies linked to structural and viscous dissipation associated with the flow mechanisms. Notice that the value of De_β is connected with the relative dominance of structural mechanisms in relation to dissipation mechanisms. As De_β tends to infinity, the dissipation mechanisms become dominant, especially at high shear rate.

The yield stress case is reached when the viscosity goes to infinity, i.e., φr = φ₀/φ_∞ ~ 0. Here, the system displays a high-compact entangled structure. So, the yield stress can be expressed in terms of the geometric Deborah number, defined in Eq. (32h):

$${\upsigma}_{\mathrm{y}}=\frac{1}{{\mathrm{De}}_{\mathrm{G}}}=\frac{1}{\sqrt{{\mathrm{De}}_{\mathrm{HS}}{\mathrm{De}}_{\upbeta}}}$$

(34)

This dimensionless number is the ratio between a driven sheared force (electrical) and a characteristic yield stress σ_y. In particular, σ_y depends on the kinetic, structural, and bulk elastic mechanism of the structured fluid. At σ_y > 1, the system is in the zone of yield stress (φ_r = φ₀/φ_∞ ~ 0), whereas at σ_y < 1, the system experiments undergo transition from a structured fluid to an elastic solid. The case when σ_y = 0, the system behaves as a structured liquid. According with Baños et al. (2021), typical restrictions employed in pulsatile electroosmotic system are as follows: To avoid possible Joule heating and electro-kinetic instabilities due to applied electrical field, the amplitude of the electrical field E_z(t) must be restricted to E₀ < 100 V/nm (Green and Morgan 1998); therefore, E₀ ~ 10³ V/m was considered. The micellar density is ρ ~ 10³ kg/m³. The microchannel length, L ~ 10⁻² m, and its height, a (=5–100) μm, are such that α ~ O(10⁻³). For the symmetric (z:z) electrolyte solution, the valence is z =1, the bulk number concentration is n_∞ = 10³ N_AM with the Avogadro number N_A = 6.022 × 10²³ 1/mol, and M is the molar concentration of the electrolyte. The dielectric permittivity is ε_r ~ O(10²), the Boltzmann constant is k_B =1.38 × 10⁻²³ J K⁻¹, the elementary charge is e = 1.602 × 10⁻¹⁹ C, and the absolute temperature is T = 298 K. The frequency ranges from ω ~ 400 Hz to 360 kHz and Debye lengths λ_D range from 15 to 300 nm are considered. The material parameters for the simulations are given in Table 1, and they were taken from Soltero et al. (1999).

Table 1 Material properties of CTAT

The dimensionless equations for axial velocity, volumetric flow rate, flow enhancement, pulsatile fluidity function, electrolytic distribution, and pulsating oscillatory function are given by the following equations.

Dimensionless theoretical equations

Continuity equation

Assuming isothermal rectilinear flow, an incompressible viscoelastic electrolytic liquid, isothermal conditions, and negligible gravitational mechanisms compared to other forces, the continuity equation is given by the following simplified form:

$$\frac{\partial vz\left(r,t\right)}{\partial z}=0$$

(35)

Equation (35) implies that there is no extensional flow in the system. The momentum balance equation can be written in the following analytical form:

$${\operatorname{Re}}_{\upomega_0}\updelta \frac{\partial vz\left(r,t\right)}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left(r{\upsigma}_{\mathrm{zr}}\right)+{\upalpha}^2\frac{I_0(ar)}{I_0(a)}E(t)$$

(36)

In Eq. (36), the parameter δ was introduced deliberately to consider the inertial mechanisms in the perturbation scheme. In Eq. (36), E(t) is the electrical mechanisms and can be represented in the following periodic function, i.e.:

$$E(t)=1+\updelta n(t)=1+\updelta \cdot \operatorname{Re}\left\{\mathrm{Exp}\left(i\upomega t\right)\right\}$$

(37)

In Eq. (37), δ can be considered as an amplitude of the oscillatory function n(t). The components of the constitutive rheological equation of state are as follows:

$${\displaystyle \begin{array}{r}\mathrm{Exp}\left[\left({\upvarphi}_{\mathrm{r}}-1\right) fr\right]{\upsigma}_{\mathrm{r}\mathrm{z}}+{\mathrm{De}}_{\infty}\left(\frac{\partial {\upsigma}_{\mathrm{r}\mathrm{z}}}{\partial t}-\frac{\partial vz\left(r,t\right)}{\partial r}{\upsigma}_{\mathrm{r}\mathrm{r}}\right)+{\mathrm{De}}_{\uplambda}{\mathrm{De}}_{\infty } fr\frac{\partial^2{\upsigma}_{\mathrm{r}\mathrm{z}}}{\partial {t}^2}=\\ {}\left(1+{\mathrm{De}}_{\uplambda} fr\frac{\partial }{\partial t}\right)\frac{\partial vz\left(r,t\right)}{\partial r}\end{array}}$$

(38)

$${Exp}\left[\left({\varphi}_{{r}}-1\right) fr\right]{\sigma}_{{zz}}+{{De}}_{\infty}\frac{\partial {\sigma}_{{zz}}}{\partial t}+{{De}}_{\lambda}{{De}}_{\infty } fr\frac{\partial^2{\sigma}_{{zz}}}{\partial {t}^2}=2{{De}}_{{HS}}\left(1+{{De}}_{\lambda} fr\frac{\partial }{{\partial t}}\right)\frac{\partial vz\left(r,t\right)}{\partial r}{\sigma}_{{r}{z}}$$

(39)

$${Exp}\left[\left({\varphi}_{{r}}-1\right) fr\right]{\sigma}_{{r}{r}}+{{De}}_{\infty}\frac{\partial {\sigma}_{{r}{r}}}{\partial t}+{{De}}_{\lambda}{{De}}_{\infty } fr\frac{\partial^2{\sigma}_{{r}{r}}}{\partial {t}^2}=0$$

(40)

$${Exp}\left[\left({\varphi}_{{r}}-1\right) fr\right]{\sigma}_{\theta \theta}+{{De}}_{\infty}\frac{\partial {\sigma}_{{r}{r}}}{\partial t}+{{De}}_{\lambda}{{De}}_{\infty } fr\frac{\partial^2{\sigma}_{\theta \theta}}{\partial {t}^2}=0$$

(41)

where the dissipation function is given by the following simplest form:

$$fr\left({\sigma}_{{zr}}\frac{\partial vz\left(r,t\right)}{\partial r}\right)=\frac{1}{1+{{De}}_{{G}}^2{\sigma}_{{zr}}\frac{\partial vz\left(r,t\right)}{\partial r}}$$

(42)

Particular cases

Linear viscoelasticity

For small deformations, the mean equation can be simplified in the Burgers constitutive equation given by the following expression:

$$\frac{\partial vz\left(r,t\right)}{\partial r}={O}_{\varphi}^{{B}}\left(\frac{\partial }{\partial t}\right){\sigma}_{{rz}}\left(r,t\right)$$

(43)

In Eq. (43), the Burgers fluidity operator can be expressed in the following manner:

$${O}_{\varphi}^{{B}}\left(\frac{\partial }{{\partial t}}\right)=\frac{\frac{\partial vz\left(r,t\right)}{\partial r}}{\sigma_{{rz}}}=\frac{1+{{De}}_{\omega_0}\frac{\partial }{\partial t}+{{De}}_{\lambda}{{De}}_{\omega_0}\frac{\partial^2}{\partial {t}^2}}{1+{{De}}_{\lambda}\frac{\partial }{\partial t}}$$

(44)

Once the last equation is substituted in the z-component of the momentum equation, the following partial differential equation is obtained:

$$vz\left(r,t\right)=\frac{O_{\varphi}^{{B}}\left(\frac{\partial }{\partial t}\right){\alpha}^2\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}}{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+{i}^2{\operatorname{Re}}_{\omega_0}{O}_{\varphi}^{{B}}\left(\frac{\partial }{\partial t}\right)\frac{\partial }{\partial t}}E(t)$$

(45)

Equation (45) can be solved using the Fourier transform, and the transfer function can be obtained from this approximation. Assuming non-slip conditions, vz(r =1,t) = 0 and symmetry of the velocity field at the center of the system ∂_rvz(r,t)|_r = 0, the following expression for the axial velocity is obtained (see Appendix 1 for the mathematical steps):

$$vz\left(r,\omega \right)=\operatorname{Re}\left[ vz\left(r,\omega \right)\right]+{iIm}\left[ vz\left(r,\omega \right)\right]={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left(\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}-\frac{I_0\left(\beta r\right)}{I_0\left(\beta \right)}\right)E\left(\omega \right)$$

(46)

where the parameter β depends on the vibratile Reynolds number Re_ω0 and the complex compliance

$$\beta =i\omega \sqrt{{\operatorname{Re}}_{\omega_0}\cdot {J}_{{B}}^{\ast}\left(i\omega \right)}$$

(47)

And the complex compliance is given in terms of the fluidity operator

$${J}_{{B}}^{\ast}\left(i\omega \right)=\frac{O_{\varphi}^{{B}}\left(i\omega \right)}{i\omega}=\frac{1}{i\omega}\frac{1+{{De}}_{\omega_0}\left(i\omega \right)+{{De}}_{\lambda}{{De}}_{\omega_0}{\left(i\omega \right)}^2}{1+{{De}}_{\lambda}\left(i\omega \right)}$$

(48)

An integrating Eq. (46) over a cross section area, the volumetric flow can be derived:

$$Q\left(\omega \right)=2\int_0^1 vz\left(r,\omega \right){dr}={T}_{{F}}\left(\omega \right)E\left(\omega \right)$$

(49)

The transfer function in Eq. (49) has the following analytical form:

$${T}_{{F}}\left(\omega \right)=\frac{Q\left(\omega \right)}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{F}}\left(\omega \right)\right]+{iIm}\left[{T}_{{F}}\left(\omega \right)\right]=\underset{{Rheology}\hbox{-} {Mechanisms}\ }{\underbrace{O_{\varphi}^{{B}}\left({i}\omega \right)}}\underset{{Electrical}\hbox{-} {thermical}\hbox{-} {Dispersion}\hbox{-} {Mechanisms}}{\underbrace{\frac{2{\alpha}^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left(\frac{I_1\left(\alpha \right)/\alpha}{I_0\left(\alpha \right)}-\frac{I_1\left(\beta \right)/\beta}{I_0\left(\beta \right)}\right)}}$$

(50)

Here, Eq. (50) is the flow transfer function of the system, where the input variable is the electrical field and the output is the volumetric flow rate. Note that Eq. (50) contains information about the thermal-electrical field and the rheological start-up mechanisms (see the mathematical deduction in Appendix 2).

Regime of small deformations and electrical mechanisms α << 1

Flow transfer function

The axial velocity, under small deformations under electrical mechanisms (α<<1), is given by the following analytical expression:

$$vz\left(r,\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{1}{{\left(i\beta \right)}^2}\left(1-\frac{I_0\left(\beta r\right)}{I_0\left(\beta \right)}\right)E\left(\omega \right)$$

(51)

With the velocity profile given by Eq. (5), the volumetric flow rate is given by

$$Q\left(\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{1}{{\left(i\beta \right)}^2}\left(1-2\frac{I_1\left(\beta \right)/\beta}{I_0\left(\beta \right)}\right)E\left(\omega \right)={T}_{{F}}\left(\omega \right)E\left(\omega \right)$$

(52)

Then, the flow transfer function at small electrical mechanism is given by

$${T}_{{F}}\left(\omega \right)=\frac{Q\left(\omega \right)}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{F}}\left(\omega \right)\right]+{iIm}\left[{T}_{{F}}\left(\omega \right)\right]=\underset{{Rheology}}{\underbrace{O_{\varphi}^{{B}}\left({i}\omega \right)}}\underset{{Electric}\hbox{-} {Thermic}}{\underbrace{\alpha^2}}\underset{{Dispersion}}{\underbrace{\frac{1}{{\left(i\beta \right)}^2}\left(1-2\frac{I_1\left(\beta \right)/\beta}{I_0\left(\beta \right)}\right)}}$$

(53)

Wall shear stress transfer function

The wall shear stress can be calculated from Eq. (43)

$${\sigma}_{{w}}=-{\left.{\sigma}_{{r}\mathrm{z}}\right|}_{{r}=1}=-{\left.\frac{1}{O_{\varphi}\left(i\omega \right)}\frac{\partial vz\left(r,\omega \right)}{\partial r}\right|}_{{r}=1}$$

(54)

Substituting the complex profile velocity from Eq. (46) into Eq. (54), the complex transfer function is obtained

$${T}_{{S}}\left(\omega \right)=\frac{\sigma_{{w}}}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{S}}\right]+{iIm}\left[{T}_{{S}}\right]=\frac{{\left(i\alpha \right)}^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left\{\alpha \frac{I_1(a)}{I_0(a)}\hbox{-} \beta \frac{I_1\left(\beta \right)}{I_0\left(\beta \right)}\right\}$$

(55)

Equation (55) relates the interaction between the electrical driven forces with the inertial-viscoelastic wall stress (see the mathematical deduction in Appendix 2). In the case of small electrical mechanisms, i.e., α << 1, we have

$${\sigma}_{{w}}={\left.\hbox{-} {\sigma}_{{r}{z}}\right|}_{{r}=1}={\alpha}^2\left(\frac{I_0\left(\beta r\right)/\beta}{I_0\left(\beta \right)}\right)E\left(\omega \right)$$

(56)

Then, the stress transfer function can be expressed in the following analytical form:

$${T}_{{S}}\left(\omega \right)=\frac{\sigma_{{w}}}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{S}}\right]+{iIm}\left[{T}_{{S}}\right]=\underset{\begin{array}{c}\mathrm{Electrical}\hbox{-} \mathrm{Thermal}\\ {}\mathrm{Mechanisms}\end{array}}{\underbrace{\alpha^2}}\underset{{Dispersion}\hbox{-} {Mechanisms}}{\underbrace{\frac{I_0\left(\beta \right)/\beta}{I_0\left(\beta \right)}}}$$

(57)

The norm of both transfer functions is given by

$$\left|{T}_{{X}}\left(\omega \right)\right|=\sqrt{{\left(\operatorname{Re}\left[{T}_{{X}}\left(\omega \right)\right]\right)}^2+{\left(\operatorname{Im}\left[{T}_{{X}}\left(\omega \right)\right]\right)}^2};X=\left\{F,S\right\}$$

(58)

Viscoelastic flow enhancement

Assuming in Eq. (50), a complex exponential function of the electrical field, i.e., E(t) = Exp[it], the Fourier transform of the electric field is given by a delta Dirac function: E(ω) = δ(ω−1); then, the volumetric flow in the time space is calculated trough the inverse of the Fourier formalism

$$Q\left(t;{{De}}_{\omega_0},{{De}}_{\lambda}\right)={T}_{{F}}\left({{De}}_{\omega_0},{{De}}_{\lambda}\right)E(t)={T}_{{F}}\left({{De}}_{\omega_0},{{De}}_{\lambda}\right)\left(1+\delta {Re}\left\{{Exp}\left[ it\right]\right\}\right)$$

(59)

The flow enhancement can be calculated through Eq. (24). It is important to note that, in the case of linear viscoelasticity, there is not an advantage to add a pulsatile contribution in the electrical field.

Steady state and homogeneous shear flow

At steady state, the system, the following equation is obtained:

$${Exp}\left[\left({\varphi}_{{r}}-1\right) fr\right]{\sigma}_{{r}\mathrm{z}}=\frac{\partial vz\left(r,t\right)}{\partial r}$$

(61)

And the zz normal component of the stress tensor can be expressed as follows:

$${\sigma}_{{zz}}=2{{De}}_{{HS}}{\left({\sigma}_{{rz}}\right)}^2$$

(62)

Developing the exponential until linear contribution, the following expression is obtained for the shear stress tensor:

$$\left(1+\left({\varphi}_{{r}}-1\right) fr\right){\sigma}_{{r}{z}}=\frac{\partial vz\left(r,t\right)}{\partial r}$$

(63)

Assuming steady state and a homogeneous flow, the shear stress tensor can be expressed in terms of the fluidity

$$\boldsymbol{\sigma} =\left(\begin{array}{ccc}2{{De}}_{{HS}}{\left({\varphi}^{\hbox{-} 1}\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)\frac{\partial vz\left(r,t\right)}{\partial r}\right)}^2& 0& {\varphi}^{\hbox{-} 1}\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)\frac{\partial vz\left(r,t\right)}{\partial r}\\ {}0& 0& 0\\ {}{\varphi}^{\hbox{-} 1}\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)\frac{\partial vz\left(r,t\right)}{\partial r}& 0& 0\end{array}\right)$$

(64)

where the viscosity function can be expressed in the following analytical form:

$${\varphi}^{-1}\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)=\frac{{{De}}_{{G}}^2{\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)}^2-{\varphi}_{{r}}+\sqrt{{\left({{De}}_{{G}}^2{\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)}^2-{\varphi}_{{r}}\right)}^2+4{{De}}_{{G}}^2{\varphi}_{{r}}{\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)}^2}}{2{{De}}_{{G}}^2{\left(\frac{\partial vz\left(r,t\right)}{\partial r}\right)}^2}$$

(65)

Material functions

At steady state and shearing flow, three material functions are obtained: (i) viscosity function (inverse of the fluidity function), (ii) first normal stress coefficient, and (iii) second normal stress coefficient. The first one can be expressed as a ratio between the shear stress and shear rate:

$$\eta \left(\frac{\partial vz}{\partial r}\right)={\varphi}^{-1}\left(\frac{\partial vz}{\partial r}\right)=\frac{\sigma_{{zr}}\left(\frac{\partial vz}{\partial r}\right)}{\frac{\partial vz}{\partial r}}$$

(66)

The first normal stress coefficient ψ₁ is defined as follows:

$${\Psi}_1\left(\frac{\partial vz}{\partial r}\right)=\frac{N_1}{{\left(\frac{\partial vz}{\partial r}\right)}^2}=\frac{\sigma_{{zz}}-{\sigma}_{{rr}}}{{\left(\frac{\partial vz}{\partial r}\right)}^2}=2{{De}}_{{HS}}{\varphi}^{-2}\left(\frac{\partial vz}{\partial r}\right)$$

(67)

According to the exponential model, the second normal stress coefficient is zero, i.e., Ψ₂ = 0, in contrast with other complex constitutive equations such as PTT and SPTT models, where Ψ₂ ≠ 0.

Shear rate

The shear rate is given by

$$\frac{\partial vz\left(r,t\right)}{\partial r}=\varphi \left({\sigma}_{{rz}}(r)\right){\sigma}_{{rz}}(r)$$

(68)

The analytical expression for the normalized fluidity function is given by

$$\varphi \left({\sigma}_{{r}{z}}(r)\right)=\frac{{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)}^2-1+\sqrt{{\left({{De}}_{{G}}^2{\sigma}_{\left({zr}\right)}^2-1\right)}^2+4{{De}}_{{G}}^2{\varphi}_{{r}}{\sigma}_{\left({zr}\right)}^2}}{2{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)}^2}$$

(69)

In Eq. (68), low and high values of the normalized shear stress have the following asymptotic limits:

$${{Lim}}_{{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)}^2\to 0}\varphi \left({\sigma}_{{r}{z}}(r)\right)={\varphi}_{{r}};{{Lim}}_{{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)}^2\to \infty}\varphi \left({\sigma}_{{r}{z}}(r)\right)=1$$

(70a, b)

Yield stress phenomena

The yield stress phenomenon is manifested at small shear strain deformations, i.e., φr = φ₀/φ_∞ ≈ 0 and ∂vz/∂r→0, so the stress tensor is given by the following form:

$${\boldsymbol{\sigma}}_{{y}}=\left(\begin{array}{ccc}{\sigma}_{{rr}}& 0& {\sigma}_{{rz}}\\ {}0& 0& 0\\ {}{\sigma}_{{zr}}& 0& 0\end{array}\right)=\left(\begin{array}{ccc}2{{De}}_{{HS}}/{{De}}_{{G}}^2& 0& 1/{{De}}_{{G}}\\ {}0& 0& 0\\ {}1/{{De}}_{{G}}& 0& 0\end{array}\right)$$

(71)

To solve the above dimensionless equation, the following perturbation scheme is proposed for the axial velocity, shear stress, shear rate, and structure parameter.

Perturbation scheme

In order to obtain analytical expressions and information about the fundamental mechanisms, the following perturbative scheme is proposed in terms of the parameter δ. Integrating the momentum balance equation with respect to the radial coordinate r, the following expression is obtained, which is a starting point of the perturbation technique:

$${\sigma}_{{zr}}\left(r,t\right)=-\alpha \frac{I_1\left(\alpha r\right)}{I_0\left(\alpha \right)}{\delta}^0+\left({\operatorname{Re}}_{\omega}\frac{\partial }{\partial t}\left(\frac{1}{r}\int_0^{{r}}\overline{r} vz\left(r,t\right) dr\right)-\alpha \frac{I_1\left(\alpha r\right)}{I_0\left(\alpha \right)}n(t)\right){\delta}^1+O\left({\delta}^1\right)$$

(72)

Accordingly, in Eq. (72), the perturbation dynamic variables are (i) axial velocity, (ii) shear stress, (ii) shear rate, (iv) fluidity function, and (v) volumetric flow rate. These variables are expanded in a power series in terms of the δ perturbation parameter, which can be associated to a small amplitude which let us to control the oscillations through the stochastic mathematical function n(t).

$$vz\left(r,t\right)={\updelta}^0{vz}_0(r)+{\updelta}^1{vz}_1\left(r,t\right)+O\left(\updelta \right)$$

(73)

$${\sigma}_{\left({rz}\right)}\left(r,t\right)={\delta}^0{\sigma}_{\left({rz}\right)0}(r)+{\delta}^1{\sigma}_{\left({rz}\right)1}\left(r,t\right)+O\left({\delta}^1\right)$$

(74)

$$\upgamma \left(r,t\right)={\updelta}^0{\upgamma}_0(r)+{\updelta}^1{\upgamma}_1\left(r,t\right)+O\left({\updelta}^1\right)$$

(75)

$$\upvarphi \left(r,t\right)={\updelta}^0{\upvarphi}_0(r)+{\updelta}^1{\upvarphi}_1\left(r,t\right)+O\left({\updelta}^1\right)$$

(76)

$$Q(t)={\updelta}^0{Q}_0+{\updelta}^1{Q}_1(t)+\cdots +O\left({\updelta}^1\right)$$

(77)

From this point, in Eqs. (73)–(77), the indices for the axial velocity, shear stress, and shear rate and the upper dot in the shear rate have been omitted, $\upgamma \left(r,t\right)=d\upgamma \left(r,t\right)/ dt=\overset{\cdot }{\upgamma}\left(r,t\right)$. In Eq. (73), the velocity profile can be separated in two contributions, one of them associated to the spatial contributions as indicated below:

$${vz}_{{j}}\left(r,t\right)={vz}_{{j}}(r)+\frac{d^{{j}\hbox{-} 1}}{dt^{{j}\hbox{-} 1}}n(t);j=1,2,3,\dots, n,n\in N$$

(78)

The volumetric flow rate to first order can be expressed as follows:

$$Q(t)=\hbox{-} \int\limits_0^1\upgamma \left(r,t\right){r}^2 dr$$

(79)

And the flow enhancement is given by

$$I\left(\%\right)={10}^2\frac{\left\langle Q(t)\right\rangle -{Q}_0}{Q_0}={10}^2\frac{\left\langle {Q}_0+\updelta {Q}_1(t)+O\left({\updelta}^1\right)\right\rangle -{Q}_0}{Q_0}={10}^2\updelta \frac{\left\langle {Q}_1(t)\right\rangle }{Q_0}+{10}^2{\updelta}^2\frac{\left\langle {Q}_2(t)\right\rangle }{Q_0}+O\left(\updelta \right)$$

(80)

Zeroth-order theory O (δ⁰)

Once the power series are substituted into the constitutive equation, the mathematical expression at zeroth order is obtained:

$${\sigma}_{\left({zr}\right)0}(r)=-\alpha \frac{I_1\left(\alpha r\right)}{I_0\left(\alpha \right)}$$

(81)

And the constitutive equation is given by the following expressions:

$$\left[1+\left({\varphi}_{{r}}-1\right) fr\right]{\sigma}_{\left({rz}\right)0}=\frac{\partial {vz}_0(r)}{\partial r}$$

(82)

And the relaxation function takes the form:

$$fr\left({\sigma}_{\left({rz}\right)0}\frac{\partial {vz}_0(r)}{\partial r}\right)=\frac{1}{1+{{De}}_{{G}}^2{\sigma}_{\left({rz}\right)0}\frac{\partial {vz}_0(r)}{\partial r}}$$

(83)

Combining Eqs. (82) and (83), a quadratic expression for the fluidity was reached, and only the positive root is considered.

$${\gamma}_0(r)=\frac{\partial {vz}_{(0)}(r)}{\partial r}={\varphi}_0(r){\sigma}_{\left({zr}\right)0}=\frac{{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)0}^2-1+\sqrt{{\left({{De}}_{{G}}^2{\sigma}_{\left({zr}\right)0}^2-1\right)}^2+4{{De}}_{{G}}^2{\varphi}_{{r}}{\sigma}_{\left({zr}\right)0}^2}}{2{{De}}_{{G}}^2{\sigma}_{\left({zr}\right)0}^2}{\sigma}_{\left({zr}\right)0}$$

(84)

where the volumetric flow to zeroth order is given by the following expression:

$${Q}_0(t)=\hbox{-} \int\limits_0^1{\upgamma}_0(r){r}^2 dr=\hbox{-} \int\limits_0^1{\upvarphi}_0(r){\upsigma}_0{r}^2 dr$$

(85)

The flow enhancement is zero, i.e., I₀ = 10² (Q₀−Q₀)/Q₀ = 0.

First-order theory O (δ¹)

To first order, Ο(δ¹), the following expressions for the rz-shear stress component is obtained:

$${\sigma}_{\left({zr}\right)1}\left(r,t\right)={\sigma}_{\left({rz}\right)1}\left(r,t\right)={\operatorname{Re}}_{\omega}\frac{1}{2}\overset{\cdot }{n}(t)r-\alpha \frac{I_1\left(\alpha r\right)}{I_0\left(\alpha \right)}n(t)$$

(86)

On the other hand, the shear rate to the first order is

$${\displaystyle \begin{array}{l}\left(\left(1-{{De}}_{{G}}^2{\left({\sigma}_{\left({r}{z}\right)0}\right)}^2+{{De}}_{{G}}^2{\sigma}_{\left({r}{z}\right)0}\right)+{{De}}_{\lambda}\frac{\partial }{\partial t}\right)\frac{\partial {vz}_1\left(r,t\right)}{\partial r}=\\ {}+{{De}}_{{G}}^2\left(2{\sigma}_{\left({r}{z}\right)0}{\sigma}_{\left({r}{z}\right)1}\frac{\partial {vz}_0(r)}{\partial r}\right)+{\varphi}_{{r}}{\sigma}_{\left({r}{z}\right)1}\\ {}+{{De}}_{\infty}\left(\frac{\partial {\sigma}_{\left({r}{z}\right)1}}{\partial t}-\frac{\partial {vz}_0(r)}{\partial r}{\sigma}_{\left({r}{r}\right)1}\right)+{{De}}_{\infty }{{De}}_{{G}}^2\left\{{\sigma}_{\left({r}{z}\right)0}\frac{\partial {vz}_0\left({r}\right)}{\partial r}\frac{\partial {\sigma}_{\left({r}{z}\right)1}}{\partial t}-{\sigma}_{\left({r}{z}\right)0}{\sigma}_{\left({r}{r}\right)1}{\left(\frac{\partial {vz}_0(r)}{\partial r}\right)}^2\right\}\\ {}+{{De}}_{\lambda}{{De}}_{\infty}\frac{\partial^2{\sigma}_{\left({r}{z}\right)1}}{\partial {t}^2}-{{De}}_{{G}}^2{\sigma}_{\left({r}{z}\right)1}\frac{\partial {vz}_0(r)}{\partial r}\end{array}}$$

(87)

At first-order theory, the normal stress follows the next partial differential equation:

$${{De}}_{\lambda}{{De}}_{\infty}\frac{\partial^2{\sigma}_{\left({rr}\right)1}}{\partial {t}^2}+{{De}}_{\infty}\frac{\partial {\sigma}_{\left({rr}\right)1}}{\partial t}+\left({{De}}_{{G}}^2{\sigma}_{\left({rz}\right)0}\frac{\partial {vz}_0(r)}{\partial r}+{\varphi}_{{r}}\right){\sigma}_{\left({rr}\right)1}=0$$

(88)

The average first-order volumetric flow rate is given by

$$\left\langle {Q}_1(t)\right\rangle =\frac{1}{2\uppi}\int\limits_0^{2\uppi}{Q}_1(t) dt=\frac{1}{2\uppi}\ \int\limits_0^{2\uppi}\left(\hbox{-} \int\limits_0^1{\upgamma}_1\left(r,t\right){r}^2 dr\right) dt$$

(89)

The flow enhancement at first-order I₁ is given by I₁ =10²δ(<Q₁(t)>/Q₀), so

$${I}\left(\%\right)=\frac{\left\langle {Q}_1(t)\right\rangle }{Q_0}=\frac{\frac{1}{2\pi}\ \int\limits_0^{2\pi}\left(\hbox{-} \int\limits_0^1{\gamma}_1\left(r,t\right){r}^2 dr\right) dt}{\int\limits_0^1{\gamma}_0\left(r,t\right){r}^2 dr}$$

(90)

Equations (81)–(86) are the key findings and show the evolution of the structure in the complex fluid. These coupled equations display the first-order contribution associated to the thermal, inertial-electrical, kinetic, shear thinning, shear thickening, yield stress, and concentration mechanisms through the characteristic dimensionless numbers. Once the dimensionless numbers are chosen, Eqs. (81), (84), and (86) are substituted into Eqs. (87) and (88); the resulting non-linear coupled differential equations were solved using the Crank-Nicolson Method applying a central difference technique (Baños et al. 2021). The dimensionless flow enhancement was solved numerically with a Gaussian quadrature technique in a Wolfram Mathematica programming code (Wolfram 2016; Medina et al. 2018; Peralta et al. 2020).

Results

In this section, the mean results of this research are showed. The results are based in the regular perturbations to zeroth, first, and second orders, as previously presented.

Shear thinning mechanisms

Figure 3a shows the effect of φ_r over the fluidity function. At low and high wall shear stress values, the system displays a constant behavior independent of the wall shear stress and for a particular value of wall stress energy. At intermediate values of the wall stress, the system shows a monotonically increasing behavior (power law–like behavior) until a second critical value where the system is independent of the wall shear stress. Physically, at low wall stress, the fluid has a compact structure with the maximum links, bonds, or entanglement in the system. At moderate values of wall shear stress, the internal surface forces destroy the microstructure due to flow. It is important to note that the dimensionless number φ_r controls the shear thinning and shear thickening mechanisms. Figure 3b shows the electrical flow enhancement as a function of the shear thinning mechanisms over the flow enhancement. The dimensionless numbers used here are given as follows: (i) De_G = 1, (ii) α = 0.1, (iii) δ = 0.1, and (iv) φ_r = {0.1, 0.4, 0.7, 0.9}. Figure 3b shows the first-order perturbation as a function of wall stress. Three important zones are clearly seen: At both low and high wall electrical shear stresses, the system exhibits a constant behavior, which corresponds to a given by the Newtonian behavior (zero flow enhancement). At a critical wall electrical shear stress, the system displays a monotonically increasing behavior until maximum peak. This resonance peak is characterized by a coupling effect between the thermal, electrical, and shear thinning mechanisms through the dimensionless number φ_r. At σ_w > σ_wR, the system shows a monotonically decreasing behavior until it approaches an asymptotic value near the unit. Here, we have made the following assumptions:

• (a) The resonance effect is controlled by the destruction of the microstructure (links, intermolecular bonds, or entanglement) and by the fluidity ratio φ_r = φ₀/φ_∞.

• (b) The form of the resonance curves depends on the fluidity function and the dimensionless number associated to the fluidity ratio φ_r = φ₀/φ_∞.

• (c) The maximum peak value is associated with a coupling of electrical-thermal, viscous, and elastic mechanisms.

Fig. 3

a The fluidity function versus wall shear stress as a function of the shear thinning mechanisms. b The flow enhancement versus wall stress for the same material conditions given in a

Shear thickening mechanisms

Figure 4a shows the fluidity function and the flow enhancement versus wall stress as a function of the shear thickening mechanisms through the dimensionless number φ_r. The other parameters employed were (i) De_G = 1 and (ii) α =1. At small and high values of wall stress, a constant fluidity function was observed. At moderate wall stress, a monotonically decreasing behavior until a critical wall stress value was observed; this is due to the structure which remains static. Physically, in the power law zone, the raising of structural points is due to a more entangled structure by effect of the driven force associated to the flow.

Fig. 4

a The fluidity function versus wall shear stress as a function of the shear thickening mechanisms. b The flow enhancement versus wall stress for the same material conditions given in a

Figure 4b shows the flow enhancement versus wall stress as a function of φ_r. The parameters used in the simulations were (i) De_G =1, (ii) α =1, (iii) δ = 0.1, and α = {10⁻², 10⁰, 10²}. When α = 10⁰, the system shows two plateaus at low and high wall stresses, respectively. In contrast to Fig. 3, the system displays its anti-resonance behavior, where the flow decreases drastically by the effect of the shear thinning mechanism due to an increase of the links or bonds associated to a more entangled structure. The effect of thermal and electric forces induces a shift in the flow enhancement. When the thermal fluctuations dominate over the electrical forces, the system needs more energy to display its anti-resonance behavior, whereas the opposite case is clearly seen when the electrical force is larger than the thermal processes. It employs less energy to reach the minimum.

Furthermore, Fig. 4 shows the flow enhancement versus wall stress as a function of the shear thickening mechanisms through the dimensionless number φ_r >1. It is clear that the shear thickening mechanisms are to decrease the volumetric flow rate by the effect of the applied electrical field. The α number shifts the anti-resonance flow by the effect of the thermal fluctuations and the driven force, which deals with the energy in the system to reach the maximum peak.

Kinetic-rupture mechanisms

Figure 5 shows the effect of the dimensionless number De_G which was associated to the electrical and material yield stress mechanisms on the fluidity function (Fig. 5a) and the flow enhancement (Fig. 5b). The dimensionless numbers employed in the simulation (a) are given by the following numerical values: (i) De_G = {0.01, 0.1, 1, 10, 100}, (ii) φ_r = 0.1, (iii) α = 1, and (iv) δ = 0.1. The dimensionless number De_G represents a competition between electrical and structural yield stress forces. It is a function of irreversible viscoelastic work and fluidity at high electrical wall stress. The effect of De_G over the flow is to control the energy associated to the driven force; when De_G << 1, the system needs more energy to break down the structure, due to the competition of the kinetic, structural, thermal, and electric forces. On the other hand, when De_G >> 1, the structure fluid changes its internal structure more easily.

Fig. 5

a The fluidity function versus wall shear stress as a function of the thixotropic mechanisms through the dimensionless number De_G. The effect of this number is associated with the critical wall stress to undergo transitions from higher to lower structure states, by effect of the elastic, kinetic, and structural mechanisms. b Flow enhancement versus wall stress for the same material conditions given in a. The system is shifted to low and high wall stress depending on the numerical value of De_G

Electric and thermal fluctuations

Figure 6a shows the dimensionless electric charge distribution versus radial coordinate with different α values. At small values of α, i.e., α << 1, the electric distribution shows a linear behavior with the radial coordinate. Here, the electric mechanisms are small in comparison to the thermal fluctuations. Nevertheless, when α >> 1, the electric distribution shows an oscillatory behavior from the center of the capillary system to the interface between the electrolytic fluid and the solid (wall). Figure 6b shows the flow enhancement versus wall stress as function of α.

Fig. 6

a Electrical charge distribution versus radial coordinate and b flow enhancement versus wall stress as a function of the dimensionless number α. The effect of the dimensionless number α is related to the energy within the system, aiming to reach its maximum peak

The numerical values used in the simulation are the same as Fig. 6a. When the system is dominated by the thermal fluctuation mechanism, the resonance peak curve is shifted to high values of the wall stress (α << 1), whereas the opposite behavior is clearly seen when the electrical forces dominate over the thermal forces. Two important points are summarized as follows: (1) The dimensionless numbers De_G and α play an important role in the kinetic and structural mechanisms within system. The first one deals with the electrical and internal yield stress mechanisms in the system, while the second one is a consequence of the electrical and thermal fluctuations. (2) One way to increase the energy to reach the maximum resonance is to modify the thermal fluctuations and the internal mechanisms of the material associated with kinetic, structural, and dissipative effects at high wall stress.

Concentration effects

Figure 7 shows the effect of CTAT concentration in weight percent on the fluidity (Fig. 7a) and the flow enhancement (Fig. 7b) versus applied wall stress. In Fig. 7a, the system shows two plateaus at low (initial fluidity) and high shear wall stress (terminal fluidity) and an intermediate power law region with an exponent close to the unit. As the CTAT concentration increases, the initial fluidity is reduced as expected. The onset of the power law region is also shifted to the right with the increase in concentration. The increase in concentration promotes a more entangled structure, which is why fluidity decreases as concentration. At a critical electrical wall stress, the internal tangential force and normal force destroy the fluid structure at moderate values of electrical wall stress (intermediate power law region). At a second critical electrical wall stress value, the system completely destroys its structure due to flow (reaching terminal fluidity). The primary effect of varying the CTAT weight concentration is to enhance the kinetic, structure, and viscoelastic effects through the dimensionless numbers De_G and φr. In Fig. 7b, the system displays resonance curves associated with the weight concentration. At every concentration, the system shows a single resonance peak at a particular electrical wall stress. The maximum of the resonance peak is associated with the extent of the power law region, with the highest peak occurring at the highest concentration. The key findings in Fig. 7b are summarized as follows:

• (a) The effect of the weight concentration is to promote a more entangled structure due to the influence of the driven force.

• (b) The smallest resonant curve is obtained at the lowest concentration. As the concentration increases, the system exhibits a more pronounced resonance zone, and the maximum peak becomes considerably larger than at the lowest concentration. The power peak is reached at high electrical wall stress.

• (c) On the other hand, the last two concentrations show the same power peak, i.e., the flow enhancement was independent of the driving force. This means that there is competition between the different disrupted states of the microstructure; however, the energy required to reach the same maximum is greater due to the presence of a similar structure in the system.

Fig. 7

The fluidity enhancement versus wall stress as a function of the CTAT weight percent concentration. The material properties used in the simulation are given in Table 1. The other parameters employed in the simulation are α = 0.1 and δ = 0.1

Yield stress mechanisms

In Fig. 8a, the fluidity function versus dimensionless yield stress number for different values of the dimensionless parameter α was plotted. Here, φ_r = 10⁻⁴. At small dimensionless Bingham number (Bi) values, the system behaves as a low viscous fluid. However, at critical Bi, the function shows a monotonically decreasing behavior, reaching a low fluidity value, which indicates a highly structured fluid (high viscosity). In contrast to the previous simulations, here the thermal fluctuation mechanisms induce a fast relaxation process. However, the electrical field dominates over the thermal fluctuations, determining the wall stress value at which the system experiments a transition from a lower to a higher structured state due to the flow. Figure 8b shows the flow enhancement versus wall stress as a function of the dimensionless number α. In all cases, the simulations show a characteristic resonance behavior and the effect of the α number is to shift the peaks to the right (high values of the Bingham number).

Fig. 8

a The fluidity and b flow enhancement versus Bingham number as a function of the electrical forces and thermal fluctuations through dimensionless number α. The thermal fluctuations induce the transition from the liquid to solid structure state

Inertial-viscoelastic regime: transfer function

In the case of a linear viscoelastic regime, the system shows resonance behavior, and for a critical frequency, it displays a dominant resonance peak followed by train of lower peaks (Fig. 9). The effect of the electrical-thermic forces through α enhances the dynamical response of the flow and stress transfer functions (T_F(ω), T_σ(ω)). Here, there is no flow enhancement, i.e., I = 0.

Fig. 9

The transfer functions versus frequency as a function of α

Pulsating volumetric flow versus time

Figure 10a shows the volumetric flow rate versus time. Here, the material parameters correspond to a shear thinning fluid with thermal mechanisms. Moreover, Fig. 10b shows the volumetric flow rate versus time as a function of the shear thinning mechanisms. The volumetric flow rates exhibit a constant behavior at small time values, and as time increases, the system begins to oscillate under an equilibrium value. In addition, the shear thinning mechanisms increase the volumetric flow up to a maximum value as the system evolves and to a minimum in a continuous oscillating behavior. It is clear when the shear thinning decreases, and the effect is the opposite.

Fig. 10

b The volumetric flow rate versus time for the shear thinning mechanisms. In b, the same simulations as in (a) are shown with different shear thinning forces. The shear thinning mechanisms have the effect of shifting the volumetric flow rate to low and high values by the effect of the reduction of the number of links, intermolecular bonds, or entanglements in the fluid structure

Local and global perturbation analysis

Figure 11a shows the effect of the concentration on the normalized flow enhancement curves; the effect of the concentration is to shift the curves to the right and increase the value of the maximum flow enhancement. A similar effect of the concentration is observed in Fig. 11b, where the non-local approximation was used. In the case of the non-local approximation, a minimum value appears in all the curves after passing the maximum value. This minimum was interpreted here as a requirement of more energy to move the fluid. The curves are also narrower in the bell region of the maximum. For a better comparison, Fig. 11c shows curves b from Fig. 11a and b where the minimum value for the non-local case is evident.

Fig. 11

Flow enhancement versus wall stress at first order in the regular perturbation

Important findings are summarized as follows:

• (a) The difference between the local and non-local perturbations is that the minimum was observed in the simulation of first-order perturbation, in contrast to what was reported previously (Herrera-Valencia et al. 2019).

• (b) This minimum is observed in the rheological constitutive equation that contains a Maxwell relaxation time which depends on the shear rate through the second invariant of the shear rate tensor.

• (c) Physically, this minimum can be interpreted as a consequence of the structural evolution associated to low and high relaxation mechanisms. These mechanisms are associated to the kinetic, structural, yield stress, thixotropic, and viscoelastic mechanisms.

Elastic mechanisms

Figure 12a shows the effect of the elasticity, through the dimensionless Weissenberg number, on the flow enhancement. The dimensionless numbers used in the simulation were φ_r = 0.1, De_G² = 7.8 × 10⁻⁴, and De_∞ = {0, 0.1, 1, 10}. As the value of the Weissenberg number increases, the system reflects the minimum value observed in the non-local approximation. It is clear that, when the elastic forces increase, the system shows a lower maximum flow enhancement value associated with the storage (elastic) mechanisms. This kind of behavior has been reported in random longitudinal vibrate pipes (Herrera et al. 2009) and in slip mechanisms. This effect is similar to the concentration effect observed in Fig. 11b, which is once again interpreted as an increase in the energy required to move the fluid and alter its structure due to the flow.

Fig. 12

a The flow enhancement versus the wall stress. b The flow enhancement versus wall stress versus CTAT weight concentration. The other numerical values employed in the simulation are (i) δ = 0.01 and (ii) α = 0.1. b The flow enhancement versus wall stress as a function of the weight concentration. The numerical values of the material parameters used in the simulation are given in Table 1

Figure 12b shows the flow enhancement versus the wall stress for different sample micellar concentrations with a fixed value of the Deborah numbers. This can be seen as a combined effect of concentration and elasticity. The effect of concentration is confirmed here as the curves shift to the right, and the value of the maximum value increases with increasing concentration. The shape of the resonance curves is highly affected by the combined effects of concentration and elasticity, resulting in a pulse-like curve with a characteristic minimum value.

The sharp transition from the maximum to the minimum value can be interpreted as thermodynamic transition associated to the relaxation and kinetic mechanisms.

Summary of the results

Finally, we summarize the key findings from the simulations (Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12), which illustrate the effect of the electrical field on the volumetric flow rate in the regimes of linear and non-linear viscoelasticity. This effect was analyzed as a function of the material parameters using dimensionless groups. We solve this physical problem using a new non-linear exponential thixo-viscoelasto-plasto rheological model, which describes changes of the fluid structure due to flow. The mean contributions are mention as follows:

Linear viscoelasticity

• The physics and rheology of the system can be represented through nine dimensionless numbers for the different mechanisms associated with the following: (i) infinity-viscoelastic (De_∞), (ii) structural (De_λ,), (iii) Helmholtz-Smoluchowski (De_HS), (iv) kinetic-structural (De_β), (v) shear thinning/thickening (φ_r), (vi) thixotropy and anti-thixotropic (φ_r, De_G = (De_HSDe_β)^1/2), (vii) yield stress mechanism (De_G), (viii) start-up/compliance (Re_ω0, De_λ, De_G = (De_HSDe_β)^−1/2, (ix) CTAT weight concentration (φ_r, De = (De_HSDe_β)^−1/2), (x) electric-thermal (α), and (xi) dispersion (β) mechanisms.

• At small deformations, the system is represented by two analytical transfer functions {T_F(ω), T_S(ω)} associated with the interactions between the driven electrical field force E(t) and the corresponding volumetric and stress-inertial outputs {Q(t),σ(t)}.

• In the viscoelastic regime, the electric-thermic mechanisms are coupled with the rheological compliance, dispersion, and start-up forces.

• At small viscoelastic and electric regimes, the transfer functions depend on the start-up mechanisms, rheology through fluidity Burgers operator, and the square of the alpha number α.

Non-linear viscoelasticity

• To solve the analytical coupled equations in the non-linear regime, a regular perturbation scheme to zeroth and first orders was proposed.

• The effect of the pulsatile electrical field is to enhance the volumetric flow rate as a function of the material conditions. The minimum value for a resonance behavior to occur is that the fluid undergoes a transition due to the normalized driving force (shear thinning mechanisms).

• The shear thickening mechanism shows the opposite effect, i.e., there is a drastic reduction in fluidity resulting in a decrease in the volumetric flow rate.

• The electrical mechanisms are associated with the energy required to reach the resonance peak. When the electrical field mechanism is weaker, the system requires more energy to reach the maximum. In contrast, when the electrical forces dominate over thermal mechanisms, the system needs less energy to reach the peak.

• The first-order perturbation shows a non-monotonic behavior, transitioning from maximum to a minimum value due to changes in the structure induced by flow. The minimum observed in the simulations can be attributed to structure instabilities, indicating a higher energy requirement for fluid flow.

• Electrical, thermal, kinetic, structure, viscosities at low and high shear rates, and concentration are associated to the thixotropy and the energy to reach the resonance peak.

• In the case of a high viscosity, the system is dominated by the inverse of a geometric Deborah number (σ_y =De_G⁻¹). This dimensionless number describes the transition from fluid to solid by effect of structural and high shear rate mechanisms, and it is related with two classical numbers (Papanastasiou (Pa) and Bingham (Bi)).

• When the fluid becomes more solid due to the elastic, concentration, and yield mechanisms, the maximum flow enhancement transitions from a smooth wide curve to a narrow cusp-shaped, accompanied by a characteristic minimum flow enhancement that indicates a higher energy requirement.

In our model, the dynamical response (peak and flow enhancement) is a consequence of the minimum and maximum thermal and electric mechanisms, which is regulated by the dimensionless number α. These mechanisms are in competition with the structural, kinetic shear thinning, shear thickening, thixotropy-rheopexy, and elasto-plasto forces manifested in the complex fluid. The rheological parameters of importance were (i) fluidities at low and high shear rate {φ₀, φ_∞}, elastic modulus G₀, structural relaxation time λ_s, and shear banding parameter {λ_B}. The specific ways to adapt these parameters are by changing the concentration and the molecular weight distribution of dissolved structural viscoelastic polymer chains. In the regime of linear viscoelasticity, to increase power peak amplitude, the thermal and inertial mechanisms must be less than the electric and viscoelastic mechanisms. In the regime of non-linear viscoelasticity, the flow enhancement is reached to shear thinning mechanisms. However, the effects of the electrical-thermal, kinetic, structure, and elasto-plasto mechanisms play an important role in thixotropy. To shift the position of the localized power plateau and width of the thermal-electric-inertia of the electroosmotic system (material-rheology mechanisms) must be tuned. To widen the power peak, the fluidities and characteristic structural-kinetic-flow times must be modified.

Conclusions

Analytical solutions in microchannels for the electroosmotic flow of viscoelastic fluids obeying a general exponential rheological model have been derived. This model couples a non-linear generalization of the Burgers model with a structured exponential equation to take into account the change in the structure by effect of the flow. The exponential structure model is proposed in order to consider the construction and destruction of the fluid microstructure by the effect of the flow. Symmetric boundary conditions with equal zeta potentials at the walls were assumed. A non-linear Poisson-Boltzmann equation governing the electrical double-layer field was included in the momentum equations.

An evaluation of the present model predictions based on transfer function and flow enhancement indicates that the new-exponential thixo-viscoelasto-plasto model possesses the necessary physics to describe the electro-thermal-inertia-rheological linear and non-linear flow enhancement conversion. The non-linear model presented here is only valid for electric fields and inertial mechanisms of sufficiently small amplitude, since under higher amplitude, non-linear instability effects may play a role. The present original research, theory model, and computations contribute to the evolving fundamental understanding of complex fluids through thermal-electro-inertial-rheological couplings.

Main findings are summarized as follows:

• The system is represented by two analytical transfer functions {T_F(ω), T_S(ω)} associated with the interactions between the driven electrical field force E(t) and the corresponding volumetric and stress-inertial outputs {Q(t),σ(t)}.

• The dynamical response (peak and flow enhancement) is a consequence of the minimum and maximum thermal and electric mechanisms, which is regulated by the dimensionless number α.

• The effect of the pulsatile electrical field is to enhance the volumetric rate flow as a function of the material conditions. The minimum condition to have the resonance behavior is that the fluid experiments transitions by effect of the normalized driven force (shear thinning mechanisms).

• The shear thickening mechanism shows the opposite effect, i.e., there is a drastic reduction of the fluidity as a consequence of this the volumetric rate flow decrease.

• The electrical mechanisms are associated with the energy required to reach the resonance peak. When the electrical field mechanism is smaller than the thermal one, the system needs more energy to reach the maximum. In contrast, when the electrical forces dominate over the thermal mechanisms, the system needs less energy to reach the maximum peak.

• The effect of the thermal mechanism is to augment the kinetic energy of the particles in the fluid, and thus, more energy is necessary to orient them in the flow direction.

• The first-order perturbation shows a non-monotonic behavior from maximum to minimum associated to the transition of the structure by effect of flow. The minimum showed in the simulations can be associated with the structure instabilities and indicates a higher energy requirement to make the fluid flow.

• In the case of a high viscosity, the system is dominated by the inverse of a geometric Deborah number (σ_y =De_G⁻¹). This dimensionless number describes the transition from fluid to solid by the effect of structural and high shear rate mechanisms, and it is related with two classical numbers (Papanastasiou (Pa) and Bingham (Bi)).

• When the fluid becomes more solid by the effect of the elastic, concentration, and yield mechanisms, the flow enhancement maximum transitions from a smooth wide curve to a narrow cusp one and a characteristic minimum flow enhancement which indicates a higher energetic requirement.

Model limitations

It is worth mentioning the following model limitations: It is worth mentioning the following model limitations (de Sousa Mendes, 2007, Matus-Rivas and Rey, 2016, Matus-Rivas and Rey, 2017, Matus-Rivas and Rey, 2019a, Matus-Rivas and Rey, 2019b)

• It does not predict second difference of normal stresses.

• It is restricted to the diluted or semi-diluted regime.

• It does not couple concentration or temperature effects.

• It does not contain the orientation through a vector director n.

Future work

It would be worthwhile to extend the theoretical predictions of the effects of the electrical-thermal, thixo-viscoelasto-plasto mechanism with mass transfer and carry out experimental studies on human blood pathologies such as (i) diabetic blood, (ii) hepatic cirrhosis, (iii) anemic blood, (iv) umbilical cord blood, and (v) (Ponalagusamy and Ramakrishna 2020). Additionally, the effects of instabilities, described by cubic equations in shear rate, shear stress, and shear banding mechanisms, play an important role and should be addressed using this new equation (Fig. 11). Therefore, a second perturbation and experiments with structured fluids must be conducted (Marttyushev and Birzina 2008).

A model coupling orientation effects such as those occurring in liquid crystals will be presented in a future (Matus-Rivas and Rey, 2016; Matus-Rivas and Rey, 2017; Matus-Rivas and Rey, 2019a; Matus-Rivas and Rey, 2019b). Second-order predictions for this system will be evaluated also in future work.

Appendices

Appendix 1. Rheological equation of state

The basic assumption of the model is given by a kinetic-physic equation, given by the following rheological equation of state associated to the upper-convected Maxwell equation.

$$S\left(r,t\right)\boldsymbol{\sigma} +\frac{1}{G_0}\overset{\nabla }{\boldsymbol{\sigma}}=2{D}$$

(91)

The structural function can be modeled in terms of a population balance model, i.e.,

$$\frac{dS\left(r,t\right)}{dt}={\left(\frac{dS\left(r,t\right)}{dt}\right)}_0-{\left(\frac{dS\left(r,t\right)}{dt}\right)}_{\infty }$$

(92)

At low shear rate, the relaxation structure model is given by the following Arrhenius-type equation:

$${\left(\frac{dS\left(r,t\right)}{dt}\right)}_0={K}_1{e}^{-{\beta}_1f\left({Invariant}\right)}$$

(93)

The kinetic expression at high shear rate can be expressed in a similar form

$${\left(\frac{dS\left(r,t\right)}{dt}\right)}_{\infty }={K}_2{e}^{\hbox{-} {\beta}_2f\left({Invariant}\right)}$$

(94)

In Eqs. (93) and (94), K₁ and K₂ are kinetic constants associated to the velocity to change the structure by effect of an external force. The parameters β₁ and β₂ can be identified such as constants related with the irreversible work to break down the structure of the system. Finally, f(invariant) is a function of an invariant. The kinetic balance is given by

$$\frac{dS\left(r,t\right)}{dt}={K}_1{e}^{\hbox{-} {\beta}_1f\left({Invariant}\right)}-{K}_2{e}^{\hbox{-} {\beta}_2f\left({Invariant}\right)}$$

(95)

The exponential functions can be developed in a Taylor’s expansion until the first order, and the following expression is obtained:

$$\frac{dS\left(r,t\right)}{dt}={K}_1\left(1-{\beta}_1f\left({Invariant}\right)\right)-{K}_2\left(1-{\beta}_2f\left({Invariant}\right)\right)$$

(96)

So, grouping all the terms of Eq. (96),

$$\frac{dS\left(r,t\right)}{dt}={K}_1-{K}_2-{K}_1{\beta}_1f\left({Invariant}\right)+{K}_2{\beta}_2f\left({Invariant}\right)$$

(97)

And

$$\frac{dS\left(r,t\right)}{dt}={K}_1-{K}_2+\left({K}_1{\beta}_1-{K}_2{\beta}_2\right)\left(-f\left({Invariant}\right)\right)$$

(98)

Identifying the following variables,

$${K}_1=\frac{\varphi_0}{\lambda_{{c}}};{K}_2=\frac{\varphi }{\lambda_{{c}}};{\beta}_1={\varphi}_{{r}}{\beta}_2;{\beta}_2=k{\lambda}_{{c}}$$

(99)

And

$${\varphi}_{{r}}={\varphi}_0/{\varphi}_{\infty }$$

(100)

The structural balance is given by

$$\frac{dS\left(r,t\right)}{dt}=\frac{\varphi_0-S\left(r,t\right)}{\lambda_{{c}}}+\left({\varphi}_0{\varphi}_{{r}}-S\left(r,t\right)\right)\left(-\frac{\beta_2}{\lambda_{{c}}}f\left({Invariant}\right)\right)$$

(101)

And

$${\varphi}_0{\varphi}_{{r}}={\varphi}_{\infty };{k}=\frac{\beta_2}{\lambda_{{c}}};-f\left({Invariant}\right)= tr\left(\sigma \cdot D\right)$$

(102)

Then,

$$\frac{dS\left(r,t\right)}{dt}=\frac{\varphi_0-S\left(r,t\right)}{\lambda }+{k}\left({\varphi}_{\infty }-S\left(r,t\right)\right) tr\left(\sigma \cdot D\right)$$

(103)

From Eq. (103), the structural balance can be expressed in terms of an exponential function

$$\left(1+{f}_{\lambda}\left(\beta tr\left(\sigma \cdot D\right)\right)\frac{d}{dt}\right)S\left(r,t\right)/{\varphi}_{\infty }=\frac{\varphi_{{r}}+\beta tr\left(\sigma \cdot D\right)}{1+\beta tr\left(\sigma \cdot D\right)}$$

(104)

And the relaxation function

$${f}_{\lambda}\left(\beta tr\left(\sigma \cdot D\right)\right)=\frac{\lambda_{{c}}}{1+\beta tr\left(\sigma \cdot D\right)}\cong \frac{\lambda_{{c}}}{{Exp}\left(\beta tr\left(\sigma \cdot D\right)\right)}={\lambda}_{{c}}{Exp}\left(-\beta tr\left(\sigma \cdot D\right)\right)$$

(105)

Combining the last equations, we have

$$S\left(r,t\right)/{\varphi}_{\infty }=\frac{{Exp}\left[\left({\varphi}_{{r}}-1\right){f}_{\lambda}\right]}{1+{f}_{\lambda}\frac{d}{dt}}$$

(106)

In the kinetic equation (Eq. 106) and the rheological equation of state, we have

$${Exp}\left[\left(\varphi r-1\right){f}_{\lambda}\right]\boldsymbol{\sigma} +\frac{1}{\varphi_{\infty }{G}_0}\left(1+{f}_{\lambda}\frac{d}{dt}\right)\overset{\nabla }{\boldsymbol{\sigma}}=\frac{2}{\varphi_{\infty }}\left(1+{f}_{\lambda}\frac{d}{dt}\right){D}$$

(107)

And generalizing the last expression

$${Exp}\left[\left(\varphi r-1\right){f}_{\lambda}\right]\boldsymbol{\upsigma} +\frac{1}{\varphi_{\infty }{G}_0}\overset{\nabla }{\boldsymbol{\upsigma}}+\frac{f_{\lambda }}{\varphi_{\infty }{G}_0}\overset{\nabla \nabla }{\boldsymbol{\upsigma}}=\frac{2}{\varphi_{\infty }}\left({D}+{f}_{\lambda}\overset{\nabla }{{D}}\right)$$

(108)

Equation (108) serves as the rheological equation of state in this research and can be deduced through a structural balance and structural energy of the system using an Arrhenius equation. This energy is used to describe the energy required (viscous or viscoelastic irreversible work to break down the structure). This is similar to Eyring equation used to describe the rate of a reaction: K = K₀Exp[−ΔG/RT] = K₀ Exp [−βσ:D] = K₀ Exp [−βtr(σ⋅D)].

Appendix 2

In this section, the volumetric flow rate as function of the electrical and thermal fluctuations in the regime of small shear rate is analyzed. The mean equation is given by the following linear differential equation:

$$\left\{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+{i}^2{\operatorname{Re}}_{\omega}{O}_{\varphi}^{{B}}\left(\frac{\partial }{\partial t}\right)\frac{\partial }{\partial t}\right\} vz\left(r,t\right)={O}_{\varphi}^{{B}}\left(\frac{\partial }{\partial t}\right){\alpha}^2\frac{I_0\left(\alpha {r}\right)}{I_0\left(\alpha \right)}E(t)$$

(109)

The mean equation is given by the following linear differential equation:

$$\left\{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+{\left(i\beta \right)}^2\right\} vz\left(r,\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(110)

The parameter, β, given in Eq. (110) is defined in the following form:

$${\beta}^2=i{\operatorname{Re}}_{\omega}\cdot \omega \cdot {O}_{\varphi}^{{B}}\left(i\omega \right)$$

(111)

The non-homogeneous contribution is obtained by solving the parametric differential equation.

$$\left\{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+{\left(\ i\beta \right)}^2\right\}{v}_{{H}}z\left(r,\omega \right)=0$$

(112)

The solution of Eq. (112) is given in terms of a Bessel function:

$${v}_{{H}}z\left(r,\omega \right)={C}_1{I}_0\left(\beta r\right)+{C}_2{K}_0\left(\beta r\right)$$

(113)

In Eq. (113), {I₀, K₀} are the modified Bessel function of first and second kinds, respectively:

$$\left\{\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}+{\left(i\beta \right)}^2\right\}{v}_{{P}}z\left(r,\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(114)

To solve Eq. (114), it is assumed that a solution for V_pz(r,ω) is in the form:

$${v}_{{P}}z\left(r,\omega \right)={AI}_0\left(\alpha r\right)$$

(115)

In Eq. (115), I₀ is the first kind modified Bessel function and it satisfies the following expression:

$$\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial r}{v}_{{P}}z\left(r,\omega \right)={\left(i\alpha \right)}^2{v}_{{P}}z\left(r,\omega \right)$$

(116)

Combining the last Eqs. (114) and (116), the following expression is obtained:

$$\left({\left(i\upbeta \right)}^2+{\left(i\alpha \right)}^2\right){v}_{{P}}z\left(r,\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(117)

Then,

$$\left({\left(i\beta \right)}^2+{\left(i\alpha \right)}^2\right){AI}_0\left(\alpha r\right)={O}_{\varphi}^{{B}}\left(i\omega \right){\alpha}^2\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(118)

Factor out the constant A,

$$A={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\frac{1}{I_0\left(\alpha \right)}E\left(\omega \right);{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2\ne 0$$

(119)

Then, the particular axial velocity is found:

$${v}_{{P}}z\left(r,\omega \right)={AI}_0\left(\alpha r\right)={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(120)

The total axial velocity is given by the following analytical expression:

$$vz\left(r,\omega \right)={C}_1{I}_0\left(\beta r\right)+{C}_2{K}_0\left(\beta r\right)+{O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(121)

Apply the boundary conditions, (i) r = 0; ∣vz∣≤ M, and (ii) r = 1, vz = 0, so the constants C₁ and C₂ take the following form:

$${C}_1=-{O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\frac{1}{I_0\left(\alpha \right)}E\left(\omega \right)$$

(122)

And

$${C}_2=0$$

(123)

Substituting the constants in Eqs. (122) and (123) into the general solution Eq. (121),

$$vz\left(r,\omega \right)={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{\alpha^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left(\frac{I_0\left(\alpha r\right)}{I_0\left(\alpha \right)}-\frac{I_0\left(\beta r\right)}{I_0\left(\beta \right)}\right)E\left(\omega \right)$$

(124)

Integrating the above equation over a cross section area,

$$Q=2\int\limits_0^1\int\limits_0^1 vz(r) drd\theta ={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{2{\alpha}^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left(\frac{I_1\left(\alpha \right)/\alpha}{I_0\left(\alpha \right)}-\frac{I_1\left(\beta \right)/\beta}{I_0\left(\beta \right)}\right)E\left(\omega \right)$$

(125)

The transfer function is given by the following expression:

$${T}_{{F}}\left(\omega \right)=\frac{Q\left(\omega \right)}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{F}}\right]+{iIm}\left[{T}_{{F}}\right]={O}_{\varphi}^{{B}}\left(i\omega \right)\frac{2{\alpha}^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left(\frac{I_1\left(\beta \right)/\beta}{I_0\left(\beta \right)}-\frac{I_1\left(\alpha \right)/\alpha}{I_0\left(\alpha \right)}\right)$$

(126)

Equation (126) relates the electrical driving force (input) with the volumetric flow rate (output).

Shear stress

The shear stress can be calculated from Eq. (121),

$${\sigma}_{{w}}=-{\left.{\sigma}_{{r}{z}}\right|}_{{r}=1}=-{\left.\frac{1}{{{O}}_{\varphi}\left(i\omega \right)}\frac{\partial vz\left(r,\omega \right)}{\partial r}\right|}_{{r}=1}$$

(127)

Substituting the axial velocity, Eq. (124) into Eq. (127), the following expression is obtained:

$${T}_{{S}}\left(\omega \right)=\frac{\sigma_{{w}}}{E\left(\omega \right)}=\operatorname{Re}\left[{T}_{{S}}\right]+{iIm}\left[{T}_{{S}}\right]=\frac{{\left(i\alpha \right)}^2}{{\left(i\beta \right)}^2+{\left(i\alpha \right)}^2}\left[\alpha \frac{I_1\left(\alpha \right)}{I_0\left(\alpha \right)}\hbox{-} \beta \frac{I_1\left(\beta \right)}{I_0\left(\beta \right)}\right]$$

(128)

Equation (128) relates the electrical driven force (input) with the inertial-viscoelastic wall stress (output).