Introduction

The quest for finding appropriate closed-form constitutive models to represent certain material behaviors has witnessed decades of rigorous research, which was initially galvanized mainly by those observed behaviors (Bingham 1916; Morrison 2001; Bird et al. 1987). Viscous, elastic, plastic, and thixotropic behaviors are commonly capable of categorizing material responses to an imposed actuation. In particular, viscoelastic materials, in which the stress response decays over some characteristic time, inherit the viscous response of fluids and the elastic one from solids. The time for the decay to occur is defined as the relaxation time of the fluid, i.e., the time needed for the material to exhibit an elastic response and relax, which leaves the material with a steady-state viscous response. Canonically, the simplest constitutive model that captures linear viscoelasticity is the Maxwell modelFootnote 1 (Morrison 2001), whose (scalar) shear stress response (\(\sigma _{21}=\sigma \)) under the imposition of a simple shear is as follows:

$$\begin{aligned} \sigma (t)+\frac{\eta }{G}\frac{\partial \sigma (t)}{\partial t}=-\eta \dot{\epsilon }(t) \end{aligned}$$
(1)

where \(\eta \) and G are the viscosity (in Pa\(\cdot \)s) and elastic modulus (in Pa), respectively, the ratio of which (\(\eta /G\)) may be thought of as a relaxation time, t is time (in s), and \(\dot{\epsilon }(t)\), in s\(^{-1}\), is the imposed deformation rateFootnote 2. In fact, the Maxwell model is derived by assembling a spring (representative of the elastic response) and a dashpot (the viscous response) in series, superimposing the deformation (\(\epsilon (t)\)) of these two elements, and solving for \(\sigma (t)\). Polymer melts with a small and narrowly distributed molecular weight under small deformations are adequately modeled by the Maxwell constitutive equation. In another canonical model, the Kelvin-Voigt assembly considers the spring-dashpot elements stacked in parallel, which is suitable for creep (stress-controlled) experiments, for instance. While these simple models are based on a single characteristic relaxation time, in real-world viscoelastic fluids, a wide range of relaxation times are commonly present. Classically, this can be addressed by assembling a number of spring-dashpot (Maxwell) branches in parallel and thus capturing a range of relaxation times, also known as the generalized Maxwell model. On the other hand, in many rheologically relevant materials such as gels and worm-like micellar solutions and a range of polymeric systems, the material exhibits a power-law response, i.e., \(\epsilon (t)\propto t^a\). Such power-law responses are not well described by canonical rheological models such as the Maxwell or Kelvin-Voigt models (Tschoegl 2012; Jaishankar and McKinley 2013).

As mentioned above, the viscoelastic response inherits the elastic response of a solid (\(\sigma (t)\propto \epsilon \)) and the viscous behavior of a Newtonian fluid (\(\sigma (t)\propto \frac{\partial \epsilon }{\partial t}\)). Scott-Blair (Scott-Blair 1947) proposed a compact way to describe viscoelasticity by borrowing the concept of fractional derivatives (Stankiewicz 2018; Jaishankar and McKinley 2013):

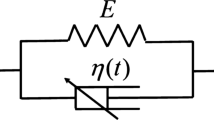
$$\begin{aligned} \sigma (t) = E\tau ^\alpha \frac{\textrm{d}^{\alpha }\epsilon (t)}{{\textrm{d}t}^{\alpha }}=\mathbb {V}\frac{\textrm{d}^{\alpha }\epsilon (t)}{{\textrm{d}t}^{\alpha }} \end{aligned}$$
(2)

where E and \(\tau \) are the elastic modulus (in Pa) and relaxation time (in s), respectively, and \(0\le \alpha \le 1\) is the fractional derivative order, effectively creating an element that interpolates between the constitutive responses of a spring and a dashpot; see Fig. 1. Such elements are usually referred to as Scott-Blair or spring-pot elements. In this formalism, the product of E and \(\tau ^\alpha \) (in Pa\(\cdot \)s\(^\alpha \)) may be thought of as a quasi-property, \(\mathbb {V}\), whose unit depends on the fractional derivative. The seemingly unphysical perception of this quasi-property (and its non-integer dimension in time) may be justified by the fact that \(\mathbb {V}\) represents the firmnessFootnote 3 of a material (Scott-Blair and Coppen 1942).

Fig. 1
figure 1

Schematic of a Scott-Blair (spring-pot) element, \(\sigma (t)\propto \frac{\textrm{d}^\alpha \epsilon (t)}{\textrm{d}t^\alpha }\), that compactly describes a material that embodies both solid (\(\alpha =0\)) and viscous (\(\alpha =1\)) responses

Full size image

Fruitful efforts have been made to approximate (and model) the observed behavior of different fluids using the concept of fractional derivatives. Highly anomalous butyl rubber (Scott-Blair 1947), soft particulate gels (Bantawa et al. 2022), cheese (Bonfanti et al. 2020; Faber et al. 2017), Xanthan gum (Jaishankar and McKinley 2014), and biological samples such as highly viscoelastic bovine serum albumin (BSA) (Jaishankar and McKinley 2013) have been successfully modeled with respective fractional models, while the classical counterparts of these models often require an exceedingly large number of the canonical Maxwell (or Kelvin-Voigt) elements and thus circumscribing the applicability of classical approaches to model viscoelastic samples with power-law responses (Tschoegl 2012; Jaishankar and McKinley 2013). Consistent and approachable methods, therefore, are called for to identify fractional models apposite to such viscoelastic samples. The issue, however, is that solution of fractional constitutive models, compared to classical ordinary differential equations that are used in rheological constitutive models, is far from trivial. As such, platforms that can automatically solve for different forms of fractional models may pave the way for further development of this class of compact models.

In a forward problem, a constitutive equation, e.g., a fractional viscoelastic model (FVEM), is at hand with all the initial conditions and parametric information, i.e., the fractional derivative order (\(\alpha \)) and quasi-properties, and the task is to solve for a rheological property such as \(\sigma (t)\). Several methods have been proposed and employed in the literature to solve FVEMs, such as the Laplace transform (Mainardi 2010; Feng et al. 2020; Fang et al. 2020), finite-difference (Shen 2020; Lin et al. 2007; Diethelm et al. 2005), finite-element (Alotta et al. 2018), and the Adomian decomposition method (Tripathi et al. 2010), among others. However, in inverse problems, measurable observations are gathered from a sample with missing information about the constitutive equation that governs the rheological process, and the goal is to recover those missing parameters by leveraging the collected data. The algorithms mentioned above, however, often struggle in the face of inverse problems and ill-posedness (Jagtap et al. 2022), meaning that a solution may be either nonexistent or not unique. The parameter recovery of generalized Maxwell models (by stacking finite spring-dashpot units) can quickly become prohibitive as the number of units increases. Data-driven methodologies, on the other hand, can tolerate ill-posedness and thus are suitable choices when tackling inverse (and forward) problems (Chen et al. 2020) to provide unified platforms for the identification and discovery of FVEMs.

Machine learning platforms have shown promise to obtain forward and inverse solutions of differential equations alike (Raissi et al. 2019; Karniadakis et al. 2021; Raissi et al. 2020; Raissi 2018; Karnakov et al. 2022; Li et al. 2022). By inducing physical intuition into the training process, physics-informed neural networks (PINNs) were developed for the forward and inverse analysis of many scientific problems (Cai et al. 2022; Lawal et al. 2022; Ishitsuka and Lin 2023; Asrav and Aydin 2023; Tang et al. 2023). By implicitly (or explicitly) informing the neural net (NN) of a rheological constitutive model, several rheology-informed neural network (RhINN) platforms were recently developed (Mahmoudabadbozchelou and Jamali 2021; Mahmoudabadbozchelou et al. 2021, 2022b, a; Saadat et al. 2022). Other efficient and promising data-driven algorithms and tools have also been developed to recover parameters in rheological problems of interest (Freund and Ewoldt 2015; Armstrong et al. 2017; Singh et al. 2019; Thakur et al. 2022; Reyes et al. 2021). Generally, RhINNs can be used to detect, construct, and solve a variety of rheological constitutive models in the form of ordinary differential equations. Nonetheless, as these platforms have not been developed and tested for fractional derivatives, this work specifically focuses on the identification of FVEMs using RhINNs in an inverse implementation.

Here, as a subset of all the possible combinations of fractional viscoelastic models, three configurations of FVEMs, namely, the fractional Maxwell model (FMM), fractional Kelvin-Voigt model (FKVM), and fractional Zener model (FZM), which is a fractional Maxwell unit connected to a spring-pot in parallel are selected. The goal is to recover the fractional derivative order of each spring-pot element, assuming that other quasi-properties are known from previous experiments or rheometry. This task is far from trivial, as inverse-problem solvers for fractional constitutive equations are yet to be popularized, and the pressing need for material discovery propels the numerical and data-driven methods to confine the parameter space of inverse problems and eventually recover those parameters. While these cases by no means encompass all the possible combinations and intricacies of FVEMs, the selected configurations nonetheless hand valuable information about the applicability of RhINNs in solving fractional inverse problems. The ultimate goal is to develop a generalizable platform for the data-driven solution of fractional constitutive models without compromising accuracy as the complexity of the underlying response/model increases.

Problem setup and methodology

In “Fractional Maxwell model,” “Fractional Kelvin-Voigt model,” and “Fractional Zener model,” the fractional Maxwell, Kelvin-Voigt, and Zener models are introduced, respectively, in terms of their fractional differential equations (FDEs) and analytical solutions. These three models are also mechanistically depicted in Fig. 2. Then, in “Rheology-informed neural networks and fractional derivatives,” the concepts behind rheology-informed neural networks (RhINNs) and the numerical procedure to solve FDEs are discussed.

In this work, the analysis is performed by studying the synthetically generated data using the analytical solutions (as opposed to seeking digitized experimental measurements from the literature) because by doing so, the ground truth fractional derivative orders can be tuned to evaluate the robustness in the recovery of fractional derivative orders.

Fig. 2
figure 2

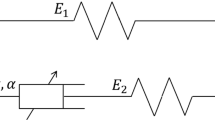
Schematic description of the fractional a Maxwell, b Kelvin-Voigt, and c Zener models using spring-pot elements. The objective of this work is to recover the fractional derivative orders, i.e., \(\alpha \) and \(\beta \) in fractional Maxwell and Kelvin-Voigt models and \(\alpha \), \(\beta \), and \(\gamma \) in the fractional Zener model

Full size image

Fractional Maxwell model

As mentioned in “Introduction,” each Scott-Blair element is characterized by two parameters (E and \(\tau \)) and a fractional derivative order, \(\alpha \). In the fractional Maxwell model (FMM), two Scott-Blair (spring-pot) elements ((\(E_1,\tau _1,\alpha \)), (\(E_2,\tau _2,\beta \))) are connected in series, similar to the element arrangement in the classical Maxwell model; see Fig. 2a. By assuming equality of stress experienced by each Scott-Blair element (\(\sigma _1=\sigma _2=\sigma \)) and additivity of deformations (\(\epsilon =\epsilon _1+\epsilon _2\)), one may derive the Maxwell FDE (Schiessel et al. 1995; Schiessel and Blumen 1993):

$$\begin{aligned} \sigma (t) + \tau ^{\alpha -\beta }\frac{\textrm{d}^{\alpha -\beta }\sigma (t)}{{\textrm{d}t}^{\alpha -\beta }} = E\tau ^{\alpha }\frac{\textrm{d}^{\alpha }\epsilon (t)}{{\textrm{d}t}^{\alpha }} \end{aligned}$$
(3)

where \(\tau = (E_1\tau _1^{\alpha }/E_2\tau _2^{\beta })^{1/(\alpha -\beta )}\) and \(E = E_1(\tau _1/\tau )^{\alpha }\). In deriving Eq. 3, it is assumed that \(0 \le \beta < \alpha \le 1\) without loss of generality (Schiessel et al. 1995).

The solution of Eq. 3 upon imposing a step strain (\(\epsilon (t)=\epsilon _0 H(t)\), where H(t) is the Heaviside step function) can be derived analytically, and the relaxation modulus, G(t), in Pa, is expressed as follows:

$$\begin{aligned} G(t) = \frac{\sigma (t)}{\epsilon _0} = E \left( \frac{t}{\tau }\right) ^{-\beta } \mathcal {M}_{\alpha -\beta , 1-\beta }\left( -\left( \frac{t}{\tau }\right) ^{\alpha -\beta }\right) \end{aligned}$$
(4)

where \(\mathcal {M}_{\kappa ,\mu }\) is the generalized Mittag-Leffler function defined as follows (Schiessel et al. 1995):

$$\begin{aligned} \mathcal {M}_{\kappa , \mu }(x) = \sum _{n=0}^{\infty } \frac{x^{n}}{\Gamma (\kappa n+ \mu )} \end{aligned}$$
(5)

where \(\Gamma (.)\) is the gamma function.

In “Fractional Maxwell model,” the solution of Eq. 3 under a unit step strain (\(\epsilon _0=1\)) is sought. In other words, \(\epsilon (t)=H(0_+)=1\), and \(G(t)=\sigma (t)\). Therefore, the solution of Eq. 3 and the analytical relaxation modulus (Eq. 4) coincide and are directly comparable.

Fractional Kelvin-Voigt model

For the case of the fractional Kelvin-Voigt model (FKVM), two Scott-Blair elements (with parameters similar to that in “Fractional Maxwell model”) are stacked in parallel; see Fig. 2b. The deformation, similar to the classical Kelvin-Voigt model, is identical in each branch, and the stresses are additive. By simply adding the stress response of two Scott-Blair elements (Eq. 2) and setting \(\epsilon _1=\epsilon _2=\epsilon (t)\), one may derive the stress response of FKVM (Schiessel et al. 1995):

$$\begin{aligned} \sigma (t) = E\tau ^{\alpha }\frac{{\textrm{d}}^{\alpha }\epsilon (t)}{{\textrm{d}t}^{\alpha }} + E\tau ^{\beta }\frac{{\textrm{d}}^{\beta }\epsilon (t)}{{\textrm{d}t}^{\beta }} \end{aligned}$$
(6)

where E and \(\tau \) continue to be defined as in “Fractional Maxwell model”. The creep compliance, J(t), in Pa\(^{-1}\), is then defined as follows:

$$\begin{aligned} \textrm{J}(t) =\frac{\epsilon (t)}{\sigma _0} =E^{-1}\left( \frac{t}{\tau }\right) ^{\alpha }\mathcal {M}_{\alpha -\beta , 1+\alpha }\left( -\left( \frac{t}{\tau }\right) ^{\alpha -\beta }\right) \end{aligned}$$
(7)

where \(\sigma _0\) is the step-stress in a creep experiment. By assuming a unit step-stress (\(\sigma (t)=\sigma _0=1\)), the solution of Eq. 6 (\(\epsilon (t)\)) and the exact solution (Eq. 7) will become identical.

Fig. 3
figure 3

Schematic illustration of the RhINN architecture. In this figure, the material response is assumed to be the relaxation modulus, G(t), which is applicable to the fractional Maxwell and fractional Zener models. For the fractional Kelvin-Voigt model, this output is replaced with the creep compliance, J(t). The fitting parameters (Params) in RhINNs, which are the fractional derivative orders, are defined trainbale

Full size image

Fractional Zener model

The classical Zener model consists of a Maxwell model in parallel with a spring. In the fractional Zener model (FZM), three fractional elements with parameters \((E_1, \tau _1, \alpha )\), \((E_2, \tau _2, \beta )\), and \((E_3, \tau _3, \gamma )\) are arranged, as displayed in Fig. 2c. The total mechanical response of the model with constraints \(0 \le \beta < \alpha \le 1\) and \(0 \le \gamma \le 1\), and by setting \(\tau = (E_1\tau _1^{\alpha }/E_2\tau _2^{\beta })^{1/(\alpha -\beta )}\), \(E_0 = E_1(\tau _1/\tau )^{\alpha }\), and \(E = E_3(\tau _3/\tau )^{\gamma }\) is given as follows (Schiessel et al. 1995):

$$\begin{aligned} \sigma (t) + \tau ^{\alpha -\beta }\frac{\textrm{d}^{\alpha -\beta }\sigma (t)}{{\textrm{d}t}^{\alpha -\beta }} = E_0\tau ^{\alpha }\frac{\textrm{d}^{\alpha }\epsilon (t)}{{\textrm{d}t}^\alpha } + E\tau ^{\gamma }\frac{\textrm{d}^{\gamma }\epsilon (t)}{{\textrm{d}t}^{\gamma }} + E\tau ^{\gamma +\alpha -\beta }\frac{\textrm{d}^{\gamma +\alpha -\beta }\epsilon (t)}{{\textrm{d}t}^{\gamma +\alpha -\beta }} \end{aligned}$$
(8)

The relaxation modulus, G(t), of FZM under a stress-relaxation test with constraints mentioned above is given by the following:

$$\begin{aligned} \textrm{G}(t) = E_0 \left( \frac{t}{\tau }\right) ^{-\beta }\mathcal {M}_{\alpha -\beta , 1-\beta }\left( -\left( \frac{t}{\tau }\right) ^{\alpha -\beta }\right) + E\frac{\left( \frac{t}{\tau }\right) ^{-\gamma }}{\Gamma (1-\gamma )} \end{aligned}$$
(9)

Similar to FMM, a stress relaxation test under a unit step strain is assumed here, i.e., \(\epsilon (t)=H(0_+)=1\), and \(G(t)=\sigma (t)\). Thus, the solution of Eq. 8 and the analytical solution (Eq. 9) can be compared side-by-side.

It is worth mentioning that the range of material response using the analytical solutions, i.e., Eqs. 4, 7, and 9, highly depends on the fractional derivative orders (and quasi-properties, which are assumed given here; see the outset of “Results and discussion”). Consequently, to keep the discussion concise, readers are encouraged to refer to the material response plots provided in “Results and discussion” for more quantitative information relevant to the respective data sets.

Rheology-informed neural networks and fractional derivatives

For all three cases introduced above, the only input to the neural network (NN) is time, t, while the NN output is the material response, which is \(\sigma (t)\) (or G(t)) for the FMM and FZM cases, and \(\epsilon (t)\) (or J(t)) for the FKVM; see Fig. 3. The neural network is composed of several hidden layers, each containing a predefined number of neurons. The trainable variables, i.e., the weights and biases of the neurons plus the fitting parameters (Params in Fig. 3), which are the fractional derivative orders in each case, are learned by minimizing a composite loss function:

$$\begin{aligned} \phi =\phi _d + \phi _{f} \end{aligned}$$
(10)

where \(\phi _d\) is the loss due to the discrepancy between the predicted material response (\(G_p\)Footnote 4) and the ground truth material response (\(G_{gt}\)), defined as the following mean-squared error (MSE):

$$\begin{aligned} \phi _d = \text {MSE}(G_p, G_{gt})=\frac{1}{n}\sum _{k=1}^{n} (G_{p,k}-G_{gt,k})^2 \end{aligned}$$
(11)

Moreover, the residual (Res in Fig. 3) between the two sides of each FDE (\(\phi _f\)) can be calculated, which is also a mean squared error. As an example, this residual for the case of FMM will be as follows:

$$\begin{aligned} {\begin{matrix} \phi _{f} &{} = \frac{1}{n_{r}}\sum _{i=1}^{n_{r}} \left( \sigma _{p,i} + \tau ^{\alpha -\beta }\frac{\textrm{d}^{\alpha -\beta }\sigma _{p,i}}{{\textrm{d}t}^{\alpha -\beta }} - E\tau ^{\alpha }\frac{\textrm{d}^{\alpha }\epsilon _i}{{\textrm{d}t}^{\alpha }}\right) ^2 \\ &{} = \frac{1}{n_{r}}\sum _{i=1}^{n_{r}} \left( \sigma _{p,i} + \tau ^{\alpha -\beta }\frac{\textrm{d}^{\alpha -\beta }\sigma _{p,i}}{{\textrm{d}t}^{\alpha -\beta }} - E\tau ^{\alpha }\frac{t_i^{-\alpha }}{\Gamma (1-\alpha )}\right) ^2 \end{matrix}} \end{aligned}$$
(12)

where \(n_r\) is the number of residual points that are used to define artificial input arrays in time. In writing the second equality in Eq. 12, a unit step-strain function is assumed for \(\epsilon _i\), where the \(\alpha ^{th}\) fractional derivative of a constant function \(y(t)=1\) is known to be \(t^{-\alpha }/\Gamma (1-\alpha )\) (Garrappa et al. 2019).

The objective in an inverse problem, as stated in “Introduction,” is to recover the fitting parameters of an embedded constitutive equation, which are the three FDEs introduced in “Fractional Maxwell model,” “Fractional Kelvin-Voigt model,” and “Fractional Zener model.” In a RhINN implementation, these FDEs are interrogated at discrete points in time (\(n_r\) in Eq. 12). To calculate the residual loss component (\(\phi _f\)), it is thus necessary to adhere to a definition of fractional derivatives best suited for the problem at hand. Among the existing definitions (or senses) of fractional derivatives (Baleanu 2016), the Riemann-Liouville (RL) and Caputo definitions seem to receive more attention (Jiang and Zhang 2020). Despite the equivalency of these two senses for certain viscoelastic cases (e.g., the fractional Zener model (Bagley 2007)), the Caputo solution is the suitable choice when (integer-order derivative) information about the boundary and/or initial conditions is available (Mainardi 2010; Li et al. 2011), which is the case here: the zeroth-order derivative of G(t) and J(t) curves is given, and thus, the initial conditions are accessibleFootnote 5. Thus, the Caputo sense is employed in this work to handle the fractional derivative of the outputs (\(\sigma (t)\) or \(\epsilon (t)\)) with respect to the input, t. The \(\alpha ^{th}\) order (\( 0 \le \alpha \le 1\)) fractional derivative of f(t) w.r.t. time in the Caputo sense is defined as follows (Baleanu et al. 2016):

$$\begin{aligned} \text {D}^{\alpha }_t f(t) = \frac{1}{\Gamma (1-{\alpha })} \int _{0}^{t} (t-1)^{-\alpha }\frac{\textrm{d}f(x)}{\textrm{d}x}\,dx \end{aligned}$$
(13)

In writing Eq. 13, the lower limit of integration is set to \(t=0\). It is worth mentioning that fractional derivative orders higher than unity are calculable using the Caputo sense; however, fractional derivatives are employed for viscoelastic materials here, and thus, the derivative order is deemed to remain within zero and one.

Equation 13 is not readily implementable on NNs, and thus, one will need to approximate the integral term. In this work, a well-established finite-difference algorithm (Diethelm et al. 2005) is used to calculate the Caputo derivative of f(t):

$$\begin{aligned} \text {D}^{\alpha }_t f(t) = \frac{1}{h^{\alpha }\Gamma (2-\alpha )} \sum _{n=0}^{n_r} a_{n,n_r}(f_{n_r-n}-f_{0}) + O(h^{2-\alpha }) \end{aligned}$$
(14)

where h is the (uniform) step size (\(h=t/n_r\)), \(f_0\) is the value of f(t) at \(t=0\), and \(a_{n,n_r}\) is the quadrature weights derived from a product trapezoidal rule:

$$\begin{aligned} a_{n,n_r} = {\left\{ \begin{array}{ll} 1, &{} \text {if }n=0 \\ (n+1)^{1-\alpha }-2n^{1-\alpha }+(n-1)^{1-\alpha }, &{} \text {if }0<n<n_r \\ (1-\alpha )n_r^{-\alpha }-n_r^{1-\alpha }+(n_r-1)^{1-\alpha }, &{} \text {if }n=n_r \end{array}\right. } \end{aligned}$$
(15)

which leads to an error of order \(h^{2-\alpha }\). The hereditary nature of the Caputo fractional derivative lies in the fact that the derivative at each point depends on the past information of f(t) in time.

Table 1 The initial conditions (ICs) for the fractional derivative orders (fitting parameters)
Full size table

In this study, \(n_r=100\) artificial points are uniformly distributed between 0.001 and 5s in time to calculate the residual loss, Eq. 12, and train RhINNs. Further increasing \(n_r\) resulted in negligible improvement in parameter recovery. One justification for selecting a small training time window is that the chosen numerical approach for the fractional derivative (Eq. 14) becomes unstable for non-uniform grids. Therefore, by increasing the time window, fewer points are available at the beginning of time, which can compromise the parameter recovery. The exact number of points is used to generate the ground truth data (G(t) or J(t)), which are then fed into the RhINNs.

One crucial step in solving inverse problems using RhINNs is the selection of NN hyperparameters, i.e., the NN parameters that are selected (and optimized) before the training process. For all three FDEs, four hidden layers, each containing ten neurons with a tanh activation function, are employed. Insignificant variation in the achieved convergence (and the execution time) was observed for other values of neuron or layer count. The trainable fractional derivative orders to be recovered are constrained to remain between 0.01 and 0.99 for numerical stability and also to respect the assumptions made to derive Eq. 14. A piecewise learning rate was employed that gradually decays in time to ensure gradient stability and also to find a compromise between the accuracy and the code execution time. Rather than a hard error threshold, the training process is halted once the recovered parameters (or the composite loss, \(\phi \)) plateaus and does not change. Each FDE inherits a particular degree of complexity, and a hard loss threshold that can effectively terminate the training process of one FDE might not apply to the other two. The initial conditions for the fitting parameters are also tabulated in Table 1. The neural network can tolerate initial conditions different than the ones tabulated below, but for unphysical initial conditions (e.g., \(\alpha <\beta \) in the FMM cases), there may be convergence issues. The loss minimization task is handled by TensorFlow’s built-in tf.keras.optimizers.Adam optimizer. The entire optimization task can also be performed using SPSVERBc1’s L-BFGS-B method in our code, but since this method is more computationally expensive than Adam, it is more convenient to perform Adam and use L-BFGS-B if need be.

Results and discussion

For all the FDE cases studied here, the compound elastic modulus (E) and relaxation time (\(\tau \)) are assumed given and were set to their respective values used when generating the exact data. The inevitability of this bold assumption lies in the fact that the (unique) recovery of fractional derivative orders, along with all the properties of the Scott-Blair elements, was infeasible for some cases. Nonetheless, assuming missing values of E and \(\tau \), the compound elastic modulus is accessible by taking the initial slope of the stress (or the relaxation modulus in a step-strain stress relaxation test) response in time. The relaxation time, in a similar fashion, is derivable by extracting the time needed for the material to relax the elastic response, which is the time range before the stress (or G(t)) plateau. Admittedly, these pieces of information may demand rounds of experiments. However, it is safe to assume that these parameters can be at least estimated with an acceptable level of confidence. Also, it is worth mentioning that our preliminary work suggests that all parameters can be recovered through RhINN solutions in the majority of the cases studied, but further work on that front is required to provide a robust and generalizable framework. As such, here and in this work, we limit the study to the recovery of fractional derivative orders. These fractional derivative orders are not readily accessible from rheometry, and RhINN is interrogated to precisely pinpoint these derivative orders.

Fractional Maxwell model

For the fractional Maxwell model, as mentioned in “Fractional Maxwell model,” RhINN is interrogated to recover the fractional derivative orders of the elements, i.e., \(\alpha \) and \(\beta \), as shown in Fig. 2a, under a stress relaxation test with a unit step-strain (\(\epsilon (t)=H(t)\)). The neural network is trained on a broad range of \(\alpha \) and \(\beta \) values with \(0 \le \beta < \alpha \le 1\). Moreover, the other two model parameters, i.e., \(E={1}\)Pa and \(\tau ={20}\)s, are assumed given; see the explanation in “Results and discussion.” In Fig. 4, the total relative absolute error (RAE) (in %) between the RhINN predictions and the ground truth values for a wide range of \(\alpha \) and \(\beta \) values is displayed. In each tile, the top and bottom numbers represent the recovered \(\alpha \) and \(\beta \), respectively, which can be cross-checked with their corresponding exact values given for each row and column. The maximum total RAE for the entire parameter space of \(\alpha \) and \(\beta \) is less than 10%, which indicates that RhINN is capable of recovering the fractional derivative order of FMMs.

Fig. 4
figure 4

Total relative absolute error (RAE) in fractional derivative order values (\(\alpha \) and \(\beta \)) compared to their respective exact values for the fractional Maxwell model under a stress relaxation test with a unit step-strain function. The numbers in each tile, from top to bottom, represent the recovered \(\alpha \) and \(\beta \) values, respectively, with their exact values given by their corresponding row and column. The upper triangle is inaccessible since in deriving Eq. 3, it is assumed that \(0 \le \beta < \alpha \le 1\)

Full size image

From a rheologist’s vantage point, having a precise fractional derivative order recovery might seem secondary to having a measurable rheological property, which is the relaxation modulus, G(t), in the case of a stress relaxation test. That is, the ultimate goal in constitutive modeling is enabling accurate prediction of material response, and as such, the absolute value of the parameters involved in a model may not necessarily mean as much. Since the ground truth formula (Eq. 4) to generate the data is available, it is possible to calculate the recovered relaxation modulus (G(t)) by inserting the recovered \(\alpha \) and \(\beta \) values along with the given values of E and \(\tau \) and then comparing the recovered G(t) with the ground truth one. Such material responses are plotted in Fig. 5 for four combinations of \(\alpha \) and \(\beta \), with the RhINN predictions and the exact G(t) values shown in solid and dashed lines, respectively. The plots in Fig. 5 indicate that even for the case of the largest RAE reported, recovered relaxation spectra is closely tracking the ground truth solution. Recalling the definition of Scott-Blair elements (Eq. 2), the lower value of the fractional derivative order (\(\beta \)) is a manifestation of the high-frequency material response, which is the elastic response in viscoelastic materials. Therefore, changing \(\beta \) should be observable in the initial G(t) response in Fig. 5. Here, The relaxation modulus is lower for the smaller values of \(\beta \) since G(t) is proportional to \(t^{-\beta }\), which decreases as \(\beta \) drops; see Eq. 4.

Fig. 5
figure 5

The relaxation modulus, G(t) of the fractional Maxwell model. The RhINN (solid line) response is calculated by inserting the recovered sets of \(\alpha \) and \(\beta \) into Eq. 4, plotting the material response for a time window equal to that of the training data (0.001 and 5s), and is compared with the ground truth (dashed line) relaxation modulus. The elastic modulus (\(E={1}\)Pa) and relaxation time (\(\tau ={20}\)s) are assumed given

Full size image

Fractional Kelvin-Voigt model

RhINNs are then applied to recover fractional derivative orders of the elements in the fractional Kelvin-Voigt model (FKVM) under a creep test using a unit step-stress function for various (\(\alpha \), \(\beta \)) combinations with constraint \(0 \le \beta < \alpha \le 1\). In each case, the other model parameters, \(E= 1\)Pa and \(\tau = 20\)s, are assumed given. The total RAE between RhINN predictions and the ground truth values for different fractional derivative orders are shown in Fig. 6. The RAE values are mostly within a 20% band, with the exception of some scenarios where the overall relative absolute inaccuracy reaches up to 50%. Note that in those examples, the small value of \(\beta \) results in a large RAE. The higher RAE scenarios were further investigated by examining the recovery of each particular fractional derivative order (as represented by the values in the tiles). It was found out that the higher order, \(\alpha \), is consistently recovered more accurately than \(\beta \). One possible reason for higher deviation in \(\beta \) recovery could be that RhINN was trained over a short time window, and the higher fractional derivative order (or more viscous element) dominates the material response in the Kelvin-Voigt model within short timescales.

Fig. 6
figure 6

Total relative absolute error (RAE) in the fractional derivative orders (\(\alpha \) and \(\beta \)) with respect to their exact values in the fractional Kelvin-Voigt model under creep compliance for various combinations of fractional derivative orders with constraint \(0 \le \beta < \alpha \le 1\). The numbers in each tile, from top to bottom, represent the recovered \(\alpha \) and \(\beta \) values, respectively, with their exact values given by their corresponding row and column

Full size image

As previously presented for the case of FMMs, and to support our interpretation, the material response is also plotted using the predicted and ground truth fractional derivative orders. In Fig. 7, the creep compliance (J(t)) is depicted for cases where there are significant differences between the predicted and ground truth fractional derivative orders. In this figure, the recovered derivative orders are inserted into Eq. 7 over a larger time window, i.e., \(1 \times 10^{-2}\le t/\tau \le 1 \times 10^{4}\) to monitor the out-of-sample response of J(t) using the recovered parameters. Across the range of derivative orders, the predicted and the ground truth responses are in good agreement at shorter times, e.g., \(t/\tau < 10\). Despite the high RAE in recovering \(\alpha \) and \(\beta \) at smaller values of \(\alpha \) (the upper left cases in Fig. 6), the J(t) response nonetheless commits a much smaller error, indicating that the combination of \(\alpha and \beta \) determines the accuracy of J(t) and not their individual values. However, disparity between the predicted and ground truth J(t) responses arises at longer times due to the relatively substantial error in recovering \(\beta \). This can also be alleviated by increasing the training time window, which was set to be within 0.001 and 5 s throughout this study.

Fig. 7
figure 7

The creep compliance, J(t), response of the fractional Kelvin-Voigt model using the recovered (solid) and exact (dashed) fractional derivative orders. Other parameters, \(E= 1\)Pa and \(\tau = 20\)s, are assumed known. The recovered derivative orders are inserted into Eq. 7 over a larger time window, i.e., \(1 \times 10^{-2}\le t/\tau \le 1 \times 10^{4}\) to assess the out-of-sample response of J(t) using the recovered parameters

Full size image

Fractional Zener model

Finally, RhINN is used in this case to recover the fractional derivative orders (\(\alpha \), \(\beta \), and \(\gamma \)) of the three Scott-Blair elements in the fractional Zener model (FZM) under a stress relaxation test using a unit step-strain function for a wide range of derivative order values with constraints \(0 \le \beta < \alpha \le 1\) and \(0 \le \gamma \le 1\). Other model parameters (\(E_0=E= 1\)Pa and \(\tau = 20\)s) remained constant, as before. The NN hyperparameters are also similar to those used in “Fractional Maxwell model” and “Fractional Kelvin-Voigt model.” Figure 8 summarizes the total relative absolute error in recovering the three fractional derivative orders. The RAE values are generally within a 30% band for the derivative orders, with the exception of a few scenarios where the relative absolute error hits 100%. In Fig. 8 b and c, these higher-error cases occur when \(\gamma \) is equal to one of the other two derivative orders (\(\beta \) and \(\alpha \), respectively). On the other hand, it should be noted that some recovered fractional derivative orders match their respective exact values. Thus, the true test of the RhINN order recovery can be done by comparing the relaxation moduli using the recovered parameters and benchmarking against the ground truth solution.

Fig. 8
figure 8

Total relative absolute error (RAE) in the recovered fractional derivative orders (\(\alpha \), \(\beta \), and \(\gamma \)) with respect to their exact values for the fractional Zener model under a stress relaxation test using a unit step-strain function for various combinations of derivative orders with constraints \(0 \le \beta < \alpha \le 1\) and \(0 \le \gamma \le 1\). The numbers in each tile, from top to bottom, represent the recovered \(\alpha \), \(\beta \), and \(\gamma \) values, respectively

Full size image

In Fig. 9, the recovered derivative orders are inserted into Eq. 9 over a larger time window, i.e., \(1 \times 10^{-3}\le t/\tau \le 1 \times 10^{4}\) to assess the out-of-sample response of the material response using the recovered derivative orders. The relaxation modulus, G(t), using both the recovered and exact fractional derivative orders, is shown in Fig. 9 for the cases in which the highest values of RAE were observed. Despite the significant relative absolute inaccuracy in the recovered fractional derivative orders, the predicted relaxation moduli closely track the exact values for all scenarios at shorter times \(t/\tau <1\). At longer times (unseen by the RhINN), however, a significant discrepancy between the predicted and actual responses is observed for these cases. Once again, this can be explained by recalling the fact that the training time window (0.001 and 5s) was not large enough to encompass all the intricacies of the material response at longer times. The selection of the time window was also constrained by the computational expenses of fractional derivatives. We remind the reader that in this particular algorithm, time has to strictly be spaced linearly, and since small time intervals are required at short times, this prevents one from a comprehensive and long time training process. Therefore, employing more versatile and efficient fractional derivative algorithms compatible with nonlinear step sizes should be at the core of future efforts on this topic. It should be stressed, though, that out-of-sample prediction using RhINNs (or any other numerical toolkit) is accurate only up to a threshold, and the numerical solver usually cannot stray too far from the data that were given during the training stage.

Fig. 9
figure 9

The relaxation modulus, G(t), of the fractional Zener model using the recovered (solid) and exact (dashed) fractional derivative orders. Other parameters (\(E_0=E= 1\)Pa and \(\tau = 20\)s) are assumed known and constant. The recovered derivative orders are inserted into Eq. 9 over a larger time window, i.e., \(1 \times 10^{-3}\le t/\tau \le 1 \times 10{4}\) to monitor the out-of-sample response of G(t) using the recovered parameters

Full size image

Conclusion

In this work, RhINNs were developed and employed to recover the fractional derivative orders of the elements in fractional viscoelastic Maxwell, Kelvin-Voigt, and Zener models based on single sets of (synthetically generated) data. Moreover, the derivative orders were used to generate the stress relaxation response of the fractional Maxwell and Zener models upon the imposition of a unit step-strain and the creep compliance response of the fractional Kelvin-Voigt model under a creep test using a unit step-stress function. A systematic study on the recovery of the derivative orders over their permitted parameter space (between zero and unity) was performed. With various combinations of the fractional derivative orders (and their respective constraints), multiple scenarios were examined in each of the three fractional models. Overall, in most situations, RhINNs are found to retrieve the fractional derivative orders of all the components in each of the models in the same range as the ground truth values used in the generation of the data. In other instances, the total relative absolute error (RAE) for some of the derivative orders is found to be substantial. However, the relaxation modulus (or creep compliance) using the recovered derivative orders closely mimics the input experiments with minimal deviations. This is mainly because the solution of these models to an applied flow protocol is not unique within the time window under question, meaning that several combinations of the derivative orders can replicate the same overall behavior. This is more noticeable when more complex models (with more spring-pot elements) are considered. As such, for the derivative order recovery of the fractional Zener model, the recovered parameters do not necessarily follow the ones used to generate the data; nonetheless, the retrieved order values do indeed result in an accurate recovery of the behavior. Also, in this work, the neural network was trained over a short time window in terms of the data provided, and in some cases, those time windows are likely not long enough for all model components to respond appropriately to an applied stimulus. Moreover, due to the hereditary nature of fractional derivatives and the need to sum all the past information to get the fractional derivative at each point, the RhINN convergence was found to be time-consuming (typically within tens of minutes, or an hour), which leaves room for further improvement in the computation time and efficiency of fractional problems using RhINNs. While this work presents a robust platform for the inverse data-driven solution of fractional constitutive models, further investigation is warranted on recovering all model parameters (including elastic moduli and relaxation times) and other flow protocols. Also, training the RhINNs over a longer time window could improve the efficiency of fractional derivative recovery.