Introduction

Surfactants are amphiphilic molecules characterised by a hydrophobic tail and a hydrophilic head, fundamental for an extremely wide range of applications, such as home- and beauty-care, everyday use goods (Baruah et al. 2015; Hargreaves 2007; Yang 2002), food (Drakontis and Amin 2020) and pharmaceutical industry, including development of drug delivery systems, such as liposomes (Garti et al. 2012; Guo et al. 2010).

Due to their complex molecular structure, as the surfactant concentration in a water solution increases, the system undergoes a series of phase changes. In detail, as soon as surfactant concentration overcomes a critical value, known as critical micellar concentration (typically order of 10−2 mM) (Hait and Moulik 2001; Mahmood and Al-Koofee 2013; Ohlendorf et al. 1986), surfactant molecules self-assemble and form micelles (spherical, rod-like or wormlike) (Davies et al. 2006; Yang 2002). Different types of micelles correspond to different morphological structures and specific rheological properties, even in the case of highly diluted micellar solutions that can be weakly viscoelastic in the case of wormlike structures (Acharya and Kunieda 2006; Imae et al. 1985; Panmai et al. 1999; Trickett and Eastoe 2008). As surfactant concentration grows (typically above 20%wt), different grades of order in the amphiphilic molecules are realised. In these conditions, molecules organise themselves in hexagonal, cubic or lamellar crystalline liquid structures (Fontell 1990) which lead to a complex physical-chemical behaviour (Richtering 2001).

Concerning rheology, concentrated surfactant-water solutions, usually defined as surfactant pastes, show a gel-like behaviour. In high concentration range, heavily different rheological behaviours are observed, with non-monotonic changes in viscosity and moduli of several orders of magnitude. These changes not only depend on concentration, but also on temperature (Acharya and Kunieda 2006, Cappelaere et al. 1994, Castaldo et al. 2019, Davies et al. 2006, Ketner and Raghavan , Kumaran et al. 2001, Li et al. 2016, Poulos et al. 2017). These two key parameters also affect other physical properties, related to the molecular order induced in the fluid.

Previous works (Johnston et al. 2015; Panoukidou et al. 2019; Rekvig et al. 2003; Skartlien et al. 2012) investigated phase diagram of water-surfactant systems, including predictions on rheological behaviour, only in silico, due to problems associated to experimental characterisation. Consequently, a detailed understanding of rheological behaviour of surfactants at different water content and, in particular, at temperatures higher than room temperature is crucial (Baruah et al. 2016, Pathak and Ojha , Kekicheff et al. 1989, Luo et al. 2012).

The main goal of this work is to fill this gap in the knowledge, providing a systematic rheological characterisation, not available in the literature, of one of the most used anionic surfactants: sodium lauryl ether sulphate (SLE3S). SLE3S is one of the main components in shampoos, detergents, toothpastes and creams, used for its emulsifying and foaming properties and for its reduced production costs. Understanding the physics of these systems plays a key role in industrial processing, which also has an important impact on production efficiency.

In this paper, in order to identify different textures of the water-based mixture, related to the SLE3S concentration, and to obtain macroscopic qualitative information on sample structure, optical anisotropy properties of each phase are observed by using polarised light microscopy (PLM). Then, the systematic rheological characterisation of each texture is performed at different temperatures, in the range 30–60 °C, in order to determine changes in shear viscosities and moduli, a key issue in ruling formulation functionality (Capaccio et al. 2020; Dehghan et al. 2015; Jiang et al. 2009). A special attention is paid to the cubic phase which exists only in a narrow concentration range and, for this reason, is not easy to identify. Consequently, cubic phase is often poorly characterised (Lavergne et al. 2011), despite being related to most of the difficulties faced in industrial processes, due to a dramatic increment in rheological parameters (viscosity and moduli) respect to the neighbouring phases.

The approach here proposed, focused on the range of concentration and temperature of industrial relevance, can be used as a simple and effective way to obtain a detailed phase map of a multicomponent mixtures exhibiting complex phase behaviour.

Materials and methods

Chemical structure

SLE3S is a sodium salt produced through the ethoxylation of the sodium lauryl sulphate (SLS), characterised by a similar structure with three extra ether groups (Cserháti et al. 2002). The hydrophilic head of SLE3S includes three ether groups and a \({\textrm{SO}}_3^{-}\) group, balanced by a Na+ counterion. According to typical behaviour of surfactant systems, depending on concentration in water, SLE3S rearrange in different morphologies, corresponding to different phases. In detail, at room temperature (25 °C), phase changes are defined in the following concentration ranges: micellar (referred as L1) in the range 0.024–28%wt, hexagonal (H) 31–56%wt, cubic (V1) ~ 58–62%wt and lamellar (Lα) 62–72%wt (Li et al. 2016).

Sample preparation

SLE3S solution is obtained from Procter and Gamble in the form of a high concentrated paste (72% weight fraction surfactant in water, as determined by vacuum drying). Samples (~5 g each) at different concentration (20, 35, 50 and 60%wt) are prepared using distilled water to dilute the surfactant raw paste using an analytical balance (sensitivity 10−4 g). Concentrations are selected to fall within the L1, H, V1 and Lα domains, respectively. The samples are carefully mixed using a spatula and centrifuged (4000 rpm for 40 min) to degas them. Centrifugation step is repeated more than one time due to the high viscous samples, until a bubble-free sample is obtained. Samples are then stored at room temperature overnight to guarantee the equilibrium and the homogeneity. Preliminary visual inspection through cross-polarisers is used to check phase uniformity in the samples.

Optical setup

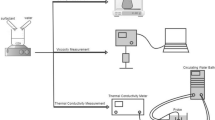
PLM is used to check texture of SLE3S samples and to identify the correlation between the concentration and the corresponding phase. Optical setup is based on an inverted microscope (Zeiss Axiovert 200, 20× objective) equipped with a high-sensitivity CCD video camera (Hamamatsu Orca AG) and a motorised stage (Marzhauser), controlled by an in-house-built software, for automated mosaic scanning of large samples (Ferraro et al. 2022).

A tiny amount of surfactant at different concentration is squeezed between a glass microscope slide and a coverslip. Sample thickness is set at 130 μm by inserting a double-side adhesive tape as a spacer between the two glass surfaces. Sample thickness is verified by measuring the focus position, by means of the microscope focus encoder, of top and bottom glass surfaces confining the surfactant paste. Two crossed polarised filters are placed before and after the sample along the optical path. 3 × 3 mosaic images are acquired at room temperature and sticked using commercial image analysis software (Image-Pro Plus). Sample birefringence, related to the ordered texture in SLE3S morphology, allows to identify different phases by simple visual comparison (see Fig. 1). Further detail on the methodology, including a cartoon of experimental setup here described, is reported in a previous work (see Fig. 1 D in Capaccio et al. 2020).

Fig. 1
figure 1

Optical experiments: five different concentrations of SLE3S are compared, at room temperature, in order to visualise four distinct phases, i.e., micellar (L1), hexagonal (H), cubic (V1) and lamellar (Lα). At the bottom of the panel, the critical concentration values denoting the transition from one phase to another are also given (~28% wt from micellar to hexagonal, ~58% wt from hexagonal to cubic and ~62% wt from cubic to lamellar)

Full size image

Rheological setup

Rheological measurements are performed at different temperatures (30, 40, 50 and 60 °C) using a stress-controlled rheometer (Anton Paar Physica MCR 301 Instruments) (Tomaiuolo et al. 2016) equipped with a double gap measuring system (C-DG26.7-20/T200/S and DG26.7/TI) for sample characterised by a low viscosity (20%wt) and a cone-plate measuring system (CP25-1/S-SN72510) for sample characterised by a high viscosity (35, 50, 60 and 72%wt). Temperature is controlled by a Peltier cooler/heater connected to a circulating water bath (Lauda) and let to equilibrate at the measuring value for 3 min before each test.

Pre-shear is run to homogenise sample structure after loading, imposing a constant shear rate (\(\dot{\gamma}\)) of 200 1/s for 1 min. For H, V1 and Lα, flow curves are run varying \(\dot{\gamma}\) in the range 0.01–200 1/s (40 data points, sampling time 15 s). Measurements are repeated varying \(\dot{\gamma}\) from 200 to 0.01 1/s. For L1, flow curves are run varying \(\dot{\gamma}\), from 10 to 200 1/s, and vice versa, to minimise noise related to rheometer sensitivity at low torque. No significant differences (hysteresis) are observed comparing the \(\dot{\gamma}\) rising and decreasing tests, for simplicity only 0.01–200 1/s data are reported in the results.

To identify the linear viscoelasticity range, strain sweep experiments are performed. Storage and loss moduli (G′ and G″, respectively) are measured at fixed angular frequency (ω = 5 rad/s) varying the strain in the range 0.01–200. For all the tests, linear viscoelasticity is verified in the range of amplitude 0.01–1 s. Frequency sweep is investigated at strain 0.1 varying frequency in the range 100–0.1 rad/s, measuring 16 data points, except for L1 where the range is 10–0.1 rad/s.

The entire characterisation required about 45 min for each T. To limit water evaporation and phase transitions due to concentration changes during the rheological measurements, sample is reloaded for each T measured.

Parallel plate rheo-optical apparatus

In order to verify the influence of shear flow on phase changes, some preliminary rheo-optical tests are run at room temperature. In particular, we focused this analysis on the SLE3S concentration that showed the most complex phase behaviour (60%wt). A simple shear flow is generated by using a parallel plate rheo-optical apparatus, widely described in previous works (Caserta et al. 2004; Caserta et al. 2006; Pommella et al. 2012). Briefly, one of the two optical glass plates is translated with respect to the other by a computer controlled motorised stage (Ludl). The flow cell containing the sample is under the field of view of an optical microscope (Zeiss Axioscope). Also in this case, two polarised filters, placed on top and on bottom of the two glass plates, are carefully crossed and fixed to visualise sample birefringence. Sample can be observed by a high-speed video camera (Hamamatsu C11440-36u) along the velocity gradient direction. Image acquisition rate is fixed to 1 image/s.

Texture evolution is investigated in a range of \(\dot{\gamma}\) similar to the one used in rheological measurements (0.01–200 1/s). In this case, \(\dot{\gamma}\) is given by the ratio between the speed of the moving plate and the gap between plates, fixed to 130 μm, in analogy with the static image acquisition (see “Optical setup” section). To quantify the texture evolution, light intensity is calculated by measuring the average grey level (I), normalised respect to image intensity at rest (I0) as function of time, at different \(\dot{\gamma}\).

Data, reported in supplementary (see Fig. S1), do not show texture variations comparable with the one induced by temperature and concentration changes. For this reason, we considered as negligible the influence of flow on sample transitions, respect to variations induced by temperature and concentration, in the range of values here investigated.

Statistical data analysis

All rheological characterisations are performed at least two times on different samples prepared independently, repeating the dilution from the same 72% batch. Data reported in the charts are expressed as mean ± standard error of the mean (SEM).

Results

The scope of this work is to provide a systematic rheological characterisation of phases exhibited in the SLE3S/H2O system, not still available in the literature. To this aim, a preliminary sample characterisation is run at room temperature by PLM in order to distinguish different phases, related to the concentration system. Each of the so identified textures is than object of a detailed rheological characterisation in a range of temperature 30–60 °C. Measuring the influence of concentration and temperature on rheological properties represents an innovative way to support industries and their processes. In the following section, experimental results are presented.

Phase characterisation

In Fig. 1, mosaics scanning images of the sample at different concentrations and, consequently, representative of different phases are reported. In fact, comparison of optical properties and image brightness provides information on the sample phase here compared (L1, H, V1 and Lα).

Lα is clearly identified by typical Maltese cross patterns, visible in the 72%wt sample. By reducing the concentration, sample at 60%wt appears almost completely black, with the sole exception of some isolated light spots, in agreement with an isotropic cubic phase, that appear already qualitatively very stiff. This phase is present in a very narrow concentration range of approximatively 58–62%wt. Further reducing SLE3S concentration, H is expected to be birefringent, as the cloudy samples corresponding to 50%wt. Sample at 35%wt denotes the transition from hexagonal to micellar phase: in this case, indeed, the texture shows a not uniform brightness, with bright domains separated by dark regions, suggesting a phase equilibrium between H and L1, as reported in most phase diagrams, differently from L1 which appears completely black.

Rheological characterisation

In this section, a detailed rheological characterisation of the system under investigation is reported. Both flow and frequency test are run using the constant stress rheometer equipped with the geometry and protocol described above (see “Rheological setup” section).

Flow curve

In Fig. 2, viscosity (η) measurements as a function of \(\dot{\gamma}\) are shown for the five concentrations here in exam (20, 35, 50, 60 and 72%wt), corresponding to four different phases (L1, H, V1 and Lα), for four different temperatures (30, 40, 50 and 60 °C). In agreement with previous measurements at room temperature reported in the literature (Castaldo et al. 2019), all the samples show a typical shear thinning behaviour, with a viscosity decrement of ~4 orders of magnitudes in the range of shear rate here investigated. In particular, viscosity of hexagonal (H, 35 and 50%wt) and lamellar (Lα, 72%wt) samples decreases as function of \(\dot{\gamma}\) from 103 to 1 Pas, with limited differences by varying T in the range investigated. In the case of micellar phase (L1, 20%wt) and cubic phase (V1, 60%wt), a stronger dependency of η from T is observed. For L1, at fixed shear rate (e.g,. \(\dot{\gamma}\) ~ 10 1/s), η increases of one order of magnitude, from 0.02 to 0.12 Pas, increasing temperature from 30 to 60 °C. This unusual increase in viscosity with temperature probably depends on increments in the contour length of micelles, in fact, at high temperatures micelles are known to grow into longer and flexible cylinders (Kalur et al. 2005). In the case of V1, at low T values (30 and 40 °C), η thins from 104 to 101 Pas with \(\dot{\gamma}\). In these conditions, V1 is more viscous respect to both H and Lα phases. On the contrary, in high T range (50–60 °C), η of cubic phase is considerably reduced. Considering data at fixed value of \(\dot{\gamma}\) (e.g. 1 1/s), η of V1 phase is about 4∙102 Pas at 30 and 40 °C, while is about 1.5∙101 Pas at 50 and 60 °C. Such a stronger decrement of η with T suggests a phase transition (Baruah et al. 2015).

Fig. 2
figure 2

Influence of shear rate and temperature (30 °C—green, 40 °C—blue, 50 °C—yellow, 60 °C—orange) on viscosity for five concentrations of SLE3S (20, 35, 50, 60 and 72%wt). Flow curves are fitted with a power-law viscosity model (fitting are reported on the right), in order to evaluate flow parameters (n and k) for each concentration at different temperatures. In detail, V1 flow curves at 50 and 60 °C are split in two sections (\(\dot{\gamma}\) < 1 1/s and \(\dot{\gamma}\) > 1 1/s) to better investigate the effect of temperature on viscosity

Full size image

To better investigate how T affects rheological behaviour of each phase, flow curves are fitted with a power-law viscosity model (\(\eta =k\bullet {\dot{\gamma}}^{n-1}\)), where k is the consistency factor and n is the flow exponent. As shown in the legends reported in Fig. 2, n < 1 for all conditions investigated, in agreement with a typical shear thinning fluid, corresponding to a linear trend in the logarithmic diagrams. Data lies on a single line in the entire range of observation (10−2 < \(\dot{\gamma}\) < 102 1/s), for surfactant concentration 20, 35 and 72%wt. In the case of L1 sample, a variation with T is observed in both fitting parameters: in particular, k increases (from 0.02 to 0.84 Pas), while n decreases with temperature (from −0.27 to −0.95), consequently viscosity radically increase heating from 30 to 60 °C. Similar increment of about 1 order of magnitude in viscosity of cationic and anionic micellar solution as function of temperature (Kalur et al. 2005) or pH (Zhang et al. 2013) is previously observed and attributed to the growth of wormlike micelles. Marginal fluctuations for the sample at 50%wt, also in the H phase region, can be observed: a variation with T is observed in both fitting parameters, in particular n increases from −0.97 to −0.66. In the case of V1 phase sample (60%wt), η at high T shows a clear discontinuity at \(\dot{\gamma}\cong\) 1 1/s. For this reason, flow curves at 50 and 60 °C are split in two sections (\(\dot{\gamma}\) < 1 1/s and \(\dot{\gamma}\) > 1 1/s), obtaining two independent values of power law fittings parameters, also reported in figure legend. From the above observation, we can state that flow parameters, referred as k and n, are a step function of T only for V1 phase, while they show minor changes for other phases, in the same range of T investigated. This observation is in agreement with the expected phase transition in this concentration and temperature range.

As regards the cubic phase, in order to better investigate the T effect on these rheological aspects, η is measured at additional temperatures (20, 45 and 48 °C). In Fig. 3, η data (y-axis) are plotted as a function of \(\dot{\gamma}\) (x-axis) and T (z-axis). As shown in the 3D plot, η show limited changes in the entire range 20–45 °C. At 48 °C, η begins to significantly decrease (~4× times) and then collapse considerably of 1 order of magnitude at 50 and 60 °C.

Fig. 3
figure 3

Influence of shear rate (x-axis) and temperature (z-axis) in the range 30–60 °C on viscosity (y-axis) of SLE3S cubic phase (60%wt)

Full size image

To estimate η-T dependency, a classical Arrhenius-like equation (Baruah et al. 2016) is used (\(\eta (T)=A{e}^{{~}^{E_a}\!\left/ \!{~}_{\mathrm RT}\right.}\)), where R (J/mol K) is the universal gas constant and Ea (J/mol) is the activation energy. As shown in Fig. 4, Ea can be estimated from the linear slope (dotted line) obtained by plotting k values, reported in Fig. 2 (i.e., \(k={\left.\eta \right|}_{\dot{\gamma}=1}\) for H, V1 and Lα and \({\left.\eta \right|}_{\dot{\gamma}=10}\) for L1), as function of 1/T. The low activation energy value indicates the presence of stable structures (Baruah et al. 2015) and of limited influence of T on η. As shown, H and Lα phases are characterised by low values of Ea, ~0, 7.6 and ~0 kJ/mol, respectively. On the contrary, due to unusual increase in viscosity with temperature, L1 (20%wt) is characterised by a negative value of Ea (~−5.1∙104 kJ/mol). As regards V1 (60%wt), three different regions can be distinguished: two regions characterised by low values of Ea (9.0 and 13.0 kJ/mol, for low and high values of 1/T, respectively), where η marginally changes in the range of T investigated; in the intermediate region, an higher value of Ea, ~4.6∙102 kJ/mol is measured, indicating the existence of a phase transition in the temperature range 45–50 °C.

Fig. 4
figure 4

For each SLE3S concentration investigated (20, 35, 50, 60 and 72%wt), viscosity is plotted as function of the inverse of temperature, in order to obtain activation energy (Ea) related to phase transition, if present. Ea is estimated from the slope of linear curve (dotted line), obtained by fitting experimental data with Arrhenius law

Full size image

Oscillatory tests

Performing frequency sweep tests, G′ and G″ are investigated as function of ω. Measurements at 30 and 60 °C are reported in Fig. 5, while frequency sweep tests at 40 and 50 °C are reported in Supplementary Materials for brevity. In the temperature range examined, G′ (triangle up) is always higher respect to G″ (triangle down) with an almost parallel trend, suggesting a weak-gel-like behaviour (Trappe and Weitz 2000) of surfactant pastes. Both moduli slightly increase with T for L1, H and Lα, while V1 shows a significant reduction of G′ and G″ going from 30 to 60 °C, confirming phase changes previously observed.

Fig. 5
figure 5

For each SLE3S concentration investigated (20, 35, 50, 60 and 72%wt), elastic (G′, Pa) and viscous (G″, Pa) moduli are reported as function of angular frequency (ω, rad/s), triangle up and down, respectively. Experimental data are reported at two different temperature, 30 and 60 °C (green symbols on the left and orange symbols on the right, respectively). In Supplementary Materials, same measurements are also reported for 40 and 50 °C

Full size image

To better investigate moduli changes, the ratio between G″ and G′, i.e., tan(δ), is evaluated and plotted as function of ω for all experimental conditions (Fig. 6 data at 30 and 60 °C, Supplementary Materials data at 40 and 50 °C). As shown, heating poorly affects tan(δ) for H and Lα, while for V1 tan(δ) increases significantly with T: in detail, at 60 °C, the ratio is about 2.8× higher respect to the value at 30 °C. Indeed, for cubic samples at high temperature the difference between the two moduli reduces, although G″ remains lower than G′.

Fig. 6
figure 6

tan(δ), calculated as the ratio between G″ and G′, is reported as function of angular frequency (ω, rad/s), at 30 and 60 °C (green and orange circles, respectively) for each SLE3S concentration investigated (20, 35, 50, 60 and 72%wt). In Supplementary Materials, same measurements are also reported for 40 and 50 °C

Full size image

Temperature effect

Measurements reported above are here used to identify rheological properties of different phases and, consequently, different surfactant concentration in water as function of a temperature range (30–60 °C) of technological relevance, in order to provide a deep characterisation of SLE3S-water system. In Fig. 7, η and complex viscosity (η*) data are plotted, at fixed \(\dot{\gamma}\) (=1 1/s) and at fixed ω (=1 rad/s), against the whole range of T for all SLE3S concentration investigated. In L1, H and Lα region, η shows a limited change as function of T, while η jumps is clearly visible in V1 data series, as previously described. In detail, SLE3S at 60%wt, at \(\dot{\gamma}\) = 1 1/s and T = 30 °C, has a η ~3.5× and ~20× higher than H and Lα phases, respectively, while at high T, e.g., 60 °C, the same concentration range shows a reduced η respect to the other phases (~0.25× and ~0.54× compared to H and Lα, respectively).

Fig. 7
figure 7

Viscosity (A) and complex viscosity (B) against temperature, as function of SLE3S concentration: 20%wt (triangle down), 35%wt (triangle up), 50%wt (circle), 60%wt (square) and 72%wt (diamond)

Full size image

In Fig. 7, complex viscosity η* is compared to η (left and right panels). The general trend of data is the same, with limited changes in both viscosities with T for all the phases except V1. However, Cox-Mertz superposition rule is not valid, as evident observing values of η* are systematically more than one order of magnitude higher respect to η. It is worth noticing temperature dependency of η* is stronger compared to η.

The same behaviour can be also observed plotting G′, G″ and complex modulus (G*) against T, parametric in SLE3S concentrations (Fig. 8). Also in this case, significant changes in rheological response of surfactant pastes are observed. In particular, moduli of V1 are significantly higher respect to L1, H and Lα phases at low T, but dramatically reduce increasing this parameter: in detail, G′ decreases from 3.6∙105 to 4.2∙103 Pa, G″ from 2.7∙104 to 4.7∙103 Pa and G* value from 2.9∙105 to 5.4∙103 Pa. In the same temperature range, moduli of other phases show only minor fluctuations. It is worth noting the phase change observed for V1 phase systems as function of T appears to be in the range 40–50 °C, observing shear viscosity jump, while oscillatory tests seem to suggest a slightly lower value of the T transition, that is measurable in the range 30–40 °C.

Fig. 8
figure 8

Elastic (A), viscous (B) and complex modulus (C) against temperature, as function of SLE3S concentration: 20%wt (triangle down), 35%wt (triangle up), 50%wt (circle), 60%wt (square) and 72%wt (diamond)

Full size image

Discussion and conclusions

Surfactants, due to their complex molecular structure, undergo a series of phase changes, depending on their concentration and temperature, affecting different parameters. In particular, a detailed characterisation of flow behaviour is needed for an adequate design of industrial processing. Despite this, such a characterisation is not available in the literature, neither for systems of common industrial use, such as sodium lauryl ether sulphate (SLE3S) here investigated.

The aim of this paper is to fill this gap in the knowledge, providing a systematic rheological characterisation of SLE3S, and demonstrate that rheology can be used in order to build such a phase diagram, being a suitable tool to recognise the phase transitions as function of concentration and temperature. In order to confirm the phase transition and to identify each phase, rheology is here supported by PLM, able to link optical anisotropy properties to different sample texture.

Sodium lauryl ether sulphate (SLE3S) is investigated in a concentration (25–72%wt) and temperature (30–60 °C) range of technological relevance, collecting 20 measurement points. Each phase (micellar, hexagonal, cubic and lamellar, referred as L1, H, V1 and Lα, respectively), at fixed temperature, shows non-monotonic changes of several orders of magnitude of distinct parameters: viscosity and complex viscosity, elastic, viscous and complex moduli. These results are obtained by analysing the system under steady and oscillatory shear flow. Increasing temperatures, H and Lα phases do not show significant rheological changes, in contrast to V1 phase. In fact, rheological parameter of SLE3S at 60%wt radically decreases by increasing temperature from 30 to 60 °C, confirming temperature-induced structural modifications.

The approach here proposed, focused on the range of concentration and temperature of industrial relevance, can be used as a simple and effective way to obtain a detailed phase map of a multicomponent mixtures exhibiting complex phase behaviour, as was partially done in literature (Chopra et al. 2002; Ilyin et al. 2020; Pasquino et al. 2013). In fact, the approach here presented can be systematically applied to fine tune the characterisation, extending the number of temperature-concentration values, and to identify, with any needed precision, values of transition among phases. It is worth mentioning that surfactant systems can be affected by polydispersity due to the different preparation conditions, consequently, specific values of concentration and temperature related to phase transition could be affected. This aspect, increasing the range of frequencies investigated in order to identify the crossover point, could benefit from a more in-depth analysis (Escalante et al. 2000; Parker and Fieber 2013; Zou et al. 2015; Zou et al. 2019) in order to quantify parameter such as relaxation times, hydrodynamic correlation length, persistence length and average entanglement, to better describe each type of microstructure. Overall, the study of the phase diagram of aqueous surfactant solutions can benefit from the combined application of rheology and PLM, with other techniques, such as electron paramagnetic resonance spectroscopy and small-angle X-ray scattering, in order to characterise each microstructure.