Modeling the density relaxation of polystyrene

Abstract

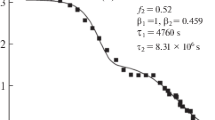
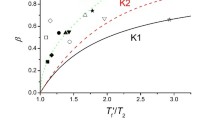
Cumulative density-relaxation data from the literature (following a thermal quench or during a constant rate of cooling) for polystyrene are analyzed. Consideration is given to four well-known models for the relaxation time as a function of temperature and fictive temperature, starting with the seminal modeling proposed by Tool in 1946. Among the numerous experimental results, those presented by Greiner & Schwarzl in 1984 are the most extensive, including their notable result that, under constant-cooling rate, the apparent glass-transition temperature (T_g,apparent) varies linearly with the log of the cooling rate (q_c). In the present paper, it is established by detailed numerical analysis that Tool's model is the one which replicates this linear dependence between T_g,apparent and log q_c. In turn, this implies that the temperature dependence of the equilibrium relaxation time (or the temperature shift factor) is purely exponential below the glass-transition temperature. This behavior is also shown to describe available experimental data in the literature (all below the nominal glass-transition temperature) for the stress relaxation of polycarbonate and the dielectric compliance of polyvinyl acetate.

Appendices

Appendix 1: Governing equations

Making use of Equations (1) and (7) from the text, we can write the governing equation for ϕ as

$$\frac{\mathrm{d}\upphi}{\mathrm{d}\mathrm{t}}=-\frac{\upphi}{\tau }+{\mathrm{q}}_{\mathrm{c}}$$

(43)

where

$${\mathrm{q}}_{\mathrm{c}}\equiv -\frac{\mathrm{dT}}{\mathrm{dt}}.$$

(44)

For the case of a thermal quench (from T_i to T_bath at t = 0), we have that q_c is a Dirac delta function (Dirac 1958; Lighthill 1959) of magnitude

$$\Delta \mathrm{T}\equiv {\mathrm{T}}_{\mathrm{i}}-{\mathrm{T}}_{\mathrm{bath}}$$

(45)

such that the solution for t > 0⁺ is simply

$$\upphi \left(\mathrm{t}\right)=\Delta \mathrm{T}\ \exp \left\{-\mathrm{Q}\left(\mathrm{t}\right)\right\}$$

(46)

where

$$\mathrm{Q}\left(\mathrm{t}\right)\equiv {\int}_{{\mathrm{o}}^{+}}^{\mathrm{t}}\frac{\mathrm{d}\overset{\sim }{\mathrm{t}}}{\uptau \left(\overset{\sim }{\mathrm{t}}\right)}.$$

(47)

Or, if the KWW (Kohlrausch 1847; Williams and Watts 1970) parameter is introduced, (46) becomes

$$\upphi \left(\mathrm{t}\right)=\Delta \mathrm{T}\ \exp \left\{-{\mathrm{Q}}^{\upbeta}\left(\mathrm{t}\right)\right\}$$

(48)

where β typically lies between 0 and 1. In this case, the equivalent differential equation becomes

$$\frac{\mathrm{d}\upphi}{\mathrm{d}\mathrm{t}}=-\upbeta {\mathrm{Q}}^{\upbeta -1}\frac{\upphi}{\uptau}$$

(49)

for t > 0⁺, subject to the initial condition

$$\upphi \left(\mathrm{t}={0}^{+}\right)=\Delta \mathrm{T}.$$

(50)

For the constant-cooling-rate case, with q_c a constant in (43) & (44), the closed-form solution (with KWW parameter included) is simply

$$\upphi \left(\mathrm{t}\right)=\frac{{\mathrm{q}}_{\mathrm{c}}}{\mathrm{u}\left(\mathrm{t}\right)}{\int}_0^{\mathrm{t}}\mathrm{u}\left(\overset{\sim }{\mathrm{t}}\right)\mathrm{d}\overset{\sim }{\mathrm{t}}$$

(51)

where

$$\mathrm{u}\left(\mathrm{t}\right)\equiv \exp \left\{{\mathrm{Q}}^{\upbeta}\left(\mathrm{t}\right)\right\}$$

(52)

and Q(t) as defined in (47). Alternatively, the governing differential equation in this case becomes

$$\frac{\mathrm{d}\upphi}{\mathrm{d}\mathrm{t}}=-\upbeta {\mathrm{Q}}^{\upbeta -1}\frac{\upphi}{\uptau}+{\mathrm{q}}_{\mathrm{c}}$$

(53)

subject to the initial condition:

$$\upphi \left(\mathrm{t}=0\right)=0.$$

(54)

In particular, the factor βQ^β-1 common to both (49) and (53) reduces to unity when β=1 (i.e., when the KWW approximation becomes an identity).

In relating the computational variable ϕ (≡ T_eff - T) to the experimentally determined variable χ (≡ υ - υ_∞), we make use of Equation (9) in the text which directly relates the two via the constant Δα^* defined in (10). That is,

$${\upalpha}^{\ast}\left(\mathrm{T}\right)\equiv \frac{\mathrm{d}\upupsilon \left(\mathrm{T}\right)}{\mathrm{d}\mathrm{T}}$$

(55)

measures the temperature sensitivity of the specific volume (throughout, it is tacitly assumed that the pressure is atmospheric). In general, α*(T) tends to be a constant, α_l^* (say), at sufficiently high T and a correspondingly smaller constant, α_g^* , at sufficiently low T.

An underlying assumption in the simulation is that the specific volume υ(t) responds instantaneously to changes in T(t) via the temperature sensitivity α_g^*. For example, in the case of a thermal quench, with T(t) undergoing a step change of magnitude ΔT down from T_i to T_bath , it is assumed that the corresponding instantaneous change in υ(t) is

$$\Delta \upupsilon =-\Delta \mathrm{T}\times {\upalpha}_{\mathrm{g}}^{\ast }$$

(56)

whereas υ_∞(t), the equilibrium specific volume, undergoes a change of

$$\Delta {\upupsilon}_{\infty }=-\Delta \mathrm{T}\times {\upalpha}_l^{\ast }.$$

(57)

Accordingly, since υ = υ_∞ initially (when the system is in equilibrium), it follows that, at t = 0⁺,

$$\upupsilon -{\upupsilon}_{\infty }=-\Delta \mathrm{T}\ \left({\upalpha}_{\mathrm{g}}^{\ast }-{\upalpha}_l^{\ast}\right),$$

that is,

$$\upchi =\Delta {\upalpha}^{\ast}\times \upphi$$

(58)

where use has been made of (8), (10) and (50). That is, (58) is the same as (9), which is assumed to apply at all t.

Furthermore, if we now consider the commonly-employed non-dimensional variable δ which, for the thermal-quench case, is typically defined as

$$\updelta \equiv \frac{\upsilon \left(\mathrm{t}\right)-{\upsilon}_{\infty}\left({\mathrm{T}}_{\mathrm{bath}}\right)}{\upsilon_{\infty}\left({\mathrm{T}}_{\mathrm{bath}}\right)},$$

(59)

it then follows from (8) and (9) that

$$\updelta =\frac{\Delta {\upalpha}^{\ast }}{\upsilon_{\infty}\left({\mathrm{T}}_{\mathrm{bath}}\right)}\upphi .$$

(60)

Typically, the coefficient in (60) is taken to be a constant, denoted as Δα, where

$$\upalpha \equiv \frac{1}{\upsilon}\frac{\mathrm{d}\upsilon }{\mathrm{d}\mathrm{T}}$$

(61)

and

$$\Delta \upalpha \equiv {\upalpha}_l-{\upalpha}_{\mathrm{g}}$$

(62)

is analogous to Δα^* in (10).

Of course, if the overall temperature range of T_bath is sufficiently small such that the variation in υ_∞(T_bath) is negligible, it is then reasonable to treat the coefficient in 60) as constant. However, in the present study we include data in which υ_∞(T_bath) varies by almost 10%. {For example, with dυ/dT ≈ 5.5 × 10⁻⁴cm³/gm°C (from third column of Table 10) and T_bath ranging from -52°C to about 100°C, it follows that υ_∞ (T) varies by about 0.084 cm³/gm overall.} Accordingly, in fitting the data, it will be more accurate to fit the data in terms of its dimensional form, χ, rather than its non-dimensional form, δ, thus avoiding the inaccuracy of treating the coefficient in (60) as a constant. This is what has been done in the present investigation.

Appendix 2: Value of ∆α* for polystyrene

Listed in Table 10 are relevant data sources from the literature for the case of polystyrene. As indicated, many of the cited results are based upon thermal-quench data which have been replotted in terms of “aging time” (ta) measured from when the specimen was quenched. In particular, such plots are given directly in Lee and McGarry (1990) and Struik (1978), whereas the remaining entries for specified ta have been obtained by cross-plotting the underlying thermal-quench data. Based upon the cumulative results, it seems that a reasonable representative value for ∆α* is 3.3 × 10-4 cm3/(gm°C), which is what has been employed throughout the simulated results in the present investigation.

Table 10 Experimental results for υ_∞ and ${\upalpha}_l^{\ast },\kern0.5em {\upalpha}_{\mathrm{g}}^{\ast}\kern0.5em \&\kern0.5em \Delta {\upalpha}^{\ast },$ in (10^-4cm³/(gm°C)), from various sources for polystyrene

Numerically, the present calculations for both the thermal-quench and constant-cooling-rate cases have been done mainly in terms of the differential-equation formulation, using a fourth-order Runge Kutta (formula 25.5.10 from Abramowitz and Stegun 1965). The results have been corroborated in many instances by using the integral formulation in terms of the simple trapezoidal rule (formula 25.4.1 from Abramowitz and Stegun 1965).