Introduction

The study of yield stress fluids and, in particular, the questions related to their transition from solid-like behavior in static condition to liquid-like behavior in viscoelastic kinetic condition, the existence or not of thixotropy, the time-dependent effects, the discordance of results obtained with different measurement methods, and the use of new measurement technologies (Balhoff et al. 2011; Bonn and Denn 2009; Bonn et al. 2017; Choi et al. 2011; Coussot 2014; Coussot et al. 2017; Dinkgreve et al. 2016; Jönkkäri and Syrjälä 2010; Ong et al. 2019; Owens et al. 2020; Sun and Gunasekaran 2009; Ulicny and Golden 2007) have been object of several investigations from some decades to today.

Generally, in experiments that probe the transition from liquid to solid, the dynamic yield stress τyd is measured according to the definition \( {\tau}_{yd}={\lim}_{\gamma \dot \to 0}\tau \left(\dot{\gamma}\right) \), namely, it is the shear stress measured in steady-state shear flow in the limit where the deformation rate (shear rate \( \dot{\gamma} \)) goes to zero, so that the extrapolation of the flow curves (τ vs \( \dot{\gamma} \)) towards the vanishing shear rate is used. However, this methodology suffers from some important limitations: wall slip occurrence (Buscall 2010; Poumaere et al. 2014), dependence on the sweep rate of shear rate (Divoux et al. 2013), and thixotropy effects depending on the preparation (Dinkgreve et al. 2018). Other researchers prefer to switch off the flow rather than progressively decreasing \( \dot{\gamma} \), determining the residual stress, but this procedure is sensibly influenced by the value of the initial applied shear rate (Lidon et al. 2017).

On the other hand, several types of experiments are also devoted to the transition from solid to liquid, in order to determine the static yield stress, i.e., the maximum stress for which solid structure is preserved during shear start up (Divoux et al. 2011). For this purpose, creep experiments are often performed: a constant shear stress is applied and strain is monitored (Møller et al. 2009). If shear γ tends to a constant value, the material remains a solid (i.e., does not flow), while if γ increases with time, the material behaves like a liquid. Therefore, the static yield stress is obtained as the maximum shear stress for which a flow is not activated. Also, in this kind of measurements, some criticisms can be underlined, since it is not categorical to establish if a steady-state is effectively reached and if the system flows or not, in particular because it could be that no apparent flow is detected for a long time before the material finally yields (Chaudhuri and Horbach 2013). Among the most studied materials, Carbopol’s hydrogel solutions have been investigated in depth for their stability, for connection with jamming in granular system and easy modeling (Gabelle et al. 2013; Péméja et al. 2019; Shafiei et al. 2018), as well as for wall slip effects (Daneshi et al. 2019; Poumaere et al. 2014), and interplay between creep and residual stresses (Lidon et al. 2017). In a recent paper (Varges et al. 2019), peculiarities of the transient and steady-state were shown, demonstrating that in Carbopol 980 the elastic effects are dominant when the system is fully structured, while viscous effects dominate after yielding. At stress just above the yield stress, thixotropic effect is observed, in contrast to the observed absence of thixotropy at large stresses. No elasticity was observed in the dispersions while unstructured, the microstructure rebuilding instantaneously after reduction of the imposed stress to a value below the yield stress. In the present investigation, experiments are conducted in such a way to reach the state of static equilibrium from dynamic conditions, or to abandon the static equilibrium, always working around stress values close to yield stress. Therefore, a thixotropic trend is expected, as well as a difference between static and dynamic yielding (Dinkgreve et al. 2017). In the same paper (Varges et al. 2019), the importance of measure times is shown, which also fits in with our results. In line with the mentioned preliminary findings, we do not consider considerable residual elastic stresses, but we took into account a possible elastic deformation only when the quasi-solid structure is present below the yield stress.

Here, we propose a new experimental technique with the aim to conduct an analysis on the basic significance of yield stress and have chosen Carbopol because it is a well-characterized material, while the aspects highlighted above remain to be clarified. The renewed experimental methodologies represent an alternative approach to the topic. Considering the listed limits of the most used methodologies to measure both dynamic and static yield stress, the proposed innovative procedure is substantially based on the following changes regarding the setting of the problem and the measurement technique:

First, we start from the fundamental physics conception that, if the static yield stress (τys) is given by the minimum shear stress necessary to start a flow of the elasto-viscoplastic material investigated and the dynamic one (τyd) is the smallest shear stress to apply in order to stop it flowing, τys and τyd are also the mutual shear stresses applied by the material studied on an object that starts to flow in it and ends flowing in it, respectively. The proposed methodology differs substantially from the standard rheological techniques because it is based on the measurement of the stress that a fluid exerts on an immersed rotating object, whereas classic methods are based on the evaluation of the stress that is applied on a fluid.

Second, the experiment for dynamic yield stress evaluation is within the basic methodology of switching off the flow, but instead of starting from a fixed initial shear rate and repeating the experiments by decreasing it, one starts from a non-equilibrium condition that automatically leads to vanishing shear rate. Thus, it is not necessary to impose a decreasing of the initial speed by a motor driving torque.

Third, the procedure for determining static yield stress lies in the basic concept of a creep experiment but, in accordance with the criterion expressed in point 1, the deformation of the solid-like material that becomes fluid is indirectly deduced from the release of a cylinder put in rotation in it.

Fourth, a torsion pendulum equipped with a magnetic dipole and a rotating cylinder immersed in the investigated material was used as the object on which the shear stress of the fluid is applied; the presence of a homogeneous magnetic field applying a twisting torque on the magnetic dipole has a fundamental role for the measurement procedure and it constitutes one of the most original aspects.

In fact, the exact knowledge of the applied magnetic torque and the induced rotation of the equipment in the fluid allow the identification of the relaxation time from a non-equilibrium flow condition to a state of static equilibrium, as well as the measurement of both static and dynamic yield stress. Experiments in different equilibrium conditions were possible thanks to the innovative magnetic field assistance. They highlighted the effects of measurement times when yield stress fluids are investigated, helping to shed light on some points of the related data of previous literature and allowing to establish a time-cadenced procedure that guarantees a reliable and repeatable quantitative evaluation of yield stresses.

To the best of our knowledge, the same possibility to determine not only static and dynamic yield stress but also time-dependent phenomena, using a single experimental setup and applying the same basic methodology, was exhibited only by large-amplitude oscillatory shear (LAOS) measurements. The fundamental difference between the two methodologies consists in the use of static equilibrium conditions in the here proposed magnetic-field-assisted torsion pendulum technique (MFATPT), while LAOS is based on the dynamic oscillation characteristic at different frequencies, static conditions being never active, and a dependence on the amplitude of the oscillations being present. Therefore, the main advantage of MFATPT is that it allows to investigate a broad range of conditions, from quasi-static state to the LAOS ones with high accuracy, while a MFATPT negative aspect consists in the considerable time necessary to take an accurate measurement, depending on the need to follow conditions of static equilibrium.

In the experimental section, the material preparation and the description of the innovative experimental apparatus are presented, with the related measure theory. The subsequent section reports the experimental results on the following: (i) the relaxation behavior from a fluid in kinetic condition to solid-like material in a static condition, for solutions at a different percentage of Carbopol; (ii) the behavior from static condition to flow condition through the increasing stimulus of a magnetic torque to determine the static yield stress; (iii) the behavior from kinetic flow to the static equilibrium for different external conditions to determine the dynamic yield stress; and (iv) round-trip cycles through successive equilibrium conditions performed at different experimental times, to highlight the importance of the latter and optimize experimental measurements.

The conclusions will detail the most significant contributions of this study, consisting of the easy and direct measurement of static and dynamic yield stresses, as well as the determination and the modeling of the behaviors over time from a fluid-like response (when flowing) to a solid-like response (when static) typical of Carbopol microgels.

Experimental

Materials

Carbopol (commercial name of polyacrylic acid) solutions were prepared starting from Carbopol® 980 NF Polymer (Lubrizol), following standard preparation protocols. In particular, Carbopol powder was dissolved in deionized water (MilliQ) and mixed with a propeller (Heidolph RZR 2102 Control) for about 15 min at 700 rpm. The so-prepared aqueous solution was neutralized with a 1 M sodium hydroxide water solution (supplied by Sigma-Aldrich). The neutralization step took place during about 1 h stirring. Carbopol solutions were prepared at different concentrations ranging between 0.07 and 0.20%wt.

Carbopol forms a colloidal dispersion when mixed with water. After neutralization, the polymer chains, interconnected by crosslinks, absorb water and partially uncoil due to the electrostatic repulsion. High molecular weight polyacrylate entanglements interconnect the chains. They lead to irreversible agglomerates (Putz and Burghelea 2009) and prevent free flowing (Taylor and Bagley 1974). The hydration produces ten times increase of the chain diameter (Kim et al. 2003). In summary, the ionization process, with the crosslink of the swollen molecules, produces a strongly bonded microgel network. The latter exists at different scale level, also at very low concentrations, as reported in several papers (Gutowski et al. 2012; Kim et al. 2003; Piau 2007) and recently demonstrated by high-resolution confocal microscopy(Graziano et al. 2020). Indeed, yield stress in Carbopol-based systems is strongly dependent on the Carbopol particle networks, the latter being at the basis of the yielding nature. A higher concentration of Carbopol can also induce a jamming transition when a 3D network is generated, the suspension behaving as a gel-like material (Dinkgreve et al. 2016; Dinkgreve et al. 2015; Paredes et al. 2013). At low stresses, the microgel agglomerates do not move relatively to each other, but are able to deform, showing a solid-like elastic behavior. Above a threshold value of the external shear stress, a relative mobility of the microgels occurs producing a liquid-like visco-plastic behavior (Ketz et al. 1988).

For this study, Carbopol® 980 has been chosen among the others since it is non-toxic and ensures the formulation of a yield stress model fluid also with a small amount of polymer, reaching a meaningful yield stress range for application (Varges et al. 2019). Sample stability was evaluated by measuring rheological properties over time, highlighting a long-term preservation of the yield stress for over a week from the preparation. Different methods can be used for the determination of the yield stress, leading to results that can vary more than one order of magnitude, in the dependence of sample handling and used method (Bonn et al. 2017). To have preliminary data on the used material, here we adopt one of the most used methods for the determination of yield stress by means of oscillatory tests. In particular, considering the curves of the elastic modulus G′ and viscous modulus G′′ as functions of shear stress at a fixed frequency of 1 Hz, the value of stress corresponding to the initial drop of G´ (5% of the difference from the plateau value) could be taken as static yield stress. Indeed, this point represents the onset of the non-linear region where the fluid is not behaving anymore as an elastic solid and flows like a liquid (Mezger 2006; Shih et al. 1999). A stress-controlled rheometer Physica MCR 301 (Anton-Paar) equipped with a titanium cone-plate system (65 mm, angle of 2°) was used. The obtained data have been used for a comparison with the results of the new methodology proposed in this work.

Once prepared, the solutions were stored in tubes sealed with para-film tape. The experimental measurements with the innovative setup were performed within 3 days of preparation. Aseptic pipettes calibrated to the tenth of a milliliter were used for the transfer inside the cylindrical ampoule of the innovative experimental apparatus described in the following section.

Experimental apparatus and theory of the measure

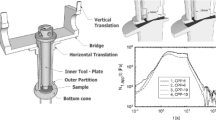
Figure 1 shows the scheme of the experimental apparatus designed to measure yield stress of a complex fluid. A nylon thread, stretched along the vertical axis (Y), constitutes a torsional pendulum together with the magnetic dipole, which has a moment μ (78 mA m2), and the inert plastic cylinder (I C), both tied, balanced and coaxial with the wire itself. Using the standard calibration curve of the elastic reaction torque for the used wire, the value of the elastic torsion constant K = 131·10−7 Nm was easily determined. The external cylinder (E C) is fixed to the ground. The radii of the inner and outer cylinders are R1 = 7.0 mm and R2 = 15.0 mm respectively. The yield stress fluid (YSF) to investigate is transferred, taking it with pipettes from the container in which it has degassed, and slowly introducing it into the cavity between the two cylinders, accurately avoiding the formation of air bubbles. This operation was continued until the inner rotating cylinder is immersed in the sample for a height h. We underline that the rotating cylinder is perfectly balanced and solidly bound with respect to the suspension axis, which is also the rotation axis, and any vertical thrust (Archimedes’ thrust, elastic reaction thrust that tends to make the cylinder float) are balanced by the tensile stress in the suspension wire.

Fig. 1
figure 1

Scheme of the prototype experimental apparatus: symbols as described in the text

Full size image

The magnetoelastic resonator (M R), whose signal is processed by a Signal Analyzer (S A), has a core consisting of an innovative nanocrystalline material. This soft ferromagnetic core is high sensitive to changes in the local magnetic field (Lanotte et al. 2000). When the pendulum rotates, the magnetic dipole, rigidly connected to it, also rotates inducing a decrease in the magnetic field component coaxial with the sensor.

Therefore, any rotation (θ) of the pendulum around the Y-axis is detected with high sensitivity (± 0.25°). This methodology has been deeply explained in reference (Lanotte et al. 2019). In that previous investigation, the damped oscillation of a similar torsional pendulum, immersed in a fluid, was studied to determine the material viscosity. In this case, instead, the measurement technique is fundamentally different since it consists of determining the condition of static equilibrium of the pendulum. Moreover, important components were added to the original apparatus. In particular, a standard system of Helmholtz Coils (HC) was integrated for applying a static magnetic induction field B along the Z-axis, which is perfectly orthogonal the suspension wire, on Y-axis, and to the magnetic dipole in the rest position (Fig. 1). Both the rotation stimulation and the equilibrium position are determined by the torque produced by the field B. The rotation angle is also directly visualized using a standard protractor that is fixed in the horizontal XZ plane and coaxial with the Y-axis. The MR sensor is not influenced by magnetic induction field B since it is sensitive only to magnetic component along X-axis. The external EC ampoule is immersed in a thermal bed, maintaining a constant temperature (20 °C) by means of a thermostatic setup (Lanotte et al. 2019). Figure 2a shows an image of the experimental equipment (snapshot from above).

Fig. 2
figure 2

a Photography of the experimental apparatus showing the torsional pendulum system -suspension wire along Y-axis + rotating magnetic dipole in the plane XZ + empty cylinder (IC)-, the external cylinder (EC), the yield stress fluid (C) which fills the cylindrical crown to a controlled level, the external ampoule (A) in which water is kept at constant temperature, the needle (N) glued to the magnetic dipole, the protractor fixed on the XZ plane and centered on the Y-axis, the position of the magnetoelastic resonator (MR) for the precise measurement of the rotation angle. b. Scheme of the scalar components of the mechanical moments along Y-axis in any equilibrium condition reached after the application of a magnetic induction field directed along Z-axis. The figure shows the sign of Y scalar components of the magnetic torque (− μ B sin(α)), the mechanical reaction torque (+ Kθ), the yield stress torque (+ τ Sd), and the internal friction torque (+Mf) in the case examined, i.e., when equilibrium is achieved through clockwise rotation

Full size image

It is possible to see the permanent magnet that constitutes the magnetic dipole μ, the internal and external cylinders (IC and EC respectively), and the Carbopol solution (C) between them. A nonmagnetic stainless-steel needle is also visible, integrated with the pendulum system and coaxial with the magnetic dipole. This needle is a guide for visualizing the rotation on a protractor (G in Fig. 2a), fixed on a horizontal plane and centered on the Y-axis, along which the nylon suspension wire is stretched.

In the case shown in Fig. 2, the applied field B ≠ 0 produces the reduction of the α angle between B and μ from the initial 90°, in the condition of B = 0, to the final 70°. Since α is complementary to the rotation angle, the latter assumes the value θ = (π/2 − α) = 20°. In fact, when a magnetic induction field is applied, the torsion pendulum is subjected to a magnetic torque μ ∧ B, whose modulus is μ·B·sin(α) inducing a clockwise rotation around Y (see Fig. 2b).

On the other side, starting from the position in which the pendulum is not subject to any external stimulus, when a rotation of θ intensity is produced, a mechanical reaction torque of modulus Κ·θ—and direction indicated in Fig. 2b—is also applied to the pendulum, being K the elastic torsional constant of the suspending wire. Moreover, when a static equilibrium is established, if there is a fluid between the internal and external cylinder, a mechanical moment also acts due to the shear yield stress (τy) applied by the fluid on the cylinder surface (τy·Sd Fig. 2b). This mechanical moment is then applied on the cylinder surface immersed in the solution (base area ΠR12 and eight h, Fig. 1) by the fluid which is in contact with this surface in static condition: the fluid not in contact with the cylinder does not apply any action on it. In the described experimental conditions, the intensity of this torque can be expressed as τy·Sd, where τy is the constant yield stress and Sd = ∫s r · dS, where S is the surface of IC wet by the fluid and r is the distance of any elementary surface dS from the rotation axis Y. In the investigated case, it results in

$$ {S}_d=2\pi {R_1}^2h+{\int}_0^{R_1}2\pi {r}^2 dr $$
(1)

Since R1 = 7 mm and h = 3 mm or h = 9 mm were used in the experimental apparatus, the values Sd = 1.6·10−6 m3 or 3.5·10−6 m3 are obtained respectively.

Ultimately, whenever the pendulum stops in static equilibrium at an angle θe, the sum of all the components along Y-axis of the applied torques must be equal to zero. Therefore, referring to the scheme in Fig. 2b, the following equation can be applied:

$$ - B\mu \sin \left(\frac{\pi }{2}-{\theta}_e\right)+K{\theta}_e+{\tau}_y\cdotp {S}_d+{M}_f=0 $$
(2)

where summarizing for the sake of clarity, τy • Sd is the torque due to the shear yield stress in the points of the static fluid in contact with cylinder IC (Fig. 1), \( - B\mu \sin \left(\frac{\pi }{2}-{\theta}_e\right) \) is the torque component applied by the external magnetic field in consequence of the presence of the magnetic dipole glued to the pendular system, Kθe is the torque component due to elastic torsional reaction of the suspension wire, and Mf is the component of the torque due to eventual mechanical internal friction, inherent in the pendulum system, and not intern to the fluid. There are no terms due to internal stress in the fluid, as well as internal friction in the fluid, because they are not applied on the rotational pendulum whose static equilibrium is considered. Any reaction relating to elastic deformation of the like-solid phase is considered contained in τy (or rather inherent to the contact shear stress itself).

In conclusion, the simple theory of the experiment provides

$$ {\tau}_y=\frac{\left(B\upmu\ \cos {\theta}_e-K{\theta}_e-{M}_f\right)}{S_d} $$
(3)

from which the yield stress value can be calculated by measuring the equilibrium angle θe, being known all the other parameters on the right side of the equation.

Results and discussion

Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress

To measure the dynamic yield stress, a first experimental investigation was devoted to the detecting of the rotation angle as a function of time. A torsion was produced up to a maximum fixed angle θmax. Afterwards, the pendulum was left under the sole action of the elastic moment recall and the rotation angle has been acquired while the static equilibrium conditions were restored.

With reference to Fig. 2a, initially, the pendulum, free from any torsional stress, was stationary at the initial angle θι = 0. By a slow progressive increase in the intensity of the B field along Z-axis, the pendulum rotation was produced up to θmax = 60°. Then, B was turned off and the rotation of the pendulum, during the approach to the new equilibrium position, was detected over time.

If the experiment is carried out in the air, the pendulum has damped oscillations and gradually stops at the equilibrium angle |θe| < 0.25°. This means that the torque due to the internal friction in the pendulum system (Mf) is negligible, since it is included in the limit of the experimental error.

When Carbopol solution is present, after an abrupt decrease of the angle in few seconds, a non-zero equilibrium angle θmin is slowly reached, as shown in Fig. 3 for different weight percentage: this clearly indicates that a shear stress occurs on the fluid-cylinder interface, preventing further sliding and balancing the mechanical moment of the elastic recall. Since the fluid initially is flowing and in final condition is stopped, we can speak of dynamic yield stress.

Fig. 3
figure 3

Decrement with time of the rotation angle during the return to the equilibrium condition, under the sole action of the moment of elastic recall. The experimental points are related to different Carbopol contents as specified in the box in the figure and refer to average θ values obtained by repeated measurements. Experimental errors are contained in the point size. Continuous curves are obtained by the analytical simulation described in the text

Full size image

Taking into account that θmin is progressively reached by a counterclockwise rotation and B is switched off, the equilibrium of torques provides:

$$ K{\theta}_{\mathrm{min}}-{\tau}_{yd}\cdotp {S}_d=0 $$
(4)
$$ {\tau}_{yd}=\frac{K{\theta}_{\mathrm{min}}}{S_d} $$
(5)

where τyd is the dynamic yield stress.

In Fig. 3, the decreasing behaviors of θ (measured by the MR sensor) with time, starting from θmax in the release position up to θmin in the final equilibrium position, are reported in the aqueous solutions of Carbopol with different weight percentages. The experimental points are obtained by averaging on reiterated measurements and are reported with the respective experimental errors. In general, it appears that after about 20 min, the equilibrium is definitively reached in all the used dilutions.

The value of the parameter h was fixed at 3 mm for all samples, except for the 0.07%wt solution for which it was necessary to use h = 9 mm in order to lengthen the evolution times towards the static equilibrium. From the measured values of θmin (Table 1), the shear stress values, due to a dynamic yield, have been obtained by applying Eq. (5).

Table 1 Average values of the dynamic yield stress τyd versus the content of Carbopol as deduced from the final equilibrium angle (θmin) applying Eq. (5). The errors concerning τyd were evaluated by means of the propagation law considering the sensitivity of the measuring devices
Full size table

When stopping from flow to static condition, Carbopol solutions change both the microscopic morphology and the physical properties from liquid-like to solid-like (Bonn et al. 2017; Shafiei et al. 2018). The establishment of a new structural configuration with different physical and chemical properties could take time, and this phenomenon is relevant in enhancing thixotropic behavior (Dinkgreve et al. 2018). Therefore, in studying the settling down of the equilibrium starting from a kinetic condition, in order to identify the dynamic yield stress, the approach to equilibrium takes time, as evidenced by the experimental results in Fig. 3. Considering the used measurement methodology, it is important to note that, when the cylinder IC (Fig. 1) is approaching to stop, the fluid in contact with the surface of the cylinder acquires a zero velocity relative to the cylinder itself. The fluid in the cavity of the two cylinders follows the classical shear flow profile, where the velocity is zero at the fixed wall and is maximum at the moving wall, so the fluid velocity takes some time to become zero everywhere. Only when the shear-flow completely ends, the cylinder IC is blocked.

It is interesting to stress from Fig. 3 that practically, the same time occurs to reach equilibrium in solutions at different Carbopol contents (for all dilution, 20 min is necessary to make the decrement of θ lower than the experimental error). This indicates that the processes governing the time evolution are the same in all the cases. Since by increasing Carbopol content, both viscosity, η, and elastic modulus, G′ increases; it is plausible that the relaxation time of the equilibrium approach results practically the same, being related to the ratio η/G′, as generally results in polymers. On the other hand, the absolute decrement appears to be linked to a different composition and consequent different viscosity and density, since they are not proportional to the content only (Lidon et al. 2017; Møller et al. 2009; Varges et al. 2019).

Effect of the application of an external torque to start a flow from the initial equilibrium condition at θ = 0: determination of the static yield stress

In the absence of liquid, starting from θ = 0, the current in the Helmholtz coils is increased to produce a magnetic induction field that applies a mechanical moment μ˄B to the torsional pendulum (B is applied along Z; see Fig. 2). Since the rotation starts at the lowest applicable current, the mechanical moment, due to the internal friction of the pendulum, is negligible to inhibit rotation, in agreement with what was observed about the free oscillations in the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section.

Then, starting from the pendulum in the initial equilibrium position (θ = 0 and B = 0) and with the fluid material covering the rotating cylinder up to a height h, a magnetic induction field B = N·ΔB is applied, with ΔB = 0.25·10−5 T and N increased progressively by one unit. After 20 min from B application, the rotation angle detected by the sensor MR (Fig. 2a) was recorded, verifying that after this wait, the stable equilibrium is obtained (the measured values of θe vs B remain stable over time). In presence of a static yield stress, the pendulum rotation is counteracted and the pendulum remains at rest up to B ≤ B°. In other words, only for B=B° + ΔB, a permanent rotation, equal to or greater than the minimum detectable one (Δθ = 0.25 ° by means of MR sensor), is detected. We have outlined “permanent” rotation, because it was always verified that by decreasing magnetizing induction field, namely, returning towards B = 0 T value, the rotation does not return to zero. In fact, if the equilibrium angle equal zero is restored, it means that the investigated solution is strained (as in an elastic solid sample) but no flow is produced. Only if rotation does not return to zero by removing magnetic induction field, we consider activating the flowing fluid adjacent to the rotating cylinder surface.

This is clarified by the data represented in Fig. 4. In fact, if a torsional cycle is performed up to B° to successively return to zero, also, the rotation angle goes to zero; on the contrary, when the maximum B value is shifted to B° + ΔB, the rotation remains partially permanent when the torsion returns to zero (Fig. 4).

Fig. 4
figure 4

For each solution with different Carbopol content, both the torque cycles, θe vs B, up to a maximum value Bo and return to zero (on the left) and the torque cycle up to a maximum Bo + ΔB and return to zero (on the right), are shown: in the first case, the rotation is completely reverted; in the second, a residual rotation is found. This indicates that Bo applies a torque producing a solid-like material deformation, which can be reverted decreasing B to zero; instead, a minimum Bo increment (ΔB) produces a greater torque which induces a flow activation with a liquid-like response, and consequently an effective rotation of the cylinder inside the fluid. In fact, the rotation is not eliminated by reducing the torsional stress to zero

Full size image

Once one finds the Bo value, by applying the equilibrium conditions (3) to the sum of the mechanical moments, with Mf = 0, we can deduce the static yield stress:

$$ {\uptau}_{ys}=\frac{B{}^{\circ}\upmu\ \cos {\theta}_e-K{\theta}_e}{S_d} $$
(6)

taking into account the Sd value for h = 3 mm, except in the case of 0.07w% solution for which h = 9 mm was used. This last choice was necessary otherwise the pendulum rotation starts for values of the magnetic induction field very close to the minimum instrumentation limit making it impossible to identify the threshold value B°.

In Table 2, the values of Bo are reported with the consequent τys values obtained from Eq. (7). The percentage difference between static and dynamic yield stress (Δτ/τyd) is also shown. The static conditions give higher values for all Carbopol content supporting the conclusion that the difference depends on the procedure only and it is not an intrinsic property of the material.

Table 2 For each aqueous Carbopol solution, the table shows the B° field value deducted from the torque cycles (θe vs B) in Fig. 4, the static yield stress consequent from Eq. (7), and the percentage increase (Δτ/τyd) of the static value with respect to the dynamic one. The errors concerning τys were evaluated by means of the propagation law considering the sensitivity of the measuring devices
Full size table

In fact, the lower value of dynamic yield stress can be understood by considering that the kinetic rotational energy of the pendular system must be canceled by the work of the fluid shear reaction forces, and this work is made by the elastic reaction of the like-solid material that is forming, so straining it and abating the equilibrium angle, θmin. As consequence, an artifact decrement of yield stress measured from Eq. (5) is produced. This effect is inactive in the static case, when only structure yielding is present. This means that there are not two different yield stresses, but that the stress value depends strictly on the measurement initial conditions: dynamic or static.

Torsion cycles and time-dependent response

The time required to change both rotating equipment and Carbopol solution from the static equilibrium to the flow regime and vice-versa has an evident impact when measuring the pendulum torsion angles in the investigated solution as a function of a magnetic field higher than the Bo threshold value.

The results of this investigation in 0.20% and 0.10% Carbopol solutions are shown in Fig. 5a and b respectively. For the measurements, two different procedures were adopted. In a first case (black squares in Fig. 5), any increase (or decrement) in field strength, ΔB, strictly necessary to reach the subsequent measuring point, was performed in a fixed interval of 5 s.

Fig. 5
figure 5

Equilibrium angle θe as a function of the magnetic induction field B in torsion cycles, as performed according to the procedure explained in the manuscript (short pauses, black points, and long pauses, red points) in 0.20% (a) and 0.10% (b) Carbopol hydrogel

Full size image

Then, after a 30-s pause, the measurement of the rotation was recorded. Thus, each experimental point corresponds to an evolution of the microscopic state that occurred in about 30 s. The same rotation can also be followed by a magnification camera on the protractor.

In a second case (red squares in Fig. 5), the same time gradients of the field (ΔB/5 s) were applied, but the pause before recording θ experimental values was extended to 20 min (thus ensuring—on the basis of the results in the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section—that the equilibrium configuration has been achieved before to perform angle measurement).

In agreement with the system evolution over time, the equilibrium torsion angle measured over short times (black curve) increases less in the growth phase of the magnetic torque (Fig. 5 →), and it decreases less in the decreasing phase of the magnetic torque (Fig. 5 ←), compared to the same variations measured over long times (red curve). The yield stress dependence on the experiment duration was already highlighted in previous investigations (Caton and Baravian 2008; Malkin et al. 2017). In particular, short-time and long-time yield stress values for Carbopol can be largely different (Benmouffok-Benbelkacem et al. 2010). Our methodology allows to determine the waiting time for the stabilization of the equilibrium and to ensure the repeatability of the results when the long pauses of the second procedure are adopted. Therefore, we consider in detail the experimental behavior provided by the red curve in Fig. 5a and the respective experimental points, in order to obtain the yield stress values (Table 3).

Table 3 Experimental data from torsion cycles in 0.20% Carbopol solution. Average values from repeated measurements of the torsion equilibrium angle, θe, as a function of the magnetic induction field, B, producing the magnetic torque, in the case of a short pause and a long pause. On the fourth row, the yield stress values are also reported, calculated by using the long pause procedure which guarantees the complete stabilization of the torsional equilibrium among elastic, magnetic and yield stress torques (red points in Fig. 5a). The errors concerning τyd* were evaluated by means of the propagation law considering the sensitivity of the measuring devices
Full size table

Concerning the interval of B values lower than 6·10−5 T (Fig. 5a), zero rotation is detected. Such a behavior demonstrates that the static yield stress is acting, counterbalancing the magnetic moment, in agreement with the “Effect of the application of an external torque to start a flow from the initial equilibrium condition at θ = 0: determination of the static yield stress” section, including the B° threshold value.

In a second range of field values increasing from B° up to Bmax (Fig. 5a), any equilibrium point should verify the Eq. (3). Therefore, taking into account Mf = 0, the values of dynamic yield stress obtained from this method—different from the evaluation performed in the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section—τyd* = (B μ cos(θe) – K θe)/Sd, have been calculated and reported in the fourth row of Table 3 (here Sd corresponds to h = 3 mm).

Overall, when the incremental ratio \( \frac{\Delta \theta }{\Delta t} \) (average shear rate) from a measuring point to the next decreases (last row in Table 3), the obtained value of τyd* increases and approaches to τys. This confirms that the difference between yield stress values obtained under static and dynamic condition can be ascribed to the kinetic energy: in fact, the lower the increment in θe and the lower the kinetic energy of the pendulum in approaching equilibrium position and more the dynamic yield stress approximates the static one.

Now, consider the experimental behavior obtained by reducing B value from Bmax down to zero. Around Bmax, the yield stress can decrease if the external destabilizing torque decreases towards the zero value, maintaining the static equilibrium condition; therefore, if the friction is bilateral, it can also change direction downwards to reach again its maximum value but acting clockwise. In other words, the sign of the mechanical torque component produced by yield stress can also be negative and the equilibrium could be established when

$$ K{\theta}_e-B\ \mu \sin \left(\frac{\pi }{2}-{\theta}_e\right)\pm \mid {\tau}_y\mid \cdotp {S}_d=0 $$
(7)

where |τy| can vary from 0 up to its maximum possible amount (τyd ), as in the standard case of static internal friction.

As matter of fact, for B = B (Table 3 and Fig. 5a), the sign of yield stress changes in negative, but decreasing the magnetic solicitation, it remains practically equal to zero. This means that yielding mechanism is not bilateral and the equilibrium is reached by decreasing θ until K θe − B μ sin(π/− θe) = 0.

Finally, for low values of the external torque moments, when B < B, the yield stresses due to the stabilization of the solution in a more rigid state become predominant. For B = 0, they assume a maximum value consistent with that previously found, blocking the θe value at 17° (Table 3 and Fig. 5a).

Obviously, the considerations made are valid if the maximum magnetic induction field provides a rotation higher of θmin determined in the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section.

For the lower weight percentage Carbopol hydrogels, the behavior is similar but with minor differences between short pause and long pause measurements. This assertion can be verified in Fig. 5b, where cycles for 0.10% Carbopol aqueous solution are shown. The other percentages are not reported for the sake of simplicity.

The data obtained from torsional cycles confirm the quality of the proposed novel methodology and, at the same time, they highlight the importance of times and procedures for measuring yield stress. Therefore, at this point, it appears appropriate to perform a comparison with numerical data resulting by means of other techniques.

The summary in Table 4 shows that the values of yield stress measured by means of MFATPT have the same trend as those found in the same samples by oscillatory tests but they are higher. The difference is greater at low percentage of Carbopol, where the increment reaches 90%. This could be ascribed to the fact that oscillatory tests directed to determine static yield stress are however performed in finite dynamic conditions (oscillations), while our method ensures measurements in the limit of zero kinetic energy at the flow stopping. In fact, the relative influence of the kinetic energy should be higher with decreasing fluid viscosity (lower Carbopol content).

Table 4 Static and dynamic yield stress obtained from the new proposed device in comparison with the values measured through rheometric oscillatory tests on the same samples and from previous literature investigations on Carbopol 980 hydro-solutions by means of different techniques
Full size table

In Table 4, the dynamic yield stress values obtained in others investigations on the same Carbopol 980 aqueous solutions are also reported. Few data are available for all the Carbopol contents, except for 0.10 wt%. In the last case, we can affirm that the value measured by the new technique is within the range of the previous evaluations. Considering that, generally, the yield stress measured in Carbopol solutions by different methodologies and with different preparation procedure can spread even up to one order of magnitude (Balmforth et al. 2014; Benmouffok-Benbelkacem et al. 2010; Curran et al. 2002; Daneshi et al. 2019; Dinkgreve et al. 2016; Poumaere et al. 2014; Roberts and Barnes 2001; Sun and Gunasekaran 2009), and taking into account the fundamental differences among the measure procedures adopted in the paper as listed in Table 4, this result is acceptable and gives credit to numerical data obtained by the new method proposed here.

Conclusive remarks

The yield stress measurement method proposed herein presents two main innovations with respect to the most commonly used techniques:

First, the measurement is carried out through the effect of shear stresses applied by the fluid on a rotating cylinder immersed in the observed solution. Using the concept of action and reaction, we define as static yield stress the maximum shear stress that the fluid can exert on the cylinder when induced to rotate, starting from static conditions. Similarly, the dynamic yield stress is defined as the maximum shear stress that the fluid can exert on the cylinder, until stopping its rotation in the fluid itself.

Second, the method adopted allows automatically setting the shear rate to zero. This avoids the difficulty of controlling a decreasing angular speed through the mechanical torque of a driving motor, as often necessary in others methods, as well as the stabilization of frequency and amplitude as in oscillatory tests. Moreover, the procedure ensures measurements in the limit of zero dynamic energy both at the start of the flow (static yield stress) and at the stop of the flow (dynamic yield stress).

The proposed new approach led to the following main conclusions:

  1. (i)

    Generally, the values of τys and τyd obtained with different methods can differ between them even of one order of magnitude (Balmforth et al. 2014; Benmouffok-Benbelkacem et al. 2010; Curran et al. 2002; Daneshi et al. 2019; Dinkgreve et al. 2016; Poumaere et al. 2014; Roberts and Barnes 2001; Sun and Gunasekaran 2009). The values obtained by the new methodology are consistent with previous data, being the obtained dynamic yield stress within the range between the previous literature data for Carbopol 980 (Gabelle et al. 2013; Kelessidis et al. 2011; Varges et al. 2019) and the values found by standard oscillatory tests in the same samples (see Table 4).

  2. (ii)

    According to the experimental results, it is confirmed that generally the dynamic yield stress is lower than the static one. This can be explained considering that the Carbopol solutions exhibit a high viscosity at low flow velocity (Balmforth et al. 2014; Benmouffok-Benbelkacem et al. 2010; Bonn et al. 2017; Curran et al. 2002). This contributes to slow down the mobile equipment before activating the structural microscopic bond at the origin of the yield stress. In particular, the behavior of τyd* evidenced in Fig. 5 and Table 3 clearly shows that the measurement of the yield stress depends strictly on the adopted procedure, even when basically the same methodology is used (the equilibrium condition of a pendulum in the case of the present investigation). In fact, it has been highlighted that significant differences are determined by the speed of approach to the equilibrium position (Table 3): the lower is the change of angle over time when approaching equilibrium, the more the dynamic yield stress value tends to the static one.

  3. (iii)

    Using the same setup, the dynamic yield stress can be measured by means of two different procedures explained in the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section and in the “Torsion cycles and time-dependent response” section. These procedures provide the value τyd (Table 1) and τyd* (Table 3) respectively. The values obtained using these two different methods show a considerable agreement and confirm the reliability and the effectiveness of the experiment modeling.

  4. (iv)

    It is possible to follow in detail the evolution of the static equilibrium approach with time (the “Temporal trends to spontaneously re-establish conditions of static equilibrium starting from flow condition: measurement of dynamic yield stress” section; Fig. 3). The equal value of the time required to reach equilibrium is justified by the process of shear flow stopping of the Carbopol suspension that is related to the velocity profile in the cavity.

  5. (v)

    Time-dependent processes have also highlighted the importance of performing long time measurements to ensure that the structural evolutions, and also, deformations have occurred. This is demonstrated by the results of the torsion cycles measured at different times (the “Torsion cycles and time dependent response” section and Fig. 5). The ability to measure the effect of time can also be useful to investigate the complex coupling between viscoplastic deformation, aging, and rejuvenation (Agarwal and Joshi 2019; Coussot 2018; Joshi and Petekidis 2018). Moreover, the methodology used appears competitive compared to some others (Kashani et al. 2015) for its simplicity.

Even the aqueous solutions of Carbopol, which in many respects can be considered as a simple fluid (flow behaviors follow the Hershel-Bulkley law), have here shown significant dependence on time. This underlines the requirement of adequate experimental protocols to obtain reproducible experimental estimates.

The proposed MFATPT technique fits in the field of rotational shear rheometry in concentric cylinders geometry. Compared to standard methodologies, its main points of innovation are the alternative direct physical approach, the effectiveness of the magnetic field assistance, the possibility of adjusting the measurement to the specific time dependency in the YSF used, and the ability to measure dynamic and static yield stress with the same experimental setup. The prerogatives listed above strongly candidate the new methodology to highlight and elaborate peculiar aspects in yield stress fluids.