Stability of bubbles in wax-based oleofoams: decoupling the effects of bulk oleogel rheology and interfacial rheology

Abstract

Oleofoams are dispersions of gas bubbles in a continuous oil phase and can be stabilized by crystals of fatty acids or waxes adsorbing at the oil-air interface. Because excess crystals in the continuous phase form an oleogel, an effect of the bulk rheology of the continuous phase is also expected. Here, we evaluate the contributions of bulk and interfacial rheology below and above the melting point of a wax forming an oleogel in sunflower oil. We study the dissolution behaviour of single bubbles using microscopy on a temperature-controlled stage. We compare the behaviour of a bubble embedded in an oleofoam, which owes its stability to both bulk and interfacial rheology, to that of a bubble extracted from the oleofoam and resuspended in oil, for which the interfacial dilatational rheology alone provides stability. We find that below the melting point of the wax, bubbles in the oleofoam are stable whereas bubbles that are only coated with wax crystals dissolve. Both systems dissolve when heated above the melting point of the wax. These findings are rationalized through independent bulk rheological measurements of the oleogel at different temperatures, as well as measurements of the dilatational rheological properties of a wax-coated oil-air interface.

Introduction

Foaming of edible oils to form oleofoams is used in the design of food products with reduced fat content (Binks and Marinopoulos 2017; Heymans et al. 2017). Oleofoams are more difficult to stabilise compared with aqueous foams, because of the limited availability of non-aqueous foaming agents (Heymans et al. 2017). Recent studies have shown that the addition to vegetable oils of crystallising agents such as fat (Brun et al. 2015; Mishima et al. 2016; Binks and Marinopoulos 2017), fatty alcohol (Fameau et al. 2015), fatty acid (Binks et al. 2016), or food-grade emulsifier (Gunes et al. 2017; Heymans et al. 2018) crystals improves the foamability and stability of the resulting oleofoams. The benefits of such systems include a long shelf-life at above refrigeration temperatures and a reduced need for additives, which are desirable features for consumers.

The stability of an oleofoam is influenced by several factors. Crystals can adsorb at the air-oil interfaces of the bubbles (Mishima et al. 2016; Heymans et al. 2017) and impart interfacial elasticity, similar to that observed for aqueous Pickering foams (Basheva et al. 2011; Beltramo et al. 2017; Binks 2002; Hunter et al. 2008; Stocco et al. 2011), therefore preventing bubble dissolution. Another contributing factor is the rheology of the bulk oleogel formed by the crystals remaining in the oil phase. The size and shape of the crystals influence the rheology of the bulk oleogel (Gunes et al. 2017; Heymans et al. 2018) surrounding the bubbles. The dominant type of crystal polymorph in the system depends on the method of preparation, involving tempering and agitating the crystal-oil mixture. For instance, it has recently been shown in a model waxy oil that the dynamic moduli of the oleogel vary non-monotonically with cooling rate (Andrade et al. 2018). The agitation conditions also affect the crystal size and shape. Low shear rates may affect the orientation of crystals and their growth rates (Heymans et al. 2017). At high shear rates, such as in whipping, the crystal sizes are reduced. Whipping also increases the probability of adsorption of crystals to the air-oil interface (Gunes et al. 2017).

The classical criteria for bubble stability in the presence of an elastic interface or a viscoelastic bulk predict certain thresholds in (interfacial or bulk) rheological properties for bubble dissolution to be retarded or arrested. Small bubbles are prone to dissolution even in a gas-saturated medium due to the capillary pressure across a curved interface, $P=\frac{2{\sigma}_0}{R}$, where σ₀ is the surface tension of the gas-liquid interface (Epstein and Plesset 1950; Duncan and Needham 2004). A bubble will continue to dissolve until the rate of change of the capillary pressure P with respect to the bubble radius R becomes zero, $\frac{\mathrm{d}P}{\mathrm{d}R}=-\frac{2{\sigma}_0}{R^2}=0$. For bare interfaces, such that σ₀ is a constant, this condition is never satisfied and bubbles dissolve completely. In the presence of an interfacial layer, the surface stress σ changes during bubble dissolution (assuming constant mass of interfacial material on the interface) and becomes dependent on R. The interfacial elasticity of the layer, ${E}_{\mathrm{d}}=\frac{\mathrm{d}\sigma }{\mathrm{d}\mathrm{ln}\kern.2em A}$, modifies the stabililty criterion: $\frac{\mathrm{d}P}{\mathrm{d}R}=-\frac{2\sigma }{R^2}+\frac{4{E}_{\mathrm{d}}}{R^2}$. If E_d ≥ σ/2, bubble dissolution can be arrested. This is known as the Gibbs stability criterion (Kloek et al. 2001), and it has been confirmed experimentally for nanoparticle-stabilized, aqueous foams (Stocco et al. 2009). The effect of an elastic bulk in retarding or arresting bubble dissolution has been described by Kloek et al. (2001). For a bubble surrounded by an infinite elastic medium with constant shear modulus G, a bubble of initial radius R₀ will keep shrinking to a relative radius ε = R/R₀ until the criterion GR₀ = 4σ₀ε³/(1 − 5ε⁴ + 4ε³) is fulfilled. Numerical predictions by Kloek et al. (2001) show that beyond this, further bubble dissolution will be arrested.

The requirement for formulated products to remain stable in varying environmental conditions poses additional challenges. Oleofoams that are stable at room temperature may be destabilized by heating both because the crystals can melt (Binks et al. 2016), and because of enhanced bubble dissolution due to the changes in gas solubility with temperature. Enhanced bubble dissolution upon changes in temperature has been previously shown to destroy particle-stabilized bubbles in water, where air solubility increases with cooling (Poulichet and Garbin 2015), and in alkanes, where air solubility increases with heating (Achakulwisut et al. 2017).

To elucidate the link between microstructure and stability imparted by crystals in an oleofoam, in this work, we performed experiments on single bubbles to decouple the bulk and interfacial rheological contributions to stability. In addition, we evaluated the effect of heating on the stability of single bubbles. The model system for this study is a wax-based oleofoam with low gas fraction to enable observation of individual bubbles. We used video microscopy on a temperature-controlled stage to visualize directly the microscale phenomena occurring at the single-bubble level for bare bubbles in oil, bubbles stabilized by an interfacial layer of wax, and bubbles stabilized both by an interfacial wax layer and a bulk oleogel phase. To rationalize the observed differences in dissolution times, we performed bulk rheological measurements on the oleogel, and dilatational interfacial rheological experiments on a wax layer at the air-oil interface.

Materials and methods

Materials

The wax used is Hydropel QB (Shamrock Technologies), a blend of paraffin and synthetic waxes. According to the manufacturer’s specifications, the mean particle diameter is 9 μm, the density is ρ_wax = 0.88 g cm⁻³ and the melting temperature range is T_m = (50 − 105) °C. The wax particles were used as received. Consumer-grade sunflower oil (Tesco) was used as received. The density of the oil was measured to be ρ_oil = 0.87 g cm⁻³ and the viscosity η_oil = 50 mPa s at T = 25 °C.

Characterisation of wax properties

To measure the contact angle of sunflower oil in air on solid wax, powdered wax was put on a glass slide and then heated on a hot plate until the wax melted. Another glass slide was placed on top of the layer of molten wax to obtain a smooth, flat surface. The wax was then allowed to cool down to room temperature and solidify. A sessile drop of sunflower oil was carefully placed on the solid wax layer in air and imaged with a custom-built optical goniometer. The contact angle measured through the oil phase was found to be θ = (50 ± 3)^∘ (n = 8 repeats) (see Suppementary Information Fig. 1a).

Differential scanning calorimetry of the wax was carried out using a DSC Q2000 instrument (TA Instruments). The sample was first brought to 20 °C and then heated to 120 °C at a rate of 1 °C/min. It was maintained at isothermal conditions for 1 min and then cooled down to 20 °C at the same rate, after which it was again left for 1 min at isothermal conditions. Similarly, two more heating cycles were carried out for the same sample at 5 °C/min and 10 °C/min. A first melting peak is observed at T ≈ 60 °C, and a second broader peak is observed at T ≈ 100 °C (SI Fig. 1b).

Foam preparation

We developed a simple protocol to make oleofoams containing a small amount of stable bubbles. We did not follow the established whipping protocol (Binks et al. 2016; Gunes et al. 2017), which produces dense, stable oleofoams, because our goal is to produce foams with low gas volume fraction, so as to be able to observe the evolution of isolated bubbles. Suspensions of wax particles in sunflower oil were obtained by agitation at room temperature. Wax concentrations in the range 0.5–7.5 wt% were used in the experiments. The suspensions were heated to a given temperature on a hotplate (UC152, Stuart). The temperature of the sample was monitored using a thermocouple (RS PRO Digital thermometer, K-type, SYS calibration). When the sample attained the required temperature, the vial was agitated using a vortex mixer (PV-1, Grant) at 3000 rpm, for a given mixing time, during which the sample cooled down. The heating temperature was varied in the range 50 − 120 °C; the mixing time was varied in the range 30 s to 3 min. The temperature of the sample was measured again with the thermocouple immediately after mixing. The sample was left to cool to room temperature for up to 2 h and was then carefully scooped from the vial using a spatula and placed onto a microscope glass slide with a polydimethylsiloxane (PDMS) spacer of thickness 1.5 mm and a glass coverslip on top. To prepare samples with wax-coated bubbles without the bulk gel network, the oleofoam was diluted by gently scooping a small sample (≈20 μL) and adding sunflower oil to a dilution factor of 12. To do so, the oleofoam was placed on a microscope slide with a PDMS spacer and sunflower oil was added dropwise to fill up the enclosure, which was then sealed with a coverslip. Except for bubbles within an oleofoam, which are held in place by the bulk oleogel network, buoyancy caused the bubbles to rise to the top of the enclosure; these bubbles were then in the immediate vicinity of the glass coverslip, but no contact line was formed.

Video microscopy with temperature control

The slides were placed into a temperature-controlled microscope stage (THMS600, Linkam) and observed with an upright microscope (BXFM, Olympus) using × 10 magnification. Images were recorded every 10 s in reflection mode with a CMOS camera (Thorlabs). Because of the low thermal conductivity of glass, the temperature in the sample cell is expected to differ from the set temperature of the metal, heating element. The temperature was therefore calibrated by comparing the set temperature of the heating element with the melting point of reference substances placed in the sample cell. The temperature in the cell was measured using the thermocouple. Two reference substances were used: ice (T_m = 0 °C) and cholesterol (Sigma-Aldrich, T_m = 147 − 150 °C). The temperatures reported in the remainder of the paper correspond to the calibrated temperatures.

Image analysis

Image analysis using MATLAB (MathWorks, Natick, MA, USA) was used to track the size of the bubbles over time. Because the bubble shape was typically not spherical, we measure the projected area of the bubble in the imaging plane and then convert it into an equivalent radius, that is, the radius of a spherical bubble with the same area. Each video frame was converted into a binary image using the function graythresh. The function bwareaopen was used to remove small objects. Finally, the function imfill was used to remove the bright spot at the centre of the bubbles due to transmitted light. The pixels within the bubble contour were counted to obtain its area.

Bulk rheology

Bulk samples were characterised in a rheometer with a water bath temperature control (MCR 302, Anton Paar) using a cone-plate geometry (diameter 50 mm, cone angle 1°). Oleofoam preparation follows the protocol described in “Foam preparation” using the optimal temperature, wax concentration, and mixing time identified in “Effect of preparation temperature and wax concentration on bubble formation.” The oleogel was produced using the same protocol, with the vortex mixer at a lower rate (750 rpm) to promote mixing but prevent bubble inclusion. The samples were then left to rest in their original vials for up to 2 h to attain room temperature. The oleogel and oleofoam were then carefully scooped and inserted in the geometry. The pure oil and the wax suspension did not require such care and were sampled using a pipette. The sample is then naturally squeezed when the cone is lowered to its measuring position.

Experiments where the temperature is varied were conducted immediately after lowering the cone and without any additional pre-shear. The sample was in direct contact with the smooth metal surfaces of the geometry to ensure good temperature control. The upper limit of the investigated temperature was limited to 95 °C. Experiments conducted at fixed temperature were performed using hydrophobic sandpaper surfaces (Sungold Abrasives, Port Washington, NY, USA) with a typical roughness of 13 μm to limit wall slip. Oscillatory measurements were conducted at a fixed frequency f = 1 Hz. All data points for both flow and oscillatory rheology represent 5 s of raw acquisitions. Significant differences were observed compared with smooth surfaces, most notably in oscillatory rheology at medium and high strains for initially undisturbed samples. An effect is also visible at very low shear rates in flow rheology (see “Rheological measurements” and Supplementary Information).

Dilatational interfacial rheology

To estimate the dilatational modulus of a wax-coated air-oil interface, we performed measurements using a pendant drop geometry and drop shape analysis techniques. Depending on whether an interfacial layer is fluid-like or solid-like, different drop shape analysis techniques are applicable. In the fluid state, the (isotropic) interfacial stress can be obtained as the effective surface tension σ(A) (Knoche et al. 2013; Hegemann et al. 2018), where A is the surface area. From the slopes of σ(A) isotherms, the classical Gibbs modulus, E_Gibbs = dσ/dln A, is obtained. A drop shape analysis method for solid-like, elastic interfaces was introduced recently (Nagel et al. 2017). In this method, called drop shape fitting elastometry (DSFE), the drop shapes are fitted to a model incorporating a pseudolinear Hookean constitutive model to extract the interfacial compression modulus, E_d, and interfacial shear modulus, G_2D (Nagel et al. 2017). Given that DSFE is an emerging technique that has received limited experimental validation so far, we have used both methods.

A custom-built optical tensiometer was used for the measurements. A pendant drop of neat sunflower oil in air was formed at the tip of a needle (inner diameter 1.70 mm, outer diameter 2.11 mm, RS Components) connected to a syringe pump (Harvard Apparatus). To deposit an interfacial layer of wax, a droplet of oleogel, pre-heated to 90 − 110 °C, was brought into contact with the pendant drop of oil using another needle (outer diameter 0.5 mm) connected to a 1-mL, hand-held syringe filled with the oleogel. Upon contact, the oleogel droplet spontaneously spread over the surface of the pure oil drop. From the time of transferring the hot oleogel into the syringe to the subsequent contact with the pendant drop, the oleogel temperature decreased by more than 40 °C, as measured by depositing a drop of the oleogel from the syringe onto the thermocouple tip.

Other methods were attempted to reproduce conditions closer to the interfacial coating on air bubbles in an oleogel, but were unsuccessful. In a control experiment, to confirm that when spreading the oleogel on an oil drop the wax crystals did not diffuse in the bulk of the drop, we performed microscopy on sessile drops placed on a glass slide. A vertical scan of the drop with the small depth of focus of the × 10 lens revealed that the crystals remained confined at the drop interface, even after a waiting time of 10 min.

The Bond number, $B\mathrm{o}=\Delta \rho g{R}_0^2/\sigma$, was in the range 0.40 ≤ Bo ≤ 0.51; the Worthington number, Wo = ΔρgV/(2πr_cσ), was in the range 0.32 ≤ Wo ≤ 0.81. Here Δρ is the density difference between the inner and outer fluids, in this case oil and air; g the gravitational acceleration, R₀ the drop radius at the apex, σ the surface tension of the wax-coated oil-air interface, V the drop volume, and r_c the needle radius. With these values of Bo and Wo, good precision can be expected in surface tension measurements from drop shape analysis (Berry et al. 2015).

The volume of the pendant drop was slowly varied in small steps using the syringe pump, at a flow rate of ±0.05 mL/s. The interfacial dilatational strain rate for each step was $\mid \dot{\alpha}\mid ={A}^{-1}\mid \mathrm{d}A/\mathrm{d}t\mid =\left(4.5\pm 0.5\right)\times 1{0}^{-3}\ {\mathrm{s}}^{-1}$, with an areal strain of ∣dA∣/A = 0.14 ± 0.01 for each step change. Upon attaining the desired volume (approx. 30 s) and allowing 60 s for the drop shape to equilibrate, an image was recorded. The characteristic time at which the surface properties are probed is then around 90 s. After this interval, the drop size was changed.

To implement the two drop shape analysis techniques, open-source routines were used. The effective surface tension was determined by fitting the drop shapes to the Young-Laplace equation, using open-source numerical routines by Nagel et al. (2017). This fitting method incorporates a Chebyshev transform filtering algorithm to improve the precision in the sampling of the interface shape. To implement the DSFE method, the library of open-source MATLAB functions developed by Nagel et al. (2017) was used.

Results

Effect of preparation temperature and wax concentration on bubble formation

We first optimised the temperature to which the suspension of wax microparticles in sunflower oil was heated prior to mixing and bubble formation. The concentration of wax was 2.5% w/v in all the experiments. After heating to the desired preparation temperature, each sample was shaken for 2 min on the vortex mixer. The temperature at the end of mixing was measured and was found to have decreased by ΔT ≈ 20 − 40 °C, corresponding to a cooling rate of 10 − 20 °C/min. The samples were allowed to cool down to room temperature after mixing and prior to imaging.

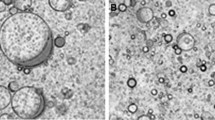
Figure 1a shows optical micrographs of samples prepared with different preparation temperatures in the range T = 50 − 120 °C. For preparation temperatures below T = 65 °C, which corresponds to the first melting peak of the wax, few or no bubbles are formed. A significant number of bubbles are formed in the range T = 80 − 115 °C. The bubbles formed in this temperature range are mostly non-spherical. At T = 120 °C, the number of bubbles is reduced again (SI Fig. 2). The bubbles formed for temperatures below T = 65 °C and at T = 120 °C tend to be spherical and to possess smooth interfaces. Micrographs with higher magnification in Fig. 1b show non-spherical shapes and buckled interfaces for T = (75 − 110) °C, which are characteristic of bubbles stabilised by elastic layers. Further, above 65 °C, fewer wax crystals were prominent in the bulk. The bulk appears like a network with fine material present in it.

Fig. 1

Effect of preparation temperature on formation of bubbles in oleogels of wax in sunflower oil. a Optical micrographs of samples (wax concentration 2.5% w/v, mixing time 2 min) after preparation and cooling to room temperature. The preparation temperature was varied in the range T = (50 − 120) °C. b Magnified images of bubbles at selected temperatures showing the non-spherical shapes and buckled interface characteristic of bubbles stabilised by elastic layers. The gel of wax crystals in the surrounding oil phase is also visible

The samples were stored at room temperature (SI Fig. 3a), and the stability of the bubbles was tested by optical microscopy after 1 week (SI Fig. 3b) and again after 4 months (SI Fig. 3c). Except for the bubbles prepared at temperatures between T = 80 − 110 °C, the bubbles in the other samples had shrunk significantly with respect to their initial size and many had disappeared at the locations where there were previously many bubbles.

We then tested the effect of wax concentration while keeping the preparation temperature and the mixing time the same for all the samples, T = 90 °C and 2 min, respectively. The wax concentration was varied in the range 0.5–7.5% w/v. Below a concentration of 2.5% w/v, the bubbles were few and they dissolved within minutes to hours (SI Fig. 4). Above 2.5% w/v, the sample became very viscous as it cooled during mixing, resulting in fewer bubbles and optically opaque samples which were difficult to image using optical microscopy.

Finally, keeping the wax concentration fixed at 2.5% w/v, the mixing times were varied from 30 s to 3 min for a narrower range of temperatures, T = 75 − 95 °C. The temperatures at the end of mixing were recorded and were found to have decreased by ΔT ≈ 30 − 40 °C for mixing times of 2–3 min. The number of bubbles increased with increasing mixing time up to 2 min. For longer mixing time, the number of bubbles did not increase significantly (SI Fig. 5).

Based on these results, we selected the parameters of the oleofoam preparation protocol to be used in the rest of the study: preparation temperature T = 90 °C, wax concentration of 2.5% w/v and mixing time of 2 min, followed by cooling to room temperature before use. All the results presented in Figs. 2, 3, 4, and 5 correspond to samples prepared with this protocol (see other details of protocol in “Results”).

Fig. 2

Dissolution behaviour of individual bubbles at different temperatures. The temperature was increased from room temperature (21 °C) to T₁ = 25 °C (blue curve) or T₂ = 74 °C (red dashed curve) at a rate of 5 °C/min. In a–c, the corresponding bubble dissolution behaviour is shown by blue open symbols and red filled symbols, respectively. a Bare bubble dissolving in oil. b Wax-coated bubble in oil. c Bubble in oleofoam. d Comparison of bubble dissolution for T₁ = 25 °C for bare bubble (grey triangles), wax-coated bubble (orange squares), and bubble in oleofoam (filled purple diamonds). The radius R is normalised by the initial effective radius R₀. Time is normalised by t^∗, the theoretical dissolution time of a bare bubble with the same initial radius in oil at 25 °C, and corrected for the effect of confinement

Fig. 3

Image sequences of evolution of bubbles at 25 °C. a A bare bubble quickly dissolves. b Solid interfacial layer unfolding around a dissolving, wax-coated bubble. c A bubble in the oleogel remains stable over the same timescale

Fig. 4

Bulk rheological properties of the oleogel. a Viscosity of the pure sunflower oil (open grey triangles), a suspension of wax particles in oil (orange squares), oleofoam (purple circles), and oleogel (yellow diamonds) as a function of temperature. Data obtained for a heating rate dT/dt =  + 10 °C/min, and applied shear rate of 50 s⁻¹ in a smooth geometry. b Flow curve of the oleogel for T = 25 °C, using a rough geometry and decreasing shear rates. A 1000 s⁻¹ pre-shear was applied for 20 s immediately before the acquisition. c Amplitude sweep of the oleogel for T = 25 °C and f = 1 Hz using a rough geometry. A waiting time of 500 s has been applied right after sample loading (no subsequent pre-shear) after which the sweep is started, first for increasing strains (filled symbols) and immediately afterwards for decreasing strains (empty symbols). Blue squares represent the storage modulus G^′ and the red circles the loss modulus G^′′. The dashed line shows G^′ ∝ γ⁻¹ for reference. d Temperature sweep of the storage and loss modulus of the oleogel for an applied strain amplitude γ = 0.05%, f= 1 Hz and a smooth geometry. The sweep was started immediately after sample loading (no pre-shear or waiting time) at a heating rate dT/dt = 7 °C/min. Same colour codes as in c

Fig. 5

Interfacial rheology of oleogel layer at the air-oil interface. a Image sequence of a pendant drop of oil coated by an oleogel layer in air undergoing compression. The labels indicate the compression state (A/A₀). The drop is attached to the needle at z = 0, and z is directed upwards, opposite to gravity. b Curvature profiles for different values of A/A₀ during compression. c Estimated compression modulus at 18 °C for the compression series using drop shape fitting elastometry ${E}_{\mathrm{d}}^{\mathrm{DSFE}}$ (filled blue triangles). The reference state is indicated by the vertical line at A/A₀ = 0.82. The interface is assumed to behave as a purely elastic 2D solid in the shaded region. The Gibbs modulus E_Gibbs is also shown in both the fluid regime (filled red squares) and, for reference, in the elastic regime (open red squares)

Microscopic imaging of single bubble dissolution during heating

We studied the dynamic evolution of the size of single, isolated bubbles upon heating. We conducted three different experiments so as to gain insights into the roles of the bulk rheology of the oleogel network and of the interfacial rheology of the adsorbed crystal layer:

• 1. Bare bubble in sunflower oil (control experiment).

• 2. Wax-coated bubble: a bubble was extracted from the oleofoam and resuspended in sunflower oil; care was taken to ensure no bulk gel and crystals were left in the oil surrounding these bubbles. The interfacial layer was still present on the bubbles, as confirmed by their buckled interface.

• 3. Bubble within oleofoam, i.e. a bubble in the sample as prepared. These bubbles were therefore coated with an interfacial layer of wax crystals and also embedded in the bulk gel network.

All bubbles considered had initial radii in the range R₀ = 100 ± 20 μm. Care was taken to observe individual, isolated bubbles, in order to prevent unwanted Ostwald ripening effects from neighbouring bubbles, particularly important for bare bubbles and wax-coated bubbles. The samples were inserted in the temperature-controlled stage at an initial temperature T₀ = 21 °C. The temperature was then increased to the desired final temperature at a heating rate of 5 °C/min. The temperature was then maintained constant while images were recorded every 10 s. The values of the final temperature were chosen below the melting range of the wax, T₁ = 25 °C, and after the first melting peak, T₂ = 74 °C.

The dissolution behaviour of the three types of samples at the two different final temperatures is shown in Fig. 2. The radius R has been normalised by the initial (effective) bubble radius, R₀. Time has been normalised by t^∗, the theoretical dissolution time of a bare bubble in oil, with the same initial radius R₀, at a reference temperature T = T₁ = 25 °C, and including a correction factor to account for the presence in the experiments of a gas impermeable wall next to the bubbles (see “Foam preparation”). This theoretical dissolution time is computed using the theory by Epstein and Plesset (1950) and is given by ${t}_{\mathrm{th}}=\frac{R_0^2}{3D{k}_{\mathrm{H}}}\left(\frac{R_0\rho }{2{M}_{\mathrm{w}}\sigma }+\frac{1}{BT}\right)$. The gas diffusivity in the liquid, D; the liquid density, ρ; the gas-liquid surface tension, σ; and Henry’s constant, k_H, are evaluated at the reference temperature T₁. M_w is the molar mass of the gas, and B is the universal gas constant. The correction for confinement effects gives t^∗ = t_th/ ln 2 (Duncan and Needham 2004).

First, the control experiment with bare bubbles in sunflower oil, shown in Fig. 2a, provides qualitative information on the net effect of the change in physicochemical properties of the air-oil system with increasing temperature. A bare bubble heated to T₂ = 74 °C dissolves approximately 5 times faster than a bare bubble held at a temperature T₁ = 25 °C. For the wax-coated bubbles, it can be seen in Fig. 2b that also in this case, the rate of dissolution increases with increasing temperature. In Fig. 2c, it can be seen that a bubble within the oleogel at T₁ = 25 °C barely changes radius over a timescale of several times the dissolution time of a bare bubble, t^∗. Bubbles within the oleogel at T₂ = 74 °C dissolve on a timescale that is only slightly slower than the case of wax-coated bubbles. Finally, in Fig. 2d, the dissolution behaviour of the three types of bubbles at T = 25 °C are compared directly: wax-coated bubbles dissolve on a much slower timescale than bare bubbles, while the dissolution of bubbles in the oleofoam is practically arrested. Additional data sets for wax-coated bubbles (n = 10) show a large variability in dissolution times, due to the variability in wax surface coverage between different bubbles. Nevertheless, the additional data (provided in Table 1 in the Supporting Information) confirm the qualitative trends shown in Fig. 2.

Figure 3 shows image sequences for three representative experiments at T₁ = 25 °C, below the melting range of the wax. The bare bubble dissolves completely (Fig. 3a). For a wax-coated bubble, the interfacial layer remained solid, and in a few instances, it could be seen unfolding around the bubble (Fig. 3b). Over the same timescale, a bubble embedded in the oleogel remains stable (Fig. 3c).

Rheological measurements

In order to understand the increased bubble stability against dissolution in the oleofoam, we have characterized the bulk rheology of the pure sunflower oil, a suspension of undissolved wax particles in oil, the oleogel, and the oleofoam. Bulk elasticity, for instance, may stabilize bubbles of all sizes as reported by Kloek et al. (2001).

Flow rheology of wax suspensions, oleogels, and oleofoams

Figure 4a provides an overview of the influence of temperature on the four systems studied. The heating rate was dT/dt = 10 °C min⁻¹. These measurements were performed using smooth boundary conditions; we therefore applied a shear rate of 50 s⁻¹ to suppress wall slip. The viscosity of the pure sunflower oil follows an Arrhenius-like behaviour (see Esteban et al. (2012)). For temperatures above 70 °C, the viscosity of all four systems is similar, confirming that most solid content has melted. For lower temperatures, the viscosity of the oleogel and oleofoam deviate significantly from the wax suspension. Repeat experiments show a sample variability of around ±30% for the oleogel and the oleofoam, confirming that the preparation protocol and rheological characterization are sufficiently controlled. Comparison with the literature on waxy crude oils (Lorge et al. 1997; Dimitriou and McKinley 2014; Geri et al. 2017) suggests that, in our system, T = 70 °C roughly corresponds to the rheological wax appearance temperature below which wax crystals nucleate and grow in the oil to a sufficient extent as to form a percolating network. The presence of bubbles in the oleogel—producing the oleofoam—does not result in a dramatic change in rheology, most probably due to the small bubble volume fraction (Ducloué et al. 2015), or possibly because the foam releases the bubbles under strong shear.

Figure 4b offers a more in-depth understanding of the rheology of the oleogel at T = 25 °C using rough boundary conditions. The flow curve has been obtained for decreasing shear rates after a 20-s pre-shear step performed at 1000 s⁻¹. Its shape is identical to the waxy crude oils below wax appearance temperature presented in Mendes et al. (2015) and Geri et al. (2017). The presence of a local stress minimum around $\dot{\gamma}=0.1$ s⁻¹ is a signature of thixotropic behaviour below which the oleogel experiences ageing. Additional experiments with smooth boundary conditions (data not shown) confirm this flow curve shape down to the local minimum, below which wall slip significantly affects the measurements. The stress minimum of 0.35 Pa can be used as an estimate of the oleogel yield stress just after being stirred.

Oscillatory rheology of the oleofoam

Figure 4c shows an amplitude sweep of the oleogel at T = 25 °C using a rough geometry. Two runs have been performed, first for increasing strain amplitudes up to γ = 1000%, then—immediately afterwards—for decreasing amplitudes. We observe that the gel is initially stiff with a shear modulus around 16 kPa and a limited linear viscoelastic plateau, up to 0.2% in deformation. Experiments conducted with smooth boundary conditions yield G^′ = 9 kPa in the linear plateau, which is most likely due to a combination of limited slip in the linear elastic regime and sample variability.

For strain amplitudes above γ = 1%, the gel quickly yields: the storage modulus G^′ decreases so steeply (with an exponent below − 1) that the applied stress amplitude decreases with increasing deformation, indicative of the oleogel failure. The stress amplitude maximum reached before failure, τ = 43 Pa, is an upper bound of the yield stress for an initially undisturbed sample. More classical estimates—for instance, the G^′ = G^′′ crossover point (Dinkgreve et al. 2016)—result in a yield stress around 21 Pa. We finally note that the data obtained for decreasing strain amplitude are not superposed to the data for increasing amplitude: after failure, the oleogel remains softer for all applied deformations. This is further evidence of thixotropic behaviour.

Finally, Fig. 4d shows the evolution of the storage and loss moduli of the oleogel during heating for an applied frequency of 1 Hz and with a smooth geometry. We set the strain to 0.05%—in the linear viscoelastic regime—to limit slip and damage to the microstructure. The temperature ramp is measured to be dT/dt = 7 °C/min. The shear modulus at T = 25 °C is slightly lower than in Fig. 4c, indicating moderate wall slip. The measured shear modulus then decreases sharply and reaches values as low as 100 Pa for T ≥ 40 °C. At this point, the instrument torque falls below 0.5 μN m, which severely limits our measurement precision.

Dilatational rheology of wax-coated air-oil interface

Interfacial rheological effects due to the wax layer (see Fig. 3b) can also contribute to bubble stability against dissolution (Kloek et al. 2001). Since such effects cannot be investigated directly on the oleofoam bubbles, we used a pendant drop geometry as model system for a wax-coated air-oil interface.

To produce a wax-coated air-oil interface on a pendant drop, we deposited a layer of hot oleogel on the surface of a clean oil drop as described in “Dilatational interfacial rheology.” After deposition of the oleogel, the drop was first expanded to facilitate spreading of the wax over the interface. The drop volume was then decreased to compress the interface, mimicking the conditions relevant to bubble dissolution. Figure 5a shows an image sequence during drop compression. The drop area, A, is normalised by the area corresponding to the maximum volume, A₀. In the experiment shown in Fig. 5, it is A₀ = 31.25 mm². Compression below A/A₀ = 0.82 led to drop shapes characteristic of elastic interfaces (Knoche et al. 2013; Hegemann et al. 2018). As shown in Fig. 5a, the effect is more pronounced for A/A₀ = 0.46. Magnified images of the drop surface reveal an interfacial layer of wax crystals, but it is not possible to assess whether it is a multi-layer or a single layer, and to confirm that it reproduces the microstructure of the layer on bubbles in an oleofoam (see Fig. 8 in Supporting Information).

The transition from liquid- to solid-like behaviour of the interfacial layer can be identified quantitatively by plotting the meridional curvature profile of the drop, κ(z). For a fluid interface, the curvature varies linearly with height, obeying the Young-Laplace equation. For an elastic interface, the profile is no longer linear (Nagel et al. 2017). Figure 5b shows that the deviation from linearity increases for decreasing A/A₀.

The interfacial compression modulus, E_d, can be estimated as the Gibbs modulus, E_Gibbs, in the range where the interfacial layer is fluid-like, and can be determined from the drop shape fitting elastometry (DSFE) in the elastic regime as ${E}_{\mathrm{d}}^{\mathrm{DSFE}}$ (see “Dilatational interfacial rheology” for details). In the DSFE, the strains are defined with respect to an elastically relaxed reference shape profile, in which the surface stress is isotropic. Compression below this state gives rise to elastic extra-stresses. We selected the reference state as A/A₀ = 0.82 based on the curvature profiles (Fig. 5b). Both the Gibbs modulus, E_Gibbs, and the compression modulus obtained from the DSFE, ${E}_{\mathrm{d}}^{\mathrm{DSFE}}$, are plotted as a function of area in Fig. 5c. Drop shape fitting elastometry, strictly applicable for purely elastic interfaces, is expected to give better estimates of E_d for compressed states below the reference state (grey shaded region) while E_Gibbs is expected to be a more reliable measure for fluid interfaces (outside shaded region). For reference, E_Gibbs is shown also in the elastic regime (empty symbols). Within the elastic regime, we find an approximate value of the compression modulus E_d ≈ 40 mN/m, to be used for testing the Gibbs criterion. The interfacial shear modulus, also found by the DSFE, was small compared with E_d, in the range 0.02 mN/m ≤G_2D≤ 0.12 mN/m.

Discussion and conclusions

Effect of temperature on bubble formation

The effect of preparation temperature on bubble formation (Fig. 1) can be understood from the oleogel bulk rheology as a function of temperature (see Fig. 4). As the viscosity of the oleogel falls with increasing temperature, mixing is enhanced and it aids to incorporate air into the material. Therefore, it can be expected that at higher temperatures, the number of bubbles will increase. Nevertheless, since the bulk modulus G^′ and the viscosity η of the gel all decrease strongly at the elevated temperatures at which mixing occurs (Fig. 4a), the bubbles are more mobile and susceptible to coalescence and buoyancy forces. This balance may explain why the bubble population increases with temperature up to T = 90 °C and then subsequently falls at higher mixing temperatures, with typically larger bubbles (Fig. 1a and SI Fig. 2).

Effect of bulk rheology on bubble stability

Typical bubbles (R₀ ≈ 100 μm) in the oleofoam are stable against dissolution at room temperature. Ignoring the effect of the interfacial layer for now, a simple analysis based on Kloek et al. (2001) would suggest that bulk elasticity of the oleogel may be responsible for the observed stability, as shown for instance by the large value of the elasto-capillary number GR₀/2σ₀ ≃ 50. For the capillary pressure, 2σ/R, to be balanced by the mechanical load τ_rr under static conditions, a stress of over 600 Pa is required, assuming σ = σ₀ = 0.031 N m⁻¹ and R = R₀ = 100 μm. However, this analysis assumes that the elastic medium may sustain infinite deformation with a constant shear modulus, while we have found that the oleogel used in our experiments flows for shear stresses above 40 Pa. The corresponding plasto-capillary number (Ducloué et al. 2015) τ_YR₀/2σ ≤ 0.15 is insufficient to arrest dissolution in the framework of Kloek et al. (2001). The dynamics of yielding around a spherically deforming bubble have been analysed by De Corato et al. (2019) for an elastoviscoplastic fluid, in the absence of thixotropy.

As the oleogel used in our experiments is thixotropic, its linear elastic modulus G^′ and yield stress τ_Y increase in time if the gel is left undisturbed or sheared too slowly. The magnitude of the strain rate around a spherical bubble of radius R(t) is ${\dot{\epsilon}}_{rr}=2{R}^2\dot{R}/{r}^3$, r being the distance to the bubble centre. Since bare bubbles in oil dissolve on a typical timescale t^∗ ≃ 4200 s, the strain rate at the bubble surface can be estimated as $2\dot{R}/R\simeq 2/{t}^{\ast }=4.8\ 1{0}^{-4}$ s⁻¹, and it decays as 1/r³ away from the bubble. This strain rate is far below the shear rate of the local stress minimum in Fig. 4b below which we should expect strong ageing of the oleogel, especially away from the bubble edge. We can then hypothesize that this ageing can be efficient enough for the yield stress of the gel to reach 600 Pa and prevent bubble dissolution at T = 25 °C whereas it is no longer the case at T = 70 °C given the drastic reduction of G^′ and G^′′ measured at that temperature.

Waxy systems also present the peculiar property of forming a stronger network after a more intense pre-shear step (see Kané et al. (2004)) which means that the more intense mixing step applied to the oleofoam might actually add to its stability. Directly applying our results to whipped oleofoams then proves extremely challenging.

Local effects vs. bulk rheology

An additional mechanism could contribute to the unexpectedly high bubble stability against dissolution in the oleofoam. In our experiment, the typical bubble size R₀ ≈ 100 μm is only around 10 times the typical crystal size (of the order of 10 μm), and we may question whether the bubble “sees” the same oleogel as the one probed at a larger scale by a rheometer. Recent experiments performed in attractive, fibrous bacterial cellulose gels (Song et al. 2019a, b) show that the critical bubble size at the onset of rising motion is larger than what is expected from bulk rheological measurements, especially for the smallest solid volume fractions. Song et al. (2019b) observed that the cellulose gel locally restructures around bubbles, all the more for looser fibre networks. This restructuring allows the gel to locally withstand the mechanical stresses associated with the bubble buoyancy; we may then speculate that it also enhances the ability of our oleogels to locally withstand the high, yet strongly localized stresses associated with bubble dissolution.

Effect of interfacial rheology on bubble stability

The presence of a wax layer at the bubble surface also has a stabilizing effect, first by reducing the surface tension σ and also through the appearance of an interfacial elasticity E_d. The Gibbs criterion (Kloek et al. 2001; Stocco et al. 2009) requires that E_{d, max} ≥ σ/2 to arrest bubble dissolution due to interfacial elasticity alone. The surface tension σ of the wax-coated interface is not known precisely, and it is not a constant as the surface coverage gradually increases during bubble dissolution. Since σ ≤ σ₀, where σ₀ is the surface tension of the bare oil-air interface, and σ₀ is known more precisely, fulfilling the more stringent condition E_{d, max} ≥ σ₀/2 also fulfils the Gibbs criterion. The DSFE measurements (Fig. 5) give an approximate value in the range E_d ≈ 40 mN/m during compression up to A/A₀ = 0.44, and therefore, the condition E_d > σ₀/2 ≈ 15 mN/m is in principle satisfied. Furthermore, in the oleofoam samples, the crystals at the bubble interface are expected to be more densely packed than in the DSFE experiments; this is qualitatively evidenced by buckled bubble interfaces observed both in the oleofoam (Fig. 1b) and wax-coated bubbles suspended in oil (Fig. 3b). The surface elasticity of these bubbles may therefore be even higher than what we estimated from the DSFE experiments, and we would expect wax-coated bubbles to be stable against dissolution. Yet our experiments show that wax-coated bubbles dissolve in pure sunflower oil at room temperature, albeit slower than bare bubbles (Fig. 2d). Interestingly, an intact interfacial layer delaminates as dissolution proceeds (Fig. 3b). The reason for this may be that as the bubble dissolves and E_d increases, it eventually becomes energetically more favourable for the wax layer to detach from the oil-air interface rather than be further compressed. The layer therefore peels intactly, exposing local bare oil-air interface with E_d = 0 mN/m, such that the wax-coated bubble dissolves. Thus, E_d > σ/2 is not a relevant criterion for dissolution arrest in this system, and Pickering stabilization is not effective in this system. This is in contrast with the observations of Gunes et al. (2017) for lipid-based oleofoams. It is therefore not possible to generalize the applicability of our findings to other types of oleofoams.

Effect of heating on oleofoam stability

At elevated temperatures, T ≥ 70 °C, the crystal network weakens as evidenced by the decreasing bulk viscosity (Fig. 4a) and moduli (Fig. 4d) of the oleogel. A similar behaviour is expected of the crystal interfacial layer, explaining why the wax-coated bubbles dissolve at a rate not too different from bare bubbles at higher temperatures (Fig. 2b) while bubbles in the oleofoam dissolve completely (Fig. 2c). The oleofoam is therefore unstable at temperatures above the peak crystal melting point (SI Fig. 1(b)), which roughly corresponds here to the rheological wax (dis)appearance temperature (Geri et al. 2017).

Summary

Our study of the dissolution of bubbles in an oleofoam, in conjunction with bulk and interfacial rheological measurements, has shown that although crystals adsorb to the interfaces of bubbles, the Pickering mechanism of stabilisation is insufficient to arrest bubble dissolution. We found that for bubbles isolated from the oleogel matrix but possessing an interfacial wax layer, even though the Gibbs criterion for bubble stability is met, dissolution is not arrested: peeling of the wax layer from the air-oil interface is energetically more favourable than elastic compression of the layer. Bulk rheological properties of the oleogel surrounding the bubbles therefore play the dominant role in arresting bubble dissolution. Measuring the oleogel bulk elastic properties that are relevant to prevent bubble dissolution is however challenging due to the thixotropic nature of the oleogel used in our experiments. Finally, given the relatively modest size ratio between the bubble size and the oleogel crystals, we may also question whether a continuous medium approach of bubble dissolution based on bulk rheological measurements is justified.