Large-amplitude oscillatory shear rheology of dilute active suspensions

Abstract

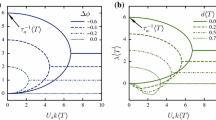
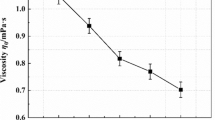
Suspensions of swimming microorganisms are a class of active suspensions that show an interesting rheological response in steady shear flow. In particular, the particle contribution to the viscosity can be negative, which has been calculated from models and measured experimentally. In this article, the material functions in large-amplitude oscillatory shear (LAOS) flow are calculated. In addition to the linear material functions, the nonlinearities are quantified analytically using the intrinsic nonlinear material functions. The particle contribution to both the storage and loss modulus can be negative. Since the suspending fluid is assumed Newtonian (and so has no storage modulus), the overall storage modulus can be negative. The intrinsic nonlinearities also show differences between passive and active suspensions. At small frequency, the active swimming can change the sign of the material functions. However, the viscous material functions are independent of the swimming motion at a very large frequency. The changes in sign of the material functions and the unique dependence on frequency may act as a rheological fingerprint of suspensions of swimming organisms.

Appendices

Appendix 1: Formula for the stress

There are two common representations of long slender objects used in the literature. The first is a series of spherical beads connected by rigid rods, in which only the positions of the beads are tracked (rotations of the spheres do not matter). This model has been extensively described in Bird et al. (1987). In the notation used in this article, the flow and Brownian contributions of the particles to the stress are

$$ \boldsymbol{\sigma}^{f} = \frac{c k_{\textrm{B}} T}{D_{r}} \frac{\lambda_{N}^{(2)}} {\lambda_{N}^{(1)}} \langle \boldsymbol{n} \boldsymbol{n} \boldsymbol{n} {\boldsymbol n} \rangle : {\boldsymbol{\kappa}}$$

(38)

$$ \boldsymbol{\sigma}^{\textrm{B}} = 3 c k_{\textrm{B}} T \left[ \langle \boldsymbol{n} \boldsymbol{n} \rangle - \boldsymbol{\delta}/3 \right] , $$

(39)

where $\lambda _{N}^{(1)}$ is the time constant of the object composed of N beads that is related to the rotational diffusivity D _r while $\lambda _{N}^{(2)}$ is a time constant related to the drag on the object. Note that the Brownian contribution is the same as that used in this article, while the flow contribution differs in the use of κ. However, κ = Γ − Ω. When inserting this into the flow contribution, the vorticity contribution equals zero since Ω is antisymmetric. Therefore, our formulas match this model with $H=\lambda _{N}^{(2)}/\lambda _{N}^{(1)}$. Values of this ratio are given in Bird et al. (1987). If hydrodynamic interactions between beads are ignored, then H = 1. If hydrodynamic interactions are included, H depends on the number and radius of the beads and can be either larger or smaller than one. How H deviates from one determines the sign of the second normal stress coefficient in steady shear flow for passive particles.

The other commonly used model of long slender objects is a spheroid with large aspect ratio. The stress in a dilute suspension of spheroids has been previously examined extensively. In the notation of this article, the Brownian contribution is (Hinch and Leal 1976)

$$\boldsymbol{\sigma}^\textrm{{B}} = 2 \mu c V_{\textrm{part}} F D_{r} \left[ \langle {\boldsymbol n} \boldsymbol{n} \rangle - \boldsymbol{\delta}/3 \right] , $$

(40)

where μ is the viscosity of the Newtonian suspending fluid, V _part is the volume of a single particle, and F is a function of the particle shape given by Hinch and Leal (1972) as

$$ F = \frac{6(r^{2}-1)}{r^{2} K_{3} + K_{1}} , $$

(41)

where r is the aspect ratio and K ₃ and K ₁ are integrals given by Leal and Hinch (1971) as

$$ K_{3} = {\int}_{0}^{\infty} \frac{r d \lambda}{(r^{2}+\lambda)^{3/2}(1+\lambda)} $$

(42)

$$ K_{1} = {\int}_{0}^{\infty} \frac{r d \lambda}{(r^{2}+\lambda)^{1/2}(1+\lambda)^{2}} . $$

(43)

The rotational diffusivity is also related to these functions as (Leal and Hinch 1971)

$$ D_{r} = \frac{k_{\mathrm{B}} T}{4 \mu V_{\text{part}}} \left( \frac{r^{2} K_{3} + K_{1}}{r^{2} + 1} \right) . $$

(44)

Placing these expressions into the Brownian stress formula leads to

$$\boldsymbol{\sigma}^{\textrm{B}} = 3 c k_{\textrm{B}} T \left( \frac{r^{2}-1}{r^{2}+1} \right) \left[ \langle \boldsymbol{n} \boldsymbol{n} \rangle - \boldsymbol{\delta}/3 \right] ,$$

(45)

which matches with the expression used in this article when $r \to \infty$.

In the notation of this article, the flow contribution is (Hinch and Leal 1976)

$$\begin{array}{@{}rcl@{}} \boldsymbol{\sigma}^{f} &= & 2 \mu c V_{\textrm{part}} \{ 2A \langle {\boldsymbol n} \boldsymbol{n} \boldsymbol{n} \boldsymbol{n} \rangle : \boldsymbol{\Gamma} \nonumber\\ && + 2B \left[ \langle \boldsymbol{n} \boldsymbol{n} \rangle \cdot \boldsymbol{\Gamma} + \boldsymbol{\Gamma} \cdot \langle \boldsymbol{n} \boldsymbol{n} \rangle \right] + C \boldsymbol{\Gamma} \} , \end{array} $$

(46)

where A, B, and C are functions of the particle shape as given in Hinch and Leal (1972) as

$$ A = \frac{J_{3}}{I_{3} J_{1}} + \frac{1}{I_{3}} - \frac{2}{I_{1}} $$

(47)

$$ B = \frac{1}{I_{1}} - \frac{1}{I_{3}} $$

(48)

$$ C = \frac{2}{I_{3}} , $$

(49)

where the I’s and J’s are integrals defined by Batchelor (1970). The limiting behaviors of these factors are given in Hinch and Leal (1972). For $r \to \infty$, they are

$$ A \sim \frac{r^{2}}{4(\ln 2r - 3/2)} $$

(50)

$$ B \sim \frac{3 \ln 2r - 11/2}{r^{2}} $$

(51)

$$ C \sim 2 . $$

(52)

In this limit, B approaches zero, C approaches a constant, while A approaches infinity. Therefore, for slender objects, we can express the flow contribution as

$$\boldsymbol{\sigma}^{f} = 4 \mu c V_{\textrm{part}} A \langle \boldsymbol{n} \boldsymbol{n} \boldsymbol{n} \boldsymbol{n} \rangle : \boldsymbol{\Gamma} . $$

(53)

This expression and the one used in the article would be the same if

$$ H = \frac{4 \mu V_{\text{part}} A D_{r}}{k_{\mathrm{B}} T} = A \left( \frac{r^{2} K_{3} + K_{1}}{r^{2} + 1} \right) . $$

(54)

In the limit $r \to \infty$,

$$ \left( \frac{r^{2} K_{3} + K_{1}}{r^{2} + 1} \right) \sim \frac{2 \ln 2r - 1}{r^{2}} . $$

(55)

Using this limit and the limit of A shows that H = 1/2 for spheroids with $r \to \infty$.

Appendix 2: Distribution function and material functions

Equations (12)–(14) express the distribution function in terms of the dependence on strain and time. In particular, the function Ψ₁ is expressed in terms of A ₁₁ and B ₁₁. The functions A ₁₁ and B ₁₁ satisfy the coupled differential equations

$$ \text{De} A_{11} = -\text{De} {\Omega}_{s} {\Psi}_{0} + \frac{1}{6} \nabla_{\boldsymbol{n}}^{2} B_{11} $$

(56)

$$ -\text{De} B_{11} = \frac{1}{6} \nabla_{\boldsymbol{n}}^{2} A_{11} . $$

(57)

To solve these equations, we follow the approach used in Bird et al. (1987) in which we expand A ₁₁ and B ₁₁ in terms of the real-valued spherical harmonics ${P_{k}^{j}} \sin (j \phi )$ and ${P_{k}^{j}} \cos (j \phi )$, where ${P_{k}^{j}}$ are the Legendre polynomials with $\cos \theta$ as their argument. The spherical harmonics are eigenfunctions of the Laplacian operator. Note that they are not eigenfunctions of the Ω _s operator, which leads to coupling between the spherical harmonics. The details of how Ω _s operates on the spherical harmonics is given in Bird et al. (1987). Since ${\Omega }_{s} {\Psi }_{0} = -{P^{2}_{2}} \sin (2 \phi ) /(8 \pi )$, then A ₁₁ and B ₁₁ will only have a single spherical harmonic and are given by

$$ A_{11} = \frac{1}{8 \pi} {P^{2}_{2}} \sin(2 \phi) \frac{\text{De}^{2}}{1+ \text{De}^{2}} $$

(58)

$$ B_{11} = \frac{1}{8 \pi} {P^{2}_{2}} \sin(2 \phi) \frac{\text{De}}{1+ \text{De}^{2}} . $$

(59)

These functions can then be used to compute the linear viscoelastic functions using Eqs. (18) and (19). This is done most simply using the fact that $n_{x} n_{y} = {P_{2}^{2}} \sin (2 \phi )/6$ and using the orthogonality of the spherical harmonics. By performing the integrals, we can show that

$$ \tilde{G}^{\prime} = \frac{M}{5} \frac{\text{De}^{2}}{1+\text{De}^{2}} $$

(60)

$$ \tilde{G}^{\prime\prime} = \frac{M}{5} \frac{\text{De}}{1+\text{De}^{2}} + \frac{2 \text{De}}{5} . $$

(61)

The solution for Ψ₁ can now be placed into the equation for Ψ₂, which becomes

$$\begin{array}{@{}rcl@{}} \frac{\partial {\Psi}_{2}}{\partial \tilde{t}} &=& \frac{-\text{De}}{2} \sin(2 \text{De} \tilde{t}) {\Omega}_{s} A_{11} - \frac{\text{De}}{2} [ 1 + \cos(2 \text{De} \tilde{t}) ] {\Omega}_{s} B_{11} \\ &+& \frac{1}{6} \nabla_{\boldsymbol{n}}^{2} {\Psi}_{2} . \end{array} $$

(62)

Using the expansion of Ψ₂ in time leads to three coupled PDEs for the angular functions that are given by

$$ \nabla_{\boldsymbol{n}}^{2} B_{20} = 3 \text{De} {\Omega}_{s} B_{11} $$

(63)

$$ \nabla_{\boldsymbol{n}}^{2} B_{22} = 12 \text{De} A_{22} + 3 \text{De} {\Omega}_{s} B_{11} $$

(64)

$$ \nabla_{\boldsymbol{n}}^{2} A_{22} = - 12 \text{De} B_{22}+ 3 \text{De} {\Omega}_{s} A_{11} . $$

(65)

These equations are solved by expanding in spherical harmonics. They are being forced by the nonhomogeneous terms with Ω _s . Therefore, we use the relationship that

$$ {\Omega}_{s} ({P_{2}^{2}} \sin(2 \phi) ) = \sum\limits_{j=0}^{4}{~}^{\prime} \sum\limits_{k=j}^{4}{~}^{\prime} a_{2k}^{2j} {P_{k}^{j}} \cos(j \phi), $$

(66)

where the primes on the sums denote that the integers are incremented by two and the coefficients $a_{2k}^{2j}$ are given in Bird et al. (1987). Incorporating these coefficients gives

$$ {\Omega}_{s} ({P_{2}^{2}} \sin(2 \phi) ) = \frac{6}{7} {P_{2}^{0}} - \frac{6}{7} {P_{4}^{0}} - {P_{2}^{2}} \cos(2 \phi) + \frac{1}{28} {P_{4}^{4}} \cos(4 \phi) , $$

(67)

which can then be used to obtain

$$\begin{array}{@{}rcl@{}} B_{20} &&= \frac{3}{8 \pi} \frac{\text{De}^{2}}{1+\text{De}^{2}} \left[ \frac{-1}{7} {P_{2}^{0}} + \frac{3}{70} {P_{4}^{0}} \right. \\ &&\left. +\frac{1}{6} {P_{2}^{2}} \cos(2 \phi) - \frac{1}{560} {P_{4}^{4}} \cos(4 \phi) \right] \end{array} $$

(68)

$$\begin{array}{@{}rcl@{}} B_{22} &&= \frac{3}{8 \pi} \frac{\text{De}^{2}}{1+\text{De}^{2}} \left[ \frac{-(1-2\text{De}^{2})}{7(1+4\text{De}^{2})} {P_{2}^{0}} + \frac{3(5-3 \text{De}^{2})}{14(25+9\text{De}^{2})} {P_{4}^{0}} \right. \\ &&\left. + \frac{1-2 \text{De}^{2}}{6(1+4 \text{De}^{2})} {P_{2}^{2}} \cos(2 \phi) - \frac{5-3 \text{De}^{2}}{112(25+9\text{De}^{2})} {P_{4}^{4}} \cos(4 \phi) \right] \\ \end{array} $$

(69)

$$\begin{array}{@{}rcl@{}} A_{22} &=& \frac{3}{8 \pi} \frac{\text{De}^{3}}{1+\text{De}^{2}} \left[ \frac{-3}{7(1+4 \text{De}^{2})} {P_{2}^{0}} + \frac{12}{7(25+9 \text{De}^{2})} {P_{4}^{0}} \right. \\ &+& \left. \frac{1}{2(1+4 \text{De}^{2})} {P_{2}^{2}} \cos(2 \phi) - \frac{1}{14(25+9 \text{De}^{2})} {P_{4}^{4}} \cos(4 \phi) \right] . \\ \end{array} $$

(70)

The solution for Ψ₂ can be placed in the equation for Ψ₃ which after using the time expansion of Ψ₃ leads to the four coupled differential equations:

$$ \nabla_{\boldsymbol{n}}^{2} A_{31} = - 6 \text{De} B_{31} + 3 \text{De} {\Omega}_{s} A_{22} $$

(71)

$$ \nabla_{\boldsymbol{n}}^{2} B_{31} = 6 \text{De} A_{31} + 6 \text{De} {\Omega}_{s} B_{20} + 3 De {\Omega}_{s} B_{22} $$

(72)

$$ \nabla_{\boldsymbol{n}}^{2} A_{33} = - 18 \text{De} B_{33} + 3 \text{De} {\Omega}_{s} A_{22} $$

(73)

$$ \nabla_{\boldsymbol{n}}^{2} B_{33} = 18 \text{De} A_{33} + 3 \text{De} {\Omega}_{s} B_{22} . $$

(74)

The nonhomogeneous terms involving Ω _s are written in terms of spherical harmonics using the a factors from Bird et al. (1987), and these equations are then solved to obtain A ₃₁, B ₃₁, A ₃₃, and B ₃₃. These functions directly determine Ψ₃. They are also used in Eqs. (20)–(23) to calculate the intrinsic nonlinearities. These averages are simplified by the fact that

$$ {n_{x}^{2}} {n_{y}^{2}} = \frac{1}{15} {P_{0}^{0}} - \frac{2}{21} {P_{2}^{0}} + \frac{1}{35} {P_{4}^{0}} - \frac{1}{840} {P_{4}^{4}} \cos(4 \phi) . $$

(75)