Linear viscoelasticity of unentangled corona blocks and star arms

Abstract

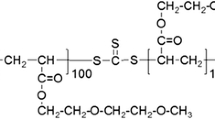
ABA-type triblock copolymers form micellar structures consisting of B-rich cores and A-rich coronas in A-selective solvents. The relaxation of A corona is known to be qualitatively similar to but quantitatively different from that of a star-shaped A chain due to the geometric (spatial) constraint by the core and the thermodynamic (osmotic) constraint. The effect of the geometric constraint on the block dynamics can be modeled by a chain with one end grafted onto an impenetrable wall. We show that the impenetrable wall slightly accelerates the end-to-end vector relaxation in a direction normal to the wall while it slightly decelerates the viscoelastic terminal relaxation. To test this prediction, we performed linear viscoelastic measurements for model systems: For polystyrene–polyisoprene–polystyrene (SIS) triblock copolymers in S-selective solvent (diethyl phthalate) forming micelles, the viscoelastic relaxation of unentangled S blocks (corona blocks) was indeed slower compared with that of star-branched S chains having the same molecular weight. Nevertheless, the deceleration was stronger than that expected from our theory, and possible reasons were discussed.

Appendix:

In this appendix, we show the detailed calculation of the correlation functions and the shear relaxation modulus for the model in the “Theory” section. We first consider the two-and four-body correlation functions defined by Eq. 20. Eqs. 10 and 11 describe the Ornstein-Uhlenbeck processes and can be formally integrated as

$$ R_{\alpha } (t)=e^{-t/\tau}R_{\alpha} (0)+{{\int}_{0}^{t}} {d{t^{\prime}} e^{-(t-{t^{\prime}})/\tau}\xi_{\alpha} ({t^{\prime}})}\quad_{(\alpha=x , y)} $$

(A1)

$$ Q_{z} (t)=e^{-2t/\tau }Q_{z} (0)+{{\int}_{0}^{t}} {d{t^{\prime}}\;e^{-2(t-{t^{\prime}})/\tau }\xi_{z} ({t^{\prime}})} $$

(A2)

where we have defined $Q_{z} (t)=R_{z} (t)-\sqrt {Nb^{2}/3}$. The two body correlation functions for R _x (t), R _y (t), and Q _z (t) can be calculated straightforwardly.

$$ \left\langle {R_{\alpha } (t)R_{\alpha} (0)} \right\rangle =\left\langle {R_{\alpha }^{2}} \right\rangle e^{-t/\tau }=\frac{Nb^{2}}{3}e^{-t/\tau}\quad_{(\alpha=x,y)} $$

(A3)

$$ \left\langle {Q_{z} (t)Q_{z} (0)} \right\rangle =\left\langle {{Q_{z}^{2}} } \right\rangle e^{-2t/\tau }=\frac{Nb^{2}}{6}e^{-2t/\tau } $$

(A4)

The two body correlation functions in Eq. 19 become

$$ C_{\alpha}^{(2)} (t)= e^{-t/\tau} (\alpha = x,y) $$

(A5)

$$ C_{z}^{(2)} (t)=\frac{3}{Nb^{2}}\left[ {\left\langle {Q_{z} (t)Q_{z} (0)} \right\rangle +\frac{Nb^{2}}{3}} \right]=1+\frac{1}{2}e^{-2t/\tau } $$

(A6)

Because R _x (t), R _y (t), and Q _z (t) are the Gaussian processes, the higher-order correlation functions can be calculated straightforwardly. Here, we note that Eq. A6 contains a non-relaxing component ($C_{z}^{(2)} \to 1$ at the limit of t → $\infty )$. The four body correlations can be factorized into the two-body correlations (Van Kampen 2007). Thus, we have

$$\begin{array}{@{}rcl@{}} C_{\alpha }^{(4)} (t)&=&\frac{9}{N^{2}b^{4}}\left[ {\left\langle {R_{\alpha }^{2} } \right\rangle^{2}+2\left\langle {R_{\alpha } (t) R_{\alpha } (0)} \right\rangle^{2}} \right]\\ &=& 1+2e^{-2t/\tau }(\alpha =x,y) \end{array} $$

(A7)

$$\begin{array}{@{}rcl@{}} C_{z}^{(4)} (t)&&=\frac{9}{N^{2}b^{4}}\left\langle {(Q_{z} (t)+\sqrt {Nb^{2}/3} )^{2}(Q_{z} (0)+\sqrt {Nb^{2}/3} )^{2}} \right\rangle \\ &&=\frac{9}{N^{2}b^{4}}\left[\left\langle {{Q_{z}^{2}} } \right\rangle ^{2}+2\left\langle {Q_{z} (t)Q_{z} (0)} \right\rangle^{2}\right.\\ &&\left.+\frac{4Nb^{2}}{3}\left\langle {Q_{z} (t)Q_{z} (0)} \right\rangle +\frac{2Nb^{2}}{3}\left\langle {{Q_{z}^{2}} } \right\rangle +\frac{N^{2}b^{4}}{9}\right] \\ &&=\frac{9}{4}+2e^{-2t/\tau }+\frac{1}{4}e^{-4t/\tau } \end{array} $$

(A8)

By substituting Eqs. A5–A8 into Eq. 19, we finally have

$$\begin{array}{@{}rcl@{}} G(t)&=&\frac{1}{5}\nu k_{\mathrm{B}} T\left[ {e^{-2t/\tau }+2e^{-t/\tau }\left( {1+\frac{1}{2}e^{-2t/\tau }} \right)} \right]\\ &+&\frac{1}{15}\nu k_{\mathrm{B}} T\left[ {6e^{-2t/\tau }+\frac{1}{4}e^{-4t/\tau }} \right]\\ & =&\nu k_{\mathrm{B}} T\left[ {\frac{2}{5}e^{-t/\tau }+\frac{3}{5}e^{-2t/\tau }+\frac{1}{5}e^{-3t/\tau }+\frac{1}{60}e^{-4t/\tau }} \right] \end{array} $$

(A9)

This gives Eq. 21.

The shear relaxation modulus calculated in the main text (and in this appendix) is for a non-interacting chain. In reality, the chains interact with each other and a chain feels the osmotic pressure field. As we discussed in the main text, this modulates the effective potential for the chain end (6). We briefly consider how this affects the shear relaxation modulus. By the addition of the extra term, the position of the minimum of the effective potential and the expansion coefficient are changed. Then, we may have the following harmonic approximation form instead of Eq 9.

$$ U_{\text{eff}} (\text{\textbf{r}})\approx \frac{3k_{\mathrm{B}} T}{2Nb^{2}}[{R_{x}^{2}} +{R_{y}^{2}} +c(R_{z} -\bar{{R}}_{\text{mp}} )^{2}]+\mbox{(const)} $$

(A10)

Here, c is a positive constant and $\bar {{R}}_{\text {mp}}$ is the most probable bond length. The use of Eq. (A9) changes the relaxation time in the z-direction (from 2 τ to c τ) as well as the average end-to-end vector size in the z-direction (from $\sqrt {Nb^{2}/3}$ to $\bar {{R}}_{\text {mp}} )$. These changes, however, do not affect the longest relaxation time of the shear relaxation modulus because the longest relaxation time arises from the coupling between the relaxation of the x- or y-direction and the time-independent component in the z-direction (The weight average relaxation time can be affected, although we expect that the effect will not be large.)