Skip to main content
SpringerLink
Log in

Entropy generation analysis of MHD nanofluid in a corrugated vertical walls enclosure with a rectangular baffle using the Brinkmann-Forchheimer model

  • Research
  • Published:
Colloid and Polymer Science Aims and scope Submit manuscript

Abstract

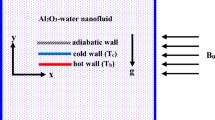
Copper is abundant and has good conductivity, corrosion resistance, and malleability. These properties affect the behavior of nanofluids by contributing to the interaction between nanoparticles and the magnetic field. This work aims to assess the thermal transfer characteristics of a Cu-water nanofluid filled in an enclosure having vertical wavy walls under the influence of natural convection. The system also experiences the existence of a constant inclined magnetic field and features an inner heated rectangular baffle. In this study, a comprehensive analysis is conducted on several thermo-physical parameters, including the Rayleigh number (\({10}^{3} \le {\text{Ra}} \le {10}^{5}\)), Hartmann number \((0 \le {\text{Ha}} \le 150),\) nanoparticle concentration \((0.00 \le \phi \le 0.09),\) and porosity \((0.2 \le \varepsilon \le 0.8)\). The Galerkin finite element method (GFEM) is employed in this study to conduct calculations, enabling a comprehensive analysis of streamlines, isotherms, entropy generation, and mean Nusselt numbers. The key findings demonstrate that raising the number of Rayleigh and porosity raises the velocity profile within the enclosure. For the various angles of the inner rectangular baffle \((\theta =0^\circ ,30^\circ ,60^\circ ,\mathrm{ and}\ 90^\circ )\) at \({\text{Ra}}={10}^{3}- {10}^{5}\), the calculated maximum increase in \({{\text{Nu}}}_{{\text{avg}}}\) are \(77.5\%, 78.3\%\), \(81.9\% ,\) and \(82.2\%,\) respectively. Furthermore, significant rise in the value of (\({S}_{{\text{Total}}}\)) up to \(96.1\%, 11.1\%\), and \(8.8\%\) is experienced when \(\left(Ra\right), \left(\phi \right),\) and \((\varepsilon )\) increase, while \(19.5\%\) decrement is observed when (\({\text{Ha}}\)) increases. Additionally, the average Bejan number \(({{\text{Be}}}_{{\text{avg}}})\) grows as the fraction volume of nanoparticle \((\phi )\) climbs and the Hartmann number \(({\text{Ha}})\) declines. The geometry configurations employed in this research have real-world applications across different engineering fields, such as energy storage, chemical processing equipment, biomedical systems, solar collectors, heat exchangers, and cooling systems for electronic devices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data availability

Not applicable.

Abbreviations

Ha:

Hartmann number

Ra:

Number of Rayleigh

Pr:

Prandtl number

\({B}^{2}\) :

Magnetic field strength

Nuavg :

Average Nusselt number

\({T}_{h}\) :

The heated surface thermal (K)

\({T}_{c}\) :

The cold surface thermal (K)

\(U,V\) :

Dimensional velocity components

\(U*,V*\) :

Dimensionless velocity components

\(g\) :

Gravitational acceleration

\(A\) :

Aspect ratio, H/W

\(\gamma\) :

Angel of inclination

\(L\) :

Average width of the cavity

\(H\) :

Height of the cavity

\({F}_{c}\) :

Forchheimer coefficient

\(K\) :

Permeability

\(a\) :

Amplitude of the wave

\(\mu\) :

Dynamic viscosity

\(\theta\) :

Dimensionless temperature

\(\phi\) :

Volume fraction of nanofluid

\({\alpha }_{{\text{nf}}}\) :

Thermal diffusivity of nanofluid

\({\sigma }_{{\text{nf}}}\) :

Electric conductivity of nanofluid

\(\rho\) :

Density

\(\lambda\) :

Surface waviness, a/W

\(\varepsilon\) :

Porosity

c:

Cold

h:

Hot

avg:

Average

nf:

Nanofluid

bf:

Basefluid

References

  1. Bejan A (1979) A study of entropy generation in fundamental convective heat transfer 718–725

  2. Bejan A (1980) Second law analysis in heat transfer. Energy 5(8–9):720–732

    Article  Google Scholar 

  3. Bejan A, Kestin J (1983) Entropy generation through heat and fluid flow. 475–475

  4. Bejan A (1996) Minimization of entropy generation 

  5. Abu-Hijleh B (2001) Natural convection and entropy generation from a cylinder with high conductivity fins. Numer Heat Transf A 39:405–432

    Article  Google Scholar 

  6. Naterer GF, Camberos JA (2003) Entropy and the second law fluid flow and heat transfer simulation. J Thermophys Heat Transfer 17:360–371

    Article  CAS  Google Scholar 

  7. Magherbi MA, Abbassi A, Brahim AB (2003) Entropy generation at the onset of natural convection. Int J Heat Mass Transfer 46:3441–3450

    Article  Google Scholar 

  8. Mahmud S, Islam AKMS (2003) Laminar free convection and entropy generation inside an inclined wavy enclosure. Int J Therm Sci 42:1003–1012

    Article  Google Scholar 

  9. Erbay LB, Altac Z, Sulus B (2004) Entropy generation in a square enclosure with partial heating from a vertical lateral wall. Heat Mass Transfer 40:909–918

    Article  Google Scholar 

  10. Andreozzi A, Auletta A, Manca O (2006) Entropy generation in natural convection in a symmetrically and uniformly heated vertical channel. Int J Heat Mass Transfer 49:3221–3228

    Article  Google Scholar 

  11. Khanafer K, Vafai K, Lightstone M (2003) Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int J Heat Mass Transf 19:3639–3653

    Article  Google Scholar 

  12. Masuda H, Ebata A, Teramae K (1993) Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles 227–233

  13. Buongiorno J (2006) Convective transport in nanofluids. 240–250

  14. Alomari MA, Farhany KA, Hashem AL, Dawody MFA, Redouane F, Olayemi OA (2021) Numerical study of MHD natural convection in trapezoidal enclosure filled with (50% MgO-50% Ag/water) hybrid nanofluid: heated sinusoidal from below. Int J Heat Tech. 4

  15. Baytaş AC (2007) Entropy generation for thermal nonequilibrium natural convection with a non-Darcy flow model in a porous enclosure filled with a heat-generating solid phase. J Porous Media. 3

  16. Slimi K (2006) Entropy generation for unsteady natural convection and radiation within a tilted saturated porous channel. Int J Exergy 2:174–190

    Article  Google Scholar 

  17. Varol Y, Oztop HF, Pop I (2009) Entropy generation due to natural convection in non-uniformly heated porous isosceles triangular enclosures at different positions. Int J Heat Mass Transf 52(5–5):1193–1205

    Article  CAS  Google Scholar 

  18. Tayebi T, Öztop HF, Chamkha AJ (2020) Natural convection and entropy production in hybrid nanofluid filled-annular elliptical cavity with internal heat generation or absorption. Therm Sci Eng Prog 19:100605

    Article  Google Scholar 

  19. Ahmed SE, Elshehabey HM (2018) Buoyancy-driven flow of nanofluids in an inclined enclosure containing an adiabatic obstacle with heat generation/absorption: effects of periodic thermal conditions. Int J Heat Mass Transf 124:58–73

    Article  CAS  Google Scholar 

  20. Alnaqi AA (2019) Effects of magnetic field on the convective heat transfer rate and entropy generation of a nanofluid in an inclined square cavity equipped with a conductor fin: considering the radiation effect. Int J Heat Mass Transf 133:256–267

    Article  CAS  Google Scholar 

  21. Rathore N, Sandeep N (2022) Darcy–Forchheimer and Ohmic heating effects on GO-TiO2 suspended cross nanofluid flow through stenosis artery. Proc Inst Mech Eng Pt C J Menh Eng 236(20):10470–10485

    Article  CAS  Google Scholar 

  22. Sridhar V, Ramesh K (2022) Peristaltic activity of thermally radiative magneto-nanofluid with electroosmosis and entropy analysis. Heat Transfer 51(2):1668–1690

    Article  Google Scholar 

  23. Hassan M, Mohyud-Din ST, Ramzan M (2019) Study of heat transfer and entropy generation in ferrofluid under low oscillating magnetic field. Ind J Phys 93:749–758

    Article  CAS  Google Scholar 

  24. Lu D et al (2018) Impact of nonlinear thermal radiation and entropy optimization coatings with hybrid nanoliquid flow past a curved stretched surface. Coatings 8(12):430

    Article  Google Scholar 

  25. Khan WA, Ali M (2019) Recent developments in modeling and simulation of entropy generation for dissipative cross material with quartic autocatalysis. Appl Phys A 125:1–9

    Article  Google Scholar 

  26. Alipour N, Jafari B, Hosseinzadeh Kh (2023) Optimization of wavy trapezoidal porous cavity containing mixture hybrid nanofluid (water/ethylene glycol Go–Al2O3) by response surface method. Sci Rep 13(1):1635

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  27. Korei Z et al (2022) MHD mixed convection and irreversibility analysis of hybrid nanofluids in a partially heated lid-driven cavity chamfered from the bottom side. Int Commun Heat Mass Transf 132:105895

    Article  CAS  Google Scholar 

  28. Azizul FM, Alsabery AI, Hashim I (2020) Heatlines visualisation of mixed convection flow in a wavy heated cavity filled with nanofluids and having an inner solid block. Int J Mech Sci 175:105529

    Article  Google Scholar 

  29. Abdelmalek Z, Tayebi T, Dogonchi AS, Chamkha AJ, Ganji DD, Tlili I (2020) Role of various configurations of a wavy circular heater on convective heat transfer within an enclosure filled with nanofluid. Int Commun Heat Mass Transf 113:104525

    Article  CAS  Google Scholar 

  30. Heidary H, Abbassi A, Kermani MJ (2013) Enhanced heat transfer with corrugated flow channel in anode side of direct methanol fuel cells. Energy Convers Manage 75:748–760

    Article  CAS  Google Scholar 

  31. Alsabery AI et al (2021) Impacts of amplitude and local thermal non-equilibrium design on natural convection within nanofluid superposed wavy porous layers. Nanomaterials 11(5):1277

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  32. Barnoon P et al (2019) MHD mixed convection and entropy generation in a lid-driven cavity with rotating cylinders filled by a nanofluid using two phase mixture model. J Magn Magn Mater 483:224–248

    Article  CAS  Google Scholar 

  33. Zidan AM et al (2022) Entropy-based analysis and economic scrutiny of magneto thermal natural convection enhancement in a nanofluid-filled porous trapezium-shaped cavity having localized baffles. Waves in Random and Complex Media 1–21

  34. Jakeer S et al (2021) Impact of heated obstacle position on magneto-hybrid nanofluid flow in a lid-driven porous cavity with Cattaneo-Christov heat flux pattern. Alex Eng J 60(1):821–835

    Article  Google Scholar 

  35. Ellahi R (2019) Numerical simulation and mathematical modeling of electro-osmotic Couette–Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry 11(8):1038

    Article  CAS  Google Scholar 

  36. Ranjit NK, Shit GC (2017) Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 128:649–660

    Article  Google Scholar 

  37. Shamshuddin MD et al (2022) MHD bioconvection microorganism nanofluid driven by a stretchable plate through porous media with an induced heat source. Waves in Random and Complex Media 1–25

  38. Medebber MA et al (2019) Numerical study of natural convection in vertical cylindrical annular enclosure filled with Cu-water nanofluid under magnetic fields. Defect and diffusion forum 392 Trans Tech Publications Ltd

  39. Radouane F et al (2020) Magneto-free convective of hybrid nanofluid inside non-Darcy porous enclosure containing an adiabatic rotating cylinder. Energ Source Part A Recovery Util Environ Eff 1–16

  40. Wakif A et al (2022) Importance of exponentially falling variability in heat generation on chemically reactive von Kármán nanofluid flows subjected to a radial magnetic field and controlled locally by zero mass flux and convective heating conditions: a differential quadrature analysis. Front Phys 10:988275

    Article  Google Scholar 

  41. Jamshed W (2021) Partial velocity slip effect on working magneto non-Newtonian nanofluids flow in solar collector’s subject to change viscosity and thermal conductivity with temperature. Plos one 16(11):e0259881

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  42. Korei Z (2023) Thermo-magnetic convection analysis of magnetite ferrofluid in an arc-shaped lid-driven electronic chamber with partial heating. J Therm Anal Calorim 148(6):2585–2604

    Article  CAS  Google Scholar 

  43. Korei Z et al (2022) Thermohydraulic and second law analyses during the cooling of an electronic device mounted in an open cavity equipped with magnetic nanofluid, magnetic field inducer, and porous media: a two-phase numerical investigation. Int Commun Heat Mass Transf 139:106497

    Article  Google Scholar 

  44. Djebali R (2021) Mesoscopic study of mixed convection and heat transfer due to crescent shape hot source under magnetic field and Joule effect. Romanian Rep Phys 72:106

    Google Scholar 

  45. Djebali R (2020) Numerical analysis of nanofluid cooling efficiency of hot multishaped cylinder in vertical porous channel. Rom J Phys 65(9–10):1–10

    Google Scholar 

  46. Ferhi M, Djebali R (2020) Appraising conjugate heat transfer, heatlines visualization and entropy generation of Ag-MgO/H2O hybrid nanofluid in a partitioned medium. Int J Numer Meth Heat Fluid Flow 30(10):4529–4562

    Article  Google Scholar 

  47. Djebali R (2019) Accurate LBM appraising of pin-fins heat dissipation performance and entropy generation in enclosures as application to power electronic cooling. Int J Numer Methods Heat Fluid Flow 30(2):742–768

    Article  Google Scholar 

  48. Ferhi M et al (2019) Conjugate natural heat transfer scrutiny in differentially heated cavity partitioned with a conducting solid using the lattice Boltzmann method. J Therm Anal Calorim 138:3065–3088

    Article  CAS  Google Scholar 

  49. Abbassi MA, Djebali R, Guedri K (2018) Effects of heater dimensions on nanofluid natural convection in a heated incinerator shaped cavity containing a heated block. J Therm Eng 4(3):2018–2036

    Article  CAS  Google Scholar 

  50. Djebali R, ElGanaoui M, Naffouti T (2012) A 2D Lattice Boltzmann full analysis of MHD convective heat transfer in saturated porous square enclosure. Comput Model Eng Sci 84(6):499

    Google Scholar 

  51. Sheikholeslami M, Bandpy MG, Ganji DD (2013) Numerical investigation of MHD effects on Al2O3–water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 60:501–510

    Article  CAS  Google Scholar 

  52. Redouane F, Jamshed W, Devi SSU, Amine BM, Safdar R, Al-Farhany K, Eid MR, Nisar KS, Aty AHA, Yahia IS (2021) Influence of entropy on Brinkman-Forchheimer model of MHD hybrid nanofluid flowing in enclosure containing rotating cylinder and undulating porous stratum. Sci Rep 1:24316

    Article  Google Scholar 

  53. Esfe MH, Arani AAA, Rezaie M, Yan WM, Karimipour A (2015) Experimental determination of thermal conductivity and dynamic viscosity of Ag–MgO/water hybrid nanofluid. Int Commun Heat Mass Transfer 66:189–195

    Article  Google Scholar 

  54. Dobrovolskaia MA (2019) Recent advances in modeling and simulation of nanofluid flows-part i: fundamentals and theory. Int J Heat Mass Transf 1:23–33

    Google Scholar 

  55. Makinde OD, Animasaun IL (2016) Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. J Mol Liq 221:733–743

    Article  CAS  Google Scholar 

  56. Rashad AM, Armaghani T, Chamkha AJ, Mansour MA (2018) Entropy generation and MHD natural convection of a nanofluid in an inclined square porous cavity: effects of a heat sink and source size and location. Chin J Phys 1:193–211

    Article  Google Scholar 

  57. Woods LC (1975) The thermodynamics of fluid systems. Oxford

  58. Chamkha AJ, Selimefendigil F (2018) MHD free convection and entropy generation in a corrugated cavity filled with a porous medium saturated with nanofluids. Entropy 20(11):846

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  59. Hussain S, Schieweck F, Turek S (2014) Efficient Newton-multigrid solution techniques for higher order space–time Galerkin discretizations of incompressible flow. Appl Numer Math 83:51–71

    Article  Google Scholar 

  60. Hussain S, Mehmood K, Sagheer M, Farooq A (2017) Entropy generation analysis of mixed convective flow in an inclined channel with cavity with Al2O3-water nanofluid in porous medium. Int Commun Heat Mass Transfer 89:198–210

    Article  CAS  Google Scholar 

  61. Donea J, Huerta A (2003) Finite element methods for flow problems. John Wiley & Sons 

  62. Nithiarasu P, Lewis RW, Seetharamu KN (2016) Fundamentals of the finite element method for heat and mass transfer. John Wiley & Sons

  63. Mansour MA, Ahmed SE, Chamkha AJ (2017) Entropy generation optimization for MHD natural convection of a nanofluid in porous media-filled enclosure with active parts and viscous dissipation. Int J Numer Methods Heat Fluid Flow 27(2):379–399

    Article  Google Scholar 

  64. Sadia A et al (2021) MHD natural convection and entropy generation of non-Newtonian ferrofluid in a wavy enclosure. Int J Mech Sci 198:106350

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Central South University, Changsha Hunan, 410083, China

    Asad Ali, Kejia Pan & Muhammad Waqas Ashraf

  2. School of Mathematics Sciences, Zhejiang Normal University, Jinhua, 321004, Zhejiang People’s Republic of China, China

    Rashid Ali

Authors
  1. Asad Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kejia Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rashid Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Muhammad Waqas Ashraf
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Literature and consolation: A.A.; methodology and supervision: K.P.; software and validation investigation: R.A.; and analysis and interpreted the data: M.W.A.

Corresponding author

Correspondence to Asad Ali.

Ethics declarations

International review board statement

Not applicable.

Information consent

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, A., Pan, K., Ali, R. et al. Entropy generation analysis of MHD nanofluid in a corrugated vertical walls enclosure with a rectangular baffle using the Brinkmann-Forchheimer model. Colloid Polym Sci (2024). https://doi.org/10.1007/s00396-024-05264-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00396-024-05264-9

Keywords

Search

Navigation