Non-Newtonian effect on heat transfer and entropy generation of natural convection nanofluid flow inside a vertical wavy porous cavity

Abstract

A numerical study on heat transfer and entropy generation in natural convection of non-Newtonian nanofluid flow has been explored within a differentially heated two-dimensional wavy porous cavity. In the present study, copper (Cu)–water nanofluid is considered for the investigation where the specific behavior of Cu nanoparticles in water is considered to behave as non-Newtonian based on previously established experimental results. The power-law model and the Brinkman-extended Darcy model has been used to characterize the non-Newtonian porous medium. The governing equations of the flow are solved using the finite volume method with the collocated grid arrangement. Numerical results are presented through streamlines, isotherms, local Nusselt number and entropy generation rate to study the effects of a range of Darcy number (Da), volume fractions (ϕ) of nanofluids, Rayleigh numbers (Ra), and the power-law index (n). Results show that the rate of heat transfer from the wavy wall to the medium becomes enhanced by decreasing the power-law index but increasing the volume fraction of nanoparticles. Increase of porosity level and buoyancy forces of the medium augments flow strength and results in a thinner boundary layer within the cavity. At negligible porosity level of the enclosure, effect of volume fraction of nanoparticles over thermal conductivity of the nanofluids is imperceptible. Interestingly, when the Darcy–Rayleigh number $Ra^*\gg 10$, the power-law effect becomes more significant than the volume fraction effect in the augmentation of the convective heat transfer process. The local entropy generation is highly dominated by heat transfer irreversibility within the porous enclosure for all conditions of the flow medium. The particular wavy shape of the cavity strongly influences the heat transfer flow pattern and local entropy generation. Interestingly, contour graphs of local entropy generation and local Bejan number show a rotationally symmetric pattern of order two about the center of the wavy cavity.

1 Introduction

Over the last several decades, heat transfer in the natural convection process has received significant impact on various engineering applications, for instance, geothermal systems, heat exchangers, cooling systems for electronic devices, solar energy collector, non-Newtonian chemical processes, chemical reactors and to name a few [1, 2]. To save energy in these systems, heat transfer enhancement has become an essential subject. A significant amount of research has been carried out to enhance the heat transfer mechanism in a close enclosure. In this regard, an innovative technique of using nanofluids becomes useful. It has higher thermal conductivity than the conventional fluids (e.g., water, oil, ethylene glycol) with either little or no pressure drop [3]. Nanofluids are a homogenous mixture of nanoparticles and base fluid (e.g., water, oil, ethylene glycol). It is made of dispersed nanometer-sized particles where the diameter varies between 1 to 100 nm. In the early 1990s, Masuda et al. [4] investigated that effective thermal conductivity can be improved by $20\%$ by adding $3\%$ nanoparticles in the base fluid. Afterward, Choi and Eastman [5] proposed the concept of nanofluid, mentioning that the nanofluids maintain high thermal conductivity compared to the base fluid used in the study. In order to acquire knowledge about the enhanced heat transfer mechanism, numerous experiments and simulations have been conducted in the past two decades. Nnanna [6] conducted an experimental study of the heat transfer characteristics of Al$_2$O$_3$-water nanofluid in a differentially heated rectangular cavity and observed that the heat transfer rate is increased even at the small volume fraction (0.2–2%).

Khanafer et al. [7] studied the enhancement of heat transfer in a square enclosure utilizing nanofluids. They found that the heat transfer rate increases with the increase of volume fraction of nanoparticles for any given Grashof number (Gr). Wen and Ding [8] reported an experimental study on TiO$_2$-water nanofluid for the Rayleigh number (Ra) less than $10^{6}$ where they found that the convective heat transfer rate decreases with the increasing volume fraction of nanoparticles. Kim et al. [9] found that a remarkable increase in heat transfer can be obtained at the modest nanoparticles dispersion while studying the pool boiling characteristics of dilute dispersions of Al$_2$O$_3$, ZrO$_2$ and SiO$_2$ nanoparticles in water. Wang and Mujumdar [10] presented the fluid flow and heat transfer behavior of nanofluids in forced and free convection flows. Abu-Nada et al. [11] observed an increase of heat transfer in horizontal annuli while simulating the natural convection heat transfer in horizontal annuli for various nanoparticles and volume fractions. Santra et al. [12] studied the behavior of heat transfer in Cu–water nanofluid in a differentially heated square cavity considering a wide range of Rayleigh numbers (Ra) from $10^{4}$ to $10^{7}$. They found that the heat transfer rate increases with an increase of volume fraction of nanoparticles.

Newtonian nanofluid has been studied with the constant viscosity and variant pressure being applied to the base fluid in the pioneering studies. Non-Newtonian nanofluids do not follow Newton’s law of viscosity. Shear-thinning and shear-thickening fluids follow inversely proportionate relation between viscosity and shear rate. The classical Ostwald-de Waele power-law model explains the characteristics of the non-Newtonian fluid [13]. A comparative study run by Kim et al. [14] between non-Newtonian nanofluids and Newtonian fluids presents the convection strength and the degree of heat transfer rate regarding the transient buoyant natural convection in non-Newtonian power-law fluids. The shear-thinning nanofluid augments the fluid circulation, and convective heat transfer compared to Newtonian fluid was found by Lamsaadi et al. [15]. Hojjat et al. [16] did a study on forced convection of non-Newtonian nanofluids inside a uniformly heated circular cylinder; the findings present significant local and average heat transfer coefficients of nanofluid compared to that of the base fluid. In a simulation experiment by Turan et al. [17] on the laminar natural convection of non-Newtonian nanofluids within a square enclosure with differentially heated sidewalls, the result showed mean Nusselt number increases with increasing Rayleigh number. Chandi and Raj [18] found that shear-thinning fluids exhibit a higher heat transfer rate than the Newtonian fluids ($n=1$). A numerical study conducted by Kaddiri et al. [19] stated the critical value of the Rayleigh number that augments with the power-law index in the Rayleigh-Bénard convection of non-Newtonian power-law fluid. Shojaeian et al. [20] revealed the findings that the heat transfer characteristics and entropy generation of non-Newtonian fluid are affected through the variance of thermophysical properties. The heat transfer rate increased with increasing Rayleigh number for shear-thinning fluid mainly. A numerical study of hybrid $Al_{2}O_{3}{-}CuO$/water nanofluid in a square porous cavity studied the magneto-hydrodynamic natural convection and heat transfer with analysis of entropy generation [21]. Similar studies of Cu–water nanofluid in an inclined porous cavity analyzed natural convection and entropy generation with respect to effect of heat source, size and corresponding location [22].

The unique contact surface of porous medium initiates special interaction between the fluid and the medium, which has encouraged several dimensions of computational fluid research. Fluids flow through the voids in a porous medium; the controlled flow feature increases the contact surface area within. Non-Newtonian nanofluids natural convection heat transfer in a porous medium is still a growing research field. One of the pioneering studies of porous medium conducted by Adrian and Khairy [23] focused on analyzing buoyancy effect stemmed from density and temperature differences in a porous medium on the phenomenon of natural convection boundary-layer flow. Gobin et al. [24] argued in their study that permeability of the porous medium serves as the impacting factor of heat and mass transfer in a semi-porous cavity for natural convection of binary fluid. A numerical study on natural convection in a trapezoidal porous enclosure with differentially heated walls found the formation of the highest heat-transfer coefficient near the corner regions of the enclosure [25]. A similar study by Sathiyamoorthy et al. [26] conducted a study of natural convection flow for a square porous cavity with sinusoidal and linear heated walls. Analysis conducted by Kuznetsov and Nield [27] focused on natural convection of a nanofluid in a horizontal porous medium and followed three-temperature model to study the effect of local thermal non-equilibrium state. Significant enhancement of heat transfer of nanofluids in a porous cavity was found for minimal Rayleigh number ($Ra=10$) from a study by Chamkha and Ismael [28]. A numerical study of significance of shape factors of nanoparticles in a fluid saturated porous annulas illustrated the increase of Rayleigh number and Darcy number at a certain aspect ratio of manifolds heat transfer rate within the cavity [29].

The above literature review indicates the existence of many studies on the natural convection of non-Newtonian nanofluid within a regular geometry such as square, rectangle, rotated square/rectangle for which the sidewalls are flat. The interaction between the fluid parcel and the enclosure walls within a thin boundary layer contact becomes complicated depending on the medium characteristics and geometric shape of the wall. The interaction becomes more complex and exciting when the active walls of the enclosure become irregular. As for irregular geometry, waviness on the sidewalls becomes popular to the CFD community. In this regard, Mahmud et al. [30] investigated the impact of surface waviness on the heat transfer mechanism within a two-sided single-undulated vertical wavy enclosure. The study found a critical value affiliated with the magnitude of surface waviness. The average heat transfer demonstrated higher value before and after the critical value point. Sheremet and Pop [31] considered a left-sided wavy porous enclosure opening at the top to investigate the effect of undulation number and the shape of the wave on nanofluid flow. They reported that the surface heat transfer becomes attenuated by increasing the undulation number for a large amount of heating of the wave troughs. Another investigation suggested that when the enclosure is made of vertically flat and horizontally wavy with several undulations, then there exist always double cell flow regimes regardless of the value of the thermal dispersion in nanofluid flow [32]. Recently, a left-sided wavy cavity with different wave numbers was investigated by Grosan and Sheremet [33] to study the thermophoresis effect on double-diffusive natural convection of a warm gas containing small particles. Investigation revealed that the heat transfer rate was augmented by decreasing the undulation number of the wavy surface and the buoyancy ratio parameter. Very recently, Acharya and Dash [34] investigated the magnetic effect on power-law non-Newtonian CuO-water nanofluid under the natural convection settings inside a square wavy cavity. Similar study has been published on the natural convection in a square cavity with wavy circular heater, depicting the proportional effect of wavy amplitude of the heat source in heat transfer pattern within the enclosure [35]. The thermal characteristics of $Al_{2}O_{3}{-}H_{2}O$ nanofluid with horizontal magnetic field applied in a wavy enclosure considering the presence of an internal heat generation source demonstrated the possible approaches to control natural convection within the cavity through tuning the heat generation source and magnetic field [36].

Deduction from the above literature review reveals that natural convection heat-transfer phenomena of non-Newtonian nanofluid in a wavy porous enclosure are still a narrowly explored field. To the best of the author’s knowledge, the natural convection of non-Newtonian nanofluids within a wavy porous enclosure has not been studied yet. Existing research works in the field of computational fluid considered either wavy or porous properties of the cavity and mostly experimented on nanofluids. This paper is unique in its consideration of non-Newtonian characteristics of the nanofluid in a medium with both wavy and porous properties. The particular undulated shape of the cavity stands out as the unique parameter to have a strong influence on the heat transfer behavior of the subjected fluid. Following the above description, the objective of the present work is to investigate the natural convection heat transfer of non-Newtonian Cu–water nanofluid in a porous medium within a differentially heated rectangular wavy cavity. When considering the study of heat transfer in real-life naturally built cavities and spaces, irregular geometry is often found in place,for example, thermal plants, fuel cell technology, micro-electronic chips, nano-medicine and many more relevant fields of application. Continuous advent of technology to produce devices seamlessly matching with natural surroundings (fold-able TVs, mobile-phones) and target to reduce sizes of the devices are creating more opportunities for further exploration of heat transfer analysis of the irregular wavy geometry cavities. This real-life established examples have motivated to conduct the study in a wavy geometry shaped cavity.

The paper is structured as follows. In Sect. 2, the physical model, the governing equations for the power-law based non-Newtonian nanofluid and the properties of nanofluid have been described. In Sect. 3, the numerical method and code validation has been described in detail. In Sect. 4, the results of the current simulation are presented in terms of the streamlines, isotherms for different pertinent parameters such as power-law index (n), Darcy number (Da), Rayleigh number (Ra). The rate of surface heat transfer calculated in terms of local Nusselt number and has been presented. Furthermore, entropy generation has been discussed in terms of the irreversibilities due to fluid-friction and heat transfer. Finally, the conclusion is given in Sect. 5.

2 Mathematical formulation of the problem

2.1 Physical model and problem description

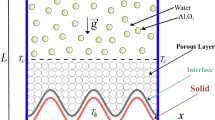
The present study considers a two-dimensional wavy porous enclosure with single undulation, as shown in Fig.1a, for the study of natural convection heat transfer phenomena of nanofluid, when different temperature conditions are applied to simulate heat transfer through fluid motion. The wavy and porous characteristics of the cavity bring a complex fluid flow and heat transfer phenomena of the non-Newtonian nanofluid within the enclosure. Dense mesh near the walls and sparse mesh at the central region of the cavity are maintained. The aspect ratio of the cavity maintains $A:\frac{H}{L}=2$, where H and L represents the height and average width of the cavity, respectively. Here, the two vertical wavy-side walls with single undulation are exposed to heat transfer activities as the left wavy wall is heated with higher temperature $(T_h)$, and the right wavy wall is subjected to lower temperature $(T_l < T_h)$, as labeled in Fig.1a. The top and bottom walls are considered to be adiabatic (no heat transfer takes place i.e. $\frac{\partial {\bar{T}}}{\partial {\bar{y}}}=0$). The nanofluid in the enclosure consists of water containing suspended Cu-nanoparticles, i.e., Cu–water nanofluid. Furthermore, the present study considers the following assumptions:

• The flow is laminar, two-dimensional, and the fluid is incompressible.

• The base fluid and nanoparticles are in thermally equilibrium state, and no relative velocity exists between the nanoparticles and base fluid molecule.

• No-slip boundary condition is applied at the enclosure or cavity walls and the system is hence established on single-phase model.

• The porosity is uniform, and nanoparticles are spherical shaped.

• Thermal conductivity of nanofluid is identical to the thermal conductivity of the porous zone in the cavity.

• The following relationship has been used to generate the curved walls and meshes within the enclosure:

  $$\begin{aligned} {\bar{x}} = X \left[ 1- 2a\cos \left( \frac{2\pi N{\bar{y}}}{H}\right) \right] , \quad 0\le {\bar{y}}\le H \quad -L/2 \le X \le L/2 \end{aligned}$$

  (1)

  where a is the amplitude of the wave, and N denotes the undulation number of the vertical wall of the enclosure.

• Thermo-physical properties of the base fluid, water, and nanofluid are listed in Table 1.

Fig. 1

Coordinate system of the present study with boundary conditions in a physical domain and b computational domain

2.2 Problem formulation in dimensional form

The natural convection heat transfer phenomenon studied in this paper takes place due to the buoyancy-driven force caused by the temperature difference maintained on the cavity’s vertical wavy walls. The two-dimensional laminar, incompressible non-Newtonian Cu–water nanofluid flow under the assumption of Boussinesq approximation is governed by the equation of continuity, momentum, and energy as given by,

$$\frac{\partial {\bar{u}}}{\partial {\bar{x}}}+\frac{\partial {\bar{v}}}{\partial {\bar{y}}} = 0$$

(2)

$$\frac{\partial {\bar{u}}}{\partial {\bar{t}}}+{\bar{u}}\frac{\partial {\bar{u}}}{\partial {\bar{x}}}+{\bar{v}} \frac{\partial {\bar{u}}}{\partial {\bar{y}}}= -\frac{1}{\rho _{n_{f}}}\frac{\partial {\bar{p}}}{\partial {\bar{x}}} +\frac{1}{\rho _{n_{f}}}\left[ \frac{\partial }{\partial {\bar{x}}}\left( 2 \mu _{eff}\frac{\partial {\bar{u}}}{\partial {\bar{x}}}\right) +\frac{\partial }{\partial {\bar{y}}}\left( \mu _{eff}\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\right)+\frac{\partial }{\partial {\bar{y}}}\left( \mu _{eff}\frac{\partial {\bar{v}}}{\partial {\bar{x}}}\right) -\mu _{eff}\frac{{\bar{u}}}{K}\right]$$

(3)

$$\begin{aligned} \frac{\partial {\bar{v}}}{\partial {\bar{t}}}+ {\bar{u}}\frac{\partial {\bar{v}}}{\partial {\bar{x}}}+ {\bar{v}}\frac{\partial {\bar{v}}}{\partial {\bar{y}}} & = -\frac{1}{\rho _{n_{f}}}\frac{\partial {\bar{p}}}{\partial {\bar{y}}}+\frac{1}{\rho _{n_{f}}}\left[ \frac{\partial }{\partial {\bar{x}}}\left( \mu _{eff}\frac{\partial {\bar{v}}}{\partial {\bar{x}}}\right) +\frac{\partial }{\partial {\bar{x}}}\left( \mu _{eff}\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\right) \right. \nonumber \\&\quad \left. +\frac{\partial }{\partial {\bar{y}}}\left( 2 \mu _{eff}\frac{\partial {\bar{v}}}{\partial {\bar{y}}}\right) -\mu _{eff}\frac{{\bar{v}}}{K}\right] +g\left( \beta _{T}\right) _{nf}\left( {\bar{T}}-T_{l}\right) \end{aligned}$$

(4)

$$\frac{\partial {\bar{T}}}{\partial {\bar{t}}}+{\bar{u}}\frac{\partial {\bar{T}}}{\partial {\bar{x}}}+{\bar{v}}\frac{\partial {\bar{T}}}{\partial {\bar{y}}} = \alpha _{nf}\left( \frac{\partial ^2 {\bar{T}}}{\partial {\bar{x}}^2}+\frac{\partial ^2 {\bar{T}}}{\partial {\bar{y}}^2}\right)$$

(5)

where ${\bar{u}}$ and ${\bar{v}}$ correspond to the velocity components of the nanofluid along the dimensional ${\bar{x}}$ and ${\bar{y}}$ directions. Other dimensional quantities are pressure ${\bar{p}}$ and the temperature ${\bar{T}}$ of the fluid. The quantities $\rho _{nf}, \mu _{eff}, K, \beta _{T}$ and $\alpha _{nf}$ represent density, effective dynamic viscosity, permeability, thermal expansion coefficient, and thermal diffusivity of the non-Newtonian nanofluid respectively. The properties of the nanofluid are discussed in detail in Sect. 2.3.

The wavy porous cavity with single undulation $(N=1)$ on vertical walls can be presented by mathematical formulation, as mentioned below. Along with the equations of the geometry, the boundary conditions associated with Eqs. 2–5 are given by:

• when ${\bar{t}}=0$,

  $$\begin{aligned} {\bar{u}}={\bar{v}}={\bar{T}}=0 \qquad \forall \, {\bar{x}}, {\bar{y}} \end{aligned}$$

  (6)

• when ${\bar{t}}>0$,

  $$\begin{aligned} {\bar{u}} = {\bar{v}}=0, {\bar{T}}=T_{h} \quad \text {on left wavy wall:} \, {\bar{x}}_{L} = -\frac{L}{2}\left[ 1- 2a\cos \left( \frac{2\pi {\bar{y}}}{H}\right) \right] , 0\le {\bar{y}}\le H \end{aligned}$$

  (7)
  $$\begin{aligned} {\bar{u}} = {\bar{v}}=0, {\bar{T}}=T_{l} \quad \text {on right wavy wall:} \, {\bar{x}}_{R} = \frac{L}{2}\left[ 1- 2a\cos \left( \frac{2\pi {\bar{y}}}{H}\right) \right] , 0\le {\bar{y}}\le H \end{aligned}$$

  (8)
  $$\begin{aligned} {\bar{u}} = {\bar{v}}=0, \frac{\partial {\bar{T}}}{\partial {\bar{y}}} = 0 \quad \text {on bottom and top wall:} \, {\bar{y}}=0 \, \& \, H, -\frac{L}{2}\left( 1-2a\right) \le {\bar{x}}\le \frac{L}{2}\left( 1-2a\right) \end{aligned}$$

  (9)

2.3 Thermophysical properties of nanofluid

The thermophysical properties of Cu–Water nanofluid used in the present study are listed in Table 1, considered at the ideal atmospheric temperature and pressure condition.

Table 1 Thermophysical properties of water and copper (Cu) nanoparticles [37]

The addition of nanoparticles in the base fluid changes the thermophysical properties of the nanofluid produced. The thermophysical properties of nanoparticles added in the base fluid, along with the base fluid and nanoparticles, volume fraction, determine the nanofluid properties. There are established experimental results depicting the non-Newtonian behavior of some particular nanofluids, such as Cu–water, carbon nanotube-water nanofluid (CNT nanofluid), $Al_{2}O_{3}$–water and $TiO_{2}$–water nanofluids. In an experiment by Chang et al. [38], the rheolgy of Cu–water nanofluid demonstrated shear-thinning fluid behavior. In another experiment [39], CNT nanofluid showed more extensive shear-thinning behavior with the addition of nanoparticle volume fraction. These experimental results state that the appearance of non-Newtonian behavior of nanofluid depends on the species of the nanoparticle and its volume fraction. Study by Santra et al. [40] showed simulation of a forced convection of Cu–water nanofluid in a channel where both Newtonian and non-Newtonian models have been projected. The power-law index applied for non-Newtonian model considered the consistent fluid coefficient and flow behavior index. A recent study of water-based non-Newtonian power-law CuO-water nanofluid analyzed the natural convection under the influence of magnetic field [34]. Also, there are latest published research exploring the non-Newtonian behavior of Cu–water nanofluid in terms of heat transfer and flow friction characteristics, as explored in [41].

In this regard, the effective density, $\rho _{nf}$ of the nanofluid is calculated by the mixture rule [42],

$$\begin{aligned} \rho _{nf} = \left( 1-\phi \right) \rho _{f}+\phi \rho _{s} \end{aligned}$$

(10)

where $\phi$ denotes the volume fraction of the nanoparticles in the base fluid, the subscripts f, nf, and s represent the properties of the base fluid, nanofluid, and nanoparticles, respectively.

The heat capacity, $(\rho C_{p})_{nf}$, and the thermal expansion coefficient,$(\rho \beta _{T})_{nf}$, of the nanofluid calculated from the mass averaging method [42], are as follows:

$$\left( \rho C_{p}\right) _{nf} = \left( 1-\phi \right) \left( \rho C_{p}\right) _{f}+\phi \left( \rho C_{p}\right) _{s}$$

(11)

$$\left( \rho \beta _{T}\right) _{nf} = \left( 1-\phi \right) \left( \rho \beta _{T}\right) _{f}+\phi \left( \rho \beta _{T}\right) _{s}$$

(12)

The Hamilton and Crosser model [42, 43] for the effective thermal conductivity of nanofluids, $k_{nf}$ is given by,

$$\begin{aligned} k_{nf} = \frac{k_{s}+(n_{e}-1)k_{f}+(n_e-1)(k_{s}-k_{f})\phi }{k_{s}+(n_{e}-1)k_{f}-(k_{s}-k_{f})\phi }k_{f}, \end{aligned}$$

(13)

where, $n_{e} = \frac{3}{\psi }$ is called the empirical shape factor related with the sphericity $\psi$ of the nanoparticles. For spherical nanoparticles, the shape factor is $n_{e}=3$ where $\psi =1$ [44, 45]. Then, the final form of thermal conductivity for Cu–water nanofluid with the spherical shaped Cu nanoparticles yields,

$$\begin{aligned} k_{nf} = \frac{k_{s}+2k_{f}+2(k_{s}-k_{f})\phi }{k_{s}+2k_{f}-(k_{s}-k_{f})\phi }k_{f} . \end{aligned}$$

(14)

Finally, the effective thermal diffusivity $\alpha _{nf}$ for a nanofluid is evaluated by,

$$\begin{aligned} \alpha _{nf} = \frac{k_{nf}}{(\rho C_{p})_{nf}} \end{aligned}$$

(15)

2.4 Power-law viscosity model

The Ostwald-de Waele power-law can predict the characteristics of time-independent non-Newtonian fluid model [13] in which the effective viscosity $\mu _{eff}$ is a function of the shear rate $\bar{{\dot{\gamma }}}$. For the non-Newtonian nanofluid case, the effective viscosity according to the power-law model can be written as,

$$\begin{aligned} \mu _{eff}= \mu _{nf}|\bar{{\dot{\gamma }}}|^{n-1}=\frac{\mu _{f}}{(1-\phi )^{2.5}}|\bar{{\dot{\gamma }}}|^{n-1} \end{aligned}$$

(16)

where, $\bar{{\dot{\gamma }}}=\frac{1}{2}\left( \nabla {\bar{u}}+(\nabla {\bar{u}})^T\right)$ is called the shear rate tensor. The magnitude of the shear rate tensor $|\bar{{\dot{\gamma }}}|$ is evaluated by the Frobenius norm as,

$$\begin{aligned} |\bar{{\dot{\gamma }}}| = \sqrt{2\left<\bar{{\dot{\gamma }}},\bar{{\dot{\gamma }}}\right>} = \sqrt{2\left( \frac{\partial {\bar{u}}}{\partial {\bar{x}}}\right) ^2 + 2\left( \frac{\partial {\bar{v}}}{\partial {\bar{y}}}\right) ^2+\left( \frac{\partial {\bar{u}}}{\partial {\bar{y}}}+\frac{\partial {\bar{v}}}{\partial {\bar{x}}}\right) ^2} \end{aligned}$$

(17)

Replacing the derived expression of $\left| \bar{{\dot{\gamma }}}\right|$ in Eq. 16, we get the following formula of effective dynamic viscosity, $\mu _{eff}$:

$$\begin{aligned} \mu _{eff}= \frac{\mu _{f}}{(1-\phi )^{2.5}}\left[ 2\left( \frac{\partial {\bar{u}}}{\partial {\bar{x}}}\right) ^2+2\left( \frac{\partial {\bar{v}}}{\partial {\bar{y}}}\right) ^2+\left( \frac{\partial {\bar{u}}}{\partial {\bar{y}}}+\frac{\partial {\bar{v}}}{\partial {\bar{x}}}\right) ^2\right] ^{\frac{n-1}{2}} \end{aligned}$$

(18)

Here, n in Eq. 18 is the power-law index, and it characterizes different non-Newtonian nanofluids. Shear-thinning, Newtonian and shear-thickening fluids are presented by the following values of n: $n<1.0$, $n=1.0$, and $n>1.0$. Effective viscosity of shear-thinning and shear-thickening fluids are higher and lower than Newtonian viscosity, respectively. A real fluid sustains the least and highest effective viscosity at a very low and high shear rate depending on the molecular structure. While the power-law model states nonsensical infinite and zero viscosity when the shear rate becomes zero or infinite for shear-thinning fluids ($n<1$) for the description of a real non-Newtonian fluid. In this regard, a modification was reported incorporating Newtonian behavior of non-Newtonian fluids at a very low and high shear rate to overcome the limitation of the power-law model [46]. The modification is based on an experimental study reported by [47], who first announced a lower and upper non-Newtonian regime for the pseudoplastic fluids against applied shear-stress.

2.5 Governing equation in non-dimensional form

The governing equation in non-dimensional expression represents the mathematical equation’s exportability in any configuration of the setup in the study. To this purpose, the following non-dimensional variables and parameters are introduced:

$$\begin{aligned} &x=\frac{{\bar{x}}}{L},\, y=\frac{{\bar{y}}}{L},\, t=\frac{\alpha _{f} {\bar{t}}}{L^2},\, u=\frac{{\bar{u}}L}{\alpha _{f}},\, v=\frac{{\bar{v}}L}{\alpha _{f}},\, \theta =\frac{T-T_l}{T_h-T_l},\, p=\frac{{\bar{p}}L^2}{\rho _{nf}\alpha _{f}^2},\nonumber \\&\quad Ra_{T} = \frac{g(\beta _T)_{f}\left( T_h-T_c\right) L^{2n+1}}{\nu _f{\alpha _f}^{n}},\quad Pr = \frac{\nu _f}{\alpha _{f}^{2-n}L^{2n-2}},\quad Da = \frac{K}{L^2} \end{aligned}$$

(19)

where u and v represent the non-dimensional velocities of the flow along with the non-dimensional x and y directions. The quantities $\nu _{f}$, $\alpha _{f}$ represents the kinematic viscosity and the thermal diffusivity of the base fluid. Employing the above dimensionless variables, the non-dimensional form of the effective viscosity yields

$$\begin{aligned} \mu _{eff}=\frac{\mu _{f}}{(1-\phi )^{2.5}} \left( \frac{\alpha _{f}}{L^2}\right) ^{n-1} |{\dot{\gamma }}|^{n-1} \end{aligned}$$

(20)

where $|{\dot{\gamma }}|$ represents the magnitude of the shear-rate in non-dimensional form as defined by,

$$\begin{aligned} |{\dot{\gamma }}| = |\bar{{\dot{\gamma }}}|/ \left( \frac{\alpha _{f}}{L^2}\right) =\sqrt{2\left( \frac{\partial u}{\partial x}\right) ^2+2\left( \frac{\partial v}{\partial y}\right) ^2+\left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) ^2} \end{aligned}$$

(21)

To overcome the infinite viscosity at rest and zero viscosity in the limits of infinite shear rate, a modified power-law viscosity model is given by [46],

$$\begin{aligned} \mu _{eff}=\frac{\mu _{f}}{(1-\phi )^{2.5}} \left( \frac{\alpha _{f}}{L^2}\right) ^{n-1} D \quad \text{ where } \quad D= \left\{ \begin{array}{ll} 1&{} {\text {if}}\; |{\dot{\gamma }}| < \gamma _1 \\ \left| {\dot{\gamma }}\right| ^{n-1}&{} {\text {if}}\; \gamma _1 \le \left| {\dot{\gamma }}\right| \le \gamma _2 \\ \left| \gamma _2\right| ^{n-1}&{} {\text {if}}\;\left| {\dot{\gamma }}\right| > \gamma _2 \\ \end{array}\right. . \end{aligned}$$

(22)

Here, the constants ${\gamma }_1=10^{-6}$ and ${\gamma }_2=10^5$ are considered to impose shear rate thresholds. Note that, the viscosity is assumed to be constant outside the threshold limit of the shear rate.

By employing Eq. 19 into Eqs. 2–5, the following system of non-dimensional governing equations are derived,

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(23)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y} = -\frac{\partial p}{\partial x} +\frac{Pr}{\left( 1-\phi \right) ^{2.5}\rho _{nf}^{*}}\left[ \frac{\partial }{\partial x}\left( 2D\frac{\partial u}{\partial x}\right) +\frac{\partial }{\partial y}\left( D\frac{\partial u}{\partial y}\right) +\frac{\partial }{\partial y}\left( D\frac{\partial v}{\partial x}\right) -\frac{uD}{Da}\right]$$

(24)

$$\begin{aligned} \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} & = -\frac{\partial p}{\partial y}+\frac{Pr}{(1-\phi )^{2.5}\rho _{nf}^{*}}\left[ \frac{\partial }{\partial y}\left( 2D\frac{\partial v}{\partial y}\right) +\frac{\partial }{\partial x}\left( D\frac{\partial u}{\partial y}\right) +\frac{\partial }{\partial x}\left( D\frac{\partial v}{\partial x}\right) -\frac{vD}{Da}\right] +Pr Ra_{T}\frac{(\beta _{T})_{nf}}{(\beta _{T})_{f}}\theta \end{aligned}$$

(25)

$$\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x} +v\frac{\partial \theta }{\partial y} = \frac{\alpha _{nf}}{\alpha _{f}}\left( \frac{\partial ^2 \theta }{\partial x^2}+\frac{\partial ^2 \theta }{\partial y^2}\right)$$

(26)

where, $\rho _{nf}^{*}=\frac{\rho _{nf}}{\rho _{f}}$ is the density ratio between nanofluid to base fluid. The non-dimensional parameters Pr, $Ra_{T}$, and Da denotes the Prandtl number of the base fluid, Rayleigh number of thermal expansion, and Darcy number of the porous medium, respectively. The non-dimensional boundary conditions associated with Eqs. 23–26 take the following form:

$$\begin{aligned} \text {when} \quad t=0, \quad u=v=\theta =0 \qquad \forall \, x, y \end{aligned}$$

(27)

when $t>0$,

$$\begin{aligned} u= & {} v=0, \theta =1 \quad \text {on left wavy wall:} \, x_{L} \nonumber \\= & {} -\frac{1}{2}\left[ 1- 2a\cos \left( 2\pi y\right) \right] ,\quad 0\le y\le A \end{aligned}$$

(28)

$$\begin{aligned} u= & {} v=0, \theta =0 \quad \text {on right wavy wall:} \, x_{R} \nonumber \\= & {} \frac{1}{2}\left[ 1- 2a\cos \left( 2\pi y\right) \right] ,\quad 0\le y\le A \end{aligned}$$

(29)

$$\begin{aligned} u= & {} v=\frac{\partial \theta }{\partial y}=0 \quad {\text {on bottom }} \& {\text{ top wall:}} \,\nonumber \\ y= & {} 0 \, \& \, A, \quad -\frac{1}{2}\left( 1-2a\right) \le x\le \frac{1}{2}\left( 1-2a\right) \end{aligned}$$

(30)

2.6 Local Nusselt number and average Nusselt number

The physical quantity such as the rate of heat transfer along the hot wavy wall in non-dimensional form is evaluated in terms of the local Nusselt number given by,

$$\begin{aligned} Nu=-\frac{k_{nf}}{k_{f}}\left( \frac{\partial \theta }{\partial \varvec{n}}\right) . \end{aligned}$$

(31)

where $\varvec{n}$ is the normal surface vector to the hot wavy wall. The average of the local Nusselt number along the hot undulating wall is given by,

$$\begin{aligned} {\overline{Nu}}=-\frac{1}{L_w}\int _0^{L_{w}} \frac{k_{nf}}{k_{f}}\left( \frac{\partial \theta }{\partial \varvec{n}}\right) ~\text {d}y, \end{aligned}$$

(32)

where $L_w$ is the length of the hot wavy wall.

2.7 Entropy generation

From the perspective of the second law of thermodynamics, each real-life heat transfer processes involve a change of entropy due to the irreversibility of the natural processes. Entropy is the qualitative presentation of the loss of work/energy in any natural phenomenon, and in heat transfer processes, it is comprehended as the finite difference in temperature [48]. In the natural convection heat transfer process, fluid flow friction and heat transfer mechanism contribute to the change of entropy [49]. For the laminar, incompressible non-Newtonian nanofluid flow, the local entropy balance equation comprises two groups of entropy generation terms based on the linear transport theory from the local thermodynamic equilibrium, and they are,

• ${\bar{S}}_{{F}}:$ Entropy generation due to fluid friction, also known as viscous irreversibility.

• ${\bar{S}}_{{T}}:$ Entropy generation due to heat transfer, also known as heat transfer irreversibility.

The dimensional form of fluid friction and heat transfer irreversibility for non-Newtonian nanofluid flow in a porous enclosure is given by,

$$\begin{aligned} &{\bar{S}}_{F}=\frac{\mu _{nf}}{T_{0}K}\left[ {\bar{u}}^2+{\bar{v}}^2\right] \\&\qquad +\frac{\mu _{nf}}{T_{0}}\left[ 2\left( \frac{\partial {\bar{u}}}{\partial {\bar{x}}}\right) ^2+2\left( \frac{\partial {\bar{v}}}{\partial {\bar{y}}}\right) ^2+\left( \frac{\partial {\bar{u}}}{\partial {\bar{y}}} + \frac{\partial {\bar{v}}}{\partial {\bar{x}}}\right) ^2\right] \\&\quad {\bar{S}}_{T}= \frac{k_{nf}}{T_{0}^{2}}\left[ \left( \frac{\partial {\bar{T}}}{\partial {\bar{x}}}\right) ^{2} + \left( \frac{\partial {\bar{T}}}{\partial {\bar{y}}}\right) ^{2} \right] . \\ \end{aligned}$$

(33)

Employing the transformation listed in Eq. 19 and using the typical characteristic scale $\frac{T_{0}^2 L^2}{k_{f} (\varDelta T)^2}$ [50], the dimensionless viscous irreversibility and heat transfer irreversibility is obtained by,

$$\begin{aligned} &S_{F} = \frac{T_{0}^2 L^2}{k_{f} (\varDelta T)^2} {\bar{S}}_{F} \\&\quad = \frac{ \lambda D}{(1-\phi )^{2.5}} \left[ \frac{u^2+v^2}{Da}+ 2\left( \frac{\partial u}{\partial x}\right) ^2+2\left( \frac{\partial v}{\partial y}\right) ^2+\left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right) ^2\right] \\&\quad S_{T} = \frac{T_{0}^2 L^2}{k_{f} (\varDelta T)^2} {\bar{S}}_{T} = \frac{k_{nf}}{k_{f}} \left[ \left( \frac{\partial \theta }{\partial x}\right) ^{2} + \left( \frac{\partial \theta }{\partial y}\right) ^{2} \right] \end{aligned}$$

(34)

where the parameter $\lambda = \frac{T_{0} \mu _{f} \alpha _{f}^{n+1}}{k_{f} (\varDelta {T})^2 L^{2n}}$ is termed as the irreversibility distribution ratio [51] for non-Newtonian nanofluid, which is defined by the ratio between viscous irreversibility to heat transfer irreversibility [52]. The local entropy generation rate ${S}_{L}$ (also called by total irreversibility) is the sum of both irreversibilities, i.e.,

$$\begin{aligned} ~ \begin{aligned} S_{L} = S_{F} + S_{T}&= \frac{ \lambda D}{(1-\phi )^{2.5}} \left[ \frac{u^2+v^2}{Da}+ 2\left( \frac{\partial u}{\partial x}\right) ^2 \right. \\&\quad +2 \left. \left( \frac{\partial v}{\partial y}\right) ^2+\left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\right) ^2\right] \\&\quad + \frac{k_{nf}}{k_{f}} \left[ \left( \frac{\partial \theta }{\partial x}\right) ^{2}+ \left( \frac{\partial \theta }{\partial y}\right) ^{2} \right] \\ \end{aligned} \end{aligned}$$

(35)

The Bejan number (Be), a dimensionless parameter defined as the ratio between heat transfer irreversibility to total irreversibility, i.e.,

$$\begin{aligned} Be_{L} =\frac{S_{T}}{S_{L}}= \frac{S_{T}}{S_{F}+S_{T}}. \end{aligned}$$

(36)

Based on the numerical value of Be, the dominance of heat transfer irreversibility and viscous irreversibility is inferred by $Be > 0.5$, and $Be < 0.5$, respectively. Numerical integration of the above irreversibilities over the entire domain produces the corresponding total quantity, and they are,

$$\begin{aligned} S_{F,T}= & {} \int _{0}^{A}\int _{0}^{1} S_{F} \,\text {d}x\,\text {d}y \, , \quad S_{T,T} = \int _{0}^{A}\int _{0}^{1} S_{T} \,\text {d}x\,\text {d}y \, ,\nonumber \\ \quad S_{L,T}= & \int _{0}^{A}\int _{0}^{1} S_{L}\,\text {d}x\,\text {d}y. \end{aligned}$$

(37)

3 Numerical method and code validation

3.1 Governing equations in curvilinear coordinates ($\xi$, $\eta$)

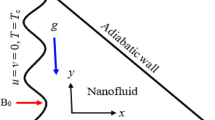
In the present study, body-fitted non-orthogonal grids are required to simplify the utilized numerical technique for the simulation purpose. In this regard, two independent new variables $\xi$ and $\eta$ are introduced in terms of the variables x and y by,

$$\begin{aligned} ~ \xi =\frac{x-x_L}{x_R-x_L}, \quad \eta =y. \end{aligned}$$

(38)

Using the above transformations, the physical domain (Fig. 1a) in the xy-plane is transformed into a rectangular domain (Fig. 1b) in the computational space $\xi \eta$-plane where the computational domain is defined by $0 \le \xi \le 1$ and $0 \le \eta \le A$. Note that the left and right wavy walls in the physical domain become coordinate lines $\xi =0$ and 1, respectively, in the $\xi \eta$-plane. Taking into account the transformation Eq. 38, the governing Eqs. 23−26 are transformed into the following form,

$$\begin{aligned}\frac{1}{|J|}\Big (A_{11}u_{\xi }+A_{12}u_{\eta }+A_{21}v_{\xi }+A_{22}v_{\eta }\Big ) = 0 \end{aligned}$$

(39)

$$u_{t}+\frac{1}{|J|}(u A_{11}+v A_{21})u_{\xi }+\frac{1}{|J|}\left( u A_{12}+v A_{22}\right) u_{\eta } =-\frac{1}{|J|}\left( A_{11}p_{\xi }+A_{12}p_{\eta }\right) +\frac{Pr}{\left( 1-\phi \right) ^{2.5}\rho _{nf}^{*}}\frac{1}{\left| J\right| ^{2}} \Bigg (A_{11}^2 \left( 2D u_{\xi }\right) _{\xi } + 2A_{11} A_{12} \left( 2D u_{\eta }\right) _{\xi } + A_{12}^2 \left( 2D u_{\eta }\right) _{\eta } + A_{21}^2 \left( D u_{\xi }\right) _{\xi } + 2 A_{21} A_{22} \left( D u_{\eta }\right) _{\xi } + A_{22}^2 \left( D u_{\eta }\right) _{\eta } + A_{11} A_{21} \left( D v_{\xi } \right) _{\xi } + A_{11} A_{22} \left( D v_{\xi } \right) _{\eta } + A_{12} A_{21} \left( D v_{\eta }\right) _{\xi } + A_{12} A_{22} \left( D v_{\eta }\right) _{\eta } - \frac{uD}{Da} \Bigg )$$

(40)

$$v_{t}+\frac{1}{|J|}(uA_{11}+vA_{21})v_{\xi }+\frac{1}{|J|}(uA_{12}+vA_{22})v_{\eta }=-\frac{1}{|J|}(A_{21}p_{\xi }+A_{22}p_{\eta }) +\frac{Pr}{\left( 1-\phi \right) ^{2.5}\rho _{nf}^{*}}\frac{1}{\left| J\right| ^{2}} \Bigg (A_{11}^2 \left( D v_{\xi }\right) _{\xi } \qquad + 2A_{11} A_{12} \left( D v_{\eta }\right) _{\xi } + A_{12}^2 \left( D v_{\eta }\right) _{\eta } + A_{11} A_{21} \left( D u_{\xi }\right) _{\xi } + A_{12} A_{21} \left( D u_{\xi }\right) _{\eta } + A_{11} A_{22} \left( D u_{\eta }\right) _{\xi } + A_{12} A_{22} \left( D u_{\eta }\right) _{\eta } + A_{21}^2 \left( 2D v_{\xi }\right) _{\xi } \qquad + 2 A_{21} A_{22} \left( 2D v_{\eta }\right) _{\xi } + A_{22}^2 \left( 2D v_{\eta }\right) _{\eta }- \frac{vD}{Da} \Bigg ) \qquad +Pr Ra_{T}\frac{(\beta _T)_{nf}}{(\beta _T)_{f}}\theta$$

(41)

$$\theta _{t}+\frac{1}{|J|}(uA_{11}+vA_{21})\theta _{\xi } +\frac{1}{|J|}(uA_{12}+vA_{22})\theta _{\eta }= \frac{\alpha _{nf}}{\alpha _f}\frac{1}{\left| J\right| ^{2}} \Bigg ((A_{11}^2+A_{21}^2)\theta _{\xi \xi } +(A_{12}^2+A_{22}^2)\theta _{\eta \eta } +2(A_{11}A_{12}+A_{21}A_{22})\theta _{\xi \eta }\Bigg )$$

(42)

where $A_{11}=y_{\eta }$, $A_{12}=-y_{\xi }$, $A_{21}=-x_{\eta }$, $A_{22}=x_{\xi }$ and |J| is the Jacobian of the above transformation Eq. 38. Subscript $\xi$ and $\eta$ indicate the partial derivative corresponding to $\xi$ and $\eta$ direction. In the above equations, the dimensionless fluid viscosity D in $(\xi ,\eta )$ coordinate system is given by,

$$\begin{aligned} D &= \Bigg [\frac{2}{\left| J\right| ^{2}} \left( A_{11} u_{\xi } + A_{12} u_{\eta } \right) ^{2} + \frac{2}{\left| J\right| ^{2}} \left( A_{21} v_{\xi } + A_{22} v_{\eta } \right) ^{2} \\&\quad + \frac{1}{\left| J\right| ^{2}}\Big (A_{21} u_{\xi } + A_{22} u_{\eta } + A_{11} v_{\xi } + A_{12} v_{\eta }\Big )^{2}\Bigg ]^{\frac{n-1}{2}}\\ \end{aligned}$$

(43)

The boundary conditions associated with Eqs. 39–42 can be written as

$$\text {when} \quad t=0, \quad u=v=\theta =0 \quad \forall \xi , \eta$$

(44)

$$\begin{aligned}&\text {when} \quad t>0 \left\{ \begin{array}{ll} u=v=0, \theta =1 &{}\quad {\text {for}}\; \quad \xi =0, \quad \text {and} \quad 0\le \eta \le A \\ u=v=0, \theta =0 &{}\quad {\text {for}}\;\quad \xi =1, \quad \text {and} \quad 0\le \eta \le A \\ u=v=\theta _{\eta }=0 &{}\quad {\text {for}}\;\quad 0\le \xi \le 1, \quad \text {and} \quad \eta =0,A \\ \end{array}\right. \end{aligned}$$

(45)

The physical interest of the heat transfer rate from the hot wall is determined in terms of the local Nusselt number (Nu) and the average Nusselt number ${\overline{Nu}}$ given by,

$$Nu = -\frac{k_{nf}}{k_{f}}\left[ \delta \left( \frac{\partial \theta }{\partial \xi } \right) \right] _{\xi =0} \quad \text {and} \quad {\overline{Nu}}= \frac{1}{L_w}\int ^{L_{w}}_0 Nu(\eta ) \, \text {d}\eta$$

(46)

where $\delta =\left( \sqrt{A_{12}^2+A_{22}^2}\right) /|J|$. In the computational domain, the fluid friction irreversibility ($S_F$) and the heat transfer irreversibility ($S_T$) can be written as,

$$\begin{aligned}&S_{F} = \frac{ \lambda D}{(1-\phi )^{2.5}} \Bigg [\frac{u^2+v^2}{Da}+ \frac{2}{\left| J\right| ^{2}} \left( A_{11} u_{\xi } + A_{12} u_{\eta } \right) ^{2} + \frac{2}{\left| J\right| ^{2}} \left( A_{21} v_{\xi } + A_{22} v_{\eta } \right) ^{2} \nonumber \\&\quad + \frac{1}{\left| J\right| ^{2}}\Big (A_{21} u_{\xi } + A_{22} u_{\eta } + A_{11} v_{\xi } + A_{12} v_{\eta }\Big )^{2}\Bigg ] \end{aligned}$$

(47)

$$\begin{aligned}&\quad S_{T} = \frac{k_{nf}}{k_{f}} \frac{1}{\left| J\right| ^{2}} \left[ \left( A_{11} \theta _{\xi }+A_{12} \theta _{\eta } \right) ^{2} + \left( A_{21} \theta _{\xi }+A_{22} \theta _{\eta } \right) ^{2} \right] \end{aligned}$$

(48)

Therefore, the total quantity of fluid-friction irreversibility ($S_{F,T}$), heat transfer irreversibility ($S_{T,T}$), local entropy generation rate ($S_{L,T}$) in the computational domain is calculated by,

$$\begin{aligned} \begin{aligned}&S_{F,T} = \int _{0}^{A}\int _{0}^{1} S_{F} |J|\, \text {d}\xi \, \text {d}\eta \, , \\&\quad S_{T,T}= \int _{0}^{A}\int _{0}^{1} S_{T} |J|\,\text {d}\xi \, \text {d}\eta \, \\&\quad S_{L,T}= \int _{0}^{A}\int _{0}^{1} \left( S_{F}+S_{T}\right) |J|\,\text {d}\xi \, \text {d}\eta \\ \end{aligned} \end{aligned}$$

(49)

3.2 Numerical procedure

The partial differential equations (PDEs) Eqs.  39–42 subject to the boundary conditions Eqs. 44–45 are solved using an implicit finite volume method. In the finite volume methods, the PDEs are discretized over a collocated grid arrangement. In this approach, the solution domain is divided into a finite number of control volumes (CV). A non-uniform grid spacing has been generated utilizing a hyperbolic tangent function, so that dense meshes appear near the walls and coarser meshes are produced in the core region (Fig. 1). By using this grid arrangement, the boundary layer characteristics can be captured very well, and higher accuracy in the overall numerical simulation can be achieved. In a 2-D finite volume method, each control volume maintains four faces (north, west, south, and east) and one central node where the flow variables are calculated [53]. The mass fluxes are calculated at cell faces using linear interpolation on the neighboring nodal values. The differential equations are integrated over each control volume yields a discretized equation at each node. In order to discretize, a three-point backward difference scheme for time derivative constant time steps $\varDelta t= 10^{-5}$, and the central difference scheme for the convective and diffusive terms has been employed. The detailed description of the numerical procedure can be found in [54, 55].

An in-house FORTRAN code is used to simulate the above mentioned numerical procedure with double precision and second-order accuracy in both space and time. A time-marching pressure correction algorithm is formulated using the Semi-Implicit Method for Pressure Linked Equation Revised (SIMPLER) algorithm of Patankar [56]. At each time step, the pressure field is updated by solving a Poisson type pressure correction equation using an incomplete Cholesky-conjugate gradient method (ICCGM) [57]. Rhie and Chow [58] interpolation is used to ensure strong pressure-velocity coupling. A Bi-Conjugate gradient Stabilized (Bi-CGSTAB) [59] solver has been used to solve the linear system of discretized equations in velocities (u, v) and temperature $(\theta )$. The simulation procedure maintains iterations until the residual tolerance is less than or equal to $10^{-6}$ for all the variables (i.e., $u,v,\theta$). This code is used for the several studies on the non-Newtonian fluids with irregular shape geometric models [60,61,62].

3.3 Grid independence test

A grid independence test is performed for numerical analysis to establish the expected solution independent of grid size. Three different grid sizes of $41\times 81$, $81\times 161$ and $161\times 321$ are considered for the test. The numerical results for the average Nusselt number $(Nu_{avg})$ along the left wall for each of the grid sizes is presented in Table 2. Results are tabulated for both Newtonian ($n=1.0$), and non-Newtonian ($n=0.7,1.4$) nanofluids ($\phi =0.05$) where the other governing parameters fixed at $Pr=6.2$, $Ra=10^{5}$ and $Da=10^{-2}$. It is evident from the Table that the percentage change in the average Nusselt number is less than $3\%$ in our test for different grid sizes. Therefore, the non-uniform grid size $81\times 161$ is chosen to conduct all simulations present in this study to ensure an optimum balance between the computational time and high accuracy.

Table 2 Grid independence test for $A=2.0, a=0.5, Pr=6.2, Ra=10^{5}, Da=10^{-2}, \phi =0.05$

3.4 Validation of numerical code

To validate the numerical code of the present study, the simulation results are first compared for the non-Newtonian pure fluids with results published by Turan et al. [17]. The comparison is made for the parameters $A=1.0$, $a=\phi =0.0$, $Pr=100$, $Ra = 10^6$, and $n=0.2,1.0,1.8$ and shows a very good agreement with the published results as shown in Table 3. Another comparison for Newtonian nanofluid within the wavy enclosure has been established with M. Esmaeilpour and M. Abdollahzadeh [49] with the pertinent parameters $A=2.0$, $a=0.25$, $n=1.0$, $Pr=6.2$(water), $Ra=Gr \times Pr$ where $Gr=10^4, 10^5$ for different volume fractions $\phi =0.00,0.05,0.10$ of Cu–Water nanofluid. Figure 2 shows that present results for isotherms are qualitatively in excellent agreement with the previous reports . Furthermore, a comparison of average Nusselt number (${\overline{Nu}}$) for the case of porous medium is presented in Table 4 for different values of Darcy number (Da) and Rayleigh number (Ra). The test shows very good agreement between the present results and the results reported by Lauriat and Prasad [63], and by Mchirgui et al. [51].

Fig. 2

Comparison for isotherms between a present study and b [49] for wavy enclosure ($a=0.25, A=2.0$) while $Pr=6.2$; $Gr = 10^4$ (left panel), $10^5$ (right panel); $\phi =0.00$ (solid line), 0.05 (dash line), 0.10 (dash-dot line)

Table 3 Comparison of the average Nusselt number $({\overline{Nu}})$ between present results and the result published by Turan et al. [17]

Table 4 Comparison between present results and results in Lauriat and Prasad [63] and by Mchirgui et al. [51]for average Nusselt number (${\overline{Nu}}$) where $A=1.0, a=0.0, Pr=1.0, n=1.0, \phi =0.0$

For entropy generation, to validate the numerical simulation, another comparison is performed with the previously published result from [52] for square geometry. The comparison is graphically presented in Fig. 3. The figure shows an excellent agreement of the present result for $S_{F}$, $S_{T}$, $S_{L}$, and Be with the previously published result for the same configuration.

Fig. 3

Comparison between a present study and b [52] for square geometry ($a=0, A=1.0$) while $Pr=0.7$ (air), $Ra = 10^5$, $\phi =N=0.0$ and $\lambda =10^{-4}$

4 Results and discussion

The present numerical study is aimed to investigate the flow physics and heat transfer phenomena of Non-Newtonian nanofluids in a rectangular porous wavy enclosure. For flow geometry, the pertinent parameters are $A=2.0, a=0.25$ and $N=1.0$. The governing parameters to investigate the flow field and heat transfer phenomena are chosen in the following range: $0.7 \le n \le 1.4$, $0 \le \phi \le 0.1$, $10^3 \le Ra \le 10^5$, $10^{-4} \le Da \le 10^{-1}$ and $Pr = 6.2$ (water). Besides, the irreversibility distribution ratio is considered by $\lambda =10^{-6}$ as like Ali et al. [51] to explore the entropy generation rate inside the porous enclosure. The following sections present the effects of the above parameters on the flow field and temperature field in terms of the streamlines and isotherms, the velocity profile along the line $y=1.0$, the local Nusselt number (Nu) and the average Nusselt number (${\overline{Nu}}$) at the left wavy wall. The total and local entropy generation rate has also been discussed for the different values of the pertinent parameters.

4.1 Effect of Rayleigh number on streamlines and isotherms of non-Newtonian nanofluids

Figure 4 displays the effect of Rayleigh number (Ra) on the streamlines feature of shear-thinning ($n=0.7$), Newtonian ($n=1.0$) and shear thickening ($n=1.4$) nanofluids of different volume fractions. In each image of the figure, the dotted lines, dashed lines and solid lines represent $0 \%$, $5 \%$ and $10 \%$ volume fraction of nanofluids.

Fig. 4

Streamlines for volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (left panel), $n=1.0$ (middle panel), $n=1.4$ (right panel), $Da=10^{-2}$ and a $Ra=10^3$, b $Ra=10^4$, and c $Ra=10^5$

Results show that, for a given value of n, the contour size of streamlines gets larger, and the boundary layer thickness gets reduced with an increase in the values of Ra. Also, increasing Ra leads to an increase in stream function’s magnitude at every location inside the enclosure. It has happened because the buoyancy-induced flow gets stronger when Ra is increased. As a result, the streamlines are concentrated near the wavy walls for higher values of Ra. Regardless of the value of Ra, the sparse appearance of streamlines at the central region indicates the lower gradient of the stream function, resulting in a slow fluid domain. The core region of the vortex shape changes from the vertical-elliptical shape to the horizontal-dumble shape, increasing the values of Ra. For the value of $Ra=10^3$, the buoyancy induced flow has less energy, and the corresponding stream function value gets the lowest. At $Ra=10^5$, the primary vortex in the central region splits into two small secondary vortices, and they move near the wavy walls in the crest region. The phenomenon indicates an increased concentration of energy in the central region.

For a given value of Ra, the flow becomes stronger for shear-thinning fluids ($n=0.7$), where the apparent viscosity is lesser than Newtonian fluids ($n=1.0$). An increase in the power-law index leads to reduce the contour size of the streamlines and increase the boundary layer thickness. The magnitude of stream function at any location decreases with increasing the power-law index (n). As we can see from the color legend, the maximum value of the stream function decreases with an increment in n. For shear-thickening fluids $(n=1.4)$, the apparent viscosity between fluid molecules becomes higher than the Newtonian viscosity ($n=1.0$). As a result, the flow gets weaken, the boundary layer becomes thickening, and the value of the stream function decreases. For a shear-thickening fluid at $n=1.4$, the flow at the center of the cavity follows an elliptic shaped steady flow for all values of Ra compared to shear-thinning $(n=0.7)$ and Newtonian (1.0) fluid.

Added volume of nanoparticle in the base fluid brought about visibly distinct effect. The contour size of the stream function is inversely proportionate to the volume fraction $(\phi )$ of nanoparticles. It becomes apparent when a representative contour label is displayed in each image. It is worth being mentioned that with an addition of nanoparticles suspended with a base fluid, the effective thermal expansion coefficient becomes lower, which lowers the buoyancy induced force. Therefore, an increase in the volume fraction reduces the strength of the flow hence the contour size. Increasing the volume fraction also increases the boundary layer thickness. For the values of $Ra=10^3,10^4$, the cell size becomes reduced with an increase of $\phi$. However, at $Ra=10^5$ and for $n=0.7, 1.0$, the shape of the contours becomes different, and the contour size is increasing with $\phi$.

Figure 5 presents the isothermal distribution for different values of Ra with the parameter settings identical to the Fig. 4. An increase in Ra increases the dominance of convective heat transfer inside the porous enclosure as the buoyancy-induced flow becomes enhanced. The feature is observed by looking into the shape of the isotherms. At $Ra= 10^3$, the isotherms become parallel to the vertical wavy walls, which suggest that convective heat transfer does not take placed yet, and a negligible effect of non-Newtonian nanofluids is observed. Instead, the conduction heat transfer processing is active inside the cavity. At $Ra=10^4$, the vertical lines are getting inclined to the horizontal direction, which indicates the commencement of the convection heat transfer processing inside the porous cavity. Further increasing the value of Ra, at $Ra=10^5$, the horizontally stratified isotherms clearly show the dominance of the convective heat transfer process. For a given n, increasing Ra leads to a decrease in the thickness of the thermal boundary layer and increases the concentration of isotherms near the wavy walls.

Fig. 5

Isotherms for volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (left panel), $n=1.0$ (middle panel), $n=1.4$ (right panel), $Da=10^{-2}$ and a $Ra=10^3$, b $Ra=10^4$, and c $Ra=10^5$

For a non-Newtonian nanofluid into consideration, the apparent viscosity plays an additional significant role in the convective heat transfer process. Results show that, for a given Ra, the dominance of convective heat transfer is reverse complemented by an increase in the power-law index value. For higher values of $Ra=10^4,10^5$, shear-thinning fluids $(n=0.7)$ show the strong dominance of convective heat transfer at this parameter settings. At $Ra=10^5$, horizontal stratification of isotherms is observed for the shear-thinning fluids in the central region of the wavy porous cavity. With increasing the power-law index n, the isotherms get vertically oriented, indicating a reduction of the convective heat transfer process as the fluid flow becomes weaken with increasing the apparent viscosity. Furthermore, the thermal boundary layer becomes thicker with an increment in the power-law index.

Adding nanoparticles in the base fluid leads to enhance the effective thermal conductivity of the mixture. The interaction between added nanoparticles and the non-newtonian characteristics of the nanofluid molecules influences the heat transfer pattern. Present results show that, in the wavy porous cavity, Cu–water nanofluids are less effective for lower values of $Ra=10^3$. Increasing Ra leads to augmenting the motion of Cu-nanoparticles, which results in an enhancement of convective heat transfer as the nanoparticles are highly thermally conductive. For a fixed value of Ra and n, the thermal boundary layer gets thicker with increasing the volume fractions ($\phi$), as we can observe in each image of the figure. Results show that isotherms for $\phi =0.1$ (solid lines) are curved more horizontally than the isotherms for $\phi =0.0$ (dotted lines) and $\phi =0.05$ (dashed lines). The feature is nicely observed for shear-thinning fluids. For shear-thinning fluids, nanofluids are highly mobile, and adding more nanoparticles increases the net heat transfer rate. For shear-thickening fluids, increasing volume fraction is observed for a higher value of $Ra=10^5$.

4.2 Effect of Darcy number on streamlines and isotherms of non-Newtonian nanofluids

In a porous medium flow, the Darcy number (Da) plays a vital role in representing the relative effect of medium permeability through its cross-sectional area. Besides, in the Brinkman-extended darcy model employed in the present study, the Darcy number stays together with the viscous term. Therefore, lowering Da leads to strengthening the viscous effect. Figure 6 shows the effect of Da on the feature of stream function for non-Newtonian nanofluids with different volume fractions $(\phi =0,0.05,0.10)$ at fixed $Ra=10^4$. Results show that, for any given n, a decrease in the values of Da leads to weakening the flow, which results in lowering the magnitude of stream function at any given location inside the porous enclosure. Indeed, decreasing Da leads to reduced buoyancy-induced flow as the fluid permeability through a cross-sectional area gets reduced; thus, the boundary layer becomes thicker gradually.

Fig. 6

Effect of Da on streamlines for volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (left panel), $n=1.0$ (middle panel) and $n=1.4$ (right panel) and $\hbox {Ra}=10^4$. In a $Da=10^{-2}$, b $Da=10^{-3}$ and c $Da=10^{-4}$

Similarly, for any given Da, the boundary layer becomes thicker progressively with an increase in the power-law index. The stream function value is also lessened as the viscous effect gets substantial, with an increase of n. Consequently, the contour cells of the wavy porous cavity are gradually reducing in size, and cells in the central region change their orientation from horizontal to vertical. However, for $Da=10^{-3}, 10^{-4}$, cells in the central region remains in the same orientation with increasing n, as the fluid flow gets restricted due to a substantial viscous effect and low porous permeability. Also, the stream function values consistently decrease with an increase in the power-law index.

Inside a porous cavity, the non-Newtonian nanofluids are highly effected by varying the volume fractions. For any given n and Da, the contour cell size gets reduced by increasing the volume fractions $\phi$. The effect is substantial in the central region compared to the boundary region of the porous cavity. Contour cells for large volume fraction $\phi =10\%$ always occupy less space in the central area of the cavity, representing slow fluid phenomena there. With an increase of volume fraction, the flow becomes more concentrated and stagnant.

Figure 7 shows the distribution of isothermal lines at different Darcy numbers for non-Newtonian nanofluids, where the Rayleigh number is fixed at $Ra=10^4$. Increasing Da leads to enhance the temperature gradient near the wavy walls. In other words, decreasing the value of Da leads to a breach of the convective heat transfer process. At $Da=10^{-2}$, the isothermal lines are bent towards the horizontal direction for shear-thinning fluids, which indicates the dominance of convective heat transfer over the conduction. With an increase in the power-law index value, the horizontal stratification becomes reduced, and so for heat convection. Three different volume fraction of nanoparticles produced distinctly visible isothermal lines. Shear-thinning fluids instantiated a lean thermal boundary layer and the consequent convective heat transfer is higher in magnitude. For $Da=10^{-3}$ and $10^{-4}$, the lines of isotherms are parallel to the wavy wall of the porous cavity. In this case, for lower values of Da, the convection process becomes reduced as the fluids are restricted to flow due to low permeability. The thermal boundary layer becomes thickening at these values of Da. At $\hbox {Da}=10^{-4}$, the negligible effect of the power-law index and volume fractions has been observed on the porous medium flow inside the wavy cavity.

Fig. 7

Effect of Da on isotherms for volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (left panel), $n=1.0$ (middle panel, $n=1.4$ (right panel) and $\hbox {Ra}=10^4$. In a $Da=10^{-2}$, b $Da=10^{-3}$ and c $Da=10^{-4}$

4.3 Variation of temperature profile along the mid-y line

Figure 8 shows the temperature distribution along the horizontal midline at $y=1.0$ inside the wavy-porous cavity for the pertinent parameters $Ra=10^3,10^4,10^5$, $Da=10^{-2},10^{-3},10^{-4}$, $n=0.7,1.0,1.4$ and $\phi =0.00,0.05,0.10$. As shown in Fig. 8a, for a lower value of $Ra=10^3$, the temperature distribution in the midline gets no effect from the non-Newtonian nanofluids with different volume fractions. Temperature is just decreasing linearly from the left wall to the right wall in this case. This phenomenon indicates the porosity’s strength and the weakening of the heat convection process along the mid-y line. For higher values of Ra in this case, the effect of non-Newtonian nanofluids becomes prominent. With increasing the power-law index, the temperature grows in the left half but reduces in the right half of the midline. A similar observation exists for increasing the volume fraction as well. For $Ra=10^4$, the non-linearity of decreasing temperature is observed for the shear-thinning fluids $(n=0.7)$, which indicates the existence of a convective heat transfer process along the midline. For Newtonian $(n=1.0)$ and shear-thickening fluids $(n=1.4)$, temperature decreases with a higher gradient than the shear-thinning fluids. For $Ra=10^5$, the non-linear phenomenon is observed for all types of fluids as the buoyancy force gets augmented. In this case, for shear-thinning and Newtonian fluids, temperature first decreases rapidly, maintains a constant temperature of $\theta =0.5$ for most of the part along the midline, and decreases rapidly to $\theta =0.0$.

Fig. 8

Temperature distribution along the horizontal mid-line (i.e. $y=1.0$) as function of Ra and Da for volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (red), $n=1.0$ (blue) and $n=1.4$ (magenta). In a $Da=10^{-2}$, b $Da=10^{-3}$ and c $Da=10^{-4}$

For lower values of $Da=10^{-3}$, the effect of the power-law index and volume fractions of nanofluids are less observed except the case $Ra=10^5$. Further decreasing the Darcy number to $Da=10^{-4}$, the negligible effect of power-law index and volume fractions are observed along the midline. However, further increasing Ra will strengthen the convection process along the mid-y line, and the effect of non-Newtonian nanofluids will be visible. It is worth being mentioned that the effect of non-Newtonian nanofluids gets prominent when the Darcy–Rayleigh number defined by $Ra^{*}=Ra \times Da \gg 10$.

4.4 Variation of Nusselt number and average Nusselt number along the hot wavy wall

Figure 9 presents the local Nusselt number (Nu) for non-Newtonian nanofluids along the hot wavy wall. The pertinent parameters for the investigations are Darcy number ($Da=10^{-2}$,$10^{-3}$,$10^{-4}$), Rayleigh number ($Ra=10^3$,$10^4$,$10^5$), power-law index ($n=0.7,1.0,1.4$) and volume fractions ($\phi$=0.0,0.05,0.10).

Fig. 9

Distribution of local Nusselt number (Nu) along the hot wavy wall for $\quad 10^3\le Ra\le 10^{5}$, $\quad 10^{-4}\le Da\le 10^{-2}$, $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines), power-law index $n=0.7$ (red), $n=1.0$ (blue) and $n=1.4$ (magenta). In a $Da=10^{-2}$, b $Da=10^{-3}$ and c $Da=10^{-4}$

In Fig. 9a, at $Ra=10^3$, the distribution of the local Nusselt number (Nu) along with the wall show near symmetric pattern for a given n and $\phi$. Nu becomes higher near the top and bottom end, i.e., in the trough region of the wavy wall. It is happened due to the low convective heat transfer process at low Rayleigh numbers. A closure view into the results shows that Nu increases with decreasing and increasing the power-law index in the lower and upper parts, respectively. More importantly, in this case, the volume fraction effect is more prominent than the power-law effect. With increasing the volume fractions, Nu increases along the hot wavy wall. However, with increasingRa, the power-law effect gets more prominent than the volume fraction effect. Besides, the symmetric pattern of Nu distribution along the hot wavy wall is broken when the Darcy–Rayleigh number $Ra^{*}=Ra \times Da\gg 10$. With increasing Ra, Nu gets augmented significantly at the bottom part but is degraded at the top part of the wavy wall. This phenomenon indicates the dominance of the convective heat transfer in the lower part of the hot wavy wall. It has happened because the buoyancy force is augmented with increasing Ra, resulting in an enhancement of the convective heat transfer process. Also, increasing Ra leads to an increase in the magnitude of the local Nusselt number. For $Da=10^{-2}$, Nu reached beyond 20 for $Ra=10^5$ in the lower part of the hot wavy-wall for shear-thinning $(n=0.7)$ nanofluids for all the volume fractions. Notwithstanding, Nu increases with increasing $\phi$ as adding nanoparticles leads to augmenting the thermal conductivity of nanofluids.

Figure 9b shows that for $Da=10^-3$ and $Ra=10^3$, the non-Newtonian fluids display no effect on the local Nusselt number, but the nanofluids effect is still persistent. In this case, the convective heat transfer process is negligible to consider, but the conductive heat transfer is noticeable. Similar to the Fig. 9a, when $Ra^{*}=Ra \times Da \le 10$, then the volume fraction effect is more prominent than the power-law effect and the distribution of the local Nusselt number (Nu) show the symmetric pattern. However, when $Ra^{*}=Ra \times Da \gg 10$, the symmetric pattern has lost, and the power-law effect becomes more prominent than the volume fraction effect. When $Ra=10^5$, the volume fraction has a negligible effect on Nu. In this case, although Ra is higher, due to the lower value of Da, the permeability gets reduced, and fluid flow becomes weakened. Further decreasing Da, as in Fig. 9c, the fluid flow becomes significantly weakened, hence the convective heat transfer gets reduced significantly. In this case, the non-Newtonian effect is only observed when $Ra=10^5$ for which $Ra^*=10$. It is worth mentioning that when $Ra^*=10$, with increasing the power-law index (n), Nu increases in the upper part but decreases in the lower part of the left wavy wall.

In Fig. 10, variations of the average Nusselt number (${\overline{Nu}}$) are illustrated for $10^3\le Ra\le 10^5$, $10^{-4}\le Da\le 10^{-2}$, $0.7\le n\le 1.4$ and $0.0\le \phi \le 0.1$. It is apparent from the results that when the porosity is high, i.e., $Da=10^{-2}$, the average Nusselt number gets augmented with the values of Ra and also exhibit proportionate enhancement in value with the volume fractions $(\phi )$ as well as the power-law index (n). For $Da=10^{-2}$ and $Ra=10^3$, the power-law index show less significant effect than the volume fraction on the enhancement of ${\overline{Nu}}$. However, when Ra get higher, and the convection becomes dominant, the power-law effect emerges significantly than the volume fraction effect. Maximum enhancement of ${\overline{Nu}}$ with Ra is always obtained for the shear-thinning fluids $(n=0.7)$, irrespective of the Darcy number. Results show that the average rate heat of transfer (${\overline{Nu}}$) from the hot wavy wall decreases with decreasing Da as the medium becomes less porous, and the viscous effect gets stronger with the lower value of Da.

Fig. 10

Variation of average Nusselt number $({\overline{Nu}})$ as a function of Rayleigh number (Ra) for $Da=10^{-2}$ (left panel), $Da=10^{-3}$ (middle panel), and $Da=10^{-4}$ (right panel); power-law index $n=0.7$ (red), $n=1.0$ (blue) and $n=1.4$ (magenta) at different volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.10$ (solid lines)

For $Da=10^{-3}$, volume fraction effect becomes prominent on the average Nusselt number for $Ra=10^{3}, 10^4$ but negligible for $Ra=10^5$. This feature suggests that the viscous effect gets stronger at the low porosity condition than the buoyance effect even for larger values of Ra. Furthermore, for the shear-thickening fluids ($n=1.4$) with a higher viscosity than the Newtonian fluids ($n=1.0$), minor enhancement of ${\overline{Nu}}$ is observed with increasing Ra. With further decreasing the values of Da, the fluid’s porosity becomes lower as well as the fluid permeability. As a result, the flow becomes least mobilized, and the convective heat transfer becomes less significant even for higher values of Ra inside the wavy porous cavity. Besides, for shear thickening fluids ($n=1.4$) when the viscosity of the fluid gets higher than the Newtonian viscosity, no variation on ${\overline{Nu}}$ is observed with increasing Ra. However, for the shear-thinning fluids ($n=0.7$), the viscosity of the fluid is lower than the Newtonian viscosity, ${\overline{Nu}}$ is increasing with increasing Ra. Results in Fig. 10 suggests that when $Ra^{*}=Ra\times Da \gg 10$, then non-Newtonian effect becomes prominent.

4.5 Entropy generation and relative dominance of local entropy generation factors

In this section, the local entropy generation ($S_{L}$), and the local Bejan number (Be) has been investigated for non-Newtonian nanofluids with the variation of pertinent parameters, namely Rayleigh number (Ra), Darcy number (Da), power-law index (n) and volume fractions ($\phi$). The local entropy generation ($S_{L}$) is evaluated summing up the local entropy generation due to fluid friction ($S_{F}$) and heat transfer ($S_{T}$).

Figure 11 shows the contours of the local entropy generation ($S_{L}$) inside the porous cavity for different Darcy number ($10^{-4}\le Da\le 10^{-2}$) with $Ra=10^5$, $n=0.7,1.0,1.4$, and $\phi =0.0,0.05,0.1$. Interestingly, the contour graphs of the local entropy generation show a rotationally symmetric pattern about the center of the cavity for all combinations of n and Da. For all three cases of Da and n, contour lines are densely appeared in the bottom-left and top-right corner of the porous enclosure, apprehending the highest rate of temperature difference in those regions. The increase of Darcy number leads to expand the contours along with the side walls. The contours of the entropy generation align more with the hot wall and cold wall with increasing Darcy number and also increases the value of entropy generation. On the other hand, the entropy generation rate decreases with an increase in power-law indexes.

Fig. 11

The Total Local Entropy Generation $S_{L}$ for different volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines) and power-law indexes at $n=0.7$ (left panel), $n=1.0$ (middle panel), $n=1.4$ (right panel), and $\hbox {Ra}=10^5$. In a $Da=10^{-2}$, and b $Da=10^{-3}$

For a given Da, the entropy generation rate is observed to be significantly higher for shear-thinning fluids $(n=0.7)$, followed by Newtonian fluid. The value is significantly low for shear-thickening fluid $(n=1.4)$. At $Da=10^{-2}$, contours are highly concentrated along the hot and cold walls of the enclosure. The entropy generation value for shear-thinning fluid reached $S_{L}=420$, making it the highest entropy generation for all three porosity cases with $Ra=10^5$. This maximum value appears near the bottom left and the top right corner of the sidewalls, closer to the adiabatic walls. With power-law index, the maximum value gradually decreases for Newtonian fluid $(n=1.0)$ at 120 and shear-thickening fluid $(n=1.4)$ at 32. The local entropy generation near the wavy walls gets reduced, and the contour distributions get sparsed with increasing the power-law index. The contour graphs get closer inside the cavity by increasing the volume fractions of nanofluids.

At $Da=10^{-3}$, the contour graphs of entropy generation show a more dispersed pattern within the enclosure. For shear-thinning fluids and Newtonian fluids, the contour graphs show a similar pattern as in $Da=10^{-2}$, i.e., two parts-one along the hot wavy wall and other along the cold wavy wall. However, the curves disperse more towards the center. For shear-thickening fluids, the restricted flow within the enclosure produces a lower entropy generation in the whole domain and hence at the bottom-left and top-right corners. Nevertheless, the highest entropy values are concentrated in the bottom-left and top-right corners, with the lowest entropy being dispersed in the central region of the cavity. This feature indicates an underflow stream for the shear thickening nanofluids in the central area in a low porous medium. With increasing the volume fractions, the contours get larger by moving towards the center of the porous cavity.

The local entropy generation ($S_{L}$) discussed above represents the sum of both fluid friction and heat transfer irreversibility. However, $S_{L}$ can not provide which irreversibility is dominating the local production of the total amount. In this regard, Fig. 12 shows the contour of the local Bejan number (Be), apprehending the significance of the pertinent parameters similar to the Fig. 11. Indeed, values of local Bejan number (Be) fall into the range $0\le Be \le 1$, indicate the dominance of the fluid friction or heat transfer irreversibility into the local entropy generation rate. The h irreversibility due to heat transfer dominates for $0.5\le Be\le 1$, while $0\le Be \le 0.5$ that indicates the dominance of fluid friction irreversibility into the local entropy generation rate.

Fig. 12

Local Bejan Number (Be) graphs for various volume fractions $\phi =0$ (dotted lines), $\phi =0.05$ (dashed lines) and $\phi =0.1$ (solid lines) and power-law indexes at $n=0.7$ (left panel), $n=1.0$ (middle panel), $n=1.4$ (right panel) and $\hbox {Ra}=10^5$. In a $Da=10^{-2}$, and b $Da=10^{-3}$

The contour plot of the local Bejan number for shear-thinning fluids at $Da = 10^{-2}$ shows a mixed dominance of the heat transfer irreversibility and fluid friction irreversibility on local the entropy generation. The heat transfer process dominates the entropy generation at the hot and cold walls and the central region of the porous cavity. Fluid friction irreversibility dominates in the top-middle and bottom-middle region of the cavity. For a Newtonian fluid, the dominance of fluid friction in local entropy generation decreases significantly. For shear-thickening fluid, the local entropy generation is entirely dominated by the heat transfer process. With increasing the volume fraction, the contour graph for local bejan number changes nominally. Nevertheless, the contours occupy the lesser area, increasing the volume fraction of Newtonian and Shear-thickening fluids. Besides, it is reasonable to say that with increasing the volume fraction, fluid friction irreversibility loses dominating the heat transfer irreversibility as the flow becomes slower than the pure fluid, but the effective conductivity enhances.

The contour graph for $Da=10^{-3}$ show densely concentrated graphs near the wall of the enclosure in Fig. 12b. Although major dominance of the heat transfer irreversibility is obvious, the contribution from viscous irreversibility also exists for shear-thinning fluids. The center of the enclosure experiences dominance of heat transfer irreversibility, while viscous irreversibility is dominant to small scale near the region of the top and bottom adiabatic walls. The viscous irreversibility presented through contour graphs gradually changes to heat transfer irreversibility with increasing the power-law index. For the Newtonian fluid case, the graphs are aligned along the enclosure’s hot and cold walls. Heat transfer irreversibility is dominantly found in the graphs for most regions in the cavity. Along the bottom and top adiabatic walls, viscous irreversibility graphs are found sparsely. For shear-thickening fluid, absolute dominance of heat transfer irreversibility is observed, which happens due to the underflow stream of non-newtonian nanofluids inside the porous cavity. The graphs are comparatively more concentrated along the middle region of hot and cold walls. The contour size gets smaller with increasing the volume fraction for non-Newtonian nanofluids. It is worth being mentioned that similar to the pattern for the local entropy generation graph in Fig. 11, the local Bejan number graphs also exhibit rotational symmetry of order two about the center of the cavity.

Table 5 presents the quantitative details of the total irreversibility due to fluid friction, heat transfer, and the sum of both for all the test cases in the present study. Values of $(S_{F,T})$, $(S_{T,T})$ and $(S_{L,T})$ are tabulated for $10^3\le Ra\le 10^5$, $10^{-4}\le Da\le 10^{-2}$ , $0.7\le n\le 1.4$ and $0.0\le \phi \le 0.1$. Enhancement of convective heat transfer and porosity in the medium by increasing the Rayleigh number and Darcy number influences the local entropy generation factors and corresponding local Bejan number. The changing values of entropy generation factors with the change of parameters helps to apprehend the reason behind thermal exchange enhancement. The quantitative values show that the fluid is almost stagnant at low Rayleigh numbers to produce a major contribution of total fluid friction irreversibility. Hence the irreversibility of heat transfer dominates a major percentage of local entropy generation. Heat transfer irreversibility is dominating when the Rayleigh number is lower, and this situation persists even when the medium’s porosity is enhanced. The tabulated result shows that the total local entropy generation ($S_{L,T}$) reduces with increasing the power-law index but augments with increasing the volume fractions.

Table 5 Total fluid friction irreversibility $(S_{F,T})$, heat transfer irreverisibility $(S_{T,T})$, and sum of them $(S_{L,T})$ for shear-thinning fluids $(n=0.7)$, Newtonian fluids $(n=1.0)$ and shear-thickening fluids $(n=1.4)$ with different volume fractions $\phi =0, 0.05, 0.10$ while $10^3\le Ra\le {10^{5}}$ and $10^{-4}\le Da\le 10^{-2}$

It is observed that the total viscous irreversibility $(S_{F,T})$ gets increasing with increasing the Rayleigh number (Ra) regardless of the strength of porosity. However, from the governing equations 34 and 35, the viscous irreversibility ($S_{F}$) and hence the total quantity, i.e., $S_{F,T}$, becomes enhanced when Darcy number (Da) is lower but the quantity gets attenuated when Da become higher. The total viscous irreversibility also arises with the volume fraction ($\phi$) for the cases when the Darcy–Rayleigh number $Ra^*=Da*Ra\gg 10$ for all power-law fluids except the case $Da=10^{-4}$. For a shear-thinning fluid at $Da=10^{-2}$ and $Ra=10^3$, the total fluid friction irreversibility is as low as 0.001 for all volume fractions. An increase in the volume fraction of nanoparticles maintains the same total viscous irreversibility for the same parameters but keeps the dominance of total heat transfer irreversibility with increasing behavior. At the same porosity level, the enhancement of the Rayleigh number increases the total irreversibility $(S_{L,T})$ significantly. In this case, $S_{L,T}$ is significantly dominated by total heat transfer irreversibility $(S_{T,T})$. With a decrease of porosity, the total local entropy generation $(S_{L,T})$ values continue to decrease for all Rayleigh numbers. For $Ra=10^5$, the total local entropy at $Da=10^{-2}$ with $\phi =5\%$ is 22.913, which decreases to 14.535 (about $36.6\%$ decrement) at $Da=10^{-3}$ and at $Da=10^{-4}$, the value decreases even more to 3.750 about $83.6\%$ decrement.

An increase in power-law index values shows a decrease in total local entropy generation for both Newtonian fluids and shear-thickening fluids compared to their corresponding shear-thinning fluid at the same value of Rayleigh number, Darcy number and volume fraction of nanoparticles. The more dilatant the fluid becomes, the fluid obstructs the entropy generation process. Total heat transfer irreversibility always dominates for all the test cases of non-Newtonian nanofluids. At increased buoyancy force and decreased porosity level, the viscous irreversibility has a significant contribution in total local entropy generation following heat transfer irreversibility.

5 Conclusion

This study has numerically investigated the natural convection heat transfer and entropy generation of non-Newtonian power-law nanofluid in a two-dimensional singly undulated wavy porous cavity. Three varied volume fractions of Cu–water nanofluid has been considered for the present study. The numerical technique employed in the present study has been a combination of an implicit finite volume method and a time-marching pressure-correction algorithm over a collocated grid arrangement. In that approach, the non-dimensional governing equations have been formed using an appropriate set of transformations. The governing equations are transformed from the physical domain to a rectangular shaped computational domain using curvilinear coordinates to use body-fitted non-orthogonal grid arrangement. An in-house FORTRAN code has been developed to implement the finite volume approach where the governing equations are integrated over the control volumes. The code has been tested for different grids to establish grid-independent results discussed in the present study. The code has been verified with the previous benchmark result for non-Newtonian nanofluids and entropy generation rate. After that, numerical investigations have been proceeded for control parameters such as Rayleigh numbers $(10^3 \le Ra\le 10^{5})$, Prandtl number (6.2), power-law index $(n = 0.7, 1.0, 1.4)$, Darcy numbers $(Da=10^{-2},10^{-3},10^{-4})$ and nanoparticle volume fraction $(\phi = 0.00, 0.05, 0.1)$. The obtained numerical results have been presented through streamlines and isotherms, Nusselt number, and entropy generation. The main conclusions drawn from the present study can be summarized as follows:

• Variation of control parameters significantly affects the flow patterns and isotherms for high porous non-Newtonian nanofluid within the wavy cavity. Flow gets strength, and the boundary layer becomes thinner with increasing the buoyancy forces and the porosity of the flow medium. Increasing the power-law index and the volume fraction of nanoparticles leads to enhance viscosity inside the flow; hence the flow becomes weaker inside the wavy enclosure.

• The buoyancy force gets more strength with increasing the Rayleigh number; as a result, the flow becomes strengthened, resulting in the development of convective heat transfer from the hot wavy wall to the enclosure through the non-Newtonian nanofluid. When Ra reaches to $10^5$, the isotherms show horizontal stratification inside the wavy enclosure for shear-thinning fluids compared to other cases, suggesting augmentation of convective heat transfer when $n<1.0$.

• For a low porous medium of $Da=10^{-4}$, isotherms pattern becomes parallel to the wavy walls, which indicates a negligible convective heat transfer process inside the enclosure. The increase of porosity significantly augments the velocity profile with the enhancement of convective heat transfer. The addition of nanoparticles increases the thermal conductivity of the non-Newtonian nanofluids, resulting in the Nusselt number’s enhancement for the high porous medium of $Da=10^{-2}$. However, when the porosity of the medium is too low such as $Da=10^{-4}$, nanoparticle addition to the base fluid shows a negligible effect in the augmentation of the heat transfer process.

• The heat transfer rate, i.e., Nu, is stronger near the bottom end of the hot wavy wall than the top end when the Darcy–Rayleigh number is much higher than 10, i.e., $Ra^*\gg 10$. For $Ra^*\gg 10$, non-Newtonian effects are more prominent than the volume fraction effect in the enhancement of heat transfer from the hot wavy wall. Otherwise, volume fraction effects are found more significant.

• The average Nusselt number increases with an increase of Darcy numbers for a certain Rayleigh number and vice versa. The increasing volume fraction of nanoparticles augments the average Nusselt number, i.e., the natural convection heat transfer enhances. The average Nusselt number decreases with increasing power-law indexes, and consequently, natural convection heat transfer reduces.

• Increase of porosity of the medium (Darcy Number (Da)) augments the local entropy generation simultaneously in the enclosure. On the other hand, the local entropy generation is diminished to considerable extent through increasing power-law index value of nanofluids. The particular wavy shape of the enclosure influences the local entropy generation pattern strongly. The maximum point of entropy generation is located by the top-right and bottom-left wavy walls, demonstrating the highest rate of heat transfer taking place at these locations.

• The local Bejan number suggests that the entropy generation of the non-Newtonian nanofluid within the wavy porous enclosure is strongly dominated by heat transfer irreversibility for all cases of pertinent parameters. Augmentation of thermal Rayleigh number (Ra) leads to enhance viscous irreversibility showing enhancement in the entropy generation due to fluid friction.

• The local entropy generation graph and local Bejan number graphs are rotationally symmetric of order two about the center of the wavy cavity. This pattern is observed for the first time in the entropy generation study of the non-Newtonian nanofluid within the porous wavy cavity.

The controlled amplitude and number of undulations in this study are followed to adapt the single-phase flow model. The study can be extended in applying a multiphase mathematical model in simulation of non-Newtonian nanofluid in a similar experimental cavity. Various investigations of multiphase flow properties and convective heat transfer phenomenon of the non-Newtonian nanofluid in varying porous cavity levels of multiple numbers of undulations, different aspect ratios, and different wave amplitude are also required.