Introduction

Magnetorheological elastomers (MREs) are hybrid materials, comprising an elastic non-magnetizable matrix, such as polydimethylsiloxane (PDMS), interspersed with magnetic fillers like iron oxide particles. First publications concerning such smart magnetorheological elastomers date back to the 1990s [1,2,3,4,5], though they still attract much attention today [6,7,8,9,10,11,12,13,14,15,16]. When applying a magnetic field, MREs undergo a reversible variation of their visco-elastic characteristics and/or undergo a reversible shape change that can be used for actuation. Consequently, MREs offer much potential for applications in adaptive damping systems, sensors, valves, and other actuators. Their inclusion in artificial muscles, robots, medical instruments, and haptic applications is also common [6,7,8,9,10,11,12,13,14,15,16]. An efficient usage of MREs for applications would be strongly facilitated by a fundamental understanding of the macroscopic and internal mechanisms under applied magnetic fields: Their physical response to external magnetic fields depends on the influence of experimental parameters such as concentration and distribution of filler particles, matrix stiffness, magnetic field strength, etc. Past theoretical and experimental studies have contributed considerably to the understanding of MRE particle-level processes [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].

Tomographic imaging of internal MRE structures has resulted in a significant understanding of internal MRE structures [29,30,31,32, 40]. This method allows tracking of single-particle movement as well as particle cluster formation [41]. These microscopic and macroscopic changes are linkable to magnetorheological properties of the material. It is known that in samples cross-linked under an applied magnetic field, even isotropic particles tend to form chain structures which result in an anisotropic Young’s modulus. Using X-ray micro-tomography, at least one research group has been able to acquire information concerning structure formation in order to quantify particle dimensions, concentration, and structural changes at a particle scale [28, 31, 32, 42]. With the help of 3D printers, new structured and well-organized MREs are producible [11, 14, 43, 44]. Simulation has assisted greatly in the computation of particle movement as well as magnetostrictive effects, thus helping to complete the overall understanding of MRE deformation mechanisms [35,36,37,38,39].

In samples similar to the ones studied here, it has been shown that non-local matrix-mediated interactions can be described in an iterative procedure inspired by the Oseen-tensor formalism in hydrodynamics [26]. Here, the system is described as an interplay between mutual magnetic forces and the opposing elastic matrix deformations caused by particle displacement. Under slowly rotating external magnetic fields, depending on the parameter space, oscillating distance between non-touching magnetic particles [24], or contact between magnetic particles due to an increasing magnetic field along the particle axis [25] occurs. For soft samples containing chains of magnetic particles, slowly rotating magnetic fields lead to a differing internal instability in the sample. In order to obtain the correct balance between magnetic and elastic forces, lateral deformations of the chain of magnetic particles (buckling) occurs [27].

However, there remains a lack of information concerning the internal dynamics of MREs. The precise determination of material parameters, such as the ratio between elastic and magnetic forces, responsible for structure formation in MREs cross-linked under zero magnetic field, is still a subject of current research. Furthermore, it is important to know whether such structures are reversible and tunable by an external magnetic field and whether microscopic deformations persist with larger particle populations.

Here, a bottom-up approach is followed, in which the system is first reduced to two particles embedded in a polymer matrix. Then, the particle numbers are successively increased, up to fourteen particles. This downscaling enables a full characterization of the system with a high spatial and temporal resolution. This bridges the gap to tomographic measurements where images are based on much larger samples, but whose analysis is far more time consuming.

In this article, focus is placed on the thorough characterization of well-defined particle systems. Therefore, the investigation concerns samples with different particle distance, matrix elasticity, and magnetic field strength. While previous work has focused either on non-touching particles or on the touching processes with increasing magnetic field strength, here the structural evolution under a rotating homogenous magnetic field is systematically followed. A new strongly magneto-active configuration, resulting from the transition from particle contact to particle separation and vice versa under small external magnetic field orientation alternations, is revealed. This is in contrast to previous works where an increasing magnetic field strength is used to cause particle collision [19, 20, 25, 45]. The foreground to this study lies in the influence of the magnetic field strength, the resulting Young’s modulus, and particle distances. In order to determine whether such strongly magneto-active states can be scaled up, the particle population is successively increased. Should it be possible to scale up such a strongly magneto-active state then the potential of such switching events for macroscopic actuators would be immense. With the fourteen particle system, it is possible to obtain insight into local chain formation, lateral deformation, and their dependance on elastic modulus, particle distance, and magnetic field strength.

Experimental

Materials

The PDMS consisted of three components [24, 25, 27]: the difunctional vinyl-terminated PDMS (DMS-V25, 500 cst Gelest Inc.), the SiH-containing crosslinker (HMS Gelest Inc.), a low molecular weight trimethylsiloxy-terminated PDMS with molecular weight 770 g/mol (Alfa Aesar), and a platinum catalyst (SIP6830.2, Gelest Inc.). A prepolymer solution was created by mixing 90.9 wt% DMS-V25 with 9.1 wt% HMS. By adding different percentages of low molecular weight PDMS, the elastic modulus of the final gel can be varied from a few Pascal up to several kilo Pascal (Table 1). Cross-linking was induced through a platinum catalyst and takes place in form of a hydrosilation reaction. The PDMS solution was always mixed in the volume ratio of 160 μl with 10 μl catalyst solution containing trimethylsiloxy-terminated PDMS with 5 wt% platinum catalyst.

Table 1 Young’s modulus dependence on the PDMS solution mixing ratio
Full size table

The magnetic nickel particle fillers were purchased from Alfar Aesar (− 100 + 325 mesh, purity 99.8 %). Low remanence (5.5 kA/m) and a saturation volume magnetization of 317 kA/m are characteristic features, which were verified by means of single-particle SQUID magnetometer measurements (Online Resource Fig. 2). The particles have a size distribution ranging from 50 to 250 μm. Tomographic scans show slightly non-spherical shapes including surface roughness and slight porosity (Online Resource Vid. 1 and Online Resource Fig. Online Resource chapter 2). Since all samples were prepared manually, the particles actually used have a much narrower size distribution and better sphericity than randomly chosen particles.

Fig. 1
figure 1

a Sketch of the experimental apparatus. The mirror guides light through the sample from below and is recorded with the camera. b Sketch of two nickel particles (dark gray) embedded in the PDMS Matrix (light gray). Red dashed lines mark the interfaces

Full size image

The two and three particle samples were always prepared according to the following scheme: First a 2-mm-thick, 2.25-cm2 layer of elastic non-magnetizable PDMS network was formed in a mold and cured at 60 ∘ C for 24 h. The PDMS consists of a prepolymer mixture with 10, 12, and 14 wt% low molecular weight PDMS added. This change in composition varies the modulus of the matrix significantly: ≈ (661 Pa; 774 Pa; 1301 Pa± 100 Pa) for 10, 12, and 14 wt% low molecular weight PDMS added (Table 1), respectively. For further information concerning the determination of such values, the reader is referred to the supplementary information (Online Resource chapter 2) and [46].

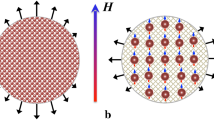
After curing the first layer, paramagnetic Ni particles were carefully deposited with a micro-manipulator in the center of the layer. Particles with similar size were selected manually and show a circularity of ≥ 0.94 (extracted by image analysis using ImageJ). Due to the PDMS softness and particle surface roughness, this procedure is not perfectly precise. The positioning accuracy of the particles was about ± 20 μm. In the final step, another layer of PDMS (of the same composition) was poured over the first, which was cured for another 24 h at 60 ∘C. Thus, the particles are fully encapsulated by the matrix material (Fig. 1 b) and figure 3 in [26]. As dimensions of the final PDMS gels exceed the particle diameters (and their typical displacements) by a factor of ≈ 10, the influence of the boundaries on the particle motion can be neglected.

For samples with more than 3 particles, the sample preparation varied slightly from the aforementioned process in order to achieve free-standing PDMS films. A free-standing film allows for more flexibility, thereby contributing to the emergence of microscopical deformations induced by particle displacement. As the cross-linking of the PDMS takes some time, a solid structure is needed to stabilize the PDMS film until solidification is finished. Afterward, the lift off process to obtain a free-standing film is not so simple to achieve due to the low Young modulus we are facing. A solution presented itself in the form of using a sacrificial layer which could be solved in water after the PDMS film had solidified. To these ends, polyvinylalcohol sheets were used as sacrificial layers to facilitate the fabrication of free-standing PDMS structures. The first step included casting a polyvinylalcohol (PVA, 113000 MW, 90 % hydrolysation) sheet by allowing a 10 wt % PVA in water solution to dry under room temperature conditions. For the solution, 10 wt% PVA was dissolved in water at 80 ∘C under continuous stirring. Following film solidification, the sample was cut into 4-cm2 square pieces and glue rims attached to prevent PDMS creep. Subsequently, a slightly modified version of the two-layer technique described above was used. For the bottom layer, 160 μl with a mixing ratio (low molecular PDMS to prepolymer) of 12 wt% was used, giving a thickness of ≈ 350 μm. Deposition and arranging of the particles took place analogous to the two particle system. Fourteen nickel particles were placed on top and positioned with a micro-manipulator to achieve equal spacing. A final 160 μl layer of a 12 % PDMS mixture was added to encapsulate the particles. Maintaining the sample under 60 ∘C for 24 h ensured sufficient cross-linking and adhesion of the layers. The final step involves solving the PVA film in water which provides a free-standing PDMS structure with thickness ≈ 700 μm stabilized only by the glue rim.

Apparatus

In order to guarantee an exposure to a homogenous magnetic field with a maximum magnetic flux density of 216 mT, a Halbach array [27] comprising two rotatable rings populated with permanent magnets was used. The magnetic field orientation can be freely rotated in the sample plane. The readout uncertainty of the magnetic field orientation is ± 0.5∘. Adding a systematic offset of the magnetic field orientation of ± 1.5∘ a total error of 𝜃 of ± 2∘ is assumed. The nickel particles were positioned near the middle of the Halbach array and exposed to a ≈ 170-mT field (measured by a Lake Shore Gaussmeter 425). This field is close to the saturation magnetization of nickel.

A × 20 Mitutoyo objective mounted on top of the CCD camera (mvBlueCOUGAR-S from Matrix Vision GmbH), enabled the visualization of the Ni particles. Transmission illumination was installed from below (Fig. 1a). The focal plane was adjusted for the maximum particle diameter. Single frames were taken following each successive 5∘ rotation of the Halbach magnet array. This implies that the images taken and presented here pertain to the final state. Dynamic effects such as magnetic moment relaxation or matrix viscosity have relaxed before taking the image and play no role in this work. In order to extract the particles’ x-y positions, the resulting video was loaded in ImageJ (https://imagej.net/Fiji) and the gray scales inverted. Consequently, the particles correspond to white circles on a dark background, which were analyzed using the plug-in TrackMate [47] in ImageJ. For this procedure, a mask diameter corresponding to the average particle diameter must be defined. However, for particles in contact, a slightly oversized mask was used to allow a slight degree of overlap. The particle center was detected more accurately with mask diameters identical to the particle diameters. Following detection, process parameters for the linking distance between each image were assigned. Linking distance is defined as the resulting maximum particle displacement between two images. This was chosen so that the position of the particle could be obtained for every picture. The error in detecting the particle center was estimated to be ± 1 pixel (corresponding to ± 2.34 μm) in the x and y directions. A measurement of ≈ 40 cycles validated this as a good approximation (Online Resource Fig. 5). The center-to-center vector between two particles (particle axis) is denoted by Δx and Δy. The center-to-center distance r is given by:

$$ r=\sqrt{({\Delta} x)^{2}+({\Delta} y)^{2}} $$
(1)

With Δx and Δy a center-to-center vector with an error of ± 4.68 μm is obtained. Additionally, after attaining the center-to-center vector connecting both particles (particle axis), the orientation relative to the x axis could be calculated. As the magnetic field orientation for every step is well known, the angular difference between particle axis and magnetic field can be computed. The particles did not change their z-position as they remained in focus throughout the measurements.

Theoretical background

The theoretical background of the particle matrix systems which combine the magnetic and elastic forces acting in the system is briefly summarized. A variety of approaches and assumptions for the theoretical description of magnetizable particle elastomer composites are proposed in the literature [17,18,19,20, 23, 25, 26, 33, 34, 48,49,50,51,52]. In the following, a few results that consider two particle systems explicitly will be mentioned. For an overview of the derivation and precise description of the theory, the reader is referred to [17,18,19,20, 25, 26, 34, 48,49,50,51,52]. The system can be divided into two characteristic states:

  1. 1.

    Ni particles are well separated;

  2. 2.

    Ni particles are able to make contact;

Forces will be discussed in relation to both states.

Magnetic interaction

Even though the Ni particles are themselves 3D objects with well-defined dimensions, the assumption to treat the magnetizable Ni particles as point-like dipoles is valid for substantial particle separation [20, 53,54,55,56]. This is also validated in [26] by comparing experimental results with a theoretical approach, where well-separated particles experience distance oscillation during rotation of the external field. Assuming identical magnetic moments m and a magnetization parallel to the applied field, the dipole interaction force between two particles i and j is given [34, 57]:

$$ \hat F_{ij}=\frac{3\mu_{0}|\textbf{m}|^{2}}{4\pi |\textbf{r}|^{4}}\left[(2 cos(\theta))\hat e_{m}+(1-5 cos^{2}(\theta))\hat e_{r}\right] $$
(2)

Here, μ0 is the magnetic permeability of vacuum, |r| is the center-to-center distance between particles, |m| the magnetic moments of particles in the sample, and 𝜃 the angle between external field orientation and the particle axis. \(\hat e_{r}\) and \(\hat e_{m}\) are unit vectors in the direction of the particle axis and the magnetic moment direction, respectively. The force in Eq. 2 depends quadratically on the magnetic moment of the particles but even stronger on the center-to-center distance. It also depends slightly on the angle between the external magnetic field orientation and the particle axis. As a direct result of this dipole interaction, a configuration with the angle difference between particle axis and external magnetic field orientation in the range of 0 to \(\sim \)54.7∘ (the magic angle) results in an attraction of the particles whereas at an angle ≥ 54.7∘ it switches to repulsion. In cases where the particles cannot follow the rotation of the magnetic field in the plane containing the particle axis, a reversal from an attractive to a repulsive magnetic force or vice versa may be experienced.

Using Eq. 2 involves a number of simplifications: Treating particles as point-like dipoles should not be valid if they are close to contact or even in contact [25]. As Eq. 2 is only an approximation, there are two additional approaches to take into consideration. Biller et al. [19] look at the spatial distribution of the magnetization in the particles induced by the field. The magnetic inter-particle energy can then be approximated by a multipole expansion beyond the dipole approximation. To obtain sufficient accuracy for contacting particles, approximately 100 multipoles are needed. This shows that short range forces differ significantly from the dipole approximation. These higher order terms lead to an attraction, depending on the counteracting elastic force, even for angles higher than the magic angle of the dipole approximation.

In a second approach, Puljiz et al. [25] use a local magnetic field by taking the stray field of the neighboring particle into account. Here, only a dipole approximation is used but many iterative steps to calculate the local field are needed in order to obtain the actual magnetic moments of the particles. With the corrected magnetic moments, the force can be calculated. The displacements in response to magnetic force create a deformation of the surrounding matrix and are similarly expressed in [26] with displaceability matrices. However, for every step, a reevaluation of the magnetic moments must be carried out. The theoretical approaches [25, 26] have proven their conformity with experiments. The goal is to provide additional experimental data for verification of the different models.

Elastic interaction mediated by the matrix

When a field is applied, the magnetic force leads to particle displacement and an elastic force arises from the deformation of the matrix. This elastic force counteracts the magnetic force. To these ends, the matrix is assumed to be homogeneous, isotropic, and infinitely extended [25, 26]. A linear elastostatic tendency (Hooke’s law) is used. This approach is limited to non-touching particles because the displacement field of the matrix would have a divergence at the point where two particles touch. Additionally, in the contacting position, nonlinear elastic, as well as magnetic, effects play a role. In contrast to Hooke’s model, a Mooney-Rivlin hyperelastic model was suggested to provide an analytical approximation of the elastic potential [19, 58]. In this system, the matrix is not only linearly deformed by particle motion but is also subjected to a torque due to rotation of particles around their own central axis. A good approximation to an incompressible, infinitely extended, isotropic, and homogenous viscoelastic medium is presented through a continuum description of a swollen polymer gel by Puljiz et al. [34]. Additionally, they showed that their formalism holds for the inclusion of net torques on the rigid particles. The specified examples for two- and three-particle systems in [59, 60] are of particular importance in providing a solid theoretical basis for the systems described in this work.

Particle motion under slowly varying homogeneous magnetic fields

These experiments reveal specific dependencies of the results on the sample characteristics such as the number of magnetic particles, elastic modulus of the surrounding gel matrix, and the typical particle distance. Figure 2a gives typical particle configurations for an experiment using two magnetic particles. In the following, results of one exemplary sample are presented and tendencies based on these results discussed. Results and tendencies were reproduced and verified by other samples produced in the same way.

Fig. 2
figure 2

a Typical two-particle system with an initial distance of 316 μm. PDMS ratio of 14%. Series of images depicting the quasi-static particle positions over a 360∘ rotation of the external magnetic field. Magnetic field orientation is indicated by the black arrows. b Schematic of the Halbach array. The red dashed line marks the magnetic field orientation; the blue dashed line the particle axis. 𝜃 defines the angle difference

Full size image

Two-particle system

In the following, the characteristics of two-particle systems under a stepwise rotated magnetic field are elaborated by means of a representative two-particle arrangement. This rotation effectively leads to a variation in the angle difference 𝜃 between particle axis and magnetic field orientation (Fig. 2b). When exposing the two-particle samples to a homogenous magnetic field, different particle arrangements were observed depending on the orientation of the magnetic field relative to the particle axis (Fig. 2a). Unless otherwise stated, measurements commenced with the magnetic field oriented parallel to the particle axis. Without a magnetic field, the particles are located apart from each other (dashed lines in Figs. 3, 4, and 5). In the following, this is called the initial state and the particle distance in that state as the initial distance. As particle pairs want to minimize their overall energy, magnetic and elastic torque is acting on the pair of particles, leading to a rotation of the particles around their common axis. Particles are also able to solely rotate around their center which is well depicted in Fig. 2a as well as through changing center-to-center distance while particles are in contact in Fig. 3. The origin of this change in the center-to-center distance lies in the roughness of the particle surface as they slide over each other. For small rotational magnetic field angles (< 3∘), a uniform rotation of the particles around their axis was observed while particles are able to follow the field. This rotation generates a counteracting elastic torque. Consequently, the axis of the particle pairs rotates less than that of the applied field resulting in an angle difference between the particle pair axis and the applied magnetic field. This changes the magnetic interaction energy. In configurations in which the magnetic attraction dominates over the elastic forces, the particles are in contact. When, due to the field rotation, the magnetic attraction reduces, elastic forces balance the magnetic attraction and the particles separate again. Thus, as the total energy is defined by an interaction between magnetic and elastic forces, a bistability effect leads to a trend toward hysteresis in the inter-particle distance over the angle difference; Fig. 3 comparable to those depicted in Fig. 5 in [19] and Fig. 3 in [25].

Fig. 3
figure 3

Same particles with different initial distance (dashed lines, 230, 241, 259 μm). The matrix composition was maintained equal for the 3 samples (Young’s modulus of PDMS: (1221 ± 100) Pa). The orange vertical line indicates the magic angle of 54.7∘. For smaller initial distance, particles remain in contact for higher angle differences 𝜃. Orange arrows indicate the direction of the experiment. Starting position was 𝜃 = 0

Full size image
Fig. 4
figure 4

Same particles for the three measurements while matrix composition differs. Young’s modulus varies from (661 to 1301)± 100 Pa. The initial distance is marked with dashed lines and was nearly equal for the 3 measurements as it ranges from 302 to 309 μm. Orange arrows indicate the direction of the experiment. Starting position was 𝜃 = 0

Full size image
Fig. 5
figure 5

a Three particles in a row. Magnetic field direction is indicated by the black arrow. b Particle distance over angle difference. Dashed lines mark the initial distance of respective system. The samples had Young’s modulus of (1221 ± 100) Pa

Full size image

The form of the hysteresis is strongly influenced by the initial distance, the elastic modulus, and the magnetic field strength (Figs. 3 and 4). In order to determine how this manifests itself, in the following, two of these parameters were maintained constant and one altered.

Leaving the elastic modulus (≈ (1221 ± 100) Pa) and magnetic field strength (≈ 170 mT) unchanged but varying the initial distance, the influence of the particle positioning on the new strongly magneto-active configuration can be obtained. Exactly the same particles were used in order to exclude any influences resulting from different particle dimensions. Positioning errors due to particle detection do not change with the measurements and are thus only depicted once in Fig. 3. Starting with the smallest center-to-center distance (Fig. 3 red curve) the particles remain in contact for angle differences 𝜃 from 0 to at least (60 ± 2)∘. This exceeds the 54.7∘ angle at which the magnetic dipole-dipole interaction changes from attraction to repulsion. In agreement with theoretical predictions of comparable particle systems [20, 21], the dipole approximation fails to reproduce such experimental results. The system shows indications that higher order terms play a significant role.

According to the magnetic dipole-dipole interaction particles repel each other for angles higher than 54.7∘. Graphically, this is discernible as center-to-center distance increases over the initial distance marked with dashed lines in Fig. 3. Diminishing the angle difference, magnetic forces increase until they are strong enough and particles jump into contact again.

For the angle of ≈ 54.7∘, the magnetic force along the particle axis should vanish. This should result in no displacement of the particles and the counteracting force through the elasticity of the matrix should vanish as well. However, for separated particles, the initial distance is reached even at angles deviating from 54.7∘ (crossing of the dashed line in Figs. 3 and 4). The non-perfect sphericality of the particles causes them to rotate individually around their own center of mass which is a possible cause of the angle aberrations.

For a larger initial distance, a higher elastic force acts on the particles in contact. If the influence of changes in the center-to-center distance of the particles due to their surface roughness can be neglected, the same attractive magnetic force simultaneously acts on particles in contact. For this reason, the particles separate at smaller angle differences, i.e., at higher attractive magnetic forces. This trend is confirmed for 230 μm an angle of (60 ± 2)∘, for 241 μm an angle of (47 ± 2)∘ and for 259 μm an angle of (42 ± 2)∘, at which a change from touching to non-touching occurs. Furthermore, the magnetic force needed to bring them into contact increases. This is shown as contact occurs at smaller distances and angles 𝜃 for particles with greater initial separation. While the particles experience a clear and sudden jump into contact for particles at relatively low initial distances, the transition becomes smoother with increased initial distance until the particles are no longer able to touch. At this point, the system is back in the state where the center-to-center distance only oscillates with rotating field [24, 61]. For initial distances smaller than ≈ 220 μm, the two-particle system approaches the state of remaining in contact for any orientation of the applied external magnetic field at this flux density. They rotate according to the field until a pairwise reorientation takes place.

After characterizing the influence of the particle initial distance and comparison with previous work, the next parameter was varied. Mixtures with 10, 12, and 14 wt% PDMS 770, resulted in matrices with Young’s moduli of ≈ 661 Pa, 774 Pa, and 1301 Pa with an error of ± 100 Pa, respectively. The initial distance was maintained roughly the same (302–309 μm). In this case, the elastic force increases through the stronger cross-linking of the matrix for the same particle displacements, while the magnetic force remains almost unchanged. Similar to an increasing initial distance, a stronger elastic force causes a smoother touching of the particles and the transition to the state where the distance only oscillates with rotating field is depicted in Fig. 4. Also, the angular difference at which separation takes place decreases for harder matrices. Consequently, both methods (changing distance and changing elastic modulus) show the same trend in the interplay between magnetic and elastic forces.

The last parameter, the strength of the magnetic interaction, was changed by altering the sample position in the Halbach magnet in the z direction, effectively diminishing the magnetic field strength. This reduces the magnetic moment because the experiments are performed below the saturation field for these particles. Consequently, the magnetic force is weakened, and particles are able to remain separated for a longer angle range. So by changing one of the three possible parameters, initial distance, matrix Young’s modulus, or magnetic field strength, the hysteresis form can be modified. Consequently, the properties of the strongly magneto-active configuration can be appropriately adapted to any specific application.

Three-particle system

Normally MREs contain a noteworthy volume of magnetic filler particles. So after thoroughly characterizing the magneto-active configuration of two particles, the system is first expanded to three particles (and later on to many) for purposes of examining the influence of an additional particle. It is expected that this additional particle should influence the displacement of the other particles, alter the hysteresis loop, and introduces the possibility of a mutual jumping into contact. Focus was placed on particle alignment along one line, in order to obtain the interaction with only the neighboring particle. This also makes it easier to adjust the inter-particle distance to be approximately identical.

Samples are produced as described in “Materials.” Based on the following representative three-particle arrangement, trends and characteristics of such three-particle systems will now be discussed. The elastic modulus of the matrix was determined to be ≈ (1221 ± 100) Pa as a 12.5 wt% mixture was used. After curing for 24 h, the samples were exposed to a stepwise rotating magnetic field of 170 mT. In order to experience as few symmetry influences as possible, all inter-particle distances were adjusted to be approximately identical. Particles were positioned in this representative case with initial distances of 238 μm and 256 μm (Fig. 5a).

With the field aligned along the particle axis, all three are in contact (Fig. 5a). The particle axis is defined as the axis between the neighboring particles 1&2 and 2&3. In contrast to simulations, particle size and distance differ slightly causing the system to be asymmetrical along the particle axis. This results in an asymmetry in the magnetic interaction as it is influenced by both as follows: The particle size affects the magnetization and thus enters the magnetic interaction with the third power of the particle radius. But since the magnetic dipole-dipole force (2) scales with the inverse fourth power of the distance, the magnetic interaction is more sensitive to a change in the distance. Therefore, at the same relative change, the distance can be assumed to have a stronger influence on the magnetic activity. Hence, differences in the initial inter-particle distance lead to the fact that systematically one particle first separates from this short chain. In fact, the particle pair with the higher initial distance was the first to separate. Observing the particle distance over the angle difference, both pairs show hysteresis (Fig. 5b). For the closer particles (2&3) and for those further (1&2) apart, a separation occurs within the bounds of error at ≈ (57 ± 2)∘. As with two, the three-particle system assumes the new strongly magneto-active configuration.

Comparing the three-particle system with the two-particle system, several similarities are discernible. The form of the 2&3 hysteresis is nearly identical to the one of the particle pair with 230 μm initial distance (Fig. 5b). At the point of separation, the angle difference reaches its maximum. Additionally, both reach the initial distance at the same angle difference. The proximity of the particle pair makes little difference in a two-particle system and the system seems to be only slightly influenced by the third particle.

In contrast, hysteresis is clearly visible in 1&2 (Fig .5b). While being separated, the pair 1&2 abruptly changes its distance and the pair 2&3 jumps apart. Thus, the non-local-mediated matrix deformation is clearly observed. This means if particle 2&3 jump apart or are in contact, it automatically influences the distance between 1&2. The initial distance is reached at ≈ (39 ± 2)∘, whereas the pair 2&3 reaches its initial distance at a much higher angle. On a particle level, the matrix-mediated interaction seems to induce a higher initial distance to the particle pair 1&2. Due to the strong distance dependency of the dipole interaction, the separation or jumping into contact of 2&3 does not vary the magnetic dipole energy of 1&2 sufficiently that this would induce a separation or contact (Fig. 6). Therefore, the altered particle movements arise mainly through a matrix mediated interaction.

Fig. 6
figure 6

Dipole-dipole-energy over angle difference. The two-particle system shows qualitatively the same trend as the three-particle system

Full size image

Consequently, the three-particle system also assumes a new strongly magneto-active configuration. For the closer particle pair, it is not different from a two-particle system, and no influence of the third particle is observed. The magnetic dipole energy and the hysteresis look similar (Figs. 5b and 6). To keep in mind, unlike the unchanged picture for the closer pair, the initially more distant pair shows some significant alterations. Upon contact, it acts according to the original parameters but separated it experiences a deformation mediated by the matrix and effectively has a larger distance to overcome. A perfect symmetrical system with spherical particles is assumed to show a magnetic activity of a two-particle system. Additionally, both particle pairs would reach the initial distance again at the same angle difference. However, any minor asymmetry will lead to a preferred magnetic activity of one of the particle pairs. Asymmetry in the magnetic interaction can arise, e.g., in the experimental setup in form of the particle size or distance. But the magnetic interaction reacts with different sensitivity to variations in those quantities as the distance enters the magnetic force (2) with the inverse power of 4 and the particle size with the power of 3. Thus, a change in the distance can be assumed to have a stronger influence. The experimental configuration allows to set the inter-particle distance only up to a certain precision, and hence an asymmetry in the initial inter-particle distance is unavoidable. In order to determine the influence of the particles size, it needs to outweigh the scattering in particle distance. Since the fabrication method used enables the selection of particles usable for the production of samples, investigation of the influence of the particle size distribution on magneto activity is possible. This would be interesting for poly-disperse particle systems but as it is a wider topic it will be addressed in future work.

14-Particle system

In the previous section, a magneto-active configuration of particles in an elastomer matrix (PDMS) was characterized, and its ability to alter the matrix deformation with only a small variation in the external field orientation was presented. For valves, actuators, etc., the creation and addressability of such sudden deformation changes can be essential. To amplify the effects, on the one hand, the sample is thinned; on the other hand, scaling up of the system is performed to obtain information concerning the deformation types of enlarged systems. The thinner system also allows the induction of surface deformations by motion of the embedded particles.

The samples were subjected to the magnetic field in the Halbach magnet. When the field is along the particle axis, longitudinal movement of the particles takes place. Thus, depending on the initial distance, contacting particle groups of two, three, or four particles arises (Fig. 7a). Selecting 5 particles, marked in Fig. 7a and b, the new magneto-active configuration of the two- and three-particle system is depicted. Comparing again the influence of neighboring particle events, for example, the separation and jumping in contact of particles 8&9 and 11&12 (marked with arrows in Fig. 7c and d on the magnetic energy of particle 9&10), it is found to be relatively minor. In most cases, the distance changes and thus the acting elastic force. Particles 11&12 show steps in the distance while separated even though neither 8&9 nor 9&10 distance changes. This is an effect of the influence of the thirteenth particle as it separates from particle 14, thus decreasing the distance between 11&12. The distance increase is then caused by contact between 12&13.

Fig. 7
figure 7

a 14 particles in a row (inset: particles 8 to 12). b Formation of particles 8 to 12 for different magnetic field orientations. c Particle 10 dipole energy varied over magnetic field orientations. Black arrows indicate contact/release of particle pairs 8&9 and 11&12 respectively. d Particle distance over different magnetic field orientations. Black arrows indicate a contact/release of particle pairs 8&9 and 11&12 respectively

Full size image

For a more detailed discussion, the particle group formations must be analyzed. Starting with a magnetic flux density of 45 mT for 0 to 360∘, an image is taken at every 5∘ of rotation. Defining groups by particles per group, it is possible to count their amount over all magnetic field angles (Fig. 8). Consequently, the graph depicts that no particle pairs form at 45 mT as elasticity counteracts the magnetic forces. Increasing the magnetic field strength stepwise up to 170 mT, the attractive magnetic interaction increases and at some point dominates over the elastic forces. Particle group formation is observed with a maximum of four particles (Figs. 7b and 8). A clear tendency to pair building is observed when comparing the chain counts over all images. This is indicated by the peak at two particles per chain for 135 mT and 170 mT in Fig. 8. Additionally, the data reveal a shift toward larger groups because at 170 mT fewer two-particle groups are counted compared to 135 mT.

Fig. 8
figure 8

Images were generated during variations in magnetic field orientation in 5∘ steps. Groups of particles were defined and their number counted (y-axis). Clear tendency to form pairs at 135 and 170 mT. Pair building does not form at lower magnetic flux densities

Full size image

So, it is unambiguously proven that it is possible to scale up the system and still be able implement the system locally in a magneto-active configuration. However, due to the building of chain segments, the global magneto activity is weaker. This is evident by comparing the distance between the edge particles while magnetic field orientation was varied. It decreases from 779 to 775 pixels which does not even resemble a 1% distance change. Furthermore, it is a smooth distance transition which does not take place suddenly.

Nevertheless, the local magnetic activity is comparable to the two- and three-particle configurations described in “Two-particle system” and “Three-particle system” and neighboring particle groups do not influence each other enough to change this. Also, by analyzing the group amounts, it is possible to depict the tendency of pair building and an increase in group size for higher magnetic field strengths.

In the next step, a comparison between the model and simulation of a ferrogel will be considered [62]. The ferrogel is modeled with a one-dimensional chain comprising magnetic particles connected by springs. The dynamics of touching and separating particles are evaluated by calculating the energy governing the system which are backed by simulation. Despite some differences between these experiments and the simulations of Goh and coworkers [62], e.g., these samples are not mechanically stretched and the particles are not evenly distributed, some important similarities in the dynamics of particles touching and detaching are found. A well-defined parameter space exists, in which pair building is preferred from the system. In the simulation, this begins with particles at the edges. In this work, the initial particle condition is the determining parameter and formation of pairs commences among the particles with the shortest center-to-center distance. As mentioned in [62], heterogeneity, which is given as the experimental samples are asymmetrical, can lead to different initiation points of

the chain formation process. Experiments have shown that increasing the magnetic field strength leads to the formation of particle groups with more than two particles. This behavior has been calculated and simulated [62]. One of the control parameters to influence this behavior was the magnetic moment m of the particles which, in this case, was varied by the magnetic field strength. As ascertained from the two- and three-particle measurements, there is an interplay between initial distance and the elastic module of the matrix which decides how many particles touch at a certain magnetic field strength.

Finally, in the resulting images, darker and brighter areas were visible around the particles. Since the matrix material is incompressible, particles jumping into contact should lead to a strong displacement of the matrix material. As the PDMS films are relatively thin, this should lead to surface arches. Through the strain caused at the interface, the light is broken differently compared to the zero magnetic field state leading to brighter and darker areas in the images. In the two- and three-particle samples, the matrix dimensions were so large that such deformations could not reach the surface and no brighter and darker areas were observed in the resulting image. Future measurements are intended to quantify the surface deformations of thin samples.

In the 14-particle chain, locally the magneto-active configuration was observed as well since particle groups form. Hereby, the formation process is similar to the two- and three-particle system and a sudden distance change between the particles was observed. But, on global sight, the magneto-active configuration does not exist since the distance between the edge particles does not change greatly with small alternation of the magnetic field orientation. Here, in contrast to the particles in the local magneto-active configuration, a smooth sinus-like distance change was observed. The particles at the edges show only an overall distance change of ≈ 1%.

Conclusion

Based on ≈ 160-μm diameter superparamagnetic nickel particles embedded in a PDMS matrix, it was possible to investigate a novel strongly magneto-active configuration, switchable by small variations in magnetic field orientation. This new configuration was thoroughly characterized as follows: Starting with the exemplary two-particle system, a transition from touching to non-touching of the particles is achieved by just a tiny alternation of the external magnetic field orientation. The particle distance demonstrates hysteresis as a function of the angle 𝜃 between magnetic field orientation and the particle axis. The shape of the hysteresis loop is strongly dependent on parameters such as elastic modulus, magnetic field strength, and particle distance. An excessive increase in any of these parameters results in a collapse of the magneto-active function into a basic state of contacting or non-contacting particles at all times. With increasing Young modulus, increasing particle distance, or decreasing magnetic moments, the configuration transits smoothly over the previous observed states of oscillating particle distance.

In a three-particle system, the new magneto-active configuration also exists, but the particle pair with greater initial distance separates first. Also, while in the three-particle system the hysteresis for the closer particle pair remains unaltered compared to the solely two-particle system, the particle pair with higher initial distance was influenced by the vicinity of the third particle and showed steps in the particle distance hysteresis.

In a 14-particle system, a clear tendency to pair formation was observed. With decreasing field strength, the magnetic force is not strong enough to overcome the elastic force and pair formation is suppressed. For a lower elastic modulus, chain formation with longer chain segments is prevalent. Since the 14 particles tend to pair building the particles were only locally in the magneto-active configuration comparable to the two- and three-particle systems. Looking at the global behavior by analyzing the distance of the edge particles, a sinus-like distance change was observed. Thus, the edge particles were not in the magneto-active configuration. As the magneto-active configuration does not lead to sudden distance changes globally, there are no macroscopic deformations to be expected suitable for use in actuation. However, at higher magnetic fields, local changes may shift to global changes as chain segments shift to higher particle numbers for higher magnetic fields (Fig. 8). Future research in this respect includes linking the particle distance changes to actual physical matrix deformations.