Abstract
Clays are not only ubiquitous in nature, but they are also used in huge quantities in a broad range of industrial applications, such as thixotropic drilling fluids, ore pelletizers, waste disposal sealants, or fillers in polymer nanocomposites. In order to model environmental processes or to design new materials on a rational base, it is of prime importance to determine and possibly modify the interfacial properties of clay platelets at the solid/electrolyte interface. In this context, the fundamental question rises how far the stoichiometric interlayer charges as determined by the composition of the silicate layer correlates with the diffuse double-layer properties. Here, this question is addressed by means of a series of purposely synthesized sodium 2:1 layered silicates with defined composition and hence interlayer charge densities, respectively. Platelets of layered silicates of large enough diameter to perform AFM colloidal probe measurements were produced by melt synthesis. For comparison also, a natural muscovite mica has been included in this study. The diffuse layer properties in electrolyte solution have been determined by direct force measurements using the colloidal probe AFM technique and by electrokinetic measurements, respectively. We find that the diffuse layer potential decreases with increasing interlayer charge of the 2:1 layered silicates. This counterintuitive finding is attributed to ion adsorption and was further corroborated by determining the quantitative adsorption of polyelectrolytes, namely poly(amidoamine) dendrimers.

Graphical abstract
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
Layered silicates are not only omnipresent in nature but also have a wide range of important applications, such as for thixotropic drilling fluids, ore pelletizers, waste disposal sealants, or fillers in polymer nanocomposites to improve their properties as gas barriers and flame retardants [1,2,3,4,5,6,7]. For many of these applications, it is not only important to tune properties such as size or aspect ratio but also their swelling behavior and surface charge density, respectively. A typical example would be the rheological properties of colloidal clay suspensions. However, mostly only indirect methods to determine the charge of the clay platelets have been applied so far [8, 9]. The commonly used technique for determining the cation exchange capacity (CEC) of clay minerals is based on the insertion of ammonium in the interlayer [8,9,10]. Neglecting potential contributions of accessory minerals and the CEC capacity of edges, charge densities can then be derived from the CEC. Alternatively, they can be determined directly by the so-called Lagaly method applying n-alkylammonium cations of increasing equivalent area [11]. While the ammonium method can only provide average charge densities, the Lagaly method is capable of indicating the degree of surface charge heterogeneities for the bulk of the sample. Both methods, however, fail to deliver information at the level of a single platelet. Moreover, neither of the two approaches provides information on the effective surface charge that is responsible for the formation of the electrical double layer in electrolyte solution, which determines interparticle interactions and dispersibility. However, in how far the stochiometric layer charge and diffuse layer charge are directly related is still an open question, in particular as ion adsorption has to be taken into account. Hence, it would be important to have a dataset comprising both charge densities, as well as the effective diffuse layer charge density for a highly defined interlayer charge density. Here, we utilize purposely synthesized 2:1 silicates with variable but defined charge density and large diameter of the platelets. Thereby, we can exclude distortions due to the edge contribution of the clay platelets, which have different surface chemistry and thus may carry different charges [12].
In colloid science, the surface charge of particles is often determined by electrokinetic methods [13]. The most prominent and commonly used electrokinetic technique is the measurement of the electrophoretic mobility where colloidal particles migrate in an external electrical field [14]. However, this technique is most quantitative if the particles have a geometrically well-defined spherical shape. Unfortunately, this condition is not fulfilled for inorganic platelets, although suitable approximations exist [15, 16]. For such colloidal objects, the measurement of the streaming current provides a more suitable approach [17, 18]. While this technique does not provide quantitative zeta-potentials, it allows for the determination of the isoelectric point and it is to a large degree independent from the geometry of the particles [19]. Common to all electrokinetic techniques is that the plane of shear cannot be determined in an unambiguous manner. In order to obtain accurate results hydrodynamic effects, which are incorporated in the Henry or the O’Brien and White theory, have to be taken into account [20]. By contrast, direct force measurements based on the colloidal probe technique with the atomic force microscope (AFM) allow for determining the diffuse layer properties in an unambiguous manner provided that the colloidal probe has been “calibrated” beforehand in a symmetric measurement in the sphere-sphere geometry. While this technique is well-established for large, flat surfaces [21, 22], there is an increasing interest to use it also for the characterization of individual inorganic clay platelets [12, 23, 24].
Here, we will use direct force measurements by means of the colloidal probe technique in order to determine the surface charge properties in a much more direct manner than it would be possible using cation exchange or the Lagaly method, respectively. These measurements will be compared to electrophoretic mobility and streaming current detection, respectively. We compare three different 2:1 silicates that have been synthesized by recently published procedures, namely a sodium brittle mica (cf. ref. 25) and two sodium-fluorohectorites (cf. ref. 26, 27) with different composition. Moreover, we included the naturally-occurring muscovite mica as an additional clay material and reference sample, as it is a commonly used 2:1 silicate material. While muscovite mica as natural material shows a large variety in properties, it is nevertheless the clay material for which the most reference data in terms of direct force and streaming potential measurements have been reported [28,29,30,31,32,33,34,35,36]. The main point to be addressed is the question in how far the diffuse layer properties correlate with the interlayer charge based on the stochiometric composition. So far, there is only a very limited number of suitable data sets available, for example for hematite [37].
A further, independent assessment of the effective diffuse layer charge is carried out by the adsorption of highly defined polyelectrolytes to the clay platelets. The adsorption of poly(amidoamine) (PAMAM) dendrimers can be easily detected by AFM [38,39,40]. Their physicochemical behavior has been described in detail by experiments and simulations [41, 42]. Moreover, the adsorption can be described by means of the random sequential adsorption (RSA) model [43,44,45,46]. Utilizing a recent extension of the RSA model, the so-called 3-body RSA, which takes the influence of a charged collector surface into account, allows to evaluate in how far polyelectrolyte adsorption is influenced by the differences in the diffuse layer properties for the different types of clays.
Experimental
Melt synthesis of clays
All three layered silicates with target compositions of [Na1.0]inter[Li1.0Mg5.0]oct[Si8]tetO20F4 (Na1.0, cf. ref. 26), [Na1.7]inter[Li1.7Mg4.3]oct[Si8]tetO20F4 (Na1.7, cf. ref. 27), and [Na4]inter[Mg6]oct[Si4Al4]tetO20F4 (Na4.0 or also known as “brittle mica,” cf. ref. 25) were synthesized via the melt possibly followed by long term annealing. Details of the synthesis and characterization have been published previously.
Briefly, the educts were mixed according to the nominal composition (≈ 0.1 mol) in a glovebox under argon into Mo-crucibles. The Mo-crucibles (Plansee, Austria) were first heated in a radiofrequency induction furnace to remove remaining traces of water. The crucible was then closed with a conical lid and sealed by welding. Subsequently, the crucible was transferred to an argon floated graphite rotary kiln (60 rpm) (Graphit HT-1900, Linn High Therm) and was ramped to 1750 °C (15–20 °C min−1), held at this temperature for 60–70 min, cooled to 1300–1250 °C (cooling rate 50–55 °C min−1), and then slowly (cooling rate < 10 °C min−1) below the melting point (800–1050 °C). Finally, it was quenched by switching off the power. The fluorohectorites (Na1.0 and Na1.7) were at last annealed at 1045 °C for 6 weeks while the brittle mica was used as received.
For reference purpose natural muscovite mica (M-mica) of V3 grade (Plano GmbH) was used as received. Prior to sample preparation all clays were pestle grinded and sieved through a stainless-steel sieve with 0.125 mm mesh.
Immobilization of clay platelets
For AFM and colloid probe measurements the clays were dispersed in Milli-Q water (1–2% w/w). Glass slides for optical microscopy were used as substrates, which were modified by means of amino-terminated silane in order to obtain positively charged but at the same time flat surfaces [47]. Here, a silane with one ethoxy-group has been used to secure the formation of a silane-monolayer only [48]. The drop of the suspension with the clay platelets was put on an amino-silanized glass slide and subsequently dried at 200–250 °C on a hot plate. To remove weekly adsorbed platelets, the slide was then rinsed with water and dried as before. RCA-cleaned [49] glass substrates were modified by a gas phase silanization (1 mbar, 4 h) with 3-aminopropyl-diisopropylethoxy-silane (abcr GmbH, Germany).
AFM imaging of native clay platelets
The surface topography of the immobilized clay platelets was determined by tapping mode AFM in air (Dimension 3100 equipped with a NanoScope V controller, Bruker). These measurements were performed with cantilevers (OMCL-AC160TS, Olympus) preselected for a tip radius below 10 nm. This selection has been performed by imaging a Nioprobe standard (Aurora Nanodevices, BC, Canada).
Colloid probe preparation and calibration
Colloid probes (CP) were prepared by recently described sintering technique using tipless silicon cantilevers (NSC12, MikroMasch, Bulgaria) and silica particles (∅ = 6.8 μm, Bangs Laboratories Inc.), respectively [50]. There a “neck” made of ludox silica nanoparticles (Ludox AM-30, Sigma-Aldrich) ensures the high mechanical stability of the attached colloid to the cantilever. The spring constant of the used cantilevers was calibrated using the thermal noise method for the sintered colloid probe [51]. The calibration of the colloidal probes’ diffuse layer properties has been achieved in the symmetrical sphere-sphere geometry, whereby the diffuse layer potential as well as the regulation parameter for the silica particle have been determined. For that similar silica particles were sintered in an analogous manner to the surface of a quartz slide.
Direct force measurements with colloid probe AFM
The measurements were conducted in the semi-closed fluid cell at MFP-3D (Asylum Research, Santa Barbara, CA). After mounting a slide with immobilized platelets in the fluid cell, it was filled with the degassed working solution (I = 1.2 mM, pH 5.5). Removal of dissolved gas was accomplished in two steps: firstly, nitrogen was purged through the electrolyte solution, and secondly, a HPLC- degassing unit was used directly before the measurements (FLOM Gastorr BG12).
The interaction force profiles were acquired for a given pair CP-clay platelet for at least 50 times in approach and retraction cycles with a velocity of 0.8 μm/s. For the given pair, no differences between the first and the last curve could be observed. The maximum loading force was in the order of 10–12 nN. Three colloid probes (k = 0.112–0.540 N/m) were used, and each probed at least 5 platelets of given types of clays.
The measurement of the interaction forces between two silica particles in the sphere-sphere geometry has been performed in the same way as for CP versus clay platelet. The two particles, one attached to the probe and one attached to the substrate, were first coarsely aligned by optical microscopy; the following fine alignment was achieved by a procedure similar to force volume plots. Further details are given elsewhere [52, 53].
The measured deflection versus piezo displacement curves were converted to force versus distance profiles by custom written procedures in IGOR PRO (Wavemetrics) based on standard algorithms [21]. In order to determine the diffuse layer potential of a platelet, 30–40 force profiles attributed to one pair interaction were averaged and normalized by the effective radius R. The F/R vs. distance profiles were fitted to the full-solution of the Poisson-Boltzmann equation with charge regulation approximation. In symmetric system, two parameters, namely diffuse double layer potential and charge regulation parameter, are being determined. In the asymmetric system, those parameters must be fixed for one surface to obtain the two parameters for another substrate [54,55,56]. More details are given in the Supporting Information. Routinely, the Debye-length obtained from these fits is compared to the nominal ionic strength of the electrolyte solution. The observed deviations for the presented results were smaller than 10%.
Electrophoretic mobility
For electrophoretic mobility measurements, we used aqueous dispersions with ca. 0.05% w/w of grinded clays (pH 5.5, total ionic strength I = 5 mM). The freshly prepared dispersion were allowed to sediment for at least 30 min in order to separate the light fraction with platelets of sub-10-μm size, resulting in a solid content of the supernatant suspensions of 0.03–0.04% w/w, which was determined gravimetrically. The supernatant was measured immediately after immersing in the cell using a commercial microelectrophoresis device (ZetaView PMX 100, ParticleMetrix GmbH). Measurement data were collected at the stationary planes for at least three times. The details on the procedure can be found elsewhere [57].
Streaming current detection
Shortly, a streaming current setup consists of a Teflon cell with two incorporated electrodes and a Teflon piston. While the clay dispersion is put into the cell the piston makes reverse translational motion to create a flow. Since colloid platelets tend to adsorb onto hydrophobic Teflon surfaces the resulting flow voltage is measurable. Upon addition of titrant the voltage between the electrodes is changing, so one can calculate the approximate surface charge and hence the potential on the surface of charged colloid species in the dispersion [17, 18].
For the measurements involving streaming current detection, aqueous dispersions with 0.1–0.2% w/w of grinded clays (pH 5.5, I = 100 (50) mM) were prepared. The streaming current detection has been performed by means of a commercial device (StabiSizer® PMX 200C, Particle Metrix GmbH), which has been used in the charge titration mode.
PAMAM dendrimer adsorption on clay platelets
PAMAM dendrimers of generation G10 were obtained from aqueous solutions (Dendritech, Midland, MI). For all dendrimer solutions, a concentration of 10 mg/L in Millipore water was used. An ionic strength of 0.1 mM with pH 4 was adjusted with HCl for dendrimer adsorption and subsequent washing solutions, respectively. Silicon wafers (CrysTec GmbH, Berlin, Germany) were silanized using 3-aminopropyldimethylethoxysilane (abcr GmbH, Karlsruhe, Germany) in a gas phase silanization procedure and then heated at 80 °C for 60 min. Dispersions of different types of layered silicates were placed on modified silicon wafers for 30 min and then dried in a stream of pure nitrogen. For dendrimer adsorption, these silicon wafers or freshly cleaved mica sheets were immersed into the dendrimer solution for 30 min and afterwards transferred into a pure solution of pH 4 for 30 s twice. Otherwise, the procedure was analogous to the one reported previously for mica sheets [40, 58].
AFM imaging after PAMAM adsorption
PeakForce tapping mode AFM images were taken in air using a Dimension Icon (Bruker Nano Inc.). Images were acquired using ScanAsyst Air cantilevers (Bruker Nano Inc.) with a nominal spring constant of 0.4 N/m and a resonant frequency of 70 kHz. Scan sizes of 1 × 1 μm2 were used for the evaluation of the number of absorbed dendrimers. The PeakForce setpoint was adjusted to 0.02 V, the PeakForce amplitude 50 nm and the PeakForce frequency 2 kHz, respectively.
The AFM images were processed with NanoScope Analysis 1.80 (Bruker Nano Inc.). The data was leveled with a first order plane fit and was flattened by subtracting a first order polynomial background. Adsorbed dendrimers were manually counted using Fiji (ImageJ) with the Cell Counter Plugin.
Results and discussion
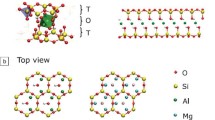
In this study, we concentrated on three different synthetic layered silicates with a 2:1 structure (cf. Fig. 1a) but different interlayer charges. These silicates carry a permanent negative charge at the basal surfaces originating from isomorphous substitution of octahedral or tetrahedral cations. The basal surfaces are terminated by chemically inert oxygen atoms that connect two tetrahedrons via edge sharing (Fig. 1b). Melt synthesis yields platelets representing stacks of hundreds of individual silicate layers with diameters exceeding 10 μm. The edges of the platelets tangling OH-groups are located and hence the edges carry a pH-dependent surface charge with points of zero charge in the range 6–7. Additionally, natural muscovite mica (M-mica) has been included as a ‘reference’ material.
Structure of 2:1 layered silicates like hectorites, micas, and brittle micas. a Stack of silicate layers comprising a platelet with interlayer space and external basal surface. b Top view of the tetrahedral layer representing the a typical external basal surface with a,b dimensions of the unit cell depicted. c Chemical structures of the 2:1 layered silicates studied here
The nominal layer charges as resulting from the average composition of the unit cells for Na1.0, Na1.7, M-mica, and Na4.0 were 1.0, 1.7, 2.0, and 4.0, respectively. These compositions cover a wide range of charge densities of the interlayer and external basal surfaces. The effective charge densities of the interlayers as derived from experimentally determined interlayer concentrations and a,b-unit cell dimensions amount to 2.20 e/nm2, 3.06 e/nm2, 4.26 e/nm2, and 6.65 e/nm2 for Na1.0, Na1.7, M-mica, and Na4.0, respectively. The charge density of the last layer in the stack representing the external basal planes is, however, only half of the values of these interlayer charge densities. The diffuse layer properties of M-mica have been determined extensively by electrokinetic techniques and direct force measurements [28,29,30,31,32,33,34,35,36]. Thus, M-mica provides a suitable “reference” to test the methodology applied in the present study.
In order to immobilize those silicate platelets to a solid substrate, it is sufficient to provide an oppositely charged surface for physisorption (cf. Fig. 2a). Figure 2b shows an exemplary AFM-image of an immobilized Na1.0 platelet. The platelet has an extension of more than 10 μm in both lateral directions. Moreover, the platelets showed a low surface roughness, albeit with a number of small terraces that bear typically a thickness over several hundreds of nanometers. The flatness of hectorite is further demonstrated by the inset in Fig. 2b, which represents a 2-dimensional zoom-in on the surface of the hectorite platelet. The monolayer steps and large areas without any corrugations are clearly visible. Similar low surface roughness has been found for the other two types of silicate platelets and freshly cleaved M-mica, respectively.
a Schematic representation of the immobilization of hectorite platelets on a silane-modified glass surface. b AFM images of an immobilized Na1.0 platelet. Both images have been acquired in Tapping Mode in air under ambient conditions at room temperature with a scan rate of 0.4 Hz (scan size of 20 × 20 μm2 and 5 × 5 μm2, respectively)
Direct force measurements
Figure 3 schematically outlines the general approach that has been followed to determine the diffuse layer (DL) properties of single hectorite platelets: firstly, the diffuse layer properties of the colloidal probe have been obtained in a completely symmetric system, namely in the sphere-sphere geometry between a silica colloidal probe and a silica particle sintered on a flat transparent substrate (cf. Fig. 3a). This determination provides the diffuse layer potential and charge regulation parameter of the probe, which is a prerequisite for a quantitative evaluation of force profiles as determined between different silicates and comparable colloidal probes (asymmetric combination). Secondly, the colloidal probe technique has been used to determine the interaction force profiles on various synthetic layered silicates and M-mica, respectively. Due to the large diameter of the hectorite platelets, these measurements can be considered as taking place in the sphere-plane geometry (cf. Fig. 3b).
Schematic illustration of the experimental approach to determine the diffuse layer properties of single silicate platelets. a First, the diffuse layer properties of the silica colloidal probe are obtained from direct force measurements against another silica particle. b Second, the diffuse layer properties of the different silicates are determined by direct force measurements on the platelets using silica colloidal probes with known diffuse layer properties
Determining the diffuse layer properties of the colloidal probes
A quantitative analysis of direct force measurements between two dissimilar surfaces requires the accurate knowledge of the diffuse layer properties for one of the surfaces. Commonly, the colloidal probe is the “known” surface and its properties have been determined beforehand in a separate set of measurements. Here, we used colloidal probes prepared by a sintering method, which provides a defined silica surface chemistry due to the heat-treatment and an enhanced mechanical stability without using any glue, which is prone to contaminations in the system [50]. In order to determine their diffuse layer properties in a completely symmetric system, we performed measurements in the sphere-sphere geometry [52, 53].
Figure 4 shows a representative force profile as acquired at pH 5.5 and an ionic strength of 1.2 mM with a sintered colloidal probe (cf. inset of Fig. 4) and an immobilized colloidal particle, respectively. Thus, the interaction geometry corresponds to a symmetric sphere-sphere geometry. The interaction forces as acquired during approach were averaged from 30 to 40 individual force profiles and have been normalized to the effective radius Reff, which is given by 1/Reff = 1/R1 + 1/R2, where R1 and R2 are the radii of the colloidal probe and the immobilized particle, respectively. Such a normalization allows to compare differently sized particle pairs and different interaction geometries (sphere-sphere vs. sphere-plane). It is based on the Derjaguin approximation, which relates the measured interaction forces F(D) at a separation D with the free interaction energy W(D) between two infinitely extended plates at the same separation by:
Exemplary force versus distance profile upon approach between a silica colloidal probe and another colloidal silica particle immobilized on a quartz slide. The force profile has been acquired at pH 5.5, I = 1.2 mM and has been averaged from about 30–40 single force profiles. The solid line indicates the fit to the full-solutions of the Poisson-Boltzmann (PB) equation including the constant regulation approximation. By contrast, the dashed lines represent the solution to classical boundary conditions of constant charge (top) and constant potential (bottom), respectively. The insert shows SEM picture of a typical colloidal probe
The interaction force profiles F(D) have been fitted to the full-solutions of the Poisson-Boltzmann (PB) equation, including the classical boundary conditions of constant charge (CC) and constant potential (CP) [59,60,61]. These two boundary conditions are represented by the dashed lines in Fig. 4. Additionally, we included the constant regulation (CR) approximation that takes the charge regulation between the approaching surfaces into account [54]. For the latter, the surface chemistry is summarized by means of the so-called regulation parameter p that has typically values in the range from 0 to 1. It can be shown that p = 0 corresponds to the boundary of CP and p = 1 to CC, respectively [54].
At large separation distances D, which can be considered here D > 20 nm, the solutions for the different boundary conditions (CP, CC, and CR) coincide. In this regime, the interaction forces are decaying in an exponential manner and the decay constant is given by the so-called Debye-length κ−1, which is defined by
where ϵϵ0 is the total permittivity of water, kBT is the thermal energy of the system, NA is the Avogadro’s number, e is the elementary charge, and I is the total ionic strength of the electrolyte solution [59, 61].
From fits to the interaction forces in a completely symmetric, i.e., between two silica particles (cf. Fig. 4), we obtain diffuse layer potentials of ψd = − 50.3 ± 0.5 mV and a regulation parameter of p = 0.74 ± 0.04. Both values fall in the range reported also by other groups, albeit the regulation parameter is slightly higher than reported elsewhere for silica particles in KCl [62]. However, we find that the regulation parameter scattered to a much larger extend than the diffuse layer potentials of the silica particles used here, which have been heat-treated during the sintering procedure [50, 63]. This treatment does lead to a different surface chemistry [20]. We attribute the scattering to the fact that the regulation is taking place for small separation distances where additional factors, such as surface roughness, play a stronger role [63,64,65,66]. However, the diffuse layer properties are not critically dependent on the regulation parameter as in this study only the interaction forces at separation distances larger than κ−1 have been evaluated. Charge regulation is known to take place primarily at separation distances < κ−1. The diffuse layer potential ψd determined here is in good agreement with values reported in other studies for silica particles under comparable conditions.
Direct force measurements on layered silicate platelets
Figure 5a shows some exemplary interaction force profiles acquired by a silica colloidal probe on individual layered silicate platelets of varying charge densities. All force profiles compiled in Fig. 5a have been obtained by the same colloidal probe and under exactly the same electrolyte conditions (i.e., pH 5.5 and I = 1.2 mM). Moreover, it has been taken care to measure the interaction forces at the center of the platelets. Platelets with large lateral dimensions (i.e., > 10 μm) have been specifically selected in order to exclude contributions of the edges and the underlying substrate, which is oppositely charged due to the aminosilane-modification. As mentioned above, the solution pH of the measurements is slightly below the point of zero charge of the edges. The edges will carry a positive surface charge while the basal plane carries a permanent pH-independent negative surface charge [12, 67]. As the lateral dimensions of the platelets are much larger than the interaction area, we nevertheless can safely assume that the measured interaction is exclusively taking place in a sphere-plane geometry, the latter represented by the external basal surface.
a Representative interaction force profiles between a silica colloidal probe and the three different synthetic layered silicates Na1.0, Na1.7, and Na4.0, respectively. Dashed lines represent the constant charge and constant potential boundary conditions, while the solid lines correspond to the fit of the data by constant regulation approximation. b Diffuse layer potentials obtained from the fits to the full-solutions of the Poisson-Boltzmann equation from interaction force profiles (cf. Fig. 5a)
Already a first qualitative examination of Fig. 5 shows that the strength of the repulsive interaction varies significantly for the different types of silicates: The force profiles show at separation distances larger than 12–15 nm the same exponential decay constant as expected for the same ionic strength and thus identical κ−1. Moreover, the repulsive nature of the interaction is in line with negative surface charges as expected for phyllosilicates of the 2:1 structure family [1]. Thus, the varying strength of repulsion has to be attributed to different diffuse layer potentials. The repulsion decreased in the order Na1.0, Na1.7, and Na4.0. This order is, however, opposite to expectations based on the interlayer charge within the platelets. A quantitative evaluation based on fits to the full solutions of the PB equation is given below, but the order of the diffuse layer potentials is already evident from the force profiles shown here. At smaller separation distances, charge regulation leads to interaction forces that are falling between the classical boundary conditions CC and CP. Only for Na4.0, we find an additional repulsive force at separation distances smaller than 5 nm. The absence of attractive forces at small separation distances due to van der Waals forces is attributed to the significant roughness of the silica particles [52, 63] and has been reported previously for a variety of surface combinations, including cases where the second surface is atomically flat on a local scale [66, 68].
The force profiles have been quantitatively evaluated by fits to the full-solutions of the PB equation in an analogous manner as for the silica particles (cf. Fig. 4). Again, the solid lines in Fig. 5a indicate fits to the CR-approximation that describes the measured interaction forces better, especially at small separation distances. However, it has to be pointed out that the fits are limited to separation distances larger than 20 nm and therefore the diffuse layer potentials obtained from these fits are only weakly depending on the regulation behavior of both surfaces involved [54, 55]. Figure 5b summarizes the diffuse layer potentials as obtained for platelets of the different types of charge density. The data shown in Fig. 5b have been compiled from diffuse layer potentials acquired on different silicate platelets (at least 3 each) and different colloidal probes (at least two different), respectively. The obtained diffuse layer potentials vary between the different types of investigated silicates. The difference in the average values are significant even despite the large standard deviations in the diffuse layer potentials for each individual type of charge density. Additionally, for comparison, the data obtained by colloidal probe measurements on M-mica have been included. This type of natural layered silicate has been well studied by direct force measurements [28,29,30] as well as by electrokinetic methods [31,32,33,34,35,36]. Most likely due to the pristine K+ counter cation, as in contrast to Na+ for the synthetic layered silicates used here, an offset in the absolute values is expected and the DL potentials cannot be compared. M-mica rather is included to validate our methods. Moreover, also a time dependence in the zeta potentials has been reported previously [30, 34, 35], which could be also observed here (cf. Fig. 5b). Within about 30 min, the DL potential, as determined by fits to the full solutions of the PB equation increased by as much as 60 mV. The DL potentials of M-mica as observed here, are, however, well in the range for the values reported previously in literature validating our method [32, 36]. Moreover, also the time dependence of the diffuse layer potentials has been reported previously [30, 36].
Variability of diffuse layer potentials
For all types of layered silicate studied here, we observed a rather large variation in the diffuse layer potentials, which is in the order of 15–25% of the average DL potential. The origin of these large variations in diffuse layer potentials demands further consideration, in particular in respect to the question if the variations arise within each individual platelet or whether it rather reflects differences between platelets. Figure 6a summarizes the DL potentials measured for different positions of a grid on a single platelet of Na1.0 in a so-called force-volume plot. The different potentials obtained from full-fits to the PB-equation are represented here by a grayscale. There is no clear correlation for the position on the platelet and the observed diffuse layer potential. It should be pointed out that due to the featureless surface topography of platelets any topographic influence cannot be made responsible for the observed variations. We find similar trends also for platelets of the other types of layered silicates investigated. A set of measurements comparing the intra-platelet variation with the inter-platelet variation indicates that the observed variations have to be attributed to a large extend to variations within each individual platelet (cf. Fig. 6b).
a Force map composed from 4 × 4 force vs. distance curves acquired on an individual Na1.0 platelet. The false color scale has been attributed on base of the diffuse layer potentials (DL) determined from the fits to PB-equation for the single force profiles. b Comparison of DL potentials acquired on individual platelets of different layered silicate types (Na1.0, Na1.7, and Na4.0) at different positions
Electrokinetic methods
In order to corroborate the counterintuitive sequence of the diffuse layer potentials, which is just opposite to the one expected from the stochiometric interlayer charge, we utilized two independent electrokinetic techniques: electrophoretic mobility and streaming current detection. Measurement of the electrophoretic mobility represents a standard technique, also for clays [69], which allows to determine the so-called ζ-potential [14]. This potential is directly related to the diffuse layer potential as it corresponds to the latter at the plane of shear of the liquid streaming around a particle while it is moving due to an externally applied electrical field [13, 14]. In the case of sufficiently large particles and ionic strengths, the Smoluchowski limit is given by κR > 100 [13, 14]. In the case of platelets instead of spherical particles, this limit can nevertheless be utilized in an approximate manner provided that the aspect ratio of the platelets is large enough and that the ionic strength of the electrolyte solution is high enough. Therefore, the ionic strength has been increased from 1.2 to 5 mM in order to suppress, at least partially, geometric contributions of the non-spherical shape of the platelets. Figure 7 a summarizes the electrophoretic mobility μeff for the different types of silicates. The same sequence for the electrophoretic mobility, which is approximately proportional to the ζ-potential, has been obtained for the different types of layered silicates. The layered silicate with the lowest stoichiometric interlayer charge density shows the highest mobility and vice versa. In order to exclude that the dimensions of the platelets of the different layered silicates have a significant influence on the electrophoretic mobility, we utilized an additional electrokinetic technique, the so-called streaming current detection. This method detects the streaming current resulting from platelets adsorbed to the hydrophobic surface from a stamp cell while moving a piston [17, 18]. Hence, it is intrinsically independent of the platelet dimension but only semi-quantitative in terms of the streaming potentials retrieved. It is used commonly to detect the iso-electric point of inorganic suspension of non-spherical shape. Here, it can be used to estimate the streaming potential of the different types of 2:1 layered silicates. By estimating the streaming potential from the streaming current via a linear relation, we have been able to confirm also by this method the sequence Na1.0, Na1.7, and Na4.0. Again, high ionic strengths have been necessary in order to guarantee a sufficiently high bulk conductivity for the streaming current [18, 19].
a Electrophoretic mobility of different types of layered silicates as determined by micro-electrophoresis. The dashed line is a guide to the eye only. b Comparison of the data obtained by the different techniques (AFM in green, electrophoretic mobility in red and streaming current in blue, respectively). The dashed lines indicate guides to the eye. In order to allow for a comparison, we normalized the data obtained by different values for the ones obtained for Na1.0 to 1 (further explanation is found in the text)
In Fig. 7b, the results from measurements by the different techniques have been summarized. In order to allow for a comparison, we assumed as 1st-order approximation a linear relationship between electrophoretic mobility and zeta potential as well as between streaming current and streaming potential, respectively. Hence, all measurement data can be considered to some degree of accuracy as related to the “potential” of the diffuse layer, albeit at different positions within the diffuse layer. We normalized the respective values from the different methods to those obtained for Na1.0, which has been set arbitrarily to 1.0. It becomes obvious that independent of the method and the solution ionic strength, the sequence of the charging states for different types of 2:1 layered silcates in solution remains constant (cf. guides to the eye in Fig. 7b). Hence, we exclude at the present state that the inverse relation between diffuse layer charge and stochiometric charge has to be attributed to measurement errors. While the sequence for the potential obtained does not change independently from the technique used, we find no perfect quantitative match for the normalized potentials of the 2:1 layered silicates. However, it should be noted that due to the different ionic strength used for the various analytical techniques, such a deviation would be expected on base of the Grahame equation, which already in its linearized form would stipulate a dependence of the potential on ionic strength by means of ψ = 2πκσ, where σ is the diffuse layer charge density on the silicate platelet. The latter can be assumed to be constant in a first order approximation.
Visualizing surface charge by adsorption of macroions
The adsorption of polyelectrolytes as macroions depends also on the surface charging state of the collector surface [70, 71]. Due to their highly defined shape and low polydispersity poly(amidoamine) (PAMAM) dendrimers are particularly well suited for adsorption studies by AFM [38,39,40]. Here, PAMAM dendrimers of generation G10 have been adsorbed to the external basal surface of the various types of layered silicate platelets under the same conditions, i.e., pH 4 and I = 0.1 mM, as reported previously [40]. Figure 8 a shows an image of the topography of PAMAM G10 dendrimers adsorbed to a M-mica surface. The cross sections shown in Fig. 8b illustrate the narrow size distribution and thus low polydispersity for these dendritic structures. The observed diameter is compatible with the dimensions reported previously. It should be noted that the diameter in the AFM image is convoluted with the shape of the AFM tip, thus, the dendrimers appear broader. For the following calculations, we used a diameter of 9.15 nm in the adsorbed state [40].
a AFM image of the surface topography of PAMAM G10 dendrimers adsorbed to M-mica. The image has been acquired by PeakForce Tapping mode in air. The white lines indicate the positions where cross-sections have been taken. b Cross- sections illustrating the narrow size distribution of PAMAM dendrimers used in this study. Each color belongs to one cross section
Figure 9 a illustrates the adsorption onto layered silicate platelets immobilized to an amino-modified solid substrate (cf. Fig. 9a). Figure 9 b shows in an exemplary manner an AFM image for Na1.0, while Fig. 9c shows a single Na1.0 platelet covered with PAMAM G10 after the adsorption procedure. The single dendrimers can be easily distinguished on flat parts of the platelet. The low fractional surface coverage is characteristic for the adsorption of PAMAM dendrimers in a highly charged state under low ionic strength conditions [40]. We could recently demonstrate that PAMAM dendrimers can be also used due to their unique shape and molecular weight distribution as probe for the surface chemistry of clay platelets [72].
a Schematic representation of a substrate with the immobilized hectorite platelets on which the adsorption of dendrimers has been carried out. b AFM image of bare Na1.0 platelets immobilized on an amino-modified wafer before the adsorption. c AFM image of a single Na1.0 platelet after adsorption of PAMAM G10. The single dendrimers are clearly visible. d, e Schematic representation of the influence of the surface charge density on the adsorption process. According to the 3-body RSA model, the adsorption of PAMAM dendrimers on higher charged surfaces are expected to be higher (d) and thus showing a higher surface coverage. Lower surface charge density (e) are expected to adsorb smaller amounts as the inter-dendrimer repulsion is larger due to the higher effective Debye-screening length (see images at bottom of d, e)
Three-body RSA
The adsorption of dendrimers to charged surfaces follows the so-called 3-body RSA model, which takes also the electrostatic influence of the collector surface into account. Thus, the adsorption of dendrimers represents a versatile approach to probe the surface charge density of the different surfaces [58, 73, 74]. The adsorption can be also described quantitatively on base of an extended RSA model [73].
The adsorbed amount of PAMAM dendrimers represents an additional, independent indicator to indirectly probe the diffuse layer charge density of the 2:1 layered silicates: According to the 3-body RSA model, the adsorption of PAMAM dendrimers on higher charged surfaces should be higher (cf. Fig. 9d, e inspired by ref. 58). The presence of more counter ions near the highly charged interface leads to an additional screening, which can be expressed by means of an reduced effective Debye-length [58, 73]. The effective screening length can then be utilized to provide a quantitative description of the adsorption in terms of the extended RSA-model as introduced by Adamczyk and coworkers [44]. Thus, the 3-body model assumes a non-ideal collector-surface in difference to the classical or extended RSA model. Thus, the adsorbed amount or fractional surface coverage of PAMAM dendrimers, easily accessible by AFM imaging (cf. Fig. 9c) allows to probe the surface of layered silicate platelets. Due to the large diameter of the platelets synthesized here, we can easily determine the number density on areas as large as 1 × 1 μm2 that are well separated from the platelet’s edges.
Figure 10 a and b shows exemplary images of PAMAM dendrimers G10 adsorbed on Na1.0 and Na1.7 platelets, respectively. The adsorption has been carried out at pH 4.0 and an ionic strength I = 0.1 mM. The image size of 1 × 1 μm2 only represents a small area of the respective silicate platelets. For comparison, we additionally imaged the dendrimers on a cm-sized sample of M-mica (cf. Fig. 8c). Based on at least 5 different platelets of Na1.0 and Na1.7, respectively, and at least two independent adsorption experiments, we obtained the surface coverages summarized in Table 1.
PeakForce Tapping Mode AFM images of different types of adsorbed PAMAM dendrimers on a Na1.0, b Na1.7, and c M-mica, respectively. Such images have been used to determine the number density for the different layered silicates (cf. Table 1)
Again counterintuitive and opposite to expectations but in line with the measurement of the DL properties, the dendrimer adsorption experiments showed that the silicate platelets with the higher stoichiometric interlayer charge density behave as if they have a lower surface charge density. Thus, the adsorbed amount of PAMAM G10 on Na1.7 is about 40% lower than for Na1.0. The adsorbed amount on M-mica is slightly higher than for Na1.7 and thus follows the order observed in the DL properties. Moreover, we find that for M-mica the fractional surface coverage is in very good agreement with previously published results under the same adsorption conditions.
Conclusions
The colloidal probe technique based on the AFM is an analytical technique that allows to probe the diffuse layer properties of clays on the single platelet level. In difference to electrokinetic techniques, it is not necessary to make additional assumptions about the plane of shear as the full interaction potential is measured. Moreover, despite the micrometer-sized colloidal probes, it is still possible to determine the diffuse layer properties in a laterally resolved manner and thereby to address questions like the heterogeneity of the charge distribution on single platelets.
Here, we studied three purposely synthesized types of 2:1 layered silicates with large platelet diameters. The most important finding of this study is that the stochiometric interlayer charge does not correspond to the diffuse layer charge as determined by the colloidal probe technique and two different electrokinetic methods. We attribute this difference to the adsorption of ions onto the silicate surface. These ions are tightly bound in the Stern layer. Similar mechanisms have been reported previously [37, 67]. This effective diffuse layer potential is also the one responsible for the adsorption of polyelectrolytes as we could demonstrate by the adsorption of highly defined PAMAM dendrimers. The findings are of high relevance especially for a rational understanding of the design and processing of composite materials, for example in relation to their rheological properties [2, 75].
References
Bergaya F, Theng BKG, Lagaly G (2006) Developments in clay science. Elsevier
Lagaly G (2006) Chapter 5 colloid clay science. In Developments in Clay Science: Handbook of Clay Science, eds. Bergaya F, Theng B K G, Lagaly G, p. 141. Elsevier
Doblhofer E, Schmid J, Rieß M, Daab M, Suntinger M, Habel C, Bargel H, Hugenschmidt C, Rosenfeldt S, Breu J, Scheibel T (2016) Structural insights into water-based spider silk protein–nanoclay composites with excellent gas and water vapor barrier properties. ACS Appl Mater Interfaces 8:25535–25543
Kodama T, Komarneni S (1999) Na-4-mica: Cd2+, Ni2+, Co2+, Mn2+ and Zn2+ ion exchange. J Mater Chem 9:33–539
Zhu J, Breu J, Hou H, Greiner A, Agarwal S (2019) Gradient-Structured Nonflammable Flexible Polymer Membranes. ACS Appl Mater Interfaces 11:11876–11883
Zammarano M, Franceschi M, Bellayer S, Gilman JW, Meriani S (2005) Preparation and flame resistance properties of revolutionary self-extinguishing epoxy nanocomposites based on layered double hydroxides. Polymer. 46:9314–9328
Edenharter A, Feicht P, Diar-Bakerly B, Beyer G, Breu J (2016) Superior flame retardant by combining high aspect ratio layered double hydroxide and graphene oxide. Polymer. 91:41–49
Lagaly G (1979) The “layer charge” of regular interstratified 2:1 clay minerals. Clay Clay Miner 27:1–10
Laird DA, Scott AD, Fenton TE (1989). Clay Clay Miner 37:41–46
Kaufhold S, Dohrmann R, Ufer K, Meyer FM (2002). Appl Clay Sci 22:145–151
Mermut AR, Lagaly G (2001). Clay Clay Miner 49:393–397
Zhao H, Bhattacharjee S, Chow R, Wallace D, Masliyah JH, Xu Z (2008) Probing surface charge potentials of clay basal planes and edges by direct force measurements. Langmuir. 24:12899–12910
Delgado AV, Gonzalez-Caballero E, Hunter RJ, Koopal LK, Lyklema J (2005). Pure Appl Chem 77:1753–1805
Hunter RJ (1989) Zeta-potential in colloid science. Zeta-potential in colloid science. Academic Press, New York
Delgado ÁV, González-Caballero F (1998). Croat Chem Acta 71:1087–1104
Thomas F, Michot LJ, Vantelon D, Montarges E, Prelot B, Cruchaudet M, Delon JF (1999) Colloids Surf A. 159:351–358
Dentel SK, Kingery KM (1988) An evaluation of streaming current detectors. AWA Research Foundation-Research Report. American Water Works Association
Barron W, Murray BS, Scales PJ, Healy TW, Dixon DR, Pascoe M (1994) Colloids Surf A 88:129–139
Walker CA, Kirby JT, Dentel SK (1996) The streaming current detector: a quantitative model. J Colloid Interface Sci 182:71–81
Kobayashi M, Skarba M, Galletto P, Cakara D, Borkovec M (2005) Effects of heat treatment on the aggregation and charging of Stöber-type silica. J Colloid Interface Sci 292:139–147
Senden TJ (2001) Force microscopy and surface interactions. Curr Opin Colloid Interface Sci 6:95–101
Butt H-J, Berger R, Bonaccurso E, Chen Y, Wang J (2007). Impact of atomic force microscopy on interface and colloid science. Adv Colloid Interface Sci 133:91–104
Yan L, Englert AH, Masliyah JH, Xu Z (2011) Determination of anisotropic surface characteristics of different phyllosilicates by direct force measurements. Langmuir. 27:12996–13007
Xing Y, Xu M, Gui X, Cao Y, Babel B, Rudolph M, Weber S, Kappl M, Butt H-J (2018) The application of atomic force microscopy in mineral flotation. Adv Colloid Interface Sci 256:373–392
Kalo H, Milius W, Braeu M, Breu J (2013) Synthesis and single crystal structure refinement of the one-layer hydrate of sodium brittle mica. J Solid State Chem 198:57–64
Stöter M, Kunz DA, Schmidt M, Hirsemann D, Kalo H, Putz B, Senker J, Breu J (2013) Nanoplatelets of sodium hectorite showing aspect ratios of ≈20 000 and superior purity. Langmuir. 29:1280–1285
Kalo H, Milius W, Breu J (2012) Single crystal structure refinement of one- and two-layer hydrates of sodium fluorohectorite. RSC Adv 2:8452–8459
Senden TJ, Drummond CJ (1995) Surface-Chemistry and Tip Sample Interactions in Atomic-Force Microscopy. Colloids Surf A 94:29–51
Nishimura S, Kodama M, Noma H, Inoue K, Tateyama H (1998) The use of AFM for direct force measurements between expandable fluorine mica. Colloids Surf A 143:1–16
Raviv U, Laurat P, Klein J (2002) Time dependence of forces between mica surfaces in water and its relation to the release of surface ions. J Chem Phys 116:5167
Pashley RM (1981) DLVO and hydration forces between mica surfaces in Li+, Na+, K+, and Cs+ electrolyte solutions: A correlation of double-layer and hydration forces with surface cation exchange properties. J Colloid Interface Sci 83:531–546
Scales PJ, Grieser F, Healy TW (1990) Electrokinetics of the muscovite mica-aqueous solution interface. Langmuir. 6:582–589
Lyons JS, Furlong DN, Healy TW (1981) The electrical double-layer properties of the mica (muscovite)-aqueous electrolyte interface. Aust J Chem 34:1177–1187
Nishimura S, Tateyama H, Tsunematsu K, Jinnai K (1992) Zeta potential measurement of muscovite mica basal plane-aqueous solution interface by means of plane interface technique. J Colloid Interface Sci 152:359–367
Nishimura S, Scales PJ, Tateyama H, Tsunematsu K, Healy TW (1995) Cationic modification of muscovite mica: an electrokinetic study. Langmuir. 11:291–295
Sides PJ, Faruqui D, Gellman AJ (2009) Dynamics of charging of muscovite mica: measurement and modeling. Langmuir. 25:1475–1481
Lützenkirchen J, Heberling F, Supljika F, Preocanin T, Kallay N, Johann F, Weisser L, Eng PJ (2015). Faraday Discuss 180:55–79
Li J, Piehler LT, Qin D, Baker JR, Tomalia DA, Meier DJ (2000) Visualization and characterization of poly(amidoamine) dendrimers by atomic force microscopy. Langmuir. 16:5613–5616
Muller T, Yablon DG, Karchner R, Knapp D, Kleinman MH, Fang HB, Durning CJ, Tomalia DA, TURRO NJ, Flynn GW (2002) AFM studies of high-generation PAMAM dendrimers at the liquid/solid interface. Langmuir. 18:7452–7455
Pericet-Camara R, Papastavrou G, Borkovec M (2004) Atomic force microscopy study of the adsorption and electrostatic self-organization of poly(amidoamine) dendrimers on mica. Langmuir. 20:3264–3270
Likos C N, Ballauff M (2005) Equilibrium structure of dendrimers - results and open questions. Top Curr Chem 245:239–252
Ballauff M, Likos CN (2004) Dendrimers in solution: insight from theory and simulation. Angew Chem 43:2998–3020
Feder J (1980) Random sequential adsorption. J Theor Biol 87:237–254
Adamczyk Z, Warszynski P (1996) Role of electrostatic interactions in particle adsorption. Adv Colloid Interface Sci 63:41–149
Adamczyk Z, Senger B, Voegel JC, Schaaf P (1999) Irreversible adsorption/deposition kinetics: a generalized approach. J Chem Phys 110:3118–3128
Senger B, Voegel JC, Schaaf P (2000). Irreversible adsorption of colloidal particles on solid substrates. Colloids Surf A 165:255–285
Ulman A (1996) Formation and structure of self-assembled monolayers. Chem Rev 96:1533–1554
Terracciano M, Rea I, Politi J, De Stefano L (2013). Optical characterization of aminosilane-modified silicon dioxide surface for biosensing. J Eur Opt Soc-Rapid 8:13075
Kern W, Puotinen DA (1970) Cleaning solutions based on hydrogen peroxide for use in silicon semiconductor technology. RCA Review 31:187–206
Kuznetsov V, Papastavrou G (2012) Note: Mechanically and chemically stable colloidal probes from silica particles for atomic force microscopy. Rev Sci Instrum. 83:116103
Hutter JL, Bechhoefer J (1993) Calibration of atomic‐force microscope tips. Rev Sci Instrum 64:1868–1873
Rentsch S, Pericet-Camara R, Papastavrou G, Borkovec M (2006) Probing the validity of the Derjaguin approximation for heterogeneous colloidal particles. Phys Chem Chem Phys 8:2531–2538
Kuznetsov V, Papastavrou G (2014) Ion adsorption on modified electrodes as determined by direct force measurements under potentiostatic control. J Phys Chem C 118:2673–2685
Pericet-Camara R, Papastavrou G, Behrens SH, Borkovec M (2004). J Phys Chem B 108:19467–19475
Popa I, Sinha P, Finessi M, Maroni P, Papastavrou G, Borkovec M (2010) Importance of charge regulation in attractive double-layer forces between dissimilar surfaces. Phys Rev Lett 104:228301
Trefalt G, Palberg T, Borkovec M (2017) Forces between colloidal particles in aqueous solutions containing monovalent and multivalent ions. Curr Opin Colloid Interface Sci 27:9–17
Helfricht N, Klug M, Mark A, Kuznetsov V, Blüm C, Scheibel T, Papastavrou G (2013) Surface properties of spider silk particles in solution. Biomater Sci 1:1166–1171
Pericet-Camara R, Cahill BP, Papastavrou G, Borkovec M (2007) Nano-patterning of solid substrates by adsorbed dendrimers. Chem Commun 3:266–268
Israelachvili JN (1992) Intermolecular and surface forces. American Press, London, New York
Butt HJ, Jaschke M, Ducker W (1995) Measuring surface forces in aqueous-electrolyte solution with the atomic force microscope. Bioelectrochem Bioenerg 38:191–201
Butt H-J, Cappella B, Kappl M (2005) Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf Sci Rep 59:1–152
Smith A, Maroni P, Borkovec M, Trefalt G (2018) Measuring inner layer capacitance with the colloidal probe technique. Colloids Interfaces 2:65–82
Valmacco V, Elzbieciak-Wodka M, Besnard C, Maroni P, Trefalt G, Borkovec M (2016) Dispersion forces acting between silica particles across water: influence of nanoscale roughness. Nanoscale Horiz 1:325–330
van Zwol PJ, Palasantzas G, van de Schootbrugge M, de Hosson JTM, Craig VSJ (2008) Roughness of microspheres for force measurements. Langmuir. 24:7528–7531
Huang X, Bhattacharjee S, Hoek EMV (2010) Is surface roughness a “scapegoat” or a primary factor when defining particle−substrate interactions? Langmuir. 26:2528–2537
Kuznetsov V, Papastavrou G (2012) Adhesion of colloidal particles on modified electrodes. Langmuir. 28:16567–16579
Preocanin T, Abdelmonem A, Montavon G, Luetzenkirchen J (2016) Charging behavior of clays and clay minerals in aqueous electrolyte solutions — experimental methods for measuring the charge and interpreting the results. In Clays, Clay Minerals and Ceramic Materials Based on Clay Minerals, InTech
Barten D, Kleijn JM, Duval J, von Leeuwen HP, Lyklema J, Stuart MAC (2003) Double layer of a gold electrode probed by AFM force measurements. Langmuir. 19:1133–1139
Çelik MS (2004) Clay surfaces: fundamentals and applications. Elsevier Ltd., London
Michna A (2017) Macroion adsorption—electrokinetic and optical methods. Adv Colloid Interface Sci 250:95–131
Netz RR, Joanny JF (1999) Adsorption of semiflexible polyelectrolytes on charged planar surfaces: charge compensation, charge reversal, and multilayer formation. Macromolecules. 32:9013–9025
Stöter M, Gödrich S, Feicht P, Rosenfeldt S, Thurn H, Neubauer JW, Seuss M, Lindner P, Kalo H, Möller M, Fery A, Förster S, Papastavrou G, Breu J (2016) Controlled exfoliation of layered silicate heterostructures into bilayers and their conversion into giant janus platelets. Angew Chem 128:7524–7528
Cahill BP, Papastavrou G, Koper GJM, Borkovec M (2008) Adsorption of poly(amido amine) (PAMAM) dendrimers on silica: importance of electrostatic three-body attraction. Langmuir. 24:465–473
Michna A, Adamczyk Z, Sofińska K, Matusik K (2017) Monolayers of poly(amido amine) dendrimers on mica – in situ streaming potential measurements. J Colloid Interface Sci 485:232–241
Luckham PF, Rossi S (1999) The colloidal and rheological properties of bentonite suspensions. Adv Colloid Interface Sci 82:43–92
Acknowledgments
We thank Carmen Kunert for the SEM imaging of the colloidal probes.
Funding
Open Access funding provided by Projekt DEAL. This work has been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the framework of SFB 840.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(PDF 99 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuznetsov, V., Ottermann, K., Helfricht, N. et al. Surface charge density and diffuse layer properties of highly defined 2:1 layered silicate platelets. Colloid Polym Sci 298, 907–920 (2020). https://doi.org/10.1007/s00396-020-04673-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00396-020-04673-w