Abstract
Water interacting with a polymer reveals a number of properties very different to bulk water. These interactions lead to the redistribution of hydrogen bonds in water. It results in modification of thermodynamic properties of water and the molecular dynamics of water. That kind of water is particularly well observable at temperatures below the freezing point of water, when the bulk water crystallizes. In this work, we determine the amount of water bound to the polymer and of the so-called pre-melting water in poly(vinyl methyl ether) hydrogels with the use of Raman spectroscopy, dielectric spectroscopy, and calorimetry. This analysis allows us to compare various physical properties of the bulk and the pre-melting water. We also postulate the molecular mechanism responsible for the pre-melting of part of water in poly(vinyl methyl ether) hydrogels. We suggest that above −60 °C, the first segmental motions of the polymer chain are activated, which trigger the process of the pre-melting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Various states of water, whose physical and chemical properties are modified by interactions with a solute, have been discussed and studied since the beginning of twentieth century [1]. It is claimed that the states of water interacting with a solute differ from those existing in bulk water in their “structure”, rotational, and vibrational dynamics and freezing temperature. One of the first observations of this distinct water in water-polymer mixtures was performed with calorimetric method [2]. It has been noticed that the enthalpy of melting of ice in water-polymer mixtures is significantly lower than that, which should result from the analytical content of water. It was hence concluded that the interactions with a polymer prevent some fraction of water from freezing. The presence of liquid water below 0 °C in polymer systems has been confirmed by X-ray experiments [3], infrared spectroscopy [4], and, more recently, by broadband dielectric spectroscopy (BDS) [5, 6]. The detection in the last method bases on the presence of dielectric depolarization (at around 18 GHz), which results from rotational reorientation of non-freezing water molecules. The non-freezing water is often linked with the water, which has rotational or translational motions restricted at room temperature due to its interactions with a solute. Although the presence of non-freezing water in polymeric solution has been confirmed with various experimental techniques, the exact relations (both qualitative and quantitative) between the non-crystallized water, the rotationally restricted water, and the water hydrogen bonded to solute molecules are still not well understood.
In this work, we analyze an evolution of intermolecular interactions between water and selected model polymer at temperatures below the freezing point of water with use of Raman spectroscopy. Then, we relate the observed evolution of these interactions with changing fraction of non-crystallized water determined by means of dielectric spectroscopy and differential scanning calorimetry.
As a model system for these studies, we have chosen series of hydrogels with various crosslinking degree prepared by electron-beam irradiation of poly(vinyl methyl ether) (PVME) [7]. PVME is an amphiphilic amorphous polymer, and its aqueous solutions reveal a number of interesting properties, particularly the presence of the lower critical solution temperature (LCST) around 37 °C [8]. Our previous work was devoted to molecular relaxations at temperatures between −60 and 50 °C in the PVME hydrogels; in particular, we have studied the transition revealed around −18 °C, whose origin had been so far unclear [9]. We have shown therein that this transition is related to the pre-melting of water induced by the segmental motions of the polymer. Such phenomenon should be associated with modification of intermolecular interactions between polymer network and water in this temperature range; this hypothesis was one of motivations for the research described in the present work.
The selection of PVME hydrogels for these studies gives us an opportunity to investigate an influence of the crosslinking degree on the content of non-freezing and pre-melting water. Moreover, we would like to compare how these two types of water differ in their thermal properties, rotational motions, and ability to form hydrogen bonds with the polymer in the range of temperatures below the freezing point of water.
Experimental
Material description
Polymer hydrogels were prepared of 50 wt% aqueous solution of PVME (Sigma-Aldrich Co.). The crosslinking was performed by mean of electron-beam irradiation. Details of the radiation synthesis as well as of the sol-gel analysis may be found in our earlier papers [7, 10, 11]. The basic physical properties of studied samples are summarized in Table 1. All the samples were studied in their equilibrium swelling degree. The equilibrium swelling degree (ESD) is defined here as:
where m p is a weight of dry polymer network and m gel is a weight of a swollen hydrogel at a time when its equilibrium swelling is attained. The polymer faction w PVME we define as ratio of m p to m gel.
Experimental techniques
Recently, it has been reported that the kinetics of the crystallization of water and formation of various crystalline forms in PVME/water mixtures strongly depends on the applied cooling rate [3, 12]. It was therefore crucial to apply similar cooling procedures in all our experiments to be allowed to compare directly the results concerning the crystallized and the non-crystallized water. Furthermore, Zhang et al. [3] have reported that above −30 °C, the crystallization temperature of water in PVME/water mixtures strongly depends on the crystallization rate and is almost independent below this temperature. For this reason, in our experiments, the hydrogel samples have been annealed for at least 40 min at the temperature of −50 °C or lower.
Raman spectra were acquired with use of JobinYvon T64000 triple-gratings spectrometer equipped with the Olympus BX40 confocal microscope. The Ar-ion laser (LEXEL) line (514.5 nm) was used as a source of sample excitation. Laser power (4–6 mW at a sample) and time of a single measurement (240–360 s) were adjusted to obtain the high quality spectra. All Raman experiments were conducted with the same microscope objective (x50, N.A. = 0.5), and the laser light was focused 30–40 μm below the sample surface. Low temperature measurements (range −163 to +10 °C) were performed in helium-nitrogen cryostat, and liquid nitrogen was used as a cooling medium. Temperature was stabilized by Lakeshore 330 temperature controller with precision ±0.1 °C. Hydrogel samples were cooled down with a cooling rate over 10 °C/min. To minimalize the water loss (low pressure in the cryostat cell was needed for good temperature stabilization and could result in partial evaporation of water), the air was pumped out from the cell just after crystallization of water (detected by appearance of the ice band in the Raman spectrum). After reaching the temperature -163 °C, and after at least 40 minutes of isothermal annealing, the sample was measured during slow, step-like heating (each step was reached with 1–2 °C/min heating rate and then the sample was measured isothermally for 6 min). Due to such procedure, one can assume that the thermal histories of the samples measured by the Raman and by the dielectric spectroscopies were almost identical.
Differential scanning calorimetry (DSC) measurements were performed using TA2920 and Q1000 calorimeters (TA Instruments Inc.). The mass of inserted samples typically varied between 3 and 6 mg. Standard DSC measurements were performed for the temperature range from −50 to 55 °C. The cooling rate was 10 °C/min and heating rate was 3 °C/min.
Broadband dielectric spectroscopy (BDS) studies were performed using a Novocontrol® Alpha Analyser Concept 80 apparatus in the range of frequency 0.1–107 Hz and in the temperature range −60 to +50 °C, with a temperature step of 3° (only the measurements conducted below 0 °C are the subject of this paper). Samples were placed between two gold-plated brass electrodes in the Novocontrol® Liquid Sample Cells BDS 1308. The liquid sample cell was used in order to maintain a good contact between the sample and the electrodes and to avoid water flowing out of a cell. The dimensions of the sample were 18-mm diameter and 1-mm thickness. A spacer ring 1 mm in thickness, 1-mm wide, and 20 mm in outer diameter, made of silica, was used to ensure stability of the dimensions of the samples.
In order to compare directly the integral intensities of the Raman bands the following mathematical procedure was applied:
-
Each spectrum was normalized in a way that the total area under the curve equals one;
-
The spectra were deconvoluted with PeakFit v4.12 (SeaSolve Software Inc., SYSTAT Software Inc.) assuming a presence of four components in the OH stretching region;
-
The comparison of particular peaks related to different water states was performed on the basis on integral intensities estimated by the deconvolution.
Results
Raman spectroscopy studies
Changes of the supramolecular structure of water and water interactions with PVME are well manifested in the spectral range 2,700–4,000 cm−1, as seen in the Raman spectra of the PVME-65 at several selected temperatures in Fig. 1. This range contains vibrational bands related to both stretching vibrations of CHx of the polymer (bands located between 2,700 and 3,050 cm−1) and stretching vibrations of OH of water (in the range 3,100–3,700 cm−1) [11]. The intense narrow band at around 3,150 cm−1 is a well-known manifestation of a crystallized water, and it is referred to the “collective band of ice” (Icol) [13]. A spectrum of a dry not-crosslinked PVME at 27 °C is additionally shown in the figure for a comparison. The shape of the multi-mode bands of CHx stretching for the frozen hydrogel (2,700–3,050 cm−1, see the inset in Fig. 1) resembles well the corresponding bands for the dry PVME. It is particularly well seen for the symmetric CH3-stretching band (νs(CH3)) at around 2,820 cm−1, which position is the same as the one in the totally frozen hydrogel at the temperatures between −125 and −55 °C. It is known from Maeda’s [14] and from our previous studies [11] that the position of this mode reflects the hydration of the PVME segments. In a neat, dry polymer, it is located at 2,820 cm−1, and in a fully hydrated polymer, it is at around 2,840 cm−1 [9, 14, 15]. The fact that this band shifts back to around 2,840 cm−1 after the cycle of cooling and heating implies also that no significant fraction of water was lost during the cycle, and all the samples studied returned to its initial hydration state.
Raman spectra acquired on heating run at several temperatures −125, −55, −15, −10, and 0 °C for the sample PVME-65; spectra were normalized to the intensity of the polymer band at ca. 2,940 cm−1. The spectrum of neat linear PVME at room temperature is shown as a reference (grey). Changes in the intensities and positions of particular bands on heating are marked with arrows
Actually, the νas(CH3) band (antisymmetric stretching, at around 2,970 cm−1 in a neat polymer) reveals similar hydration-dependence of the spectral position. Yet, the shift is not as clearly visible for the νas(CH3) band as for the νs(CH3) band because the former one is broader and less intense than the latter. These spectral features indicate that in the fully frozen hydrogel, below −55 °C, the polymer chain is dehydrated.
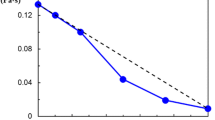
On heating of the sample, despite of the shift of the νs(CH3) and νas(CH3) bands to the higher wavenumbers also the center of the collective ice band at around 3,150 cm−1 shifts to the higher wavenumbers and the intensity of this band diminishes. The shift of the center of the collective band of ice with temperature is a well-known feature of the spectrum of the ice type I [13]. It is interpreted as the result of weakening of hydrogen bonds and coupling between adjacent OH oscillators. Hence, the similar effect observed in frozen hydrogels will not be discussed here. The evolutions of the integral intensity (AI) of the collective band of ice and of the position of the band νs(CH3) on heating in the samples PVME-22 and PVME-65 are summarized in Fig. 2. It is apparent that in both samples, the values of integral intensity AI are constant up to ca. −60 °C. Above this temperature, the value of AI monotonously decreases down to its minimum at 0 °C when all the ice melts. This observation confirms an existence of the phenomenon of pre-melting of ice and points out that the pre-melting processes start already at around −60 °C.
The temperature dependence of the position of the νs(CH3) band of PVME (full symbols, right y-axis) and of the integral intensity of IC band of ice (empty symbols, left y-axis) in the sub-zero range of temperature for sample PVME-22 (squares) and PVME-65 (triangles); lines connecting points are as guide for eyes; temperature of the change in the tendency is marked with the dashed line. One should note that according to Loozen et al. [15, 16] the νs(CH3) band in the neat, uncrosslinked PVME shows a small temperature dependence, shifting to higher wavenumber by ca. 0.03 cm−1/deg with decreasing temperature. The data presented are therefore corrected for that temperature shift with respect to the wavenumber of the νs(CH3) band at 25 °C
One may also see in Fig. 2 that the position of the νs(CH3) band and the value of AI are both approximately constant at the lowest temperatures up to ca. −60 °C and above this threshold strong changes in both quantities occur. In both frozen hydrogels below ca. −60 °C, the νs(CH3) is approximately equal 2,819 cm−1. That means that up to that temperature the PVME chains are dehydrated. Above −60 °C the νs(CH3) band clearly shifts with temperature to higher wavenumbers. In the sample PVME-65 the center position of the νs(CH3) band is around 2,840 cm−1 at ca. −20 °C indicating that the PVME chain is fully hydrated above this temperature. One can conclude that although at −20 °C, there is still significant fraction of ice (AI = 0.1), the amount of pre-melted water in the sample is sufficient to reestablish the network of hydrogen bonds around polymer chains.
Taking into account the known dependence of the position of the νs(CH3) band on the hydration of PVME segments at room temperature [6, 8, 16], we may estimate the local hydration degree of the polymer segments in the temperature range from −120 to 0 °C. We may assume that below 0 °C, the analyzed system is composed of two phases: the network of PVME chains surrounded by not frozen water molecules and the ice crystals. Then, the positions of νs(CH3) should reflect the local concentration of PVME in the liquid phase \( {w}_{{\mathrm{PVME}}_{\mathrm{local}}} \). When a fraction of PVME in a whole sample w PVME is known (see Table 1), the fraction of liquid water in the whole sample w liqH2O may be estimated using the following formula:
The values of w liqH2O determined in such a way were used to estimate the hydration number N (the number of water molecules in liquid state per monomer unit) in different temperatures with use of the formula (3):
where MPVME = 58.08 is a molar mass of the monomer unit of PVME and MH2O = 18.02 is a molar mass of water and w PVME is a polymer fraction derived from sol-gel analysis (Table 1). We assume here that the chemical structure of the PVME monomer unit remains unchanged after radiation crosslinking. The results shown in Fig. 3 clearly indicate that for all samples studied, the hydration numbers are close to 0 below −60 °C, and above this temperature, they abruptly grow up to values 5–8 at −5 °C.
Dielectric spectroscopy studies
In our previous studies of molecular relaxations in PVME hydrogels with use of dielectric spectroscopy in the range 0.1–107 Hz we have noticed an apparent plateau in the plot of the real part of the permittivity (ε’) at high frequencies (f > 105 Hz) [5, 11] (Fig. 4). It is due to the reorientation of water dipoles at gigahertz and sub-gigahertz frequencies, which contributes to dielectric constant in the studied frequency range. Shinyashiki et al. [5] has studied polymer-water mixtures of different compositions (including aqueous solutions of linear PVME) with use of time domain reflectometry (TDR) in the temperature range −55 to +25 °C. They have shown that the dielectric process related to water reorientations decelerates from around 1010 Hz at −2 °C down to around 107 Hz at −30 °C and has the major contribution to dielectric depolarization in the frequency range 105–107 Hz. In addition to the deceleration of liquid water band, they observed a drop in intensity of liquid water band at −5 °C, which was related to the crystallization of the major fraction of water. After partial crystallization of water, the remaining fraction of liquid water continued to decelerate its rotational reorientation on further cooling.
In the isochrones at 106 Hz of PVME hydrogels, which are shown in Fig. 5, one can notice the peculiar changes in the values of dielectric strength ∆ε with temperature; ∆ε = ε r–ε ∞, where ε r and ε ∞ are unrelaxed and relaxed values of dielectric constant, respectively. Given the fact that in the samples studied concentration of water is between 86 and 96 wt%., ∆ε values were calculated assuming that ε ∞ equals its theoretical value for liquid water, i.e., ε ∞ = 1.78. For the samples PVME-22 and PVME-35, the dielectric strength slowly and monotonously increases from −20 up to −3 °C, and at −3 °C, the value of ∆ε abruptly jumps. For the sample PVME-65, we may notice the monotonous growth of ∆ε from −20 to 0 °C. From the Shinyashiki’s TDR studies [5], we may conclude that it is the non-crystallized water, which mostly contributes to the ∆ε at 1 MHz. Hence, the value of the ∆ε below −20 °C should correspond to the non-freezing water. The increase in the ∆ε value between −20 and −3 °C we assign to pre-melting of water and abrupt jumps in ∆ε at −3 °C to the melting of the remaining ice crystals. These results are in a very good agreement with our Raman studies, which demonstrates that at 0 °C all ice in PVME-65 is already melted (see Fig. 2). Both methods (BDS and Raman) show also that in PVME-22, significant fraction of ice starts to melt at 0 °C.
Then, to relate the dielectric strength of water reorientation to the concentration of rotationally unrestricted water c in the sample, we have applied here the Cavell equation [17]:
where: ε is relative permittivity, ε 0 the permittivity of vacuum, N0—Avogadro’s constant, kB—Boltzmann constant, and μ eff—an effective dipole moment. According to Eq. (2), the dielectric strength of the process is proportional to the number of rotating dipoles; in presented case ∆ε at 1 MHz is proportional to c. The quantity of this water may be determined following the Shinyashiki’s assumption that ∆ε would theoretically depend linearly on temperature also below the freezing point providing that all the water stays liquid. We may derive such fictitious value of ∆ε all by linear extrapolation of ∆ε from the positive to the negative temperature range (the result of the extrapolation is marked in Fig. 5 with dashed lines). Taking the abovementioned assumptions, one can calculate a fraction of liquid water w ucw in the hydrogels with the use of the following formula:
where w PVME is a weight fraction of polymer in a hydrogel determined with sol-gel method (see Table 1). The obtained liquid water fraction w ucw can be easily recalculated into the hydration number N of polymer monomer unit with use of the formula (3) if we substitute w liqH2O with w ucw. The BDS determined hydration number vs. temperature for PVME-22, PVME-35, and PVME-65 are plotted in Fig. 6. In all samples studied, the hydration number is practically temperature independent in the range from −50 to −20 °C and equals less than 1 for PVME-22 and PVME-35 and around 3 for PVME-65. N value monotonously grows between −20 and −3 °C and for PVME-22 and PVME-35 equals around 3 at −3 °C. Above −3 °C, the melting of ice takes place in these two samples. In the densely crosslinked PVME-65, we cannot detect typical fusion of ice; instead the fraction of liquid water steeply grows between −20 and 0 °C.
Differential scanning calorimetry studies
DSC-based estimation of an amount of unfrozen water in a system presumes that the enthalpy of melting of ice ∆H all is proportional to amount of water which crystallizes. In the case of the PVME hydrogels, the values of ∆H all (normalized to the fraction of water in a sample) are always lower than the enthalpy of melting of ice for distilled water ∆H H2O. This indicates the presence of some fraction of not frozen water below 0 °C in these systems. The exemplary thermogram (second heating run) for the PVME hydrogel is presented in Fig. 7. The detailed analysis of the thermogram allows distinguishing three different states of water present in a sample:
-
“Normal” bulk water, which melts on heating around 0 °C, with enthalpy ∆H o; in Fig. 7, it is marked by left-slanting lines.
-
Water which crystallizes on cooling but on heating “pre-melts” around −18 °C with the enthalpy ∆H prem.; in Fig. 7, it is marked by right-slanting lines.
-
Water which does not crystallize on cooling and its fraction in a system is described with the formula:
where w b.w. is a weight fraction of water bound to a polymer, w H2O is a total weight fraction of water in a hydrogel, and the enthalpy of melting of ice for distilled water ∆H H2O equals 333 J/g.
The fractions of the non-freezing bound water w b.w in the hydrogel samples were calculated with the use of the formula (6). Then, w b.w substituted w liqH2O in the formula (3) to be expressed as a hydration number N (shown in Fig. 8).
Quantity of this part of water which exhibit pre-melting was also determined from the standard DSC thermograms and is plotted in Fig. 8 as an average number of water molecules per monomer unit of polymer network. One can notice that both values of N have a weak dependence on the irradiation dose for doses up to 42.5 kGy (for samples PVME-22, PVME-35, and PVME-42, N is around 2) and for hydrogels crosslinked with higher irradiation doses these values are higher; in PVME-50, there are around four non-freezing water molecules and around seven pre-melting water molecules per monomer unit. In sample PVME-65, there are four non-freezing water molecules and around six pre-melting water molecules per monomer unit.
Discussion
The general temperature dependence of the frequency of the mode νs(CH3) is similar in all investigated systems. The onset of the blue shift of this band with temperature is located in the range −60 to −30 °C. Such evolution of the position of the νs(CH3) band indicates that on heating from −60 to 0 °C, hydration of PVME segments gradually increases. It is important to note, that the blue shift of this band is accompanied by simultaneous decay of the intensity of the collective band of ice (Fig. 2). The coincidence of these two phenomena points out that when ice starts to pre-melt the produced liquid water immediately constitutes hydrogen bonds with hydrophilic sites at polymer chains.
It is also worthy to note that the increasing hydration of the polymer segments coincides with increasing segmental mobility of PVME. This can be explained by the fact that the α process is associated with the pre-melting of ice, as it was shown in our previous work [9]. Hence, considering calorimetric, dielectric and Raman results the most probably scenario goes as follow: heating of the hydrogel over −60 °C activates the polymer chains mobility which is, however, initially restricted by presence of the ice crystals. Upon further heating, the mobile polymer segments move also some of the neighboring molecules of frozen water what triggers the process of the pre-melting. In the next step, the molecules of liquidized water establish hydrogen bonds with polymer chains. From that point, the polymer chains can move cooperatively with H-bonded water molecules. That cooperativity was manifested as an increase in dielectric strength of the α process of PVME, what we have reported in our previous work [9].
We have studied with use of Raman spectroscopy, dielectric spectroscopy, and calorimetrically, how the amount of non-crystallized water in PVME hydrogels increases with temperature between −50 and 0 °C. The outcomes of our analyses are summarized in Fig. 9, which presents the hydration number N determined with these methods in three hydrogels: PVME-22, PVME-35, and PVME-65. Values obtained by DSC are shown only at −50 °C (the fraction of unfrozen bound water) and at −1 °C (the fraction of unfrozen bound water plus pre-melted water). These temperatures were selected because −50 °C was the lowest point measured by DSC and −1 °C was the highest point below the fusion of ice.
The summary plot presenting the evolution of the hydration number N of the PVME monomer unit in PVME-22 (grey), PVME-35 (empty), and PVME-65 (black) with temperature, determined by DSC (squares), BDS (circles), and Raman spectroscopy (triangles); the values obtained by DSC are plotted at −50 °C (non-freezing bound water) and at −1 °C (non-freezing bound water + pre-melted water). The temperatures were selected arbitrary, −50 °C as the lowest point measured by DSC and −1 °C as the highest point below the fusion of ice; the lines are plotted for eye guidance of the points obtained from Raman spectroscopy
The comparison reveals good qualitative agreement between the results obtained with different techniques. In all studied samples we observe the presence of some fraction of liquid water at −50 °C, i.e., there are around 1–2 water molecules per monomer unit in PVME-22 and PVME-35 and three to four water molecules per monomer unit in PVME-65. Above −50 °C, the hydration number gradually increases with temperature in all hydrogels due to the pre-melting of ice, but this increase is the most pronounced in PVME-65. The differences between N in particular hydrogels should be related to different density of their polymer networks. Hence, the higher amount of unfrozen bound water in the denser crosslinked samples can be a result of confinement of water molecules in tight meshes of these networks. It may imply that in a very dense network, in which some quantity of water is trapped in nanoscopic voids, the nanodroplets of water may be formed. Such nanodroplets can reveal thermodynamic properties very different to these of the “normal” ice and as a consequence melt much below 0 °C [18]. It should be noted that the concept of hydration number N is applicable principally to homogenous liquid systems. As we already mentioned the process of radiational crosslinking composes of generation and recombination of macroradicals. These processes lead to formation of defects such as additional end groups and nods of a polymer network. As a consequence, the thus obtained hydrogel constitutes a highly inhomogeneous system. The hydration of both types of defects is different from the hydration of a monomer unit. As a result, the determined by us hydration numbers are in fact the averaged hydration numbers of various species existing in the PVME networks (regular monomer unit, nod of a network, free end group). These effects are obviously the most apparent in the sample PVME-65.
The applied techniques are tools able to observe different properties of frozen and unfrozen water: their vibrations, rotations in electric field, and thermal properties. From Fig. 9 it is clear that evolution of unfrozen water with temperature seen by all these techniques is qualitatively very similar. Quantitatively, there is also a good agreement between hydration number N determined calorimetrically and N derived from dielectric depolarization. Yet, one may notice some inconsistency concerning the Raman results with those obtained by DSC and BDS. Differences in quantitative data can be due to different accuracy of each technique and assumptions used for the analysis. Raman spectroscopy is especially sensitive to local conformation of molecules (here, the environment of methoxy groups). Increase in a number of unfrozen water molecules is therefore “early detected” and the accuracy of the determination of N is the best in the low temperature range (where the fraction of liquid is the smallest). On further heating, the additional molecules of liquid water are more distant from the polymer chains and thus they are changing the vibrational states of CH3 groups in smaller and smaller degree. On the contrary, the dielectric spectroscopy, in which rotations of dipoles are observed, is the most uncertain in the low temperature region. As we already concluded, the water molecules which pre-melt quickly arrange hydrogen bonds with hydrophilic sites at polymer chain and therefore their rotations are strongly restricted [6]. Hence, they do not contribute to dielectric depolarization, and as a result, those water molecules are “invisible” in dielectric spectra.
Summary and conclusions
We studied states of water at temperatures below 0 °C in PVME hydrogels of various crosslinking degrees. With the use of dielectric spectroscopy, we estimated fraction of water able to rotate in the range of negative temperatures, while the DSC allowed us to determine the amounts of both non-freezing and pre-melting water. We found a good agreement between the DSC and the BDS-based estimations of the hydration number of the PVME monomer unit.
Thanks to high sensitivity of Raman spectroscopy to a local environment of molecules, we perceived that between −163 and −60 °C, the PVME chains are fully dehydrated. We noticed that the pre-melting process starts in significantly lower temperature than was observed by BDS and DSC, i.e., around −60 °C and proceeds with simultaneous reconstruction of hydrogen bonding between the polymer and water molecules.
Based on presented herein results, we postulate the triggering mechanism of the pre-melting process. Namely, we suggest that above ca. −60 °C, the first segmental motions of the polymer chain are activated. Next, these mobile segments move some of the neighboring molecules of frozen water, which triggers the process of the pre-melting.
References
Eisenberg D, Kauzmann W (1969) The structure and properties of water. Oxford classics texts in the physical sciences. Clarendon, Oxford
Magne FC, Portas HJ, Wakeham H (1947) A calorimetric investigation of moisture in textile fibers. J Am Chem Soc 69(8):1896–1902
Zhang T, Li T, Nies E, Berghmans H, Ge L (2009) Isothermal crystallization study on aqueous solution of poly(vinyl methyl ether) by DSC method. Polymer 50:1206–1213
Loozen E, Van Durme K, Nies E, Van Mele B, Berghmans H (2006) The anomalous melting behavior of water in aqueous PVME solutions. Polymer 47:7034–7042
Shinyashiki N, Shimomura M, Ushiyama T, Miyagawa T, Yagihara S (2007) Dynamics of water in partially crystallized polymer/water mixtures studied by dielectric spectroscopy. J Phys Chem B 111:10079–10087
Cerveny S, Colmenero J, Alegria A (2005) Dielectric investigation of the low-temperature water dynamics in the poly(vinyl methyl ether)/H2O system. Macromolecules 38:7056–7063
Janik I, Ulanski P, Rosiak JM (1999) Pulse radiolysis of poly(vinyl methyl ether) in aqueous solution. Formation and structure of primary radicals. Nucl. Inst. Methods Phys. Res., Section B: Beam Interactions with Materials and atoms. Elsevier Science 151(1–4):318–323
Schafer-Soenen H, Moerkerke R, Berghmans H, Koningsveld R, Dusek K, Solc K (1997) Zero and off-zero critical concentrations in systems containing polydisperse polymers with very high molar masses. 2. The system water-poly(vinyl methyl ether). Macromolecules 30:410–416
Pastorczak M, Wübbenhorst M, Dominguez-Espinosa G, Okrasa L, Pyda M, Kozanecki M, Kadlubowski S, Ulanski P, Rosiak JM, Ulanski J (2012) Relaxation processes and intermolecular interactions in PVME hydrogels in sub-zero temperatures: glass transition and pre-melting of ice. Polymer 53(1):161–168
Pastorczak M, Kadlubowski S, Okrasa L, Kozanecki M, Boiteux G, Rosiak J, Ulanski J (2007) Molecular relaxations in radiationally crosslinked poly(vinyl methyl ether) hydrogels. J Non Cryst Solids 353(47–51):4536–4540
Pastorczak M, Kozanecki M, Ulanski J (2009) Water-polymer interactions in PVME hydrogels—Raman spectroscopy studies. Polymer 50(19):4535–4542
Zhang T, Nies E, Todorova G, Li T, Berghmans H, Ge L (2008) Isothermal crystallization kinetics study on aqueous solution of poly(vinyl methyl ether) by FTIR and optical microscopy method. J Phys Chem B 112:5611–5615
Green JL, Lacey AR, Sceats MG (1986) Spectroscopic evidence for spatial correlation of hydrogen bonds in liquid water. J Phys Chem 90:3958–3964
Maeda Y (2001) IR spectroscopic study on the hydration and the phase transition of poly(vinyl methyl ether) in water. Langmuir 17:1737–1742
Van Durme K, Loozen E, Nies E, Van Mele B (2005) Phase behavior of poly(vinyl methyl ether) in deuterium oxide. Macromolecules 38:10234–10243
Loozen E (2009) The influence of hydrogen bonds on the phase behaviour of water soluble polymers. Ph.D. thesis, Katholieke Universiteit Leuven, Leuven
Cavell EAS, Knight PC, Sheikh MA (1971) Dielectric relaxation in non aqueous solutions. Part 2. Solutions of tri(n-butyl)ammonium picrate and iodide in polar solvents. Trans Faraday Soc 67:2225–2233
Marechal Y (2007) The hydrogen bond and the water molecule—the physics and chemistry of water, aqueous and bio media. Elsevier, Amsterdam
Acknowledgments
The authors are deeply grateful to Professor Naoki Shinyashiki and Professor Michael Wübbenhorst for fruitful discussions and their helpful comments. This work was financially supported by The Polish Ministry of Science and Education (grants No. 3TO8E02730 and NN209200738) and National Science Centre (grant No. 2013/09/B/ST4/03010).
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is dedicated to Prof. Friedrich Kremer on the occasion of his 65th birthday.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Pastorczak, M., Dominguez-Espinosa, G., Okrasa, L. et al. Poly(vinyl methyl ether) hydrogels at temperatures below the freezing point of water—molecular interactions and states of water. Colloid Polym Sci 292, 1775–1784 (2014). https://doi.org/10.1007/s00396-014-3283-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00396-014-3283-z