Abstract
The Tibetan Plateau (TP), often referred to as the “Roof of the World”, has experienced rapid warming in recent decades. This warming has had significant impacts on downstream regions, while its effects on upstream regions are less well-defined. This study explores the relationship between TP warming and the occurrence of summer heat stress days in Europe, with a particular focus on Eastern Europe (EEU). Our analysis reveals a robust correlation between TP warming in both the summer and the preceding spring, and the frequency of heat stress days in EEU, demonstrating a significant interannual connection. During the spring, pronounced warming in the southern TP generates a strong local Rossby wave source, triggering a substantial divergence anomaly that amplifies the warming effect. This mechanism weakens the subtropical jet and strengthens the polar jet during the summer, setting the stage for anticyclonic anomalies over EEU. Furthermore, anomalies induced by TP warming, characterized by local upward movement and divergence at upper levels, intensify convergence and sinking airflow in the upstream region, leading to increased adiabatic heating in EEU. The dynamic response of the summer circulation anomaly, exemplified by the anticyclone anomaly over EEU, to prior TP warming is further corroborated through numerical simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The increasing incidence of heat-related fatalities in Europe has brought heat to the forefront of weather-related causes of death (Ebi et al. 2021; Lin et al., 2022). These fatalities are attributed to heat stress days (HSDs) during the summer, characterized by extended periods of hot and dry weather. The profound impact of HSDs on human health, agriculture, and the environment is a growing concern (Perkins-Kirkpatrick and Lewis 2020; Masson-Delmotte et al., 2021, van Daalen et al. 2022). Europe has experienced severe HSD events in the past, notably in 2003 (Black et al. 2004), 2010 (Bastos et al. 2014; Rasmijn et al. 2018), and 2015 (Duchez et al. 2016), with recent years repeatedly breaking historical records for extreme high temperatures (Blunden and Boyer, 2021). A particularly alarming event occurred in 2022 when Europe faced a devastating heatwave, resulting in over 60,000 heat-related deaths between May 30 and September 4 (Ballester et al. 2023), a toll comparable to the excess deaths recorded during the 2003 heatwaves (Robine et al. 2008). This situation underscores the critical need for improved temperature monitoring systems and a deeper understanding of the fundamental mechanisms driving these extreme events.
The occurrence of HSDs in Europe is influenced by various large-scale circulation patterns, with many of these HSDs associated with anticyclonic anomalies over regions experiencing increased temperatures (Stefanon et al. 2012). These anticyclonic anomalies primarily raise surface air temperature through two pathways: first, by providing non-adiabatic heating through reduced cloud cover and intensified solar radiation via strong upper-level divergence, and second, by imparting adiabatic heating through enhanced sinking airflow (Xu et al. 2020; Zschenderlein et al. 2020). The regulation and energy transfer of large-scale circulation patterns, such as atmospheric blockings and jet streams, play a pivotal role in maintaining these local anticyclonic anomalies over Europe (Baldi et al. 2006; Deng et al. 2018; Zhang et al. 2020; Rousi et al. 2022). The weakening of westerly winds amplifies Rossby waves and promotes the formation of atmospheric blockings, creating conditions conducive to sustaining and amplifying extreme high temperatures in Europe (Kornhuber et al. 2017). Moreover, the Tibetan Plateau (TP), with its unique topography and geographic location, significantly impacts the Eurasian climate, particularly the jet stream, through thermal and mechanical forcing (Kang et al. 2019; You et al. 2020a).
In this context, significant research attention has been directed towards unraveling the intricate influence of atmospheric teleconnection patterns on the climate over the TP and its neighboring regions, along with the reciprocal impact of the TP on upstream climate (Zhang et al., 2024). Rodwell and Hoskins (1996, 2001) proposed a linkage between the Mediterranean climate response and Indian summer monsoon heating through the propagation of Rossby waves. Moreover, model experiments involving the presence or absence of mountains effectively replicate the dry or moist climates over central Asia, respectively, driven by the South Asian monsoon circulation during summer, primarily induced by the TP (Broccoli and Manabe, 1992). TP heating has been identified as a key driver of Pakistan monsoon rainfall variability, modulated via Rossby waves in the upper troposphere and weakened water vapor transport in the upstream region (Wang et al. 2019). Drawing primarily from numerical simulations, Lu et al. (2018) demonstrated that summer TP heating may impact upstream climate by intensifying ascending motion over the TP and inducing descending airflow over Europe (Lu et al. 2018). TP heating can exert a profound influence on upstream climate variations ranging from the North Atlantic to West Asia (Liu et al. 2020). However, the specific nexus between TP warming and the heightened occurrence of HSDs in Europe remains an area requiring further elucidation and detailed exploration.
While a prior study posits that the diminishment of summer snow cover over the TP can elucidate over 30% of the total variance in summer elevated temperature variability in both southern Europe and Northeast Asia (Wu et al. 2012, 2016), the underlying causal relationship and the dynamic mechanisms linking these factors remain enigmatic. The objective of this study is twofold: first, to investigate whether a causal relationship indeed exists between the increasing frequency of HSDs in Europe and the warming of the TP; and second, to delve into the way TP warming influences the occurrence of HSDs in the upstream region and the dynamic mechanisms that underpin this intricate connection.
To investigate these critical issues, this study employs wet bulb temperature as the defining metric for HSDs and uncovers their dynamic relationship with TP warming in the preceding spring. The subsequent sections of this paper are organized as follows: Sect. 2 introduces the data and methods used in this research, Sect. 3 presents the findings and results of the study, and Sect. 4 offers a comprehensive discussion of the results and draws conclusions based on the research findings.
2 Data and method
2.1 Data
We utilized the Ensembles daily gridded observational dataset (E-OBS) for the period 1979–2022 to analyze observed daily maximum surface air temperature, sea level pressure, and relative humidity in Europe. This dataset enables the calculation of daily maximum wet bulb temperature, essential for detecting HSDs (Cornes et al. 2018). E-OBS is widely employed for climate monitoring in Europe, especially for assessing the frequency and magnitude of daily extremes. The data is characterized by a horizontal resolution of 0.25°× 0.25°. Summer in this study refers to June-July-August.
To assess the warming of the TP, we used a monthly near-surface air temperature dataset with a high spatial resolution of 0.1°×0.1° (You and Yang, 2023). This dataset offers an extended temporal coverage and fine-grained spatial resolution, making it ideal for studying long-term temperature changes on the TP. The dataset was generated using a deep learning method based on adversarial networks, leveraging observed data from the Climate Research Unit (Jones et al. 2012). Notably, the accuracy of temperature data, especially over the western TP, is enhanced compared to the gridded air temperature data from the Climate Research Unit.
To characterize large-scale atmospheric conditions, we employed the European Centre for Medium-Range Weather Forecasts Reanalysis v5 (ERA5), which encompasses daily geopotential height (Z), horizontal wind (U and V), and temperature in multiple levels (T). ERA5 is a valuable resource for investigating circulation anomalies and diagnosing dynamic processes (Hersbach et al. 2020). Notably, previous research has indicated that the circulation anomalies associated with HSDs in Europe and the main characteristics of the jet stream remain consistent across different reanalysis datasets (Kobayashi et al. 2015; Yin and Zhang, 2021). In this paper, we ensured a uniform horizontal resolution of 1°×1° for the reanalysis dataset using bilinear interpolation.
2.2 Definition of HSDs
Previous research has consistently highlighted that, under equivalent temperature conditions, an increase in air humidity can markedly decrease an individual’s tolerance to heat stress (Zhang et al. 2021; Cvijanovic et al. 2023). To quantitatively assess the impact of HSDs on human health and tolerance, we define HSDs as days when the wet bulb temperature reaches or exceeds 28 °C. For individuals dressed in standard clothing and exposed to low air velocities, a wet bulb temperature of 28 °C represents the upper limit for engaging in moderate levels of physical work (Coco et al. 2016; Brimicombe et al. 2023).
In our calculation of wet bulb temperature, we apply Normand’s rule (Wallace and Hobbs 2006). This method involves determining the lifting condensation level (LCL), where the temperature and dewpoint coincide, on a thermodynamic chart for a parcel of air. Subsequently, we trace the moist adiabat from the LCL back down to the surface to obtain the temperature at the surface, which represents the wet-bulb temperature (Knox et al. 2017). The LCL computation involves several steps, including: (1) determining the dewpoint from the LCL pressure and initial mixing ratio, (2) calculating the LCL pressure using the starting temperature and dewpoint, and (3) iterating until convergence is achieved (Iribarne and Godson 1981; Bohren and Albrecht, 1998; Al-Ismaili and Al-Azri 2016).
2.3 Dynamical diagnosis
This paper uses two-dimensional wave activity flux (WAF) (Takaya and Nakamura 2001) to analyze the propagation of atmospheric Rossby wave trains related to HSDs in Europe and TP warming. The specific calculation equation is as follows:
In the formula, (\({\upphi }\), \(\lambda\)) are the latitude and longitude; p is the pressure;\({p}_{0}\)= 1000-hPa; \(\mathbf{U}\) = (U, V) is the basic flow; a is the radius of the earth;\({\psi }^{{\prime }}=\frac{{\varPhi }^{{\prime }}}{f}\) is the disturbance of geostrophic streamfunction relative to basic flow, in which the \(f\) means the coriolis parameter and the \(\varPhi\) indicates the geopotential.
The intensity of transient disturbance activity is usually represented by the transient kinetic energy (Ke) at the synoptic scale. Referring to Murakami (1979), the calculation formula for Ke is:
\(u\) and \(u\) are zonal and meridional winds respectively, and the superscript “\({\prime }\)” represents the disturbance component, which is obtained from 2.5 to 6 d band-pass filtering of daily wind field data (Murakami 1979). The overbar represents the summer averaged value. The high value of Ke reflects the strong transient wave activity.
To reveal the mean flow variation caused by transient disturbances, referring to Hoskins and Wang (2006), the Eliassen-Palm flux (E-P flux) is calculated as follows:
The divergence of the E-P vector corresponds to the strengthening of the mean westerly airflow, and vice versa corresponds to the weakening of the westerly wind.
Using the wave source equation derived by Sardeshmukh and Hoskins (1988), the distribution of the Rossby wave source (RWS) related to TP warming was diagnosed. The calculation formula of RWS is as follows:
In which, the \(\varvec{u}=(u, v)\) indicates the horizontal wind; \({\nabla }_{H}\)is horizontal gradient operator; \(\zeta\) represents the relative vorticity; the subscript “\(\chi\)” represents the divergent wind component.
The heating forcing caused by preceding TP warming was diagnosed by calculating atmospheric apparent heat sources:
\(T\) means temperature; \(t\) and \(\omega\) represent the time and vertical velocity, respectively; \(\overrightarrow{V}\) is the horizontal wind and the \(\sigma =\frac{RT}{{C}_{p}p}-\frac{\partial T}{\partial p}\) means the static stability, in which the \(R\) is the gas constant, \(p\) is the pressure, and the \({C}_{p}\) is the specific heat at constant pressure.
The horizontal jet core number is used to determine the climatological position of the jet stream axis, which is defined as the number of days in which the wind speed at a given grid point is greater than the surrounding 8 grid points (Xiao et al. 2016).
2.4 Idealized numerical simulations
We used a Linear Baroclinic Model (LBM) to explore the potential influence of heating forcing resulting from preceding warming of the TP on the development of anticyclonic anomalies over Europe. The LBM serves as a valuable tool to comprehend complex feedback mechanisms by isolating the nonlinear aspects of atmospheric dynamic processes, allowing for the calculation of a stable linear response to prescribed forcing, among other capabilities.
The dynamic component of the LBM is constructed based on the dynamic core of the CCSR/NIES Atmospheric General Circulation Models (AGCM) version 5.4 g. A comprehensive description of the model and the linearization equations used can be found in Watanabe and Kimoto (2000). It’s worth noting that prior studies have demonstrated the effectiveness of the LBM in reproducing circulation responses in the mid-high latitudes of the Northern Hemisphere when subjected to prescribed forcing (Yasui and Watanabe 2010; Hayashi and Watanabe 2017). For this study, the model employs a horizontal resolution scheme of T42 (2.8125°×2.8125°) and a vertical height layer consisting of 20 layers.
To verify the robustness of the results based on LBM, we also utilized the Community Atmosphere Model version 5.3 (CAM5.3, the atmospheric component of Community Earth System Model), to assess the impact of TP warming on the European region with a horizontal resolution of 1.9° x 2.5°and 30 vertical levels. Similar to Guo et al. (2011) and Li and Liu (2015), two sets of sensitive experiments are designed.
The first set, referred to as low TP warming experiments, Ex_LTPW), suppressed the surface sensible heat flux when the TP surface sensible heat flux was greater than zero over the TP region. This implies that the TP surface does not transfer sensible heat to the atmosphere in the numerical integration, and the land–atmosphere heat exchange ceases. In the second set, known as high TP warming experiments, Ex_HTPW), the atmospheric sensible heat over the TP region was enhanced by 30%. Each set of sensitive experiments was integrated from spring to the end of summer and include 15 members to minimize the dependence on the initial field. The differences between the mulit-member ensemble mean results (mean results of Ex_HTPW minus that of Ex_LTPW) of the two sets are considered as the effects by the TP warming forcing.
3 Results
Based on the definition outlined in Sect. 2.2, the study conducted an analysis of the spatial distribution of HSDs over Europe, depicted in Fig. 1a. The climatological distribution of summer HSDs across Europe illustrates two distinct regions with elevated values. The first region encompasses the southwestern part of Europe, including Portugal, Spain, France, and neighboring areas. The second most prominent region is Eastern Europe (EEU). Prior research has provided substantial evidence regarding the significant influence of atmospheric teleconnections over Eurasia on the elevated temperatures experienced in EEU (Kornhuber et al. 2019; Zhao et al. 2020). Additionally, thermal anomalies originating from the TP play a crucial role in the interannual variations of these teleconnections (Zhao et al. 2012; Lu et al. 2018). Consequently, this study specifically focuses on analyzing the occurrence of HSDs in EEU within the defined latitude and longitude ranges (15°E-30°E, 40°N-55°N).
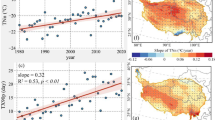
Over the period spanning from 1979 to 2022, the average frequency of HSDs in EEU was approximately one day per year per grid point. Moreover, the analysis revealed a robust increasing trend in HSD frequency (Fig. 1b), displaying an increase of 0.3 days per decade (P < 0.01), accompanied by notable interannual variability. Furthermore, the study’s findings establish that HSDs based on wet bulb temperature serve as a reliable indicator for identifying extreme high-temperature events in EEU. Specifically, the HSD series for the summers of 2007, 2010, 2012, 2021, and 2022 all exhibited remarkable positive anomalies (exceeds than 2 times the standard deviation), highlighting the increasing occurrence of heat stress events in recent years.
(a) Spatial pattern depicting the climatological distribution of summer Heat Stress Days (HSDs) across Europe (unit: days) based on E-OBS dataset. The dashed frame outlines the Eastern Europe (EEU) domain (15°E, 40°N − 30°E, 55°N). (b) Mean summer frequency of HSDs in EEU. The black solid line represents the linear regression of HSD frequency (the regression slope is statistically significant at the 0.01 significance level). The black dashed line denotes the two times the standard deviation of HSD.
The occurrence of large-scale HSDs in EEU is not solely determined by local circulation patterns characterized by anticyclonic anomalies but is also influenced by both upstream and downstream circulation systems. Figure 2 provides critical insights into the circulation anomalies during the preceding spring and summer, shedding light on their pivotal role in contributing to a higher frequency of HSD events in EEU.
In the preceding spring (Fig. 2a), EEU found itself situated in front of a high-pressure ridge, with adiabatic subsidence motion induced by northwest airflow. This meteorological setup potentially resulted in dry and hot conditions over EEU, setting the stage for the subsequent summer HSD events. Similar circulation anomalies also extended their influence on the TP. The frequent occurrence of summer HSDs in EEU is linked to the local anticyclonic anomaly (Fig. 2b). Simultaneously, a noteworthy anticyclonic anomaly is observed over the northern TP. These circulation anomalies spanning the Eurasian region exhibit a saddle-shaped pattern, characterized by stronger stability, which in turn makes it more conducive for maintaining elevated temperatures.
Linear regression analysis of (a) spring and (b) summer geopotential height (Z) (shadings; unit: gpm; dotted areas indicate significance at the 95% confidence level) and horizontal wind (vectors; unit: m s− 1; only displaying significant values at the 95% confidence level) at 300 hPa relative to the frequency of summer Heat Stress Days (HSDs) in Eastern Europe (EEU). Black dashed box denotes the domain of EEU.
The observed circulation anomaly patterns over Eurasia strongly suggest a potentially close relationship between summer HSDs in EEU and the warming of the TP. The analysis unveils a significant positive correlation between the frequency of summer HSDs and the surface air temperature over the TP during both summer and the preceding spring (Fig. 3). This robust relationship is not only evident in their consistent visible upward trend (Fig. 3a and c) but also in the significant interannual correlation between the two (Fig. 3b and d). Despite the removal of the linear trend, a significant correlation persists between HSD and TPTI in Eastern Europe. The subsequent regression analysis opted to eliminate the linear trend from the original data to highlight the interannual component. This implies that as the TP experiences warmer conditions during both the preceding spring and summer, the frequency of summer HSDs in the EEU region increases.
However, understanding the dynamic mechanism through which the TP, positioned in the downstream region, influences the occurrence of summer HSDs in EEU necessitates further investigation. For a more focused analysis, we selected a specific area that exhibits a high positive correlation with HSDs (spanning from 80°E to 95°E and 27°N to 35°N) and calculated the regional average of surface air temperature in this region, defining it as the Tibetan Plateau Temperature Index (TPTI). This TPTI will be employed for a more in-depth investigation into the intricate relationship between TP warming and the heightened occurrence of summer HSDs in the EEU region.
Spatial distribution of correlation coefficient between summer frequency of Heat Stress Days (HSDs) in Eastern Europe (EEU) and spring Tibetan Plateau Temperature Index (TPTI) with trend (a) and without trend (b). Panels (c) and (d) show the same analysis as in (a) and (b) but for HSD frequency and summer TPTI. Dotted areas denote significance at the 95% confidence level
Both the TP and EEU are situated in the mid-high latitudes, and their circulation anomalies are influenced by the westerly jet, as depicted in Fig. 2b. Figure 4a provides a climatological representation of the summer jet stream over Eurasia, revealing two belt-shaped regions with maximum wind speeds. One region encompasses the area where the subtropical jet stream is active (20°E-110°E, 32°N-47°N), while the other corresponds to the region housing the polar jet stream (10°E-80°E, 55°N-70°N). We calculate the regional averaged wind speed in these two regions, defining them as the subtropical jet stream index and the polar jet stream index (Fig. 4b). Following Huang et al. (2014), we consider the difference between these indices as the Jet Stream Index (JSI). Given the significant negative correlation (-0.72, P < 0.01) between the intensity of the subtropical jet stream and the polar jet stream, a high JSI value is associated with a strong subtropical jet stream and a weak polar jet stream (Fig. 4c). This corresponds to the circulation anomalies characterized by fewer summer HSDs in EEU (Fig. 4d). The weakening of the subtropical jet and the strengthening of the polar jet act as crucial links connecting the increased occurrence of HSDs in EEU to the warming TP (Fig. 5a). Figure 5b illustrates the distribution of the correlation coefficient matrix among HSDs, the jet stream, and TPTI, further affirming the intricate relationship. The TPTI exhibits strong continuity from spring to summer, notably influencing summer jet streams based on its spring values. Additionally, a significant correlation is observed between jet streams and Eastern European HSD. Interestingly, the year 2010, marked by red dots in Fig. 5a and c, corresponds to a period when EEU experienced a notably high frequency of HSDs. This observation reaffirms the conclusions drawn from the analysis, which include anticyclonic anomalies over the TP and EEU, alongside a weakened subtropical jet stream and an intensified polar front jet stream.
(a) Summer climatological distribution of horizontal jet core number (HJCN, shadings) and windspeed (green contours; unit: m s− 1). The black dashed boxes highlight the primary regions of the subtropical jet and polar jet. (b) Normalized index of the polar jet stream and subtropical jet stream. Linear regression of zonal wind at 300 hPa on (c) Jet Stream Index (JSI) and (d) frequency of summer Heat Stress Days (HSDs) in Eastern Europe (EEU) multiplied by -1. Dotted areas indicate significance at the 95% confidence level. Black dashed boxes in (c) and (d) denote the domain of EEU.
(a) Boxplot presenting Heat Stress Days (HSDs) frequency, summer jet stream index, Tibetan Plateau Temperature Index (TPTI) in spring, and TPTI in summer. The red points mark the respective values for the year 2010. Black circle is the outlier point of year 2012 (beyond the 1.5x upper quartile bounds). (b) Correlation coefficients between the time series. (c) Geopotential height (Z) anomalies (shadings; unit: gpm) and horizontal wind (vectors; unit: m s− 1) anomalies at 300 hPa for the year 2010
It is interesting to find out the connection between the warming of the TP in spring and the subsequent increase in the frequency of HSDs in EEU. Figure 6 presents the circulation anomalies response to the TP warming in spring and the associated dynamic processes. When the TP experiences warming in spring, it triggers local anticyclonic anomalies in the upper levels of the atmosphere. These anomalies manifest as westerly wind anomalies in the north of the TP and easterly wind anomalies in the south of the TP (Fig. 6a and b). Moreover, the warming of the TP also gives rise to robust RWS anomalies and induces negative vorticity forcing (Fig. 6c and d). These circulation anomalies play a pivotal role in not only amplifying but also sustaining the warming of the TP, extending its influence into the subsequent summer season (Fig. 7a and b).
Controlled by this distinct circulation pattern, a southeast wind anomaly prevails during summer, driving negative humidity advection and positive temperature advection towards EEU (Fig. 7d and f). Consequently, these atmospheric conditions create dry and hot circumstances, establishing a favorable background for the occurrence of HSDs in EEU. Furthermore, previous studies have indicated that plateau heating affects the summer circumglobal teleconnection across the Northern Hemisphere, consequently influencing the summer climate over EEU through downstream effects (Zhang et al., 2018).
Linear regression of spring (a) zonal wind (unit: m s− 1), (b) Wave Activity Flux (WAF) (vectors; unit: m2 s− 2) and geopotential height (shadings; unit: gpm), (c) RWS (unit: 10− 11 s− 2), and (d) relative vorticity (unit: 10− 6 s− 1) at 300 hPa onto spring Tibetan Plateau Temperature Index (TPTI). Dotted areas are significant at the 95% confidence level
Linear regression of (a) spring and (b) summer geopotential height (Z) (shadings; unit: gpm; dotted areas are significant at the 95% confidence level) and horizontal wind (vectors; unit: m/s; only show the significant values at the 95% confidence level) at 300 hPa on spring Tibetan Plateau Temperature Index (TPTI). (c), (d) and (e), (f) are the same as (a) and (b), but for humidity advection (10 − 5 g kg − 1 s − 1) and temperature advection (K s− 1) at 700 hPa, respectively
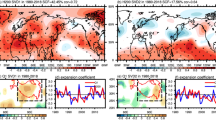
The warming of the TP during summer corresponds to a wave train anomaly that propagates from northwest to southeast over Eurasia, with strong WAF anomalies flowing from EEU to the TP region (Fig. 8a and b). The wave train links the anticyclonic anomalies over EEU and TP, forming the zonal circulation cells (Fig. 8d). This suggests that the warming of the plateau strengthens the descending motion over Eastern Europe, thereby exacerbating the high temperatures in that region. The wave train pattern is characterized by the regional average values in highly correlated regions (R1: 5°E-25°E, 45°N-65°N; R2: 42°E-62°E, 35°N-55°N; R3: 67°E-87°E, 27°N-47°N; R4: 90°E-110°E, 20°N-40°N) of the meridional wind anomalies at 300 hPa. Specifically, the Meridional Wind Index (VI) is defined as follows:
.
VI exhibits a significant positive correlation with various key factors, emphasizing its crucial role in linking the frequent summer HSDs in EEU and the warming of the TP. Specifically, VI displays a strong positive correlation with the TPTI in summer (correlation coefficient: 0.59, P < 0.01), TPTI in the preceding spring (correlation coefficient: 0.37, P < 0.05), and HSDs (correlation coefficient: 0.58, P < 0.01). These correlations highlight the important mediating role played by the wave train in driving the influence of TP warming on the increased occurrence of HSDs in the upstream region (Fig. 8d).
The warming of the TP results in a strong upward movement anomaly over the western TP (Fig. 8d), generating divergent forcing at the upper levels. This, in conjuction with the easterly anomalies (Figs. 7d and 8b), further amplifies the strong convergence and sinking airflow over EEU (Fig. 9c and d). This process promotes the occurrence of HSDs in EEU. Furthermore, the anticyclonic anomaly associated with TP warming weakens the upper atmospheric kinetic energy north of the TP (Fig. 9a and b). This reduction contributes to the weakening of the subtropical jet, thereby amplifying the temperature gradient in the mid-to-upper troposphere (Huang et al. 2014). Consequently, this fortifies the polar front jet stream over Eurasia (Fig. 4d). The change in the westerlies creates a favorable circulation pattern that sustains anticyclonic anomalies over EEU by strengthening the passage of stationary waves through the region (Lu et al. 2018).
Linear regression of summer (a) meridional wind (unit: m s− 1; dotted areas are significant at the 95% confidence level) and (b) stream function (shadings; unit: unit: s− 1; dotted areas are significant at the 95% confidence level) and wave activity flux (vectors; unit: m2 s− 2) at 300 hPa on summer Tibetan Plateau Temperature Index (TPTI). (c) Scatter distribution of Meridional Wind Index (VI) and TPTI and their probability density distribution. (d) Vertical cross-sections of the linear regression of geopotential height (contours; unit: gpm; the white solid lines represent the significant values at the 95% confidence level), zonal wind (shadings; unit: m s− 1; dotted areas are significant at the 95% confidence level) and meridional-vertical wind (vectors; m s− 1) on summer TPTI.
Linear regression of summer (a) transient kinetic energy (unit: m2 s− 2) at 300 hPa, (b) Eliassen-Palm (EP) flux divergence (unit: 10− 5 m s− 2) at 300 hPa, (c) divergence (unit: 10− 6 s− 1) at 300 hPa, and (d) omega (unit: hPa s− 1) at 700 hPa on summer Tibetan Plateau Temperature Index (TPTI). Dotted areas are significant at the 95% confidence level
To mitigate potential interference from feedback effects and confirm the dynamic response of atmospheric circulation to TP warming, we conducted an idealized numerical simulation utilizing the LBM described in Sect. 2.4. In this simulation, we employed a threshold of 0.75 times the standard deviation of the TPTI to select 10 years with positive TPTI anomalies (1981, 1998, 2006, 2007, 2009, 2010, 2012, 2013, 2016, and 2018), as shown in Fig. 10a. Subsequently, we calculated the summer-averaged atmospheric apparent heat source anomalies over the TP during these years and introduced heating forcing into the simulations to mirror observed locations and intensities (Fig. 10b). The shape of the forcing was defined as a circle with a center at 90°E, 32°N and a horizontal radius of 5°.
The model was initiated with the summer climatological circulation as the initial field and progressed through integration. The average circulation anomalies from 16 to 20 days of time integration were considered as steady responses to the specified forcing (Fig. 11). The heating of the TP directly induced significant anticyclonic anomalies over the local region, extending to create anticyclonic anomalies in the EEU region through the upstream effect of atmospheric blocking. A comparison between Figs. 8 and 11 reveals that the LBM simulation results successfully replicate the observed circulation pattern, notably the saddle-shaped structure over Eurasia. This correspondence suggests that TP warming significantly strengthens the wave train propagating from northwest to southeast, as depicted in the observation results (Figs. 8a and 11b). Both the simulated and observed outcomes affirm that preceding TP warming serves to amplify summer HSDs in EEU.
Simulation results based on CAM5.3 highlight that the increased sensible heating over the TP region during spring leads to significant anticyclonic anomalies in the local upper-level atmosphere (Fig. 12a). This condition favors the sustained warmth over the TP region, extending into the summer. Furthermore, it results in anticyclonic anomalies over the northeastern TP and cyclonic circulation anomalies over the western TP during the summer. These correspond to the reinforcement of the polar front jet stream and the weakening of the subtropical jet stream (Fig. 12b). Through meridional stationary wave propagation, this triggers anticyclonic circulation anomalies that exert control over the upstream East European region. Consequently, the summer wet bulb temperature exhibits a notable positive anomaly in the East European region, leading to a significant increase in HSD frequency (Fig. 12c and d). These simulation results corroborate the potential physical mechanisms proposed in the observational analysis (Fig. 13).
Ensemble mean differences of simulated (a) spring circulations, (b) summer circulations (shadings for geopotential height in unit of gpm; vectors for horizontal wind in unit of m/s and only show the significant values at the 95% confidence level), (c) summer wet bulb temperature (WBT, in unit of °C), and (d) frequency of heat stress day (HSD, in unit of day) between in Ex_HTPW and in Ex_LTPW. Dotted areas are significant at the 95% confidence level
4 Concluding remarks
In recent years, EEU has witnessed a significant increase in summer high temperatures. This study establishes a robust link between frequent HSDs in EEU and the warming of the TP during the preceding spring. The investigation delves into the dynamic mechanism underlying this connection: (1) During spring, warming in the southern part of the TP triggers a local Rossby wave source anomaly, setting off negative vorticity forcing and anticyclonic anomalies. These anticyclonic anomalies, in turn, amplify the warming of the TP during the summer. (2) Throughout the summer, the anticyclonic anomaly weakens the subtropical jet stream, establishing a saddle-shaped circulation pattern that sustains the anticyclonic anomaly over EEU. Simultaneously, the warming of the TP induces upward airflow, causing local divergence at upper levels and leading to a convergence anomaly over EEU. This intensified convergence anomaly further reinforces adiabatic sinking motion in EEU, contributing to increased surface temperatures and the occurrence of summer HSD events.
Furthermore, the numerical simulations successfully reproduce the dynamic response of the circulation pattern over Eurasia to the heating forcing over the TP, emphasizing the critical role of TP warming in driving the more frequent summer HSDs in EEU. The findings indicate that an unusually warm TP in spring may serve as a precursor signal of more frequent summer HSDs in EEU. Considering the relatively short memory of the atmosphere, it’s likely that plateau snow cover (Figure S4) and soil moisture (Figure S5) play a significant role in the sustained warmth from spring to summer (Shen et al. 2015; Yang and Wang, 2019; You et al. 2020a, b). It is important to note, however, that the TP is located downstream of EEU. Consequently, the increased frequency of HSDs in EEU further promotes TP warming through the propagation of the wave train. There appears to be a strong interaction between the two processes (Liu et al. 2020; Yang et al. 2021; Zhou and Yuan 2022). While this study sheds light on the dynamic impact of TP warming on the upstream region through observational diagnosis and numerical simulation, further research is needed to better understand and quantify this contribution.
Data availability
Gratitude is extended to the European Climate Assessment & Dataset (ECA&D) project (https://www.ecad.eu/download/ensembles/download.php), China Meteorological Data Service Center (https://data.tpdc.ac.cn/zh-hans/data/3220c0db-1295-4bac-b245-bb209b2d73bb), and ECMWF (https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5) for providing the relevant data used in our study. The calculations of wet bulb temperature can be realized through the Metpy package of the Python language (https://unidata.github.io/MetPy/).
References
Al-Ismaili AM, Al-Azri NA (2016) Simple iterative approach to calculate wet-bulb temperature for estimating evaporative cooling efficiency[J]. Int J Agric Innovations Res 4(6):1013–1018
Baldi M, Dalu G, Maracchi G et al (2006) Heat waves in the Mediterranean: a local feature or a larger-scale effect?[J]. Int J Climatol 26(11):1477–1487
Ballester J, Quijal-Zamorano M, Méndez Turrubiates RF et al (2023) Heat-related mortality in Europe during the summer of 2022[J]. Nat Med, : 1–10
Bastos A, Gouveia CM, Trigo RM et al (2014) Analysing the spatio-temporal impacts of the 2003 and 2010 extreme heatwaves on plant productivity in Europe[J]. Biogeosciences 11(13):3421–3435
Black E, Blackburn M, Harrison G et al (2004) Factors contributing to the summer 2003 European heatwave[J]. Weather 59(8):217–223
Blunden J, Boyer T (2021) State of the climate in 2020[J]. Bull Am Meteorol Soc, 102(8)
Brimicombe C, Lo CHB, Pappenberger F et al (2023) Wet Bulb Globe Temperature: Indicating extreme heat risk on a global grid[J]. GeoHealth, 7(2): e2022GH000701
Broccoli AJ, Manabe S (1992) The effects of orography on midlatitude Northern Hemisphere dry climates[J]. J Clim 5(11):1181–1201
Coco A, Jacklitsch B, Williams J et al (2016) Criteria for a recommended standard: occupational exposure to heat and hot environments[J]. DHHS (NIOSH) Publication
Cornes RC, van der Schrier G, van den Besselaar EJM et al (2018) An ensemble version of the E-OBS temperature and precipitation data sets[J]. J Geophys Research: Atmos 123(17):9391–9409
Cvijanovic I, Mistry MN, Begg JD et al (2023) Importance of humidity for characterization and communication of dangerous heatwave conditions[J]. NPJ Clim Atmospheric Sci 6(1):33
Deng K, Yang S, Ting M et al (2018) An intensified mode of variability modulating the summer heat waves in eastern Europe and northern China[J]. Geophys Res Lett, 45(20): 11,361 – 11,369.
Duchez A, Frajka-Williams E, Josey SA et al (2016) Drivers of exceptionally cold North Atlantic Ocean temperatures and their link to the 2015 European heat wave[J]. Environ Res Lett 11(7):074004
Ebi KL, Capon A, Berry P et al (2021) Hot weather and heat extremes: health risks[J]. Lancet 398(10301):698–708
Guo X, Yang K, Chen Y (2011) Weakening sensible heat source over the Tibetan Plateau revisited: effects of the land–atmosphere thermal coupling[J]. Theoret Appl Climatol 104:1–12
Hayashi M, Watanabe M (2017) ENSO complexity induced by state dependence of westerly wind events[J]. J Clim 30(9):3401–3420
Hersbach H, Bell B, Berrisford P et al (2020) The ERA5 global reanalysis[J]. Q J R Meteorol Soc 146(730):1999–2049
Hoskins B, Wang B (2006) Large-scale Atmospheric Dynamics[M]. The Asian monsoon. Springer, Berlin, Heidelberg, pp 357–415
Huang DQ, Zhu J, Zhang YC et al (2014) The different configurations of the east Asian polar front jet and subtropical jet and the associated rainfall anomalies over eastern China in summer[J]. J Clim 27(21):8205–8220
Iribarne JV, Godson WL (1981) Atmospheric Thermodynamics. Springer, p 260
Jones PD, Lister DH, Osborn TJ et al (2012) Hemispheric and large-scale land‐surface air temperature variations: an extensive revision and an update to 2010[J]. J Geophys Research: Atmos 117:D5
Kang S, Zhang Q, Qian Y et al (2019) Linking atmospheric pollution to cryospheric change in the Third Pole region: current progress and future prospects[J]. Natl Sci Rev 6(4):796–809
Knox JA, Nevius DS, Knox PN (2017) Two simple and accurate approximations for wet-bulb temperature in moist conditions, with forecasting applications[J]. Bull Am Meteorol Soc 98(9):1897–1906
Kobayashi S, Ota Y, Harada Y et al (2015) The JRA-55 reanalysis: General specifications and basic characteristics[J]. J Meteorological Soc Japan Ser II 93(1):5–48
Kornhuber K, Petoukhov V, Petri S et al (2017) Evidence for wave resonance as a key mechanism for generating high-amplitude quasi-stationary waves in boreal summer[J]. Clim Dyn 49:1961–1979
Kornhuber K, Osprey S, Coumou D et al (2019) Extreme weather events in early summer 2018 connected by a recurrent hemispheric wave-7 pattern[J]. Environ Res Lett 14(5):054002
Li X, Liu X (2015) Numerical simulation of Tibetan Plateau heating anomaly influence on westerly jet in spring[J]. J Earth Syst Sci 124:1599–1607
Liu Y, Lu M, Yang H et al (2020) Land–atmosphere–ocean coupling associated with the Tibetan Plateau and its climate impacts[J]. Natl Sci Rev 7(3):534–552
Lu M, Yang S, Li Z et al (2018) Possible effect of the Tibetan Plateau on the upstream climate over West Asia, North Africa, south Europe and the North Atlantic[J]. Clim Dyn 51:1485–1498
Masson-Delmotte V, Zhai P, Pirani A et al (2021) Climate change 2021: the physical science basis[J]. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change, 2
Murakami M (1979) Large-scale aspects of deep convective activity over the GATE area[J]. Mon Weather Rev 107(8):994–1013
Perkins-Kirkpatrick SE, Lewis SC (2020) Increasing trends in regional heatwaves[J]. Nat Commun 11(1):3357
Rasmijn LM, Van der Schrier G, Bintanja R et al (2018) Future equivalent of 2010 Russian heatwave intensified by weakening soil moisture constraints[J]. Nat Clim Change 8(5):381–385
Robine JM, Cheung SLK, Le Roy S et al (2008) Death toll exceeded 70,000 in Europe during the summer of 2003[J]. CR Biol 331(2):171–178
Rodwell MJ, Hoskins BJ (1996) Monsoons and the dynamics of deserts[J]. Q J R Meteorol Soc 122(534):1385–1404
Rodwell MJ, Hoskins BJ (2001) Subtropical anticyclones and summer monsoons[J]. J Clim 14(15):3192–3211
Rousi E, Kornhuber K, Beobide-Arsuaga G et al (2022) Accelerated western European heatwave trends linked to more-persistent double jets over Eurasia[J]. Nat Commun 13(1):3851
Shen SSP, Yao R, Ngo J et al (2015) Characteristics of the tibetan Plateau snow cover variations based on daily data during 1997–2011[J]. Theoret Appl Climatol 120:445–453
Stefanon M, D’Andrea F, Drobinski P (2012) Heatwave classification over Europe and the Mediterranean region[J]. Environ Res Lett 7(1):014023
Takaya K, Nakamura H (2001) A formulation of a phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow[J]. J Atmos Sci 58(6):608–627
van Daalen KR, Romanello M, Rocklöv J et al (2022) The 2022 Europe report of the Lancet countdown on health and climate change: towards a climate resilient future[J]. Lancet Public Health 7(11):e942–e965
Wallace JM, Hobbs PV (2006) Atmospheric Science: an introductory survey, 2nd edn. Academic, p 504
Wang Z, Yang S, Duan A et al (2019) Tibetan Plateau heating as a driver of monsoon rainfall variability in Pakistan[J]. Clim Dyn 52:6121–6130
Watanabe M, Kimoto M (2000) Atmosphere-ocean thermal coupling in the North Atlantic: a positive feedback[J]. Q J R Meteorol Soc 126(570):3343–3369
Wu Z, Jiang Z, Li J et al (2012) Possible association of the western tibetan Plateau snow cover with the decadal to interdecadal variations of northern China heatwave frequency[J]. Clim Dyn 39:2393–2402
Wu Z, Zhang P, Chen H et al (2016) Can the tibetan Plateau snow cover influence the interannual variations of eurasian heat wave frequency?[J]. Clim Dyn 46:3405–3417
Xiao C, Zhang Y, Lofgren BM et al (2016) The concurrent variability of east Asian subtropical and polar-front jets and its implication for the winter climate anomaly in China[J]. J Geophys Research: Atmos 121(12):6787–6801
Xu P, Wang L, Liu Y et al (2020) The record-breaking heat wave of June 2019 in Central Europe[J]. Atmospheric Sci Lett 21(4):e964
Yang K, Wang C (2019) Seasonal persistence of soil moisture anomalies related to freeze–thaw over the Tibetan Plateau and prediction signal of summer precipitation in eastern China[J]. Clim Dyn 53(3–4):2411–2424
Yang X, Zeng G, Zhang S et al (2021) Relationship between two types of heat waves in northern East Asia and temperature anomalies in Eastern Europe[J]. Environ Res Lett 16(2):024048
Yasui S, Watanabe M (2010) Forcing processes of the summertime circumglobal teleconnection pattern in a dry AGCM[J]. J Clim 23(8):2093–2114
Yin J, Zhang Y (2021) Decadal changes of east Asian jet streams and their relationship with the mid-high latitude Circulations[J]. Clim Dyn 56:2801–2821
You Q, Chen D, Wu F et al (2020a) Elevation dependent warming over the Tibetan Plateau: patterns, mechanisms and perspectives[J]. Earth Sci Rev 210:103349
You Q, Wu T, Shen L et al (2020b) Review of snow cover variation over the Tibetan Plateau and its influence on the broad climate system[J]. Earth Sci Rev 201:103043
You Q, Yang Y (2023) Dataset of 0.1°monthly surface air temperature over the Tibetan Plateau (1901–2020). National Tibetan Plateau Data Center. https://doi.org/10.11888/Atmos.tpdc.300228
Zhang J, Jiang Y, Chen H et al (2018) Double-mode adjustment of Tibetan Plateau heating to the summer circumglobal teleconnection in the Northern Hemisphere[J]. Int J Climatol 38(2):663–676
Zhang R, Sun C, Zhu J et al (2020) Increased European heat waves in recent decades in response to shrinking Arctic Sea ice and eurasian snow cover[J]. NPJ Clim Atmospheric Sci 3(1):7
Zhang G, Zeng G, Liang XZ et al (2021) Increasing heat risk in China’s urban agglomerations[J]. Environ Res Lett 16(6):064073
Zhang J, Chen H, Fang X et al (2024) Warming-induced hydrothermal anomaly over the Earth’s three poles amplifies concurrent extremes in 2022[J]. Npj Clim Atmospheric Sci 7(1):8
Zhao P, Yang S, Wu R et al (2012) Asian origin of interannual variations of summer climate over the extratropical North Atlantic Ocean[J]. J Clim 25(19):6594–6609
Zhao W, Zhou N, Chen S (2020) The record-breaking high temperature over Europe in June of 2019[J]. Atmosphere 11(5):524
Zhou S, Yuan X (2022) Upwind droughts enhance half of the heatwaves over North China[J]. Geophysical Research Letters, 49(2): e2021GL096639
Zschenderlein P, Pfahl S, Wernli H et al (2020) A lagrangian analysis of upper-tropospheric anticyclones associated with heat waves in Europe[J]. Weather Clim Dynamics 1(1):191–206
Acknowledge
The research presented in this paper is a contribution to the project supported by Swedish Research Council (VR: 2019–03954 and 2021-02163). Guwei Zhang is founded by the National Natural Science Foundation of China (42,205,170). Cheng Shen is supported by the Sven Lindqvists Forskningsstiftelse and Research Fund Adlerbertska Stiftelse.
Funding
Open access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by XY and CS. The original draft of the manuscript was written by XY. All authors reviewed and revised the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no conflicts of interest relevant to this study.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, X., Shen, C., Zhang, G. et al. Enhanced spring warming of the Tibetan Plateau amplifies summer heat stress in Eastern Europe. Clim Dyn 62, 6173–6188 (2024). https://doi.org/10.1007/s00382-024-07197-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-024-07197-z