1 Introduction

Orographic gravity waves (OGWs) are atmospheric waves sourced by the orography of a planet. Orographic gravity waves (OGWs) are ubiquitous in the atmosphere, propagate vertically and partly horizontally influencing the dynamics and transport across atmospheric layers. Horizontal scales of OGWs largely reflect horizontal scales of the orography variations. Namely, OGWs have horizontal wavelengths from a few to thousands of kilometres (spanning from non-hydrostatic to inertia-gravity wave modes), and therefore, a significant part of their spectrum cannot be resolved even in the current state-of-the-science global climate models. Hence, the effects of OGWs from the subgrid scale orography need to be parameterized.

The OGW parameterization schemes supplement the models with the OGW induced decelerations of the model winds. This orographic gravity wave drag (OGWD) arises as a reaction to the force exerted by the flow on the topography, which is then propagated upwards in a form of the vertical flux of the horizontal wave momentum (Teixeira 2014). When the wave dissipates, the flux converges and a drag is exerted on the background winds. All of these processes are parameterized based on a set of assumptions that are well justified to a leading order (Plougonven et al. 2020) and come along with free parameters of the schemes that are subject to tuning. Many OGW parameterization schemes have been developed to date and although they often share the basic concepts, they can differ in the formulation of the momentum flux, tuning of free parameters or in the variety of physical mechanisms considered in addition to the free propagation of OGWs. Therefore, as yet unquantified differences in the resulting drag can be expected.

Parameterized OGWD plays an important role for stratospheric dynamics and transport in global climate models (GCMs) (Eichinger et al. 2020; Sacha et al. 2021). This importance stems predominantly from the fact that OGWD in those particular GCMs is the dominant force in the wintertime midlatitude lower stratosphere above the subtropical jet, a so-called valve layer (Kruse et al. 2016), where it controls the planetary wave propagation from the troposphere to the stratosphere. This layer is located at altitude from 15 to 25km (\(\sim\) 120–50 hPa). This is one mechanism from the set of interactions between resolved and unresolved drag in the models that has been identified analytically and in idealized simulations by Cohen et al. (2013, 2014), i.e. the compensation mechanism between resolved and unresolved drag.

In this paper, we study the differences between the magnitude and vertical distribution of the parameterized OGWD from the CMIP6 - Coupled Model Intercomparison Project Phase 6 model simulations (Eyring et al. 2016). Of the 9 models studied, 7 use different OGW parameterizations and the schemes of the remaining two are tuned differently. The individual OGW parameterization schemes are briefly reviewed in the methodology section, focusing especially on the definitions of the momentum flux and the free propagating mode components. We have also been able to get the information on specific settings of the free parameters in the schemes from the modelers, a unique research effort to date. In Sect. 5 we compare the OGWD differences between the simulations and trace back the reasons behind the intermodel differences in distribution and magnitude of the parameterized drag to the unique information established in the review part. Finally, we show how the OGWD differences affect the differences in zonal winds and resolved waves in the stratosphere of the models. The study is concluded by highlighting the directions for future research.

2 Methodology

We analyze utendogw—the tendency of eastward wind due to OGWs (further referred as OGWD) from the Coupled Model Intercomparison project Phase 6 (CMIP6) simulations (Eyring et al. 2016), the first model intercomparison project providing the parameterized drags on a 3-D grid as monthly means at 19 pressure levels. A summary of the participating models with the data needed for our analysis is given in Table 1. Models at our disposal are CanESM5, CESM2, CNRM-CM6-1, GFDL-ESM4, HadGEM3-GC31-LL, IPSL-CM6A-LR, MIROC-ES2L, MRI-ESM2-0 and UKESM1-0-LL. Note that the resolution of each model is different, which is also a factor affecting resulting OGWD from parametrizations. We analyze data from the Atmospheric Model Intercomparison Project (AMIP) simulations (prescribed sea surface temperature and sea ice concentrations) spanning the period 1984–2014 and besides OGWD we analyze also zonal mean zonal winds and Eliassen-Palm flux divergence (EPFD) and individual flux components. For some models, an ensemble of AMIP simulations has been produced using different versions and realizations of the model, but since the resulting OGWD is similar between the configurations of each model we will focus only on the comparison between different models in this study.

Table 1 List of the models and specific variants used for CMIP6 with information on horizontal resolution according to CMIP6 database and OGW parameterization scheme
Full size table

3 Basic concept of the OGW parametrizations

State-of-the-science OGW parametrization schemes include a set of the subgrid-scale orography drag processes, but here our main focus will be on the part of the schemes accounting for vertically propagating OGWs and the resulting OGWD. For parameterizing this process, the schemes employ many assumptions [monochromatic waves, instantaneous vertical propagation, instability criterion and others, see Plougonven et al. 2020].

We illustrate the basic concept of the OGW parametrization following the pioneering work of Pierrehumbert (1986). Considering a terrain obstacle, such as a mountain with the maximum height h, and a flow with a constant wind speed U that arrives on the obstacle, we can non-dimensionalize the horizontal distances by L—half of the width of the obstacle, vertical distances by U/N and time by L/U. Then the system can be characterized with two non-dimensional numbers—an inverse Froude number,

$$ F_i=\frac{Nh}{U},$$
(1)

where N is the Brunt–Väisälä frequency, and a nondimensional measure of vertical motions

$$\begin{aligned} b=\frac{NL}{U}. \end{aligned}$$
(2)

If \(b>>1\), we can use the hydrostatic approximation and \(F_i\) solely characterises the problem.

Generally, the wave drag terms appear in the momentum equations after the Reynolds decomposition as a divergence of the Reynolds stress terms. For vertically propagating GWs, the drag force results from a convergence of two Reynolds stress components \(\tau _x\) and \(\tau _y\) that are the vertical fluxes of zonal and meridional wave momentum defined as:

$$\begin{aligned} \begin{aligned} \tau _x=\frac{1}{ \delta x\delta y}\iint \limits _S{\overline{\rho }} u'w' \ \textrm{d}x\ \textrm{d}y,\\ \tau _x=\frac{1}{ \delta x\delta y}\iint \limits _S{\overline{\rho }} v'w' \ \textrm{d}x\ \textrm{d}y, \end{aligned} \end{aligned}$$
(3)

where \(\delta x\) and \(\delta y\) are the width and the length of the grid, \({\overline{\rho }}\) is the background density and \(u'\), \(v'\) are the perturbations of zonal and meridional wind velocity components and \(w'\) is the perturbation of the vertical velocity. S is the grid area over which the average is computed.

As the prime quantities are unresolved by the model the task is now to estimate the drag using resolved quantities. In the first step, we can estimate how much of the wave momentum flux can be propagated upwards given the background configuration (variable U and N). For this, the saturation hypothesis (Lindzen 1981; Holton 1982) is widely used in the schemes. According to this hypothesis, there is a limited amount of momentum flux that can be carried by a wave through a level of the atmosphere. When this limit is reached, the exceeding momentum flux has to be dissipated. This limiting momentum flux is called the saturation flux.

The saturation flux over the length l can be estimated from

$$\begin{aligned} \tau _s=\int _{-\frac{l}{2}}^{\frac{l}{2}}\ {\overline{\rho }} u'w' \ \textrm{d}x\approx {\overline{\rho }} \left[ u'\right] \left[ w'\right] l, \end{aligned}$$
(4)

where \([u']\) and \([w']\) are the typical magnitudes of velocities for a wave. Let us say L is the characteristic horizontal scale of a wave and D is the vertical one. Given that vertical and horizontal perturbations have the same frequency, we can then say that \([w']\approx (D/L)[u']\) and also we expect that the magnitude of the zonal wind fluctuations reaches \([u']=U\) at the point where the wave breaks. In the hydrostatic limit, assuming slowly varying background in the vertical, we can estimate D locally as \(D=U(z)/N(z)\). Substituting those terms back to the equation, we get an estimate for the saturation flux:

$$\begin{aligned} \tau _s=\frac{\rho U^3 \alpha }{N}. \end{aligned}$$
(5)

\(\alpha \propto 1\) stands for a dimensionless constant depending on the shape of the obstacle. For a monochromatic plane wave, \(\tau\) is conserved during the vertical propagation unless the dissipation occurs. To estimate the location of breaking levels, the vertical profile of \(\tau _s\) can be used. As Pierrehumbert (1986) notes, the first breaking region generally occurs for a wide range of background conditions and mountain profiles less than a vertical wavelength away from the ground (hereinafter the low level wave breaking), due to the convective instability. In the hydrostatic limit, the convective instability emerges when the value of \(F_i\) exceeds some critical value (typically \(F_c\approx 0.8\) (Bacmeister and Pierrehumbert , 1998)). A portion of the momentum flux is then deposited and only the rest is transported vertically by a freely propagating wave.

As the density decreases exponentially, the wave breaking must occur somewhere in the free atmosphere. Nevertheless, the strong dependence of the saturation flux on the background wind (third power of U), which generally increases with height in the atmosphere, competes with the density decay and has a pronounced impact on the breaking height.

Assuming that the momentum flux of the freely propagating wave is slightly smaller than the saturation flux, the wave can be prone to breaking with a small decrease of \(\tau _s\) at any height. In the troposphere in midlatitudes, the wind speed generally increases with altitude until reaching the center of the upper tropospheric—lower stratospheric (UTLS) jet. Here the wind speed starts to decrease and inevitably the saturation limit is reached and wave breaking is set to occur. The portion of the momentum flux larger than the saturation flux is deposited and the wave propagates further upwards only with the value of \(\tau _s\). If the wind speed starts to grow again with height, the saturation limit increases and the wave propagates again freely upwards conserving its momentum flux.

So far we have omitted the estimation of the sourced momentum flux. We have done so ostensibly because the situation is complicated by the nonlinear relation between the surface drag on the mountain, low level flux and the location and existence of breaking. However, using the scaling arguments developed for the estimation of the saturation flux, the momentum flux of freely propagating OGWs, \(\tau _0\), can be estimated as

$$\begin{aligned} \tau _0=\frac{\rho U^3}{N \delta x}G\left( F_i\right) , \end{aligned}$$
(6)

where G is some function of the inverse Froude number that contains the information on the mountain height and its value scales the amount of momentum fluxed by freely propagated OGWs.

For \(F_i<<1\), i.e. a linear flow without breaking, we can assume that \(u'\) and \(w'\) are proportional to the height of the ridge and write

$$\begin{aligned} G(F_i)=EF_i^2=E\left( \frac{Nh}{U}\right) ^2, \end{aligned}$$
(7)

where E stands for an efficiency constant depending on the shape of the mountain. After substituting to (6), we finally get

$$\begin{aligned} \tau _0=E\frac{\rho UNh^2}{\delta x}. \end{aligned}$$
(8)

The basic ideas presented in the text above are used in the core of most CMIP6 model OGW parameterization schemes. In the following section we provide more detailed information about each of the schemes.

4 Details of individual schemes and their set-up

In this section we briefly describe the individual schemes. However, the existing information is often limited by available papers and documentation related to each model. Hence, in some cases, personal communication with the model developers was needed to obtain the necessary details, especially regarding the simulation-specific tuning of the free parameters in the schemes. However, we have not been able to establish the tuning details for all models.

The following description is concerned particularly with the scheme/model-specific treatment of the topography, surface momentum flux and additional mechanisms like the wave blocking, low-level breaking and of parameters controlling the vertical distribution, such as \(F_c\). In some schemes, \(F_c\), as we defined it, is replaced by other parameters which represent wave blocking or breaking limits. We adjusted them in our description to have a uniform notation, which is in accordance with the original definitions and settings in the schemes.

4.1 MIROC-ES2L

MIROC-ES2L employs the OGWD parametrization scheme based on McFarlene (1997). The surface momentum flux at a reference level, \(\sigma ^r\), is defined as

$$\begin{aligned} \mathbf {\tau }\left( \sigma ^r\right) =\mathbf {\tau }_0=-E\frac{\kappa _e}{2}h_e^2\rho _0N_0\mathbf {U_0}, \end{aligned}$$
(9)

with \(\sigma ^r=\frac{p_r}{p_s}\), where \(p_{r/s}\) is the pressure at the reference level and at the surface respectively. \(\textbf{U}\) is the horizontal wind velocity, \(\kappa _e\) is a representative horizontal wavenumber, \(h_e\) is the effective height, which determines the wave amplitude limited by \(F_c\) and is defined as \(h_e=min(2S_d,F_cU_0/N_0)\), with \(S_d\) being a standard deviation of the sub-grid scale orography. All terms indexed by 0 are taken at the reference level.

E is the efficiency parameter, which is always less than one. \(E\kappa _e/2\) taken together present a tunable parameter which we denote K. And as we can see, it corresponds with (8), so that \(1/\delta x=\kappa _e/2\).

The vertical distribution of the momentum flux is controlled by the saturation hypothesis, and we can write the vertical profile of the momentum flux as

$$\begin{aligned} \mathbf {\tau }(\sigma )=\mathbf {\tau }_0\left( \frac{A(z)}{h_e}\right) ^2\frac{\rho NU}{\rho _0N_0U_0}, \end{aligned}$$
(10)

where; the wind speed U is a projection of background winds to the direction of the low level wind (\(U=\textbf{U} \cdot \textbf{U}_0/|\textbf{U}_0|\)) and A(z) is the wave amplitude at height z. The amplitude varies with altitude, however, it is constrained to be less than the critical value of convective overturning, \(A(z)\le F_cU/N\). If the amplitude does exceed this value, momentum is deposited in accordance with the saturation hypothesis. Saturation momentum flux is equal to (10) after taking \(A(z)=F_cU/N\).

Even though this scheme considers wave blocking effects on the effective height, it does not explicitly add any drag caused by the blocking. Parameters in this scheme have following values, \(F_c=0.707, K=8\times 10^{-6} \textrm{m}^{-1},\sigma ^r=0.985\). We have confirmed, that in the analyzed simulation, \(F_c\) has the same value and \(K=3.75\times 10^{-5} \textrm{m}^{-1}\).

4.2 MRI-ESM2-0

This model uses the scheme introduced by Iwasaki et al. (1989). It is similar to the previous scheme of the model MIROC-ES2L, but in the updated scheme two monochromatic OGW modes are launched instead of one. First mode is supposed to account for effects of waves with \(\lambda \sim\)100   km—type A, with the main influence in the stratosphere. Second mode accounts for effects of short waves with \(\lambda \lesssim\)10   km—type B with the main influence in the troposphere.

The momentum at the reference level is defined in the same way as (9), but this time we need to distinguish between the type A and B of the waves. For each type, a different reference level is chosen. The momentum is then written as

$$\begin{aligned} \mathbf {\tau _{0i}}\left( \sigma _i^r\right) =-K h_{ei}^2\rho _{0i}N_{0i}\textbf{U}_{0i}, \end{aligned}$$
(11)

where all variables are set depending on the reference level - \(\sigma ^r\), with subscript i being A or B. \(h_e\) is defined similarly as in McFarlene (1997), \(h_{ei}=min(S_{di},0.5F_cU_{0i}/N_{0i})\). \(S_{dA}\) is defined as the standard deviation of mean height and \(S_{dB}=0.5(h_{max}-h_{min})\), both taken over the grid area. Note the factor 0.5 in the definition of effective height. Iwasaki et al. (1989) states that it is due to the vertical drop of the flow over sinusoidal terrain. This drop should be twice the amplitude of the wave.

The tunable parameter K is set to \(2\times 10^{-5}\) for type A and \(5\times 10^{-5}\) for type B. \(F_c\) in this scheme is tuned separately for wave blocking \(F_c=0.67\) and for amplitude limitation concerning saturation hypothesis \(F_c=1\). Other parameters are \(\sigma _A^r=0.9\) and \(\sigma _B^r=0.97\). Explicit choice of these values was not confirmed for the analyzed simulation. Note, that the type B reference level is set lower. This is based on the assumption that shorter waves are formed at lower altitudes.

The vertical evolution of the momentum flux for type A follows again the saturation hypothesis. For type B it is defined as

$$\begin{aligned} \mathbf {\tau }_B(\sigma )={\left\{ \begin{array}{ll} 0 &{} \sigma _B \le 0.3, \\ \mathbf {\tau }_B\left( \sigma _B^r\right) \frac{(\sigma -0.3)^2}{0.7^2} &{} \sigma _B >0.3. \end{array}\right. } \end{aligned}$$
(12)

Type B waves are mostly reflected by the upper troposphere downward to the surface where they can be again reflected until they dissipate. As we can see, the momentum flux is larger as we go lower, with \(\sigma =0.3\) being in the upper troposphere around 9km.

4.3 HadGEM3-GC31-LL and UKESM1-0-LL

These two models are described together because they use the same scheme defined by Webster et al. (2003). Instability is constrained by the saturation hypothesis as in Gregory et al. (1998). Anisotropy of the subgrid-scale orography is considered in the scheme, taking into account the dependence of the subgrid-scale orography elevation on the direction. For this reason, \(\phi _{xx},\phi _{xy}\) and \(\phi _{yy}\) are defined as

$$\begin{aligned} \begin{aligned}&\phi _{xx}=\left( \frac{\partial h(x,y)}{\partial x}\right) ^2, \\&\phi _{xy}=\frac{\partial h(x,y)}{\partial x}\frac{\partial h(x,y)}{\partial y},\\&\phi _{yy}=\left( \frac{\partial h(x,y)}{\partial y}\right) ^2, \end{aligned} \end{aligned}$$
(13)

where h is the height of the topography. The anisotropic handling of the subgrid orography aims to improve the resulting parameterized OGW momentum fluxes.

The surface stress accounting for the anisotropy of the orography is defined as

$$\begin{aligned} \begin{aligned}&\tau _{0x}=-K \rho _0N_0u_0\left( \phi _{xx} \cos {\chi }+\phi _{xy} \sin {\chi }\right) , \\&\tau _{0y}=-K \rho _0N_0v_0\left( \phi _{xy} \cos {\chi }+\phi _{yy} \sin {\chi }\right) , \end{aligned} \end{aligned}$$
(14)

where \(\tau _{0x}\) is the zonal component and \(\tau _{0y}\) is the meridional component of the surface momentum flux and \(\chi\) is the direction of the wind near the surface relative to the west.

To include wave blocking, \(h_e\) is defined similarly to the previous cases, \(h_e=F_cU_0/N_0\). Finally we obtain the surface OGW stress in the form

$$\begin{aligned} \mathbf {\tau }_{gw}=\mathbf {\tau }_0\left( \frac{h_e}{h}\right) ^2, \end{aligned}$$
(15)

which is the residual momentum flux that is propagated upwards. The momentum that is dissipated due to the low-level breaking and or blocking,

$$\begin{aligned} \mathbf {\tau }_b=\mathbf {\tau }_s-\mathbf {\tau }_{gw}, \end{aligned}$$
(16)

is included in the model and is deposited uniformly up to the altitude h. The drag from blocking is explicitly implemented to the wind fields to numerically stabilise the scheme (Walters et al. 2011). In this scheme, the recommended setting of free parameters is \(K\sim 10^{-5}\) and \(F_c=0.5\). However, for HadGEM3-GC31-LL, we have confirmed a choice of \(F_c\) to be separately 0.25 for the blocking and 4 for the saturation criterion.

4.4 CESM2 and CanESM5

The OGW parameterizations of CESM2 and CanESM5 are generally based on the same scheme Scinocca and McFarlene (2000), which bases on the scheme by Lott and Miller (1997). The parameterization scheme consists of three components (a part for freely propagating waves, for the low-level breaking and for the wave blocking). Here, we will focus on the freely propagating OGWs only.

Two wave modes are used to propagate the momentum flux. We will denote the momentum flux for each wave as \(\mathbf {\tau }^+\) and \(\mathbf {\tau }^-\), where one is the positive half of the integral from which the momentum flux is derived and the other is the negative half, i.e. one is for \((0; \; \pi /2)\) and the other for \((-\pi /2; \; 0)\). Starting from a pressure drag by a constant flow on the topography, Scinocca and McFarlene (2000) derive the momentum fluxes in the form,

$$\begin{aligned} \begin{aligned} \mathbf {\tau }^+=-\frac{\kappa ^+}{2}\rho _0N_0\textbf{U}_0\cos {\theta ^+}\left( h_e^+\right) ^2,\\ \mathbf {\tau }^-=-\frac{\kappa ^-}{2}\rho _0N_0\textbf{U}_0\cos {\theta ^-}\left( h_e^-\right) ^2, \end{aligned} \end{aligned}$$
(17)

where \(\theta\) is the angle that the drag vector makes with the x-axis, so that the cosine stands for the efficiency constant E. Effective height is defined as

$$\begin{aligned} \begin{aligned} h_e^+=\cos {\theta ^+}min\left( h_e,F_cU_0/N_0\right) ,\\ h_e^-=\cos {\theta ^-}min\left( h_e,F_cU_0/N_0\right) . \end{aligned} \end{aligned}$$
(18)

In comparison with a one-wave scheme, this scheme transports up to \(30\%-50\%\) more of momentum flux to the middle atmosphere.

Critical Froude number for this parameterization is recommended to be \(F_c=0.707\). We were not able to find the value of a parameter related to the wavelength \(\kappa\).

For the analyzed CanESM5 simulation we have established from personal communication a specific choice of \(F_c=0.22\). Smaller Froude critical number was employed, because 0.707 caused a negative wind bias compared to observations in the NH winter lower stratosphere in midlatitudes, causing wave breaking, which further reinforced deceleration of the winds (Scinocca, J.,personal correspondence). For the CESM2 simulation we have confirmed from personal communication a specific setting \(F_c=1\), hence much lager than for the CanESM5 simulation. However, it must be stressed that the resolution and dynamical core of the models is different.

4.5 IPSL-CM6A-LR

This model uses the scheme by Lott (1999), which is also based on Lott and Miller (1997). The parameterization concerns freely propagating waves and a blocked flow. The effective height \(h_e\) is computed according to

$$\begin{aligned} \int ^{h_{max}}_{h_b} \ \frac{N}{U} \ \textrm{d}z \le F_{c}, \end{aligned}$$
(19)

where \(h_b\) is the blocking height. The drag force from this blocked flow is distributed in levels below \(h_b\).

The residual momentum flux is then calculated as

$$\begin{aligned} \mathbf {\tau }= & {} -E\left( h_{max}-h_b\right) ^2\rho _0 N_0\textbf{U}_0\frac{\sigma }{4S_d}\left( B\cos {\psi }^2\nonumber \right. \\{} & {} \left. \quad +C\sin {\psi }^2;(B-C)\cos {\psi }\sin {\psi })\right) , \end{aligned}$$
(20)

where \(\sigma , \psi\) are the slope of the obstacle and the angle between the flow and the direction of the obstacle. B and C are constants dependent on \(\gamma\), which is a measure of the anisotropy of the orography. These are as follows

$$\begin{aligned} \begin{aligned}&B = 1-0.18\gamma -0.04\gamma ^2 \\&C = 0.48\gamma + 0.3\gamma ^2. \end{aligned} \end{aligned}$$
(21)

The vertical distribution of the drag is controlled by the saturation hypothesis. To account for the drag from the low-level wave breaking, a parameter \(\beta\) is introduced. The momentum flux then decays by this parameter up to the level of 850   hPa. In Lott (1999) the free parameters of the scheme are chosen as \(F_c=1\) for blocking and \(F_c\approx 2\) for saturation, \(E=1\) and \(\beta =0.5\). We were only able to confirm the simulation specific choice of the parameter for blocking \(F_c=0.7\).

4.6 CNRM-CNM6-1

Parts of the OGW parameterization scheme used in this model are described in Déqué et al. (1994) and Geleyn et al. (1994), with additions in Catry et al. (2008). A brief description can be found in a paper describing the whole model (Roehrig et al. 2020).

The parameterization captures not only the dissipation due to the wave breaking, but also the resonance and reflection effects. A complete vertical profile of the momentum flux is given as

$$\begin{aligned} \mathbf {\tau }(z)=\left( \Gamma _1(z)+\Gamma _2(z)+\Gamma _3(z)\right) \mathbf {\tau }_0, \end{aligned}$$
(22)

where \(\mathbf {\tau }_0\) is the already known surface stress and \(\Gamma _1, \Gamma _2, \Gamma _3\) stand for the dissipation, reflection by a neutral or unstable level, and damping or amplification by the resonance, respectively. The latter two effects have not been included in any other model scheme so far. The surface stress is defined according to Boer et al. (1984).

$$\begin{aligned} \mathbf {\tau }_0=-K_{GW}\rho _0N_0h_{rms}\textbf{U}_0, \end{aligned}$$
(23)

where \(h_{rms}\) is the root-mean-square of the variance of the orography, and \(K_{GW}\) is a dimensionless tuning parameter, which can be rewritten as \(K_{GW}=Eh_{rms}/l\), where l is the typical distance between topographical features in the grid. Assuming this to be the possible horizontal wavelength of OGWs, we get the same definition as we saw in some of the previous schemes.

With the Froude number \(F_i(z)=N(z)h_{rms}/U(z)\) and U(z) as in (10) we can write for the vertical distribution of \(\Gamma _1\)

$$\begin{aligned} \Gamma _1(z)=max\left[ 0, \min _{z'<z}\Gamma \left( z'\right) \right] , \ \Gamma (z)=\frac{\rho (z)N(z)U(z)/F_i^2}{\rho _0N_0\left\Vert \textbf{U}_0\right\Vert /F_{i0}^2}. \end{aligned}$$
(24)

We will not detail the derivation of \(\Gamma _2\) and \(\Gamma _3\), i.e. the reflection and resonance components, but we must consider their effects. Namely the reflection implies a larger momentum flux deposition at the low-level breaking levels, resulting in a smaller momentum flux propagating freely upwards. The inclusion of resonance means possible amplification or damping of stress in the vicinity of a breaking level depending on the vertical wavelength scale relative to the depth of the breaking layer.

The scheme also accounts for wave blocking by multiplying the final momentum flux by a coefficient dependent on the depth of blocking layer, which is in turn dependent on \(F_c\). Above the blocking layer the coefficient is equal to 1. This shall enhance the drag near the surface in the case of wave blocking. For this model, we were able to establish the specific choice of \(F_c=0.5\) and \(K_{GW}=1.5\times 10^{-3}\), which can be related (as shown earlier) to \(h/\delta x\) or Kh in previous definitions.

4.7 GFDL-ESM4

This model uses a parameterization scheme of Garner (2005), as described in Zhao et al. (2018) that uses a Fourier transform of the terrain. A potential \(\chi\) is introduced such that \(\nabla \chi =\rho _0\textbf{U}'\), where \(\textbf{U}'\) is a perturbation of the horizontal velocity, with nabla in this case being a purely horizontal operator.

\(\chi\) can be expressed as a function of wave numbers, or in spatial coordinates as follows

$$\begin{aligned} \chi (\textbf{x})=-\frac{\rho N}{2\pi }\iint \frac{h\left( \mathbf {x'}\right) }{\left|\textbf{x}-\mathbf {x'}\right|} \ \textrm{d}x'\ \textrm{d}y'. \end{aligned}$$
(25)

Garner (2005) shows that we can use Fourier transform of topography to get \({\hat{h}}(\textbf{k})\), where \(\textbf{k}\) is the horizontal wave vector. Amplitudes of this transform give us the spectrum of possible OGWs. \({\hat{h}}(\textbf{k})\) can be also expressed in spatial coordinates, \(h(\mathbf {x'})\), which is the term emerging in the definition of the potential \(\chi\). After rescaling,

$$\begin{aligned} \tilde{\chi }=\frac{\rho _0 N_0}{\rho N}\chi . \end{aligned}$$
(26)

we can define the base vertical flux of horizontal momentum as

$$\begin{aligned} \mathbf {\tau }_0=\frac{\rho N}{\rho _0 N_0}\left[ \nabla \tilde{\chi } (\nabla h)^T\right] \textbf{U}, \end{aligned}$$
(27)

where \(\nabla \tilde{\chi } (\nabla h)^T\) could be transcribed as a matrix. This term includes anisotropy, variance as well as the amplitude of the topography.

The parameterization scheme also considers the drag from the wave blocking and deflection, where the blocked layer is defined using \(F_c\). With a small difference that the authors do not take the mean height as an average of a grid cell, but take h as a variable within each grid so that it corresponds with the assumed distribution of mountains. The drag from the low-level blocking and breaking is distributed near the surface. We can then divide the total momentum flux into the freely propagating and blocked components

$$\begin{aligned} \mathbf {\tau }=a_p\mathbf {\tau }_0+a_b\mathbf {\tau }_b, \end{aligned}$$
(28)

where \(a_p,a_b\) are considered to be tunable parameters.

The critical number in this scheme is tuned to \(F_c=0.7\), and we have confirmed this number for the analyzed simulation as well. The other two parameters are \(a_p=1\) and \(a_b=5\), where the large value for the low-level drag was chosen due to the low resolution of the model (see Table 1).

5 Results

5.1 Intermodel comparison of parameterized OGWD

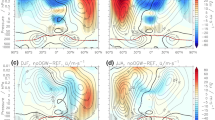
In this section we analyze whether the described differences between parameterization schemes of the CMIP6 models and their tuning lead to pronounced differences in the parameterized OGWD. We focus especially on the parameter \(F_c\), which is known to have a large impact on the resulting drag (Webster et al. 2003, Scinocca, J. personal correspondence, Ridley, J. personal correspondence) and is used in all parameterizations. Naturally, one needs to be careful, when attributing the differences, as other factors like different dynamical cores, or resolution of the models may play a role as well. First, we focus on the horizontal OGWD distribution (shown for two particular models in Fig. 1). From a visual inspection, the horizontal distribution is very similar between all analyzed models and schemes (not shown), allowing identification of major hotspots connected with significant topography of the Earth. Note, however, the scale of the colorbar in Fig. 1, which points to great differences in the magnitudes of OGWD between the models. Further in the manuscript we show only the results from the zonal mean analysis. In the Appendix A we provide the same figures also for major hotspot regions to confirm that the results are consistent across the globe.

Fig. 1
figure 1

Yearly climatological (1984–2014) horizontal distribution of OGWD at 70 hPa for models MRI-ESM2-0 and IPSL-CM6A-LR

Full size image
Fig. 2
figure 2

Mean (1984–2014) SH (on the left) and NH (on the right) winter vertical distribution of zonal mean OGWD for the available CMIP6 models in the latitudinal band of a maximal drag

Full size image
Fig. 3
figure 3

Winter zonal mean OGWD climatology from 1984 to 2014 in the NH for the available CMIP6 models averaged over the low-level drag region (on the left) and over the lower to mid-stratospheric region (on the right)

Full size image

Focusing on the magnitude and vertical distribution of the drag, in Fig. 2 we show for all the models the zonally averaged OGWD over the regions in midlatitudes in both hemispheres, where the strongest hotspots are located (see Fig. 7 in the Appendix A for locations of the hotspots). In the majority of models we can clearly identify in Fig. 2 three regions with locally maximal OGWD. The first layer of pronounced OGWD is located near the surface and is connected with the low-level breaking and blocking. The second is caused by breaking of freely propagating OGWs above the center of the UTLS jet starting at \(\approx\) 100   hPa. This is in agreement with our estimation of breaking levels based on the saturation hypothesis and the climatological zonal mean zonal wind field. Finally, the remaining flux is deposited in the upper stratosphere above 10   hPa, this region will not be investigated further in the manuscript. The vertical distribution is similar between both winter hemispheres, but the magnitude of the zonal mean OGWD in SH is generally smaller than in NH, which is due to the higher fraction of ocean sampled in the zonal mean. Locally, OGWD above Andes exceeds the values seen for the hotspots in NH (Figs. 8 and  9 in the Appendix A). However, note that for some models (CESM2 in particular) the difference between the magnitude of zonal mean OGWD in NH and SH is smaller than for the other models.

To analyze intermodel differences in the near surface and lower stratospheric drag while accounting for possible differences in the vertical structure of the atmosphere and in the vertical distribution of OGWD from different schemes and tuning, we compute a mean OGWD across pressure levels around those two vertical regions and show its latitudinal distribution in Fig. 3. (See Figs. 10 and  11 in the Appendix B for vertical distribution of all models.) Starting with the low-level zonal mean OGWD in boreal winter in NH (Fig. 3, upper left panel), we can see pronounced discrepancies between the models approximately from 30\(^{\circ }\)N to 60\(^{\circ }\)N. The models with largest drag (suggesting early deposition of the momentum flux) are CNRM-CM6-1, IPSL-CM6A-LR and MRI-ESM2-0. For IPSL-CM6A-LR, the reason for such a large low-level drag stems probably from the method of how the drag from breaking and blocking is distributed within the scheme in vertical, depending on the decaying parameter \(\beta\). In the literature, it is stated that this parameter is effective up to about 850   hPa (Lott 1999). However, the exact value used in the simulation is not known and also it must be considered that the topography locally reaches much higher altitudes (lower pressures), which allows the low-level drag to affect higher levels in the mean. Also, the choice of \(F_c=0.7\) for blocking in this model would suggest only a medium amount of drag to be redistributed and created near the surface. In the case of CNRM-CM6-1, the pronounced low-level drag is consistent with the choice of \(F_c=0.5\). Hence, a large portion of the momentum flux cannot propagate higher and is dissipated near the topography. In the MRI-ESM2-0 parameterization scheme, the drag from blocking is not considered explicitly. Larger low-level drag values in this simulation are most likely due to the type B waves (modes with short wavelengths) that are trapped in the troposphere and enhance the low-level drag. For this model we were not able to establish exact values of the free parameters of the scheme used for the simulation.

On the other end, CanESM5, HadGEM3-GC31-LL and UKESM1-0-LL, give almost no drag near the surface. HadGEM3-GC31-LL and UKESM1-0-LL share a parameterization that handles the low-level drag differently than other models and puts a great emphasis on this process (Webster et al. 2003). Also, given the small value of \(F_c=0.25\) that is employed (for UKESM1-0-LL this has not been confirmed) we should see pronounced drag from blocking. It is very likely that the drag from blocking for those two models is not included in the OGWD CMIP6 data.

This is also possible in the case of CanESM5, where we have been informed that the critical Froude number has been chosen as 0.22, which would imply large low-level drag values. CanESM5 employs a similar OGW parameterization scheme as CESM2, which uses \(F_c=1\), suggesting smaller low-level drag values than for CanESM5, but we see the exact opposite.

MIROC-ES2L gives only slightly higher low-level drag values than the previous three models. This is in line with the fact, that the low-level blocking and low-level breaking are not considered in its parameterization explicitly. For this model and CanESM5, the lower horizontal resolution of 500km compared to other models can be a factor as well.

The moderate low-level drag values of GFDL-ESM4 are connected with the specific handling of deflection and wave blocking in its parameterization scheme and the larger value of the parameter \(a_b\) chosen for this simulation. Since \(F_c=0.7\) we can expect a large part of the momentum flux to propagate vertically into the free atmosphere.

Next we turn our attention to the intermodel agreement in the lower stratosphere in NH (Fig. 3, top right panel), where in boreal winter a pronounced OGWD region is to be expected due to the breaking of freely propagating modes. We can again see pronounced differences between the models—four models give negligible values of OGWD and continue to do so up to the upper stratosphere (see Fig. 2). For IPSL-CM6A-LR and CNRM-CM6-1 this is clearly due to the deposition of the majority of momentum flux in the low-level breaking region as a consequence of the choice of \(F_c\) or in the case of IPSL-CM6A-LR also due to the decaying parameter. However, HadGEM3-GC31-LL and UKESM1-0-LL show the smallest values from the comparison also for the low-level drag. As discussed earlier, it is likely that the two models do not report the drag from the blocking and other low-level processes to the OGW drag output. We were not able to confirm this, but from the communication with the model developers and users, it is the most likely explanation. If true, we could say again that most of the momentum was already deposited near the surface and did not propagate to the lower stratosphere. This is confirmed in Fig. 12 in the Appendix B, where we show estimates of the launched momentum fluxes connected with the freely propagating modes using the vertical integration of the OGWD. Otherwise, the only plausible explanation would be that their OGW parameterization scheme underestimates the net orographic drag compared to other models and schemes.

The largest drag from freely propagating waves is produced by CESM2, GFDL-ESM4, and MIROC-ES2L, with MIROC-ES2L giving absolutely largest peak of the drag in midlatitudes at the poleward flank of the UTLS jet. This group of models was giving also moderate amounts of the low-level drag. For MRI-ESM2-0 the situation is different and not as much tuning-dependent. The low-level drag is caused by a different part of the wave spectrum than the drag in the stratosphere (A-type modes with wavelengths around hundred kilometers). CanESM5 gives smaller OGWD than CESM2, which is in line with the choice of \(F_c=0.22\) for the low-level drag in CanESM5 and suggests that the low-level drag was indeed not included in the OGWD output for the model. In the stratosphere, the two-wave scheme of CanESM5 is known for allowing more momentum flux to be propagated to the stratosphere from the surface Scinocca and McFarlene 2000) resulting in moderate OGWD values in the lower stratosphere.

In SH, during the austral winter, we start the discussion with the meridional distribution of the zonal mean drag from freely propagating OGWs in the lower stratosphere (Fig. 3, bottom right panel). Compared to NH, where the OGWD has an almost Gaussian distribution centred between 30 and 40\(^{\circ }\)N, for SH we see two latitudinal bands of pronounced OGWD—one from 20 to 50\(^{\circ }\)  S peaking more equatorward (around 30\(^{\circ }\)S) than for NH and the other in the polar region. These two regions are separated by the OGWD gap. The OGWD gap is a direct result of the columnar approach with the strictly vertical propagation assumption employed in the parameterizations. This deficiency of the current OGW parameterizations gets more pronounced in SH than in NH due to the continental distribution. The intermodel differences generally follow the situation from NH, only in MIROC-ES2L we see that it produces not only stronger OGWD than other models, but its distribution is also different. This is probably due to the comparatively coarse resolution of this model, which may fail to capture smaller scale features of the highly variable orography in SH (especially concerning Antarctic and southern Andes). The intermodel differences in low-level drag in SH (Fig. 3, bottom left panel) are almost similar equatorward from the OGWD gap to the situation in NH midlatitudes. However, large intermodel differences can be seen for low-level drag distribution and magnitude in Antarctic, where we can see chaotically oscillating large values of positive and negative OGWD that even exceed the magnitude of the OGWD from freely propagating OGWs aloft. This is an unprecedented situation compared to NH and SH equatorward from the OGWD gap. We cannot provide any explanation for this feature with the data available. However, being localized only to the one specific region while emerging in majority of the models, it is most likely not connected with a particular OGWs parameterization type or specific choice of the free parameters.

5.2 Dynamical impact

In this subsection we link the differences in the parameterized OGWD with the differences in resolved wave dynamics in the stratosphere of the models. In the Appendix B—Figs. 13,  14, and  15 we document that the below discussed relations between the resolved and unresolved drag are not caused indirectly by intermodel differences in the zonal mean circulation that would influence both the resolved and unresolved wave forcing. The only clear signals can be found in the vertical column of the OGWD maximum—the direct proportion between OGWD in the valve layer and lower tropospheric winds (stronger lower tropospheric winds, stronger lower stratospheric OGWD), which is due to the partitioning between the near surface drag and freely propagating momentum fluxes in the schemes, and the indirect proportion (weaker winds, stronger OGWD) in the lower stratosphere marked by significant correlations (with r from 0.63 to 0.78 and p-values from 0.01 to 0.07). In this region the relationship between OGWD and zonal mean zonal winds has a two-fold nature. Zonal wind is a crucial input to the parameterization on the one hand and OGWD is a dominant wind tendency term in this region on the other (though not for all models, as shown in the previous section).

The OGWD impact on the resolved wave activity in the stratosphere has been already highlighted in the literature (Cohen et al. 2013, 2014; Eichinger et al. 2020; Sacha et al. 2021). The set of interactions between parameterized OGWD and EPFD has been conceptualised by Cohen et al. (2013), Cohen et al. (2014), from which explicitly the alteration of the resolved wave propagation has been shown to dominate in particular GCMs (Eichinger et al. 2020; Sacha et al. 2021). Indeed, we can see strong and statistically significant correlations between intermodel differences of OGWD in the valve layer and the climatological resolved wave drag (represented by EPFD) between 100hPa and 30hPa in the stratosphere both southward and poleward from the maximal OGWD region in both hemispheres, Fig. 4. Due to the limited EPFD CMIP6 data availability, this plot does not include CNRM-CM6-1 and MIROC-ES2L.

Fig. 4
figure 4

Scatter plot of model specific boreal winter zonal mean climatologies of OGWD and EPFD at the selected latitudinal bands, OGWD taken over maximum: 30\(^{\circ }\)–45\(^{\circ }\)N and 37\(^{\circ }\)–22\(^{\circ }\)S, 1984–2014

Full size image

In NH, in agreement with the well established compensational mechanism between resolved and unresolved drag and previous GCM based studies (Eichinger et al. 2020; Sacha et al. 2021), we see a clear sign of compensation between OGWD and EPFD equatorward from the OGWD region (Fig. 4, top-left panel), with models having the strongest OGWD having also the weakest resolved wave drag and vice-versa. This is in perfect agreement with the causal effect of the lower stratospheric forcing suppressing the upward and equatorward propagation of resolved waves around the subtropical jet (see Sacha et al. 2016 to document the causality). Poleward from the OGWD region, starting at 45\(^{\circ }\) N, the relationship is equally strong and robust but reversed, with the models that have stronger OGWD in the valve layer having also stronger drag from resolved waves. Hence, this effect has an opposite sense from the compensation mechanism. The possibility of such amplifying interaction has been noted already by Cohen et al. (2014), with relation to the expansion of the surf zone by OGWD at its edge. But, Eichinger et al. (2020) and Sacha et al. (2021) attributed this effect also to changes in resolved wave propagation due to the modification of the lower stratospheric refractive index by OGWD. Such effect of a localized forcing in the lower stratosphere, has been demonstrated also by Samtleben et al. (2019) and Samtleben et al. (2020) for particular suitable OGWD hotspot configurations. We analyze the reasons for the amplifying interaction later in the manuscript.

In SH (Fig. 4, bottom panels) we see qualitatively similar relationships between the intermodel differences in the resolved drag and OGWD. But, the correlations are smaller and only weakly significant. Note that the regions for averaging of OGWD and EPFD are different from NH, reflecting the existence of the OGWD gap and pronounced OGWD values in the polar region. Setting the regions similarly to NH leads to further weakening of the signal (not shown). Besides the different OGWD distribution, the weaker relationship between OGWD and EPFD in SH can be caused by the stronger influence of non-OGW parameterization on the resolved wave field documented by Scheffler and Pulido (2015) and Polichtchouk et al. (2018).

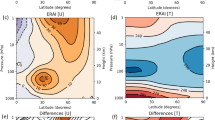
Based on the available literature on dynamical impact of lower stratospheric OGWD in SH, the dominant mechanism behind the emerging link between OGWD and resolved dynamics is the influence on the region of upward propagation of resolved waves. Eichinger et al. (2020) attributed the existence of the amplifying interaction in polar region and compensating interaction southward from the OGWD region to the latitudinal distribution of the refractive index in the lower stratosphere in SH. In their reference simulation (with the OGW parameterization), the refractive index has been maximal and sharply bounded in the OGWD gap region—a feature that was almost missing in simulations without the OGW parameterization. Similar effect has been seen by McLandress et al. (2012), where after applying an additional drag to the OGWD gap region, the upward propagation of resolved waves has been reduced. Due to the limited availability of the Eliassen-Palm flux (EPFz) data in the models, which can be used to access the vertical propagation, we cannot reproduce the correlation analysis to test this. But, we can document the effect of OGWD on the vertical propagation of resolved waves by visual comparison of the EPFz field below and inside the valve layer (Fig. 5). In SH (upper panels) we can clearly see that the meridionally broad region of vertical propagation in the upper troposphere gets confined by the OGWD region in the lower stratosphere.

Fig. 5
figure 5

Zonal mean of Eliassen-Palm flux vertical component (colors) with mean and variance of OGWD across models (grey) at two vertical levels, boreal winter, 1984–2014

Full size image

In NH (lower panels), the meridional distribution of the EPFz field in the upper troposphere is very similar to SH, but the situation is slightly different in the lower stratosphere. The vertical propagation of resolved waves is also suppressed equatorward from around 40\(^{\circ }\) N, but the propagation is no longer confined by the existence of OGWD in polar regions as in SH and the region of pronounced EPFz shifts poleward. Similar effect for meridional propagation of resolved waves can be illustrated by vertical profiles of Eliassen-Palm flux (EPFy) in the latitudinal band of the OGWD maxima in both hemispheres, Fig. 16 in the Appendix B. The equatorward pointing EPFy vanishes when reaching the lower stratospheric OGWD region.

The OGWD impact on the resolved wave field is most likely connected with the modification of the lower stratospheric refractive index for propagation of planetery waves, as documented in the scatter plot in Fig. 6 (see Figs. 17 and  18 in the Appendix B for refractive index distributions in individual models). The refractive indices were calculated according to Andrews et al. (1987), eq. 5.3.7, with the scale height \(H={7000}\,{\hbox {m}}\) and for wavenumber \(s=1\), but the emerging relationship is valid also for other wavenumbers. For NH we see an exceptionally strong and robust link between the OGWD magnitude in the valve layer and the collocated mean refractive index in the model. The stronger OGWD in the model the smaller the refractive index, meaning less propagation of resolved waves. In the polar region of NH, where the amplifying interaction takes place, we can see an opposite relation between the local refractive index and OGWD in the valve layer—the stronger OGWD in the model, the higher is the refractive index.

In SH, our results agree with the findings of McLandress et al. (2012); Eichinger et al. (2020) regarding the refractive index in the OGWD gap region—right panel in the second row of Fig. 6, with the models that have stronger OGWD in the lower stratospheric maxima having also higher values of the refractive index. Furthermore, we have found equally strong correlations between model OGWD and refractive index above the subtropical jet—left panels in the first two rowes and in the polar region—bottom of the figure. Note that in the SH polar region the refractive index is generally small and for models with strongest OGWD even negative, completely inhibiting the upward propagation. This particular finding concerns only the planetary wave mode one, though.

Fig. 6
figure 6

Scatter plot of model specific winter zonal mean climatology of OGWD and RI index taken at the selected latitudinal bands, OGWD taken over maximum: 30\(^{\circ }\)–45\(^{\circ }\)N and 37\(^{\circ }\)–22\(^{\circ }\)S, 1984–2014

Full size image

6 Summary and conclusions

In our study, we reviewed and briefly described 7 different OGW parameterizations, which are used in 9 CMIP6 models that provided the requested OGW parameterization output for AMIP simulations. The underlying physical mechanisms and tuning of the free parameters were detailed for each scheme, in some cases using unique (previously unpublished) information obtained through personal communication with the model developers. Then, we have analyzed the resulting parameterized OGWD in detail and performed an intermodel comparison of the magnitude and distribution of the drag. As the models agreed well regarding the horizontal distribution of OGWD revealing all major hotspots around the globe, we base the rest of the study on a zonal mean analysis.

We have found striking differences between the individual models in the magnitude and vertical distribution of the zonal mean OGWD. From the theory we expected to find two pronounced regions of OGWD—near the surface and in the lower stratosphere. This was however not the case for all the simulations. Some models produce either too much or too little dissipation near the surface which consequently leads to a likely over—or under-estimation of OGWD in the lower stratosphere. We also indicated two models that strongly underestimate the drag in both vertical regions, although it is very likely that they simply have not included the drag from the near-surface blocking to the OGWD output. For each model and OGW parameterization set-up we provided a tentative explanation for its performance, informed by the physics and tuning of each scheme.

Finally, we have studied whether the pronounced differences in the parameterized OGWD project into the climatological differences of the dynamics in the stratosphere between the models. Indeed, we have documented a clear link between the magnitude of OGWD in the valve layer and the drag from the resolved waves both in the subtropics (inversely proportional) and polar regions (direct proportion) in both winter hemispheres. The most likely mechanism behind this link is the modification of resolved wave propagation due to the OGWD effect on the refractive index in the lower stratosphere around the UTLS jet.

As an interesting aspect, we have found that climatological zonal mean zonal winds (and winds at 10 hPa, 60\(^{\circ }\) N in particular (not shown)) in the winter stratosphere are to a large extent insensitive to the strength of the OGWD and the resolved wave drag in polar regions of the models (see Figs. 14 and 15 in the Appendix B). A possible explanation can be that at a leading order the intermodel differences in the climatological polar vortex strength are linked with differences in diabatic heating between the models via the thermal wind balance. This climatological view can, however, mask the fact that the representation of Sudden Stratospheric Warmings (SSWs) in the models can be very sensitive to small nuances of the model dynamics. Hence, the lack of significant correlation between resolved wave drag and zonal mean wind climatology in the polar stratosphere does not rule out that resolved wave drag differences can influence the differences in SSW frequencies (Hall et al. 2021). This is supported by the connection of our results showing the strong link between OGWD and refractive index in the valve layer with the results of Wu and Reichler (2020), who showed that the refractive index differences just above the subtropical jet are important for the SSW frequency differences in CMIP5 and CMIP6 models. Considering also the intermittency of the OGWD (Kuchar et al. 2020), we intend to analyze the link between intermodel differences in OGWD and SSW frequencies in a follow up study.

The link between parameterized OGWD and resolved wave field in the models can be of great importance also for the representation of transport processes in the models. As made explicit by the Transferred Eulerian Mean equations (Andrews et al. 1987), the Stokes drift from the resolved wave field has a leading order effect on the advective transport in the extratropical stratosphere. By controlling the propagation of resolved waves to the stratosphere, differences in OGWD may affect also the intermodel differences in residual mean circulation in the extratropical stratosphere in the models (as illustrated in Fig. A1 in Sacha et al. (2019)). Another transport process, where parameterized OGWD can possibly play a role is the quasi-horizontal mixing, which is especially important for the representation of the stratosphere-troposphere exchange in the models. Additionally to influencing the propagation of resolved waves, intermittent OGWD effects have been shown to impact also the transience of the resolved wave field in one particular model with exceptionally strong OGWD (Sacha et al. 2021). However, the possible link between parameterized OGWD and quasi-horizontal mixing in the models has not been examined so far in detail. Research of parameterized OGWD with all of its tuning on transport processes is also of utmost importance, because the performance of current generation chemistry-climate models depends strongly on a precise representation of transport processes.