Abstract
The El Niño Southern Oscillation (ENSO), as one of the largest coupled climate modes, influences the livelihoods of millions of people and ecosystems survival. Thus, how ENSO is expected to behave under the influence of anthropogenic climate change is a substantial question to investigate. In this paper, we analyze future predictions of specific traits of ENSO, in combination with a subset of well-established precursors—the Trade Wind Charging and North Pacific Meridional Mode (TWC/NPMM). We study it across three sets of experiments from a protocol-driven ensemble from CMIP6—the High Resolution Model Intercomparison Project (HighResMIP). Namely, (1) experiments at constant 1950’s radiative forcings, and (2) experiments of present (1950–2014) and (3) future (2015–2050) climate with prescribed increasing radiative forcings. We first investigate the current and predicted spatial characteristics of ENSO events, by calculating area, amplitude and longitude of the Center of Heat Index (CHI). We see that TWC/NPMM-charged events are consistently stronger, in both the presence and absence of external forcings; however, as anthropogenic forcings increase, the area of all ENSO events increases. Since the TWC/NPMM-ENSO relationship has been shown to affect the oscillatory behavior of ENSO, we analyze ENSO frequency by calculating CHI-analogous indicators on the Continuous Wavelet Transform (CWT) of its signal. With this new methodology, we show that across the ensemble, ENSO oscillates at different frequencies, and its oscillatory behavior shows different degrees of stochasticity, over time and across models. However, we see no consistent indication of future trends in the oscillatory behavior of ENSO and the TWC/NPMM-ENSO relationship.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The El Niño Southern Oscillation (ENSO) is one of the largest modes of coupled ocean–atmosphere variability and has large-scale impacts on climate patterns across the globe. A large body of research has connected ENSO to significant variations in temperature, precipitation and pressure patterns both in the Tropical Pacific and beyond (Rasmusson and Carpenter 1982; Dai and Wigley 2000; Alexander, et al. 2002; Cai et al. 2011). Therefore, the better we understand and characterize ENSO and its behavior, the easier it becomes for affected communities to prepare and thus increase their resilience in the face of ENSO-related climatic impacts. In this endeavor, the ability to predict the occurrence of ENSO events in a timely manner would prove extremely helpful. This is the reason why the scientific community has been extensively investigating the atmospheric and oceanic conditions that precede ENSO events and initiate the transition between its different states (Wang, Deser, Yu, DiNezio, and Clement 2017).
In this study, we focus on a specific set of initiating mechanisms, namely the extra-tropical anomalies related to the North Pacific Oscillation (NPO) (Anderson 2003). In particular, the sea-level pressure (SLP) anomalies that accompany a positive NPO phase weaken the subtropical high in the northern Pacific Ocean, thus reducing the strength of the off-equatorial trade winds. These anomalies in the trades trigger a combined dynamic and thermodynamic response within the underlying ocean that has been shown to initiate a positive ENSO event (i.e. an El Niño). Dynamically, NPO-induced Trade Wind Charging (TWC) causes convergence of warm water in the equatorial subsurface that subsequently shoals in the eastern equatorial Pacific and initiates a positive ENSO event (Anderson and Perez 2015).
Thermodynamically, the NPO-induced North Pacific Meridional Mode (NPMM) (Chiang and Vimont 2004; Amaya 2019) connects to the onset of ENSO through the formation of equatorial Kelvin waves that propagate along the thermocline (Amaya et al. 2019; Thomas and Vimont 2016; Alexander, et al. 2010; Liu and Xie 1994). By contrast, anomalies connected to a negative NPO lead to a negative ENSO event (i.e. a La Niña). Since both the TWC and NPMM anomalies arise from NPO events, they will be henceforth referred to as TWC/NPMM variations. Recent studies on the relationship between ENSO and TWC/NPMM have shown that it is non-stationary in time both in historical data (Pivotti and Anderson 2021) and in control experiments of CMIP6 HighResMIP (Pivotti, et al. 2023).
Further, while variability of ENSO, its precursors, and its teleconnections are still topics of investigation, it is now apparent that anthropogenic global warming further complicates their evolution and interactions. Numerical models have been a fundamental tool to understand how these modes and their relations behave now and will in the future. A paper by Yeh, et al. (2018) provides a comprehensive overview of recent findings on ENSO projected changes, based on the simulations from the third and fifth Coupled Model Intercomparison Projects—CMIP3 and CMIP5 respectively. The main conclusion is that the impacts of global warming on ENSO are not well constrained, but ever-evolving, and model simulations do not agree on how the teleconnections will change in scale and intensity. A more recent study by Beobide-Arsuaga, et al. (2021) instead focuses on ENSO amplitude across CMIP5 and CMIP6 models and shows how inter-model variability is reduced in the latest CMIP6. Other studies have focused on multiple characteristics of future ENSO events, such as its amplitude (Wang, Deser, Yu, DiNezio, and Clement 2017), its variability (Collins et al. 2010), and how the characteristics of these different events affect weather patterns (Wang, et al. 2017). Furthermore, a large body of literature has looked specifically at the predicted changes in the frequency and number of extreme ENSO event occurrences (Cai, et al. 2014; Cai, et al. 2015; Marjani et al. 2019). One important aspect that has not been investigated at length is the frequency of the oscillatory ENSO signal, both with regard to changes in the range of its periodicities as well as its behavior, i.e. stochastic versus oscillatory. In Timmerman et al. (1999) the ENSO frequency was predicted to increase because of global warming. However, using historical data, Pivotti and Anderson (2021) showed that even in the absence of anthropogenic forcing the behavior of ENSO can show internal multi-decadal shifts between stochastic and oscillatory phases and that these shifts mirror changes in the strength of the TWC/NPMM-ENSO relationship.
Our objective here, then, is to examine future changes in the characteristics of ENSO in relation to the TWC/NPMM-ENSO coupling under the influence of increased human-induced climate forcings, as well as changes in the frequency of the oscillatory ENSO signal since, historically, they have shown to vary together. This is carried out using a state-of-the-art model ensemble called High Resolution Model Intercomparison Project (HighResMIP) which is part of the CMIP6 protocol. In particular, in Sect. 2 we describe in details the HighResMIP model ensemble and the experiments we employ, as well as the different methodologies that we utilize in the study. In Sect. 3 we present the results that we then summarize and discuss them in Sect. 4.
2 Data and method
2.1 Data
The model ensemble for this analysis is the one developed for the High Resolution Model Intercomparison Project (HighResMIP), which is endorsed by CMIP6 and thoroughly described in (Haarsma et al. 2016). This ensemble is meant to investigate the effects that increased horizontal resolution may have on model performance. In a previous study on the same ensemble (Pivotti et al. 2023) it was shown that horizontal resolution does not play a significant role in the representation of the TWC/NPMM-ENSO relationship. Therefore, we again use the HighResMIP as an ensemble, since we know its ensemble members well capture the TWC/NPMM-ENSO coupling, and because it has he added value of it being protocol-driven, but will not engage in a discussion on resolution. We utilize three experiments for each model, with one run per experiment, namely: (1) control-1950, a 100 years long simulation with constant 1950’s radiative forcing levels which correspond to a global radiative forcing of ~ 0.5 W/m2 (Myhre, et al. 2013); (2) hist-1950, an experiment with prescribed radiative forcings from 1950 to 2014; and (3) highres-future, a simulation that continues from where hist-1950 ends until 2050, with external forcings prescribed to follow the RCP8.5 scenario from the fifth IPCC. In this pathway no mitigation efforts are implemented (Pachauri and Alle 2014) and the radiative forcing increase relative to pre-industrial levels reaches 8.5 W/m2 by 2100 (Riahi et al. 2011). For brevity, we will refer to experiment (1) as the control and to the 101 years of combined hist-1950 and highres-future as the transient run henceforth. According to the HighResMIP protocol, each institution runs all experiments at a standard and an enhanced horizontal resolution. The details of the models, the institutions responsible and their specific resolutions are presented in Table 1. Importantly, from previous studies using datasets of comparable (~100 year) length (Pivotti and Anderson 2021; Pivotti et al. 2023), we find the length of the HighResMIP simulations to be adequate to investigate the temporal features of the TWC/NPMM-ENSO relationship both in the control and transient simulations.
For the current analysis, the variables of interest are sea surface temperature, SST, and zonal wind stress, τX. The first variable is used to capture the variability of ENSO, the latter for TWC/NPMM (Chakravorty et al. 2020). We limit our focus to the Tropical Pacific, between latitudes 20S and 20N and longitudes 120E and 70W, where both ENSO and TWC/NPMM are active, following the lead of Anderson and Perez (2015) and Larson and Kirtman (2013). Temporally, we calculate winter means over the months during which ENSO and TWC/NPMM are most active: November-January for ENSO (SST) (Trenberth 1997) and November-February for TWC/NPMM (τX) (Anderson and Perez 2015) respectively. Lastly, it is important to note that since we are interested in the τX mode that precedes ENSO events by 1 year (Anderson 2003), the two variables are lagged accordingly.
2.2 Method
Across the study we have utilized three main analytical diagnostics. The first is a variation of the classic Canonical Correlation Analysis (CCA) called the CCA in the basis of Principal Components (PC’s) (Bretherton, Smith, and Wallace 1992). In particular, as in the classic version of the CCA, this method is used to isolate the most highly correlated modes between two variables, in this case the detrended winter means of SST and the detrended winter mean τX during the prior year. In this version, the CCA is applied not to the full fields, but only to a subset of their respective PC’s, obtained through an Empirical Orthogonal Functions (EOF) analysis. Furthermore, we exclude from the CCA the PC of τX that has the highest correlation with the concurrent Niño3.4 index, as we want to remove the influence from concurrent ENSO events on the zonal wind stress as in Chakravorty, et al. (2020), and Larson and Kirtman (2014). We use the CCA in the basis of PC’s to understand whether and how each ensemble model reconstructs the relationship between ENSO and its extra-tropical precursor TWC/NPMM. This method is described in further details in previous articles by the authors where we analyzed the relationship between ENSO and the TWC/NPMM precursor in the SODAsi.3 reanalysis dataset (Pivotti and Anderson 2021) and in the control runs of the HighResMIP ensemble (Pivotti et al. 2023).
Secondly, we calculate the Center of Heat Index (CHI) of ENSO (Giese and Ray 2011) to better understand its spatial characteristics. We chose CHI because it provides multiple spatial characterizations of ENSO in a robust, well-tested and coherent manner. In this analysis we calculate the amplitude and the longitude, as well the area of each ENSO event. In each of these calculations we include all the years that satisfy the CHI requirement, namely the years in which the area over which the SST anomalies are greater than \(0.5\) (\(<-0.5\) respectively) is larger than the Niño 3.4 area (5S-5N 170–120W)—further details can be found in (Giese and Ray 2011).
Finally, to investigate whether the power and oscillatory behavior of the ENSO signal show trends across the ensemble, we turn to the Continuous Wavelet Transform (CWT) and apply it to the first PC of Tropical SST anomalies (Pivotti and Anderson 2021). To study the resulting time/periodicity maps W(p,t) (where p is the periodicity and t time), we calculate three indicators that mirror how the CHI characterizes the SST spatial anomaly maps. As a first step, to guarantee significance, we consider only the values that lie within the cone of influence. Then, to reduce noise, we exclude the values whose periodicity is higher than 10 years and whose power is less than the standard deviation of W(p,t).The first indicator we calculate is P(t), which captures the power of the signal over time. To do so, at each time point t, we sum the power across periodicities for each time-point analogous to the calculation of the CHI-amplitude.
As a second indicator, C(t), we estimate the “central periodicity” at each time point, similarly to the calculation of the CHI-longitude, by calculating the weighted mean of the periodicity, where for each (p,t) the weight is the normalized power W*(p,t).
where
Finally, as a third indicator S(t), we estimate the weighted spread around the estimated center of periodicity C(t).
3 Results
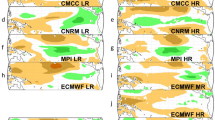
We apply the CCA in the basis of PC’s to the winter means of τX and SST, and obtain pairs of time series called Canonical Variables (CV). These time series are in decreasing order of correlation value, which means that the first pair captures the modes showing the highest correlation. In this case, the pair of CV’s has a 1 year lag by construction and represent a mode of τX (CVτx(t–1)) and a mode of SST (CVSST(t)) respectively. In order to illustrate the spatial characteristics of these highly correlated modes, we regress CVτx(t–1) and CVSST(t) against the normalized anomaly fields of their respective variables and obtain for each experiment two anomaly maps. We do not show here the 40 individual regressed maps for each experiment, (which for the control experiments can be found in Pivotti et al. (2023)). Instead we illustrate how the ensemble behaves as a whole by calculating the ensemble-wide average maps of τX and SST for control and transient experiments separately. The resulting maps are shown in Fig. 1, panels (a, b) for the control experiments (TXC, SC) and panels (d, e) for the transient (TXT, ST) respectively. The first interesting result is that both TXC and TXT capture a positive anomaly in the zonal component of the northern Tropical Pacific trades, while SC and ST reconstruct a positive SST anomaly in the eastern portion of the Equatorial Pacific. This confirms that across the ensemble the most highly correlated modes of lagged τX and SST are the TWC/NPMM precursor and ENSO in both control and transient experiments, as it is in the historical data (Pivotti and Anderson 2021). Moreover, their spatial characteristics are largely unaltered by the increase in anthropogenic forcings, as indicated by the high spatial correlations between patterns: ρ(TXC,TXT) = 0.93 and ρ(SC, ST) = 0.97, respectively. Furthermore, in order to better capture the ensemble behavior, for each set of experiments, we calculate the spatial correlation between the map of each individual model against the corresponding ensemble mean map. The results are presented on the right-hand side of Fig. 1, in panels (c, f). These results indicate that the correlation values for the SC and ST maps are higher across the ensemble for both control and transient runs, as compared to the correlation values for the TXC, TXT maps. This suggests a greater inter-model agreement in the reconstruction of ENSO patterns, when compared to TWC/NPMM patterns. Furthermore, models with a standard resolution (LR) and those with an increased resolution (HR) show no significant difference in their correlation values, which leads us to conclude that the difference in horizontal resolution does not affect a model’s ability to reconstruct the spatial characteristics of the TWC/NPMM-ENSO relationship, either in the control, or in the transient runs. In addition, we investigated the significantly lower spatial correlation for ENSO in the transient experiment of CNRM LR, and we uncovered overall weaker SST anomalies, as well as null anomalies around 150W. However, this is a map averaged over many ENSO events and, as the next steps look at isolated ENSO events, we decided not to exclude CNRM LR from the following analyses.
Ensemble mean maps of normalized anomalies of τX and SST regressed against their respective first Canonical Variable for control (a, b) and transient runs (d, e). (a, d) maps of τX. Positive (negative) values are shaded in brown (green). Magnitude of normalized τX (unitless) are given by the color bar on the r.h.s of the panel. (b, e) maps of SST. Positive (negative) values are shaded in red (blue). Magnitude of normalized SST (unitless) are given by the color bar on the r.h.s of the panel. In panels (c, f) the values of spatial correlation between the regression maps from each model and the ensemble mean maps. In brown the values for TWCX in blue those for ENSO
Having established that TWC/NPMM is a consistent ENSO precursor in this ensemble, we want to characterize its influence upon ENSO events. We do this by calculating three components of CHI of ENSO: amplitude, longitude and area (Giese and Ray 2011). We then compare average ENSO events against the ones initiated by TWC/NPMM. We define average ENSO events as those years during which the winter means of SST satisfy the CHI requirement (details in the Sect. 2.2). These events will be referred to as CHI-ENSO events. Among the CHI-ENSO events, we select those that are preceded by a TWC/NPMM event. We identify these years T as those for which either
holds true, and these events will be referred to as TWC/NPMM-charged CHI-ENSO.
The results of these calculations are shown in Figs. 2, 3, 4 which all have 4 panels. In Fig. 2a, b we plot, for each experiment, the mean CHI amplitude of all CHI-ENSO events on the x-axis against the mean CHI amplitude of the TWC/NPMM-charged CHI-ENSO events on the y-axis. Panel (a) shows the results for the control experiments and panel (b) shows them for the transient ones. In Fig. 2c, d instead we still look at the CHI-amplitude, but the means are calculated across type of experiment, with results for the control on the x-axis, and for the transient on the y-axis. In panel (c), we show the results for CHI-ENSO events and in panel (d) we show them for TWC/NPMM-charged events. Figure 3 has the same structure as Fig. 2, but shows the results for the CHI longitude, while Fig. 4 shows an estimate of the CHI-area. In all plots we also show the mean calculated across the ensemble. Starting with the CHI-amplitude in Fig. 2a, b, we find that all the points are located above the 1–1 line (significant for 9/10) which indicates an ensemble-wide agreement that ENSO events initiated by TWC/NPMM are stronger than the average ENSO events, and that this difference holds true both in the control and the transient experiments. Further comparison of CHI amplitude for the controls against transient experiments indicates that there is no trend in the CHI amplitude for either average CHI-ENSO events or TWC-charged ones, indicating that the influence of TWC/NPMM on ENSO amplitude is not enhanced (nor reduced) as a result of anthropogenic forcings.
Amplitude of the Center of Heat Index (CHI). For each model, we calculate the CHI-amplitude of all winter (NDJ) events that satisfy the CHI-criterion (CHI-ENSO) as well as for the CHI-ENSO events that have a strong TWC event the preceding winter (TWC-charged CHI-ENSO). Markers show the average CHI values, and the standard error of the mean is shown by the black dashed lines. Red markers represent LR models and blue represent HR models, in black the ensemble mean. The y = x line is shown in dotted black. In (a, b) the mean CHI-amplitude of the average ENSO events (x-axis) plotted against the mean CHI-amplitude of the TWC-charged CHI-ENSO events (y-axis), for the control runs (a) and the transient runs (b). In (c, d) the comparison is between the results for the control experiments (x-axis) and those for the transient experiments (y-axis). For all CHI-ENSO events (c) and limited to the TWC-charged CHI-ENSO events (d)
Same as Fig. 2, except showing the CHI longitude instead of the amplitude
Same as Figs. 2, 3, except showing an estimate of the CHI area. Since the models have different resolutions, we show here the ratio between the extension of the SST anomalies and the extension of the Niño3.4 area. It is important to remember that, because of the CHI requirement, all areas included in the calculation are larger than the Niño3.4 area, which means that all values are greater than 1 by default
With regard to the longitude of ENSO events, Fig. 3a shows that the TWC/NPMM-charged CHI-ENSO events have their center of heat situated more westward than CHI-ENSO events in the control runs (significant for 8/10 models). However, this result does not hold true in the case of the transient runs in Fig. 3b. Plotting the control values against transient ones in Fig. 3c, d, we find that the center of heat of CHI-ENSO events moves westwards in the presence of anthropogenic forcings, but remains unaltered for TWC/NPMM-charged events. Combining these results suggests that average ENSO events will align westward where the TWC/NPMM-charged events already have their center of heat.
Finally, from Fig. 4a, b we see that the SST anomalies of the TWC/NPMM-charged events cover a larger area both in the control runs (significant for 6/10 models) as well as in the transient runs (significant for 9/10 models). Furthermore, CHI-ENSO events cover larger areas in the transient experiments compared to the controls, whether they are initiated by TWC/NPMM Fig. 4d (significant for 7/10 models) or not Fig. 4c (significant for 6/10 models).
The results of Figs. 3, 4 led us to further consider whether there was a relationship between the CHI-area and CHI-longitude values. Thus, we plot them for all CHI-ENSO events in Fig. 5. We find a significant negative correlation between them suggesting that the westward shift of the center of heat results from the fact that a larger portion of the equatorial Pacific SST is affected by ENSO variability, which consequently moves the center of heat. As such, this apparent shift westward does not result from a shift towards CP-type ENSO events.
CHI area (x-axis) plotted against the corresponding values of the CHI longitude (y-axis). Markers show the average CHI values. Red markers represent LR models, blue represent HR models, and the ensemble mean in black. Empty markers represent the control runs and filled markers represent the transient ones. In black the fitted regressed line whose coefficients are significant at α = 0.95
To summarize the results above, we find the amplitude of TWC/NPMM-charged events remains consistently larger whether under the influence of external forcings or in the control runs. In addition, the TWC/NPMM-charged events have larger area and hence are shifted more westward than standard events in the control run, however this difference disappears as the standard events grow larger and hence shift more westward under the influence of external forcings.
So far, we have analyzed the influence of the TWC/NPMM-ENSO relationship on the spatial characteristics of ENSO. To complete the characterization of the TWC/NPMM-ENSO relationship, we investigate the relative amount of TWC-charged events. In particular, we calculate the ratio between the number of TWC-charged CHI-ENSO events and the total amount of CHI-ENSO events for control and transient experiments separately. We show the results in Fig. 6 where we plot the value for the control simulation on the x-axis, against the value for the transient one on the y-axis. Overall, we see a lack of inter-model agreement as the models are evenly split on whether the frequency of TWC-charged events are increasing or decreasing in the presence of increasing forcings. In both sets of runs, the TWC-charged events represent approximately 30% of the total CHI-ENSO events (mean of the relative amount of TWC-charged events calculated over all of the experiments), but can be as many as 40% in some simulations and as little as 10% in others (as shown in Fig. 6).
Markers show the ratio between the number of TWC-charged CHI-ENSO events and CHI-ENSO events. On the x-axis the value for the control runs, on the y-axis for the transient ones. Red markers represent LR models, blue represent HR models, and in black is the ensemble mean. The y = x line is shown in dotted black
In the second portion of our analysis, we now turn to the oscillatory behavior of ENSO, as previous results indicate that the strength of the TWC/NPMM-ENSO coupling can influence the stochasticity of ENSO variability in both historical data (Pivotti and Anderson 2021) and model simulations (Pivotti et al. 2023). To capture potential future changes in the oscillatory behavior of ENSO variability, we look at how the power of the ENSO signal is spread across frequencies by calculating the Continuous Wavelet Transform (CWT) of the leading principal component of Tropical SST anomalies (PC1). We use PC1 to isolate ENSO, because it is more representative of a model’s specific equatorial variability than a geographically fixed index like Niño3.4 would be, as evidenced by the intra-model spatial variability in ENSO reconstructions shown in Fig. 1. Furthermore, the PC1 time series is more consistent with the previous portion of our analysis, where we utilize principal components in the CCA.
To study the time–frequency CWT matrices obtained for both control (CWTC) and transient (CWTT) experiment, we calculate the power of the signal P(t), the center of periodicity C(t), and the spread around C(t), S(t) (details in the Sect. 2.2). First, we show P(t) in Fig. 7, along with any slope that is significant at α = 0.90. Looking at the slopes, 6 out of 10 models indicate a future increase in the mean power of ENSO, and only one among them shows a trend of the same sign in the control run, suggesting that for at least 5 models such an increase is not a result of the model’s internal variability as opposed to external forcing, which is consistent with the results from Fig. 2c. We compare the trends of this estimate of the power with another one, namely the standard deviation of the Niño3.4 index, in Table 2, and we see that, when the values are significant, the two estimates agree on the sign of the trend.
Time-series of the total power P(t), calculated as the sum of the power W(p,t) at each time point t across periodicities of the Continuous Wavelet Transform (CWT) – see text for details. Results from the control runs are in blue and those for the transient in dashed red. The thin lines represent trends, when significant at α = 0.90, of the slope, whose value is written at the top of each panel. The power of CWT in K2 on the y-axis
We then show the centre of frequency C(T) in Fig. 8 from which we draw two main observations: (1) the centre of ENSO frequency for a given model remains consistent between control and transient runs, with the only exception of HadGEM HR where ENSO oscillates at slightly shorter periodicities during the transient experiment; and (2) there are no ensemble-wide trends towards higher or lower periodicities as the external forcings increase. Finally, in Fig. 9 we show S(T) to see how ENSO periodicity spreads around C(T) across the ensemble. In some cases, the periodicity of the signal is narrowly constrained around C(T) (e.g. CNMR LR transient)—indicative of a more oscillatory behaviour—and in other cases it is spread over a wider range (e.g. HadGEM HR control)—indicative of a more stochastic behaviour—and sometimes the system transitions between these two kinds of behaviour (e.g. CMCC HR control). Once again, we see signs of internal variability, but no ensemble-wide indication of a trend that predicts the system will move towards either a more stochastic and/or oscillatory behaviour. Given that previous results have shown enhanced TWC/NPMM-ENSO coupling leads to more stochastic ENSO variability (Pivotti and Anderson 2021; Pivotti, et al. 2023), the lack of consistency in the transition of ENSO variability to either more or less stochastic (and hence less or more oscillatory) under the influence of external forcings agrees with the earlier findings in Fig. 6. To confirm this result, we calculate the running 30 years correlation between (1) the time series we have used throughout the analysis to isolate ENSO—the leading principal component of Tropical SST anomalies (PC1,SST)—and (2) the time series we built to isolate TWC/NPMM—the first canonical variable of τX (CV1,τx). As above, we find no inter-model agreement regarding the presence of trends in the strength of TWC/NPMM-ENSO coupling under the influence of external radiative forcing (not shown).
Same as Fig. 7, except for the center of periodicity C(t) of the Continuous Wavelet Transform (CWT)—see text for details. Periodicity in years on the y-axis
4 Summary and conclusion
In this paper, we study how the models participating in the HighResMIP protocol reconstruct the relationship between ENSO and its extra-tropical precursor TWC/NPMM.
In a previous study we had assessed that the control experiments reconstruct the coupling, by comparing them with historical reanalysis. Here, we continue our analysis by including experiments with increasing prescribed forcings between 1950 and 2050.
First, in our spatial characterization of the reconstruction of the TWC/NPMM-ENSO relationship, we show that the ENSO events initiated by TWC/NPMM are consistently stronger and cover a larger area than average ENSO events, and that this relation holds true both in the presence and absence of external forcings. As far as the area influenced by SST anomalies, we identify a projected increase in all future ENSO events. This increase is accompanied by a subsequent westward shift of the center of heat, such that in the transient experiments the center of heat for average ENSO events aligns with the position of TWC/NPMM-charged ones, which were positioned relatively more to the west in the control runs as well. At the same time, we see a lack of agreement on whether the relative amount of TWC-charged events—which represent on average the 30% of all ENSO events—is deemed to increase or decrease in the presence of increasing forcings. Recent contributions (Jiang, et al. 2021; Planton, et al. 2021) have pointed out how CMIP6 models, albeit improved in their ENSO simulations, still persistently extend ENSO SST anomalies more westward than in observations. Here, we also identify a westward shift, however, it is a relative shift in relation to the control experiments, indicating it is not driven by the mean state, but by the impact of increased radiative forcings. Furthermore, the shift is not a westward movement of all ENSO events, but it is confined to ENSO events that are not TWC/NPMM driven, which suggests the direction of the shift is not a result of a mean state bias (otherwise it would have affected all ENSO events similarly).
Given the known relation between TWC/NPMM-ENSO variability and the oscillatory behaviour of ENSO itself, we then study how the power of ENSO spreads across different periodicities. We do that by constructing CHI-analogous indices to compare across TWC time-periodicity maps. In the analysis, we find that the majority of models agree on an increase of the overall power of ENSO, which confirms our spatial analysis above. However, this power trend is not due to specific trends in how the ENSO system oscillates. In particular, we see no clear trends in the frequency of ENSO variability under warmer conditions; and, similarly, we see no clear trends towards a more oscillatory nor stochastic ENSO variability. Furthermore, this ensemble is not predicting a shift in the strength of the TWC/NPMM-ENSO relationship, which agrees with a previous results (Pivotti and Anderson 2021) that shows that these two features vary jointly over multi-decadal time-scales. As previously mentioned, the HighResMIP ensemble has the advantage of being protocol-driven. That said, it would be of value to extend this analysis to the larger ensemble of CMIP6 models. Particularly, given the multi-decadal time scale of internal variations in the TWC/NPMM-ENSO coupling, longer experiments could provide further insights on the future of this relation. In addition, it would be of interest to further investigate the CHI-analogous indices we constructed to study the TWC time-periodicity maps, and test their usability in frequency analysis of climate time series beyond ENSO.
Data availability
All data utilized in this analysis are available at https://esgf-node.llnl.gov/projects/cmip6/.
References
Alexander MA, Bladé I, Newman M, Lanzante JR, Lau N-C, Scott JD (2002) The atmospheric bridge: the influence of ENSO teleconnections on air-sea interaction over the Global Oceans. J Clim. https://doi.org/10.1175/1520-0442(2002)015%3c2205:TABTIO%3e2.0.CO;2
Alexander MA, Vimont DJ, Chang P, Scott JD (2010) The impact of extratropical atmospheric variability on ENSO: testing the seasonal footprinting mechanism using coupled model experiments. J Clim 23:2885–2901. https://doi.org/10.1175/2010JCLI3205.1
Amaya DJ (2019) The Pacific meridional mode and ENSO: a review. Curr Clim Change Rep 5:296–307. https://doi.org/10.1007/s40641-019-00142-x
Amaya DJ, Kosaka Y, Zhou W, Zhang Y, Xie S-P, Miller AJ (2019) The North Pacific pacemaker effect on historical ENSO and its mechanisms. J Clim 32:7643–7661. https://doi.org/10.1175/JCLI-D-19-0040.1
Anderson BT (2003) Tropical Pacific sea-surface temperatures and preceding sea level pressure anomalies in the subtropical North Pacific. J Geophys Res Atmos. https://doi.org/10.1029/2003JD003805
Anderson BT, Perez RC (2015) ENSO and non-ENSO induced charging and discharging. Clim Dyn 45:2309–2327
Anderson BT, Perez RC, Karspeck A (2013) Triggering of El Niño onset through trade wind–induced charging of the equatorial Pacific. Geophys Res Lett 40:1212–1216. https://doi.org/10.1002/grl.50200
Ashok K, Guan Z, Saji NH, Yamagata T (2004) Individual and combined influences of ENSO and the Indian ocean dipole on the Indian Summer Monsoon. J Clim. https://doi.org/10.1175/1520-0442(2004)017%3c3141:IACIOE%3e2.0.CO;2
Bellenger H, Guilyardi E, Leloup J, Lengaigne M, Vialard J (2014) ENSO representation in climate models: from CMIP3 to CMIP5. Clim Dyn 42:1999–2018. https://doi.org/10.1007/s00382-013-1783-z
Beobide-Arsuaga G, Bayr T, Reintges A, Latif M (2021) Uncertainty of ENSO-amplitude projections in CMIP5 and CMIP6 models. Clim Dyn. https://doi.org/10.1007/s00382-021-05673-4
Bretherton CS, Smith C, Wallace JM (1992) An intercomparison of methods for finding coupled patterns in climate data. J Clim. https://doi.org/10.1175/1520-0442(1992)005%3c0541:AIOMFF%3e2.0.CO;2
Cai W, van Rensch P, Cowan T, Hendon HH (2011) Teleconnection pathways of ENSO and the IOD and the mechanisms for impacts on Australian rainfall. J Clim 24:3910–3923. https://doi.org/10.1175/2011JCLI4129.1
Cai W, Borlace S, Lengaigne M et al (2014) Increasing frequency of extreme El Niño events due to greenhouse warming. Nat Clim Change 4:111–116. https://doi.org/10.1038/nclimate2100
Cai W, Santoso A, Wang G, Yeh S-W, An S-I, Cobb KM, Wu L (2015) ENSO and greenhouse warming. Nat Clim Change. https://doi.org/10.1038/nclimate2743
Chakravorty S, Perez RC, Anderson BT, Giese BS, Larson SM, Pivotti V (2020) Testing the trade wind charging mechanism and its influence on ENSO variability. J Clim. https://doi.org/10.1175/JCLI-D-19-0727.1
Chiang JC, Vimont DJ (2004) Analogous Pacific and Atlantic meridional modes of tropical atmosphere-ocean variability. J Clim. https://doi.org/10.1175/JCLI4953.1
Collins M, An S-I, Cai W, Ganachaud A, Guilyardi E, Jin F-F et al (2010) The impact of global warming on the tropical Pacific Ocean and El Niño. Nat Geosci. https://doi.org/10.1038/ngeo868
Dai A, Wigley TM (2000) Global patterns of ENSO-induced precipitation. Geophys Res Lett. https://doi.org/10.1029/1999GL011140
Dai A, Fyfe JC, Xie S-P, Dai X (2015) Decadal modulation of global surface temperature by internal climate variability. Nat Clim Chang 5:555–559. https://doi.org/10.1038/nclimate2605
Donat MG, Peterson TC, Brunet M, King AD, Almazroui M, Kolli RK, Al-Mulla AY (2014) Changes in extreme temperature and precipitation in the Arab region: long-term trends and variability related to ENSO and NAO. Int J Climatol 43:581–592. https://doi.org/10.1002/joc.3707
EC-Earth Consortium (2018) EC-earth-consortium EC-Earth3P-HR model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.4548
EC-Earth Consortium (2019) EC-Earth-consortium EC-Earth3P model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.4547
Giese BS, Ray S (2011) El Niño variability in simple ocean data assimilation (SODA), 1871–2008. J Geophys Res Oceans. https://doi.org/10.1029/2010JC006695
Giese BS, Seidel HF, Compo GP, Sardeshmukh PD (2016a) An ensemble of ocean reanalyses for 1815–2013 with sparse observational input. J Geophys Res Oceans 121:6891–6910
Giese BS, Seidel HF, Compo GP, Sardeshmukh PD (2016) An ensemble of ocean reanalyses for 1815–2013 with sparse observational input. J Geophys Res Oceans. https://doi.org/10.1002/2016JC012079
Graham NE, Michaelsen J, Barnett TP (1987) An investigation of the El Niño-Southern Oscillation cycle with statistical models: 1. Predictor field characteristics. J Geophys Res Oceans 92:14251–14270
Haarsma RJ, Roberts MJ, Vidale PL, Senior CA, Bellucci A, Bao Q, Corti SE (2016) High resolution model intercomparison project (HighResMIP v1.0) for CMIP6. Geosci Model Dev 9:4185–4208. https://doi.org/10.5194/gmd-9-4185-2016
Jeevanjee N, Hassanzadeh P, Hill S, Sheshadri A (2017) A perspective on climate model hierarchies. J Adv Model Earth Syst 9:1760–1771. https://doi.org/10.1002/2017MS001038
Jiang W, Huang P, Huang G, Ying J (2021) Models, origins of the excessive westward extension of ENSO SST simulated in CMIP5 and CMIP6. J Clim. https://doi.org/10.1175/JCLI-D-20-0551.1
Jin F-F (1997a) An equatorial ocean recharge paradigm for ENSO. Part I: conceptual model. J Atmos Sci. https://doi.org/10.1175/1520-0469(1997)054
Jin F-F (1997b) An equatorial ocean recharge paradigm for ENSO. Part I: conceptual model. J Atmos Sci 54:811–829. https://doi.org/10.1175/1520-0469(1997)054%3c0811:AEORPF%3e2.0.CO;2
Kao H-Y, Yu J-Y (2009) Contrasting Eastern-Pacific and Central-Pacific types of ENSO. J Clim 22:615–632. https://doi.org/10.1175/2008JCLI2309.1
Kessler WS (2001) EOF representations of the madden–Julian oscillation and its connection with ENSO. J Clim 14:3055–3061. https://doi.org/10.1175/1520-0442(2001)014%3c3055:EROTMJ%3e2.0.CO;2
Kim ST, Yu J-Y (2012) The two types of ENSO in CMIP5 models. Geophys Res Lett. https://doi.org/10.1029/2012GL052006
Larson S, Kirtman B (2013) The Pacific Meridional Mode as a trigger for ENSO in a high-resolution coupled model. Geophys Res Lett 40:3189–3194. https://doi.org/10.1002/grl.50571
Larson SM, Kirtman BP (2014) The Pacific meridional mode as an ENSO precursor and predictor in the North American multimodel ensemble. J Clim. https://doi.org/10.1175/JCLI-D-14-00055.1
Liu Z, Xie S (1994) Equatorward propagation of coupled air-sea disturbances with application to the annual cycle of the Eastern Tropical Pacific. J Atmos Sci 51:3807–3822. https://doi.org/10.1175/1520-0469(1994)051%3c3807:EPOCAD%3e2.0.CO;2
Marjani S, Alizadeh-Choobari O, Irannejad P (2019) Frequency of extreme El Niño and La Niña events under global warming. Clim Dyn 53:5799–5813. https://doi.org/10.1007/s00382-019-04902-1
McGregor S, Timmermann A, Jin F-F, Kessler WS (2016) Charging El Niño with off-equatorial westerly wind events. Clim Dyn. https://doi.org/10.1007/s00382-015-2891-8
Myhre G, Shindell D, Bréon F-M, Collins W, Fuglestvedt J, Huang J et al (2013) Anthropogenic and natural radiative forcing. Cambridge University Press, Cambridge
National Research Council (2012) Chapter: 3 Strategies for developing climate models: model hierarchy, resolution, and complexity. In: A national strategy for advancing climate modeling. The National Academies Press, Washington DC, pp 63–80. https://doi.org/10.1722/13430
Pachauri, R. K., & Alle, M. R. (2014). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. IPCC, Geneva
Pivotti V, Anderson BT (2021) Transition between forced and oscillatory ENSO behavior over the last century. JGR Atmos. https://doi.org/10.1029/2020JD034116
Pivotti V, Anderson BT, Cherchi A, Bellucci A (2023) North Pacific trade wind precursors to ENSO in the CMIP6 HighResMIP multimodel ensemble. Clim Dyn. https://doi.org/10.1007/s00382-022-06449-0
Planton YY, Guilyardi E, Wittenberg AT, Lee J, Gleckler PJ, Bayr T, McPhaden MJ (2021) Evaluating climate models with the CLIVAR 2020 ENSO metrics package. Cover Bullet Am Meteorol Soc. https://doi.org/10.1175/BAMS-D-19-0337.1
Quadrelli R, Wallace JM (2002) Dependence of the structure of the Northern Hemisphere annular mode on the polarity of ENSO. Geophys Res Lett. https://doi.org/10.1029/2002GL015807
Rasmusson EM, Carpenter TH (1982) Variations in Tropical Sea Surface temperature and Surface wind fields associated with the Southern Oscillation/El Niño. Mon Wea Rev. https://doi.org/10.1175/1520-0493(1982)110
Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, Rafaj P (2011) RCP8.5-A scenario of comparatively high greenhouse gas emissions. Clim Change. https://doi.org/10.1007/s10584-011-0149-y
Roberts M (2017a) MOHC HadGEM3-GC31-HM model output prepared for CMIP6 HighResMIP. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.446
Roberts M (2017b) MOHC HadGEM3-GC31-LL model output prepared for CMIP6 HighResMIP. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.1901
Scoccimarro E, Bellucci A, Peano D (2018a) CMCC CMCC-CM2-HR4 model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.3748
Scoccimarro E, Bellucci A, Peano D (2018b) CMCC CMCC-CM2-VHR4 model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.3749
Suarez MJ, Schopf PS (1988) A delayed action Oscillator for ENSO. J Atmos Sci 45:3283–3287. https://doi.org/10.1175/1520-0469(1988)045%3c3283:ADAOFE%3e2.0.CO;2
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. J Geophys Res 106:7183–7192. https://doi.org/10.1029/2000JD900719
Thomas EE, Vimont DJ (2016) Modeling the mechanisms of linear and nonlinear ENSO responses to the Pacific meridional mode. J Clim. https://doi.org/10.1175/JCLI-D-16-0090.1
Timmerman A, Oberhuber J, Bacher A, Esch M, Latif M, Roeckner E (1999) Increased El Niño frequency in a climate model forced by future greenhouse warming. Nature. https://doi.org/10.1038/19505
Timmermann A, An S-I, Kug J-S, Jin F-F, Cai W, Capotondi A, Lengaigne M (2018) El Niño-Southern Oscillation complexity. Nature 559:535–545. https://doi.org/10.1038/s41586-018-0252-6
Trenberth KE (1997) The definition of El Niño. Bull Am Meteor Soc 78:2771–2778
Ummenhofer CC, Kulüke M, Tierney J (2018) Extremes in East African hydroclimate and links to Indo-Pacific variability on interannual to decadal timescales. Clim Dyn. https://doi.org/10.1007/s00382-017-3786-7
Voldoire A (2019a) CNRM-CERFACS CNRM-CM6-1 model output prepared for CMIP6 HighResMIP control-1950. Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.3946
Voldoire A (2019b) CNRM-CERFACS CNRM-CM6-1-HR model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.22033/ESGF/CMIP6.3947
von Storch J-S, Putrasahan D, Lohmann K, Gutjahr O, Jungclaus J, Bittner M, Wieners K-H (2018a) MPI-M MPI-ESM1.2-XR model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.2203/ESGF/CMIP6.10295
von Storch J-S, Putrasahan D, Lohmann K, Gutjahr O, Jungclaus J, Bittner M, Wieners K-HE (2018b) MPI-M MPI-ESM12-HR model output prepared for CMIP6 HighResMIP control-1950. Earth Syst Grid Fed. https://doi.org/10.2203/ESGF/CMIP6.6485
Wang B, Wang Y (1996) Temporal structure of the Southern Oscillation as revealed by waveform and wavelet analysis. J Clim 9:1586–1598. https://doi.org/10.1175/1520-0442(1996)009%3c1586:TSOTSO%3e2.0.CO;2
Wang C, Deser C, Yu J-Y, DiNezio PN, Clement A (2017) El Niño and Southern Oscillation (ENSO): a review. In: Glynn Peter W, Manzello Derek P, Enochs Ian C (eds) Coral reefs of the Eastern Tropical Pacific: persistence and loss in a dynamic environment. Springer, Dordrecht
Weisberg RH, Wang C (1997) A Western Pacific Oscillator Paradigm for the El Niño-Southern Oscillation. Geophys Res Lett 24:779–782. https://doi.org/10.1029/97GL00689
Yeh S-W, Cai W, Min S-K, McPhaden MJ, Dommenget D, Dewitte B, Kug J-S (2018) ENSO atmospheric teleconnections and their response to greenhouse gas forcing. Rev Geophys 56:185–206. https://doi.org/10.1002/2017RG000568
Zhang W, Mei X, Geng X, Turner AG, Jin F-F (2018) A nonstationary ENSO–NAO relationship due to AMO modulation. J Clim 32:33–43. https://doi.org/10.1175/JCLI-D-18-0365.1
Acknowledgements
This work was supported by the National Science Foundation (AGS-1547412). We wish to thank Annalisa Cherchi and Alessio Bellucci for their help navigating the HighResMIP dataset.
Funding
Open access funding provided by Malmö University.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Data collection and analysis were performed by VP. The first draft of the manuscript was written by VP and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pivotti, V., Anderson, B.T. Assessing the future influence of the North Pacific trade wind precursors on ENSO in the CMIP6 HighResMIP multimodel ensemble. Clim Dyn 62, 1487–1500 (2024). https://doi.org/10.1007/s00382-023-06976-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-023-06976-4