1 Introduction

The ongoing global warming acts to increase and strengthen heatwaves (IPCC 2021). In Europe, severe heatwaves have been experienced in 2003 (Robine et al. 2008), 2010 (Barriopedro et al. 2011) and 2018 (Hoy et al. 2020), for instance. High summer temperatures generally co-occur with anticyclonic flow anomalies (e.g., Kim et al. 2018). Heatwaves are typically further amplified by diabatic heating, in particular by the increased flux of sensible heat from drought-afflicted surface (Seneviratne et al. 2013) and strong insolation resulting from low cloudiness (Tang et al. 2012). In the present study, we derive heatwave projections for Europe from bias-corrected output data of a wide ensemble of global climate model (GCM) simulations participating in Phase 6 of the Coupled Model Intercomparison Project (CMIP6, Eyring et al. 2016).

Severe heatwaves tend to increase human mortality (Gasparrini et al. 2017; Merte 2017; Ruuhela et al 2018), particularly in elderly population (Ruuhela et al. 2017; Kollanus et al. 2021). For example, the western European heatwave in 2003 may have caused 70,000 extra deaths (Robine et al. 2008) and the Russian heatwave in 2010 about 55,000 deaths (Barriopedro et al. 2011). The adverse health impacts of high temperatures can be substantial in a cool climate as well (Ruuhela et al. 2017); for example, the exceptionally warm summer of 1972 caused approximately 800 additional deaths in Finland (Näyhä 2005). Moreover, excessive heat impairs outdoor labour productivity, especially in agriculture and construction (Orlov et al. 2019).

Furthermore, high temperatures inflict agricultural production (Battisti and Naylor 2009; Lesk et al. 2016). For instance, the global production of wheat is assessed to decrease by 6% per 1.0 \(^\circ\)C of additional global warming (Asseng et al. 2015). In buildings, the risk of overheating increases in hot weather, and greater amounts of energy are consumed for cooling (Velashjerdi Farahani et al. 2021). Coal-fired and nuclear power plants require water for cooling, and therefore shortage or an excessive temperature of water may result in reduction of the electricity production (van Vliet et al. 2012). Heatwaves are associated with an elevated risk of wildfires (e.g., Lehtonen et al. 2014), and the fires may severely deteriorate the quality of air (Konovalov et al. 2011).

In Europe, observations indicate an increasing trend in the frequency and intensity of heatwaves (Wang et al. 2022), and there is robust evidence that human influence has contributed to the change (Seneviratne et al. 2021). Even during the hiatus period of global warming in the early 21st century, high temperature extremes have become more common in wide areas of the Northern Hemisphere continents (Johnson et al. 2018). Otto et al. (2012) showed that the recent past warming has substantially increased the likelihood of severe heatwaves. For example, the expected frequency of such an extreme heatwave that was experienced in Russia in 2010 was in that time approximately three times as large as in the 1960s. Also, heatwaves simultaneously affecting multiple regions of the world have become more frequent and severe (Rogers et al. 2022).

In the future, it is very likely that the intensity and frequency of hot extremes, such as warm days and heatwaves, will increase in Europe, even at the 1.5 \(^\circ\)C global warming (Seneviratne et al. 2021). In particular over the mid-latitude continents, projected changes in high temperature extremes are larger than changes in the global mean temperature. Hence, compared with historical climate, strong increases in the heatwave area, duration and magnitude are projected. More severe heatwaves for the future are projected at a regional level as well, for example, for multiple European subregions (e.g., Kim et al. 2018; Lhotka et al. 2018; Ouzeau et al. 2016). According to Ouzeau et al. (2016), an intense heatwave similar to that experienced in France in 2003 will be a typical event at the end of this century.

In the literature, a hot day is mainly defined by either the daily mean (Kim et al. 2018; Kollanus et al. 2021; Sambou et al 2021; Ouzeau et al. 2016; Vogel et al. 2020) or maximum temperature (Cardell et al. 2020; Hoy et al. 2020; Kyselý 2010; Lhotka and Kyselý 2015; Lhotka et al. 2018; Perkins-Kirkpatrick and Gibson 2017; Russo et al. 2015; Tomczyk and Bednorz 2019). The benefit of employing daily means is that temperatures of both hot daytime hours and stifling nights are considered. Hot weather in day is not equally disastrous if nighttime coolness allows the human body to recover from the heat stress (Cardell et al. 2020; Zhu et al. 2022, and references therein). Buildings get less overheated, and it is often possible to schedule work journeys and free-time outdoor activities for morning and late afternoon beyond the mid-day heat. Moreover, all the CMIP6 GCMs do not provide usable data for the daily minimum and maximum temperatures (Ruosteenoja 2021). Hence, it is possible to widen the model ensemble analysed by studying the daily mean rather than maximum temperatures.

The threshold temperature of a hot day may be either fixed or a selected quantile of the frequency distribution. A fixed threshold temperature is straightforward to interpret and constitutes a reasonable choice when exploring a limited area, such as Czechia (Kyselý 2010), Finland (Kim et al. 2018) or Poland and Germany (Tomczyk and Bednorz 2019). However, a percentile-based threshold temperature is more appropriate than the fixed one when one studies wide areas consisting of multiple climate zones. For example, in the present work the domain covers the entire European continent, and therefore it is impossible to find a common fixed temperature threshold that would be functional in both the cool Scandinavian and hot Mediterranean climate. Moreover, a percentile-based threshold temperature makes it possible to calculate spatial averages of hot weather indices over areas with divergent climates.

Here, we study European heatwaves at four levels of global warming, namely 0.5, 1.0, 1.5 and 2.0 \(^\circ\)C above the preindustrial temperatures. In current climate change studies, fixed global warming levels are used very commonly (Seneviratne et al. 2021), for example, since the impact of overly rapid or slow rates of global warming simulated by some GCMs can then be neutralised (Hausfather et al. 2022). Consequently, the projections are only influenced by inter-model differences in how the fixed global warming is distributed over the various regions and seasons. For example, this approach has been used by Perkins-Kirkpatrick and Gibson (2017) and Vogel et al. (2020) to derive changes in selected heatwave indices from previous-generation CMIP5 GCM simulations.

The large number of GCM runs analyzed in the present study makes it possible to produce statistically highly robust projections (e.g., Stolpe et al. 2021); this is a major advantage of the work. Changes in both the time-mean heatwaves and extreme heatwaves occurring once in up to 100 years in the baseline climate are considered. The main measures of the heatwave severity are the duration and extremity index of the hot spell; the extremity index consists of a cumulative sum of temperature anomalies above the threshold temperature. Changes in the date of the strongest annual heatwave are explored as well.

The paper is organized as follows. Section 2 describes the GCM output data, the bias correction method, the time points of exceeding the 0.5–2.0 \(^\circ\)C global warming levels and the definitions of heatwave indices. A brief comparison of the model-derived and observational heatwave characteristics is included as well. Section 3 provides projections for the time-mean heatwave climate and Sect. 4 for the occurrence of extreme heatwaves. In Sect. 5, we assess the sensitivity of the findings to alternative heatwave definitions: the number of permissible break days within the heatwave and the choice of the threshold temperature. Section 6 discusses the physical interpretation of the findings and potential sources of uncertainty. The paper is closed with the Conclusions Sect. 7.

2 Data and methods

2.1 GCM data and bias correction

Heatwave projections were derived from the time series of daily mean temperatures simulated by 25 CMIP6 GCMs (Table 1). For each GCM, 1–4 parallel runs were included, yielding a total of 60 GCM runs. In the parallel runs, the forcing is identical but the runs are initiated from a different time point of the preindustrial control run, so that the initial conditions diverge (e.g., Eyring et al. 2016). Data for the years 1961–2014 were extracted from historical runs and the years 2015–2100 from SSP2–4.5 scenario runs (SSP = Shared Socio-economic Pathway, O’Neill et al. 2016).

Table 1 Climate model runs analyzed in the study: the ordinal number, acronym and country of origin of the model, and the count of parallel runs examined
Full size table

In selecting the GCMs, it was required that the European recent past climate and historical trends in the global mean temperature have to be reasonably consistent with observations; future projections for four SSP scenarios needed to be concordant as well (Ruosteenoja 2021, Figs. 1, 3 and 6). Moreover, in order to reduce inter-model dependencies, at most two model versions were included from any individual research centre. As shown in Ruosteenoja (2021), 28 CMIP6 GCMs were found that met these conditions, but three of these did not provide temperature data at the daily level. Accordingly, 25 GCMs fit for the analyses remained.

Before conducting any further analyses, a bias correction was performed. First, climatological monthly means and temporal standard deviations of daily temperatures during the calibration period 1961–2010 were made consistent with the E-OBS analyses (Daily gridded land-only observational dataset over Europe, version 23, Haylock et al. 2008). Next, the resulting correction coefficients were applied to adjust GCM data for the period 2011–2100. The bias-correction (method M7) is described in Räisänen and Räty (2013). The key advantage of this correction method is that modelled future changes in the temporal mean and standard deviation of daily temperatures in the original GCM simulation data remain undistorted. Ruosteenoja et al. (2016) gave details in applying the procedure to the CMIP simulation data, especially to ensure that the long-term temperature trend is unaffected by the correction. As well, they showed that for the calibration period 1961–2010, bias correction makes the climatological monthly means and temporal standard deviations of temperature in all the GCMs virtually identical to those in the observational analyses. This is illustrated in Fig. 1 of Ruosteenoja et al. (2016), which shows mean temperatures produced by a GCM before and after the bias correction, as well as their difference. In particular, GCMs cannot adequately discern the low mean temperatures prevailing in mountainous areas, while in the corrected data this bias is effectively fixed. In the highest mountain areas, mean temperatures are up to 10 \(^\circ\)C colder in the corrected than uncorrected data, whereas in the low-lying areas immediately surrounding mountain ranges bias correction tends to increase temperatures to some extent.

2.2 Global warming levels

Here, heatwave characteristics will be examined under four global warming levels: 0.5 \(^\circ\)C, 1.0 \(^\circ\)C, 1.5 \(^\circ\)C and 2.0 \(^\circ\)C. The last two levels are equal to the targets of the Paris Climate Agreement in 2015. In order to make the heatwave projections for the different warming levels strictly comparable, it was required that data should be available from all 25 GCMs for every warming level. Therefore, higher warming levels (e.g., 3.0 \(^\circ\)C) could not be studied, because in quite many GCMs the SSP2–4.5 runs did not reach such levels before 2100. In other respects, the use of a single SSP scenario is not a restriction, since changes in temperature-related variables at a specified warming level are nearly independent of the path of emissions (Seneviratne et al. 2021).

For each bias-corrected model simulation, 20-year periods representing the four global warming levels were identified. According to the HadCRUT4.6-analyses (Morice et al. 2012) used in Fig. SPM.1 of IPCC (2021), the global mean temperature was on average 0.52 \(^\circ\)C higher in 1961–2010, the bias correction calibration period applied here, than in 1850–1900, the period used by IPCC (2021) to represent pre-industrial climate. Hence, the bias correction forces the calibration-period global-mean temperature to be 0.52 \(^\circ\)C above the observational preindustrial level in all the adjusted GCM output files. The first global warming level of 0.5 \(^\circ\)C, used here as a baseline, is reached in the 20-year period of 1977–1996. The above-mentioned higher global warming levels correspond to an additional warming of 0.48, 0.98 and 1.48 \(^\circ\)C relative to the baseline period, respectively.

Finding the years of exceeding the selected global warming levels was performed basically in a similar manner as in the IPCC report (e.g., Seneviratne et al. 2021, Cross-Chapter Box 11.1), with the exception that owing to the bias correction, warming before the period 1977–1996 was fixed in all the adjusted GCM data. The 20-year running mean global temperatures proved to increase monotonically in all the GCM output files, and therefore the years when the warming levels were exceeded could be determined unambiguously. As can be seen in Table 1, the years of exceedance vary substantially across the GCMs. These years represent the mid-points of the 20-year periods for which the heatwave occurrence will be studied. For example, if the warming level is crossed in 2028, the period examined is 2018–2037.

Thanks to the bias correction, the baseline-period climate is virtually identical in all the adjusted GCM output files. Accordingly, it is possible to concatenate the GCM data, yielding a 60 \(\times\) 20 = 1200-year-long sample representing the baseline climate. The large size of the sample involves the benefit that all the parameters describing climate, for example, the return levels of extreme heatwaves, can be determined very robustly.

Pooled bias-corrected 1200-year-long time series can likewise be built for three higher global warming levels. Unlike in the baseline climate, these time series include uncertainties induced by both (1) interannual variability and (2) inter-GCM differences in how the the fixed global warming manifests itself in the European warm-season climate.

For the interpretation of indices describing heatwave characteristics and their future changes, it is helpful to have a picture of the average temperature climate. Figure 1 shows the 25-GCM average of the mean and temporal standard deviation of daily temperatures in June–August in the baseline climate (0.5 \(^\circ\)C global warming), along with changes in these statistics by the 2.0 \(^\circ\)C global warming level. The standard deviations were first calculated for each calendar month and then averaged over June–August. The mean temperature of summer ranges from less than +10 \(^\circ\)C over the Scandinavian mountains to 20–24 \(^\circ\)C in southern Europe. Temporal fluctuations are weakest in coastal areas in the south and west and largest in the north-eastern inland. The multi-model mean temperature response to the additional global warming ranges from about 1.5 \(^\circ\)C over the British Isles to >3.0 \(^\circ\)C in south-eastern Europe. The temporal variations of temperature mostly remain nearly unchanged but amplify slightly in central and western Europe. Owing to the bias correction, the baseline-period statistics are very similar in the various GCMs while the projected changes diverge.

2.3 Heatwave indices

In this paper, days with the mean temperature above the 90th percentile (\(T_{p90}\)) of the frequency distribution of June–August 1961–2000 were classified as hot days. The percentile was first determined separately for the 25 GCMs, but due to the bias correction, inter-model differences in \(T_{p90}\) proved to be rather small (Fig. S1). Accordingly, we henceforth use the 25-GCM mean of \(T_{p90}\) (Fig. 2) as the threshold temperature of a hot day in all the GCMs. For a sensitivity assessment, some calculations were repeated by using higher threshold temperatures (Sect. 5).

Note that in determining \(T_{p90}\), the last 10 years (2001–2010) of the calibration period were excluded. These years are most strongly affected by the ongoing global warming. The small inter-GCM differences (Fig. S1) indicate that the 40-year period is long enough for the percentiles to be determined robustly.

In the literature, percentile-based threshold temperatures have been either seasonally varying (Baldwin et al. 2019; Russo et al. 2015; Perkins-Kirkpatrick and Gibson 2017; Sambou et al 2021; Vogel et al. 2020) or temporally invariant, derived from the frequency distribution of summer (Cardell et al. 2020; Kollanus et al. 2021; Lhotka and Kyselý 2015; Lhotka et al. 2018) or annual (Ouzeau et al. 2016) daily temperatures. Here, we decided to use a time-invariant rather than a seasonally varying threshold temperature, for example, because this choice sounds more suitable for considering the adverse health impacts of heat. Accordingly, the threshold temperature only depends on position. The lowest values of \(T_{p90}\), 12–18 \(^\circ\)C, occur in northern and western Scandinavia while locally in the southern Iberian Peninsula and Turkey \(T_{p90}>\) 28 \(^\circ\)C (Fig. 2).

For a heatwave event, we employ the commonly-used definition that the event must consist of at least three consecutive hot days with the mean temperature above the threshold (Cardell et al. 2020; Kim et al. 2018; Lhotka et al. 2018; Perkins-Kirkpatrick and Gibson 2017; Tomczyk and Bednorz 2019; Sambou et al 2021). The heatwave was allowed to continue until there are two successive days below the threshold temperature. Here some examples of heatwaves with varying lengths, “X” denoting a day with the mean temperature above and “–” below \(T_{p90}\):

figure a

The definition is equivalent to the basic option of Baldwin et al. (2019). In addition, we made sensitivity experiments by using alternative definitions allowing either no breaks or breaks of at most two days within the spell (Sect. 5). Analogous heatwave definitions with several sub-episodes interspersed by one or a few cooler days have been applied in Hoy et al. (2020) and Ouzeau et al. (2016).

All the days belonging to a heatwave event, both hot days above and discrete break days below the threshold temperature, are regarded as heatwave days. Accordingly, the number of heatwave days within the spell is equivalent to the duration of the period. A justification for this choice is that a single cooler day within the warm spell does not yet enable an adequate recovery of the human organism (Baldwin et al. 2019) or notable cooling of buildings (Ramamurthy et al. 2017), for instance. On the other hand, in order the adverse impacts of heat to become apparent in full, the spell must last several days.

For assessing the severity of a heatwave event, the main metrics are the duration and strength of the event. As a measure for the strength, we use the heatwave extremity index:

$$\begin{aligned} EX = \sum _{t=t_o}^{t_e} \max (T_{day}(t) -T_{p90}, 0) \end{aligned}$$
(1)

where \(T_{day}\) is the daily mean temperature and \(t_o\) and \(t_e\) stand for the onset and termination dates of the event. Accordingly, all the temperature differences above the threshold are summed up but negative anomalies are not subtracted. The definition is analogous and unit the same (degree days) as in the temperature accumulation of the thermal growing season (e.g., Ruosteenoja et al. 2016). The magnitude of EX depends on both the duration and temperature anomalies of the heatwave event. Henceforth, the extremity index is the principal indicator of the strength of a heatwave. For example, the strongest annual heatwave is that manifesting the largest extremity index.

To facilitate interpretation of the values of EX, Fig. 3 depicts the observational extremity indices of the strongest heatwave of the year for four summers with substantial heatwaves in Europe. The Russian heatwave in 2010 was by far the most severe of these, the extremity index locally exceeding 200 \(^\circ\)C d. In 1972, very anomalous temperatures occurred in the northernmost Scandinavia, yielding the values of EX higher than 100 \(^\circ\)C d. In the French warm spell in 2003 and the Scandinavian spell in 2018, the largest index values amounted to 80 \(^\circ\)C d.

Cumulative temperature-anomaly indices identical or analogous to (1) have been used in numerous previous studies, but the identifier of the index has varied widely. Examples: “heat wave amplitude” (Cardell et al. 2020), “sum of daily excess temperatures” (Hoy et al. 2020), “cumulative Tmax excess” (Kyselý 2010), “extremity index” (Lhotka et al. 2018), “global intensity” (Ouzeau et al. 2016), “heat-wave magnitude index” (Russo et al. 2015) and “heat wave severity index” (Sambou et al 2021). As many impacts of heat are experienced at a local level, EX is calculated here separately for each grid point. Alternative definitions, taking the spatial extent into account as an additional dimension, are also introduced in the literature (e.g., Lhotka et al. 2018; Vogel et al. 2020).

As stated above, the threshold temperature \(T_{p90}\) was derived from the June–July–August daily temperatures. Even so, heatwaves outside of these three summer months were also considered in calculating the heatwave indices, but it is the same fixed threshold temperature that is applied in all seasons. Therefore, the proportion of such non-summer heat events is fairly small, particularly in the baseline climate, and they mainly occur in May and September (see Sect. 6.2).

For studying changes in the time-mean heatwave characteristics (Sect. 3), we calculated 20-year means of the total annual number of heatwave days and the sum of the extremity index. In addition, changes in the average date of the most intense heatwave of the year were examined. For studying changes in the most severe heatwave of the year, we first examined the frequency distributions of the annual maximum extremity index in the baseline climate (0.5 \(^\circ\)C global warming) and determined the 2–100 year return levels from the 1200-year-long concatenated GCM output dataset. Next, probabilities for exceeding these return levels were assessed at the 1.0–2.0 \(^\circ\)C warming levels. In addition, the frequencies of exceedance were determined for two fixed index values, \(EX=80\) and 200 \(^\circ\)C d.

The projections will be presented in the form of spatial distributions and, more concisely, regional averages. The study domain covers land areas within 35–71.5 \(^\circ\)N, 10.25 \(^\circ\) W–45 \(^\circ\) E, including Europe and small areas of the northernmost Africa and western Asia (Fig. 2). Note that some areas, such as the Anatolian inland, were excluded due to the incomplete E-OBS data. The domain was further divided into six subregions (Fig. 4): south-western, south-eastern, western, eastern and northern Europe and the British Isles. The southern boundary of the northern subregion is 54 \(^\circ\) N and the northern boundary of both Mediterranean regions 45 \(^\circ\) N. The eastern and western subregions are bordered by 18 \(^\circ\) E. Northern African grid points were not included in the subregions. By contrast, to avoid the south-eastern subregion to be much smaller than the remaining ones, most of the Asian grid points within the domain were considered. The sub-division is essentially the same as applied in Ruosteenoja et al. (2018) for studying soil-moisture projections.

2.4 Evaluation of model-derived heatwave indices

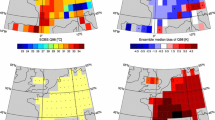
In Fig. 5, the model-derived baseline-period mean annual sums of three heatwave indices are compared with their counterparts derived from the E-OBS analyses, considering all-European spatial means. A similar comparison is shown for six subregions in Supplement Figs. S2–S4.

For the European mean, the GCMs on average slightly overestimate the annual number of heatwave days and total extremity index, whereas the count of discrete heatwave events agrees well. Inter-model scatter is of the same order of magnitude as the multi-GCM mean versus observation differences.

The high agreement between the model-derived and observational index values is largely explained by the bias correction, which forces both the time mean and standard deviation of modelled daily temperatures to match with the observational estimate. The emerging differences may be caused by potential dissimilarities in the higher moments of the frequency distributions and temporal clustering of hot days, for instance. Moreover, due to the fairly short time interval used in the comparison, parameters derived from observations and the output of individual models are substantially affected by internal variability in the climate system. This notion is supported by the fact that both the inter-model scatter and deviations from the E-OBS-derived estimates tend to be larger for the individual subregions than for the all-European domain (Figs. S2–S4); internal variability most strongly affects small spatial scales.

3 Evolution of time-mean heatwave indices

3.1 Mean heatwave day number and extremity index

The average annual count of heatwave days and the sum of the extremity index over all the heatwave episodes of the year are shown in Figs. 6 (the spatial means of six subregions for all four global warming levels) and 7 and 8 (geographical distributions at the 0.5 and 2.0 \(^\circ\)C warming levels and their difference in both absolute and percent terms). We first calculated 20-year means of the indices for the periods representing the 0.5, 1.0, 1.5 and 2.0 \(^\circ\)C warming levels (Table 1) for each individual GCM run, and these were used to calculate means over the 1–4 parallel runs. The multi-model means were then calculated by giving equal weights to all GCMs, following the recommendation of Weigel et al. (2010). Besides the multi-model means, Fig. 6 depicts multi-model medians as well as the second-lowest and second-highest time-mean index values among the 25 GCMs, which nominally define the 6–94% uncertainty intervals of inter-model scatter. The multi-model means and medians are nearly identical, or the median is slightly smaller, reflecting the skewness of the inter-model frequency distribution.

In the baseline-period climate, the average annual number of heatwave days is 5–7 everywhere in Europe (Figs. 6a, 7a). As expected, the number increases monotonically as a function of global warming (Fig. 6). At the 2.0 \(^\circ\)C global warming level compared with the baseline climate, the 25-GCM mean number of heatwave days is three to fourfold in the north and more than sixfold in the south-east. In absolute terms, this indicates an increase of about 2 weeks in the north and more than 30 days in the south (Fig. 7).

The baseline-period mean total annual extremity index ranges from less than 10 \(^\circ\)C d in the south to about 15 \(^\circ\)C d in the north (Figs. 6b, 8a). At the 2 \(^\circ\)C warming level, the index becomes approximately fourfold in northern and more than tenfold in southern Europe (Fig. 8). Potential reasons for the larger increase of the heatwave indicators in the south than north are discussed in Sect. 6.1.

The number of heatwave days increases nearly linearly as a function of the global mean temperature, while for the total extremity, the growth quickens with additional warming (Fig. 6). A straightforward explanation for this is that the extremity index (1) is proportional to both the duration of the heatwave events and the daily temperature anomalies above to the threshold (\(T_{day}(t)-T_{p90}\)), both tending to increase with amplifying warming.

For the 1.5 \(^\circ\)C global warming level, the geographical distributions of change were qualitatively similar to those in Figs. 7 and 8, albeit smaller in magnitude. For the 1.0 \(^\circ\)C warming, somewhat larger spatial differences occurred, particularly in the total extremity index. These may be due to the low signal-to-noise ratio in the responses to small global warming.

Although the level of global warming is similar, in the responses of the heatwave indices there are substantial differences across the GCMs (Fig. 6). For example, in south-western Europe under the 2.0 \(^\circ\)C global warming level, the uncertainty interval in the count of heatwave days ranges from 31 to 49. Inter-model differences result from the divergent impact of global warming on the European warm-season temperatures, for instance. In addition, differences in the shape of the frequency distribution of daily mean temperatures and the aggregation of hot days into heatwave events contribute to the inter-model scatter. Despite these differences, the GCMs are virtually unanimous on the direction of change.

The annual number of discrete heatwave events approximately tripled when comparing the 2.0 \(^\circ\)C warming level with the baseline climate, to somewhat lesser degree in the north (not shown). Consequently, the change is far smaller than in the count of heatwave days or the total extremity index. While additional heatwaves emerge in the early and late warm season, mid-summer heatwaves tend to amalgamate, which partly cancels the increase. This inference is in accord with the findings of Perkins-Kirkpatrick and Gibson (2017).

We likewise calculated changes in the count and total extremity index of heatwave days relative to the 1.0 \(^\circ\)C global warming level, representing the climate that prevailed in the 2010s. Substantial increases in both quantities are evident in this case as well, the number of heatwave days approximately doubling (Fig. S5) and the total extremity becoming 2–3.5-fold (Fig. S6). Again, changes are strongest in southern Europe.

In a qualitative sense, the present results are in good agreement with the findings of Perkins-Kirkpatrick and Gibson (2017) and Cardell et al. (2020). In those studies, exploring models belonging to older generations, it was likewise concluded that various heatwave indices increase more strongly in southern than northern Europe.

3.2 Date of the most extreme annual heatwave

Besides the severity of heatwave events, global warming affects the point of time of their occurrence during the summer season. Figure 9 shows the average mid-point date of the strongest heatwave of the year at the 0.5 and 2.0 \(^\circ\)C global warming levels and their difference. In the baseline climate, the strongest heatwave typically occurs near 10 July in northern European inland areas, between 15 and 25 July in central Europe and near the turn of July–August in the southernmost Europe. It is interesting to note that in northern Europe the most popular holiday month is July and in western and southern Europe August. To some extent, this coincides with the schedule of the strongest warm spells.

As global warming continues, in wide areas of central and eastern Europe the point of time of the most severe heatwave is delayed by about 1 week, there being a high inter-model agreement on the sign of change (Fig. 9c). Conversely, in the Mediterranean area and northern Europe, the shifts are minor. In this respect, central Europe seems to move closer to the seasonal cycle that has prevailed recently in southern Europe. It is striking that heatwaves tend to be delayed in the same areas where substantial reductions are projected for the soil moisture content (Ruosteenoja et al. 2018). It might be interesting to learn whether there is some physical linkage between these phenomena, for example, by exploring changes in the components of the surface heat balance. However, this topic is beyond the scope of the present work.

Chen et al. (2019) reported a delay of 5–10 days in the annually warmest day for some areas of central Europe, but agreement on the sign of change among the 25 CMIP5 GCMs studied was low. Liu et al. (2020) found that mid-latitude ocean areas tend to warm most strongly in August–October and least in January–April. Thus, air masses advected from oceans to continents would be, in a relative sense, warmer in the late than early summer. This might be one factor acting to delay the warmest phase of summer. On the other hand, Ouzeau et al. (2016) reported no significant changes in the point of time of the most frequent occurrence of heatwaves, but that study only analysed the regional downscalings of five GCMs and thus did not cover the full inter-model scatter.

4 Projections for extreme heatwaves

To elaborate projections for the occurrence of very intense heatwaves, we first looked for the heatwave events having the largest extremity index of each year. The frequency distributions of the annual maximum extremity index for four global warming levels are shown in Fig. 10 (European averages) and S7 (six subregions). Owing to the large size of the concatenated datasets, 1200 modelled years for every warming level, the distributions are very regular. In the baseline climate, in more than 60% of years the maximum heatwave extremity index equals zero, indicating that there is not a single hot spell lasting for 3 days (Fig. 10a). At the 2.0 \(^\circ\)C warming level, the proportion of heatwave-free summers declines to 8%, while the strongest heatwaves have extremity indices far above 200 \(^\circ\)C d (Fig. 10d), the index value of the Russian 2010 spell (Fig. 3).

The smoothness of the frequency distributions in Figs. 10 and S7 implies that the return levels of the annual maximum extremity index can be determined very robustly directly from the distributions. As an illustration, the 10 and 100-year baseline-period return levels are shown in Fig. 11. By analogy with the long-term mean extremity index (Fig. 8a), the return levels are largest in northern Europe.

As global warming proceeds, heatwaves exceeding the various baseline-period return levels rapidly become far more frequent (Fig. 12). In the eastern European subregion, for instance, at the 1.0 \(^\circ\)C global warming level there is a 36% probability that the baseline-period 10-year return level would be exceeded; under 1.5 \(^\circ\)C a 58% and under 2.0 \(^\circ\)C a 73% probability. Heatwaves more extreme than the 100-year return level would correspondingly have probabilities of 9%, 22% and 38% under these warming levels. Accordingly, in a relative sense, the most extreme heatwaves get increasingly common faster than the moderate ones, in accord with the findings reported in Seneviratne et al. (2021). The likelihood of severe heatwaves invariably increases most rapidly in south-eastern Europe, followed by south-western Europe and both the central European subregions. The increase is slowest in both northern subregions. Accordingly, the geographical distribution of the response is similar to that in the time-mean indices reported in Sect. 3.

Figure 12 also provides an estimate of how the probabilities of extreme heatwaves increase between the 1.0 \(^\circ\)C (representing the 2010s) and higher warming levels. For example, by inspecting the lowermost (red) curve in Fig. 12c (south-western Europe), one can see that a heatwave with a 10 year return level under the 1.0 \(^\circ\)C global warming would have a probability of about 31% at the 1.5 \(^\circ\)C and 53% at the 2.0 \(^\circ\)C global warming level.

Furthermore, we explored probabilities for the occurrence of heatwaves that in their extremity surpass two well-known historical warm spells; the French heatwave of 2003 with the extremity index of 80 \(^\circ\)C d and the Russian 2010 spell with \(EX=200\,^\circ\)C d (see Fig. 3). Table 2 shows annual probabilities for that such a heatwave would occur in at least 10% of the area of the subregion. Both heatwave categories are rare in the baseline climate, but the probabilities increase strongly in the course of warming. The annual probability of a \(EX>80\,^\circ\)C d heatwave is, depending on the subregion, 8–29% under the 1.5 \(^\circ\)C and 16–61% under the 2.0 \(^\circ\)C warming level. Again, the probabilities increase most rapidly in the southeast. Even the very extreme heatwave episodes with \(EX>200\,^\circ\)C d would be far from exceptional under the 2.0 \(^\circ\)C warming level, with the annual probabilities ranging from 0.6 to 6.3% (Table 2). Note that the probabilities given in Table 2 are not directly comparable with those depicted in Fig. 12, since the latter probabilities consist of spatial means over the subregion.

Table 2 Annual probabilities (in %) for the occurrence of a heatwave with the extremity index larger than a 80 \(^\circ\)C days and b 200 \(^\circ\)C days over more than 10% of the area of the subregion under the 0.5, 1.0, 1.5 and 2.0 \(^\circ\)C global warming levels
Full size table

5 Sensitivity analyses

5.1 Heatwaves with 0, 1 or 2 break days

As stated in Sect. 2.3, according our default definition a heatwave event starts with at least three consecutive days with the mean temperature above the threshold, and extension days are included if there is no longer than one day break between. In Baldwin et al. (2019), the acronym used for this definition is “311”. In this section, we explore two alternative definitions, namely “321”: two break days are allowed without interrupting the heatwave; and “300”: even one day below the threshold temperature terminates the event.

The number of permissible break days affects the average annual count of heatwave days; the longer the breaks permitted, the larger the number of heatwave days (Fig. 13). Conversely, the impact of admissible break days on the total extremity index is negligible (Fig. S8). For example, a long heatwave event interspersed with 1-day breaks between manifests itself as a single heatwave under “311” but as several shorter events under the “300” definition, the total number of heatwave days being smaller in the latter case. In contrast, all the sub-periods lasting at least 3 days contribute to the total extremity index equally under both definitions.

Inclusion of extension days affects the total annual duration and extremity index in a very similar manner at all four global warming levels. Therefore, in a relative sense, the projected increases of these indices are virtually identical regardless of which of these three definitions is used (Figs. 13, S8).

Secondly, we assessed the impact of allowing or refusing breaks within an event on the projections of extreme heatwaves. For that purpose, we first determined the 2–100 year return levels for the annual maximum heatwave extremity index under the baseline climate (quantities analogous to those depicted in Fig. 11) using all three definitions. Then, the probabilities of exceeding these return levels were calculated at the different global warming levels for the alternative definitions (Fig. S9). We can see that the definition has a very minor effect on the probabilities. The explanation is straightforward: it turned out that at the 0.5 \(^\circ\)C (2.0 \(^\circ\)C) warming level, in \(\sim\) 95% (80–90%) of the years it is the same heatwave event that obtains the largest extremity index regardless of which of those three definitions is used. In the majority of these cases, even the values of EX were identical.

5.2 Impact of the threshold temperature

Next, heatwave projections were re-calculated by using higher threshold temperatures for the hot days: the 95th and 99th percentiles of summer daily-mean temperatures. Of course, the higher thresholds produced far shorter durations and smaller extremity indices for the baseline-period heatwaves than the \(T_{p90}\) threshold. By contrast, in relative terms, projected changes were substantially larger. For example, using the \(T_{p90}\) threshold, in the East-European subregion the average total annual duration of heatwaves under the 2.0 \(^\circ\)C warming level was 5-fold compared with that under 0.5 \(^\circ\)C. For the higher threshold temperatures, the factors of increase were about 8 for \(T_{p95}\) and 21 for \(T_{p99}\). For the mean annual sum of the extremity index, the corresponding factors were 8 (\(T_{p90}\)), 12 (\(T_{p95}\)) and 31 (\(T_{p99}\)).

Conversely, when examining changes in the occurrence of intense heatwaves surpassing selected baseline-period return levels, the impact of the threshold temperature is not that substantial. For the \(T_{p99}\) threshold, the frequency of such heatwave events increases only slightly less rapidly than when using the \(T_{p90}\) threshold (Fig. S10). An evident explanation for this is that, regardless of the threshold temperature, it is the same heatwave event of the summer that has the largest extremity index. At the 0.5 \(^\circ\)C global warming level in >90% and at 2.0 \(^\circ\)C in >80% cases, the days belonging to the annual maximum heatwave event above the \(T_{p99}\) threshold temperature coincide within the corresponding \(T_{p90}\) event. Note, however, that at the 0.5 \(^\circ\)C warming level in particular, in most summers there is no \(\ge\)3-day hot spell with the mean temperature above \(T_{p99}\). For that reason, the 2–4 year return levels would be equal to zero and are therefore not depicted in Fig. S10.

6 Discussion

6.1 Reasons behind heatwave changes and their spatial distribution

One main finding of the present work is that while in the baseline-period climate the heatwave extremity index is largest in the north, both considering the long-term means and intense heatwaves, the projected increases in the extremity and duration of heatwave episodes are stronger in southern than northern and northwestern Europe (Figs. 6, 7, 8, 11, 12). There are at least three factors that can explain the future increases and their geographical distribution: (1) the increasing mean temperatures, (2) the strength and future changes in the temporal variability of daily temperatures, and (3) the contrast between the high-summer versus early/late summer mean temperatures. These three factors are examined in more detail below.

Quite a trivial explanatory factor is the projected increase in summer mean temperatures, which is strongest in southern Europe (Fig. 1c). Nonetheless, the southern European warming is strongest in inland rather than coastal areas, but such a disparity is not seen in the heatwave index responses in Figs. 7 and 8. One source of this discrepancy is the weak temporal variability of daily temperatures in coastal areas (Fig. 1b). A small temporal standard deviation implies that the difference between the 90th percentile and temporal mean of the baseline-period temperatures is likewise small (Fig. 14a).

To gain a deeper insight into this idea, we calculated the ratio of projected warming to the difference between the threshold temperature \(T_{p90}\) (defined in Sect. 2.3) and the baseline-period mean temperature:

$$\begin{aligned} \frac{\overline{T}_{mean}(2.0^\circ C) - \overline{T}_{mean}(0.5^\circ C)}{T_{p90}- \overline{T}_{mean}(0.5^\circ C)} \end{aligned}$$
(2)

where \(\overline{T}_{mean}\) is the local June–August mean temperature at the specified global warming level. By comparing the spatial pattern of the ratio (2) (Fig. 14b) with changes in heatwave indices (Figs. 7d, 8d), we can see that the distributions are qualitatively very similar: the largest values occur in the Mediterranean area, particularly near the coasts, and the smallest values in the north. In wide areas in the south, the ratio (2) is close to one; this indicates that at the 2.0 \(^\circ\)C global warming level, the mean temperature of summer will rise close to the heatwave threshold temperature \(T_{p90}\). Accordingly, at that future warming level, in southern Europe a large proportion of summer days will have mean temperatures above the threshold temperature. This results in a strong increase in the number of heatwave days and the extremity of warm spells in the south. Conversely, in northern Europe the ratio (2) is much smaller than one, so that in the majority of days \(T_{day}\) will be well below \(T_{p90}\) even at the 2.0 \(^\circ\)C warming level.

Changes in the number and extremity of heatwave days are also affected by future changes in the temporal variability of temperatures. Figure 1d shows that the temporal standard deviation is slightly amplified in central and western Europe, which tends to intensify temperature anomalies in both relatively cool and relatively warm days. This acts to increase the number and extremity of very hot days. For example, the increasing temporal variability of daily temperatures may explain why increases in the heatwave indices in Figs. 7c, d and 8c, d are stronger in northern France and southern Brittany than Scandinavia, even though the increase in summer mean temperatures is similar.

An additional factor contributing to the geographical disparity in the responses is that in the north, the summer is “sharp” in a sense that heat is strongly clustered in the high summer. As can be seen in Fig. S11, in north-eastern Europe the mean temperature of July is 2–3 \(^\circ\)C higher than the average of the mean temperatures of June and August. As the threshold temperature \(T_{p90}\) has been derived from the frequency distributions of the entire June–August season, in the north there is a relatively large number of high-summer days in which the mean temperature is far above \(T_{p90}\) even in the baseline climate. This contributes to the large values of the baseline-period extremity index in the north (Fig. 8a). Conversely, in the early and late warm season, the daily mean temperatures are generally much lower, and the threshold temperature is fairly seldom exceeded even in the future climate; this is one additional factor that explains the slow increase of the count and extremity of heatwave days in the north (Figs. 7, 8d). In wide areas of central and southern Europe, by contrast, the mean temperatures of all three summer months are fairly close to one another (Fig. S11). In these areas, the total extremity index is therefore fairly small in the baseline climate, but there are numerous days with \(T_{day}\) only slightly below \(T_{p90}\). Consequently, there is a large potential for the duration and extremity of heatwaves to increase substantially under global warming.

6.2 Potential sources of uncertainty

Table 1 reveals that the times of exceeding the specified global warming levels diverge substantially among the GCMs. For example, in three GCMs the 2.0 \(^\circ\)C level is reached as early as in the mid-2020s, in one GCM not until the 2070s. In GCMs with an early crossing time, the rate of warming during the 20-year time span examined is relatively rapid compared with GCMs simulating a late crossing. A rapid warming within the period implies that in such GCMs heatwave climate within the 20-year period is inhomogeneous in a sense that hot days and heatwaves tend to be clustered for the second half of the period. This may reduce the total number of heatwave episodes but increase the proportion of the longest and most intense events. In GCMs simulating slow global warming, this issue is of lesser importance.

Moreover, owing to the large thermal capacity of oceans, continents tend to warm more and oceans less strongly under transient warming than in a steady-state climate (IPCC 2021, p. 56). Thus, in the transient simulations the European continent is likely to warm stronger than in an equilibrium state with the same global warming level. Accordingly, the values of the heatwave indices likewise may be larger than in an equilibrium climate; this should be borne in mind when interpreting the findings.

For the bias correction, multiple methods have been developed; examples are discussed in Räisänen and Räty (2013). In the present work, we have employed a fairly simple method that adjusts the temporal mean and standard deviation of simulated daily temperatures to agree with the observational analysis. The use of a percentile-based threshold temperature reduces the sensitivity to the bias correction method applied. In fact, it would have been possible to perform the present analyses even without any bias adjustment, but adjustment involves the significant benefit of allowing a common threshold temperature to be used for all the GCM runs. This facilitates interpretation of the findings.

The threshold temperature of hot days (\(T_{p90}\)) was derived from the \(T_{day}\) data of June–August, but in searching the heatwaves, hot days within the entire warm season were considered. This does not inflict any contradiction, since in the majority of the domain less than 10% hot days fall outside of the three summer months, mainly on May and September. Therefore, it indeed appears reasonable to (1) derive the temperature thresholds from the June–August daily-mean temperatures but (2) also include heatwave events occurring outside of these 3 months in the projections.

Alternatively, heatwave projections might have been derived from simulations performed with regional climate models (RCMs). A RCM simulation is largely constrained by the GCM supplying the boundary conditions, and dynamical downscalings are typically available only for a small fraction of GCMs. Multi-GCM ensembles thus usually contain a far larger number of independent realizations than RCM ensembles. Moreover, the occurrence of heatwaves is mainly determined by large-scale atmospheric dynamics, and in studying heatwaves at European level, the high spatial resolution of RCMs does not provide such an additional value as in the simulations of heavy precipitation events, for instance.

If one explores perceived temperatures including the impact of air humidity, “disturbingly” severe hot days generally tend to increase even more rapidly than when studying the pure air temperature (Zhu et al. 2022). Nevertheless, especially in southern Europe where the heatwave indices manifest very large increases, relative humidity is projected to decrease substantially in summer (IPCC 2021, Fig. 4.23), which may mitigate many adverse impacts of the exacerbating heat.

7 Conclusions

During the next few decades global warming continues ineluctably, and even under the most optimistic scenarios the global mean temperature will increase at least 1.5 \(^\circ\)C relative to the pre-industrial level (IPCC 2021). However, the 1.5 \(^\circ\)C target would require very drastic and urgent reductions in greenhouse gas emissions. Hence, we have to be prepared to adapt ourselves to at least the 2.0 \(^\circ\)C global warming. The present analysis indicates that under that warming level the duration and extremity of European heatwaves increase substantially. In northern Europe, the average annual number of heatwave days is projected to become three to fourfold and the total annual heatwave extremity index approximatively fourfold. In southern Europe, the corresponding increase factors are about six and ten, respectively. An intense heatwave occurring once in 100 years at the 0.5 \(^\circ\)C warming level has an annual probability of about 20% in northern and 60% in southern Europe under 2.0 \(^\circ\)C. As discussed in Sect. 6.1, the stronger response in the south is not only a trivial consequence of the more rapid warming in the south but also influenced by weaker temporal variability of daily temperatures and small differences in the climatological mean temperatures among three summer months.

The annual probability estimates for even very intense heatwaves could be assessed very robustly owing to the use of bias-corrected output data from 60 CMIP6 GCM runs. Thereby we were able to create a homogeneous 1200-year-long sample that represents an abundant number of synoptically independent yearly weather conditions representing the baseline climate or 0.5 \(^\circ\)C global warming relative to the pre-industrial level. The robustness of the annual probability estimates for even very extreme heatwaves is evidenced by the absence of notable random noise in Fig. 10. Analogous time series derived from observations only cover a few decades and would thus be much more liable to stochastic fluctuations. The probabilities of intense heatwaves can also be derived from similar 1200-year samples representing higher global warming levels (1.0 \(^\circ\)C, 1.5 \(^\circ\)C and 2.0 \(^\circ\)C). However, in these datasets variations are not only induced by interannual variability in weather conditions but also, despite the fixed global warming, by the different degree of summer warming in Europe in the various GCMs.

The longer and more extreme heatwaves projected for the future in themselves inflict exacerbating health issues for people prone to high temperatures. In addition, urban heat islands tend to be at their strongest during the heatwave periods (Ramamurthy et al. 2017), and consequently the globally increasing urban population in particular will be affected by heat. Even so, the adverse health impacts can be significantly mitigated by adaptation. According to observations, the additional mortality induced by heatwaves may have declined with time (Kyselý and Plavcová 2012; Ruuhela et al. 2017). For example, after the disastrous heatwave of 2003 in France, the awareness of population of the danger of excessive heat was improved and the activities of authorities during heatwave events were rationalized, which evidently led to a substantial reduction of heat-induced deaths during the next heatwave in 2006 (Fouillet et al. 2008). The analysis of Zacharias et al. (2015) showed that even physical acclimatization of human bodies can significantly reduce heat-induced deaths projected for the late 21st century. According to Landreau et al. (2021), if the future socio-economic development is favourable enough to reduce the vulnerability of population and global warming is restricted at a tolerable level, the health risks caused by high temperatures may even decline. Nevertheless, many other heat-induced issues, such as ecological damages, wildfires and loss of agricultural production, may be more difficult to control by adaptation.

In this paper, global warming levels exceeding the targets of the Paris Climate Agreement in 2015 were not studied, because in quite many GCMs considered, the SSP2–4.5 runs do not reach such levels before 2100. However, if the efforts to curtail the emissions of greenhouse gases do not succeed adequately, our planet may warm even more than 2 \(^\circ\)C relative to the preindustrial level. In that case, heatwaves would exacerbate still more seriously than projected in the present work.

Fig. 1
figure 1

Multi-model means of the bias-corrected monthly a mean temperature and b temporal standard deviation of the daily temperatures under the 0.5 \(^\circ\)C global warming level (period 1977–1996); averages of June–August. c Changes in summer mean temperature from the 0.5 to 2.0 \(^\circ\)C global warming level; d the ratio of the standard deviation under the 2.0 \(^\circ\)C global warming level to that under 0.5 \(^\circ\)C

Full size image
Fig. 2
figure 2

The 90th percentile of the June–August daily-mean temperatures, calculated from the bias-corrected GCM output data for the period 1961–2000: a multi-model mean

Full size image
Fig. 3
figure 3

Extremity indices of four major heatwave events that occurred in Europe in a 1972, b 2003, c 2010 and d 2018. The temperature data are extracted from the E-OBS-analyses

Full size image
Fig. 4
figure 4

The six European subregions for which the heatwave projections are produced: NEU Northern Europe, BRI the British Isles, WEU Western Europe, EEU Eastern Europe, SWE South-Western Europe, SEE South-Eastern Europe

Full size image
Fig. 5
figure 5

Annual sum of a the heatwave extremity index, b heatwave days and c discrete heatwave events above \(T_{p90}\) averaged over the entire European domain. The temporal means over the period 1977–1996 (the 0.5 \(^\circ\)C global warming level) derived from the the bias-corrected output of individual GCMs are denoted by grey bars. The 25-GCM means are shown by red solid lines and the corresponding temporal means derived from the E-OBS analyses by green dashed lines. The ordinal numbers of the GCMs are given in Table 1

Full size image
Fig. 6
figure 6

a The average number of heatwave days per year and b the mean annual sum of the heatwave extremity index under the global warming levels of 0.5 \(^\circ\)C (blue), 1.0 \(^\circ\)C (green), 1.5 \(^\circ\)C (yellow) and 2.0 \(^\circ\)C (red); spatial averages for the six subregions defined in Fig. 4. The coloured bars depict multi-model means, black dots multi-model medians and error bars the 6–94 % uncertainty intervals derived from the model simulations. Breaks of at most 1 day within a heatwave event are allowed

Full size image
Fig. 7
figure 7

The multi-model 20-year mean number of heatwave days above \(T_{p90}\) per year in Europe under the global warming levels of a 0.5 \(^\circ\)C and b 2.0 \(^\circ\)C and the projected c absolute and d percent changes in the number. Note the different contour interval in a and b. Breaks of at most 1 day within a heatwave event are allowed

Full size image
Fig. 8
figure 8

The multi-model 20-year mean of the annual sum of heatwave extremity index above \(T_{p90}\) under the global warming levels of a 0.5 \(^\circ\)C and b 2.0 \(^\circ\)C and the projected c absolute and d percent changes in the index. Note the different contour interval in a and b

Full size image
Fig. 9
figure 9

The average mid-point date of the most intense heatwave of the year in Europe under the global warming levels of a 0.5 \(^\circ\)C and b 2.0 \(^\circ\)C and c the projected change in the date; multi-model means. In a and b, the dates are expressed with respect to 30 June; for example, 20 denotes July 20 and 32 August 1. In c, positive values indicate a delay (in days) and the areas where at least 80% of the models agree on the sign of change are dotted

Full size image
Fig. 10
figure 10

Frequency distributions (in %) of the extremity index of the most intense heatwave of the year (above \(T_{p90}\); unit \(^\circ\)C d) under the global warming levels of a 0.5 \(^\circ\)C, b 1.0 \(^\circ\)C, c 1.5 \(^\circ\)C and d 2.0 \(^\circ\)C; multi-model means averaged over the entire European domain. Breaks of at most one day within the heatwave event are allowed. The frequency classes are 0–8 \(^\circ\)C d, 8–16 \(^\circ\)C d,... 312–320 \(^\circ\)C d; in the inset of d 160–168\(^\circ\)C d,... 392–400 \(^\circ\)C d. Note the different scale of the y axis in the various panels

Full size image
Fig. 11
figure 11

The a 10-year (left panel) and b 100-year (right panel) return levels of the extremity index of the most intense heatwave of the year (above \(T_{p90}\); unit \(^\circ\)C days) under the 0.5 \(^\circ\)C global warming level, derived from the concatenated multi-model frequency distribution

Full size image
Fig. 12
figure 12

Probabilities for the occurrence of an annual maximum heatwave (above \(T_{p90}\)) with the extremity index larger than that occurring once in 2, 4, 10, 20, 50 or 100 years (see the legend in d) in the baseline climate (0.5 \(^\circ\)C global warming) as a function of the level of global warming. The probabilities derived from the pooled multi-model frequency distributions are shown separately for the various European subregions: a BRI; b WEU; c SWE; d NEU; e EEU; f SEE

Full size image
Fig. 13
figure 13

The average total number of heatwave days per year under the global warming levels of 0.5 \(^\circ\)C (three bars on the left), 1.0 \(^\circ\)C (the second three-bar cluster), 1.5 \(^\circ\)C (the third cluster) and 2.0 \(^\circ\)C (three bars on the right); the spatial averages of the six subregions depicted in Fig. 4: a BRI; b WEU; c SWE; d NEU; e EEU; f SEE. The left (grey) bar in the three-column cluster gives the number of days when using a definition permitting no breaks within the heatwave event. The mid (yellow) and right (green) bars show the corresponding counts when breaks of at most 1 or 2 days are allowed, respectively. The bars depict multi-model means and error bars the 6–94% uncertainty intervals derived from the bias-corrected model simulations

Full size image
Fig. 14
figure 14

a Difference between the quantities shown in Figs. 1a and 2, that is, the 90th percentile of summer daily-mean temperatures minus the mean temperature of summer in the baseline climate (0.5 \(^\circ\)C global warming level). b The ratio of the multi-model mean summer temperature increase (from the 0.5 to 2.0 \(^\circ\)C warming level, shown in Fig. 1c) to the 90th percentile minus the time-mean difference depicted in a. The analytic expression for b is given in Eq. (2) and for a in its denominator

Full size image