Low-frequency variability enhancement of the midlatitude climate in an eddy-resolving coupled ocean–atmosphere model. Part I: anatomy

Abstract

This study investigated the coupling of the wind-driven ocean gyres with the atmospheric westerly jet using an idealised, eddy-resolving, coupled model. An empirical orthogonal function analysis of the low-pass filtered data showed that the ocean gyre variability is dominated by meridional shifts of the western boundary current extension (WBCE) and changes in the strength of the subtropical inertial recirculation zone. On the other hand, the atmospheric potential vorticity (PV) variability is dominated by the growth of standing Rossby wave patterns, while its pressure variability is dominated by a zonally-asymmetric meridional shift of the atmospheric jet. Damping sea surface temperature (SST) variability in the atmosphere was shown to weaken its PV variability and reduce the zonal asymmetry of the jet-shift mode. Singular value decompositions revealed a positive feedback between meridional shifts of the WBCE and the growth of standing Rossby wave disturbances in the atmospheric jet. The atmosphere’s response is controlled by shifts in the meridional eddy heat flux over the SST front which triggers the growth of baroclinic instabilities. This instability growth eventually leads to a large-scale, barotropic pressure response over the eastern ocean basin, or an aforementioned meridional shift of the atmospheric jet. Reduction in the atmospheric resolution inhibits the ability of atmospheric eddies to resolve length scales associated with meridional shifts of the SST front and WBCE. The lack of resolution consequently weakens the influence of ocean gyre variability on the atmospheric jet and reduces the strength of the positive feedback.

1 Introduction

1.1 Motivation

Western boundary currents (WBCs), such as the Kuroshio in the North Pacific and Gulf Stream in the North Atlantic, are fast, narrow currents that reside on the western boundary of every major ocean basin. These currents, and their associated WBC extension (WBCE) and inertial recirculation zones, show vigorous variability ranging from interannual to decadal time-scales. In addition, The convergence of warm and cold waters by the WBCs create sharp SST gradients, or a front, leading to persistent wintertime surface heat fluxes into the overlying atmosphere. Recent research suggests that resolving the so-called ‘atmospheric mesoscale’, on the order of 10–100 km, over these regions may lead to improvements in modelling of the midlatitude climate variability and strengthen SST-induced forcing of the upper-troposphere (Czaja et al. 2019). This claim is backed up by current observational estimates which show that the influence of WBC variability on the troposphere is considerably stronger than earlier estimates (Frankignoul et al. 2011; Taguchi et al. 2012; Révelard et al. 2018).

Although coupled general circulation models (GCMs) and observations are vital for the progressions in our understanding of the climate, idealised, quasigeostrophic, coupled models provide a unique, and often under-utilised, perspective into the midlatitude climate variability, owing to their relatively cheap cost to run and transparency under analysis. However, studies using these class of models are yet to be run under resolutions that adequately resolve the mesoscales in both the ocean and atmosphere. Furthermore, advances in modelling of the quasigeostrophic wind-driven circulation in the past decade or so now allow for much more realistic, turbulent circulations to be achieved (e.g., Deremble et al. 2011; Berloff 2015). This warrants a significant re-investigation into the midlatitude climate variability using such models.

We will begin with a brief background on the subject, followed by a description of the models and methods used in Sect. 2. Section 3 will show the reference solutions to the benchmark modelled climate and, Sect. 4 will decompose its variability. The lagged covariability and ocean–atmosphere interactions are investigated in Sect. 5, with a final discussion of results given in Sect. 6.

1.2 Background

In the past, attributing drivers of the midlatitude coupled climate variability has proven to be complex in nature, with much of the early literature in disagreement about the role played by the midlatitude ocean circulation, even those using the same or similar models (e.g., see Latif and Barnett 1994, 1996; Schneider et al. 2002, for the classic example). It is argued that most of the midlatitude oceans act as a white-noise integrator of high-frequency atmospheric forcing through a first-order Markov process (Hasselmann 1976; Frankignoul and Hasselmann 1977). Low-frequency sea surface temperature (SST) anomalies damp surface heat fluxes, which consequently increases the surface temperature variability of the ocean and atmosphere (Battisti et al. 1995; Barsugli and Battisti 1998; Saravanan and McWilliams 1997; Kushnir et al. 2002). For example, the basin-scale tripole SST anomalies observed in the North Atlantic and Pacific are often partly attributed to this process (Mantua et al. 1997; Okumura et al. 2001; Alexander 2010; Schneider and Fan 2012). Indeed, earlier review studies of the midlatitude coupled climate variability did not find evidence for a strong response of the extratropical atmosphere to large-scale SST anomalies (Kushnir et al. 2002; Kwon et al. 2010). In these studies, it was proposed that SST variability is excited by basin-scale modes of atmospheric variability which then weakly feedback on the atmosphere.

In recent times it has become more clear that the white-noise integrator hypothesis is insufficient in explaining climate variability over regions of the ocean such as the WBCs and WBCEs (Smirnov et al. 2014). For starters, these regions of the ocean show persistent wintertime SST anomalies which increase the surface heat flux variability (Tanimoto 2003; Taguchi et al. 2012). Furthermore, recent reanalysis data shows the influence of this SST variability on the atmosphere is now significantly stronger than previous estimates (Frankignoul et al. 2011; Taguchi et al. 2012; Révelard et al. 2018).

The variability of WBCs and WBCEs have been suggested to be controlled by: (1) large-scale atmospheric forcings that trigger decadal responses in the ocean gyres, either through advective effects (Dewar 2003) or westward-propagating baroclinic Rossby waves (Taguchi et al. 2007; Sasaki et al. 2013; 2) intrinsic interannual variability due to chaotic, turbulent behaviour of WBCEs (Nonaka et al. 2016; Bishop et al. 2017; Small et al. 2019; Laurindo et al. 2019). This time-scale dependence of WBC variability has been shown by Nonaka et al. (2020). These changes in strength and position of WBCEs then impact local coupling with the overlying storm track and atmospheric jet through shifts in the low-level baroclinicity (Nakamura et al. 2004; Brayshaw et al. 2008; Sampe et al. 2010; O’Reilly and Czaja 2015). The dynamics of these regions of the ocean are strongly controlled by mesoscale ocean dynamics, which must be dynamically-resolved by the model in order to fully diagnose their effects.

Furthermore, there is now research to suggest that models which resolve the so-called ‘atmospheric mesoscale’, on the order of 10–100 km, may also be required, rather than just resolving the Rossby deformation scales, which are on the order of $1000\,\text {km}$ (Ma et al. 2016, 2017; Siqueira et al. 2021). It is postulated that as the atmospheric mesoscales are better resolved, oceanic forcing of the upper-troposphere will be enhanced (Czaja et al. 2019). For example. Famooss Paolini et al. (2022) showed that increases in atmospheric resolution leads to a westerly jet response to SST anomalies that is more similar to reanalysis data. This improved response of the downstream westerly jet was to move in the same direction as the SST front displacement. Such a response is opposite to what is expected from the linear theory (Hoskins and Karoly 1981), implying the anomalous diabatic heating associated with the SST front shift is mainly balanced by transient eddy forcing (Peng et al. 1997; Peng and Whitaker 1999). We note here that despite recent improvements in atmospheric GCMs, eddy-mean flow feedbacks still show complicated, nonlinear responses to SST anomalies (Seo et al. 2017) and increasing atmospheric resolution does not necessarily lead to circulations that are closer to observations (Czaja et al. 2019).

Within the framework of eddy-resolving, idealised ocean models driven by fixed winds, the importance of mesoscale eddies in ocean gyre variability is well-known through detailed analyses of the underlying potential vorticity (PV) dynamics (e.g., Berloff and McWilliams 1999a; Hogg et al. 2005; Berloff et al. 2007b; Deremble et al. 2011; Berloff 2015; Shevchenko et al. 2016; Kurashina et al. 2021). Furthermore, the importance of mesoscale ocean eddies in the midlatitude climate variability has been shown through studies using idealised coupled models. For example, Dewar (2001) showed that mesoscale eddy variability feeds back strongly on ocean Ekman pumping, peaking at decadal time-scales, and thus controls the SST response and atmospheric variability. Time-scale control of atmospheric variability has also been shown to be important by Hogg et al. (2006) and Berloff et al. (2007a), with preferred decadal time-scales selected by nonlinear adjustment of the ocean gyres (Dewar 2003). This is able to set the consequent time-scale of decadal coupled oscillations through transitions between pairs of preferred atmospheric states (Kravtsov et al. 2007). For example, Kravtsov et al. (2007) found that as the westerly atmospheric jet switches from a poleward to an equatorward state, nonlinear adjustments of the WBCE to anomalous forcing lead to a persistent SST anomaly forming. This SST anomaly anchors the atmosphere to remain in its equatorward latitude state through strong surface heat fluxes until the anomaly dissipates. After the SST anomaly dissipates, the atmosphere returns to its more preferred poleward state, forcing the WBCE back poleward. Suppressing mesoscale ocean eddies had a weakening effect on the coupled variability, further supporting the view that mesoscale ocean eddies are vital in not only in controlling ocean variability but also the overlying atmosphere. Furthermore, Kravtsov et al. (2006) and Farneti (2007) showed a westward-propagating, coupled, phase-locked Rossby wave which acted on an interannual time-scale associated with the basin crossing time. This coupled interaction was shown to not require the atmosphere to transition between two preferred states (Kravtsov et al. 2006) and was akin to the positive feedback mechanism proposed by Goodman and Marshall (1999). However, an important point to note is that none of these studies have modelled climates which adequately resolve both the ocean and atmosphere mesoscales. Furthermore, none have investigated the influence of atmospheric resolution on the modelled climate, nor have they detected modifications in atmospheric modes of variability by the ocean circulation.

This paper will re-establish the anatomy of the low-frequency climate variability in a quasigeostrophic coupled model run under much higher resolutions than those in previous studies (Dewar 2001; Hogg et al. 2006; Kravtsov et al. 2006, 2007; Berloff et al. 2007a). Our main aim in this study is to then see whether any novel coupled behaviours are observed and attempt to explain the mechanisms involved.

2 Model and methods

2.1 The Quasi-Geostrophic Coupled Model (Q-GCM)

The model we will be using for this study is version 1.5.0 of the Quasi-Geostrophic Coupled Model (Q-GCM) which was first described and implemented in Hogg et al. (2003). It is designed to mimic aspects of the midlatitude climate system and consists of a wind-driven, double-gyre box ocean coupled to a periodic, channel atmosphere through mixed layers that allow for transfers of heat and momentum. The model is similar to the one used in Kravtsov and Robertson (2002) and Kravtsov et al. (2007) but also includes a dynamically-active atmospheric mixed layer.

2.1.1 Notation

Before we move into describing the model, we will introduce the notation used in this paper which is identical to the one used in Hogg et al. (2003). Left-superscript, given by ‘o’ or ‘a’, indicates ocean or atmosphere variables and right-subscript, given by ‘m’ or integer i, indicates the mixed layer or i-th isopycnal layer, respectively. Layers are counted away from the ocean–atmosphere interface.

2.1.2 Model Geometry

The box ocean model consists of 3 isopycnal layers with depths ${}^oH_1=350\,\text {m}, {}^oH_2=750\,\text {m}$ and ${}^oH_3=2900\,\text {m}$. The benchmark solution has a nominal ocean resolution of $5\,\text {km}$ for a basin with lateral dimensions $4800\,\text {km}\times 4800\,\text {km}$. This gives a discretised grid of size $961\times 961$ points representing cell vertices in the longitudinal and latitudinal directions, respectively. Within the upper-isopycnal ocean, there is a mixed layer of fixed depth ${}^oH_m=100\,\text {m}$. The channel atmosphere also consists of 3 isopycnal layers with depths ${}^aH_1=2000\,\text {m}, {}^aH_2=3000\,\text {m}$ and ${}^aH_3=4000\,\text {m}$. The benchmark solution has a nominal atmosphere resolution of $20\,\text {km}$ for a channel with lateral dimensions $30\,720\,\text {km}\times 7680\,\text {km}$. This gives a discretised grid of size $1537\times 385$ points representing cell vertices in the longitudinal and latitudinal directions, respectively. Within the lower-isopycnal atmosphere, there is also another mixed layer of variable depth with an unperturbed thickness of ${}^aH_m=1000\,\text {m}$.

Parameters in Tables 1 and 2, such as eddy viscosity and boundary condition coefficients, have been chosen such that a realistic and turbulent circulation is achieved. For example, it is well known that different choices of these parameters have large and profound effects on the ocean circulation (e.g., Haidvogel et al. 1992; Berloff and McWilliams 1999a, b; Hogg et al. 2005; Deremble et al. 2011), so care has been taken to pick the correct parameter choices.

2.1.3 The quasigeostrophic (QG) layers

The QG equations for the ocean and atmosphere may be written in terms of PV anomalies and dynamic pressure anomalies. For example in the ocean, they are denoted in vector form as ${}^o\textbf{q}=({}^oq_1, {}^oq_2, {}^oq_3)^T$ and ${}^o\textbf{p}=({}^op_1, {}^op_2, {}^op_3)^T$, respectively. Ocean PV anomalies are defined as

$$\begin{aligned} {}^o\textbf{q} = \frac{1}{f_0}\nabla ^2{}^o\textbf{p}-f_0A{}^o\textbf{p} \end{aligned}$$

(1)

where $f_0=9.37\times 10^{-5}$ s$^{-1}$ is the Coriolis parameter and A is a matrix which defines interactions between layers through dynamic pressure anomalies or buoyancies

$$ A = \begin{bmatrix} \frac{1}{H_1g^{\prime}_1} &{} -\frac{1}{H_1g^{\prime}_1} &{} 0 \\ -\frac{1}{H_2g^{\prime}_1} &{} \frac{1}{H_2}\left( \frac{1}{g^{\prime}_2}+\frac{1}{g'_1}\right) &{} -\frac{1}{H_2g^{\prime}_2} \\ 0 &{} -\frac{1}{H_3g^{\prime}_2} &{} \frac{1}{H_3g^{\prime}_2} \end{bmatrix} $$

(2)

with $g_i'$ as the reduced gravities. In the ocean, $g_1'=0.0222\,\text {ms}^{-2}, g_2'=0.0169\,\text {ms}^{-2}$ which correspond to Rossby deformation radii of $40.0\,\text {km}$ and $20.6\,\text {km}$, respectively. The definition of PV anomaly in the atmosphere is the same as the ocean apart from the addition of land orography which is given in Appendix 1.

We use (x, y) as our zonal and meridional coordinates where x is always measured increasing eastwards from the western boundary of the model domain; y is measured increasing polewards from the central latitude $y_0$.

Dynamic pressures in the i-th isopycnal ocean may be converted to the transport streamfunction through the relation

$$\begin{aligned} {}^o\Psi _i = \frac{{}^oH_i}{f_0}{}^op_i \end{aligned}$$

(3)

Zonal and meridional velocities are computed through taking derivatives of ${}^op_i$

$$\begin{aligned} {}^ou_i=-\frac{1}{f_0} \frac{\partial {}^op_i}{\partial y}\,,\;{}^ov_i=\frac{1}{f_0}\frac{\partial {}^op_i}{\partial x} \end{aligned}$$

(4)

Atmospheric velocities may be computed in an identical manner.

We may now write the quasigeostrophic equations for the ocean as

$$\begin{aligned}{} & {} {}^o\textbf{q}_t+\frac{1}{f_0}J({}^o\textbf{p}, {}^o\textbf{q})+\frac{\beta }{f_0}{}^o\textbf{p}_x\nonumber \\{} & {} \quad =B\textbf{e}+\frac{{}^oA_2}{f_0}\nabla ^4_H{}^o\textbf{p}-\frac{{}^oA_4}{f_0}\nabla ^6_H{}^o\textbf{p} \end{aligned}$$

(5)

where ${}^oA_2=50\,\text {m}^2\text {s}^{-1}$ and ${}^oA_4=2.0\times 10^9\,\text {m}^4\text {s}^{-1}$ are the Laplacian and biharmonic diffusion coefficients, respectively. The Jacobian operator is given by $J(\textbf{f}, \textbf{g})=\textbf{f}_x\textbf{g}_y-\textbf{f}_y\textbf{g}_x$ and the horizontal Laplacian and biharmonic operators are given by $\nabla ^4_H$ and $\nabla _H^6$, respectively. The forcing in the QG layers is defined by the 3$\times$4 matrix B and the $4\times 1$ entrainment vector ${}^o\textbf{e}$. The QG equations for the atmosphere are similar except for the aforementioned forcing terms which we will now describe.

Table 1 Parameters for the double-gyre ocean model

2.1.4 Entrainment vectors

In the ocean, the matrix B is given by

$$ ^{o} B = f_{0} \left[ {\begin{array}{*{20}l} {\frac{1}{{H_{1} }}} & { - \frac{1}{{H_{1} }}} & 0 & 0 \\ 0 & {\frac{1}{{H_{2} }}} & { - \frac{1}{{H_{2} }}} & 0 \\ 0 & 0 & {\frac{1}{{H_{3} }}} & { - \frac{1}{{H_{3} }}} \\ \end{array} } \right] $$

(6)

In the atmosphere, we simply have $^aB=-^oB$. The entrainment vectors ${}^o\textbf{e}$ and ${}^a\textbf{e}$ for the ocean and atmosphere, respectively, are given by

$$\begin{aligned} ^o\textbf{e}= \begin{bmatrix} ^ow_{\text {ek}} \\ -\frac{\Delta ^o_mT_o}{2\Delta _1^oT}{}{^o}w_{\text {ek}} \\ 0 \\ \frac{\delta _{\text {ek}}}{2f_0}\nabla ^2_H{}{^o}p_3 \end{bmatrix} \;, \quad ^a\textbf{e}= \begin{bmatrix} ^aw_{\text {ek}} \\ \frac{F_m^{\uparrow }+F_k^{\downarrow }-F_N^{\uparrow }}{{}^a\rho } \\ 0 \\ 0 \end{bmatrix} \end{aligned}$$

(7)

These forcing vectors correspond to vertical velocities into each QG layer. Within the upper-isopycnal ocean layer, we combine the adiabatic and diabatic forcing as a single term to simplify our subsequent analysis. We call this term the upper-ocean total entrainment¹

$$\begin{aligned} ^oe_{\text {total}} = {}^oe_0-{}^oe_1={}^ow_{\text {ek}}+\frac{\Delta _m^oT}{\Delta _1^oT}{}^ow_{\text {ek}} \end{aligned}$$

(8)

Ekman pumpings in the ocean and atmosphere are computed as the curl of surface stress (dropping left-superscripts)

$$\begin{aligned} w_{\text {ek}} = \frac{1}{f_0}(\tau _x^y-\tau _y^x) \end{aligned}$$

(9)

The ocean and atmosphere surface-stresses are computed as a linear combination of lower-isopycnal atmosphere velocities (Hogg et al. 2014). This means that ocean Ekman pumping depends only on the atmospheric flow and does not explicitly depend on the ocean circulation.²

The atmosphere diabatic entrainment $^ae_1$ in (7) contains radiative heat flux terms that occur due to changes in the atmospheric mixed layer. When an unstable stratification occurs, the entrainment ${}^ae_1$ is adjusted with a correction term (Hogg et al. 2014).

2.1.5 Boundary conditions

Partial-slip boundary conditions are applied on the lateral boundaries (Haidvogel et al. 1992) by

$$\begin{aligned} {}^op_{i_{nn}} = -\frac{{}^o\alpha _{\text {bc}}}{\Delta ^o x} {}^op_{i_{n}}\,,\; {}^op_{i_{4n}} = -\frac{{}^o\alpha _{\text {bc}}}{\Delta ^o x} {}^op_{i_{3n}} \end{aligned}$$

(10)

where $\alpha _{\text {bc}}$ is the non-dimensional partial-slip boundary condition parameter (see Tables 1, 2) and $\Delta ^o x$ is the horizontal grid spacing. The subscript n denotes outward normal partial derivatives. We choose a partial-slip boundary condition parameter that is close to free-slip as this gives a more realistic representation of the nonlinear dynamics in the WBCs, see Deremble et al. (2011) for details.

There are also mass and momentum conservation constraints applied to the lateral boundaries (McWilliams 1977; Hogg et al. 2014).

Table 2 Parameters for the channel atmosphere model

2.1.6 Radiative heat fluxes

The entire model is driven by solar radiation which is fixed in time and depends on latitude. A linearised radiation scheme then redistributes heat throughout the atmosphere (Hogg et al. 2014).

2.1.7 Sensible and latent heat fluxes

Sensible and latent heat fluxes are parametrised by a single term

$$\begin{aligned} ^aF_{\lambda }=\lambda ({}{^o}T_m-{}{^a}T_m) \end{aligned}$$

(11)

where $\lambda =35\,\text {Wm}^{-2}$ is the sensible and latent heat flux coefficient.

2.1.8 The ocean surface mixed layer

The SST evolution in the ocean surface mixed layer, denoted by $^oT_m$, is given by

$$\begin{aligned}{} & {} {}{^o}T_{mt}+({}{^o}u_m{}{^o}T_m)_x+({}{^o}v_m{}{^o}T_m)_y={}{^o}K_2\nabla ^2_H{}{^o}T_m \nonumber \\{} & {} \quad -{}{^o}K_4\nabla ^2_4{}{^o}T_m-\frac{{}{^o}w_{\text {ek}}({}{^oT_1+{}{^o}T_m})}{2{}{^o}H_m}+\frac{^oF_0+{}^oF_m^{e+}}{{}{^o}\rho {}{^o}C_p{}{^o}H_m} \end{aligned}$$

(12)

where ${}{^o}T_m$ denotes SST and $({}^ou_m, {}^ov_m)$ are the mixed layer velocities. These are computed through the Ekman balance integrated over the mixed layer depth.

We also have $^oT_1, {}^oT_2, {}^oT_3$ which are fixed, constant temperature of the isopycnal layers. We will present $T_m$ as a deviation from a temperature constant which is obtained through radiative balance (Hogg et al. 2014). For our model parameters, this constant temperature for the ocean mixed layer is $27.0\,^{\circ } \text {C}$. Note that (12) also contains Laplacian and biharmonic diffusivities given by ${}^oK_2$ and ${}^oK_4$, respectively (see Table 1). The forcing terms in (12) contain thermal forcing at the ocean surface $^aF_0$ and entrainment heat flux out of the bottom of the ocean mixed layer ${}^oF_m^{e+}$.

2.1.9 The atmosphere surface mixed layer

The temperature evolution of the atmospheric mixed layer is given by a similar equation to (12) except the forcing terms are slightly different (Hogg et al. 2014). Heat flux at the top of the atmospheric mixed layer is given by ${}^aF_m$ and surface forcing given by $^aF_0$.

2.2 Partially-coupled climate

In order to attribute features of the modelled climate and pinpoint sources of variability to ocean-induced or coupled effects, we run a partially-coupled modelled climate alongside our fully-coupled climate simulation. This is done by changing a parameter $X_C$ which controls the coupling between the atmospheric mixed layer and the lower-isopycnal atmosphere. When $X_C=1$, the model is fully-coupled. On the other hand, when $X_C=0$, the atmosphere is decoupled from atmospheric mixed layer variability (see Appendix 2 for details). This will be our parameter choice for our partially-coupled climate. This coupling parameter is useful as any SST-driven variability will be suppressed while purely atmosphere-driven variability will remain. Note that mechanical interactions between the ocean and atmosphere are implemented identically to the fully coupled case.

2.3 The inter-gyre boundary

An inter-gyre boundary that partitions the ocean basin is computed by following the time-averaged pressure contour emanating from the western boundary. This approximates the position of the WBCE as it separates from the western boundary and extends into the open ocean. This inter-gyre boundary will be used to highlight the location of vorticity fluxes into the ocean gyres which arise as a result of the atmospheric variability.

2.4 Filtering data

Before any statistical techniques are applied to the data, a 2-year low-pass filter is applied to remove high frequency oscillations. This allows for any low-frequency signal to be picked up more easily in the subsequent analysis.

2.5 Empirical orthogonal functions (EOFs)

An empirical orthogonal function (EOF) analysis is performed by computing an eigendecomposition of a covariance matrix obtained from the oceanic/atmospheric state variables (von Storch and Zwiers 1999). This gives from most to least important, the patterns of variability (EOFs) that explain the most variance in the data. We will present the explained variance by each EOF as a percentage of the total variance. The filtered data set is then projected onto the EOFs to obtain the principal components (PCs), which give information about the temporal evolution of the EOFs. Analysing the power spectra will also indicate the most important time-scales at play.

2.6 Lagged singular value decompositions (SVDs)

Although EOFs are useful in decomposing single field variability, they lack information regarding modes of covariability in the modelled climate, e.g. ocean–atmosphere interactions. In order to pick out these modes of covariability, a singular value decomposition (SVD) analysis is performed on a lagged cross-covariance matrix constructed using two state variables (Bretherton et al. 1992). Similar to the EOF decomposition, the data is first 2-year low-pass filtered and both fields are subsampled onto an $80\,\text {km}$ grid. This is to save on memory cost as cross-covariances matrices require considerably larger storage than covariance matrices. By maximising squared covariance fraction with respect to time-lag, the likely time-scale for any delayed response may also be obtained, if one exists. Analogous to the EOF decomposition, a SVD produces patterns that maximise the cross-covariance in the data. Note that as we are concerned with pairs of fields, two sets of patterns are produced in the decomposition- one for each field. These are called the singular vectors or SVD modes. Again, by projecting the original data sets onto these modes, we obtain two sets of temporal coefficients. These may be correlated to obtain a measure of the strength of the coupling between the pair of singular vectors. A description of the required SVDs will be given in Sect. 5.

Fig. 1

Unfiltered ocean PV anomalies $(\text {s}^{-1})$ and transport streamfunction (Sv) for the benchmark modelled double-gyre circulation in statistical equilibrium. Panels from left to right show upper to lower layers, respectively. Panels in the upper half of the figure show instantaneous fields and panels in lower half show time-averaged fields. a–c Instantaneous ocean transport streamfunction fields. d–f Instantaneous ocean PV anomaly fields. g–i Time-averaged ocean transport streamfunction fields. j–l Time-averaged ocean PV anomaly fields

3 Modelled climate

Reference solutions for the benchmark and partially-coupled modelled climates are computed for a 120-year simulation length with a 20-year spin-up period and data saved every 5 days. Full list of parameters are presented in Tables 1 and 2. The simulation was started from rest and in radiative balance. Note that barred variables $\left( \overline{\circ }\right)$ denote time-averaged variables.

3.1 Ocean circulation

The modelled wind-driven, double-gyre ocean circulation is presented in Fig. 1. The upper-isopycnal ocean is spun up by both adiabatic Ekman pumping and diabatic entrainment which creates the subpolar and subtropical gyres (see Fig. 3). Western intensification leads to the formation of powerful WBCs and downstream inertial recirculation zones and WBCE. The basin shift and addition of land orography has created a larger, but weaker, subtropical gyre and has deflected the jet-axis tilt slightly poleward. The jet-axis tilt is determined by the relative strengths of the recirculation zones with the stronger recirculation zone tending to pull the jet towards itself (Moro 1988; Hogg et al. 2005). The middle-isopycnal ocean is forced only by the diabatic entrainment term (7) which creates gyres of weaker circulation with PV of the opposite sign.

Fig. 2

Unfiltered atmospheric PV anomalies $(\text {s}^{-1})$ and dynamic pressure anomalies $(\text {m}^2\text {s}^{-2})$ for benchmark modelled channel atmosphere in statistical equilibrium. Upper and lower panels show instantaneous and time-averaged fields; panels on the left-hand side show the lower-isopycnal layer, panels on the right-hand side show the middle-isopycnal layer. Square box outlined by black dashed line represents the position of the ocean basin. Regions $0\le x\le {}{^a}X/4$ and $3{}{^a}X/4\le x\le {}{^a}X$ are omitted where ocean–atmosphere interactions are assumed to be weak. This is repeated for subsequent figures unless stated otherwise. a, e Instantaneous and time-averaged lower-isopycnal atmosphere dynamic pressures. b, f Instantaneous and time-averaged lower-isopycnal atmosphere PV anomalies. c, g Instantaneous and time-averaged middle-isopycnal atmosphere dynamic pressures. d, h Instantaneous and time-averaged middle-isopycnal atmosphere PV anomalies

3.2 Atmosphere circulation

The modelled midlatitude, channel atmosphere circulation may be seen by looking at Fig. 2. Latitudinally varying solar radiation generates a PV gradient in the lower and middle-isopycnal atmosphere layers, which leads to the formation of a highly turbulent, zonally inhomogeneous westerly jet. The zonal inhomogeneity of the jet is created by the ocean basin shift and addition of land orography. The westerly jet formed in the middle-isopycnal atmosphere dominates the circulation with its momentum supporting the lower-isopycnal layer via baroclinic instabilities (Hogg et al. 2003). The upper-isopycnal atmosphere is not forced directly by diabatic entrainments, and is only driven by eddies, so we will neglect its dynamics for the purposes of our study. Average speeds in the middle-isopycnal atmosphere are around $20\,\text {ms}^{-1}$, while they are around $6\,\text {ms}^{-1}$ in the lower-isopycnal atmosphere. This difference in circulation strengths is responsible for the sign change in PV in the lower-isopycnal layer. The circulation in the middle-isopycnal atmosphere dominates despite receiving weaker forcing than the lower-isopycnal atmosphere because it is not spun down by frictional wind-stresses, and the effect of considerably lower reduced gravities at the layer-2,3 interface allows for enhanced PV generation via the corresponding interface displacements that occur.

Fig. 3

Unfiltered ocean SST and wind-induced forcing reference solutions for benchmark modelled climate in statistical equilibrium. Top and bottom panel rows correspond to instantaneous and time-averaged fields, respectively. a, e Ocean SST. b, f Ocean Ekman pumping. c, g Ocean diabatic entrainment. (d, h): upper-ocean total entrainment

3.3 Ocean mixed layer

Instantaneous and time-averaged fields of SST anomalies, wind-induced ocean forcing and surface stresses are shown in Figs. 3 and 14. The subtropical and subpolar gyres in the ocean mixed layer are clearly visible and separated by a sharp SST front across the WBCE (Fig. 3a, e). The WBCE acts as a partial inter-gyre barrier, separating warmer waters in the subtropical gyre from the cooler waters in the subpolar gyre. Inter-gyre exchanges of warm and cool waters by mesoscale activity is also visible.

Surface stresses generate wind-curls that drive the ocean gyres in the form of both adiabatic Ekman pumping and diabatic entrainments. Although the sum of these forcings, i.e. the upper-ocean total entrainment $^oe_{\text {total}}$, has roughly equal vorticity flux into each gyre, the adiabatic Ekman pumping component dominates in the subpolar gyre (see Fig. 3f, h). These positive and negative vorticity fluxes over the subpolar and subtropical gyres, respectively, are fuelled by the atmosphere through frictional wind-stresses. However, the sign of PV anomalies in the lower-isopycnal layer is inconsistent with the sign of Ekman pumping since negative PV anomalies sit at lower latitudes and increase as they move poleward³ (see Fig. 2b). Hence, the PV driving the ocean gyres must originate from the middle-isopycnal layer which is consistent with our findings so far (and by Hogg et al. 2003) that the lower-isopycnal atmosphere is driven from above through momentum transfers that take place via baroclinic instabilities.

Fig. 4

Unfiltered atmospheric mixed layer reference solutions for benchmark modelled climate in statistical equilibrium. a, b Instantaneous and time-averaged ASTs. c, d Instantaneous and time-averaged diabatic entrainments in the middle-isopycnal atmosphere. e, f Instantaneous and time-averaged sensible and latent heat fluxes into the atmosphere. Positive heat flux indicates heat gained by the atmosphere. g Time-averaged meridional eddy heat flux. e, f Show heat fluxes over ocean basin region

3.4 Atmosphere mixed layer

Figure 4 shows atmospheric surface temperatures (ASTs), atmosphere diabatic entrainments and sensible and latent heat fluxes. The ASTs appear to be mostly controlled by the atmospheric circulation except over the ocean basin where the WBCs and double-gyre circulation leave an imprint through the surface heat fluxes. Upward transfers of heat are given by positive heat fluxes, i.e. ocean warming atmosphere, and downward transfers of heat are given by negative heat fluxes, i.e. atmosphere warming ocean. We confirm that the sensible and latent heat fluxes give realistic patterns (Shaman et al. 2010; Kwon et al. 2010) which are strongest near the WBC separation point and WBCE, and hence, strongly controlled by the ocean gyre circulation. The time-average effect of these heat fluxes appear to be the warming and cooling of ASTs over the subtropical and subpolar WBCs, respectively. This consequently leads to a sharpening in meridional AST gradients over the ocean basin through the convergence of warm and cold waters by WBCs. Similar patterns of surface heat fluxes are obtained in Kravtsov et al. (2007) but ours show higher variability and time-averaged fluxes that extend well into the ocean interior due to the powerful WBCE. The position of these strong sensible and latent heat fluxes over the WBCs and WBCE coincides with the narrowing of meridional eddy heat fluxes in Fig. 4g. This eddy heat flux implies the convergence of ASTs due to eddies in the atmosphere mixed layer. Meridional eddy heat fluxes are active over the entire atmospheric jet, but it acts over a wider latitudinal band outside the ocean basin region, where synoptic scale turbulence destroys the low-level baroclinicity. The narrowing of this eddy heat flux latitudinal band by sharp SST gradients due to the WBCs is important in anchoring the westerly jet and increasing the low-level baroclinicity of the atmosphere (Nakamura et al. 2004, 2008). Enhancement of time-averaged atmosphere diabatic entrainment due to increased land-sea contrast and the addition of land orography is clearly visible in Fig. 4d.

Our modelled climate is qualitatively similar to those modelled by Hogg et al. (2006) and Kravtsov et al. (2007). However, some differences such as significantly increased turbulent activity in both the ocean and atmosphere are important to note. In the ocean, this leads to a strengthened WBCE via enhanced eddy backscatter in the inertial recirculation zones. This allows for greater amounts of heat transport by the jet as it is able to penetrate further into the ocean interior. This gives a greater longitudinal region for the ocean to thermally feedback onto the atmosphere, where previously, only regions close to the western boundary were able to supply large enough heat fluxes to the atmosphere such as to measurably impact upon its dynamics. Furthermore, the effects of eddies in the lower-isopycnal behaviour must also not be ignored. The convergence of heat by meridional heat fluxes over the WBCs and WBCE plays an important role in restoring the low-level baroclinicity. Mesoscale SST variability also appears well captured by the atmospheric mixed layer due to the high nominal resolution of the atmosphere.

4 Variability of modelled climate

We will now decompose the variability of the low-pass filtered ocean and atmosphere data. Furthermore, we must look at the variability of mixed layer variables that are responsible for mediating ocean–atmosphere interactions. These include forcings such as wind-induced Ekman pumping, ocean and atmosphere diabatic entrainments, as well as transfers of heat and momentum through wind-stresses and surface heat fluxes. Although similar analysis is performed in Hogg et al. (2005, 2006), our modelled ocean and atmosphere circulation is significantly more turbulent so this analysis is necessary for the purposes of this study.

Fig. 5

Leading EOFs of filtered upper-layer oceanic PV. a ${}^oq_1$ EOF 1. b ${}^oq_1$ EOF 2. c Power spectra of PC 1 for coupled $(X_C=1)$ and decoupled $(X_C=0)$ simulation. d Power spectra of PC 2 for coupled $(X_C=1)$ and decoupled $(X_C=0)$ simulation

Fig. 6

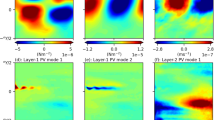
Leading EOFs of filtered upper-layer oceanic transport streamfunction and their phases of oscillation defined as $\pm 1\sigma$ over the mean circulation for the fully-coupled, reference modelled climate $(X_C=1)$. Upper panels represent modes associated with meridional shifts of the WBCE; lower panels represent modes associated with changes in strength of the subtropical recirculation zone. The standard deviations $\sigma$ is computed using the corresponding PC of the EOF. a, f $^oT_m$ EOFs 1 and 2, respectively. b, g $^aF_{\lambda }$ EOFs 2 and 1, respectively. c, h ${}^o\Psi _1$ EOFs 1 and 2. d, i Positive phases ($+1\,\sigma )$ of ${}^o\Psi _1$ EOFs 1 and 2, respectively. e, jNegative phases ($-1\,\sigma )$ of ${}^o\Psi _1$ EOFs 1 and 2, respectively

4.1 Upper-isopycnal ocean variability

The leading EOFs for the filtered upper-isopycnal ocean PV anomaly $^oq_1$ from the benchmark modelled climate are given in Fig. 5. EOFs 1 and 2 (Fig. 5a, b) explain 24.5% and 18.1% of the total variance in the data, respectively, with strong power at low frequencies (see Fig. 5c, d). EOF 1 consists of strong negative PV anomalies situated along the meandering WBCE. EOF 2 consists of similar, but more zonally-symmetric, negative PV anomalies along the WBCE. EOF 1 also appears to show a change in the subtropical gyre PV concentration, and EOF 2 very weakly so, but these are secondary to the strong variability of the WBCE. Comparing the power spectra of the corresponding PCs from the decoupled simulation shows that coupling of the atmosphere to its mixed layer has a strong effect on the ocean gyre variability (see Fig. 5c, d). Both EOFs have increased variability across almost all low frequencies through coupling. Such changes in variability are likely a consequence of thermal feedbacks between the ocean and atmosphere but it is unclear why this is so without further analysis of the lagged cross-covariability (see Sect. 5).

Although it is evident that these EOFs control WBCE variability, it is less clear how they affect the gyres by looking at the EOFs alone. In such situations it is better to overlay the EOFs onto the mean flow to show positive and negative phases of an oscillation generated by each EOF. However, we found that this was also not very insightful since the yielded PV anomaly fields still looked very similar. This is largely due to the fact that the PV anomaly fields are more homogenised throughout the ocean basin in comparison to streamfunction fields which are considerably stronger around the WBCE and recirculation zones. Thus, it is more useful to look at the leading EOFs of filtered upper-isopycnal transport streamfunction $^o\Psi _1$ which gave EOFs that were highly correlated to the EOFs obtained from the filtered upper-isopycnal PV anomaly data. Positive and negative phases are defined by a $\pm 1\sigma$ oscillation on top of the time-averaged circulation where $\sigma$ represents 1 s.d. of the corresponding PC.

We found that ${}^oq_1$ EOF 1 was correlated to ${}^o\Psi _1$ EOF 2 with correlation coefficient 0.85 and ${}^oq_1$ EOF 2 was correlated to ${}^o\Psi _1$ EOF 1 with correlation coefficient of also 0.85. The positive and negative phases of the upper-isopycnal ocean transport streamfunction EOFs are presented in Fig. 6 along with the original EOFs and explained variances. From this figure, it is now apparent that ${}^oq_1$ EOF 1 affects the strength of the subtropical recirculation zone which coincides with a change in the subtropical gyre PV concentration. Changes in the subpolar gyre and recirculation zone appear very small or negligible. In the positive phase, the subtropical recirculation zone strengthens, leading to an increase in the jet meander as the jet is consequently deflected more strongly equatorward as it separates from the western boundary, and the size of the subtropical gyre shrinks. In the negative phase, the opposite happens. The subtropical recirculation zone weakens, the jet is deflected less as it separates from the western boundary, and the size of the subtropical gyre increases. The maximum volume transports achieved by the positive and negative phases for $^o\Psi _1$ EOF 1 are $70\,\text {Sv}$ and $65\,\text {Sv}$, respectively.

On the other hand, ${}^oq_1$ EOF 2 (or ${}^o\Psi _1$ EOF 1) appears to affect the meridional displacement of the WBCE, with the entire jet shifting poleward in its positive phase and equatorward in its negative phase (see Fig. 6c, d, e). The magnitude of this meridional displacement appears to be $\sim 100\,\text {km}$ from its mean position and is similar to observed values (Sasaki et al. 2013). There is also a smaller but measurable change in the strength of the subtropical gyre, recirculation zones and WBCE in the different phases of ${}^oq_1$ EOF 2 than what is observed in ${}^oq_1$ EOF 1. The maximum volume transports achieved by the positive and negative phases for $^o\Psi$ EOF 2 are slightly less than EOF 1 with values of $67\,\text {Sv}$ and $63\,\text {Sv}$, respectively, for phases at $\pm 1\,\sigma$. Sasaki et al. (2013) also found this increase in jet-strength as the WBCE moved poleward. These are intrinsic modes of ocean gyre variability, with similar modes observed by Hogg et al. (2005), Hogg et al. (2006) and Berloff et al. (2007b). Our interests in subsequent sections lie in understanding how these modes of variability may couple with the overlying atmosphere through lagged responses and coupling.

4.2 Ocean mixed layer variability

Analysis of SST $^oT_m$ and surface heat flux $^aF_{\lambda }$ variability found similar EOFs to those seen in Fig. 5 and are presented in Fig. 6a, b, f, g. These EOFs are highly correlated to the EOFs in Fig. 5 and are similar, but not identical, in structure to each other. The main difference being that $^aF_{\lambda }$ EOF 2 does not have the corresponding negative heat flux due to cooling of the subtropical gyre in $^oT_m$ EOF 2 (see Fig. 6f, g). This is likely an effect of damped surface heat fluxes in the ocean interior due to the white-noise integrator effect (Hasselmann 1976; Frankignoul and Hasselmann 1977). The top row of panels in Fig. 6, $^oT_m$ EOF 2, $^aF_{\lambda }$ EOF 2 and $^o\Psi _1$ EOF 1, are correlated to $^oq_1$ EOF 2; the bottom row of panels in Fig. 6, $^oT_m$ EOF 1, $^aF_{\lambda }$ EOF 1 and $^o\Psi _1$ EOF 2, are correlated to $^oq_1$ EOF 1. All of the respective correlation coefficients are greater than 0.8 indicating that all the EOFs correspond to the same changes in the underlying ocean gyre circulation. Similar patterns due to $^o\Psi _1$ EOF phase changes were found for $^aF_{\lambda }$ phase changes. It appears that in the positive phases of $^aF_{\lambda }$ EOFs 1 and 2, the total sensible and latent heat flux due to the subtropical WBCs increase by 4% and 2%, respectively. In the negative phase, the sign of the anomaly flips and the total sensible and latent heat fluxes decrease by the same amount.

4.3 Atmosphere and diabatic entrainment variability

Fig. 7

Leading EOFs of atmosphere diabatic entrainment $^ae_1$ and filtered lower- and middle-isopycnal atmosphere PV. a ${}^ae_1$ EOF 1. b ${}^aq_1$ EOF 1. c $^ap_1$ EOF 2. d $-{}^ae_1$ EOF 1. e ${}^aq_2$ EOF 1. f $^ap_2$ EOF 1. g Corresponding power spectra of EOF in panel b for coupled $(X_C=1)$ and decoupled $(X_C=0)$ simulations. h Corresponding power spectra of EOF in panel e for coupled $(X_C=1)$ and decoupled $(X_C=0)$ simulations

Fig. 8

Leading EOF of filtered lower-layer atmospheric dynamics pressure. a:${}^ap_1$ EOF 1 for benchmark modelled climate. b ${}^ap_1$ EOF 1 for partially-coupled modelled climate. c Relative power spectra of the respective PCs

The leading EOFs of the filtered atmospheric variability, namely lower- and middle-isopycnal atmosphere PV and dynamic pressures, as well as their associated diabatic entrainments are presented in Fig. 7. These EOFs, which are all highly correlated to each other,⁴ consist of a wavenumber-6 mode that affects the meander and zonal symmetry of the atmospheric jet with an east–west dipole anomaly sitting over the ocean basin. This mode is a synoptic scale Rossby wave that forms in the atmosphere through growing instabilities in the westerly jet. Similar modes of variability were found in Hogg et al. (2006) with a pair of EOFs identified as a travelling-wave mode pair. We also found similar modes shifted out of phase in the longitudinal direction but these were omitted since they appeared mostly unaffected by coupling of the atmosphere to its mixed layer and had significantly lower explained variances. For example, $^aq_1$ EOF 1 (Fig. 7b) has an explained variance of 21.0% in the fully-coupled modelled climate $(X_C=1)$, but only has an explained variance of $10.8\%$ in the equivalent EOF from the partially-coupled modelled climate $(X_C=0)$. This doubling of the explained variance is apparent in the power spectra of the respective PCs in Fig. 7g with increases in variability seen over the 5–16-year band range (increased variability over longer time-scales $>20$-year are less certain). The increase in variability of this frequency band indicates the most dominant time-scales that are likely associated with ocean–atmosphere interactions. Similar changes in explained variance and power spectra were found for the corresponding EOFs in the middle-isopycnal layer (see Fig. 7h) when comparing the coupled and partially-coupled modelled climates. Yet, no such change in explained variance was observed for the omitted phase-shifted EOFs. The question now arises why the variability of one EOF is amplified while the other is not. It is natural to expect that the time-varying diabatic entrainment would increase the atmospheric variability of these two leading EOFs with roughly equal measure as their structures are very similar. The fact that the EOFs in Fig. 7b, c, e, f alone appear affected is indicative of the influence of ocean gyre dynamics on this particular mode of variability. Due to these reasons, we will treat the EOFs in Fig. 7 as separate EOFs from their phase-shifted counterparts.

The corresponding diabatic entrainment mode, or atmospheric forcing, that generates these modes of atmospheric variability are presented in Fig. 7a, d. In fact, they are the same EOF but sign-flipped since the lower- and middle-isopycnal layers receive proportional but opposite-signed forcings (7). These diabatic entrainments generate the strongest circulation response in the middle-isopycnal layer, with the PV response pattern advected eastwards of the diabatic entrainment forcing by the jet before reaching maximum strength. The corresponding dynamic pressure anomalies in the middle-isopycnal layer are of the correct sign with cyclonic circulations for positive PV anomalies and anti-cyclonic circulations for negative PV anomalies. Momentum transfers into the lower-isopycnal layer via baroclinic instabilities flip the sign of the circulation anomalies in the lower-isopycnal, despite receiving forcing of the opposite sign, such that the flow becomes more barotropic. The atmosphere diabatic entrainment EOF 1 is strengthened and more coherent over the ocean basin with enhanced forcing first appearing over the western boundary near the WBCE separation region. These then reach a maximum strength over the eastern boundary before they quickly decay. We interpret this as the generation and growth of baroclinic instabilities over the ocean basin due to land-sea contrast and strong surface heat fluxes generated by the presence of WBCs and SST front (see Fig. 4f, g). The decay of this mode to the east of the ocean basin is associated with strong eddy mixing of heat by turbulence of the jet that destroys the increased baroclinicity created by the land-sea contrast. This tendency of the atmosphere to reduce meridional temperature gradients and low-level baroclinicity has been posed by Hoskins and Valdes (1990). Although it is clear that the atmospheric westerly jet is interacting with the SST front and WBCs, it is unclear through this analysis alone what role the SST variability plays. In summary, the strongest mode of atmospheric variability is controlled by the growth of Rossby wave modes through baroclinic instabilities that are enhanced by the presence of the SST front.

When the low-pass filtered, lower-isopycnal atmosphere pressure variability ${}^ap_1$ was decomposed in our model, the leading EOF was a standing wave, meridional jet shift mode (see Fig. 8a) explaining a large 37.3% of the total variability. This mode is similar to the jet-shift mode found in Kravtsov and Robertson (2002) and Kravtsov et al. (2003) but with weak circulation anomalies sitting in-between strong circulation anomalies. These weaker circulation anomalies are regions that are largely unaffected by the anti-cyclonic circulations and increase the zonal asymmetry of the mode. Over the ocean basin, this mode corresponds to a strong anti-cyclonic circulation anomaly over the eastern basin and a much weaker, almost stagnant, anti-cyclonic anomaly over the western basin. The differences in structure with the equivalent EOF obtained from the partially-coupled modelled climate are notable with a more zonal structure and no such weak circulation anomalies, i.e. more similar to modes found by Kravtsov and Robertson (2002) and Kravtsov et al. (2003). Indeed the EOF in Fig. 8a appears similar in structure to $^aq_1$ EOF 1 in Fig. 7b as it is of the same wavenumber. Since ocean gyre dynamics has already been posed as the likely culprit in increasing the variability of this particular EOF, it is also likely that it is responsible for the changes in structure between Fig. 8a, b.⁵ Such a change in zonal structure an atmospheric mode of variability through coupling has yet to be seen in such models with Hogg et al. (2006), Kravtsov et al. (2007) and Berloff et al. (2007a) only being able to find a modification of the preferred time-scales, rather than a change in structure of the EOF itself.

4.4 Oceanic forcing variability

Fig. 9

Leading EOFs of filtered ocean forcing and associated ocean surface stresses. a $^ow_{\text {ek}}$ EOF 1. b $^oe_1$ EOF 1. c ${}^oe_{\text {total}}$ EOF 1. d $^o\tau ^x$ EOF 2. e $^o\tau ^y$ EOF 1. Black dashed line indicates time-averaged position of the inter-gyre boundary. All EOFs that are plotted in this figure are highly correlated to each other

Finally, we decompose the variability of the wind-induced ocean forcing. Namely we look at ocean Ekman pumping $^ow_{\text {ek}}$, ocean diabatic entrainment $^oe_1$, and in the case of the upper-isopycnal ocean, the upper-ocean total entrainment $^oe_{\text {total}}$. This is left until after the atmospheric variability is decomposed as it turns out that ocean forcing variability is controlled by the atmosphere at lag-zero. The leading EOFs and their associated ocean surface stresses are presented in Fig. 9. Unlike the variability of the diabatic atmosphere entrainment, which is correlated at lag-zero to the modes of lower atmosphere PV variability, ocean forcing does not correlate at lag-zero to modes of ocean gyre variability due to its large inertia. The leading EOF of the filtered ocean Ekman pumping, ocean diabatic entrainment and upper-ocean total entrainment explain 11–12% of the total variance (see Fig. 9a–c). These modes looks similar and are correlated (correlation coefficients $>0.7$) to the leading EOF of ${}^aq_1, {}^aq_2$ in Fig. 7b, e. These EOFs consists of an east–west positive–negative dipole vorticity flux over the ocean basin. The positive anomaly is situated over the WBCE and the negative anomaly is situated over the eastern basin. The centroid of both anomalies shift north and south of the inter-gyre boundary depending on whether we are looking at Ekman pumping (Fig. 9a) or diabatic entrainment (see Fig. 9b).⁶ The shifting of these anomalies is due to the aforementioned misalignment of the SST front and the zero wind-curl line (see Sect. 3.3). The ${}^oe_{\text {total}}$ EOFs are advected slightly further downstream of the atmospheric westerly jet compared to the ${}^aq_1$ EOFs which is due to Ekman layer effects when computing surface stresses in the mixed layers. The signs of the anomalies is such that losses of PV in the lower-isopycnal atmosphere correspond to gains of PV in the ocean. However, the responsible PV flux must be generated by the middle-isopycnal atmosphere where the signs are correct, i.e. positive vorticity fluxes in the ocean must be due to positive PV anomalies that arise in the atmosphere otherwise enstrophy is not conserved. This pathway where circulation anomalies in the middle-isopycnal layer transfer momentum to the lower-isopycnal atmosphere and into the ocean is again consistent with our earlier findings (see Sect. 3.2). The responsible surface stress patterns (Fig. 9d, e) are EOF 2 of zonal surface stress $^o\tau ^x$ and EOF 1 of meridional surface stress $^o\tau ^y$. The wind-stress anomalies give cyclonic surface stresses for positive vorticity fluxes and anti-cyclonic surface stresses for negative vorticity flux as expected. The leading EOF of zonal wind-stress, $^o\tau ^x$ EOF 1 consists of a zonal shear pattern (omitted). The zonal shear appears strongest over the eastern basin with the sign of the shear corresponding to a cyclonic wind-stress pattern.

Analysis of ocean forcing variability has yet to be looked at in detail using this model. This is likely because ocean gyre variability has been, so far, only explained as intrinsic modes of variability (e.g. Hogg et al. 2006) or within ocean-only simulations where the atmosphere model is switched off (Hogg et al. 2005). However, in order to be able to understand the role of the ocean gyres within any coupled interaction. Modes of atmospheric and ocean forcing variability must be related to delayed modes of ocean gyre variability.⁷ Indeed, Kravtsov et al. (2007) identified monopolar Ekman pumping forcing anomalies over the ocean basin to be part of a coupled mode associated with meridional shifts of the atmosphere westerly jet preceding shifts in the WBCE through nonlinear adjustments of the recirculation zones (Dewar 2003). The structure of the ocean forcing EOFs in this study are different since there are zonal asymmetries present which make it more difficult to diagnose its effects on the gyres. The zonal structure of these forcing modes is more similar to those discussed in Jin (1997). However, the ocean model used in their study consisted of a linear Rossby wave model which does not take into account the complex nonlinear dynamics present in the ocean gyres.

5 Disentangling causes of climate variability

Although we have made some progress in understanding the modelled climate variability, we still have some work to do in understanding how certain aspects of it interact. Namely, we are most interested in the ocean gyre response to forcing as well as how the associated surface heat flux anomaly affects the atmosphere diabatic entrainment. The ocean gyre response to forcing will be looked at by computing SVDs of the relevant data fields under different time-lags, with forcing leading response variables.

Fig. 10

Leading SVD modes when ocean entrainment $({}^oe_{\text {total}})$ leads upper-isopycnal ocean PV anomaly $({}^oq_{1})$; diabatic ocean entrainment $+{}^ae_1$ leads middle-isopycnal ocean PV anomaly $^oq_2$. a, d SVD Mode Pair 1 ($^oe_{\text {total}}$ leading $^oq_1$). b, e SVD Mode Pair 2 ($^oe_{\text {total}}$ leading $^oq_1$). c, f SVD Mode Pair 1 ($^oe_{\text {total}}$ leading $^oq_2$). g Lag correlations and scaled covariance of leading SVD mode temporal coefficients for $^oe_{\text {total}}$ leading $^oq_1$. h Lag correlations and normalised covariance of leading SVD mode temporal coefficients for $+^oe_1$ leading $^oq_2$

5.1 Ocean gyre response to wind-induced forcing

When the leading SVD modes were computed for upper-ocean total entrainment $^oe_{\text {total}}$ leading upper-isopycnal ocean PV anomaly $^oq_1$, two different leading SVD modes were found for a wide band of time-lags ranging from 0 to 16-years (see Fig. 10a, b, d, e). Longer time-lags were found to decorrelate with known EOFs and became too noisy to interpret. The two sets of SVD modes were aggregated for different time-lags by averaging over them with equal weights, i.e. computing their ensemble average. The $^oe_{\text {total}}$ component of both of these SVD modes (Fig. 10a, b) were found to have average correlation coefficients of 0.72 and 0.78 with $^oe_{\text {total}}$ EOF 1, respectively. Indeed both of these patterns are spatially correlated with the corresponding EOF (positive anomaly in the western basin and negative anomaly in the eastern basin) but the SVD mode appears both noisy and sheared in the anti-cyclonic direction. This shearing of the forcing pattern is either part of the noise or an important feature of the signal such as an effect of coupling.⁸ Although the responsible entrainment EOF is the same for the pair of presented SVD modes, where they differ is in the upper-isopycnal PV anomaly response. In fact, the upper-isopycnal ocean gyre response of every computed leading SVD mode, except the 12-year lag, was found to be either one of the following two responses. The first mode, shown in Fig. 10d, is anti-correlated to $^oq_1$ EOF 1 with a correlation coefficient of $-0.96$ while the second mode, shown in Fig. 10e, is correlated to $^oq_1$ EOF 2 with a correlation coefficient of 0.85. Both of these ocean gyre responses were found to have very low correlations of $<0.25$ (for any time-lags up to 16-year lags in both directions) indicating that the responses are likely governed by distinct mechanisms.

The maximum lagged coexplained variance of the computed SVD modes peaks at a 2–3-year lag (Fig. 10g) with the upper-isoypcnal ocean PV response found to be correlated to the meridional jet shift mode in Fig. 10. The zero-lag and 1-year lag upper-isopycnal ocean PV response was found to be correlated to Fig. 10d indicating the response of the subtropical inertial recirculation zone and gyre acts at a faster time-scale. There is some uncertainty in predicting this dominant time-scale response which is likely due to high levels of mesoscale ocean turbulence. Despite a peak in maximum covariance at 2-year, we notice that both the lagged covariances and correlations of the temporal SVD coefficients persist for up to 16-year, much longer than the expected upper-isopycnal ocean gyre response time-scale (typically less than 5-year, see Hogg et al. 2005; Berloff et al. 2007a; Kravtsov et al. 2007). We attribute this to likely repeated feedbacks of the ocean gyres with the atmosphere. In addition, the sign of the response always remains consistent, with either a weakening or a poleward shift of the WBCE detected for this particular forcing pattern implying a positive feedback signal.

For the middle-isopycnal ocean, the PV anomaly response largely consists of $^oq_2$ EOF 1 activated by the diabatic component of the upper-isopycnal ocean forcing which is given by $+{}^oe_1$ EOF 1. The PV response is contained within the subtropical gyre as this is where diabatic entrainment dominates (see Figs. 3g, 9b, g). The average correlations are 0.64 for $^oe_1$ EOF 1 and 0.99 for $^oq_2$ EOF 1. Note the sign change in vorticity fluxes is consistent with the forcing in the upper-isopycnal layer. The middle-isopycnal ocean PV response shows a negative PV anomaly protruding out from the western boundary extending out into the ocean basin and a similar positive PV anomaly extending out from the eastern boundary. This pattern was found to be correlated to the upper-isopycnal subtropical recirculation zone weakening in the upper-isopycnal layer (Fig. 10d). By checking the streamfunction response in the middle-isopycnal layer, the western and eastern circulation anomalies correspond to cyclonic and anti-cyclonic anomalies, respectively. Such a circulation response in the middle-isopycnal layer hence implies that these circulation anomalies do not arise as a result of diabatic entrainment forcing in the middle-isopycnal layer, but must be due to momentum transfers from the upper-isopycnal layer due to changes in the subtropical gyre circulation. The middle-isopycnal layer response to meridional shifts of the WBCE were not detected when looking at PV anomalies but were detected for transport streamfunction responses. The pattern of the response was similar to Fig. 10e and also occur due to momentum transfers from the upper-isopycnal layer. The time-scale of the middle-isopycnal ocean PV response is less clear than the upper-isopycnal (see Fig. 10). There appears to be a small peak in maximum covariance at the 1-year lag, perhaps associated with a fast barotropic response along the WBCE (e.g. Dewar 2003), but this peak is small and not much greater than the other values of computed maximum covariances (see Fig. 10).

In summary, the east–west positive–negative upper-ocean total entrainment mode induces a weakening of the subtropical recirculation zone and/or a poleward shift of the WBCE in the upper-isopycnal layer. The middle-isopycnal layer response seems largely to be controlled by momentum transfers that occur due to baroclinic instabilities through the much stronger upper-isopycnal circulation response. Furthermore, the ocean does not appear to respond at any preferred time-scale and instead acts over a wider interannual to interdecadal band time-scale. This is likely due to reduced predictability of the model induced by high levels of mesoscale ocean turbulence (Nonaka et al. 2016). The east–west dipole forcing mode is difficult to compare to most studies of wind-induced ocean gyre variability which mostly focus on monopole forcings (e.g., Dewar 2003; Kravtsov et al. 2007). Both the ocean forcing and response modes are complex in nature and further analysis of the processes involved is required. Since the forcing mode may be split into two separate anomalies, one in the western and the other in the eastern basin, we hypothesise that the two uncorrelated ocean gyre responses are a result of two distinct mechanisms responding independently to the two ocean forcing anomalies. Further dynamical interpretation of this ocean gyre response is outside the scope of this paper and we leave this to Kurashina and Berloff (2023). Instead, we focus our attention on the associated SST response and how this affects the atmospheric circulation.

5.2 SST-induced atmosphere diabatic entrainment

Fig. 11

Leading lag-zero SVD modes of sensible and latent heat flux and diabatic atmosphere entrainment at lag-zero in the lower-isopycnal atmosphere. a, b SVD mode 1 with $^aF_{\lambda }$ mode presented in a and $^ae_1$ mode presented in b. c, d SVD mode 2 with $^aF_{\lambda }$ mode presented in c and $^ae_1$ mode presented in d

As the ocean gyre responses in the previous Subsection induce changes in the shape and location of the WBCE, it is natural to check how the associated SST front changes affect the atmospheric circulation. Since we know the associated sensible and latent heat flux response to the discussed modes of ocean gyre variability (see Fig. 6), we would now like to see what atmosphere diabatic entrainments are associated with them.

Figure 11 shows the sensible and latent heat fluxes $^aF_{\lambda }$ and the consequently generated atmosphere diabatic entrainments $^ae_1$ over the ocean basin. Only lag-zero SVDs are checked since the atmospheric response time-scale is short in comparison to the ocean. The polarities of these SVD modes correspond to the aforementioned, wind-induced changes in the ocean gyre circulation. We have only computed these SVDs using atmosphere diabatic entrainment data over the ocean basin region where the effect of sensible and latent heat fluxes are strongest. Only the positive atmosphere diabatic entrainment situated over the eastern subtropical gyre is unaccounted for by the sensible and latent heat fluxes, but it is present in the associated SST EOF (see Fig. 6f). The damped surface heat fluxes over the subtropical gyre are likely due to the white-noise integrator effect (Hasselmann 1976). The $^aF_{\lambda }$ modes in Fig. 11a, c are highly correlated to $^aF_{\lambda }$ EOFs 1 and 2 with correlation coefficients 0.9 and 0.73, respectively. The $^ae_1$ modes in Fig. 11b, d are correlated to $^ae_1$ EOFs 3 and 1 with correlation coefficients of 0.87 and 0.64, respectively. The temporal coefficients of the SVD mode 1 and 2 themselves are also correlated highly with coefficients of 0.85 and 0.85, respectively.

The leading SVD mode pair of $^aF_{\lambda }$ and $^ae_1$ (Fig. 11a, b) is associated with the weakening of the subtropical recirculation zone and the expansion of the same gyre. The negative sensible and latent heat flux anomaly is associated with a deformation of the recirculation zone and a change in the shape of the WBCE and SST fronts, while the positive heat flux anomaly is associated with a warming of the eastern subtropical gyre as it expands. On the other hand, the second SVD mode pair (Fig. 11c, d) is dominated by strong, positive sensible and latent heat fluxes over the SST front as the WBCE shifts poleward of its average position. This heat flux generates a strong diabatic entrainment anomaly over the same region with a strong diabatic entrainment response of similar meridional scale in the form of an anomalous line source of vorticity (the sign of this depends on whether we are looking at the lower- or middle-isopycnal layer). Although there does appear to be some mixing of this temperature anomaly in the atmospheric mixed layer, the narrow meridional scale of diabatic entrainment is maintained well. This is likely due to the influence of meridional eddy heat fluxes that are anchored to the location of the SST front (Fig. 4g).

5.3 Inertial response of westerly jet to diabatic entrainment forcing over ocean basin

Fig. 12

Leading lag-zero SVD modes of atmosphere diabatic entrainment and lower-isopycnal atmosphere dynamic pressure anomaly at lag-zero. Top panel row shows the SVD modes for $20\,\text {km}$ atmosphere while bottom panel row shows the SVD modes for $80\,\text {km}$ atmosphere. Left-hand side panels show $^ae_1$ modes while right-hand side panels show $^ap_1$ modes

Next, we look at the response of the atmosphere to diabatic entrainments. Although we have already correlated EOFs of these fields to each other in Sect. 4.3, we now isolate impacts of SST variability on the atmosphere by spatially subsampling over the ocean basin. This will allow us to better determine the atmospheric response to the line source of vorticity identified in the previous paragraph.

To do this, we computed lag-zero SVDs of atmosphere diabatic entrainment $^ae_1$ and atmosphere PV $^aq_1, {}^aq_2$. Similar SVDs with entrainment and dynamic pressure anomalies $^ap_1, {}^ap_2$ are also computed to see the inertial effects on the atmospheric jet. In the case that influence of SST variability on the atmosphere is small or negligible, we would expect to see the computed SVDs will be similar or identical to the EOFs shown in Fig. 7, i.e. no difference in atmosphere response when subsampling data over the ocean basin. In addition, to ascertain any impact of atmospheric eddies on the response to diabatic entrainments, we also computed a supplementary coupled climate with a moderately reduced atmospheric resolution of $80\,\text {km}$ (see Table 3 in Appendix 4). The ocean model parameters are identical to the benchmark modelled climate. The same sets of analysis was performed using data obtained from this supplementary modelled climate.

The leading SVD modes for the $20\,\text {km}$ and $80\,\text {km}$ lower-isopycnal atmosphere dynamic pressure responses to diabatic entrainments correlated to $^ae_1$ EOF 1 are presented in Fig. 12. Firstly, the atmosphere diabatic entrainment modes (Fig. 12a, c) are highly correlated to equivalent EOFs to the one shown in Fig. 7a with correlation coefficients $>0.9$. We already know that this mode of diabatic entrainment, in the benchmark modelled climate, is well correlated to meridional shifts of the SST front and WBCE (e.g. Figure 11c, d). We found that the structure of the modes for the corresponding PV response in both atmospheric resolutions were similar to those already shown in Fig. 7, so they are omitted. However, we found that the dynamic pressure or inertial response of the $20\,\text {km}$ atmosphere to this diabatic entrainment was significantly different in structure to the EOFs shown in Fig. 7. In particular, the lower-isopycnal pressure response shows an asymmetry in the strength of the anomalous response over the western and eastern basins.⁹ Over the western basin, there is a weaker cyclonic anomaly, while over the eastern basin, there is a stronger anti-cyclonic anomaly. This is in contrast to the EOFs in Fig. 7c, f which are computed over the entire atmosphere. The EOFs computed in Fig. 7 do not show this asymmetry in response of the westerly jet to diabatic entrainments because ocean–atmosphere interactions are given less importance, in a statistical sense, as the variability of the entire atmosphere is being considered.

Reduction of the atmosphere model resolution, and a consequent damping in eddy-induced behaviours, leads to a reduction in this asymmetric response (Fig. 12d), with the lower-isopycnal pressure response correlated to EOFs of the same structure as those in Fig. 7. On the other hand, the asymmetric inertial response of the $20\,\text {km}$ westerly jet (Fig. 12b) appears to be occur as a result of SST variability on the atmospheric westerly jet with the inertial response now correlated to both $^ap_1$ EOF 1 and 2 with correlation coefficients 0.70 and 0.62, respectively. Note that the correlation to $^ap_1$ EOF 1 was undetectable in the EOF analysis in Sect. 4.3. This atmospheric response is akin to those seen in Taguchi et al. (2012) and Famooss Paolini et al. (2022) with the an anti-cycloncic pressure anomaly downstream of the jet. Furthermore, for poleward shifts of the WBCE, the atmospheric westerly jet experiences acceleration at higher latitudes and deceleration at lower latitudes which may have influences on atmospheric blocking (Famooss Paolini et al. 2022). The opposite may be seen for equatorward shifts of the WBCE. Indeed, this ocean feedback is so strong that it likely leads to the reduced zonal structure of the atmospheric westerly jet meridional shift mode seen in Fig. 8 which has a similar spatial structure to Fig. 12b. The structure of the pressure response may also explain the zonally sheared ocean forcing patterns observed in Fig. 10a–c.

Fig. 13

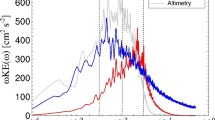
Conditionally time-averaged meridional eddy heat fluxes over years for WBCE in poleward and equatorward positions. Top panels show fluxes for a $20\,\text {km}$ atmosphere while bottom panels show fluxes for a $80\,\text {km}$ atmosphere. a, d Conditionally time-averaged meridional eddy heat fluxes for WBCE in poleward position. b, e Conditionally time-averaged meridional eddy heat fluxes for WBCE in equatorward position. c, f Anomalous heat flux between the poleward and equatorward states. The black contours show the time-averaged meridional heat flux profile over the entire simulation period

We found that $^ae_1$ EOF 3 (Fig. 11d), or changes in strength of the subtropical recirculation zone, did not appear to strongly invoke modes of atmospheric variability despite spatial subsampling over the ocean basin region. We found some evidence of coupling to the westerly jet meridional shift modes in Fig. 8 but correlation of any computed SVD modes to this EOF was low ($\sim 0.4$) so these modes were omitted. This does not necessarily mean that this SST anomaly has no measured effect on the atmospheric circulation, but rather, the response of the atmosphere to this particular anomaly is likely more strongly controlled by eddy-mean flow feedbacks. In other words, the response of the atmosphere to this SST anomaly is likely more dependent on the background flow state and is hence nonlinearly related to the strength and sign of the SST anomaly.

Finally, to better understand why improved resolution of atmospheric eddies increases the asymmetry in the strength of the lower-isopycnal atmospheric pressure response, we compare the meridional eddy heat fluxes of the $20\,\text {km}$ and $80\,\text {km}$ atmospheres that are conditionally time-averaged over years where the WBCE is in its poleward and equatorward states, i.e. greater than or less than $\pm 1\sigma$ of their measured mode variabilities. These meridional eddy heat fluxes, and their difference between the poleward and equatorward WBCE states are shown in Fig. 13. Reduction of the atmospheric resolution to $80\,\text {km}$ severely inhibits the atmosphere’s ability to resolve the underlying meridional shifts in the SST front (see Fig. 13c, f), despite the time-averaged state itself being fairly well resolved. The anomalous fluxes between the poleward and equatorward states of the SST front are both smaller in magnitude and their zonal extent. Furthermore, the meridional eddy heat flux profiles for the WBCE in the poleward and equatorward states are almost identical for the $80\,\text {km}$ atmosphere. Since the ocean circulation is almost identical with the nominal $5\,\text {km}$ resolution maintained in both climates, this difference is attributed, in part, to the lack of the atmospheric eddies’ ability to resolve the small meridional scales associated with shifts in the SST front. Indeed, the magnitude of the meridional shift between the two states is around $200\,\text {km}$ which is poorly resolved by the $80\,\text {km}$ atmosphere. Consequently for the $80\,\text {km}$ atmosphere, this leads to a $70-80\%$ reduction in strength of the anomalous line sources of heat and vorticity in Fig. 11c, d. Around half of this reduction in strength is due to a corresponding weaker SST anomaly which is likely due to damped positive feedbacks in the $80\,\text {km}$ atmosphere climate. The other half of the reduction is unaccounted for and is likely due to inhibited atmospheric eddies. The correlation of the associated temporal SVD coefficients also drops from 0.85 in the $20\,\text {km}$ atmosphere to 0.59 in the $80\,\text {km}$ atmosphere. This difference in strength of the anomalous line source of vorticity likely explains the two different inertial responses of the atmospheric jet with the increased zonal asymmetry acting as a proxy for the atmosphere’s sensitivity to underlying shifts of the SST front. Indeed, if the SST front was fixed in its meridional position, which is similar to the response of the $80\,\text {km}$ atmosphere, we would expect to see pressure anomalies of similar strength over the western and eastern ocean basin. In addition, the reduction in correlation between the surface heat flux anomaly and associated westerly jet response is indicative of a stronger dependence on the background flow state (Peng et al. 1997; Peng and Whitaker 1999; Seo et al. 2017).

5.4 Summary of ocean gyre influences on the climate variability

Our analysis has revealed the following positive feedback mechanism for enhanced low-frequency climate variability:

• 1. East–west positive–negative PV anomalies arise in the middle-isopycnal atmosphere over the ocean basin as part of a wavenumber-6 Rossby wave disturbance.

• 2. This propagates into the lower-isopycnal atmosphere via baroclinic instabilities, and surface stresses generate positive and negative vorticity fluxes over the western and eastern ocean basins, respectively. The growth of baroclinic instabilities is significantly strengthened over the ocean basin due to the presence of the SST front.

• 3. The ocean gyres respond through a weakening of the subtropical recirculation zone and a poleward meridional shift of the WBCE. Full dynamical interpretation of this ocean gyre response may be seen in Kurashina and Berloff (2023), but preliminary analysis indicates that these two responses are governed by distinct mechanisms.

• 4. SST anomalies are generated as a consequence of shifts in the inter-gyre boundary and deformations of the WBCE. This then leads to sensible and latent heat flux anomalies that generate strong diabatic entrainment anomalies in the atmosphere. The sensitivity of the atmosphere to underlying SST front shifts is highly dependent on resolution.

• 5. The diabatic entrainments trigger baroclinic instabilities that grow downstream of the westerly jet and eventually leads to a strong barotropic circulation over the eastern basin. This atmospheric response is shown to be modified by eddies and dependent on the atmosphere’s ability to resolve meridional scales associated with the SST front shift.

• 6. This atmosphere response then reinvigorates the PV variability and generates a positive feedback onto the gyres.

6 Summary and discussion

Motivated by the increasing body of evidence for coupling of atmospheric jets to WBCEs (Frankignoul et al. 2011; Taguchi et al. 2012; Révelard et al. 2018) and the potential of atmospheric mesoscales to strengthen tropospheric forcing (Czaja et al. 2019), we investigated the low-frequency, midlatitude climate variability using an idealised, eddy-resolving coupled model. Although the model we have used in this study is highly idealised, e.g., lack of moisture, simple model geometry, lack of overturning circulation and vertical motions, proper capturing of complex eddy dynamics in the ocean and atmosphere have revealed relevant coupled interactions that enhance the low-frequency variability. We believe these models play an important role in understanding the midlatitude climate and that this study opens up more avenues of future work.

Part I of this two-paper study focused on the effects of ocean–atmosphere coupling on the modelled climate and established the anatomy of the low-frequency climate variability. EOF analysis of the 2-year low-pass filtered, atmosphere PV variability showed two wavenumber-6 Rossby wave modes shifted out of phase in the longitudinal direction. These EOFs consisted of patterns with alternating-signed circulation anomalies, similar to those found in Hogg et al. (2006). Despite these EOFs appearing at first to form a travelling-wave pair, the disparity in the total explained variance in temporal behaviour meant that the EOFs should be treated separately. The difference in explained variance is due to stronger coupling of one of the modes with the ocean gyre circulation. Ocean gyre coupling with the atmosphere also likely leads to the reduced zonal symmetry of the atmospheric jet meridional shift pattern in the benchmark modelled climate. Previously, only time-scale modifications of atmospheric modes have been found using this class of models (e.g., Hogg et al. 2006) so this finding is, to our knowledge, new and important.

EOF analysis of the filtered, upper-ocean PV variability data showed the two leading EOFs consisted of changes in strength of the subtropical inertial recirculation zone and meridional displacements of the WBCE. These EOFs were both found to be strengthened significantly by coupling over the entire low-frequency spectrum. Such modes of variability have been seen frequently in QG models (Hogg et al. 2005; Berloff et al. 2007b) as they appear from the intrinsic low-frequency variability of the ocean gyres.

The ocean was found to respond in two possible ways to the east–west positive–negative dipole forcing over the basin: (1) weakening of the subtropical recirculation zone and shrinking of the respective gyre at a relatively fast $0-1$-year response time-scale; (2) a poleward meridional shift of the WBCE at a relatively slow 2–3-year response time-scale. However, the estimation of this response is uncertain with the associated correlation coefficients remaining at fairly similar levels over the entire range of computed time-lags. This is likely due to high levels of mesoscale turbulence that reduce ocean gyre predictability (Nonaka et al. 2016) and repeated positive feedbacks present in the modelled climate. The sensible and latent heat flux response associated with the meridional shift of the WBCE generated atmosphere diabatic forcings that reinforced the initial dipole forcing, and thus, reinvigorate the ocean gyre modes. Again, this is consistent with our findings of increased, broadband ocean gyre variability through coupling. The nature of this positive feedback between the ocean and atmosphere bears some resemblance to the interannual coupled interaction found by Goodman and Marshall (1999), Kravtsov et al. (2006) and Farneti (2007). This coupled interaction involves the westward propagation of coupled Rossby waves and enhanced interannual variability due to positive feedbacks. The time-scale of this interaction is found to be controlled by the basin crossing time of the ocean baroclinic Rossby wave. The coupled interaction in our model appears similar, with an initial ocean gyre response time-scale of 2–3-year which may be due to wave propagation, but positive feedbacks persist for up to much longer interdecadal time-scales. In addition, the atmospheric mode of the coupled interaction in our model appears to be a standing wave Rossby wave mode, rather than a phase-locked mode seen by Goodman and Marshall (1999), Kravtsov et al. (2006) and Farneti (2007). In fact, the coupled interaction observed in this paper more closely resembles the positive feedback found in more recent reanalysis data Taguchi et al. (2012) between the Subarctic Frontal Zone (SAFZ) and Pacific North American (PNA) pattern. This PNA pattern response to shifts in the SAFZ has also been verified in atmospheric GCMs (Tatebe et al. 2017; Okajima et al. 2018), albeit at a weaker magnitude, which is most likely due to the relatively low resolution of the models used. Similar responses have also been observed for Gulf Stream shifts in the North Atlantic using a high-resolution atmospheric GCM by Famooss Paolini et al. (2022). Their findings show a circulation response that is closer to observations.

The asymmetry in the atmosphere response, where the westerly jet is displaced less over the western basin and more over the eastern basin, is strongest in the lower-isopycnal layer due to the reduced momentum of the lower-isopycnal jet. The final pressure anomaly in the lower-isopycnal atmosphere is a barotropic circulation anomaly over the eastern basin. This asymmetry in the response is so much so that the lower-isopycnal pressure response is now also correlated to the modified westerly jet meridional shift mode. This mode was only detected after computing SVDs using data subsampled over the ocean basin region only, rather than the entire atmosphere. The structure of this westerly jet meridional shift EOF is different in structure to modes seen in Kravtsov et al. (2007) because it is less zonally symmetric.

The response of the atmosphere to meridional shifts in the SST front was also found to be dependent on the atmospheric resolution. For resolutions where the meridional scale of the shift is well-resolved, shifts in the low-level baroclinicity translate to a weaker inertial deflection of the jet over the SST front and a stronger inertial deflection of the jet downstream. The asymmetric inertial deflection of the jet is likely due to downstream organisation of the eddy-induced, line source of vorticity generated by the SST front shift. When the meridional scale of the SST front shift is poorly resolved, it is now unable to detect the changes in the low-level baroclinicity as well. So although an entrainment mode still exists, this mode is no longer controlled by meridional shifts of the WBCE, and the anomalous line source of vorticity is significantly weakened. Note that although the diabatic entrainment is still strengthened by the presence of the SST front which restores the low-level baroclinicity, the control of the variability is now handed over to the atmosphere, likely through a stronger dependence of the atmospheric response to the background flow state. This lack of atmospheric sensitivity to meridional shifts in the SST front at $80\,\text {km}$ resolution may be a contributing factor to why previous studies using this model struggled to capture many of these feedbacks of SST variability on the atmosphere (Hogg et al. 2006). Inability of atmospheric eddies to resolve shifts in the SST front may be a contributing reason to weaker-than-observed PNA responses observed by Tatebe et al. (2017), Okajima et al. (2018).

The results in this paper are also consistent to findings by Piazza et al. (2016), O’Reilly et al. (2017) where more realistic, sharper SST fronts lead to greater poleward excursions of the atmospheric jet. Greater poleward excursions of the jet have been explained by increased eddy heat fluxes due to a sharper SST front (O’Reilly et al. 2017). This then leads to a greater anomalous line source of vorticity which is advected downstream by the atmospheric jet.

Although Part I of this study has revealed the anatomy of delayed, wind-induced ocean gyre variability, we are yet to show the ocean processes driving the ocean gyre modes. We have proposed that certain patterns of ocean forcing activate modes of ocean gyre variability but exactly how they do this is still unclear and further analysis of the underlying dynamics is required. To do this, Part II of this study will require a series of ocean-only simulations run under fixed wind-stresses and thermal forcings to determine whether we are able to reproduce the effects of ocean entrainment observed in the coupled model. An analysis of ocean PV budgets will also be required to quantify the sources and sinks of PV within each of the gyres (see Kurashina and Berloff 2023, for details).

Appendices

Appendix 1: Breaking artificial symmetries in ocean forcing

It has been shown that QG ocean models with anti-symmetric wind-forcing show suppressed low-frequency behaviour (Berloff and McWilliams 1999a). In order to break the artificial symmetries in the ocean model forcing we made two adjustments to the model. Firstly, we shifted the ocean basin south by 480 km, which corresponds to 10% of the basin width. This creates a smaller region of forcing over the subpolar gyre. Secondly, we added land orography located to the west of the ocean basin which is added to mimic a continental land mass, such as the North American continent, and deflect the axis-tilt of the atmospheric jet poleward over the ocean basin. The addition of land orography, which is built-in to the model, is denoted $^aD(x,y)$ and is prescribed as a cosine hat

$$\begin{aligned} {}^aD(x,y)=500\,\cos \left( \frac{\pi (x-x_c)}{2r_0}\right) \text { m} \text { , if } \Vert x-x_c\Vert <r_0 \end{aligned}$$

(13)

where $x_c=9060$ km is the central longitude of the land mass and $r_0=3900$ km determines its width.

Appendix 2: Partially-coupled experiments

The coupling parameter $X_C$ controls the strength of the coupling between the atmospheric mixed layer and atmosphere. More specifically, $X_C$ adjusts the layer-1 entrainment through the the following term (FIg. 14):

$$\begin{aligned} {}{^ae_1} = \frac{X_CF^{\uparrow }+(1-X_C)\overline{F^{\uparrow }}}{^a\rho {}{^a}C_p\Delta _1^aT} \end{aligned}$$

(14)

where $F^{\uparrow }$ is instantaneous diabatic heating and $\overline{F^{\uparrow }}$ is the time-averaged diabatic heating obtained from a fully-coupled simulation.

Appendix 3: Modelled wind-stresses for benchmark modelled climate

Fig. 14

Unfiltered ocean surface stresses for benchmark modelled climate in statistical equilibrium. Top and bottom panel rows correspond to instantaneous and time-averaged fields, respectively. a, b Zonal ocean surface stress. c, d Meridional ocean surface stress

The time-averaged wind-stress is largely zonal with strong eastward wind-stresses focused in a fairly narrow band that sits predominantly over the subpolar gyre (Fig. 14). The meridional wind-stress has time-averaged stresses of just over a quarter in magnitude of the zonal wind-stress with an average forcing in the poleward direction. This is associated with the addition of land orography west of the ocean basin which creates a mean flow that has a poleward wind-stress component. This figure has been retained for the purposes of Kurashina and Berloff (2023) where the time-averaged wind-stresses are used to define the forcing for an ocean-only configuration of Q-GCM.

Appendix 4: Reduced atmospheric resolution parameters

See Table 3.

Table 3 Parameters for the channel atmosphere model in reduced atmospheric resolution modelled climate. Parameters that are different from the benchmark atmospheric model have an asterisk * added next to the value