Abstract
Given paleoclimatic evidence that the Atlantic Meridional Overturning Circulation (AMOC) may affect the global climate system, we conduct model experiments with EC-Earth3, a state-of-the-art GCM, to specifically investigate, for the first time, mechanisms of precipitation change over the Euro-Atlantic sector induced by a weakened AMOC. We artificially weaken the strength of the AMOC in the model through the release of a freshwater anomaly into the Northern Hemisphere high latitude ocean, thereby obtaining a ~ 57% weaker AMOC with respect to its preindustrial strength for 60 model years. Similar to prior studies, we find that Northern Hemisphere precipitation decreases in response to a weakened AMOC. However, we also find that the frequency of wet days increases in some regions. By computing the atmospheric moisture budget, we find that intensified but drier storms cause less precipitation over land. Nevertheless, changes in the jet stream tend to enhance precipitation over northwestern Europe. We further investigate the association of precipitation anomalies with large-scale atmospheric circulations by computing weather regimes through clustering of geopotential height daily anomalies. We find an increase in the frequency of the positive phase of the North Atlantic Oscillation (NAO+), which is associated with an increase in the occurrence of wet days over northern Europe and drier conditions over southern Europe. Since a ~ 57% reduction in the AMOC strength is within the inter-model range of projected AMOC declines by the end of the twenty-first century, our results have implications for understanding the role of AMOC in future hydrological changes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Atlantic Meridional Overturning Circulation (AMOC) plays a crucial role in the climate system by redistributing heat, carbon and salinity globally (e.g., Buckley and Marshall 2016; Weijer et al. 2019; Zhang et al. 2019; Srokosz et al. 2021; Jackson et al. 2023). In response to past changes in net radiation, it has been shown that the Earth’s climate experienced periods of rapid cooling that in several cases led to partial or total glaciation (e.g., Rahmstorf 2002, Clement and Peterson 2008). Abrupt changes in AMOC strength are believed to have substantially amplified these global temperature anomalies, if not led to them (Broecker 1997, Broecker 2003, Moffa-Sanchez et al. 2019). Idealized box models also support the hypothesis that the AMOC may exist in multiple states of equilibrium, specifically there would exist a state in which the AMOC is strong, similar to today’s climate, but also states in which the AMOC is much weaker or even reversed (Lenton et al. 2013; Johnson et al. 2019). Although multiple equilibria in the AMOC have not been directly observed, it is thought that in past climates the AMOC existed in a much weaker state, or even completely shut down, such as during Dansgaard-Oeschger events (e.g., Dansgaard et al. 1993; Burckel et al. 2015; Henry et al. 2016). Further, proxy records corroborate that global patterns of abrupt past climate change reflect variability in the AMOC, especially for the Younger Dryas and many of the Heinrich events (see Lynch-Steglitz et al. 2017 for a complete overview, and references therein).
In response to increasing concentrations of greenhouse gases, climate models simulate a steady decline in the strength of the AMOC; however, the amount, the rate and the effects of this decline are highly uncertain across models (Collins et al. 2013; Weijer et al. 2020; Bellomo et al. 2021; Lee et al. 2021; Fox-Kemper et al. 2021; Arias et al. 2021). Although simulations archived in the Coupled Model Intercomparison Project (CMIP) do not in general predict a shutdown of the AMOC, even when forced with quadrupled concentration of CO2 with respect to the preindustrial climate (Bellomo et al. 2021), it has been hypothesized that models may overlook this possibility (Liu et al. 2017). In fact, some recent studies have shown that AMOC’s strength may be at its weakest in the last millennium (Rahmstorf et al. 2015; Caesar et al. 2021; Thornalley et al. 2018), while numerous research efforts investigate potential precursors of an AMOC shutdown (Caesar et al. 2018; Jackson et al. 2020) and early warning signals (Jackson and Wood 2020; Boers et al. 2021). Direct observations of AMOC strength are too short to corroborate an hypothetical AMOC shutdown, in fact some recent work questions a declining trend (e.g., Worthington et al. 2021). The collapse of the AMOC is nevertheless considered a ‘low-likelihood, high-impact’ outcome (e.g., Arias et al. 2021), thus understanding its impacts relative to those of global warming is of utmost importance.
To investigate the potential impacts of an AMOC shutdown, previous studies have performed coupled climate model simulations in which the AMOC is artificially weakened through the release of freshwater into the North Atlantic or Arctic Oceans. These experiments are typically referred to as ‘water hosing’ simulations, and have been carried out both in preindustrial background conditions, or in conjunction with rising concentrations of greenhouse gases (e.g., Manabe and Stouffer 1997, Zhang and Delworth 2005, Dahl et al. 2005, Jacob et al. 2005, Levermann et al. 2005, Stouffer et al. 2006, Vellinga and Wood 2008, Brayshaw et al. 2009, Kuhlbrodt et al. 2009, Woollings et al. 2012a, Woollings et al. 2012b, Jackson et al. 2015, Liu et al. 2020). These studies have mainly focused on the seasonal or annual mean climate response, finding similar results in independent models. In all previous studies, following collapse of the AMOC or a significant weakening, the models simulate a widespread cooling in the Northern Hemisphere, which is only slightly compensated by a moderate warming in the Southern Hemisphere, especially in the South Atlantic. The cooling at the Earth’s surface is accompanied by precipitation decrease in the Northern Hemisphere, especially in the Atlantic sector and over Europe (Jackson et al. 2015).
Previous modeling experiments showed that a weakened AMOC causes a reduction in northward ocean heat transport (OHT), which is compensated by an increase in northward atmospheric heat transport (AHT). The increase in AHT is accomplished through an intensification of the northern branch of the Hadley cell. As a consequence, models also simulate a southward shift in the annual mean ITCZ, which migrates towards the Southern Hemisphere (e.g., Kang et al. 2008, Vellinga and Wood 2008, Frierson et al. 2013, Marshall et al. 2014). Prior model experiments also showed a strengthening and eastward extension of the Atlantic eddy-driven mid-latitude jet stream, which corresponds to an increased storm activity over the European continent (Brayshaw et al. 2009, Woollings et al. 2012a). These studies found that enhanced and eastwardly displaced storm tracks are due to an increased meridional temperature gradient south of the British Isles, leading to increased baroclinic instability, which fuels storm development. In addition, in water hosing experiments the subtropical high strengthens, whereas no significant changes in the Icelandic low occurs, thus suggesting an increase in North Atlantic Oscillation positive phase (NAO+) events (Jackson et al. 2015), although a previous study by Brayshaw et al. (2009) found no statistically significant changes in the frequency of the NAO.
While previous studies focused on the mean climate response to an AMOC collapse, the impacts at daily timescales remain unknown. To address this question, we perform water hosing simulations with EC-Earth3, a state-of-the-art climate model participating in the Coupled Model Intercomparison Project phase 6 (CMIP6; Eyring et al. 2016). Here we investigate mechanisms of precipitation change in the model at daily timescales in boreal winter (DJFM) and over the Euro-Atlantic sector through an analysis of the atmospheric moisture budget and of weather regimes.
2 Data and methods
2.1 Model and experimental design
We carry out model experiments with EC-Earth3, a state-of-the-art GCM participating in the CMIP6 archive and developed by a consortium of European research institutions (Döscher et al. 2022). EC-Earth3 includes the ECMWF IFS cy36r4 atmospheric model, the land-surface scheme H-TESSEL (Balsamo et al. 2009), the NEMO 3.6 ocean model (Madec 2015) and the LIM3 sea-ice component (Rousset et al. 2015). The OASIS3-MCT coupler version 3.0 exchanges fields between the model components (Craig et al. 2017). We use the standard resolutions of TL255L91 for the atmosphere and ORCA1L75 for the ocean (same as in CMIP6). These settings correspond to an atmospheric horizontal resolution of ~ 80 km and 91 vertical levels, and an oceanic horizontal resolution of ~ 100 km and 75 vertical levels.
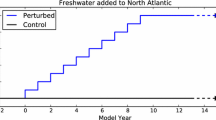
We run an experiment under preindustrial control conditions (hereafter referred to as ‘control’) for 150 years. In this experiment the external radiative forcing is fixed at the level of representative year 1850, thus all simulated climate variability is internally driven. We compare the control simulation with an experiment in which a freshwater anomaly of 0.3 Sv is uniformly added poleward of 50°N in the Atlantic and the Arctic oceans for 140 years (see Fig. 1). After this time, the hosing is halted and the model is left to freely evolve for an additional 70 years, for a total experiment length of 210 years. Hereafter, this experiment will be referred to as ‘water hosing’. We obtain the freshwater anomaly by applying a virtual salinity flux:
where S0 is the local salinity in the upper layer, dz0 is the upper layer thickness, and h is the water hosing field (\(h=\frac{H}{{A}_{R}})\). Here, the denominator (\({A}_{R}\)) is the area of the region in which the water hosing is applied (the North Atlantic and the Arctic in our case), while the numerator (H) is the strength of the freshwater flux anomaly (0.3 Sv = 0.3 \(\bullet\) 106 m3s−1). Then, the following water hosing correction is applied to conserve the total amount of salt throughout the rest of the ocean to the 3D salinity field:
which represents the total added flux divided by the total ocean volume (\({V}_{o})\).
We note that the strength of freshwater flux used in this study is deemed unrealistic: however, since current climate models are unable to reproduce AMOC bi-stability and might overestimate AMOC stability (Liu et al. 2017), similar to prior studies we apply a rather large freshwater hosing to force a much weaker AMOC and explore its impacts on the climate system. Note that this forcing has been tested in previous studies (Jackson and Wood 2018), and similar water hosing model simulations of EC-Earth3 were carried out as part of the North Atlantic Hosing Model Intercomparison Project (NAHosMIP, Jackson et al. 2023). In Jackson et al. (2023), the use and validity of water hosing experiments to investigate AMOC mechanisms is further discussed.
2.2 Response of the AMOC
Figure 2a shows the AMOC index in the experiments, defined as the annual mean maximum in the meridional overturning stream-function between 25.5°N and 27.5°N, and below 500 m. The dark purple curve is the AMOC index in the control simulation. The horizontal dark purple line represents the climatological mean value of the AMOC index, which over the span of the control simulation corresponds to 17.66 Sv. The light purple curve represents the AMOC index in the water hosing experiment. The horizontal light purple line represents the value corresponding to a 50% reduction in strength compared to the control climate (8.83 Sv). Also plotted in Fig. 2 is the ocean meridional mass stream-function in the Atlantic/Arctic sector of the control experiment (Fig. 2b), and the average of the years 100 -159 of the water hosing experiment (Fig. 2c). Years 100–159 in the water hosing experiment (shaded in Fig. 2a) are those in which the low-pass filtered (10 years running mean) AMOC index is more than 50% weaker than the control simulation. As expected, the stream-function associated with the AMOC circulation is much reduced in the water hosing experiment (Fig. 2c).
AMOC diagnostics. a The dark purple curve shows the timeseries of the AMOC strength in the control experiment, while the light purple curve shows the same index but in the water hosing experiment. Superimposed to annual mean values are 10 years running averages of the timeseries. b Mean of the ocean meridional overturning mass stream-function in the Atlantic/Arctic sector for the control experiment; c same as (b) but for the water hosing experiment averaged over the years 100–159 (corresponding to the filled light purple area in panel a). The AMOC strength in panel a is calculated as the maximum strength of the overturning meridional stream-function between 25.5°N and 27.5°N, and below 500 m
We note that similar to some other GCMs, EC-Earth3 does not simulate a steady decline in high-latitude surface temperature as the AMOC weakens due to hosing, but rather shows periods in which the Arctic warms (in particular, in the first 50 years). We advance an hypothesis for a possible physical mechanism responsible for this in the Supplemental Information (SI). However, here, since the focus is to investigate the effects of a weakened AMOC, for the water hosing experiment we analyze the years 100–159 (shaded in Fig. 2a) in which the AMOC is more than half weaker (< 50%) of its original mean strength. By making this choice, we eliminate from our analysis the possible effects of the transient warm anomalies and sea-ice decrease (fig. S1) on large-scale atmospheric circulation and precipitation patterns (see SI). This leaves us with an adequate sample size (60 years) to compute robust statistical significance against the control experiment at monthly and daily timescales.
2.3 Statistical significance
For all diagnostics, the anomalies are computed with respect to the mean control climate. We retain all 150 years of the control simulation for our calculations. We note that the AMOC (Fig. 2a) as well as global mean surface temperature exhibits centennial timescale fluctuations in EC-Earth3. Meccia et al. (2022) attribute the oscillatory behavior of the AMOC in the EC-Earth3 model to a self-sustained ocean variability. Enhanced OHT, and consequently increased sea-ice melting, are linked to a strong AMOC phase, leading to a build-up of freshwater anomalies in the central Arctic. This anomaly is then released by liquid freshwater transport through the Arctic boundaries, yielding to a freshening of the North Atlantic and a decrease in deep water formation and AMOC strength. A similar mechanism was found by Jiang et al. (2021) for the IPSL-CM6A-LR model, which shares the same ocean model (NEMO) as EC-Earth3, while self-sustained AMOC fluctuations also appear in intermediate complexity models (Mehling et al. 2022).
Centennial AMOC variability in the aforementioned studies is shown to have a large influence on subpolar temperature and sea ice anomalies. In our analysis, we average the control simulation over a period of 150 years, which covers a full AMOC oscillation. Hence, the influence of the centennial fluctuations on the computation of climatological means from the control run is not likely to affect our results. Moreover, the departure of the AMOC in the water hosing experiment from the mean control climate is much larger than the amplitude of the AMOC fluctuations (Fig. 2a). In fact, Meccia et al. (2022) estimated in a 2000 year long preindustrial control run of EC-Earth3 that the average amplitude of centennial fluctuations is ~ 3 Sv, while the departure of the hosed AMOC compared to the control AMOC strength in this study is more than 8.83 Sv.
We further account for the possible influence of the centennial AMOC fluctuations by performing statistical tests. To assess the statistical significance of the averages of the changes in the gridded anomalies (i.e., temperature, precipitation and moisture fields) in the years 100–159 of the water hosing experiment against the control mean climate, we compute averages of 30 years length taken from the control simulation, starting each one of them 5 years apart. Thus, we obtain for each grid point a distribution of 30 averages, which represent the estimated internal variability in the control run. We deem the anomaly in the water hosing experiment statistically significant if it exceeds 2 standard deviations of the distribution of the 30 averages computed from the control simulation. In the figures, we use hashes to indicate where changes are statistically significant according to this test. We tested whether significance is sensitive on the choice of period lengths of 30 years and starting 5 years apart, with different periods ranging from 20 to 60 years and starting them 2, 5, or 10 years apart. We found that our conclusions were not affected. We note that the initial AMOC strength from which the water hosing experiment is started from, may influence the time required by the water hosing to force a weakened AMOC state: however, here we do not focus on mechanisms and timescales of AMOC response to the water hosing forcing (c.f. Jackson et al. 2023), but on its impacts. Finally, although the water hosing anomalies are much larger than the model’s AMOC internal variability, we note that more ensemble members could help corroborate our findings.
2.4 Moisture budget
To investigate mechanisms of precipitation change, we compute the atmospheric moisture budget following D’Agostino and Lionello (2020). A similar moisture budget formulation can also be found in Seager et al. (2010), while a thorough derivation can be found in Trenberth and Guillemot (1995). The moisture budget (precipitation minus evaporation) for the control mean climate can be written as:
where P and E are the precipitation and evaporation respectively, u is the wind vector, q is specific humidity, p is pressure, \({\rho }_{w}\) is the density of water, and g is the standard gravity. Overbars indicate monthly means, while primes indicate sub-monthly variability. Subscript s indicates values at the surface. For all variables, we use daily data output. The first integral on the RHS of Eq. (3) is the convergence of moisture due to the mean flow, while the second integral on the RHS is the convergence of moisture due to the turbulent flow (transient eddies). We refer to the last term on the RHS as S: this term involves surface quantities representing the deformation of the surface moisture transport by the surface pressure gradient. By computing the moisture budget for both experiments using Eq. (3), the change in moisture budget in the water hosing experiment can be approximated as:
where \(\delta\) indicates the difference between the water hosing and the control experiment. \(\delta S\) is the term involving surface quantities, and tends to be significant in the presence of steep orography. In this analysis, all terms except \(\delta S\) are calculated explicitly. \(\delta S\) is computed as the residual of the other terms.
In the first integral on the RHS of Eq. (4), the contributions of thermodynamics can be separated from those of dynamics: all terms involving a difference in q but not in u are due to thermodynamic processes, while the terms involving a difference in u but not in q are due to dynamic processes. We can rewrite the moisture budget equation as:
where:
\(\delta TH\) and \(\delta DY\) represent the thermodynamic and dynamic contributions to the moisture budget, respectively. The transient eddies term \(\delta TE\) = \(-{\int }_{0}^{\overline{{p }_{s}}}\nabla \bullet \delta \left(\overline{{{\varvec{u}} }^{\boldsymbol{^{\prime}}}{q}^{^{\prime}}}\boldsymbol{ }\right)dp\) is computed as a covariance, thus it is not straightforward to split this contribution into thermodynamic and dynamic terms. As in previous studies, we leave it as is (c.f. Seager et al. 2010). In this study, because the nonlinear term \(\delta NL=-{\int }_{0}^{\overline{{p }_{s}}}\nabla (\delta \overline{q }\delta \overline{{\varvec{u}} })dp\) is small, we incorporate it with the term due to transient eddies. This term contains both thermodynamic and dynamic processes as well.
The term \(\delta TH\) (Eq. 6) represents the change in atmospheric moisture budget that is due to the change in vertically integrated mean humidity. It consists of two components: the first one is the advection of moisture \(\delta {TH}_{A}=-{\int }_{0}^{\overline{{p }_{s}}}\left(\boldsymbol{ }{\overline{{\varvec{u}}} }_{\mathrm{control}}\bullet \nabla \delta \overline{q }\right) dp\), and is related to the change in the humidity gradient (e.g., land-sea contrast) along the mean flow. The second component is defined as \(\delta {TH}_{D}=-{\int }_{0}^{\overline{{p }_{s}}}\left(\boldsymbol{ }\delta \overline{q}\boldsymbol{ }\nabla \bullet {\overline{{\varvec{u}}} }_{\mathrm{control}}\right) dp\), and is related to the change in mean humidity in areas of mean flow convergence (upward air motion) or divergence (downward air motion). The term \(\delta DY\) (Eq. 7) represents the change in atmospheric moisture budget that is due to the change in the mean flow. Similar to \(\delta TH\), it consists of two components: the first advective component \(\delta {DY}_{A}=-{\int }_{0}^{\overline{{p }_{s}}}\left(\delta \overline{{\varvec{u}} }\bullet \nabla \overline{{q }_{\mathrm{control}}}\right) dp\) is related to the change in mean wind flow in the presence of spatial gradients of humidity. The second component \(\delta {DY}_{D}=-{\int }_{0}^{\overline{{p }_{s}}}\left(\overline{{q }_{\mathrm{control}}}\boldsymbol{ }\nabla \bullet \delta \overline{{\varvec{u}} }\right) dp\) is the convergence or divergence of moisture due to the change in the mean flow. The terms of the moisture budget computed for the control climate of EC-Earth3 from Eq. (3) are consistent with previously published results, including residuals (e.g., Seager et al. 2010, D’Agostino and Lionello 2020), and will not be discussed here. A review of possible sources of errors in the computation of the moisture budget can be found in Seager and Henderson (2013). Finally, we note that the moisture budget framework does not take into account precipitation recycling (Brubaker et al. 1993). Precipitation recycling contributes to the moisture budget over land areas, and tends to be less important when considering large-scale processes such in the present study: it would be nonetheless possible in a future work to further disentangle mechanisms of precipitation changes over land using a moisture tracking formulation.
2.5 Weather regimes
To further characterize the mechanisms of precipitation change, we investigate the association of precipitation anomalies with wintertime (DJFM) Euro-Atlantic weather regimes (WRs) (e.g., Hannachi et al. 2017; Straus et al. 2017; Dawson et al. 2012). In our study, WRs are computed using clustering as described by Fabiano et al. (2020). Following their methods, we calculate WRs from daily geopotential height at 500 hPa (hereafter z500) in the Euro-Atlantic sector (30°N–90°N, 80°W–40°E). We obtain z500 daily anomalies (z500’) by removing the daily mean seasonal cycle smoothed with a 20-day running mean. Since WRs are related to large-scale atmospheric circulation, to reduce complexity arising from variability at small scales, we first compute the first 4 EOFs of the z500’, which explain ~ 55% variance in the control simulation.
We then apply K-means clustering on the principal components (PCs) associated with these EOFs to derive 4 cluster centroids. Each centroid corresponds to a WR. Each day in the control simulation is then assigned to the closest centroid based on the minimum Euclidean distance. We obtain patterns of z500’ associated with each WR by compositing over all days in each cluster. In agreement with a large number of previous studies (e.g., Vautard 1990; Michelangeli et al. 1995; Cassou 2008; Dawson et al. 2012; Strommen et al. 2019; Fabiano et al. 2020), we set the a priori number of centroids (i.e., WRs) to be 4, corresponding to the positive phase of the North Atlantic Oscillation (NAO +), Scandinavian Blocking (SBL), negative phase of the North Atlantic Oscillation (NAO−), and Atlantic Ridge (AR). The z500’ composites associated with each WRs in the control simulation are shown and discussed in Sect. 3.4. Fabiano et al. (2020) found that all climate models show biases in the simulation of WRs in the historical period, nevertheless WRs are quite consistent with reanalyses. EC-Earth3 was found to lie well within the inter-model spread (Fabiano et al. 2021).
We compute WRs in the water hosing experiment assigning each day to one of the 4 centroids obtained from the control simulation. The z500’ in the water hosing experiment are obtained with respect to the control climatology. To avoid the chance that changes in the WRs in the water hosing simulation are caused by a change in z500, rather than changes in variability, we linearly detrend the northern hemisphere z500 at each grid point (c.f. fig. S3), although we note that detrending does not alter our results. The z500’ anomalies are then projected onto the 4 EOFs computed from the control simulation, thereby producing 4 pseudo-PCs. Each day in the water hosing experiment is then assigned to a centroid based on the minimum Euclidean distance between the 4 pseudo-PCs and the control centroids. Statistical significance of the difference in the number of days and persistence in each WRs with respect to the control simulation is computed using the 99% probability threshold of the Welch’s t-test.
We note that to test the robustness of our choices, we tried setting the variance explained by the EOFs to be 80% in the control experiment to obtain the reduced dimensionality space, instead of choosing the a priori number of EOFs to be 4. With this choice, we obtain a total number of 12 EOFs, but we find that our results are not affected. Here, WRs in the water hosing experiment are computed using the control climatology as reference to compare the changes in atmospheric circulation patterns with respect to the control experiment. Computing WRs in the water hosing experiment using the water hosing climatology itself as reference, leads to largely similar WRs patterns. However, the question of how the spatial patterns may change in the new water hosed climate is not specifically addressed here.
3 Results
3.1 Changes in the annual mean climate
Figure 3 depicts an overview of annual mean changes in the global climate associated with the artificially weakened AMOC strength in the EC-Earth3 model. Due to the AMOC weakening, the global near-surface air temperature cools by an average of − 1.09 °C. Most of the cooling occurs in the Northern Hemisphere, which experiences an average decrease in temperature of − 2.09 °C. Regional warming in the Southern Hemisphere, such as in the South Atlantic Ocean, partially compensates, resulting in a weaker cooling of only − 0.10 °C. Changes are largest in the Northern Hemisphere in winter with a cooling of − 2.42 °C (c.f. fig. S4). Figure 3c shows the annual mean precipitation change, while Fig. 3d shows the zonal mean precipitation climatology (black curve) and the zonal mean precipitation change (blue curve). Precipitation decreases over most of the Northern Hemisphere, especially over the North Atlantic, while tropical precipitation exhibits a southward shift in the zonal mean annual mean Intertropical Convergence Zone (ITCZ) (Fig. 3d). For completeness, fig. S4 shows maps of near-surface temperature and precipitation changes in boreal winter and summer.
Annual mean changes (water hosing minus control). a Change in near-surface air temperature, hashes indicate statistical significance; (c) same as (a) but for precipitation; (b) change in atmospheric zonal mean meridional stream-function. In b the control climatology is superimposed in contours; (d) zonal mean precipitation change: in black the control climatology, in blue the water hosing anomaly
The southward shift of the ITCZ (Fig. 3d) corresponds to an intensification of the northern branch of the Hadley cell that expands towards the south in the annual mean (Fig. 3b). The zero crossing of the ascending branch of the annual mean Hadley cell at 700 hPa in the control simulation occurs at 4.5°N, while in the water hosing experiment it migrates towards the Southern Hemisphere and occurs at 1°S. Sea level pressure (SLP) generally increases over the Euro-Atlantic sector (fig. S5), while it decreases over the Southern Hemisphere. The resulting change in the pressure gradients modifies the surface winds, resulting in a clockwise circulation anomaly over the Icelandic low and a slightly stronger clockwise circulation over the subtropical high. Cross-equatorial surface wind anomalies are evident throughout the tropics and consistent with the southward shift of the Hadley cell and the zonal mean ITCZ.
These findings largely agree with previous work, corroborating the important role of OHT by the AMOC in regulating tropical precipitation patterns through its influence on AHT and the position of the annual mean Hadley cell north of the equator (e.g., Zhang and Delworth 2005, Kang et al. 2008, Frierson et al. 2013, Marshall et al. 2014, Vellinga and Wood 2008). After confirming that our model experiments agree with similar experiments in the literature, in the following sections we focus our analysis on previously unexplored mechanisms of wintertime (DJFM) precipitation changes in the Euro-Atlantic sector.
3.2 Analysis of precipitation anomalies
Figure 4 shows the change in winter precipitation (Fig. 4a), evaporation (Fig. 4b) and net precipitation (Fig. 4c), here defined as precipitation minus evaporation. Given the large reduction in vertically integrated atmospheric moisture (Fig. 4d), we may expect a decrease in net precipitation. Instead, because the decrease in evaporation (Fig. 4b) is much larger than the decrease in precipitation over the mid-latitude North Atlantic Ocean, the net precipitation locally increases. We note that despite the overall drying, there is a small region off the coasts of western Europe where the precipitation anomaly is slightly positive (Fig. 4a). Net precipitation is also slightly positive over the UK, Ireland and some regions over continental western Europe (Fig. 4c). This suggests that in some areas there is an increase in precipitation anomalies, albeit very small. In Fig. 4c we plot 3 boxed areas, which indicate representative regions that we will examine in more detail. We name these regions: ‘NWEU’ (Northwestern Europe), ‘NEEU’ (Northeastern Europe), and ‘SWEU’ (Southwestern Europe). We choose these boxes over more common regions used in the IPCC reports (Iturbide et al. 2020) because they encompass uniform changes in precipitation anomalies over land, and we will show that precipitation change in each region is associated with the same drivers.
Precipitation and moisture anomalies (water hosing minus control). a Precipitation change in the Euro-Atlantic sector in DJFM; (b) same as (a) but for evaporation; c same as (a) but for net precipitation (precipitation minus evaporation); d Vertically integrated change in humidity (shading) and humidity transport (vectors) in DJFM. In all panels, hashes indicate statistical significance. Contours in panel c highlight regions of positive and negative anomalies, and range from − 2.4 to 2.8 mm/day with intervals of 0.4 mm/day
To characterize the precipitation increase that we notice in some regions in the Euro-Atlantic sector at daily timescales, we compute the change in the number of wet days exceeding the 75th percentile of daily precipitation between the water hosing experiment and the control simulation in DJFM. First, we compute for each grid point the 75th percentile of the precipitation anomalies in the control simulation (Fig. 5a). Then, we count the number of days exceeding the 75th percentile threshold at each grid point in the water hosing simulation. In Fig. 5b we show the change in the number of days between the water hosing experiment and the control climate. Although there is widespread moisture deficit in the water hosing experiment (Fig. 4d), Fig. 5b shows that the number of wet days increases in some regions, particularly off the coasts of northwestern Europe. We note that the number of wet days also increases over northern Africa and on the central and eastern side of the continental U.S, although we do not examine these further.
3.3 Mechanisms of precipitation change
The amount of moisture in the atmosphere is thermodynamically constrained by the Clausius-Clapeyron relation (e.g., Held and Soden 2006). Hence, from thermodynamic considerations alone the colder air temperature caused by the decline in the AMOC would be responsible for a decrease in the overall precipitation, as previously hypothesized (e.g., Jackson et al. 2015). However, precipitation exhibits a more complex pattern of change. Specifically, there exist regions that experience an increase in anomalously wet conditions during winter despite the overall mean drying, as shown in Fig. 5. This indicates that there is an interplay of thermodynamic and dynamic processes responsible for precipitation changes. Here we investigate the relative role of each of these mechanisms using the moisture budget framework (as described in detail in the “Methods” section).
Figure 6 shows the relative contributions of each term in the moisture budget to the change in net precipitation δ(P-E) (Fig. 4c). The influence of the thermodynamic term δTH (Fig. 6a) is scattered over the European continent: it contributes to wetter conditions over the Iberian peninsula, southern Europe and the northern coasts of Scandinavia. Over the rest of the European continent, the contribution of δTH is less clear. Over the ocean, δTH is more uniformly distributed, showing a zonal dipole of wet/dry change in the west/east mid-latitude North Atlantic Ocean. δTH contributes to dry also some regions located off the coasts of France, the British Isles and Scandinavia.
Moisture budget (DJFM). Change due to (a) thermodynamic, (b) dynamic, (c) transient eddies plus nonlinear, and (d) surface processes. All terms sum up to the change in net precipitation (Fig. 4c)
Recalling Eq. (6), we plot the individual contributions of \(\delta TH\) in Fig. 7a, b. The \({\delta TH}_{D}\) term (Fig. 7b) shows a clear increase in the moisture budget by the mean divergent flow in the subtropics. The divergent flow in the control climate tends to dry the subtropics, but since the moisture deficit is larger upstream of the atmospheric flow in the eastern side of the North Atlantic when the AMOC is weakened (Fig. 4d), in the presence of this gradient the overall effect downstream towards the regions of convergence (i.e., ITCZ) is an enhancement of the moisture budget. \({\delta TH}_{D}\) also explains the drying off the coasts of France, the British Isles and Scandinavia. The wet/dry contrasts between these coasts and the adjacent seas seem to be related to a change in land-sea breeze. Above 45°N over the oceans, \({\delta TH}_{A}\) dominates the sign of \(\delta TH\) because the moisture field shows a larger decrease in the eastern side of the North Atlantic basin compared to the western side (Fig. 4d), hence the advection is reduced towards the eastern side, and an increase in the moisture budget is favored on the western side of the ocean basin. Over the European continent both \({\delta TH}_{A}\) and \({\delta TH}_{D}\) contribute to the overall scattered pattern, with \({\delta TH}_{A}\) generally favoring wetter conditions due to the change in the moisture gradient (Fig. 4d) and the land/sea contrast with the Mediterranean Sea.
The dynamic term δDY contributes to a moistening of central and northern Europe, moderate drying of southern Europe, and moistening of the southeastern United States. From Eq. (7), the dynamic term can also be split into advective (\({\delta DY}_{A}\)) and divergent (\({\delta DY}_{D}\)) terms, which are shown in Fig. 7c, d, respectively. Both \({\delta DY}_{A}\) and \({\delta DY}_{D}\) contribute to moister conditions over northern Europe, however, the drying over southern Europe is due mainly to the divergent contribution, indicating a possible connection with the southward shift of the ITCZ. We note that the combination of the dynamic and thermodynamic terms fails to fully account for the precipitation deficit over Europe. Instead, Fig. 6c shows that the transient eddies term (δTE + δNL) provides a uniform drying contribution throughout the European continent, and a moistening offshore, between the coasts of northern Europe and Greenland.
In Fig. 8, we compute averages of each moisture budget term in the 3 representative regions of precipitation change (boxed in Fig. 4c), considering only grid points over land. Over Southwestern Europe (SWEU) we see a reduction in δ(P-E), which is contributed by the dynamic and transient eddies term, while the thermodynamic and surface terms oppose the change. Over Northwestern Europe (NWEU), the slight increase in δ(P-E) is largely due to the dynamic term, while the thermodynamic and transient eddies would favor drier conditions. In Northeastern Europe (NEEU), the reduction in δ(P-E) comes from the thermodynamic and transient eddies term, while the dynamic term would again favor increased net precipitation. In all cases, δTE is responsible for drier continental conditions, while δDY contributes to increased moisture budget over northern Europe. Figure 8 also shows error bars estimated by calculating the standard deviation of the moisture budget computed separately for 6 consecutive and non-overlapping 10 years long periods of the water hosing experiment over the years 100–159 (same period analyzed throughout the analysis). This helps us estimate uncertainty in the computation of the moisture budget, although internal variability is large at decadal timescales and longer integrations would provide us with better uncertainty estimates. Finally, we note that the surface term δS (Fig. 6d) reflects the effect of the wind circulation around boundary conditions, such as orography over land, while over the ocean it retains the sign of the largest term in our calculations (i.e., δTE). While this term contributes to the overall budget, it is of difficult interpretation since it is calculated as a residual (see Eq. 3).
Moisture budget in selected regions. Each bar indicates the averaged contribution of each term over the boxed regions in Fig. 4c. Red colors indicate positive values, while blue colors indicate negative ones. Averages are computed taking into account only grid points over land. Error bars are estimated by calculating the standard deviation of the moisture budget (see main text for further details)
In Fig. 9 we show changes in dynamic atmospheric variables to help elucidate the role of δDY and δTE in driving moisture budget changes. Enhanced precipitation over northern Europe is consistent with an eastward extension of the jet-stream and enhanced wind speed at upper-levels (Fig. 9a), which explain the term δDY (see also fig. S6). We see an increase in the frequency of storm tracks (Fig. 9b), which also exhibit a slight southeastward extension towards the European continent. The enhancement of the storm tracks is in apparent contradiction with the sign of δTE, considering that more storms would imply larger precipitation anomalies over land, whereas the contribution of δTE is to dry the continent (c.f. Fig. 6c). The opposite effect of storm tracks over Europe, where they dry, and over the ocean, where they enhance moisture, is due to the pattern of evaporation change and moisture transport (Fig. 4). Because over the ocean the decrease in evaporation exceeds the decrease in precipitation, storms are more intense and enhance the moisture budget. Instead, over land the precipitation deficit is larger than evaporation, hence storms are more intense but drier.
To conclude, enhanced wind speed together with a moisture deficit explain the pattern of net precipitation changes over Europe. Although the effect of δTH per se is scattered over the European continent, its indirect effect on storm activity causes the decrease in precipitation over land. The increase in the number of wet days in some regions (above the 75th percentile, Fig. 5) is explained by the enhanced storm track activity and wind speed (δDY). Over the ocean, the δTE is the dominating factor in explaining the overall δ(P-E), whereas over the European continent δDY explains the wetter conditions over the northern parts of western Europe, while both δDY and δTE explain the drier conditions over southern Europe. We now further investigate how these precipitation mechanisms may be related to changes in atmospheric circulation patterns at daily timescales.
3.4 Changes in weather regimes
From the moisture budget analysis, we find that the dynamic contributions (i.e., δDY and δTE) to precipitation change play a crucial role in determining δ(P-E). Hence to better understand the origin of the dynamic terms, we now investigate changes in daily weather regimes (WRs) and their association with precipitation patterns. We use the methodology developed by Fabiano et al. (2020) and described in the “Methods” section, to compute the 4 most dominant wintertime WRs. The first 4 WRs in the control climate are plotted as composites in Fig. 10. We note that percent values in Fig. 10 refer to the average fraction of days in each regime in DJFM computed over the 150 years of the control climate. The first WR corresponds to the positive phase of the NAO (NAO +), which in the control simulation occurs 26.66% of the time in winter. The second WR is the Scandinavian Blocking (SBL) pattern, occurring with a frequency of 25.09%. The third WR is the negative phase of the NAO (NAO−), which resembles the NAO + but with opposite polarities, and occurs 24.75% of the time. The fourth WR is the Atlantic Ridge (AR) with a frequency of occurrence of 23.49%.
Weather regimes in the control simulation. WRs obtained through clustering. Indicated in %, the average fraction of days assigned to each regime in DJFM: a North Atlantic Oscillation (positive phase), (b) Scandinavian Blocking, (c) North Atlantic Oscillation (negative phase), (d) Atlantic Ridge (AR)
Figure 11 shows the WR frequency in DJFM in the two experiments, where the boxplots span 25th to the 75th percentiles and the whiskers the 10th to the 90th percentiles of the frequency distributions. The colored dots and horizontal lines in each boxplot are the mean and median, respectively. Here the mean control values (blue dots) correspond to the average percent frequency reported in the captions of the panels in Fig. 10. While the mean frequency of the other WRs regimes decrease in the water hosing experiment, the average frequency of NAO + grows from 26.66% to 42.85%. Table S1 reports the change in the mean frequency for all WRs, and the values associated with the boxplots in Fig. 11. Except for AR, the changes in the frequency of occurrence of the other WRs are statistically significant.
Weather regimes frequency distributions. a NAO + : colored dots indicate mean values, horizontal lines indicate median values, boxes span the inter-quantile range, while whiskers span the 10th–90th percentiles of the distribution; (b) same as (a) but for SBL; (c) same as (a) but for NAO−; (d) same as (a) but for AR. Stars under the water hosing boxes indicate whether the change is statistically significant according to the Welch’s t-test at the 99% probability threshold
The average persistence of days within each WRs is plotted in Fig. 12 for the control simulation and the water hosing experiment. In our calculation, persistence is defined as the number of consecutive days in which z500’ are clustered within the same regime. The anomaly needs to persist for at least two consecutive days in another regime to be reassigned to a new regime. The average persistence of NAO + changes from 5.0 days to 6.8 days, with the inter-quartile range changes from 2–6 days to 2–9 days. The 90th percentile changes from 11 to 15 days, suggesting an increase in extreme events associated with NAO + . The average persistence in the other WRs decreases. We note that the change in the persistence is statistically significant for all WRs, except again for AR. Table S2 reports statistics associated with the boxplots in Fig. 12. Notably, all mean values related to NAO + increase, while they decrease for the other WRs.
Weather regimes average persistence. a NAO + : colored dots indicate mean values, horizontal lines indicate median values, boxes span the inter-quantile range, while whiskers span the 10th–90th percentiles of the distribution; (b) same as (a) but for SBL; (c) same as (a) but for NAO−; (d) same as (a) but for AR. Stars under the water hosing boxes indicate whether the change is statistically significant according to the Welch’s t-test at the 99% probability threshold
Because the change in NAO + occurrence is much larger than the other WRs, and the NAO is also the regime that explains most of the wintertime precipitation anomalies in reanalyses (Seager et al. 2020), in Fig. 13 we show composites of precipitation anomalies associated with NAO + in the control (Fig. 13a) and water hosing (Fig. 13b) experiments. The precipitation composites relative to the other WRs are shown in supplemental fig. S7. The composite of precipitation anomalies during days classified as NAO + in the control simulation (Fig. 13a) resembles the well-known pattern of precipitation anomalies that we expect from a reinforcement of the Icelandic low pressure and Azores high pressure systems, which push the mid-latitude jet stream towards higher latitudes, thus promoting wetter conditions in northern Europe and drier conditions over southern Europe.
If we compare this composite with the composite obtained from the water hosing experiment for NAO + (Fig. 13b), we see an overall drying associated with the mean temperature decrease. However, we can clearly see increased precipitation located downstream of the enhanced mid-latitude jet stream (Fig. 9a), which promotes wet conditions over northwestern Europe. The precipitation anomalies associated with NAO + in the water hosing experiment are remarkably consistent with the anomalies associated with the dynamic term in moisture budget (Fig. 6b) and with the regions where we find an increase (or zero change) in the number of wet days (Fig. 5b). This indicates that in the water hosing experiment a more prevalent NAO + in winter, both in terms of frequency of occurrence and persistence, contributes to increase the precipitation anomalies associated with the dynamic term in the moisture budget. In contrast, the reduction in NAO- days is associated with a reduction in wet anomalies over southern Europe and of dry anomalies over northern Europe (fig. S7), also consistent with δDY.
4 Discussion
The impacts of a weakened AMOC in the annual mean climate found in this study largely resemble those in previous studies using different climate models and with various degrees of AMOC strength declines. For example, one of the most recent studies (Jackson et al. 2015) used HadGEM3 with a higher resolution than in our study (~ 60 km in the atmosphere) and obtained a ~ 2.5 °C global mean cooling with a much weakened AMOC strength (~ 2/3 Sv) at 26.5°N. For comparison, we obtain a reduction in global mean temperature of − 1.09 °C, but with a weaker AMOC decline (average of 7.55 Sv for 60 years). Despite the difference in the AMOC weakening, in both studies the North Atlantic is the region exhibiting the strongest cooling and there is a global southward shift in the ITCZ. The jet speed is enhanced and the jet is found to extend eastward towards Europe. Also, the storm tracks are enhanced in both studies (also in Brayshaw et al. 2009).
Woollings et al. (2012a) analyzed a water hosing experiment together with simulations from the CMIP archives finding that the storm track response to the AMOC decline is consistent across models and related to the AMOC strength, in support of the present study. Bellomo et al. (2021) also found a correlation between the amount of AMOC decline and the mid-latitude upper level jet stream, which is closely linked to changes in the storm tracks at mid-latitudes. Jacob et al. (2005) examined ECHAM5 coupled to MPI-OM together with a regional climate model to specifically investigate climate impacts over Europe. They found that in response to an AMOC weakening, the maritime influence on the European climate is larger compared to today’s climate, but also brings cooler conditions because the sea surface temperature cools. In agreement with Jacob et al. (2005), we find an enhanced influence of the ocean on the European continent driven by changes in the jet-stream and storm tracks (also supported by the findings in Brayshaw et al. 2009). Overall, we can conclude that for all of the above mentioned aspects, the results obtained with the EC-Earth3 model lie well within the simulated response to an AMOC suppression found in previous studies.
Our results are also consistent with the models analyzed in Stouffer et al. (2006), who presented an inter-model comparison of water hosing experiments carried out by both GCMs and earth system models of intermediate complexity (EMICs). As mentioned earlier, in some of the models analyzed by Stouffer et al. (2006) there is a partial recovery of OHT and northward migration of the deep water formation sites in the transient AMOC response, as in EC-Earth3. A study by van der Berk et al. (2021) using EC-Earth2.2 also finds that enhanced convection in the Nordic Seas can inhibit the effect of the water hosing on the AMOC strength.
However, ours is the first study that explicitly calculates changes in the atmospheric moisture budget and WRs in a water hosing experiment. Jackson et al. (2015) examined mean SLP change following a collapse of the AMOC in the HadGEM3 model. They argued that winter SLP changes and the strengthening of the storm tracks suggest a mean state that looks more like the positive NAO, although they did not calculate a NAO index explicitly. An earlier study by Brayshaw et al. (2009) investigated the impacts of an AMOC collapse in another version of the Met Office unified model, HADCM3. Using EOF analysis and stationary box indices methods they found no significant changes in the variability of the NAO, although they found that changes in the mean flow project onto the NAO + phase, similar to our results and Jackson et al. (2015). Brayshaw et al. (2009) found an eastward extension of the NAO pattern in the AMOC collapse run, which is consistent with our analysis of SLP change (fig. S5). However, we must take into consideration the fact that using WRs as in the present study is quite different than isolating the NAO using the methods used in Brayshaw et al. (2009). In fact, computing the NAO by using EOFs isolates the mode of variability that explains most of the variance on inter-annual timescales, which includes coupling with the ocean. The use of WRs instead better isolates atmospheric patterns at daily timescales, hence the two methods are not directly comparable.
For what concerns the impacts of NAO on precipitation, Seager et al. (2020) analyzed the ERA-Interim reanalysis over the years 1979–2017 to investigate mechanisms of precipitation variability in winter over Europe. They found that the positive phase of the NAO index is associated with wet anomalies over the British Isles and Scandinavia, and dry anomalies over southern Europe. They applied a moisture budget decomposition, and found that precipitation anomalies associated with the NAO are mainly driven by the mean flow moisture convergence anomalies, and offset by transient eddies moisture fluxes. Although in our context we specifically investigate the impacts of an AMOC weakening, we find an increase in the NAO + events together with an enhancement of wet anomalies over the British Isles and Scandinavia. In our case, the terms δDY explained the increase in wet anomalies, while δTE opposed it over those regions. Therefore, our results are consistent with the mechanisms found by Seager et al. (2020) for inter-annual variability.
Some of the impacts of a weakened AMOC on the aspects that we investigated here could also be partly consistent with impacts related to Atlantic Multidecadal Variability (AMV) or variability in models in which the AMOC exhibits enhanced multidecadal or centennial variability. An interesting parallel with the results obtained here could also be made with studies investigating the response of WRs to future climate change. Fabiano et al. (2021) examined WRs in historical simulations and future projections in the CMIP5 and CMIP6 archives, showing that models project an increase in NAO + frequency and persistence. They found a decrease in the SBL and AR regimes, and a slight increase in the NAO− phase. This indicates that except for the NAO−, the influence of future climate change on WRs has the same sign as the influence of an AMOC decline. Fabiano et al. (2021) further note that the increase in NAO + is consistent with a contraction of the mid-latitude jet towards the central position (see also Peings et al. 2018; Oudar et al. 2020). Moreover, Bellomo et al. (2021) and Woollings et al. (2012a) found a strong influence of the AMOC on the position of the jet in projections of future climate change. Hence, we argue that the response of WRs in future scenarios could be influenced by the decline of the AMOC in addition to feedbacks related to the increase in greenhouse gases. In this study, we specifically assessed the role of a weakened AMOC in a preindustrial climate setting, but we suggest that the role of a weakened AMOC in future climate change especially regarding the aforementioned aspects should be further investigated with ad-hoc model experiments.
Finally, we note that horizontal resolution may influence the results presented herein. Fabiano et al. (2020) compared standard and higher resolution of the models participating in PRIMAVERA, including EC-Earth3. While higher resolutions generally lead to improved representation of WRs, they point out that other biases, such as mean SSTs and geopotential fields, may also contribute to the models’ ability in reproducing realistic WRs. The impact of the ocean model resolution may also affect the pathways and adjustment processes in the transient response of the AMOC to the water hosing (e.g., Jackson et al. 2020; Mecking et al. 2016; Swingedouw et al. 2022). Higher resolutions in both the atmosphere and the ocean influence the air-sea interactions, ultimately affecting precipitation impacts, especially over coastal areas or complex topography (e.g., Tsartsali et al. 2022; Bellucci et al. 2021; Haarsma et al. 2019). Reproducing these experiments with higher model resolution and in different models could thus help us gain further insights and advance the results of this study.
5 Conclusions
Previous studies investigated the global and regional impacts of a possible AMOC collapse by artificially weakening the AMOC strength through the release of a freshwater anomaly into the North Atlantic and Arctic (e.g., Jackson et al. 2015). Most of these studies were carried out using single model experiments, but inter-model comparisons have also been conducted (Stouffer et al. 2006). We perform experiments with EC-Earth3, forcing a 57% reduction of the AMOC strength for 60 model years. We find that the changes in mean surface temperature and precipitation exhibit similar patterns and amplitude compared to previous studies, but for the first time we conduct an in-depth analysis of precipitation anomalies at daily timescales in the Euro-Atlantic sector in winter (DJFM).
Our results show that when we artificially weaken the AMOC compared to the preindustrial climate, the global temperature cools especially in the Northern Hemisphere. Net precipitation decreases over most of the European continent, although in some regions there is a slight net precipitation increase. We further characterize precipitation change by examining the number of days exceeding the 75th percentile of precipitation anomalies computed from the control climate. This analysis indicates while over most of the Euro-Atlantic sector precipitation decreases, in some regions the number of wet days increases following a decline of the AMOC, especially over northwestern Europe.
We apply the moisture budget framework to investigate mechanisms of precipitation change. We find that changes in the dynamics of the atmosphere, in particular the enhancement of the mid-latitude jet stream and its eastward extension towards northwestern Europe explains the increase in wet days anomalies. On the other hand, it is not simply the deficit in moisture that explains the widespread drying over Europe, but the transient eddies term. Transient eddies are responsible for the drying: in fact, despite storm tracks are enhanced, the moisture they carry is reduced, resulting in overall drier storms, even if more intense.
Finally, to further characterize precipitation anomalies and their connection with the large-scale atmospheric circulation, we analyze changes in weather regimes. We find a large increase in the persistence and frequency of occurrence in NAO + events. Through composite analysis of precipitation anomalies over all NAO + days, we find that precipitation associated with NAO + exhibits a pattern of enhanced precipitation over northwestern Europe, and reduced precipitation over southern Europe, consistent with the dynamic contributions in the moisture budget analysis and the enhancement of the jet stream.
To summarize, our study demonstrates that in the event of an AMOC weakening, widespread drying over the European continent is to be expected mainly from intensified but drier storms, and regions of wetter anomalies arise from the change in the location and intensity of the mid-latitude jet in association with an increase in NAO + days. Because a ~ 57% reduction in AMOC strength is within the projected range in AMOC decline in scenarios from the CMIP6 archive, our results have implications for understanding the role of AMOC decline in future climate change (e.g., Bellomo et al. 2021; Liu et al. 2020).
Data availability
The datasets used in study can be requested by writing to the corresponding author.
References
Arias PA et al (2021) Technical Summary. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In: Masson-Delmotte V, Zhai P, Pirani A, Connors SL, Péan C, Berger S, Caud N, Chen Y, Goldfarb L, Gomis MI, Huang M, Leitzell K, Lonnoy E, Matthews JBR, Maycock TK, Waterfield T, Yelekçi O, Yu R, Zhou B (eds)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp. 33−144, https://doi.org/10.1017/9781009157896.002.
Balsamo G, Beljaars A, Scipal K, Viterbo P, van den Hurk B, Hirschi M, Betts AK (2009) A revised hydrology for the ECMWF model: verification from field site to terrestrial water storage and impact in the integrated forecast system. Hydrometeorology 10:623–643. https://doi.org/10.1175/2008JHM1068.1
Bellomo K, Angeloni M, Corti S, von Hardenberg J (2021) Future climate change shaped by inter-model differences in Atlantic meridional overturning circulation response. Nat Commun 12:3659. https://doi.org/10.1038/s41467-021-24015-w
Bellucci A, Athanasiadis PJ, Scoccimarro E, Ruggieri P, Gualdi S, Fedele G, Haarsma RJ, Garcia-Serrano J, Castrillo M, Putrahasan D, Sanchez-Gomez E, Moine MP, Roberts CD, Roberts MJ, Seddon J, Vidale PL (2021) Air–sea interaction over the gulf stream in an ensemble of highresmip present climate simulations. Clim Dyn. https://doi.org/10.1007/s00382-020-05573-z
Berk JVD, Drijfhout SS, Hazeleger W (2021) Circulation adjustment in the Arctic and Atlantic in response to Greenland and Antarctic mass loss. Clim Dyn 57:1689–1707. https://doi.org/10.1007/s00382-021-05755-3
Boers N (2021) Observation-based early-warning signals for a collapse of the Atlantic meridional overturning circulation. Nat Clim Change 11:680–688. https://doi.org/10.1038/s41558-021-01097-4
Brayshaw DJ, Woollings T, Vellinga M (2009) Tropical and extratrop- ical responses of the North Atlantic atmospheric circulation to a sustained weakening of the MOC. J Clim 22(11):3146–3155. https://doi.org/10.1175/2008jcli2594.1
Broecker WS (1997) Thermohaline circulation, the Achilles heel of our climate system: Will man-made CO2 upset the current balance? Science 278(5343):1582–1588. https://doi.org/10.1126/science.278.5343.1582
Broecker WS (2003) Does the trigger for abrupt climate change reside in the ocean or in the atmosphere? Science 300(5625):1519–1522. https://doi.org/10.1126/science.1083797
Brubaker KL, Entekhabi D, Eagleson PS (1993) Estimation of continental precipitation recycling. J Clim 6:1077–1089
Buckley MW, Marshall J (2016) Observations, inferences, and mechanisms of the Atlantic Meridional Overturning Circulation: a review. Rev Geophys 54:5–63. https://doi.org/10.1002/2015RG000493
Burckel P, Waelbroeck C, Gherardi JM, Pichat S, Arz H, Lippold J, Dokken T, Thil F (2015) Atlantic Ocean circulation changes preceded millennial tropical South America rainfall events during the last glacial. Geophys Res Lett 42:411–418. https://doi.org/10.1002/2014GL062512
Caesar L, Rahmstorf S, Robinson A, Feulner G, Saba V (2018) Observed fingerprint of a weakening Atlantic Ocean overturning circulation. Nature 556:191–196. https://doi.org/10.1038/s41586-018-0006-5
Caesar L, McCarthy GD, Thornalley DJR et al (2021) Current Atlantic Meridional Overturning Circulation weakest in last millennium. Nat Geosci 14:118–120. https://doi.org/10.1038/s41561-021-00699-z
Cassou C (2008) Intraseasonal interaction between the Madden-Julian oscillation and the north Atlantic oscillation. Nature 455(7212):523
Clement AC, Peterson LC (2008) Mechanisms of abrupt climate change of the last glacial period. Rev Geophys. 46:RG4002. https://doi.org/10.1029/2006RG000204
Collins M, Knutti R, Arblaster J et al (2013) Long-term climate change: projections, commitments and irreversibility. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Doschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 1029–1136. https://doi.org/10.1017/CBO9781107415324.024
Craig A, Valcke S, Coquart L (2017) Development and performance of a new version of the OASIS coupler, OASIS3-MCT_3.0. Geosci Model Dev 10:3297–3308. https://doi.org/10.5194/gmd-10-3297-2017
D’Agostino R, Lionello P (2020) The atmospheric moisture budget in the Mediterranean: mechanisms for seasonal changes in the Last Glacial Maximum and future warming scenario. Quater Sci Rev 241:106392. https://doi.org/10.1016/j.quascirev.2020.106392
Dahl KA, Broccoli AJ, Stouffer RJ (2005) Assessing the role of North Atlantic freshwater forcing in millennial scale climate variability: a tropical Atlantic perspective. Clim Dyn 24:325–346. https://doi.org/10.1007/s00382-004-0499-5
Dansgaard W et al (1993) Evidence for general instability of past climate from a 250-kyr ice-core record. Nature 364:218–220. https://doi.org/10.1038/364218a0
Dawson A, Palmer T, Corti S (2012) Simulating regime structures in weather and climate prediction models. Geophys Res Lett 39(21):20
Döscher R et al (2022) The EC-Earth3 Earth system model for the Coupled Model Intercomparison Project 6. Geosci Model Dev. 15:2973–3020. https://doi.org/10.5194/gmd-15-2973-2022
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev 9:1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Fabiano F, Christensen HM, Strommen K et al (2020) Euro-Atlantic weather Regimes in the PRIMAVERA coupled climate simulations: impact of resolution and mean state biases on model performance. Clim Dyn 54:5031–5048. https://doi.org/10.1007/s00382-020-05271-w
Fabiano F, Meccia VL, Davini P, Ghinassi P, Corti S (2021) A regime view of future atmospheric circulation changes in northern mid-latitudes. Weather Clim Dynam 2:163–180
Fox-Kemper B et al (2021) Ocean, cryosphere and sea level change. In: Masson-Delmotte V, Zhai P, Pirani A, Connors SL, Péan C, Berger S, Caud N, Chen Y, Goldfarb L, Gomis MI, Huang M, Leitzell K, Lonnoy E, Matthews JBR, Maycock JK, Waterfield T, Yelekçi O, Yu R, Zhou B (eds) Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 1211–1362. https://doi.org/10.1017/9781009157896.011
Frierson D et al (2013) Contribution of ocean overturning circulation to tropical rainfall peak in the Northern Hemisphere. Nat Geosci 6:940–944. https://doi.org/10.1038/ngeo1987
Haarsma RJ, García-Serrano J, Prodhomme C, Bellprat O, Davini P, Drijfhout S (2019) Sensitivity of winter north Atlantic-European climate to resolved atmosphere and ocean dynamics. Sci Rep 9(1):1–8. https://doi.org/10.1038/s41598-019-49865-9
Hannachi A, Straus DM, Franzke CL, Corti S, Woollings T (2017) Low-frequency nonlinearity and regime behavior in the northern hemisphere extratropical atmosphere. Rev Geophys 55(1):199–234
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19(21):5686–5699
Henry L, McManus JF, Curry WB, Roberts NL, Piotrowski AM, Keigwin LD (2016) North Atlantic ocean circulation and abrupt climate change during the last glaciation. Science 353(6298):470–474. https://doi.org/10.1126/science.aaf5529
Iturbide M, Gutiérrez JM, Alves LM, Bedia J, Cerezo-Mota R, Cimadevilla E, Cofiño AS, Di Luca A, Faria SH, Gorodetskaya IV, Hauser M, Herrera S, Hennessy K, Hewitt HT, Jones RG, Krakovska S, Manzanas R, Martínez-Castro D, Narisma GT, Nurhati IS, Pinto I, Seneviratne SI, van den Hurk B, Vera CS (2020) An update of IPCC climate reference regions for subcontinental analysis of climate model data: definition and aggregated datasets. Earth Syst Sci Data 12:2959–2970. https://doi.org/10.5194/essd-12-2959-2020
Jackson LC, Wood RA (2018) Hysteresis and resilience of the AMOC in an eddy permitting GCM. Geophys Res Lett 45:8547–8556. https://doi.org/10.1029/2018GL078104
Jackson LC, Wood RA (2020) Fingerprints for early detection of changes in the AMOC. J Clim 33(16):7027–7044
Jackson LC, Kahana R, Graham T et al (2015) Global and European climate impacts of a slowdown of the AMOC in a high resolution GCM. Clim Dyn 45:3299–3316. https://doi.org/10.1007/s00382-015-2540-2
Jackson LC, Roberts MJ, Hewitt HT et al (2020) Impact of ocean resolution and mean state on the rate of AMOC weakening. Clim Dyn 55:1711–1732. https://doi.org/10.1007/s00382-020-05345-9
Jackson LC, Alastrué de Asenjo E, Bellomo K, Danabasoglu G, Haak H, Hu A, Jungclaus J, Lee W, Meccia VL, Saenko O, Shao A, Swingedouw D (2023) Understanding AMOC stability: the North Atlantic hosing model intercomparison project. Geosci Model Dev Discuss. https://doi.org/10.5194/gmd-2022-277
Jacob D, Goettel H, Jungclaus J, Muskulus M, Podzun R, Marotzke J (2005) Slowdown of the thermohaline circulation causes enhanced maritime climate influence and snow cover over Europe. Geophys Res Lett 32(21):L21. https://doi.org/10.1029/2005gl023286
Jiang W, Gastineau G, Codron F (2021) Multicentennial variability driven by salinity exchanges between the Atlantic and the arctic ocean in a coupled climate model. J Adv Model Earth Systems 13:e2020MS02366. https://doi.org/10.1029/2020MS002366
Johnson HL, Cessi P, Marshall DP, Schloesser F, Spall MA (2019) Recent contributions of theory to our understanding of the Atlantic Meridional Overturning Circulation. J Geophys Res Oceans 124:5376–5399. https://doi.org/10.1029/2019JC015330
Kang SM, Held IM, Frierson DMW, Zhao M (2008) The response of the ITCZ to extratropical thermal forcing: idealized Slab-ocean experiments with a GCM. J Clim 21(14):3521–3532
Kuhlbrodt T, Rahmstorf S, Zickfeld K, Vikebø F, Sundby S, Hofmann M, Link P, Bondeau A, Cramer W, Jaeger C (2009) An integrated assessment of changes in the thermohaline circulation. Clim Change 96(4):489–537. https://doi.org/10.1007/s10584-009-9561-y
Lee J-Y et al. (2021) Future Global Climate: Scenario-Based Projections and Near-Term Information. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In: Masson-Delmotte V, Zhai P, Pirani A, Connors SL, Péan C, Berger S, Caud N, Chen Y, Goldfarb L, Gomis MI, Huang M, Leitzell K, Lonnoy E, Matthews JBR, TK
Lenton TM, Held H, Kriegler E, Hall JW, Lucht W, Rahmstorf S, Schellnhuber HJ (2013) Tipping elements in the Earth’s climate system. Proc Nat Acad Sci USA 105:1786–1793. https://doi.org/10.1073/pnas.0705414105
Levermann A, Griesel A, Hofmann M, Montoya M, Rahmstorf S (2005) Dynamic sea level changes following changes in the thermohaline circulation. Clim Dyn 24(4):347–354. https://doi.org/10.1007/s00382-004-0505-y
Liu W, Xie S-P, Liu Z, Zhu J (2017) Overlooked possibility of a collapsed Atlantic Meridional Overturning Circulation in warming climate. Sci Adv 3:e1601666
Liu W, Fedorov A, Xie S-P, Hu S (2020) Climate impacts of a weakened Atlantic Meridional Overturning Circulation in a warming climate. Sci Adv 6:eaaz4876
Lynch-Stieglitz J (2017) The Atlantic meridional overturning circulation and abrupt climate change. Ann Rev Mar Sci 9(1):83–104
Madec G (20150 NEMO ocean engine, Note du Pole de modelisation de l'Institut Pierre-Simon Laplace No. 27.
Manabe S, Stouffer RJ (1997) Coupled ocean-atmosphere model response to freshwater input: Comparison to Younger Dryas Event. Paleoceanography 12(2):321–336. https://doi.org/10.1029/96PA03932
Marshall J, Donohoe A, Ferreira D, McGee D (2014) The ocean’s role in setting the mean position of the Inter-Tropical Convergence Zone. Clim Dyn 42:1967–1979. https://doi.org/10.1007/s00382-013-1767-z
Meccia VL, Fuentes-Franco R, Davini P et al (2022) Internal multi-centennial variability of the Atlantic Meridional Overturning Circulation simulated by EC-Earth3. Clim Dyn. https://doi.org/10.1007/s00382-022-06534-4
Mecking JV, Drijfhout SS, Jackson LC et al (2016) Stable AMOC off state in an eddy-permitting coupled climate model. Clim Dyn 47:2455–2470. https://doi.org/10.1007/s00382-016-2975-0
Mehling O, Bellomo K, Angeloni M, Pasquero C, von Hardenberg J. (2022) High-latitude precipitation as a driver of multicentennial variability of the AMOC in a climate model of intermediate complexity. Res Sq https://doi.org/10.21203/rs.3.rs-1832272/v1.
Michelangeli PA, Vautard R, Legras B (1995) Weather regimes: recurrence and quasi stationarity. J Atmos Sci 52(8):1237–1256
Moffa-Sánchez P, Moreno-Chamarro E, Reynolds DJ, Ortega P, Cunningham L, Swingedouw D, Amrhein DE, Halfar J, Jonkers L, Jungclaus JH, Perner K, Wanamaker A, Yeager S (2019) Variability in the Northern North Atlantic and Arctic Oceans across the last two millennia: a review. Paleoceanogr Paleoclimatol 34:1399–1436. https://doi.org/10.1029/2018PA003508
Oudar T, Cattiaux J, Douville H (2020) Drivers of the Northern Extratropical Eddy-Driven Jet Change in CMIP5 and CMIP6 Models. Geophys Res Lett 47:e2019GL086695. https://doi.org/10.1029/2019GL086695
Peings Y, Cattiaux J, Vavrus SJ, Magnusdottir G (2018) Projected squeezing of the wintertime North-Atlantic jet. Environ Res Lett 13:074016. https://doi.org/10.1088/1748-9326/aacc79
Rahmstorf S (2002) Ocean circulation and climate during the past 120,000 years. Nature 419(6903):207–214. https://doi.org/10.1038/nature01090
Rahmstorf S, Box JE, Feulner G, Mann ME, Robinson A, Rutherford S, Schaffernicht EJ (2015) Exceptional twentieth-century slowdown in Atlantic Ocean overturning circulation. Nat Clim Change 5:475–480. https://doi.org/10.1038/nclimate2554
Rousset C, Vancoppenolle M, Madec G, Fichefet T, Flavoni S, Barthélemy A, Benshila R, Chanut J, Levy C, Masson S, Vivier F (2015) The Louvain-La-Neuve sea ice model LIM3.6: global and regional capabilities. Geosci Model Dev 8:2991–3005. https://doi.org/10.5194/gmd-8-2991-2015
Seager R, Naik N, Vecchi GA (2010) Thermodynamic and dynamic mechanisms for large-scale changes in the hydrological cycle in response to global warming. J Clim. 23:4651e4668
Seager R, Liu H, Kushnir Y, Osborn TJ, Simpson IR, Kelley CR, Nakamura J (2020) Mechanisms of winter precipitation variability in the European–Mediterranean region associated with the North Atlantic oscillation. J Clim 33:7179–7196. https://doi.org/10.1175/JCLI-D-20-0011.1
Srokosz M, Danabasoglu G, Patterson M (2021) Atlantic meridional overturning circulation: reviews of observational and modeling advances—an introduction. J Geophys Res Oceans 126:e2020JC016745. https://doi.org/10.1029/2020JC016745
Stouffer RJ, Yin J, Gregory JM, Dixon KW, Spelman MJ, Hurlin W, Weaver AJ, Eby M, Flato GM, Hasumi H, Hu A, Jungclaus JH, Kamenkovich IV, Levermann A, Montoya M, Murakami S, Naw-rath S, Oka A, Peltier WR, Robitaille DY, Sokolov A, Vettoretti G, Weber SL (2006) Investigating the causes of the response of the thermohaline circulation to past and future climate changes. J Clim 19:1365–1387
Straus D, Molteni F, Corti S (2017) Atmospheric regimes: the link between weather and the large scale circulation. Nonlinear Stochast Clim Dyn. 105–135
Strommen K, Mavilia I, Corti S, Matsueda M, Davini P, von Hardenberg J, Vidale PL, Mizuta R (2019) The sensitivity of Euro-Atlantic regimes to model horizontal resolution. Geophys Res Lett 46(13):7810–7818. https://doi.org/10.1029/2019GL082843
Swingedouw D, Houssais M-N, Herbaut C, Blaizot A-C, Devilliers M, Deshayes J (2022) AMOC recent and future trends: a crucial role for oceanic resolution and greenland melting? Front Clim. https://doi.org/10.3389/fclim.2022.838310
Thornalley DJR, Oppo DW, Ortega P et al (2018) Anomalously weak Labrador Sea convection and Atlantic overturning during the past 150 years. Nature 556:227–230. https://doi.org/10.1038/s41586-018-0007-4
Trenberth KE, Guillemot CJ (1995) Evaluation of the global atmospheric moisture budget as seen from analyses. J Clim 8(9):2255–2272
Tsartsali EE, Haarsma RJ, Athanasiadis PJ et al (2022) Impact of resolution on the atmosphere–ocean coupling along the Gulf Stream in global high resolution models. Clim Dyn 58:3317–3333. https://doi.org/10.1007/s00382-021-06098-9
Vautard R (1990) Multiple weather regimes over the north Atlantic: analysis of precursors and successors. Mon Weather Rev 118(10):2056–2081
Vellinga M, Wood R (2008) Impacts of thermohaline circulation shut-down in the twenty-first century. Clim Change 91(1–2):43–63. https://doi.org/10.1007/s10584-006-9146-y
Weijer W, Cheng W, Drijfhout SS, Federov AV, Hu A, Jackson LC et al (2019) Stability of the Atlantic meridional overturning circulation: a review and synthesis. J Geophys Res Oceans 124:5336–5375. https://doi.org/10.1029/2019JC015083
Weijer W, Cheng W, Garuba O, Hu A, Nadiga B (2020) CMIP6 models predict significant 21st century decline of the Atlantic Meridional Overturning Circulation. Geophys Res Lett 47:e2019GL086075. https://doi.org/10.1029/2019GL086075
Woollings T, Gregory JM, Pinto JG, Reyers M, Brayshaw DJ (2012a) Response of the North Atlantic storm track to climate change shaped by ocean–atmosphere coupling. Nat Geosci 5(5):313–317. https://doi.org/10.1038/ngeo1438
Woollings T, Harvey B, Zahn M, Shaffrey L (2012b) On the role of the ocean in projected atmospheric stability changes in the Atlantic polar low region. Geophys Res Lett 39(24):L24. https://doi.org/10.1029/2012gl054016
Worthington EL, Moat BI, Smeed DA, Mecking JV, Marsh R, McCarthy GD (2021) A 30-year reconstruction of the Atlantic meridional overturning circulation shows no decline. Ocean Sci 17:285–299. https://doi.org/10.5194/os-17-285-2021
Zhang R, Delworth TL (2005) Simulated tropical response to a substantial weakening of the Atlantic thermohaline circulation. J Clim 18(12):1853–1860. https://doi.org/10.1175/JCLI3460.1
Zhang R, Sutton R, Danabasoglu G, Kwon Y-O, Marsh R, Yeager SG et al (2019) A review of the role of the Atlantic Meridional Overturning Circulation in Atlantic Multidecadal Variability and associated climate impacts. Rev Geophys 57:316–375. https://doi.org/10.1029/2019RG000644
Acknowledgements
The weather regimes were computed using the WRTool package publicly available at https://github.com/fedef17/WRtool. The simulations shown in this work were carried out at ECMWF under the special projects SPITBELL and SPITMEC2.
Funding
Open access funding provided by Politecnico di Torino within the CRUI-CARE Agreement. KB has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101026907 (CliMOC). The simulations shown in this work were carried out at ECMWF under the special projects SPITBELL and SPITMEC2. SML is supported by NSF Grant AGS-1951713. VM, FF, JvH and SC acknowledge funding for this project from European Union’s Horizon 2020 research and innovation programme under grant agreement No. 820970 (TiPES). This is TiPES contribution #159. This work has also received funding from the Italian Ministry of Education, University and Research (MIUR) through the JPI Oceans and JPI Climate “Next Generation Climate Science in Europe for Oceans”–ROADMAP Project (D. M. 593/2016).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Model setup and experiments with EC-Earth3 were performed by Virna L. Meccia and Jost von Hardenberg. Data collection and analysis was mainly performed by Katinka Bellomo, with input and help from all authors. The tool to compute weather regimes was developed by Federico Fabiano and Susanna Corti. The initial tool to compute the atmospheric moisture budget was developed by Roberta D’Agostino and later adapted by Katinka Bellomo. The manuscript was written by Katinka Bellomo, with input from all coauthors. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bellomo, K., Meccia, V.L., D’Agostino, R. et al. Impacts of a weakened AMOC on precipitation over the Euro-Atlantic region in the EC-Earth3 climate model. Clim Dyn 61, 3397–3416 (2023). https://doi.org/10.1007/s00382-023-06754-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-023-06754-2