1 Introduction

Land surface characteristics influence local and regional climates across various timescales (Dirmeyer 2011). Soil moisture ‘memory’ is a key factor that can enhance the predictability of regional climate (Koster et al. 2011). Land–atmosphere interactions have specific signatures over different areas around the globe (Guo et al. 2016 and Dirmeyer 2011). It is therefore essential to evaluate the current generation of climate models, such as those participating in the sixth phase of the Climate Model Intercomparison Project (CMIP6), across various climate regimes.

As models gain more prominence in supporting decision-making for various socio-economic applications (Lee et al. 2021), it is paramount to evaluate critical processes as a basis for model improvement and users’ awareness of the uncertainties associated with climate model outputs (Merchant et al. 2017). Although model development may be a preserve for scientists, information on land surface forcing of the climate is an aspect that societies can appreciate based on their land use practices. Existing research suggests that land–atmosphere coupling ‘hotspots’ are usually located in typical semi-arid regions with pronounced convective rainfall events (Zheng et al. 2015). Such areas have abundant radiation but limited soil moisture. For instance, meridional temperature gradients in the Sahel trigger the development of intense rainfall storms, Taylor et al. (2011).

On sub-seasonal to seasonal timescales, anomalous soil moisture leads to enhanced surface latent heat flux, which results in boundary-layer moistening and cooling (Hohenegger 2020). Convection may be enhanced or suppressed depending on the pre-existing thermodynamic conditions (Muller et al. 2022), potentially intensifying the soil-moisture precipitation feedback loop. Further, intra-seasonal dry anomalies of soil moisture have been demonstrated to enhance local to regional temperatures by about 1.5 °K in the Sahel (Talib et al. 2022). This is related to increases in the Bowen ratio as soil moisture declines. The impact of soil moisture anomalies has been demonstrated to influence local to regional climate beyond planetary boundary layer (PBL) variables. Over East Africa, Abera et al. (2020) noted that land surface characteristics such as leaf area index and soil moisture control about 47% of the temporal variability of surface temperatures. Moreover, Dirmeyer et al. (2009) reported that soil moisture memory persisted for up to about 40 days in Southern Africa. Experimental results by Cook et al. (2006) indicated that during the rainfall season in Southern Africa, an increase in soil moisture creates negative feedback through partitioning the surface energy budget; increasing the evaporative fraction triggers surface cooling that leads to high surface pressure and a stable atmosphere.

Over the Sahel, Nicholson (2000) noted that the strong meridional gradient in soil moisture between the Sahara and Guinea coast sustains regional temperature gradients that initiate the development of the African Easterly Jet (AEJ) (Cook 1999). Klein and Taylor (2020) also noted that soil moisture anomalies enhance the development of local and propagating convective storms in this region. Feedbacks between the land and atmosphere, especially where soil moisture anomalies sustain rainfall events, are related to inter-annual rainfall persistence in the Sahel (Nicholson 2000). Based on CORDEX-Africa for CMIP5, Soares et al. (2019) indicated that the Sahel hotspot of land–atmosphere coupling is projected to extend southwards due to an expected increase in aridity in West Africa. With declining global trends of soil moisture, except for the northern hemisphere winter latitudes (Dirmeyer et al. 2013), it is foreseen that corresponding feedbacks will enhance extreme events such as heat waves and droughts. This motivates the need for process-based evaluation of the models used for future climate projections, James et al. (2018)

This paper evaluates the characteristics of coupling between the land and the atmosphere in Africa for selected global models participating in CMIP6. The historical simulations provide the opportunity for process-based assessment against observations. Herein, we trace the land–atmosphere coupling processes through the impact of soil moisture characteristics on surface heat fluxes and the subsequent effect of the fluxes on temperature and precipitation. These are usually defined as the terrestrial and atmospheric pathways of the land–atmosphere interactions (Santanello et al. 2018). The subsequent sections of the paper are as follows; Sect. 2 presents the Data and Methods, Sect. 3 presents the Results, Discussion follows in Sect. 4, and finally, Conclusions are summarized in Sect. 5.

2 Data and methods

2.1 Observational and reanalysis data

Variables considered in this study are monthly means of leaf area index (LAI), soil moisture (SM), rainfall (PR), evapotranspiration (E), 2-m temperature (TAS), and latent heat flux (HFLS), Table 1. Most regions across Africa lack long-term observations relevant to a detailed study of the regional climate and model evaluation (Aloysius et al. 2016; Crowhurst et al. 2020). In this regard, researchers have relied on satellite observations and reanalysis datasets to study land–atmosphere characteristics (Miralles et al. 2012), especially on regional to global scales. The European Centre for Medium Range Forecasting (ECMWF) version 5 reanalysis (ERA5) at 0.25-degree resolution (Hersbach et al. 2020) was obtained from the Climate Data Store (CDS) of the Copernicus Climate Change Service (C3S) for all variables of interest over the period 1979–2014. ERA5 has a better representation of land surface variables such as soil moisture and vegetation than the previous version, ERA-Interim (Hersbach et al. 2020). In addition, monthly LAI at 0.25-degree resolution was obtained from Global Inventory Modeling and Mapping Studies (GIMMS). The GIMMS LAI3g version 2 (Zhu et al. 2013) is a global biweekly satellite-derived product aggregated to monthly means from 1981 to 2015. This data was sourced from the Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC) of the National Aeronautics and Space Administration (NASA). For comparison with ERA5, the Climate Hazards Group InfraRed Precipitation with Stations version 2 (CHIRPS v2) at 0.05° resolution rainfall dataset was used (Funk et al. 2015). CHIRPS v2, a blend of satellite and gauge records available from 1981 to present, has been shown to accurately characterize the spatiotemporal patterns of rainfall over Africa (Dinku et al. 2018; Shen et al. 2020).

Table 1 Overview of the observational and reanalysis datasets utilized in the study
Full size table

Both evaporation and soil moisture are key parameters in the moisture and energy cycles. A globally harmonized in-situ, satellite, model, and reanalysis land evaporation dataset generated by utilizing the Reliability Ensemble Averaging (REA) technique at 0.25 degrees, Lu et al. (2021), herein referred to as REA-ET, was used. Merging multiple evaporation datasets is one technique used to generate high-precision datasets (Yao et al. 2014). In addition, the European Space Agency Climate Change Initiative Soil Moisture (ESA CCI-SM), version 06.1 (Dorigo et al. 2017 and Gruber et al. 2019) was obtained for the period 1979–2014 at monthly timescales. This soil moisture dataset measures up to 5 cm in depth and is generated from multiple passive and active sensors from 1978 to 2020 at 0.25-degree resolution.

The period considered was 1979–2014 to coincide with CMIP6 (Sect. 2.2) or the earliest equivalent 36-year period depending on data availability (for reference datasets only).

2.2 CMIP6 models

CMIP6 models provide the state-of-the-art global climate model outputs that form the basis for several global initiatives, including the IPCC’s scientific assessment of the climate. For this work, eight coupled models were selected and used for the historical period. Guided by data availability at the CEDA archive, uniform physics and initializations were chosen across the models (p1 and i1, respectively), while three forcings (f1, f2 and f3) and two realizations (r1 and r10) were considered (Table 2) over a 36-year historical period. f1 includes prescribed time-varying aerosol and ozone fields, while f3 is characterized by interactive aerosol-cloud processes (Smith et al. 2020). The historical simulations are largely forced by observations, including volcanic activity, solar variability, and anthropogenic forcing (Eyring et al. 2016).

Table 2 Overview of the Eight selected CMIP6 models analyzed in this study
Full size table

2.3 Methods

Comparative analysis of the annual cycle of the balance between rainfall and evapotranspiration, i.e., effective precipitation, soil moisture and leaf area index, were applied to investigate the response of soil water content and vegetation characteristics to the availability or deficit of rainfall. The characterization of annual cycles is also useful to gauge the representation of the seasonality of native land–atmosphere processes in models. The effective rainfall, represented as the moisture convergence in the atmosphere, was defined as the difference between the total rainfall and the evapotranspiration (P–E) used by Byrne et al. (2015). Except for the annual cycle analysis and soil moisture regimes, all datasets were aggregated into seasonal means for March to May (MAM) and June to August (JJA) for the rest of the study.

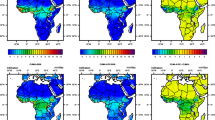
Figure 1 shows the regions of interest in this study. Dense vegetation exists in Central Africa (CA) and parts of West Africa (WA). Areas in Eastern Africa, the Sahel (SH) and Southern Africa (SA) have a much lower density of vegetation. The Sahara has the least vegetation in Africa. LAI, which is a crucial parameter in climate models, plays an important role in controlling the fluxes of energy, moisture, and carbon (Richardson et al. 2013). Underscoring the importance of soil moisture and evaporative fraction as drivers of the interactions between the land and the atmosphere, Seneviratne et al. (2010) and Koster et al. (2011) have used a soil moisture-evaporative fraction framework to characterize the interaction regimes. This study used latent heat flux (HFLS) instead of evaporative fraction (EF). Wet regimes are characterized by sufficient soil moisture above the critical value (SMCRIT) but with limited net radiation (Rn), while dry regimes feature too little soil moisture below the wilting point (SMWILT) and abundant net radiation. Depending on the prevailing season, transitional zones between the dry and wet regimes may have varying relationships between soil moisture and radiation amounts. Wet regimes are likely in equatorial Africa and some coastal regions, while the Sahara is a dry regime with too little moisture to influence turbulent fluxes at the surface. The key forcings of vegetation, net radiation in humid zones, precipitation in arid and semi-arid climates, and temperature in extra-tropics (Nemani et al. 2003) are also helpful in characterizing soil moisture regimes.

Fig. 1
figure 1

Mean leaf area index over Africa based on GIMMS-LAI3g version 2 for MAM season over the period 1981–2015 (Focus areas were identified following Soares et al. 2019)

Full size image

The terrestrial coupling index (TCI) was computed as the product of the standard deviation of soil moisture and the correlation coefficient between soil moisture and latent heat flux as defined by Dirmeyer (2011). This is necessary to account for the variability of soil moisture as the forcing variable. In regions with little variability, such as deserts or persistently saturated soils, the TCI is at a minimum as soil moisture is not a factor in the variability of latent heat flux (Halder et al. (2018)). The atmospheric leg of the coupling process, the atmospheric coupling index (ACI), was computed similarly with the TCI, multiplying the correlation between temperature and latent heat flux with the standard deviation of temperature for ACItas and rainfall for ACIpr. The significance of the correlations was assessed at a 95% confidence level. The TCI and ACI indices are direction specific, with positive (negative) feedback indicated by positive (negative) values. Negative TCI indicates a lack of soil moisture forcing on surface fluxes, implying that net radiation, controlled by cloud cover, could be the major forcing (Soares et al. 2019).

The uppermost soil layer was considered for all the datasets. This corresponds to 7 cm for ERA5, 5 cm for HadGEM3-G31-LL and ESA CCI-SM, and 10 cm for the rest of the CMIP6 models. Using CMIP5, Dirmeyer et al. (2013) also noted that this depth was readily available and useful for intercomparison studies between models. The surface layer is affected through direct evaporation, while the root zone depth drives the transpiration in vegetation (Anderson et al. 2012). Therefore, vegetation indicators, such as the Normalized Difference Vegetation Index (NDVI) or LAI, may also be used as a proxy for the root zone soil moisture. For consistency with the reference datasets, the conversion of model soil moisture from gravimetric to volumetric units was done (Xu et al. 2018).

3 Results and discussion

The results are presented and discussed in three parts. We begin by examining the annual cycles of P–E, SM and LAI to assess the mean representation of these parameters over regions identified in Fig. 1. The rest of our results focus on two seasons, MAM and JJA, which are active rainfall seasons over equatorial and western Africa, respectively. We then examine regimes of soil moisture and latent heat. Finally, we present the spatial analysis of the coupling indices between the land and the atmosphere.

3.1 Annual cycles of various parameters

We first examined the annual cycle of P–E, SM and LAI presented in Figs. 2, 3, 4, respectively. In Fig. 2, the analysis indicates a bimodal P–E pattern over CA, with the principal peak in November (ERA5 and most models) and a secondary one in March (ERA5, CHIRPS-ET, and most models). Bimodal patterns are also observed in both KE and SO for models and observations, with peaks in April/May and October/November. ERA5 and CHIRPS-ET closely match over KE, but differences are notable over SO, where CHIRPS-ET magnitudes are larger than ERA5. Positive P–E exists over KE during the rainfall seasons, MAM and October to December (OND), while negative P–E dominates SO for most times of the year, with the exception of October for all models and reference datasets considered. Both WA and SH show unimodal P–E seasonality in observations with fair model agreement during the dry seasons and a large spread during the West African monsoon season. SA has a unimodal pattern of P–E, peaking in January with pronounced model differences during the rainfall season, December to January (DJF), compared to the rest of the year. Overall, we hypothesize that climate models overestimate evaporative moisture loss, as evidenced by the larger magnitudes of negative P–E across regions during the dry seasons, especially in CA and KE.

Fig. 2
figure 2

Annual cycle of spatially averaged P–E for different CMIP6 models and observational datasets over CA (a), KE (b), SO (c), WA (d), SH (e) and SA (f) for the period 1979–2014. CHIRPS-ET is P–E using CHIRPS rainfall and Lu et al. (2021) evaporation dataset. (Due to strongly varying P–E climatologies, each sub-region has unique y-axis labels)

Full size image
Fig. 3
figure 3

Annual cycle of spatially averaged soil moisture for different CMIP6 models and observational datasets over CA (a), KE (b), SO (c), WA (d), SH (e) and SA (f) for the period 1979–2014. (Due to strongly varying SM climatologies, each sub-region has unique y-axis labels)

Full size image

The annual cycle of soil moisture, Fig. 3, shows good agreement between ERA5 and ESA-CCI over KE and WA, and consistent disparity in magnitudes of up to 1.5 m3m−3 in CA, SO, SH and SA. HadGEM3-GC31-LL, due to consideration of a shallower depth, has more soil moisture for all regions except in the Sahel, Fig. 3f. GISS-E2-1-G tends to have the least amounts of soil moisture throughout the year for all regions. Though with differing magnitudes, models show consensus in capturing the seasonality of soil moisture across Africa. For all the regions, we also note that the evolution of soil moisture is in phase with rainfall (Fig. 2). We also note that in bimodal rainfall regions, the range of soil moisture between the two peaks is relatively similar.

In Fig. 4, ERA5 and GIMMS vegetation seasonality show good agreement, except in SO and SH. In SO, ERA5 is nearly constant throughout the year, while GIMMS shows a bimodal pattern. On the other hand, GIMMS indicates a sharp increase between February to September, and a decline after that, while ERA5 shows little increase and decay before and after the September peak over the Sahel. Unlike P–E and SM, models show a large disparity in simulating vegetation seasonality over Africa. For instance, CanESM5 depicts a LAI reduction between January and April in Central Africa, contrary to observations and the rest of the models. In addition, UKESM1-0-LL showed little month-to-month variability across all regions studied while GISS-E2-1-G, though with similar seasonality in terms of P–E and SM with the rest of the models, vegetation was grossly underestimated all-year round across Africa. Using CMIP5-ESMs, Mahowald et al. (2016) reported that some models do not clearly show the precipitation-vegetation response, as currently reported in the Sahel. This is despite the expectation that LAI in the tropics is controlled by moisture availability, unlike in the higher latitudes where the control of moisture by temperature is dominant (Zeng et al. 2013). The lack of such a relationship may point to a weakness in the model configurations, which may cause an inaccurate representation of the boundary layer processes and the budgets of surface water, energy, and carbon (Park and Jeong 2021).

Fig. 4
figure 4

Annual cycle of spatially averaged leaf area index for different CMIP6 models and observational datasets over CA (a), KE (b), SO (c), WA (d), SH (e) and SA (f) for the period 1979–2014. (Due to strongly varying LAI climatologies, each sub-region has unique y-axis labels)

Full size image

3.2 Soil moisture regimes

To characterize the soil moisture regimes, soil moisture-latent heat scatter plots with Locally Weighted Scatterplot Smoothing (LOWESS) are presented in Fig. 5 for MAM. The LOWESS technique is useful for non-linear smoothing and identifying relationships in hydro-meteorological applications, Smith et al. (2002). During MAM, ERA5 indicates that Central Africa is a wet regime at high soil moisture levels, eastern Africa (KE and SO), and west and southern Africa are transitional zones while the Sahel is dry. Dry regimes have too little soil moisture to trigger any variability in latent heat flux. In contrast, in wet regimes, with abundant soil moisture, this does not initiate forcing in surface fluxes. On the other hand, transitional zones, which fall between dry and wet regimes, are potential hotspots for L–A coupling, Seneviratne et al. (2010). Herein, these regions are characterized by LOWESS lines that run nearly parallel to the diagonal. In regions like Central Africa, the variability of HLFS is, therefore, largely controlled by cloud cover modulation of the surface energy budget, Small and Kurc (2003). There is a large model spread in this region, where GFDL-CM4, CanESM5, and MIROC6 have reversed or flat curves indicating that the lack of HFLS response to SM variability could be attributed to model weakness in simulating atmospheric processes that control the energy budgets.

Fig. 5
figure 5

Scatter diagrams for soil moisture and latent heat flux with LOWESS lines for the months of MAM over CA (a), KE (b), SO (c), WA (d), SH (e) and SA (f) for the period 1979–2014. In CA, HadGEM3-GC31-LL soil moisture is indicated in the top axis. LOWESS lines that run close to the diagonal are indicative of potential L–A coupling due to a limited soil moisture environment (Due to strongly varying SM and HFLS climatologies, each sub-region has unique x and y-axis labels)

Full size image

It should be noted that a region can show attributes of either of the three regimes depending on the prevailing season (Seneviratne et al. 2010). For instance, based on ERA5, the Sahel is a dry regime in MAM (Fig. 5) but enters a transitional regime in JJA (Figure S1) due to the recharge of soil moisture by the summer rainfall. In JJA, WA changes to a general dry regime based on ERA5. Models portray similar seasonal characteristics moving from MAM to JJA; an increase in soil moisture range over the Sahel accompanied by a strong latent heat response and a reduction in soil moisture over the rest of the regions, and consequently, a reduction in the gradient of the LOWESS curves. L–A interactions are, therefore, region and season specific. For both seasons, model agreement is noted in transitional regimes, but huge differences are evident in wet and dry regimes. Based on the SM-HFLS regimes, we note that L–A interactions exist over the Sahel, East Africa, and to some degree, West and Southern Africa during certain periods of the year, depending on the seasonality of soil moisture.

3.3 Land–Atmosphere coupling indices

3.3.1 Terrestrial coupling index (TCI)

TCI shows the direction and strength of soil moisture control to surface fluxes. Figure 6 and Figure S2 present the TCI results for MAM and JJA, respectively. ERA5 indicates that during MAM, L–A coupling exists over Eastern and Southern Africa and the Guinea Coast region. The model multi-model ensemble (ENS) shows broad spatial agreement with ERA5, though with stronger intensity. CNMR-CM6-1 and GISS-E2-1-G have the weakest TCI, though signals are noted over parts of Southern and Eastern Africa. Over these regions, the rest of the models show consensus with ERA5, though with relatively stronger signals. Over the region spanning from the Horn of Africa to the Guinea Coast, intermodal differences exist with HadGEM3-GC31-LL and UKESM1-0-LL showing the most robust latent heat sensitivity to soil moisture, while the signal is damped for GFDL-CM4. Finally, we note that models with the strongest TCI also portrayed a strong SM-HFLS response (Fig. 5).

Fig. 6
figure 6

MAM TCI over Africa for selected CMIP6 models for 1979–2014. Hatching highlights regions of significant correlations in models and ERA5, while for ENS, hatching shows areas where all models agree on positive TCI. TCI values were scaled by 10.2

Full size image

Despite having the highest amounts of SM, there is no SM forcing on HFLS over CA during MAM. Given the seasonal and vegetation characteristics in this region, we suggest that evapotranspiration, driven by net radiation, is the primary driver of surface fluxes over CA. GFDL-CM4, MIROC6, and CanESM5, which had the weakest or reversed SM-HFLS response (Fig. 5), also have an extensive negative TCI over CA to southern parts of East Africa in MAM, unlike ERA5. However, these models do not correctly simulate the SM-HFLS de-coupling in CA. In the Sahara and Sahel, there are marginal amounts of SM to trigger any HFLS response, despite the presence of significant correlations in some parts.

During the north-hemisphere summer, Figure S2, the Sahelian region across West to Eastern Africa is identified as a coupling hotspot in both ERA5 and ENS (Soares et al. 2019), with the ENS coupling being stronger than ERA5. We note the consistency in models across different seasons. Like in MAM, CNRM-CM6-1 and GISS-E2-1-G have the least strength of TCI across Africa, and the MOHC models, HadGEM-GC31-LL and UKESM1-0-LL tend to overestimate the strength of TCI over most regions in Africa. The latter group consistently does not represent soil moisture forcing on surface fluxes over the study domain, while in the former, this response is over-estimated (Figure S1).

Regions with strong TCI, such as the Sahel and East Africa, that also tend to have limited vegetation and abundant net radiation have a strong chance of SM loss through E. In this regard, SM loss through E is the primary depletion mechanism of P, especially over WA and SH (Marshall et al. 2012; Douvile 2002). We note that the mean annual cycle of vegetation, soil moisture, and P–E is weakest across all regions for GISS-E2-1-G, which points to an inherent model inability to properly simulate the climate over Africa. On the other hand, HadGEM-GC31-LL shows a substantial month-to-month variability across Africa (Fig. 4). This analysis, therefore, indicates that the TCI is a valuable parameter to evaluate model characteristics in representing the climate processes over Africa. However, we underscore that the current results are metric-dependent, and considering multiple analyses would be beneficial.

3.3.2 Atmospheric coupling index—temperature (ACItas)

Figure 7 indicates consensus between ERA5 and ENS on the existence of latent heat control of 2-m temperature over parts of Eastern and Southern Africa during MAM. We note large inter-model differences over Eastern Africa, where the HadGEM3-GC31-LL and UKESM1-0-LL, which have the strongest TCI, have the weakest ACItas similar to GISS-E2-1-G. Only GISS-E2-1-G has stood out to consistently underestimate the TCI, ACItas, and other attributes earlier presented. All models, ENS and ERA5, though at differing magnitudes, agree on the Southern Africa latent heat control of surface temperature. The coupling, as measured by ACItas, is not present for the ENS over the Sahel during MAM, though some models and ERA5 have weak signals. In parts of Central Africa, MIROC6 and GFDL-CM4 show erroneously positive feedback between latent heat and temperature. Though consistent with earlier results in Fig. 5a, 6, these two models do not correctly simulate the surface flux climatology over Central Africa. However, we note small regions over Central Africa where ERA5 is consistent with findings from Gallego‐Elvira et al. (2019), that over wet and forested regions, the overlaying air could warm faster than the land surface.

Fig. 7
figure 7

ACItas for MAM season for selected CMIP6 models. Hatching highlights regions of significant correlations in models and ERA5, while for ENS, hatching shows areas where all models agree on negative ACItas

Full size image

During JJA, Figure S3, neither ERA5 nor ENS clearly highlights regions of strong coupling. We note that the Sahel’s overall temperature variability is not strongly influenced by surface fluxes, based on ERA5 and ENS. Although the Sahel is a coupling hotspot during JJA (Berg et al. 2017), this is not the case in the ENS due to mixed signals in individual models, such as GISS-E2-1-G and UKESM1-0-LL. However, MRI-ESM2-0 and GFDL-CM4 indicate strong ACItas over the Sahel and parts of Eastern and Southern Africa. The rest of the models show weak signals, while for CNRM-CM6-1, the spatial distribution of ACItas spans through northern parts of Central Africa to the Sahel. Comparing these results with Sect. 3.3.1, we note that negative feedback between latent heat flux and temperature generally exists in regions of positive feedback between SM and HFLS. Earlier results by Taylor et al. (2007) identified West Africa as a coupling hotspot, whereby regions of positive soil moisture anomalies were about 3 K cooler.

Although some models, such as HadGEM3-GC31-LL and UKESM1-0-LL, had the strongest TCI over Eastern Africa and the Sahel during the respective rainfall seasons, the signal for ACItas was weakest. MRI-ESM2-0 and GFLD-CM4 overestimated ACItas over the Sahel but could not accurately simulate the unique signature of the TCI during JJA. It implies that some models cannot accurately represent processes related to surface fluxes control of boundary layer variables, especially during the rainfall seasons. Further, the inter-model difference between TCI and ACItas shows that it is useful to evaluate all key processes rather than relying on metrics focused on a single feature.

3.3.3 Atmospheric coupling index (ACIpr)

The atmospheric coupling index based on rainfall, ACIpr, indicates some degree of coupling over parts of Eastern and Southern Africa during MAM (Fig. 8) and the Sahel during JJA (Figure S4) in ERA5. These are regions where precipitation responds to surface fluxes, indicating the overall L–A feedbacks are key climate processes over parts of Eastern and Southern Africa. Although seasonal rainfall is primarily driven by synoptic features, these results suggest that land surface feedbacks are key forcings in the intra-seasonal timescales. For instance, a reduction in the Bowen ratio over more moist boundary layers, accompanied by a drop in temperature, creates a shallower PBL where convection is favorable (Taylor et al. 2018).

Fig. 8
figure 8

ACIpr for MAM season for selected CMIP6 models. Hatching highlights regions of significant correlations in models and ERA5, while for ENS, hatching shows areas where all models agree on positive ACIpr

Full size image

The ENS is generally weaker for both seasons while indicating spatial agreement with ERA5. There are notable intermodal differences, especially over West Africa and south of the Sahel in MAM, but with consensus over Eastern and Southern Africa. Except for CNRM-CM6-1 and GISS-E2-1-G, the rest of the models indicates good agreement on the spatial characteristics of ACIpr over the Sahel during JJA. Compared with the other indices, inter-model differences are less pronounced for ACIpr in both seasons. Models with strong TCI do not necessarily depict strong ACIpr. However, these metrics are consistently weaker in both seasons for ERA5 than individual models.

4 Discussion

In general, there is consistency in the spatial variability of the different coupling indices, TCI, ACItas and ACIpr, across the models and ERA5. Despite differences in magnitudes and spatial characteristics, the current results indicate that L–A coupling hotspots are located over Eastern Africa and the regions south of the Sahel during MAM and in the Sahel during JJA (Dirmeyer et al. 2013). The coupling patterns are sensitive to the prevailing climate conditions. In off-season regions such as the Sahel during MAM, the soils are dry and thereby do not drive the variability of the local climate, while in Southern Africa, the presence of L–A coupling during MAM and JJA is indicative of SM memory from the preceding months (Dirmeyer et al. 2009). Indeed, based on the annual cycle, we note that Southern Africa has the smallest range of SM variability, indicating a slow decay from a peak in February to a minimum in September/October, just before the start of the southern hemisphere summer rainfall.

Over regions of strong coupling in the Sahel and Eastern Africa, land–atmosphere coupling has been linked with the increase in surface temperatures during anomalously low SM events at sub-seasonal to seasonal timescales (Talib et al. 2022; Abera et al. 2020). This is related to SM controlling the partitioning of latent and sensible heat flux in transitional zones (Gallego‐Elvira et al. 2019). Furthermore, in the Sahel, spatial gradients of soil moisture have been linked to convective initiation (Taylor et al. 2011), hence positive SM—rainfall feedback, as presented in the current study. L–A hotspots are, therefore, key regions where feedbacks within the climate system could enhance extreme climate events such as rainstorms, heat waves, and droughts (Taylor et al. 2007; Durre et al. 2000). Therefore, it is essential to study L–A interactions, especially at sub-seasonal timescales where high frequency and intensity variabilities can be identified.

The coupling characteristics in ERA5 can be explained by the interannual variability of the forcing variables, SM and HFLS (Supplementary Figures S5 and S6). Indeed, significant forcing can only be exerted if the forcing variable is not constant and a degree of variability is triggered in the response variable. Given that correlations are significant in most African regions, including a measure of variability is useful to overcome the weakness of simple linear relationships. The high interannual variability of soil moisture and latent heat over Eastern Africa, stretching to western Africa and parts of Southern Africa, coincides with strong TCI and ACI indices. GISS-E2-1-G had minimum variability of both the soil moisture and latent heat (Supplementary Figures S2 and S3), and consequently, the strength of the coupling indices is damped. The substantial variability in HadGEM3-GC31-LL soil moisture may be attributed to a much shallower depth of 5 cm resulting in a strong TCI. For the different L–A coupling indices considered, the spatial patterns are controlled by the standard deviation (interannual variability) of the respective variables (Supplementary Figures S5 to S10).

We noted general model consensus on the representation of coupling indices, especially over Eastern and Southern Africa during MAM and the Sahel in JJA. This points to a realistic behavior of the models at the extremes of the SM spectrum. Most models overestimate the terrestrial coupling leg over the Sahel, Eastern, and Southern Africa. Indeed, previous results by Lei et al. (2018) and Dirmeyer et al. (2018) show that most global models are biased to overestimate the strength of the coupling. Models that over-estimate L–A coupling also tend to erroneously amplify temperature extremes (Ukkola et al. 2018). GLACE-CMIP5 results by Zhou et al. (2019) indicate that soil moisture coupling amplifies drought events in historical and future timescales. Historical observations have also confirmed that prolonged droughts are usually located in regions of strong L–A coupling (Cook et al. 2010 and Miralles et al. 2014). Miralles et al. (2014) noted that even with pre-existing synoptic conditions, negative anomalies of soil moisture played a role in the intensification of the major heatwave events of 2003 and 2010 in Europe. It is, therefore, paramount that models accurately represent the L–A interactions to provide reliable information on the current and future climate hazards.

We found that L–A coupling is prominent in Africa's arid and semi-arid lands during the respective rainfall seasons. This underscores the findings of Santanello et al. (2018) that in arid and semi-arid regions, the performance of the land surface models outweighs the boundary layer parameterizations, unlike in the wet regimes. SM anomalies could, therefore, potentially enhance the severity of respective rainfall and temperature anomalies in these regions, such as droughts and heat waves. This understanding could further be exploited for sub-seasonal to seasonal predictability. Models showed enhanced sensitivity to land surface forcing compared to ERA5, especially over the Sahel and East Africa, and problematic coupling over Central Africa. The overestimation of the coupling of the indices could be related to the strong inter-annual variability of SM and HFLS. This study suggests a need for an improved understanding of drivers of inter-annual variability in models, together with biases, to inform model improvements, especially on land surface forcing to the lower atmosphere. The evaluation of L–A interactions in this study can inform the development of robust land surface models in the next-generation climate models beyond CMIP6.

5 Conclusion

We have evaluated the land–atmosphere coupling in selected CMIP6 models over diverse climatic zones in Africa. The annual cycle over different regions indicated good agreement between ERA5 and other reference datasets, including CHIRPS rainfall, ESA-CCI soil moisture, REA-ET evaporation, and GIMMS LAI datasets. In models, the seasonality in P–E, SM, and LAI is generally well represented, despite biases in magnitudes and seasonality. Inter-model differences in the annual cycles, especially in LAI, point to weaknesses of the specific model parameterizations. Models showed agreement in the seasonal biases of P–E over East Africa, where P–E was greater in the short rains than in long rains. Model biases in P–E were highest during the respective rainfall seasons and could also be traced to SM and LAI. Models tend to overestimate the P–E during the peak rainfall months over Africa except for the long rains over Eastern Africa.

Models accurately represented the soil moisture-limited regime over Eastern Africa and the Sahel, while for the wet regime in Central Africa, half of the models could not simulate the SM-HFLS regime. This indicates that interactive processes, such as the coupling between the SM and HFLS in models, are sensitive to the local climate. This may be controlled by the specified land surface and boundary layer parameterizations. Though there are significant inter-model differences, models tend to overestimate the terrestrial segment of the land–atmosphere coupling. Inter-model discrepancies, related to the model inter-annual variability, are more pronounced for the atmospheric coupling indices, unlike the terrestrial. We note that rainfall is an important factor in L–A interactions, as pronounced land–atmosphere interactions were identified during the respective rainfall seasons over the Sahel, Southern and Eastern Africa. Comprehensive process-based diagnostics are necessary to understand model characteristics and should be a priority for research on L–A interactions over Africa.