1 Introduction

The contribution of cloud cover to the Earth’s energy budget (the cloud radiative effect; CRE) has long been of interest to climatologists. In general, clouds trap longwave radiation emitted from the surface and exert a warming effect on the surface (a positive longwave CRE). However, clouds can also exert a cooling effect on the surface because cloud particles reflect shortwave radiation from the sun (a negative shortwave CRE). The sum of positive longwave CRE and negative shortwave CRE is called net CRE (or simply CRE). If the CRE is strongly positive, the increased cloudiness will significantly warm the surface, while a strongly negative CRE will cool the surface. The CRE therefore indicates how the surface temperature will respond to changes in cloud cover. In practice, the CRE is calculated by the difference in incoming longwave or shortwave radiative flux between cloudy and clear (cloud-free) conditions (Liou 2002).

In current climate models, the greatest source of uncertainty in global cloud feedback is associated with tropical upper-level clouds (TUCs) (Mauritsen and Stevens 2015; Sherwood et al. 2020). This is because TUCs have various optical thicknesses and vast coverage, while the CRE of TUCs has a poorly understood impact on climate, contrary to the shortwave-sensitive deep convective core (Gasparini et al. 2019). TUCs are often produced by the outflow of convective cloud tops, and readily spread downwind in the upper troposphere. TUCs also persist for longer than any other clouds due to the low saturation vapor pressure of ice particles (Houze 2014) and therefore have a major impact on climate.

With respect to TUCs’ responses to surface temperature, it is unclear how clouds respond to changes in surface temperature. Lindzen et al. (2001) (hereafter LCH01) initially suggested the “iris hypothesis”, in which cirrus outflow decreases due to increased precipitation efficiency in response to surface warming. Subsequent studies reported that a decrease in TUC area is associated with self-aggregation of convection following an increase in temperature (Wing and Emanuel 2014; Muller and Bony 2015). Clear shrinkage of TUC cover in response to warmer surface temperatures was found in CloudSat observations (Igel et al. 2014). The shrinkage of TUCs was revisited by a study of NASA’s A-train satellite and Tropical Rainfall Measuring Mission (TRMM) data (Choi et al. 2017). In large-scale dynamics, shrinkage of TUC cover may be associated with a tropical ascent motion of Hadley circulation (Su et al. 2017). The climatic impact of shrinking TUC cover is fundamentally dependent on whether the CRE of TUCs is positive or negative. How TUCs affect the entire climate system by modulating the radiation balance remains unclear (Lindzen and Choi 2021).

The conventional wisdom was that TUCs have a positive CRE due to the dominance of longwave over shortwave radiation (assuming the TUCs are optically thin in the shortwave band). However, TUCs are sometimes optically thick at short wavelengths, as in the case of cirrus and near-cumulonimbus or -nimbostratus clouds, for which the CRE is nearly zero or negative. That is, the magnitude of shortwave CRE immediately changes the sign of net CRE. For this reason, previous studies that used satellite observations to investigate the CRE of TUCs have come to disparate conclusions. For example, Ramanathan and Collins (1991) claimed a negative CRE of TUCs acts as a natural thermostat regulating sea surface temperatures (SSTs) by shielding shortwave radiation. According to Choi and Ho (2006), a negative CRE is associated with TUCs with a total-column cloud optical depth ≥ 10, which applies to cumulonimbus, nimbostratus, and TUCs overlying cumulus clouds. Meanwhile, a positive CRE is common in the Moderate Resolution Imaging Spectroradiometer (MODIS) and Clouds and the Earth’s Radiant Energy System (CERES) datasets regardless of region and season over the tropics.

Several attempts have been made to determine the CRE of TUCs. L’Ecuyer et al. (2019) found optically thin upper-level clouds exert a positive CRE (a net warming effect of + 2.0 W m−2 for area-weighted global average) based on CloudSat and Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) observations from 2007 to 2010. Hartmann and Berry (2017) claimed to find neutrality in the CRE for TUCs due to compensation for a negative CRE in initially thick TUCs and a positive CRE for thinning and rising TUCs during the life cycle of TUCs based on the CALIPSO-CloudSat-CERES-MODIS (CCCM) dataset. Hartmann et al. (2018) further confirmed a neutral CRE by simulating a horizontally homogeneous elevated ice cloud in a two-dimensional framework using a cloud-resolving model. However, Kang et al. (2020) suggested that these satellite-based CRE estimates for TUCs should result in a positive CRE, as CREs are easily underestimated due to the presence of the negative shortwave CRE of low-level clouds below TUC cover. According to Ito and Masunaga (2022), who tested physical processes to explain the shrinkage of TUC cover in warmer climates—one test involved precipitation efficiency and the other upper-tropospheric stability using a CCCM dataset—a neutral CRE for TUC cover resulted due to the offset between longwave and shortwave CREs of TUCs when averaged over a diurnal cycle. The CRE values of TUCs from multiple previous studies appear to be inconsistent. However, the lack of agreement among these studies may be a result of differences between observed TUC cover (instantaneously changed to surface temperatures) and expected TUC cover (eventually adjusted during the equilibration toward a warmer climate state). Investigation of the CRE of the latter TUCs is the purpose of this study.

To investigate the CRE of TUCs with respect to global warming, this study explores the CRE in the framework of a radiative-convective equilibrium (RCE) model in which TUCs are constrained by 18 years of daily MODIS cloud data. The model was first proposed by LCH01, but was tested with different coefficient settings in this study. The model is described in greater detail in the next section. Previous studies have reached contrary conclusions compared with those of LCH01, despite using the same RCE model. Lin et al. (2002) (hereafter L02) concluded that the dominant radiative effect of TUCs was a shortwave negative CRE. Chambers et al. (2002) also posited a negative CRE when they applied CERES data to the RCE model, while the opposite was true in LCH01. Chou et al. (2002) demonstrated that differences in the estimates of regional reflectivity and outgoing longwave radiation can lead to different assumptions about feedback from TUCs. Specific reasons for the different results of LCH01 and L02 are explained in greater detail in the Results section.

2 Materials and methods

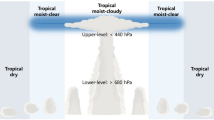
Figure 1 illustrates the structure of the RCE model (LCH01) used in this study. It includes moist and dry tropical regions and the extratropics. The tropical moist regions include two sub-regions (clear-moist and cloudy-moist regions). The main difference between the two sub-regions is the existence of upper-level clouds. In our RCE model, upper-level cloud cover varies with changes in moist air based on the nearly linear positive relationship between upper-level clouds and humidity described by Udelhofen and Hartmann (1995). Upper-level clouds are primarily cirrus clouds, which spread horizontally more than 50 km from the convective core, where considerable portion of upper-level clouds are consisted of thin cirrus clouds (cloud optical depth <  ~ 10) (Choi and Ho 2006). Only upper-level clouds exist in cloudy-moist regions, while other regions in the tropics are assumed to have only lower-level clouds. As shown in in Fig. 1, upper-level cloud cover was initially set to a fraction of 22% and an albedo of 0.24, while lower-level clouds were set to a fraction of 25% and an albedo of 0.42 (LCH01). Values for cloud fraction and cloud albedo are selected to be consistent with the global mean temperature being 288 K and match Earth Radiation Budget Experiment (ERBE) observations (Barkstrom 1984). We not only used these values, but also tested other values based on observations.

Fig. 1
figure 1

Conceptual design of a radiative-convective equilibrium (RCE) model. The model includes 22% upper-level clouds with an albedo of 0.24 and 25% lower-level clouds with an albedo of 0.42 in the tropical moist regions and only lower-level clouds with identical properties in the tropical dry regions. Reflectivity for the tropics and extratropics are 0.24 and 0.40, respectively. Equations written on each box indicate the emission temperatures for the regions. We assume upper-level clouds only in the cloudy and moist regions in the tropics

Full size image

With two cloud layers, tropical moist regions can involve four types of zones: single-layered upper-level clouds, single-layered lower-level clouds, multi-layered clouds, and clear sky. Study LCH01 gave the reflectivity of tropics, extratropics and tropical clear-sky of 0.24, 0.40 and 0.13, respectively, to match a surface temperature (Ts) of 288 K, with a planetary reflectivity of 0.31 using ERBE measurements. We assumed that these regional reflectivity values remain valid. The emission temperature (Te), considering regional differences in lapse rate and humidity, is similarly prescribed by reflectivity and written on the top of each box in Fig. 1.

We calculated the incoming solar radiation (ISR) for each region in Fig. 1 based on reflectivity, which is modulated by the fraction of the constituent clouds:

$${\text{ISR}}= \, {\text{S}}_{\rm{0}}{(}{\text{Q}}_{\rm{tropics}}\left({\text{A}}_{\rm{m}}\left({1}-{\text{tr}}_{\rm{m}}\right)+ {\text{A}}_{\rm{d}} \left({1}-{\text{tr}}_{\rm{d}}\right)\right){+}{\text{Q}}_{\rm{extratropics}}{\text{A}}_{\rm{extratropics}}{(1}-{\text{tr}}_{\rm{extratropics}}{))}$$
(1)

where ISR is determined by the solar constant (S0), relative solar irradiation (Q), area (A) and total reflectivity (tr) of each region. Subscripts m and d in the first term of Eq. (1) indicate tropical moist and dry regions, respectively. The value for tr is defined by the sum of the fraction of clouds in the regions and their reflectivity (\(\mathrm{tr}=\sum \text{(}{\text{Fraction}}_{\text{cloud}}{) \times ({\rm Ref}}_{\text{cloud}}{)}\)). For example, in the case of the reflectivity for tropical moist regions (trm):

$${\text{tr}}_{{\text{m}}}\, =\, {\text{Fraction}}_{{{\text{upper}} - {\text{level cloud}}}} \times {\text{Ref}}_{{{\text{upper}} - {\text{level cloud}}}} + {\text{ Fraction}}_{{{\text{lower}} - {\text{level cloud}}}} \times {\text{Ref}}_{{{\text{lower}} - {\text{level cloud}}}} + {\text{ Fraction}}_{{{\text{multi}} - {\text{layered cloud}}}} \times {\text{Ref}}_{{{\text{multi}} - {\text{layered cloud}}}} + {\text{Fraction}}_{{{\text{clear}} - {\text{sky}}}} \times {\text{Ref}}_{{{\text{clear}} - {\text{sky}}}}$$
(2)

Here, the area for multi-layered clouds is determined by the product of fraction of upper- and lower-level clouds (Fractionupper-level cloud⋅Fractionlower-level cloud). Each reflectivity of areas with clouds is calculated based on albedo and transmissivity of constituent clouds and clear-sky reflectivity in the Tropics For example, Refupper-level cloud = Albedoupper-level cloud + Transmissivityupper-levelcloud2⋅Refclear-sky/(1 − Albedoupper-level cloud⋅Refclear-sky). Here, transmissivity of each upper- and lower-level clouds is defined using their albedo (transmissivity = 1 − (albedo + 0.07)). Albedo of multi-layered clouds is calculated using properties of both upper- and lower-level clouds (Albedomulti-layered cloud = Albedoupper-level cloud + (Transmissivityupper-level cloud⋅Albedolower-level cloud/(1 − Albedoupper-level cloud⋅Albedolower-level cloud)). Transmissivity due to multi-layered clouds is calculated as follows (Transmissivitymulti-layered cloud = Transmissivityupper-level cloud⋅Transmissivitylower-level cloud/(1 − Albedoupper-level cloud⋅Albedolower-level cloud)).

The total amount of outgoing longwave radiation (OLR) is determined by the Stefan–Boltzmann constant (\(\sigma\)), the area of each region (A) and fourth power of Te following the Stefan–Boltzmann law in Eq. (3):

$${\rm OLR} = \sigma {{\rm (A}_ {{\rm cloudymoist}}}{\rm{T}}_{\rm{ecloudymoist}}^{4}+ {\rm A}_ {\rm{clearmoist}}{\rm{T}}_{\rm{eclearmoist}}^{4}+ {\rm A}_ {\rm{dry}}{\rm{T}}_{{\rm edry}}^{4}+ {\rm A}_ {\rm{extratropics}}{\rm{T}}_{{\rm eextratropics}}^{4})$$
(3)

We then equated OLR with ISR to keep the RCE. The model calculates a value for Ts under the RCE, which demonstrates the balance between atmospheric heating by deep convection and radiative cooling of the atmosphere by radiation. In other words, OLR must be the equivalent to ISR to achieve an energy balance.

Finally, we defined the TUCRE by the adjusted global surface temperature (Ts) in K per the corresponding TUC change in %, as expressed in Eq. (4). Consistent with the common concept of the CRE, the TUCRE by can immediately indicate warming or cooling effects of TUCs:

$${\text{TU}}{\text{CRE}} \,\equiv \frac{\Delta\text{T}_{\text{s}}}{\Delta\text{TUC}}\text{ [K}/\%]$$
(4)

where the changes in Ts that meets the RCE, and those in TUC cover, are denoted as ∆. The change in TUC is \(\pm\) 30% of the initial fraction. Here, a positive (or negative) TUCRE means that Ts increases (or decreases) with increasing TUC.

As discussed in previous studies, the TUC fraction is the key factor in determining ISR. As the TUC fraction not only takes part in the CRE, but also modulates tropical reflectivity in this simulation, we attempted to apply a realistic cloud fraction to the simulations, applying TUC fractions from 18 years of daily satellite observations from MODIS over the entire tropics (30° N to 30° S). We chose to utilize MODIS-observed cloud products, a level-3 MODIS gridded atmosphere daily global joint product (MYD08_D3). From this product, we utilized cloud top pressure and cloud fraction. There have been numerous studies that reported CO2 slicing technique of the MODIS cloud retrieval algorithm has improved the detection of microphysical properties of upper-level clouds (Menzel et al. 2008; Kim et al. 2019). Also 1.38-\(\upmu\)m channel of MODIS sensor is well known for its sensitivity to the identification of cirrus for daytime in viewing conditions (Ackerman et al. 2002), as the peak of this band is at the strong water vapor absorption region a 1.38-\(\upmu\)m reflectance is sensitive to the presence of thin cirrus (Gao et al. 1993). Using such advantage, Choi and Ho (2005) has reported that MODIS-observed upper-level clouds include more this cirrus fraction compared to the Geostationary Meteorological Satellite-5 (GMS). To take upper-level clouds over the tropics, we limited cloud-top pressure of less than 440 hPa to the cloud fraction by referring to ISCCP cloud classification (Rossow and Schiffer 1991). Here, deep convective cores will not take a great part in this fraction (12.72% among tropical cirrus clouds), which has already supported by the satellite observations (Choi and Ho 2006).

There have been numerous reports dealing possible linkage between tropical upper- and lower-level clouds. For example, lower-level clouds may be linked to upper-level clouds in their development features by tropical convective aggregation (Wing and Emanuel 2014; Muller and Bony 2015). Also, subsidence due to the Hadley circulation could decrease the lower-level clouds over the Tropics when upper-level clouds decrease (Myers and Norris 2013). Accordingly, we refer to this link to as “the coupling strength” (C) that is also considered in our TUCRE calculation. Choi et al. (2017) reported the correlation between upper- and lower-level clouds over the Pacific warm pool (130° E–170° W, 20° S–20° N) using the CALIOP cloud fraction. Based on Choi et al. (2017), we developed an equation for lower-level clouds over tropical moist regions in correlation with the MODIS-observed TUC:

$${\text{Fraction}}_{{{\text{lower}} - {\text{level cloud}}}} {\text{in the tropical moist regions }} = {\text{Fraction}}_{{{\text{lower}} - {\text{level cloud}}}} + {\text{C}}\cdot{\text{Fraction}}_{{{\text{upper}} - {\text{level cloud}}}}$$
(5)

where C is the coupling strength, which varies from − 0.2 to + 0.2. It is to involve the simultaneous fraction change in upper- and lower-level clouds over the Tropics. Even though two cloud layers vary independently by different mechanisms, the initial source for not only upper-level clouds but also lower-level clouds is tied to the sea surface temperature (Bretherton et al. 2013; Klein and Hartmann 1993). Therefore, we referred Choi et al. (2017) which investigated the correlation between tropical upper- and lower-level clouds within the latitude from 20° N to 20° S using satellite observations. They confined their analysis to the subregion of the Tropics to exclude subtropical Hadley subsidence. In other words, when the domain largens to the 30° N to 30° S, inflow of warm and dry air from subtropical Hadley subsidence will weaken the correlation between upper- and lower-level clouds. For this reason, we assure that the coupling strength between the clouds will be within the range suggested by Choi et al. (2017). Based on this coupling strength, we aimed to reflect the possible coupling relation between tropical upper- and lower-level clouds in the model. The lower-level cloud fraction in the tropical moist regions can therefore be calculated using the TUC fraction and C with the initial lower-level cloud fraction (Fractionlower-level cloud, 25%). In tropical moist regions, when TUC cover expands, lower-level clouds also develop or conversely shrink, depending on the sign of C. If the coupling strength is positive (or negative), the lower-level cloud increases (or decreases) as TUC cover increases in tropical moist regions. When the coupling strength is zero (C=0), upper-level and lower-level clouds are independent. Since upper-level clouds exist only in tropical moist regions, the coupling strength is only applicable with these regions. Therefore, we keep other conditions but lower-level clouds identical to the conditions of simulation when coupling strength is not applied.

For the 18 years of daily TUC fractions observed by MODIS, we analyzed the resulting TUCREs in the model using box plots. This allowed us to explore how the different coupling strengths between upper-level and lower-level clouds in the tropical moist regions changed the TUCRE. Because it is challenging to confirm how upper-level and lower-level clouds develop in tropical moist regions, coupling strengths applied in this study could provide only a feasible range for the TUCRE.

3 Results

Previous studies have shown that the TUC fraction (Fractionupper-level cloud) and tropical reflectivity (trm and trd) in the RCE model are crucial to estimating the TUCRE. To understand the sensitivity of the TUCRE to these factors, we first used the key input parameters from previous studies, LCH01 and L02 (Table 1), and calculated the Ts response to the change in TUCs for the input parameters (Fig. 2). LCH01 and L02 produced completely opposite results (a positive TUCRE from LCH01 and a negative TUCRE from L02). Consistent with these studies, our results also show that Ts rises in response to an increase in TUC cover (a positive TUCRE) when applying input parameters in LCH01, while the opposite was shown for L02 (a negative TUCRE). The TUCREs for LCH01 and L02 were + 0.22 K/% and − 0.05 K/%, respectively, implying a 1% increase in TUCs’ contributions to Ts changes of + 0.22 K and − 0.05 K, respectively.

Table 1 Input parameters in LCH01 and L02
Full size table
Fig. 2
figure 2

RCE model simulation results of changes in Ts in response to changes in the TUC fraction using inputs from Lindzen et al. (2001) (black circles) and Lin et al. (2002) (open circles). Differences in TUC fraction and reflectivity are compared in Table 1

Full size image

The LCH01 study reported that the area of TUC cover per unit area of cumulus clouds decreased by approximately 22% for every degree Celsius increase in the mean SST of cloudy regions (cloud-weighted SST) using observed brightness temperatures measured at the 11-µm and 12-µm channels of the Japanese Geostationary Meteorological Satellite. In the case of L02, the authors stated that the total area of clouds with a brightness temperature < 260 K was found to be 10% using CERES on board the TRMM (Simpson et al. 1996). For tropical reflectivity, L02 utilized CERES observation data, while LCH01 calculated the parameters based on the portion of constituent clouds and their reflectivity in each region, with albedos of 0.24 and 0.42 for the upper- and lower-level clouds, respectively, to match ERBE observations. L02 derived the reflectivity of tropical dry regions by averaging the largest 50% pixels of the OLR and reflectivity in the total TRMM CERES data, assuming that a large OLR corresponds to a dry atmosphere. LCH01 specified the reflectivity of each region individually in consideration of the detrainment of cumulus clouds and the moistening of upper troposphere. The resulting reflectivity values over tropical moist and dry regions (trm and trd) were 0.27 and 0.21 for LCH01 and 0.31 and 0.15 for L02. A comparison of the two studies suggests that the TUCRE in the present model is extremely sensitive to the choices of trm, trd, and Fractionupper-level cloud.

We then applied the TUC fraction and tropical reflectivity based on satellite observational constraints to the RCE model to conduct a thorough inquiry of the TUCRE. By changing the TUC fraction in Eq. (1), both Am and trm can be updated, resulting in different ISRs. In Fig. 3, the shading indicates the range between the maximum and minimum of the variables, and the black line indicates the daily average. The reference is indicated by the dashed horizontal lines for corresponding values of LCH01 (red) and L02 (blue). (Fig. 3c, has no reference for L02 because their results are out of the range shown in the y axis.) Fig. 3a represents the daily TUC fraction (Fractionupper-level cloud), which varied from 10.91% to 28.03%. Their mean value was 0.21 with standard deviation of 0.02. In Fig. 3b, reflectivity for tropical moist regions (trm) is calculated using Eq. (2) and the TUC fraction in Fig. 3a. Reflectivity for tropical dry regions (trd) was constant at 0.21 as set by LCH01, as there were no TUCs. It was clear that the change in reflectivity for tropical moist regions (trm) follows that in the TUC fraction, because the TUC fraction is one of the key factors for calculating trm in Eq. (2). The values in Fig. 3b showed their mean and standard deviation as each 0.27 and 0.01. Finally, the calculated TUCREs using Eq. (4), which were based on the observational constraints in Fig. 3a,b, are plotted in Fig. 3c. We found small changes in the TUC fraction and reflectivity for tropical moist regions (trm) led to a wide range of TUCREs, from 0.19 to 0.33 K/%. The mean of TUCREs was 0.22 with the standard deviation of 0.01. Although we conducted additional experiments with different assumptions for simulation conditions, all values remained in the positive range. The following sections contain the simulation results and detailed explanations.

Fig. 3
figure 3

a MODIS-observed daily Fractionupper-level cloud over the tropics (30º N–30º S) (TUC Fraction) for 2003–2020. b Reflectivity of tropical moist regions (trm) based on the TUC fraction in (a). c TUCREs simulated using TUC fractions in (a) in the RCE model. Shading indicates maximum and minimum values for each variable. The black line represents a daily average of each variable over 18 years. The red (or blue) broken line is the value and result from Lindzen et al. (2001) (or Lin et al. 2002) used for the reference. There is no reference from Lin et al. (2002) in (c) because the result is out of range (\(-\) 0.05 K/%)

Full size image

We tested TUCREs by taking into account the coupled strengths between the two cloud layers in the RCE model. When the coupling strength (C) was positive (or negative), lower-level clouds decreased (or increased) when TUC cover decreased. Figure 4 represents the observationally constrained TUCREs with C using box plots. Coupling strength was applied only within the tropical moist regions, as there were no upper-level clouds in other regions. In the simulation, we based TUC cover on the MODIS-observed daily upper-level cloud fraction, while lower-level cloud cover was based on Eq. (5). Parameters in other regions were identical to the former simulations. In Fig. 4, each box includes the minimum, maximum, first and third quartiles, and the mean value of the TUCREs for a given coupling strength on the x axis. Compared with the TUCRE range, and without consideration of coupling between upper- and lower-level clouds (from 0.19 to 0.33 K/%), the TUCRE involving C between two cloud layers ranged from 0.14 to 0.40 K/%. This is larger than the simulation result when we manipulated single-layered TUC cover in isolation due to the interaction between upper- and lower-level clouds, which resulted in different TUCREs. For the TUCRE when C=0 (no dependency between upper- and lower-level clouds), the TUCRE ranged from 0.19 to 0.33 K/%. This result is identical to that supplied in Fig. 3c. When C was negative, the TUCRE was larger because more ISR is incoming due to the smaller reflectance of shortwave radiation resulting from decreased lower-level cloud cover. For C= − 0.2 and − 0.1, the TUCRE ranged from 0.25 to 0.40 K/% and from 0.22 to 0.37 K/%, respectively. For a positive C, the TUCRE was smaller due to the interplay of both upper- and lower-level cloud cover. When they both increased, the ISR becomes smaller due to both the screening of upper-level clouds and the reflectance of lower-level clouds. As two cloud layers trap OLR together, the resulting TUCRE is small. For C = 0.2 and 0.1, the TUCRE ranged from 0.14 to 0.27 K/% and from 0.17 to 0.30 K/%, respectively. Consequently, simulated TUCREs involving diverse lower-level cloud covers coupled with the upper-level clouds in tropical moist regions were also positive, which implies a significant longwave effect of the TUCs.

Fig. 4
figure 4

The TUCRE as calculated based on the coupling strength (C) between TUCs and lower-level clouds in tropical moist regions. The box plot includes a minimum, a maximum and quartiles of TUCRE. C is assigned to the satellite observational TUC with different coupling strengths. A positive (or negative) C indicates a decrease (or increase) in lower-level clouds when upper-level cloud cover decreases in the tropical moist regions. C is 0 when two cloud layers are independent

Full size image

Figure 5 illustrates how the TUC fraction and tropical reflectivity (trm and trd) affect the TUCRE in the RCE model. Fifteen combinations of trm and trd are shown in the legend. The x and y axes represent the TUC fraction and resulting TUCREs, respectively. Shading indicates observationally constrained TUCREs in Fig. 4 (from 0.14 to 0.40 K/%). As constituent clouds in tropical moist and dry regions both have an impact on the reflectivity of each region, we broke down the impact of reflectivity and the TUC fraction separately.

Fig. 5 
figure 5

TUCRE estimates based on simulations with 15 combinations of reflectivity between tropical moist and dry regions (trm: trd) and 5 different TUC fractions on the x axis. The shading indicates the range of observationally constrained TUCREs in Fig. 4

Full size image

First, we analyzed how the albedo of TUCs in tropical moist regions can affect the TUCRE. The stronger (or weaker) the albedo of TUCs, the more (or less) it will affect trm. Specifically, when the TUCs are too thin to reflect solar radiation, there may be a little change in ISR when the TUC fraction varies because most of the shortwave radiation can penetrate the clouds regardless of their fraction. However, if the TUCs are thick enough to have a high albedo, the ISR will increase in response to contractions of the clouds. However, the trapping effect (the difference in absorbed longwave radiation emitted by TUCs from the surface and re-emitted longwave radiation by the far colder TUCs), is sensitive to the fraction of TUCs. In other words, although the surface emits energy corresponding to the absorbed heat to maintain the energy balance, TUCs keep the energy in the atmosphere according to their top temperature. Consequently, changes in thin TUCs with a low albedo result in a larger TUCRE due to the substantial difference in the incoming shortwave radiation while the outgoing longwave radiation is nearly the same.

To determine the impact of the TUC fraction on variation in the TUCRE, we simulated TUC cover of different fractions from 10 to 50% with 15 combinations of trm and trd values. The cases with a larger cloud fraction showed smaller differences among the TUCREs across diverse combinations of tropical reflectivity. For example, as shown in Fig. 5, when we compared the cases where trm:trd = 0.35:0.15 but with 10% and 20% TUC cover (\(\times\) markers in the columns for 10% and 20%), the resulting Ts change was different even though incoming solar radiation was identical in both cases. In the former case, due to smaller TUC cover, clear-moist regions and dry regions in the tropics were affected more by changes in Ts compared with how cloudy-moist regions responded to longwave emissions. This is because regions with higher emission temperatures contributed more to longwave emissions; Ts decreased when TUC cover increased, resulting in a negative TUCRE. The latter case, which was simulated with relatively larger TUC cover, resulted in a positive TUCRE. This indicates that the effect of a relatively larger TUC fraction is more powerful, transcending the impact of a large difference between trm and trd.

By comparing TUCREs with 5 TUC fractions and 15 combinations of trm and trd, we explored how these factors affected the TUCRE in the RCE model. TUCREs varied widely, from a weak negative to strong positive, depending on the combinations of trm and trd, even with the same TUC fraction. For example, the case where trm:trd = 0.35:0.15 with 10% of TUC cover (\(\times\) marker in the columns for 10% TUC fraction), TUCRE resulted in the negative value. It is due to the strong reflectivity of tropical moist regions with small TUC fraction. Consequently, different combinations of reflectivity have stronger (or weaker) impacts on the TUCRE when the TUC fraction is relatively small (or large).

4 Discussion

Observationally constrained TUCREs were strictly positive, ranging from 0.19 to 0.33 K/% in the framework of an RCE model. When we considered the impact of C between upper- and lower-level clouds, the TUCRE was smaller due to the stronger C. This is because the increase in both upper- and lower-level cloud cover due to the stronger coupling strength reflected a higher ISR, resulting in less heat reaching the atmosphere. The OLR will be also decreased to maintain the RCE, leading to smaller changes in Ts, and a small TUCRE. The increased ISR due to the reduced lower-level cloud cover when C is negative means the TUCRE is large, just as in the cases when C is positive. Consequently, reflecting C between upper- and lower-level clouds, a TUCRE resulted in a range of 0.14 to 0.40 K/%. By applying 18 years of daily satellite observations of the TUC fraction, we found that the net TUCRE was positive, which implies that TUCs have stronger longwave than shortwave effects when TUCs increased. In particular, the positive TUCRE range from our experiments also involves a linkage between upper-level and lower-level clouds. Based on these results, we concluded that climate system warm when TUC cover increases.

For using MODIS-observed TUC, there was no separation of thin and thick upper-level clouds in this study. It is because of the small fractional area of deep convective cores among upper-level clouds (Choi and Ho 2006). However, if deep convective cores are excluded from the TUC, reflectivity of tropical moist regions will be decreased, leading to the stronger TUCRE (Fig. 5). In this point, we again highlight that TUCREs considering the separation of thin and thick clouds may highly be in the positive range, when we refer the average value of reflectivity of tropical moist regions is 0.27.

When calculating the TUCRE, we confirmed a linear relationship between the TUC fraction and Ts (Fig. 2). This is because the TUC fraction and trm have a linear relationship, as expressed in Eq. (2), and both are key factors for determining ISR, as expressed in Eq. (1). Ts varies linearly with the TUC fraction because the atmosphere maintains RCE state by emitting OLR, a quantity expressed in Eq. (3). On the other hand, we found a non-linear relationship between the TUC fraction and the TUCRE (Fig. 5). Although the TUC fraction and Ts have a linear relationship, because the absolute Ts differs according to the choice of trm, trd, and TUC fraction, the TUC fraction and TUCRE have a non-linear relationship.

The RCE model can be criticized as it is based on simplified physics and dynamics compared with complex climate models. However, it is affordable and can generate detailed estimates of TUCREs and offers the following advantages. First, the RCE model can investigate changes in global mean Ts by using TUCs alone, not by clouds in a total column. Second, it is possible to manipulate not only the cloud fraction but also specific microphysical properties of clouds, such as albedo. Using TUC cover, which is our primary variable in the simulation, we were able to project diverse fractions and albedos using direct settings. Such advantages allow us to apply satellite-observed TUC fractions to the simulation. This made it possible to determine the feasible range of the TUCRE rather than its absolute value. Third, the RCE model can involve multi-layered clouds in the simulation. Although potential contributions from multi-layered clouds over the tropics to the radiative equilibrium have been being highlighted by multiple studies (L’Ecuyer et al. 2019; Kang et al. 2020), there is a lack of tools to making inquiries about aspects of the TUCRE, including multi-layered clouds. We were able to couple two cloud layers using coupling strength as the RCE model simulates upper- and lower-level clouds using independent settings. As a result, we successfully derived a practical TUCRE range based on the how the low cloud cover is coupled to TUC cover. Finally, the model reflects realistic atmospheric backgrounds by fixing the moist adiabatic lapse rate at 6.5 K km−1. This minimized the uncertainty due to the unstable radiative equilibrium temperature profile of a dry adiabat. By fixing the lapse rate, we were able to incorporate thermal large-scale motions of air masses absorbing sensible and latent heat from the underlying surface into the simulation. As a result, the model sets the Ts at 288 K, with annual mean conditions, and assumes the tropical (or extratropical) surface temperature was 10 K warmer (or colder) than the Ts. The model characteristically assigned each emission temperature for the regions from the Ts of tropics and extratropics, referring to ERBE measurements. Specifically, the model considered convective adjustments in the TUCRE calculation by fixing the relation between Ts and the temperature at featured emission levels to maintain the lapse rate.

The model resulted in a TUCRE from 0.19 to 0.33 K/% using estimates of Ts change corresponding to incoming and outgoing radiation at the top of the atmosphere in response to the variations in TUC cover. We manipulated the predominant factors—TUC fraction, tropical reflectivity, and the coupling strength of upper- and lower-level clouds—in the simulations to determine their potential contribution to the variation in the TUCRE. Our results show that TUC cover exerts a warming effect when the TUC cover increased. By applying satellite-observed TUC fractions, and combining plausible coupled lower-level clouds and upper-level clouds based on coupling strength, we confirmed that the climate can warm due to increased TUC cover. Our results provide a plausible range of TUCREs for projecting future climate scenarios. These results are conceptual features of the TUCRE that may prove useful if compared with TUCREs estimates based on climate model output.