1 Introduction

The climate of Central Africa is of particular importance to global climate, and the region remains very sensitive to climate variability and change, as over most of Africa (Barros et al. 2014). Central Africa also suffers from a lack of attention from researchers in climate initiatives compared to other African regions (Washington et al. 2013; Creese and Washington 2016), despite its importance. Central Africa is one of three key sources of diabatic heating that drives the tropical overturning circulation (Webster 1983), and experiences the highest lightning strike frequency on the planet (Jackson et al. 2009). Also, due to the density of its forest, it represents a vast carbon reserve and is a crucial element in the global carbon cycle (Williams et al. 2007; Dargie et al. 2017). In light of the important role played by Central African climate, understanding general circulation model (GCM) functioning over the region is particularly important to improve prediction (James et al. 2018) of future changes (James et al. 2015; Rowell et al. 2015; Baumberger et al. 2017), which is crucial to populations of the region as they are reliant to rain-fed agriculture (Samba and Nganga 2012).

Studies have advanced understanding of seasonal climatology over Central Africa (Nicholson and Dezfuli 2013; Dezfuli and Nicholson 2013) and dominant rainfall variability processes (Cook et al. 2020, Hua et al. 2019; Longandjo and Renault 2019; Alber et al. 2021, Moihamette et al. 2022). Despite this progress, very few studies (Creese and Washington 2018; Tamoffo et al. 2019, 2021b; Taguela et al. 2022a, b) have evaluated models based on processes responsible for rainfall formation in order to understand reasons behind rainfall biases. Using Regional Climate Models (RCMs), Tamoffo et al. (2019) found representation of rainfall seasonality over the region to be consistent with observed rainfall. Nevertheless, global models from the Coupled Model Inter-comparison Project (CMIP) phase 5 (CMIP5) appear to poorly reproduce regional rainfall distribution during the September to November (SON) rainy season (Creese and Washington 2018). The difficulty in simulating rainfall over the region may be partly due to the complexity of Central African climate processes which are not well represented in coupled models (Creese and Washington 2016, 2018; Crowhurst et al. 2020, 2021; Taguela et al. 2022b). The interconnection of the Central African climate with the climate of other regions such as southern Africa (Kuete et al. 2019; Howard and Washington 2019) may also contribute to the difficulty of models in representing rainfall over the region. One key process known to have a central influence on rainfall formation across the region is the African Easterly Jet (AEJ).

Recent studies using reanalysis data have highlighted the important role of the AEJ-N (Pokam et al. 2012; Dezfuli and Nicholson 2013; Nicholson and Dezfuli 2013) and AEJ-S (Jackson et al. 2009; Kuete et al. 2019) in rainfall variability. Process-based assessment has shown that model rainfall biases are partly associated with bias in location and intensity of AEJ (Creese and Washington 2018; Tamoffo et al. 2019). Creese and Washington (2018) assessed dynamical processes related to model wetness over the eastern Congo basin. Results of their study showed that wet models have a weaker AEJ-N with the mean core located poleward than in reanalyses. Meanwhile a stronger and equator-ward AEJ-N in dry models contributes to a suppression of rainfall in this part of the basin. With a special emphasis on the climatological characteristics of moisture flux convergence, Tamoffo et al. (2019) established that dry biases in Congo basin rains are associated with stronger moisture divergence at mid-troposphere, driven by a strong AEJ at the western boundary, and weaker moisture convergence at the eastern boundary driven by a weak AEJ. Tamoffo et al. (2020) showed that improved RCM simulation of precipitation relative to GCMs over Central Africa is a result of better representation of AEJs. These previous findings suggest model rainfall biases over Central Africa are associated with representation of the AEJs.

The dynamics of the jets in coupled models (Creese and Washington 2018) were analysed using CMIP5 models, and the emphasis was on understanding how the jets are driven, by examining their location and core intensity through representation of the surface gradient in temperature. Their study did not investigate elements explaining the maintenance mechanisms (Chen 2004; Kuete et al. 2019) of AEJs, thus there is limited understanding of the jet dynamics in coupled models (Creese and Washington 2018) compared to reanalyses (Chen 2004; Adebiyi and Zuidema 2016; Kuete et al. 2019).

This study focuses on understanding how the new version of coupled models (CMIP6) represents drivers of AEJ, in order to explain the evolution observed in the previous version of the models (Creese and Washington 2018) compared to the new version. Understanding AEJ dynamics in models could help scientists to improve simulations, to understand models’ rainfall biases, and temperature biases through assessment of the surface temperature gradient and surface heat fluxes.

Previews research has shown that the AEJ is maintained in association with surface heating and dry convection. In the Saharan region, the heat low is important in accelerating the AEJ-N (Cook 1999; Thorncroft and Blackburn 1999; Chen 2004). Following studies from Munday and Washington (2017); Adebiyi and Zuidema (2016) and Howard and Washington (2018, 2019) of the Angola heat low dynamics, Kuete et al. (2019) revealed the crucial role of the Kalahari heat low and southern subtropical westerly waves on the maintenance of the AEJ-S. Future changes in the strength of Sahara and Kalahari heat lows have been examined by Dunning et al. (2018) and results indicated an increase in the strength of both heat lows. As these features significantly contribute to climate variability over Central Africa through modulation of the AEJ components, such future changes are likely to impact on the region’s climate.

Our analyses in the current research have shown the importance of understanding surface temperature bias in models, an aspect that is generally neglected in assessment of coupled models, since emphasis is more often on understanding rainfall bias. This is important for the AEJ system, as previous studies showed that the observed amplified warming over the Sahara heat low (Cook and Vizy 2016) and over the Kalahari heat low (Adebiyi and Zuidema 2016) is increasing the meridional temperature gradient and the AEJ is strengthening. Therefore understanding how coupled models represent mechanisms regulating temperature above the Earth’s surface will advance understanding of AEJ dynamic in coupled models and improve reliability of future projections.

Model evaluation studies in Central Africa have revealed large differences among CMIP5 models, particularly in their historical rainfall estimates during SON (Creese and Washington 2018; Crowhurst et al. 2021). This large variation in model rainfall during SON provides an opportunity to further explore the regional circulation elements controlling the models' rainfall climatology. A common feature is the role of the AEJ components which are well developed during SON.

The first aim of this paper is to better understand the climatological structure of the AEJ components in the new CMIP6 simulations (Eyring et al. 2016; O’Neill et al. 2016) and in their CMIP5 predecessors, and we will answer to the following question:

  1. 1.

    What is the climatological structure of the African Easterly Jet during SON in reanalyses and models?

    The rest of the paper focuses more specifically on the CMIP6 models and will answer the following two questions:

  2. 2.

    What are the drivers responsible for the jet strength variation in models?

  3. 3.

    What are the reasons behind the differences between the drivers in the models and the simulated AEJs?

The paper is structured as follows: Sect. 2 describes the data and methods used in this study. Section 3 describes location and intensities of AEJs. We explore representation of surface temperature gradients in models in Sect. 4. We examine maintenance mechanisms in Sects. 5 and 6. We discuss the results and summarize in Sect. 7.

2 Data and methods

This study is based on monthly mean outputs from sixteen historical experiments of GCMs: 8 simulations from CMIP5 (Taylor et al. 2012) and 8 simulations from the newly developed CMIP Phase-6 (CMIP6) (Eyring et al. 2016; O’Neill et al. 2016). Historical simulations are analysed over the period 1980–2005 for CMIP5 and 1980–2010 for CMIP6, with a focus on SON. Table 1 provides details of the CMIP5 and CMIP6 models included in this study. Models have been selected because they have been frequently used in the literature and therefore will be of interest for comparison with previous work. In particular some CMIP5 models have been identified as representing the region well in previous literature, or showing an unusual representation or interesting biases to be explored. In addition, a comparison of all CMIP5 and CMIP6 models from a process-based perspective is not plausible, at least not in one paper. It is made clear in the conclusions that the results apply to a subset of models from the CMIP ensembles. To assess the capabilities of CMIP models, two reanalysis data are used, ERA-5 (Hersbach et al. 2020) and MERRA-2 (NASA 2017).

Table 1 Name and description of CMIP5 and CMIP6 models and reanalysis data used in this study
Full size table

We analyse monthly averages of mid-tropospheric easterly winds to indentify AEJ. Mean intensity and location of jet core is define as easterly wind speeds exceeding 6 m s−1 (Chen 2004; Adebiyi and Zuidema 2016; Kuete et al. 2019). Process based metrics from previous studies (Cook 1999; Hsieh and Cook 2007; Chen 2004; Kuete et al. 2019) are used to investigate the skill of CMIP models to capture the dynamics associated with the AEJ. This involves investigating how the intense surface heating associated with the subcontinental thermal heat low drives the meridional surface temperature gradient and results in the mid-level AEJ. As the whole AEJ system is supported by a mid-tropospheric thermal circulation, we then show in Sects. 5 and 6 how dry thermal convection over the Namib-Kalahari and Sahara dryland thermal lows supports strong rising motion forming mid-level highs associated with anticycloninc circulation and divergent centres. This process approach is important for the maintenance of the AEJ. Analyses in this study also focus on surface heat flux such as downward solar radiation, sensible heat flux, latent heat flux, and surface upward long-wave radiation.

3 Jet locations and intensities in models

Figure 1 shows the latitude–longitude mean core locations of the two jets for SON in reanalyses and models. Analyses will focus on the longitudinal band 10° E–30° E encompassing Central Africa. There is a good agreement between reanalyses in the mean SON position of AEJ-N and AEJ-S. Both reanalyses present the same east–west variation with an AEJ-N core starting at about 30° E. The AEJ-N core varies latitudinally between 9 and 10.5° N in ERA-5 and between 9 and 10° N in MERRA-2; and the AEJ-S core ranges from 4 to 11.5° S in ERA-5 and 3° S to 11.5° S in MERRA-2. Many CMIP5 simulations fail to locate the latitude of the AEJ-N over northern Central Africa. Exceptions are BCC-CSM1-1-m, MIROC5 and HadGEM2-ES, which simulate a jet position close to that of reanalyses, with the best performance for MIROC5. Other CMIP5 models simulate the jet either farther north (CNRM-CM5-2, GFDL-CM3) or farther south (MRI-ESM1, GISS-E2-R, HadGEM2-CC) compared to reanalyses. Over West Africa, several models miss the southeast-northwest orientation of the AEJ-N core, leading to a gap of around 6° in the location of the jet (e.g. BCC-CSM1-1-m, HadGEM2-CC and GISS-E2-R) between 6 and 12° N. Most CMIP5 models also fail to locate AEJ-S over southern Central Africa. Some models (e.g. GISS-E2-R, MRI-ESM1, HadGEM2-ES, GFDL-CM3, HadGEM2-CC) simulate a jet position close to reanalyses only over western Central Africa between 10 and 20° E, and other models (CNRM-CM5-2 and BCC-CSM1-1-m) simulate a jet position farther north (between 10 and 28° E) compared to reanalyses.

Fig. 1
figure 1

Long-term mean (1980–2010) September to November latitudinal/longitudinal mean core locations of maximum easterly wind (≤ − 6 m s−1) speed at 700 hPa in region of AEJ-N (northern hemisphere) and at 600 hPa in AEJ-S region (Southern Hemisphere). Models are presented in dashed lines and the reanalyses in thicker continuous lines

Full size image

In general, the spread of simulated AEJ location around reanalyses is larger for CMIP5 compared to CMIP6 (Fig. 1), indicating improvement from CMIP5 to CMIP6. CNRM shows a very strong improvement in its CMIP6 version by capturing well both AEJ-N and AEJ-S location compared to reanalyses (Fig. 1), GFDL-CM4 and MIROC6 also show improvement in the AEJ-N. Other models (MRI-ESM2-0, GISS-E2-1-G, UKESM1) locate the jet farther south than reanalysis with a strong latitudinal variation of its core. HadGEM3-GC31-LL simulates an almost constant latitudinal location of the AEJ-N. While CMIP6 models shows an improvement in locating AEJ-N over Central Africa, the spread of the jet locations around reanalyses remain strong over West Africa. The SON climatological AEJ-S is also better simulated by most CMIP6 models compared to CMIP5, but still present some bias relative to reanalyses. For example, GISS-E2-1-G locates the northernmost jet over Central Africa and the southernmost jet over western Equatorial Africa.

Figure 2 illustrates the annual cycle of the AEJs. Improvement of the location of AEJ-N by CMIP6 models spans the SON season, with good representation of north–south annual migration of the jet core (Fig. 2a, b), in agreement with reanalyses. Over Central Africa, AEJ-N is discernible throughout the year, but from December to February, the strength of the jet is relatively weak and its core lies between 0 and 3.5° N in ERA-5 and MERRA-2 (Fig. 2a, b). A northward migration from March to August is observed when AEJ-N intensity strengthens reaching 8 m s−1 in ERA-5 and MERRA-2 with maximum strength of its core in July through August. During these months, the jet reaches its most northern location, and starts shifting south from September to December, with core speeds reaching almost 10 m s−1 in ERA-5 and MERRA-2 (Fig. 2e, f).

Fig. 2
figure 2

Mean intensity in (m/s) and location in (degrees latitudes) of monthly averages of the AEJ-N and AEJ-S jet cores in reanalyses, CMIP5 (a, c, e and g) and CMIP6 (b, d, f and h). Models are presented in dashed lines and the reanalyses in thicker continuous lines. The numbers 91 m s and 42 m s at the top of the panels represent the area between the curve of the annual cycle of jet cores locations in models versus reanalyses, in CMIP5 and CMIP6 respectively

Full size image

AEJ-S is best defined during September to November in MERRA-2 but only present during October and November in ERA-5 (Fig. 2c, d). The jet core location is close in the two reanalyses and ranges from 80S in September to 10° S in November. Its core intensity is less than 7.5 m s−1 in ERA-5 while it reaches 9 m s−1 during October in MERRA-2 (Fig. 2g, h).

To quantify the improvement in AEJ-N core location from CMIP5 to CMIP6 (Fig. 2a, b), the deviation of the jet core location through the year from reanalysis is computed using the trapezium method. This method consists of calculating a numerical integration based on linear interpolation by intervals between January and December. This determines the area between models and reanalysis curves in the annual cycles of AEJ locations (Fig. 2). The area between CMIP6 models and reanalyses curves is small compared to that of CMIP5 and reanalyses. As shown in Fig. 2, where the unit of the area is the multiplication of the time axis unit in second by the latitude position in meter, the spread in location (latitude positions in meters) of AEJ-N through the year in CMIP5 compared to reanalysis is 91 s m (second meter), about twice that of CMIP6 around reanalysis (42 s m). This result shows that location of AEJ-N in CMIP6 models is closer to reanalyses compared to CMIP5 models.

There are differences in AEJ-S location among CMIP5 models with several models simulating the existence of the AEJ-S over more months than ERA5 (CNRM-CM5-2, GISS-E2-R, MRI-ESM1, GFDL-CM3). The GISS-E2-R model presents a strong bias in the AEJ-S location by simulating the existence of its core over the whole year, but a good improvement is observed in its CMIP6 version with a core well pronounced between August through November. However, the CMIP6 version fails to locate the jet core, which is too far north, ranging between 5 and 7° S. The BCC-CSM1-1-m model presents an AEJ-S in February through April (Fig. 2c), but the jet is better located in its CMIP6 version (BCC-CSM2-MR), in September and October. Mean core location of the AEJ-S is generally better simulated in CMIP6 than CMIP5, with some models simulating the existence of AEJ-S over the same months as ERA5 and the spread among models around reanalyses is smaller.

In GISS-E models, AEJ intensities are overestimated in both CMIP5 and CMIP6 versions (Fig. 2e–h), but with a slight decrease in CMIP6. MIROC models also overestimate AEJ-N intensities in CMIP5 and CMIP6, but MIROC5 presents no AEJ-S and its intensity increases in MIROC6 but remains underestimated. In CMIP6 simulations, some models (GISS-E2-1-G, MRI-ESM2-0 and MIROC6) overestimate AEJ-N annual mean core intensity with peaks during June to August. UKSEM1 and HadGEM3-GC31-LL underestimate AEJ-N intensity from June to September but are close to reanalyses during October and November. CMIP6 models also present differences in AEJ-S intensities compared to reanalyses, this is the case of GISS-E2-1-G and CNRM-CM6-1 models, that fail to locate the jet core, and are the two models with the strongest AEJ-S with their core intensities reaching 9.5 m s1. MIROC6 features the smallest AEJ-S with core speeds ranging between 6 and 7 m s−1 in September and October.

Analyses of the jet core locations and intensities has revealed improvements from CMIP5 to CMIP6, but some remaining differences between models and reanalyses, with some models (GISS-E2-1-G, MIROC6 and CNRM-CM6-1) depicting a jet core too far north or south and an overestimation in terms of intensity (too strong). These differences will now be investigated by examining meridional temperature gradients in the lower troposphere.

4 Surface temperature and jet strength in models

AEJs are thermal winds that result from a surface meridional temperature gradient. AEJ-N results from a surface meridional gradient between the hot and dry Sahara and the sub-humid Congo Basin, while AEJ-S results from a meridional thermal gradient between the hot Kalahari and humid Congo basin. It follows that investigation of the driving meridional temperature gradient is an important step in the analysis of AEJ characteristics.

Figure 3 presents the latitude/time annual evolution of the 850 hPa meridional gradient in temperature in reanalyses, and model biases with reference to ERA-5. The brown solid lines in both hemispheres represent the region (outer contour) of maximum surface temperature gradient in ERA5. The maximum meridional surface temperature gradient in the northern hemisphere is positive from north to south and located between 3 and 18° N with the strongest values within the 13–15° N band in August, which corresponds to the month when AEJ-N is at its most northern location. AEJ-N (shown by the black line) forms at the southern (equatorward) boundary of the maximum meridional surface temperature gradient and follows its cross-latitude migration through the annual cycle. The meridional surface temperature gradient in the southern hemisphere is of opposite sign because the gradient is calculated from north to south and, in the case of the southern hemisphere, the warmer temperatures are to the south over the Namib-Kalahari region. AEJ-S (shown by the red line) forms at the northern (equatorward) boundary of the meridional temperature gradient. The climatological structrure of AEJ-S in ERA-5 appears during two months (September–October).

Fig. 3
figure 3

Latitude/time annual evolution of surface 850 hPa temperature gradient (K m−1) climatology in reanalyses (first row), averaged in the longitude range of [14° E–24° E]. With overlay locations of AEJ-N (black contour in the northern hemisphere) and AEJ-S (red contour in the southern hemisphere). Bias of temperature gradient in models against ERA-5 is also represented. To show bias in location of the jets in reanalysis compared to models, we represent in green contour line mean climatology of AEJ-N and AEJ-S in ERA5. We also represent the maximum contour of temperature gradient in ERA5 (dark red line)

Full size image

Most CMIP5 and CMIP6 models underestimate the surface temperature gradient over AEJ-N region with a negative bias (brown shading), except in the MIROC5 and CNRM-CM5-2 models where the bias is positive (turquoise) throughout the annual cycle. In CMIP6 this positive bias persists in MIROC6, but it decreases in CNRM-CM6-1. MIROC therefore has the strongest surface temperature gradient, but with a slight improvement in MIROC6. In most models, the bias is improved from CMIP5 to CMIP6. This could explain why AEJ-N is reasonably well simulated in most CMIP6 models.

In the AEJ-S region, MIROC6 and CNRM-CM6-1 presents the strongest temperature gradient (Fig. 3 shown by the negative shadings). The strong temperature gradient in CNRM-CM6-1 explains improvement of its jet’s core location from CMIP5 to CMIP6, while in MIROC6, AEJ-S intensity varies oppositely to the surface temperature gradient.

To better understand the relationship between temperature gradients and jet strength/location, we performed long-term seasonal means correlation analyses. If these temperature gradients are responsible for the jets intensity in each model, a strong positive correlation between this thermal contrast and the jets strength is expected. The long-term seasonal means are calculated for AEJ intensity and temperature gradient over the domain 14–28° E of longitude and 5–15° S of latitude for AEJ-S and 3–20° N for AEJ-N in each model.

Figure 4 shows long-term means correlation between 850 hPa maximum surface meridional temperature gradient and AEJs intensities for SON, representing the season when the two jets are strong over Central Africa, and when the relationship between mean AEJs intensities and temperature gradient is most pronounced over the region. Figure 4 highlights that, in the AEJ-S region (Fig. 4a, c, e), the surface temperature gradient is strongly correlated with the jet strength during November in reanalyses (r = 0.62 in ERA-5 and r = 0.56 in MERRA-2). During September, ERA-5 and MERRA-2 both present weak correlations, but these strengthen in October. Surface temperature gradient and AEJ-S strength are not always well correlated in most coupled models, except for HadGEM3-GC31-LL, which presents a good correlation higher than 0.5 during the months of September to November. CNRM-CM6-1, GISS-E2-1-G and MRI-ESM2-0 which simulated the existence of AEJ-S during September, October and November, better correlate their jet strength with the surface gradient during October and November but the correlation is weak in September. MIROC6 which locates a maximum jet core intensity over Central Africa during September and October presents a high correlation greater than 0.8 only during October.

Fig. 4
figure 4

Scatter plots showing relationship between September to November long-term mean (1980–2010) 850 hPa surface temperature gradient (K m−1) and AEJs intensities (m s−1) for models and reanalysis. Each dot represents the yearly value in each model

Full size image

For AEJ-N (Fig. 4b, d, f), ERA-5 has higher correlations than MERRA-2. MIROC6 which had the strongest surface temperature gradient, presents strong correlations during September and October. The GISS-E2-1-G model, which simulated the strongest jet from September to November, but had the smallest surface gradient, presents a good correlation only during September. MRI-ESM2-0 and GFDL-CM4 models show good correlations during the three months, while some models (BCC-CSM2-MR, UKESM1 and CNRM-CM6-1) show correlations only during 2 months.

Figure 4 therefore illustrates correlations between surface temperature gradients and jet strength, but in some models the mean strength of the jet intensity do not always relate to the temperature gradient. This suggests that the jets are driven by the surface temperature gradient plus other mechanisms. We will now explore the contribution of other features to both AEJ-N and AEJ-S maintenance, namely the atmospheric energetics analysis and mid tropospheric high located in the vicinity of the jet.

5 African Easterly Jet dynamics in models.

5.1 Atmospheric energetic interactions of divergent and rotational flows

Another mechanism known to have a crucial influence in the AEJ maintenance is the energetic interactions of atmospheric divergent and rotational flows, developed by Chen and Wiin-Nielsen (1976) and further assessed by Wiin-Nielsen and Chen (1993). Chen (2004) highlighted that meridional divergent circulation that spills out of the North African divergent center and accelerates towards the AEJ-N core generates divergent kinetic energy. Divergent circulation is deflected westward under the Coriolis effect at the jet core and leads to conversion of divergent kinetic energy into rotational kinetic energy that accelerates the AEJ-N over West Africa during North African summer. Kuete et al. (2019) evaluated the contribution of this mechanism to the maintenance of the AEJ-S, and showed that, due to the dominance of rotational circulation over divergent circulation at mid troposphere in the AEJ-S region during SON, the contribution of conversion of divergent kinetic energy into rotational kinetic energy was ten times less important in the AEJ-S compared to its contribution to the maintenance of the AEJ-N.

Figure 5 shows vertical profiles of the atmospheric energetic interactions as estimated in Kuete et al. (2019). Conversions exhibit centers of positive values at the AEJ-N core around 700 hPa in ERA-5 and MERRA-2. The AEJ-N is located south of the downward branch of the meridional circulation and associated with uplifts below 700 hPa over the Saharan heat low. Saharan meridional northerlies induce Coriolis acceleration that maintains the AEJ-N as indicated by the mid tropospheric positive values of conversion over the AEJ-N core (green shading). Dry convection over the Kalahari heat low in the south (Howard and Washington 2018) is evident from the surface to 600 hPa (shown by vectors) and links to a peak of divergence. Both zonal and meridional divergent wind components contribute to this divergent center but due to the strong development of the zonal rotational wind component, values of conversions are very weak over AEJ-S core (Kuete et al. 2019), as shown in ERA-5. In MERRA-2, values of conversion are higher over AEJ-S region, due to a stronger acceleration of the divergent flow towards AEJ-S core at 600 hPa. The CNRM-CM6-1 model simulates the energetics well and looks relatively similar to MERRA2 over both AEJ-N and AEJ-S cores. This is generally less consistent in other models which look more like ERA5, with some (e.g. MIROC6, GFDL-CM4 and BCC-CSM2-MR) showing strong positive centers of conversions over the AEJ-N core and very weak peaks over AEJ-S and others (MRI-ESM2-0, GISS-E2-1-G, UKESM1 and HadGEM3-GC31-LL) slightly close to ERA-5 and MERRA-2 over AEJ-N core, but still weak over AEJ-S region.

Fig. 5
figure 5

Latitude/height cross-sections of the atmospheric energetics interaction, representing conversion of divergent kinetic energy into rotational energy (shading in m−2 s−3). AEJs components (black contours in m s−1) and meridional divergent circulation (vectors, vD,w) are overlaid. All variables are averaged over [14° E–24° E] representing the longitudinal core of AEJ in this study

Full size image

Weak peaks of this energetic analysis over the AEJ-S’s core in MIROC6 can be linked to the very weak acceleration of this jet over Central Africa during SON, compared to CNRM-CM6-1 which overestimates AEJ-S intensity and better simulates its mean core location during SON and presents strong values of conversion over the jet core. As a first order diagnostic of the jet's acceleration, most coupled models better simulate the atmospheric energetic interactions over AEJ-N region that leads to its strong contribution to AEJ-N maintenance compared to AEJ-S.

5.2 Mid-tropospheric highs over Africa

As a second step in understanding the dynamics of the AEJ acceleration mechanisms, we investigate the role of the North African mid-level Saharan high in the maintenance of the AEJ-N and the mid-level Botswana high in the AEJ-S. Their formation and maintenance dynamics are also explored.

5.2.1 Saharan high

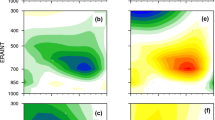
The Saharan high is a conspicuous element of the North African mid tropospheric circulation. The high develops over the land surface and centered at about 20° N described briefly by Cook (1999). The AEJ-N is located at the southern rim of this mid-level anticyclone. We use stream function as a diagnostic variable for the anticyclone during SON. At 700 hPa (Fig. 6) two high pressure systems are depicted over North Africa, the Saharan high around 20° N, 0–20° E and the Arabian high 25° N, 45° E. To show the rotational flow associated with these high-pressure systems, we use total vorticity at 700 hPa in ERA-5 and MERRA-2. In the Northern Hemisphere, vorticity is strong with negative centers at the two highs cores (brown shading). To the south of the Saharan anticyclone, strong positive meridional pressure gradient increase zonal easterly flow from 28° E, marking the entrance into the AEJ-N region in reanalyses. The spatial quadrature of the Saharan high and its associated anticyclonic circulation is well represented in ERA-5 and MERRA-2, with a more easterly extension of the high in MERRA-2.

Fig. 6
figure 6

a Saharan mid-level high represented with stream function (brown contours) at 700 mb. The first contour is at 0 and the contour interval is 1.5. Horizontal wind speed at 700 mb is illustrated by vectors (at 6 m/s). Shading shows total vorticity in reanalyses (first row) and vorticity bias in models against ERA5, to show strength of the anticyclonic circulation associated with the mid-level high. b Botswana mid-level high represented with stream function (brown contours) at 600 mb. The first contour is at 6 and the contour interval is 2. Also is represented the horizontal wind speed at 600 mb (vectors at 6 m/s). Shading shows total vorticity in reanalyses (first row) and vorticity biases in models against ERA5, to show strength of the anticyclonic circulation associated with mid-level high

Full size image

We represent in Fig. 6 total vorticity bias in models against ERA-5. The spatial formation of the Saharan and Arabian highs are well represented in CMIP6. Most coupled models locate the Sahara high pressure system core further west compared to ERA-5 and MERRA-2, except in CNRM-CM6-1 whose core is located further east. GISS-E2-1-G shows a very strong meridional pressure gradient southeast of the Saharan high core between 10 and 25° E compared to ERA-5 and MERRA-2.

The anticyclonic circulation (represented by vorticity bias relative to ERA-5) is underestimated at the core of the Saharan high in all coupled models, but the vorticity bias increases in GISS-E2-1-G at the outer contour of the high pressure at about 25° E, showing a strong rotational flow at this level in the model. The Arabian high pressure also shows a strong meridional pressure gradient west (35° E) of the high pressure marking entrance of the AEJ-N in this model. Thus, AEJ-N acceleration in GISS-E2-1-G is supported by the strong and positive pressure gradient. GFDL-CM4, BCC-CSM2-MR and MIROC6 models present the same circulation as the GISS-E2-1-G model with an increase in total vorticity bias east of the Sahara high pressure system. However, the meridional pressure gradient strong in these models compared to GISS-E2-1-G but close to ERA-5 and MERRA-2. The UKESM1, HadGEM3-GC31-LL and MRI-ESM2-0 models present similar anticyclonic circulation around the Sahara high pressure with a strong meridional gradient south of the high pressure associated with an increase in vorticity bias thus accelerating AEJ-N at its entrance into the jet region at 35° E and maintaining it up to 10° E where the gradient weakens. This mechanism is stronger in MRI-ESM2-0 thus explaining the well simulated and strong AEJ-N (Fig. 2) in this model.

The stream function field associated with the vorticity biases shows rotational flow of the Saharan and Arabian Highs in the models, thus accelerating AEJ-N. On the east side of the Saharan high is the North African divergent center (20° N) which accelerates northerly flows into lower latitudes that are then converted into rotational flow maintaining AEJ-N (Fig. 5). Since this divergent center is formed and maintained in response to heating induced by the Saharan thermal heat low, and the North African divergent center is spatially linked to the Saharan high, this differential heating serves in this study as a formation and maintenance mechanism of the Saharan high. This dynamic process has been described by Chen (2004) and Spinks et al. (2014). Figure 7a presents a vertical profile of atmospheric parameters describing the dynamic process of formation of the mid-level Saharan high. We use vertical velocity (red line) to show vertical uplifts induced by the Saharan thermal heating. To illustrate the vertical representation of the mid-level high and its circulation, we show the stream function (dark green) and total vorticity (cyan). Saharan thermal heating causes air to be warm at the surface, warm air is lifted into the mid troposphere below 600 hPa, illustrated by negative values of vertical velocity from the surface (925 hPa). The change in vertical velocity sign at 600 hPa is associated with sinking cooler air from the upper troposphere, which converges with uplifts from the surface, forming the mid level anticyclone of the Sahara with its peak located at 700 hPa, illustrated by the vertical structure of the stream function.

Fig. 7
figure 7

a Vertical profile of total vorticity (cyan), Omega (red) and stream function (dark green). Variables are for SON and averaged in the core of the Saharan high (18° N–25° N of latitude and 14° E–25° E of longitude). b Vertical profile of total vorticity (cyan), Omega (red) and stream function (green). Variables are calculated for SON and averaged in the core of Botswana high (16° S–22° S of latitude and 14° E–25° E of longitude)

Full size image

The vertical structure of total vorticity shows negative peaks in the mid troposphere between 600 and 700 hPa, indicating the strong anticyclonic circulation at this level associated with the Saharan high. ERA-5 and MERRA-2 present similar vertical structures of these parameters. Most of the coupled models fairly reproduce the vertical structure of the stream function and total vorticity, showing the capability of capturing the horizontal and vertical distribution of the mid-level Saharan high (Fig. 6a) and the anticyclonic circulation associated to it. MRI-ESM2-0 and GISS-E2-1-G show a similar vertical velocity structure associated with positive values of omega over the entire atmospheric column, thus showing a predominance of subsidence from the top of the troposphere to the surface, but more intense in GISS-E2-1-G. Verifications of this dynamic process was performed using an east–west circulation (Fig. S2). We computed the circulation using the magnitude of zonal wind (u) and omega (w). The upward motion caused by the Saharan thermal heating is very weak in MRI-ESM2-0 and GISS-E2-1-G, but the east–west circulation is dominated by subsidence in GISS-E2-1-G and associated with strong easterly flow at the surface in MRI-ESM2-0.

This analysis indicates that the Saharan high, which accelerates strong AEJ-N in MRI-ESM2-0 and GISS-E2-1-G through the associated meridional pressure gradient and vorticity at the southern rim of the high, forms for the wrong reasons.

5.2.2 Botswana high

During SON, the Botswana High is a semi-permanent anticyclone occurring at mid-level (e.g. 600–500 hPa) over Botswana/Namibia. It is formed and maintained in response to heating of the Kalahari heat low, which strengthens upward motion from surface to mid troposphere. Kuete et al. (2019) demonstrated how this high pressure system is connected to the maintenance of AEJ-S. Figure 6b illustrates the 600 hPa stream function field (solid contours) during the SON in reanalyses and models. A ridge of high pressure is shown extending across Botswana/Namibia. ERA-5 and MERRA-2 show similar representations but more intense in MERRA-2. Kuete et al. (2019) suggest that this high pressure forms earlier in the year with an anticyclone becoming evident in August and strengthens through September and October. This is consistent with Kalnay et al. (1996), who identified a high pressure system over the southern landmass of Botswana during August through October, but located slightly higher at 500 hPa, namely the Botswana high. The Botswana high is also formed in response to thermal heating and located southwest of high rainfall regions of Congo (Reason 2016), this suggests a link between the high pressure identified by Kuete et al. (2019) and the Botswana high in the Southern hemisphere. Very few studies have focused on its dynamics (Driver and Reason 2017) except regarding rainfall over the Zimbabwe region (Matarira 1990; Unganai and Mason 2002). ERA-5 and MERRA-2 shows on Fig. 6b a strong south-north positive gradient in the stream function field at the northwest rim of the high pressure core, marking the AEJ-S region.

The meridional pressure gradient associated with total vorticity which induces anticyclonic circulation at the core of the high pressure accelerates AEJ-S located north of the high. The rotational flow is more intense in MERRA-2 indicating the stronger AEJ-S compared to ERA-5. Model biases in vorticity are shown in Fig. 6b. Most coupled models capture the location and intensity of the high well, although some models (GISS-E2-1-G, MRI-ESM2-0, BCC-CSM2-MR) have a too intense core. GISS-E2-1-G which has the strongest AEJ-S, underestimates total vorticity at the core of the high pressure system compared to ERA-5. But the vorticity bias is strong and positive north of the high pressure and in the AEJ-S region, indicating strong rotational flows that accelerate the jet north of the high. MIROC6, which had the smallest AEJ-S, underestimates anticyclonic circulation with a negative bias of total vorticity, and a weak pressure gradient, thus explaining the very low strength of the jet. GFDL-CM4, MRI-ESM2-0 and BCC-CSM2-MR present a similar circulation with an overestimation of the rotational circulation at the core of the high pressure, which becomes weaker north of the high pressure showing a strong rotation flow in these models at the high’s core compared to the circulation in the AEJ-S region. The dynamic associated with the formation of the mid-level high is analyzed in Fig. 7b through the vertical structure.

Vertical profiles of omega show variations in uplift from the lower-troposphere that converge with cool upper tropospheric air, forming the high pressure system. During SON, the semi-arid landscapes of the Kalahari region are characterized with strong and dry convection associated with surface heating, which occurs in the form of sensible heat, strengthening updrafts below 500 hPa. This is shown in Fig. 7b from the vertical profile of the vertical velocity of ERA-5 and MERRA-2. CMIP6 models represent this mechanism well, detecting peaks of vertical velocity between 800 and 700 hPa, reinforcing updrafts from these levels. The formation of the mid-level high in coupled models is strongly supported by updrafts, with weaker downward motions at upper levels except for the MIROC6 models where a similar pattern of downward motion to reanalyses is observed. To better understand how cool upper-troposphere air converges with lower-troposphere uplifts induced by surface heating, we present in Figure S3 a meridional circulation using meridional components of the horizontal wind (v) and omega (w), superimposed with vertical velocity (colors). ERA-5 and MERRA-2 show strong updraft motions from surface to 500 hPa south of 20° S which are then decelerated by the upper tropospheric subsidence associated with the downward branch of the Hadley cell south of 10° S, thus forming the mid level high. This supports findings of the mid tropospheric Botswana high which also forms in response to surface heating. From the vertical structure and dynamics associated with the mid tropospheric high located at 600 hPa that is described in this study, we hypothesized that this mid level high is linked to the Botswana high located at 500 hPa. Most of the models show consistent pattern of the Botswana high with the observed data. Its formation mechanism is well linked to the representation of the high. This indicates that the simulated AEJ-S in models is consistent with the representation of the high and the anticyclonic circulation to which it is associated. AEJ system is driven a mid-level thermal circulation that is supporter by surface radiative effect. An effort is made in the next section to understand how dry thermal convection over the Namib-Kalahari and Sahara dryland thermal lows supports strong rising motion forming mid-level highs associated with anticycloninc circulation and divergent centres.

6 Heat lows and jets strength in models.

The 850 hPa surface temperature is used to analyze the heat lows. This temperature field is closely related to the atmospheric layer of the Kalahari heat low dynamic described in Howard and Washington (2018), and to the low level atmospheric thickness of the Saharan thermal low described in Lavaysse et al. (2009). No criteria was used to track and detect heat low as in these previous studies, but the temperature field used in our study gives a simple definition of the heat low similar to Chauvin et al. (2009) who used it to characterize the Saharan heat low.

Figure 8 presents the SON climatology of 850 hPa temperature in ERA-5 and MERRA-2, and temperature biases in models against ERA-5. Strong heating is observed over the Sahel, Arabia and Kalahari regions in ERA-5 and is more intense in MERRA-2 over the Kalahari region. CNRM-CM6-1 and GFDL-CM4 underestimate temperatures over the Sahel and throughout North Africa and Congo Basin. But, some slight positive temperature bias is observed in the Kalahari region showing an intensification of Kalahari heat low in these models compared to reanalyses. MRI-ESM2-0 presents a positive temperature bias localized in the region of maximum temperature, but the bias is negative over the northern Sahel. This negative temperature bias over the Sahel reinforces the hypothesis that the acceleration of the AEJ-N is due to an intensification of the Saharan high that is formed for the wrong reasons. GISS-E2-1-G, HadGEM3-GC31-L, MIROC6, BCC-CSM2-MR and UKESM1 models are very hot and show positive temperature bias against ERA-5 over the whole region including the Congo Basin, but the bias is greater in GISS-E2-1-G and MIROC6. The positive temperature bias over the Congo Basin in GISS-E2-1-G is thought to be responsible for the weak surface temperature gradient, as shown in Fig S4. Although the surface temperature gradient is small in GISS-E2-1-G, both jets remained strong and are maintained by high pressure systems in the mid-troposphere, as formation and intensification of these high pressures and their associated circulations are controlled by surface thermal heating due to the reinforcement of the heat low.

Fig. 8
figure 8

Sahara and Angola heat lows represented by the mean SON 850 hPa temperature in reanalyses (top panel) and bias in models against ERA-5. The black contour line shows heat low locations in models represented by the 296 Kelvin temperature value in the north and 297 Kelvin temperature value in the south

Full size image

As surface heating over Sahara and Kalahari regions is important in the generation and maintenance of the jets, understanding how coupled models represent different behavior of surface heating is an open question for this study. The primary component of insolation that drives surface heating is commonly referred to as surface downward shortwave radiation. We present in Fig. 9 the SON climatology of surface solar downward radiation in ERA-5 and MERRA-2, and biases of solar radiation in models against ERA-5. ERA-5 and MERRA-2 show a similar representation of solar radiation, but it is very strong in MERRA-2 in the Southern Hemisphere compared to central Sahel.

Fig. 9
figure 9

Mean September to November surface solar downward radiation in reanalyses (first row only) and bias in models against ERA5 (second and third rows). Values are shown in W m−2. The black contour line shows heat low locations in models represented by the 296 Kelvin temperature value in the north and 297 Kelvin temperature value in the south

Full size image

Solar radiation is strongly overestimated in UKESM1 and HadGEM3-GC31-L over the Sahel, North Africa and Congo basin, with a slight negative bias at the eastern Congo basin over the Rift Valley, and over southern Kalahari. In contrast, MRI-ESM2-0 and BCC-CSM2-MR show a strong overestimation of solar insolation over the southern Kalahari, which extends to central Congo Basin in MRI-ESM2-0, and a negative bias in the northern Sahel in BCC-CSM2-MR. GISS-E2-1-G, MIROC6, GFDL-CM4 and CNRM-CM6-1 show a nearly homogeneous negative bias over the entire heat low region delimited by the black contour. The negative bias is stronger in GISS-E2-1-G but does not explain the hot temperature bias in layers above Earth's surface observed in this model or MIROC6.

The Earth’s surface exchanges energy with near surface and upper layers through processes such as emission of radiation by the surface, which is associated with an energy flux. Energy heat flux transfer can either occur as sensible heat or latent heat. Figure 10 presents the spatial representation of sensible heat flux during SON, and model biases against ERA-5. ERA-5 and MERRA-2 present the same spatial distribution of surface sensible heat flux, but the energy heat flux is stronger over southeast Kalahari in MERRA-2 compared to ERA-5. The Sahel and Congo basin present very weak values of sensible heat flux in reanalyses, indicating that dry soil is not a controlling component of surface heating over these two regions during SON. The model biases show a different spatial structure in the two hemispheres, with the largest negative biases in the southern hemisphere. An exception is in GISS-E2-1-G, which presents a strong positive bias with a very strong sensible heat compared to other models. Thus enabling the ascent of warm air associated with dry convection which reinforces heating in layers above earth's surface in this model, and therefore intensifies the heat low (Fig. 8). MIROC6 and other models show weak negative biases in surface sensible heat flux over southern Kalahari, indicating that the ascent of warm air that strengthens heating above the surface is not associated with dry soil.

Fig. 10
figure 10

Mean September to November surface upward sensible heat flux in reanalyses (first row only) and bias in models against ERA5 (second and third rows). Values are shown in W m−2. The black contour line shows heat low locations in models represented by the 296 Kelvin temperature value in the north and 297 Kelvin temperature value in the south

Full size image

To describe the type of heat transfer from the surface in these models, we estimate in Fig. 11 the Bowen ratio, representing in models the ratio of the energy heat flux between the sensible heat and the latent heat. The value of the ratio is higher over the northern Sahara arid region in models and reanalyses. This indicates that, more energy is dissipated into the atmosphere as sensible heat rather than latent heat from the surface. Over Southern Kalahari, models also present important values of Bowen ratio. GISS-E2-1G and CNRM-CM6-1 present very strong values of the ratio greater than 10 over southern Kalahari. This shows that, these models are relatively dry and hot compared to other models. But the ratio is very weak in MIROC6 indicating that the climate is relatively cool and moist. A greater proportion of the available energy at the surface passed into layers above the surface as latent heat (Fig. S6) than as sensible heat. We also suggest that heat release above the surface that reinforces the heat low may be supported by long wave thermal radiation. This is shown in Fig. 12. The emission of thermal radiation by the surface represents an important mechanism for heat transfer. Understanding the mechanism by which heat radiated away from Earth’s surface to the atmosphere and between its surface layers will help to understand how the Earth's energy balance works to regulate our climate. Most coupled models present a positive bias of thermal radiation and this is very strong in MIROC6 compared to reanalyses. Although thermal radiation and surface temperature represent a fundamental characteristic of the Earth’s climate, their linear relationship is still yet poorly investigated. Our result shows that thermal radiation is a robust feature of surface heat transfer, thus explaining the increasing temperature in MIROC6. This indicates that the higher temperature bias in this model is associated with overestimation of surface thermal radiation that strengthens the heat low intensity and therefore the temperature gradient through Central Africa.

Fig. 11
figure 11

Mean September to November Bowen ratio in models and reanalyses, representing the ratio between surface sensible heat flux and surface latent heat flux

Full size image
Fig. 12
figure 12

Mean September to November surface upward longwave radiation heat flux in reanalyses (first row only) and bias in models against ERA5 (second and third rows). Values are shown in W m−2. Values are shown in W m−2. The black contour line shows heat low locations in models represented by the 296 Kelvin temperature value in the north and 297 Kelvin temperature value in the south

Full size image

7 Discussion and summary

In this study, an assessment based on processes related to the dynamics of the northern and southern components of the African Easterly Jets has been made, to investigate the representation of the mean state climatology of these jets in coupled models. The analysis is focused on the largest rainy season from September to November, defining the period when both jets are present and strong over Central Africa, and play a prominent role in the region’s climate variability. A comparison of jet core locations show the AEJ-N is reasonably well located over Central Africa in most CMIP6 models compared to AEJ-S with good improvement from CMIP5 to CMIP6. However, AEJ-N intensity is overestimated in GISS-E and MIROC models, in both CMIP5 and CMIP6. We gave close attention to these models through the rest of the analysis. The intensity of the southern jet is also overestimated in GISS-E but, MIROC5 presented no AEJ-S and its intensity increases in MIROC6 and remains underestimated. The CNRM-CM6-1 model also presents a very good improvement in the AEJ-N and AEJ-S locations from CMIP5 to CMIP6.

Analysis of the meridional gradient in 850 hPa temperature in coupled models indicates that, AEJs are thermal winds of the mid troposphere that owe their existence to a low level meridional gradient in temperature and are located slightly equatorward of the region of maximum temperature gradient. In the Northern Hemisphere, CMIP5 models (CNRM-CM5-2 and MIROC5) that locate an AEJ-N core more northward compared to reanalyses feature a stronger and more poleward peak in meridional temperature gradient. This corroborates results found by Creese and Washington (2018) that models that are dry in the east of Congo basin, with equatorward maximum easterly wind speed at mid level, were associated with equatorward shift in maximum gradient in potential temperature. A good relationship between AEJ strength and temperature gradient has also been found in RCMs by Tamoffo et al. (2021b).

However, in this study, results show that improvement in the AEJ strength and core location are not always linked to a better simulation of the maximum meridional gradient in surface temperature. GISS-E2-1-G features the strongest AEJ-N and AEJ-S but weakest meridional gradient in temperature. MIROC6 features a strong AEJ-N associated with a strong gradient, but a weak AEJ-S that is associated to a strong gradient in the southern hemisphere. Since the temperature gradient that is associated with the AEJs does not always explain the jet locations and intensities in models or the change from CMIP5 to CMIP6, other processes were examined.

Strong heat lows promote strong uplifts to mid level (e.g. 600–500 hPa), that converges with subsidence from the upper troposphere forming strong high pressure systems (Saharan high and Botswana high). This is important in GISS-E2-1-G which features strong highs that are associated with an anticyclonic circulation that accelerates easterly winds at mid-troposphere southeast of the Saharan high (AEJ-N) and northwest of the Botswana high (AEJ-S). Upward motion that converges with downward motion from upper levels to form the Saharan high are not well captured in GISS-E2-1-G, we conclude that the pressure system accelerates the strong AEJ-N for the wrong reasons. But this dynamic associated with the formation of the Botswana high in the south is better captured in GISS-E2-1-G.

Over the AEJ-N region, models exhibit strong and positive centers of the conversion of divergent kinetic energy into rotational kinetic energy due to Coriolis acceleration. While over the AEJ-S region, most models like GISS-E2-1-G present very weak centers of conversion, around 10 times weaker compared to values of conversion over AEJ-N region.

Surface heating is very important in understanding the acceleration mechanism of AEJs, as these jets are thermal winds and are strongly reliant on surface temperature. We find that CMIP models have large biases in temperature. Explanations of surface temperature bias in CMIP6 models are understood by examining the incoming shortwave solar radiation at the surface, and energy heat fluxes that reinforce heat lows strength in layers above the Earth’s surface. In the GISS-E2-1-G model, the incoming solar radiation is underestimated due to strong cloud cover but is not a key control of the strong heat low. Dry soil is responsible in reinforcing surface heating which is very strong in GISS-E2-1-G, enabling heat release associated with dry convection reinforcing heating and intensifying the heat low.

The MIROC6 model’s strong temperature gradient in the southern hemisphere is due to an overestimation of temperature values in the Kalahari relative to the Congo Basin, resulting in a strong heat low over Kalahari and a strong gradient towards Congo basin. MIROC6 shows strong development of both Saharan and Botswana highs and better captures their dynamic. The atmospheric energetic interactions of divergent and rotational flows over the AEJ-N region also exhibit strong and positive centers of conversion, while over the AEJ-S region MIROC6 has very weak centers of conversion. By examining surface sensible heat flux and the Bowen ratio and we showed that sensible heat is underestimated indicating that near-surface heating above is not associated with dry soil and that a greater proportion of the available energy at the surface to be passed to the layers above the surface as latent heat than as sensible heat. This indicates that in MIROC6 the heat release above the Earth’s surface that reinforces heat low is supported by the long wave thermal radiation.

An exception in the atmospheric energetic analyses is observed in CNRM-CM6-1 model over AEJ-S region, which exhibits strong values of conversion close to MERRA-2, supporting improvement in the simulated AEJ-S in this model from its CMIP5 to its CMIP6 version.

Investigations of AEJs dynamics in coupled models is of particular importance to understand mid -level circulation in models over Africa, as AEJs are considered as key Pan-African features, (James et al. 2018), through their interconnection to climate of other regions such as West Africa and Sahel (Chen 2004), Central Africa and South Africa (Kuete et al. 2019; Howard and Washington 2019). Dynamics of both jets has been assessed in previous studies using reanalysis data (Nicholson and Grist 2003; Kuete et al. 2019), global models (Creese and Washington 2018) and regional models (Tamoffo et al. 2019, 2021b). Despite this progress, our understanding of models representation of AEJ is still limited. We have shown that studies must go beyond analyzing the meridional temperature gradient to diagnose biases in the mean state climatology, location, and core intensity of both jets.

This study has suggested possible causes of the simulated AEJ locations, strength, and their associated dynamics in models (Creese and Washington 2018), and also possible directions for models assessment and development. In particular, investigations of processes regulating the energy balance that raises the near-surface temperature, rather than focusing only on processes explaining rainfall bias in models in particular over Central Africa (e.g. Dommo et al. 2018; Fotso-Kamga et al. 2020, Fotso-Nguemo et al. 2016, 2017; Creese and Washington 2018, 2019; Tamoffo et al. 2019, 2021a, b; Taguela et al. 2020, 2022a, b). These surface thermal processes depend strongly on insolation, vegetation cover and albedo. They can also be associated with an energy heat flux such as net surface irradiance, ground heat flux, sensible heat flux, latent heat and long wave radiation. Understanding the energy balance at the Earth’s surface is necessary to understand local climate and regional circulation, and arguably to improve simulations of this region.