1 Introduction

One of the most striking features of paleoclimatology is the replication of heavy glaciations at roughly 100-ky intervals during the late Pleistocene (past 800 ky), performing a strongly nonlinear sawtooth pattern—i.e. slow buildup in the ice mass followed by rapid terminations—as firstly observed by Broecker and Van Donk (1970).

The so-called astronomical theory on ice ages, popularized by the Serbian astronomer Milankovitch, states that the main cause of this fascinating pattern resides in the secular variation of solar radiation due to the wobbles in: (i) eccentricity of the earth orbit (main periods at T = 100 ky, and T = 400 ky); (ii) earth’s axial tilt (41 ky); (iii) precession (19–23 ky). Yet, since the first direct paleoceanographic discoveries about succession and magnitude of ice ages coming from the analysis of fossil foraminifera (Emiliani 1955, 1966; Emiliani and Shackleton 1974), it emerged that, although the orbital forcing plays a role in phase locking (Hays et al. 1976), the main causes of the oscillations are far to be elucidated definitively. The current literature is in fact aware that the power spectrum of global ice mass, derived from \(\delta ^{18}O\) variations (Berger et al. 1994), shows a notable (linear) imprint of the 41-ky obliquity forcing (actually, dominant in the early Pleistocene) and a weaker imprint of the 19-to-23-ky precession forcing (Imbrie et al. 1993). However, the wobbles in eccentricity are instead too weak to support an imprint in the ice mass oscillation at T = 100 ky as well. This is also stated as the 100-ky problem, further reinforced by the full missing of a 400-ky signature in the paleoclimatic records.

This conundrum has favored the quest for other mechanisms, involving several feedbacks grounded in the climate functioning, such as: ice-albedo feedback, stochastic resonance (Sutera 1981), role of the CO\(_2\) vertical mixing in ocean (Gildor and Tziperman 2001), isostatic adjustment under ice-sheets and calving catastrophe (Saltzman and Verbitsky 1992; Marshall and Clark 2002), nonlinear phase locking to Milankovitch forcing (Tziperman et al. 2006), the effect of the stripping of basal regolith on ice sheet thickness and timescales (Clark and Pollard 1998), the role of the salty bottom waters on the continental Antarctic ice margin in storing carbon in the deep ocean (Adkins et al. 2002; Paillard and Parrenin 2004), and silicate leak hypothesis (Brzezinski et al. 2002). Despite these numerous efforts, no single definitive theory is exhaustive in explaining the timing of the 80 ppm oscillation in the atmospheric CO\(_2\) concentration between ice ages and interglacial times (Archer 2010). The picture is further complicated by the fact that the Pleistocene has seen just eight 100-ky cycles, too few to be considered a statistically robust pattern.

In this perspective, Saltzman (2002, p. 300) argued that the oscillations are so affected by an internal instability of the climate systems (probably in the carbon cycle), that the Earth-orbital variation is not a necessary condition for the occurrence of the ice ages. Arguments supporting relaxation-oscillation dynamics were also invoked by other authors (Crucifix 2011, 2012; Paillard 2015). The development of low-order dynamical or conceptual models have allowed to fairly reproduce a few leading modes that dominate the spatial-temporal dynamics of ice ages. These models are typically composed by a set of ordinary differential equations which describe the slow manifolds of climate dynamics in a lumped spatially-integrated manner. Typical candidates for the prognostic state variables are the global ice volume \(V_i\) or ice mass \(M_i\) and the antarctic ice area A. Other slow variables are atmospheric or oceanic concentration of carbon dioxide (C), and deep ocean temperature \(T_o\). Dynamical models are constructed by following a truncation procedure of the partial differential equations of fluid dynamics and thermodynamics (Saltzman 2002), while conceptual models are proposed to test hypotheses based on observations (Crucifix 2012). Comprehensive reviews are reported in Fowler (2001), Paillard (2001), Cane et al. (2006) and Crucifix (2012).

A caveat of this modelling approach is that both dynamical and conceptual models often need to be tuned, in order to ensure realistic behaviors, through the calibration of the model coefficients. However, random variability of the climatic system may play a role in making these models more robust than they were firstly expected. To this aim, random noise is conveniently added to dynamical and conceptual models, and noise-induced phenomena may occur, such as stochastic resonance or coherence resonance (Ridolfi et al. 2011).

Stochastic resonance succeeded in reproducing millennian Dansgaard–Oeschger oscillations (Alley et al. 2001; Ganopolski and Rahmstorf 2002). However, although it was initially introduced by Benzi et al. (1982) to explain the 100 ky periodicity of glacial cycles, this phenomenon predicts symmetric ice ages (Matteucci 1989), so it is inconsistent with the observations of the late Pleistocene. On the contrary, coherence resonance allowed a single prototypical equation for atmospheric temperature (i.e., a fast variable) to accurately reconstruct the climate variability in the Vostok ice cores (Pelletier 2003). In this spirit, we will investigate the tuning effect of coherence resonance due to additive random noise in the equations for prognostic slow variables. Unlike the more commonly known stochastic resonance, the coherence resonance phenomenon does not require an interaction with an external periodic forcing, but it is a process that entirely relies on the coexistance of random noise, bistability of the internal dynamics and delay feedback (Tsimring and Pikovsky 2001). Basically, random noise in a dynamical system can accumulate a sequence of small jumps in the same direction so that the system shifts from an attraction basin to another one. Delay feedbacks and nonlinearity allow the pace of shifting to occur which produce a kind of periodicity in the system behaviour.

The possible role of coherence resonance in the scale break of the frequency of glacial-interglacial cycles have been recently analysed by Ditlevsen et al. (2020), who used the FitzHugh-Nagumo prototypical model originally proposed by Pikovsky and Kurths (1997) for excitable systems. In the present work, we expand and deepen the search of the coherence resonance mechanism in three physically-based low order models that were specifically designed for paleoclimatic purposes. Our aim is to show that they are more robust than generally expected and that a specific—somewhat arbitrary—setting of the parameter is not necessary to reproduce the 100 ky oscillations.

As clearly explained by Saltzman (2002), stochastic forcing in low-order models rises from time averaging and the truncation procedure of the fundamental equations because of non-systematic random departures from the mean values and aperiodic components (Monin and Yaglom 1975). More importantly, the averaging period of interest in paleoclimatology (\(\sim {0.1}\)–1 ky) rises the necessity to add noise to indirectly consider the smaller-scale phenomena, as already envisioned by Sutera (1981). The separation of temporal scales, or the central limit theorem, are usually invoked to justify the use of white (i.e. non-correlated) Gaussian noise. They are useful hypotheses, but not quite well justifiable, since there are many good reasons to invoke much more complex stochastic forcings in climate sciences (e.g., Graham et al. 2015). However, white Gaussian noise remains a commonplace in these cases, since it is a convenient and practical hypothesis.

We will consider to add white Gaussian noise to three popular models, that were indicated as the most representative in the review by Crucifix (2012): (i) The three-dimensional dynamical model by Saltzman and Maasch (1990; (ii) The three-dimensional conceptual model by Paillard and Parrenin (2004; iii) The two-dimensional conceptual model proposed in Crucifix (2012), based on a biased Van der Pol oscillator. Henceforth the three models will be referred to SM, PP and VdP, respectively. Although these three models address different aspects of the climatic dynamics (e.g., the first two involve the carbon cycle, but not the latter), they are self-oscillatory models that commonly share the feature of relaxation oscillations, when properly set. In this perspective, we aim to address the dynamical structure of these internal oscillations, through the understanding of the unforced regime (i.e., without orbital forcing). We will instead disregard other remarkable comprehensive models that are non-self-oscillatory (e.g., Imbrie and Imbrie 1980; Verbitsky et al. 2018; Daruka and Ditlevsen 2015).

In what follows, we begin by providing an insight on the three lumped model herein considered (Sect. 2), and analyse their stability conditions, depending on the variability of the model parameters (Sect. 3.1). Secondly, we show how these models can give rise to coherence resonance once forced with a stochastic noise, depending on the values of the model parameters (Sect. 3.2), and even thought they are not subjected to the orbital forcing. Focusing on the peculiar 100 ky pulsation, we investigate its occurrence and the dependency on the optimal noise intensity in different regions of the parameter space (Sect. 3.3). Finally, we investigate how this noise-driven oscillation interacts with the radiative forcing imposed by the orbital variation of the Earth (Sect. 3.4). Conclusions are drawn in Sect. 4.

2 Methods

Over the years, Saltzman and co-workers developed a series of different models for the Pleistocene oscillations, which are widely discussed in his book (Saltzman 2002). The model to which we refer here is the one initially presented by Saltzman and Maasch (1990), in what follows referred to as SM-model, that includes: i) an equation for the ice mass response (\(M_I\)) to CO\(_2\) changes (greenhouse feedback), and the deep ocean temperature (\(T_o\)) as negative feedbacks; ii) an equation for the CO\(_2\) (C) dynamics with a cubic nonlinearity; iii) an equation for the Antarctic ice area (A) that accounts for the negative ice albedo feedback. In order to keep the model as simplest as possible, we avoid here to include a fourth equation related to the calving catastrophes discussed in Saltzman and Verbitsky (1992). In this framework, the non-linearity of the model is fully contained in the atmospheric CO\(_2\) balance equation and implicitly simulates the feedbacks due to a variable stratification of the deep ocean, and their effect on the ability of the ocean to absorb and stock CO\(_2\). A first technical investigation of the oscillations performed by this model, when forced by additive noise on the equation for the deep ocean temperature, has been recently presented in Alexandrov et al. (2020).

The feedbacks between the ocean dynamics and its stratification were explicitly modelled by Paillard and Parrenin (2004), who included an oceanic switch forced by the “salty bottom waters formation efficiency” parameter (F). The leading idea of this latter work—henceforth referred to as the PP-model—is indeed that the enhanced stratification of the oceans depends on the formation of extremely dense bottom waters by brine rejection above continental margins of Antarctica, a process that would cease once that the ice mass reaches the continental shelves.

Finally, the Van der Pol toy model is a celebrated dynamical systems of two coupled differential equations, that was firstly adopted in electronic circuit modeling. Its use in paleoclimatology has been proposed by Crucifix (2011) and Crucifix (2012), in the so-called biased variant,—henceforth simply referred to as the VdP-model—because of the presence of the constant bifurcation parameter \(\theta\), where the response of an ice variable (say \(V_i\)) is coupled with an ocean variable (say \(T_o\)).

We here represent the three above-mentioned models through a unified mathematical framework, under the form of a (3D- or 2D-) vector stochastic differential equation

$$\begin{aligned} \dot{{\mathbf {Y}}}={\mathbf {L\!\cdot \!{Y}}}+{\mathcal {N}}({\mathbf {Y}})-{\varvec{\alpha }}R_{65}(t) +\sigma {\varvec{{\Gamma }}}(t), \end{aligned}$$
(1)

where \({{\mathbf {Y}}}\) is a vector containing the dimensionless form of the prognostic state variables (\({{\mathbf {Y}}}_{\text {SM}}\)=\(\{M_{\text {i}},C,T_{\text {o}}\}\), \({{\mathbf {Y}}}_{\text {PP}}\)=\(\{V_{\text {i}},C,A\}\), \({{\mathbf {Y}}}_{\text {VdP}}\)=\(\{V_{\text {i}},T_{\text {o}}\}\)), dot refers to time derivative, \(R_{65}\) is the orbital forcing considered in Berger et al. (1994), namely the insolation at 65\(^\circ\) N the 21\(^{\text {st}}\) June (where \({\varvec{\alpha }}_{\text {SM}}\)=\(\{0.5,0,0\}^T\), \({\varvec{\alpha }}_{\text {PP}}\)=\(\{0.33,0.3,0\}^T\), \({\varvec{\alpha }}_{\text {VdP}}\)=\(\{1.5,0,0\}^T\)). Following Saltzman and Maasch (1990), t has been made dimensionless with the time constant of ice-sheets (\(\sim {10}\) ky). The term \({\mathbf {\Gamma }}(t)\) is an array of white Gaussian processes with unitary standard deviation and \(\langle {\mathbf {\Gamma }}(t){\mathbf {\Gamma }}(t')\rangle\)=\({\varvec{\delta }}(t-t')\), and \(\sigma\) sets the noise intensity (see later). The linear and nonlinear components of the deterministic part of equation (1) read, respectively,

$$\begin{aligned} \mathbf {L_{\text {SM}}}= \begin{bmatrix} -1 &{} -1 &{} -v\\ 0 &{} r &{} -p\\ -q &{} 0 &{} -q\\ \end{bmatrix},\quad \mathbf {L_{\text {PP}}}=\begin{bmatrix} -\tau _v^{-1} &{} -x\tau _v^{-1} &{} 0\\ -\beta \tau _c^{-1} &{} -\tau _c^{-1} &{} 0\\ \tau _a^{-1} &{} 0 &{} -\tau _a^{-1}\\ \end{bmatrix},\quad \mathbf {L_{\text {VdP}}}=\frac{1}{\tau }\begin{bmatrix} 0 &{} -1\\ \xi &{} \xi \\ \end{bmatrix}, \end{aligned}$$
(2)
$$\begin{aligned} {\mathcal {N}}_{\text {SM}}= \begin{bmatrix} 0 \\ sC^2-{C}^3 \\ 0 \\ \end{bmatrix},\quad {\mathcal {N}}_{\text {PP}}= \begin{bmatrix} z\tau _v^{-1} \\ \delta \tau _c^{-1}+\gamma \tau _c^{-1}{\mathcal {H}}[-F]\\ 0 \\ \end{bmatrix},\quad {\mathcal {N}}_{\text {VdP}}=\frac{1}{\tau } \begin{bmatrix} \theta \\ -\frac{\xi }{3}T_o^3\\ \end{bmatrix}. \end{aligned}$$
(3)

Quantities with lower case in the above equations refer to the coefficients appearing in the original papers (values reported in Table 1). The function \({\mathcal {H}}[-F]\) refers to the Heaviside function, whose argument reads F=\(aV_i-bA-cR_{60}+d\), \(R_{60}\) being the daily insolation at 60\(^{\circ }\) S the 21st February (South hemisphere summer). In the following, equation (1) will be integrated numerically, namely

$$\begin{aligned} {\mathbf {Y}}_{t+dt}={\mathbf {Y}}_{t}+\left[ {\mathbf {L\!\cdot \!{Y}}_t}+{\mathcal {N}} ({\mathbf {Y}}_t)-{{\varvec{\alpha }}}R_{65}(t)\right] dt+\sigma {d{\mathbf {W}}(t)}, \end{aligned}$$
(4)

where \({\mathbf {W}}(t)\) stands for the Wiener process, dt is the numerical time step, where the Euler-Maruyama method (Kloeden and Platen 1992) allows to set \(d{\mathbf{W}}(t) = {\mathbf{N}}\left( {0,\sqrt {dt} } \right)\), being \({{\mathbf {N}}}(0,1)\) the standard normal random vector.

Of course, there are infinite different combinations of noise intensities that could be added to the equations composing each of the three models. For example, Alexandrov et al. (2020) forced only one of the three equations of the SM-model. Since the state variable are all properly made dimensionless, they are numerically comparable, so we opted for the simplest choice, namely the random additive terms—albeit statistically independent—share the same intensity \(\sigma\).

Table 1 Values of the model parameters as given by the reference settings for the three models, i.e. providing the periodograms presented in Fig. 1
Full size table

3 Results

3.1 Free and forced deterministic response

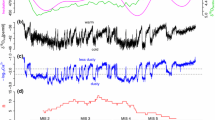
Let us firstly consider the original settings of the models, as reported in the Table 1, without any external influence, i.e. no orbital forcing and no stochastic forcing (\(\sigma\)=\({\varvec{\alpha }}\)=0). This case refers to the free response of the model. The corresponding periodograms are reported in the right part of Fig. 1. For reference, the periodogram of the \(\delta ^{18}{O}\) paleoclimatic record by Imbrie et al. (1984), a proxy for the ice mass, is overlapped on the computed ones (red line). We see that the original setting enables an autonomous dominant oscillation for all the models—not forced by external factors—that is equal to 105 ky, 133 ky and 103 ky, for SM, PP and VdP, respectively (black lines).

Fig. 1
figure 1

Free and forced response of the three lumped models considered. a, b SM-model; c, d PP-model; e, f VdP-model. Left: time series of a proxy of mass/volume ice in normalized units (observational data of \(\delta ^{18}\)O are reported in dashed-red, while the synthetic simulations of the deterministic response of the model due to the orbital forcing are reported in solid lines). Right: periodograms of real data (dashed-red), free response of the models (black solid lines), forced response of the model (blue solid lines). The temporal series of the prognostic variables reported in the left part have been normalized with the standard deviation. The periodograms have been computed through the Fast Fourier Transform

Full size image

We also remark that harmonics (i.e., oscillations with shorter period than the dominant one) are also present in the spectra of the free response. For instance, it is noteworthy that the PP’s spectrum provides four other peaks, with decreasing intensity. When the orbital forcing is added (so-called forced response, see blue solid lines in the left panels of Figure 1) the time series gain a more realistic pattern. As expected, in this case, the main components of the forcing (19-ky, 23-ky and 41-ky) appear in the corresponding periodograms. For the PP model, the dominant mode of the free response is shifted and matches the 100-ky oscillation of the real data. For SM and VdP the dominant 100-ky mode is instead not particularly influenced by the orbital forcing.

The time series and the periodograms presented in Fig. 1 illustrate how the three models are able to capture the main features of the Pleistocene climate, by combining an intrinsic instability of the system and its interaction with an external radiative forcing. The advantage of their simplicity however is overshadowed by the need of tuning several parameters, whose values can dramatically alter the model outcomes. To investigate this aspect we then explore the behavior of the three dynamical systems through a local stability analysis of the fixed points of the deterministic autonomous ODEs (Glendinning 1994). Accordingly, a generic fixed point \(\mathbf{{Y}}_0\) is a solution of the equation \({\mathbf {L\!\cdot \!{Y}}}+{\mathcal {N}}({\mathbf {Y}})=0\), and the local stability of the system around \(\mathbf{{Y}}_0\) is provided by the solutions \(\lambda\) of the characteristic equation \(det[\mathbf{{J}}-\lambda \mathbf{{I}}]\) = 0, where \(\mathbf{{J}}\) = \(\mathbf{{L}}+\mathcal{{N}}'(\mathbf{{Y}}_0)\) is the Jacobian of equation (1) and dash refers to derivation with respect to \(\mathbf{{Y}}\). The Hartman–Grobman theorem states that, if there are no eigenvalues with zero real parts, the dynamical system in a neighbourhood of the fixed point is topologically equivalent to the orbit structure of the linearized dynamical system. In particularly, the fixed or equilibrium point \({\mathbf {Y}}_0\) is asymptotically stable if all the eigenvalues have negative real part. Otherwise, excursions in the phase space are expected, away from the fixed points.

We have applied these principles by restraining our attention to a two-dimensional parameter space. In doing this, we excluded from our analysis the parameters that have a clear physical meaning and we only considered the ones influencing the stability of the equilibrium point. The analysis is made up of two features: (i) the linear stability analysis and ii) the numerical integration of the models, in order to identify the range of parameters in which oscillatory modes appear. For the SM model, we essentially summarized the analysis reported in Saltzman (2002, p. 285), adopting r and s as free parameters. As shown in Fig. 2a, the r–s space is divided into regions where the equilibrium points are all linearly stable, and where the model is linearly unstable, therefore exhibiting oscillatory behavior with varying characteristic periods, depending on the values of the parameters. The same analysis has been replicated for the PP. In this case we chose x and \(\beta\) as free variables for two reasons. Firstly, we excluded the parameters only appearing in the argument of the Heaviside function, in fact they do not affect the stability, since \({\mathcal {H}}'[\mathbf{Y}_0]\)=\(\delta (F[\mathbf{{Y}}_0])\)=0, for any value of a, b, c, d. Among the remaining parameters (see Table 1), and according to Paillard and Parrenin (2004), the three time-scales \(\tau _v\), \(\tau _c\), and \(\tau _a\) may be also ruled out, since their relative variations have a very weak influence on the model behavior. The x–\(\beta\) parameter space is clearly divided into (linearly) stable and unstable regions (Fig. 2b). Across these two, there is a region within which the model exhibits an oscillatory behavior, that mainly extends within the linearly unstable region, albeit it is not fully included in it. Finally, concerning the VdP model, once the typical time scale \(\tau\) is excluded, the choice is straightforward. Again, the results show that the \(\xi -\theta\) plane is clearly divided into a stable and an unstable region, within which the model can oscillate with varying periods (Fig. 2c).

Fig. 2
figure 2

Description of the model response in the parameter space, by discriminating the domains where the fixed points \(\mathbf{{Y}}_0\) are linearly stable or unstable. The contour lines instead refer to the time period of the dominant oscillatory mode (i.e., the one corresponding to the highest peak in the periodograms) performed by the fully-nonlinear numerically-computed time series (from Eq. 4). a SM; b PP; c VdP. The black dots refer to the parameter setting adopted in Fig. 4.

Full size image

The sensitivity analysis in the parameter space reported above shows that the three models are able to perform a dominant oscillatory mode close to 100 ky, provided a particular setting of the characteristic parameters, for each model. Otherwise, the oscillatory mode may differ from 100 ky significantly. Beside the criticism that might be raised about the arbitrariness of a specific setting of the parameters, if one supposes that these parameters are underlying some (unspecified) physical meaning, it is likely and reasonable that they should assume a relatively wide range of values. It follows that, due to the natural variability of the parameters, a deterministic description of the model response is not sufficient to solve the 100-ky problem. In the following section we will see that, through the mechanism of coherence resonance, a stochastic description may be instead functional to this aim.

3.2 Stochastic response and coherence resonance

Fig. 3
figure 3

Effects of an increasing noise intensity on the VdP model results without the orbital forcing (\(\xi\)=30, \(\theta\)=1.2). Left: time series of dimensionless ice mass (blue) when forced by noise (black). Right: Periodograms after averaging the FFT of twenty-five 1 My-long simulations

Full size image

When adding a stochastic noise, the system gives rise to patterns that cannot be predicted a priori, and that depend on both the model setting and the intensity of the noise. To give an insight, we first consider the VdP model (Fig. 3), by choosing a parameter setting providing a (linearly) stable deterministic behaviour (\(\xi\) = 30, \(\theta\) = 1.2, marked with a dot in Fig. 2c). If noise intensity is small (Fig. 3a), its effect shows up as a simple superposition of small scale fluctuations, i.e. whose amplitude is similar to that of the additive noise added in the equation, whereas the system is otherwise stuck around its original equilibrium point. In the resulting spectrum, these oscillations are shown to be spread over a wide range of frequencies (Fig. 3b). When increasing the intensity however, the noise dramatically alters the system behaviour, due to a non-linear interaction between stochasticity and system dynamics. In fact, the noise can bring the system away from its equilibrium point, and eventually shifts the state of the system towards a different basin of attraction.

Mathematically, this implies bistability in the autonomous dynamical system (namely the occurrence of two or more stable equilibrium points) or that the system is close to a Hopf bifurcation. The system can therefore wander around the phase space, sustained by the combined forcing of the noise, until shifting again to the original attraction basin and newly attaining its original equilibrium point. These trajectories in the phase space draw a typical temporal pattern with a peculiar statistical behavior, characterised by the rising of oscillations with a well-defined (and repeatable) period, a phenomenon known as coherence resonance. In the case of the VdP model (Fig. 3c), this dynamics result in the occurrence of cycles with a saw-tooth behaviour, which, interestingly, are qualitatively similar to those observed in paleo-climatic records. As evidence by Fig. 3d, this typical pattern gives rise to a low-frequency dominant oscillation that clearly show up in the spectral analysis. Notice however that this feature occurs just in a range of noise intensities (Fig. 3e). In fact, if noise is further increased, these cycles are disrupted and the system evolves as a kind of random walk, amplified by the system non-linearity. Qualitatively, the spectrum (Fig. 3f) recovers then the behaviour observed when forcing the system with low intensity noise (Fig. 3b).

All the three models considered herein actually exhibit coherence resonance. A global picture is reported in Fig. 4, where we plot the ice mass (or ice volume) variations as provided by the three lumped models including an additive white noise, but without orbital forcing. Of course, in this case, we avoided comparing the time series of the simulated signal with \(\delta ^{18}\)O record, since the presence of the noise makes the process non-deterministic and the search for the timing of the ice ages is not an issue anymore when using this approach. Left panels report the temporal paths of the three models, together with the steady solution provided by deterministic responses (i.e. with same model settings and without the noise), and the white noise intensity. The right panels of Fig. 4 show the periodograms of the stochastic simulations, compared to the periodogram of the \(\delta ^{18}\)O record. For each model, two spectra are computed. One is referring to a single signal computed over 800 ky (an approximate temporal extent of the duration of the 100 ky glacial period in the Pleistocene). A second spectrum represents instead an ensemble average of 100 spectra, each of them referring to a 800 ky simulation.

Indeed, the comparison of the spectra of the modelled signal with those obtained by observational time-series rises the question about the repeatability of these time series. More specifically, given the small number of glacial cycles in the Pleistocene, we can wonder whether the 100 ky peaks in the real spectra is just a statistical artefact, due to the limited temporal extent of the sample, rather than an intrinsic time scale of the system dynamics. This is why we have performed an ensemble of 100 realisations.

Fig. 4
figure 4

Coherence resonance in the three models. Left panels: Simulated time series obtained with equation (4), neglecting the orbital forcing, and using a parameter setting that provides linearly stable conditions (see dots in Fig. 2) with (blue line) and without (red-dashed line) additive noise. Right panels: periodograms (computed by excluding the initial 10–300 ky) referring to the \(\delta ^{18}\)O record of the last 800 ky (black-dashed lines), a single simulation lasting 800 ky (blue line), i.e. the blue time-series on the left panel, and 50 repetitions of the same 1My-long simulation (green lines)

Full size image

As expected, results for the SM model (Fig. 4a, b) show that, when producing several realizations of 800 ky-long simulations, the dominant period induced by the coherence resonance (i.e. the one peaking in the spectra) differs from one iteration to another. Among all the results, the blue lines reported in Fig. 4a–c refer to the ones providing the best match with the 100 ky peak provided by \(\delta ^{18}O\) records. After averaging, the resulting periodogram (the green one) still exhibits the main 100 ky peak, whose intensity is slightly smoothed and slightly shifted to a lower frequency, of approximately 120 ky. An insight of the residence time of the system in the phase space (\(M_i, C, T_o\)) is presented in Fig. 5a, illustrating the dichotomy in the system behaviour, close to a stable equilibrium point, around which the system persists most of the time, and another unstable equilibrium.

Fig. 5
figure 5

Residence time observed in a typical noise-induced dynamics performing stochastic coherence. a Residence time reported in the phase space of the SM-model. b Residence time reported in a two-dimensional projection of the PP-model phase space. Given the models setting, the deterministic response of the model would lead the system to a stable attraction point, as evidence by the trajectories identified by black curves

Full size image

The noise-induced dynamics in the PP model look different, since the resonance is induced by the capability of the trajectory to cross a specific threshold, which is given by the argument of the Heaviside function. Once ‘activated’, the Heaviside function allows the trajectory to skip to another attraction basin and to seek for another equilibrium.

When this threshold is crossed, the system tends to approach a second (stable) equilibrium point, that, in order to be reached, requires however the threshold to be crossed again. The system is then led back to its original equilibrium. In this dynamics, the second equilibrium lays in a region of the phase space which is not experienced by the system during its oscillations (see Fig. 5b). Single realization over 800 ky of the PP model provide spectra with a peak around 100 ky (Fig. 4c, d), but with variations that are wider than those observed for the SM model. As a consequence, when considering 100 different realizations of a 800 ky Pleistocene, the ensemble averaged spectrum presents a peak which is smoothed, shifted to lower frequencies and less pronounced with respect to both the \(\delta ^{18}\)O records and the results of the SM model.

Even for the VdP model (Fig. 4e-f) we observe the rising of a peak with a period around 100 ky, when considering a single 800 ky-long realization. The ensemble averaged spectrum is instead shifted to lower frequencies, with a peak around 150 ky whose magnitude is similar to that observed for the PP model (i.e., less pronounced than that for the SM model).

3.3 Sensitivity analysis

Basically, the coherence resonance occurs when the reference state of the system is close to a Hopf bifurcation, which happens to be triggered by the effect of the noise on the system dynamics. A key question is therefore to understand how sensitive is the coherence resonance occurrence with respect to: (i) the distance of the system from the bifurcation in the parameter space and (ii) the noise intensity. To this aim, we performed a sensitivity analysis, based on an ensemble of 1-My long simulations, by varying the noise intensity and the parameter setting, in order to cover the whole two-dimensional parameter space considered in Fig. 2.

Fig. 6
figure 6

Box plots representing on the vertical axis the statistics of the dominant oscillations, as returned by the models, for different noise intensities (horizontal axis), and referring to a sample of 50 realisations for each noise. The parameter setting is the same as in Fig. 4. The red lines refer to the median value of the oscillations over the simulation sample, whereas the box borders refer to ± three times the standard deviations around the mean. Red crosses represent outliers

Full size image

As a first step, we focus on the same case analysed in the previous paragraph. We therefore fix the models parameters (i.e. the same as those used in Fig. 4) and evaluate the systems response to different noise intensities. For each value of the latter, we performed 50 simulations and we recorded the period of the dominant pulsation resulting in the corresponding spectrum. The results of this analysis are presented in Fig. 6, where we show, for each noise intensity, the statistics of the period of the main pulsation through a box plot representation. The margins of the box (± 3 times the standard deviation), as well as the number of outliers, provide a quantification of the variability of the model response to a varying noise. The SM model shows a very little variability compared to PP and VdP (Fig. 6). In fact, the SM model produces dominant oscillations that are essentially bordered in the range \(100 \pm 30\) ky, for a wide extent of the noise intensities. Essentially, with the exception of the case with noise intensity smaller than 0.1, the SM model provides oscillations around 100 ky for the whole range of noise intensities investigated, with a variability that is lower than \(\pm 30\) ky.

The response of PP and VdP is instead different. For the PP model, we can identify a range of noises in which the median lays in the range \(100 \pm 30\) ky, but with only one intensity for which both the median and the whole box lay in that range. Outside the range \(100 \pm 30\) ky, the PP model returns oscillations distributed at higher periods and spanning over a range of values which is considerably larger than the SM model. Finally, for the VdP model, the median is always larger than 130 ky, and the model variability is qualitatively similar to that of the PP model. Based on these considerations, we can therefore state that the SM model looks as the most robust one among the three in reproducing the 100 ky oscillation.

To push our analysis further, we have then repeated this kind of analysis by considering, for each model, the whole parameter spaces represented in Fig. 2. This implies performing 50 simulations for (i) each noise intensities and (ii) for a couple of the parameters laying outside the regions referred to as ‘harmonic’ in Fig. 2. For each parameter setting explored, we then identified the occurrence of an ‘optimal’ noise, as the minimal noise triggering oscillations with a median in the range \(100 \pm 30\) ky.

Notice that our definition of ‘optimal’ noise differs from that commonly adopted in the literature (e.g., Pikovsky and Kurths 1997; Ridolfi et al. 2011), and according to which the optimal noise intensity, associated to a characteristic frequency of the coherence resonance, is the one that maximises the regularity of stochastic oscillations. Our approach here has to be different, since our focus is on the dominant pulsations arising only in the range \(100 \pm 30\) ky. Nonetheless, the two criteria might sometime overlap (see for example, right panels of Fig. 3).

The results (Fig. 7) show that, for the whole part of the parameter space where the SM model is linearly stable, it gives rise to coherence resonance with a 100 ky pulsation. Close to the margins of the linearly unstable and harmonic region, the resonance is activated with a low noise intensity (around 1% of the large scale oscillations). By increasing the values of both parameters r and s, the noise intensity required to activate coherence resonance increases very little moving away from the boundary of the unstable harmonic region. For the PP model the picture is very different. The portion of the parameter space \(x-\beta\) providing the resonance is bounded to two regions bordering the unstable harmonic region, i.e. in a large part of the parameter space the resonance is not activated, no matter how intense the stochastic forcing is. Notice also that the resonance is activated for noise intensities that are smaller than those required by the SM model, i.e. around 0.5 % of the amplitude of the large scale oscillations. The VdP-model provides the simplest picture. The resonance is activated for a minimal intensity (of the same order as for the PP-model) for equilibrium points bordering the unstable harmonic region, i.e. for \(\theta \ge 1\). Moving further away from this border, for \(1\le \theta \le {1.25}\), the noise intensity required for the resonance progressively increases monotonically. For \(\theta \ge 1.25\), there is no evidence of a resonance with a 100 ky period (see also Fig. 2).

To sum up, the SM model is able to give rise to coherence resonance for a wider parametric range than the PP and VdP models. It is also worth noticing that, for the SM model, the noise intensity activating the resonance is generally larger than the one that triggers oscillations for the PP and VdP models. In these two latter models indeed, the extent of the region of the parameters space that potentially induces the resonance shows negligible sensitivity to an increased noise intensity.

Fig. 7
figure 7

Results of the sensitivity analysis. Contour plot the noise intensity triggering coherence resonance with a main oscillation period of 100 ± 30 ky, for varying values of the model parameters

Full size image

3.4 Combining the orbital and stochastic forcing

A last feature that is worth discussing is the combined role of radiative forcing and noise on the system dynamics. Notably, we can question how the model outcomes reported in Fig. 4 may be altered by the presence of a periodic forcing, as induced by the Earth orbital variations. To that purpose, for each model, we compared the outcomes of three simulations: (i) including the orbital forcing and setting the pre-factor \(\varvec{\alpha }\) in the model equation (1) as in the original publications (see Sect. 2), (ii) setting \(\varvec{\alpha }\) equal to zero, i.e. neglecting the orbital forcing, as in case of the results presented in Fig. 4, and (iii) imposing a range of values for the forcing amplitude in between of the previous two conditions. As for the cases discussed in Fig. 4, the simulations were ran over a period of 1 My, by repeating 50 times each simulation. Results are presented in Fig. 8 and show that, in all the three models, the orbital forcing amplifies the oscillations associated to the periods that are typical of tilt variations (41 ky) and precession (19–23 ky), but has almost no influence on the 100 ky pulsation. The overall periodogram is therefore composed by oscillations with lower periods that represents a linear response of the model to the orbital forcing, and a dominant 100 ky oscillation as the product of a coherence resonance. Apart from the linear response triggered by the orbital forcing, the picture is therefore very similar to the ensemble average spectra reported by the green lines of Fig. 4, thus implying that the orbital forcing has a marginal effect on the 100-ky oscillation. At the same time, this also confirms that the three models maintain distinctive features, even when forced both stochastically and orbitally. In particular, the SM-model is the one which exhibits a higher energy at the dominant oscillation, very close to the 100-ky period appearing in the \(\delta ^{18}\)O record, which is fairly distinguishable from the other peaks. PP instead performs a dominant oscillation which is less evident, since the spectral energy is more spread over a wide range of frequencies. In this picture, the performance of the VdP model can be instead considered in between SM and PP.

Fig. 8
figure 8

Response in the periodograms from the three model forced by both the noise and the orbital forcing, with different intensities: the bold dashed blue line refers to the case without orbital forcing, the bold blue continuous line to the case with ‘full’ orbital forcing, i.e. values of \(\varvec{\alpha }\) given for Eq. (1). Light blue shaded lines represents varying orbital forcing in-between. Left ordinate axis refers to ensemble average of 50 simulations, that are ran over 1 My, right ordinate axis refers to the power density of the paleoclimatic records (\(\delta ^{18}\)O), represented by a black dashed line on the graph. The parameters of the three models are the same as in Fig. 4

Full size image

4 Discussion and conclusions

Climate simulations at the 1 My timescale can be successfully addressed with low-order lumped models, in which parameters and variables arise from long-term and global averaging and the number of equations are necessarily limited. It follows that just a few elements of the climate system can be accounted for, with a limited selection of possible interactions and feedbacks. The goodness and reliability of this approach is usually tested by comparing the deterministic response against observational records of paleoclimatic proxies, based on which the model parameters can be conveniently tuned. Since this kind of tuning is somewhat arbitrary, as far as the physical correspondence of the parameter variability is not completely clear, there is no interest in stating which of these is ‘the best model’ or which is the ‘the best parameter setting’. We can instead ask ourselves how sensitive the response of the models are depending on the variability of the model settings, and eventually on the addition of a stochastic noise to their dynamics.

Indeed, in lumped models, due to the averaging process, spatial heterogeneity and small scale temporal fluctuations are ruled out from the dynamics (Monin and Yaglom 1975). The role of these fluctuations can be reintroduced by two additional features: (i) by considering the intrinsic variability of the model parameters; (ii) by adding a stochastic forcing in the equations. We investigated the role of these two features on the response of lumped paleoclimatic models, and the robustness of three representative models in reproducing the hallmark of the Pleistocene climate, i.e. the occurrence of the 100 ky pulsation as a product of the feedback mechanism of the climate system. In doing this, we pushed the model parameters far from their optimal setting as identified by their relative authors, i.e. providing the best fit between model results and paleoclimatic records.

Our analysis shows that the interactions between additive Gaussian noise and the internal dynamics trigger a noise-induced resonance mechanism in all the three models. This mechanism allows the models to reproduce realistic periodic oscillations (including the 100-ky) even though, given the parameter setting, their deterministic response would lead them to steady fixed points. The sensitivity of the models is different with respect to the range of variability of the parameters and noise intensity. The SM model turns out to be the most robust one and the most susceptible to coherence resonance, since a Pleistocene oscillation noise-induced response was obtained for a wide range of the parameters, with relatively low values of noise intensity (up to 10% of large scale oscillations).

Although coherence resonance was observed even in the PP model, this model is much less susceptible than SM, since the portion of the parameter space \(x-\beta\) providing the resonance was quite bounded, while in a large part of the parameter space the resonance was not activated. This model was conceived to express mathematically the idea that peculiar dynamics of the southern ocean would induce abrupt climate changes—known as terminations—as produced by the intimate link between (i) ocean stratification, (ii) deep ocean–ocean mixed layer–atmosphere–CO\(_2\) exchanges, (iii) greenhouse effect and temperature rise. Mathematically speaking, this abruptness is represented through an Heaviside function, encapsulating the whole nonlinearity of the model. Such a peculiarity makes the PP model less suited in producing large scale noise-induced oscillations. A lack of robustness in the PP-model is evidenced when considering ensemble average of many realizations, with and without the orbital forcing (see Figs. 4 and 8). In this framework, in fact, a well-defined peak around 100-ky is less evident.

Finally, the VdP model shows up as a good example of how a simple toy model can produce noise-induced saw-tooth oscillation, mimicking Pleistocene climate dynamics. However, when testing its response to model variability this simplified approach reveals its shortcomings, since the portion of the parameter space providing the resonance is bounded to the range \(1\le \theta \le {1.25}\). The averaging of spectra of ensemble of many simulations with and without orbital forcing has not cancelled out a fairly-visible peak, although it is located at a period a bit larger than 100 ky and less pronounced than the SM model.

For all the three models, the role of the orbital forcing was confined to a linear triggering of the oscillations associated to tilt variations (41 ky) and precession (19–23 ky), leaving the rest of the spectrum almost unaffected.

The above comparison evidences the larger robustness of SM, when forced with both stochastic and orbital forcing. In our opinion, such a strength of the SM-model is apparently the effect of its internal mathematical structure, which was specifically designed to reproduce Hopf bifurcations and bistability, by operating through a particular choice of the nonlinear terms in the CO\(_2\)-ocean feedback. The physical interpretation of this choice was questioned nevertheless by Crucifix (2012). It seems therefore that the Landau-Stuart imprint in the SM-model represents both its strength and weakness.

To conclude, the results herein presented suggest that lumped models can respond to stochastic forcing in a manner that is far from their original conception, giving rise to interesting unexpected noise-induced behaviors. Notably, their predisposition to trigger coherence resonance in a wider range of parameters with respect to their ‘factory setting’ may open to new insights about the mechanisms underlying the occurrence of the 100-ky pulsation in the late Pleistocene.