An adaptive approach to quantify weather-within-climate rainfall characteristics

Abstract

Knowledge of subseasonal-to-seasonal (S2S) rainfall characteristics such as onset, duration, and demise of the rainfall cycle, and characteristics of dry periods that are between rainfall seasons, can provide important insight for the agriculture, health, disaster, and energy industries. Several methods have attempted to calculate temporal characteristics of rainfall and few have worked with intermittent dry periods and calculate intermittent dry period characteristics. Issues arise when applying these methods for complex rainfall regimes, or regions that have one or more of the following: (1) multiple rainfall seasons in a given year, (2) a relatively wet dry season, (3) unclear transitions between wet and dry seasons. This study develops a new and comprehensive method for calculating S2S rainfall characteristics, especially for regions that have complex annual rainfall cycles. The method consists of three steps: (1) create the annual cycle climatology of rainfall and classify its modality by the presence or absence of intermittent dry period(s), (2) identify seasonal windows of the rainfall cycle based on its climatological modality, (3) calculate yearly intermittent dry period characteristics and calculate temporal rainfall characteristics for each year using information on daily rainfall amount and the concurrent rate of change. Application and results of the method are given for the Caribbean, which exhibits the properties of a region with complex rainfall regimes. The method can be utilized under a meteorological or agronomical lens and is able to delineate false meteorological and agronomical onsets and demises. Meteorological onsets and demises that are calculated via each year’s Early-Rainy Season (ERS) and Late-Rainy Season (LRS) mean thresholds effectively characterize the seasonal evolution of mean onsets and demises in the Caribbean. The year-to-year variability of Mid-Summer Drought (MSD) characteristics, and onsets and demises that are calculated by climatological ERS and LRS mean thresholds resemble the variability of seasonal rainfall totals in the Caribbean and are statistically significantly correlated with the identified dynamical processes that impact each seasonal component of the rainfall cycle. The method has important implications for prediction, modeling capabilities, and understanding the variability of rainfall across timescales.

1 Introduction

Subseasonal-to-Seasonal (S2S) rainfall characteristics such as onset, demise, and strength and duration of intermittent dry periods, or relative dry periods between rainfall seasons, provide important insight for the agriculture, health, disaster, and energy industries. These characteristics are classified as S2S because they exhibit S2S variation in their interannual variability, or the characteristic is within a rainfall season that spans a few weeks to a few months. These characteristics are examples of what are known as “weather within climate”, or characteristics of weather that lead to climate anomalies such as floods and agricultural droughts (Moron et al. 2019). Generally speaking, temporal characteristics of the annual rainfall cycle are more useful than rainfall amounts for farmers (Marengo et al. 2001; Ingram et al. 2002). The onset and demise of the annual rainfall cycle is significant for rainfed agriculture. In this case agricultural planning and consequently food production are heavily affected by changes to the start and end of the rainfall season (Camberlin and Diop 2003; Boyard-Micheau et al. 2013; Diaconescu et al. 2015; Obarein and Amanambu 2019). The timing of the annual rainfall cycle also impacts water consumption, human health via water-borne diseases, and energy generation (Li and Fu 2004; Bombardi et al. 2020, hereafter B20). Changes in the duration and magnitude of intermittent dry periods impact planting dates and crop yields that are important for growing and harvesting seasons (Hastenrath 1966; Magaña et al 1999; Van der Zee Arias et al. 2012; Pons et al. 2016). These S2S rainfall characteristics are especially important for complex rainfall regimes, or regions that have one or more of the following: (1) multiple rainfall seasons in a given year, (2) a relatively wet dry season, (3) unclear transitions between wet and dry seasons. However, forecasts on the temporal and intermittent dry period rainfall characteristics of the annual rainfall cycle are not readily available from local weather or climate services to which a majority of stakeholders turn for forecasts on the annual rainfall cycle (Vaughan and Dessai 2014).

Temporal and intermittent dry period characteristics of the annual rainfall cycle are valuable for investigating atmospheric dynamics and simulating rainfall in models. In most regions, monsoon and large-scale patterns are responsible for the wet and dry seasons. Temporal variations in the monsoonal or large-scale patterns affect the timing of the annual rainfall cycle (Marengo et al. 2001; Bombardi et al. 2017), and intermittent dry periods (Anderson et al. 2019) In some regions, the interannual variability of the onset and demise is related to the interannual variability of the total seasonal rainfall (Marengo et al. 2001; Li and Fu 2004). Hence, accurately characterizing temporal and intermittent dry period characteristics of rainfall can enhance the understanding of what dynamical mechanisms contribute to the annual rainfall cycle and how they affect its variability. In addition, research on temporal and intermittent dry period characteristics can improve the detection of biases that models have in simulating the annual rainfall cycle and its interannual variability (Liebmann et al. 2007; Anderson et al. 2019).

Meteorological methods are one of two types of methods for calculating temporal characteristics of rainfall. Meteorological methods typically use a geographically-fixed observation from one variable such as rainfall, outgoing long wave radiation, or moisture fluxes to detect the timing of the rainfall season. A commonly-used meteorological method is from Liebmann and Marengo (2001) which defines the onset and demise dates based on accumulated rainfall anomalies relative to the climatological annual mean. Several studies adapt the Liebmann and Marengo (2001) method for their region (Camberlin and Diop 2003; Liebmann et al. 2007; Bombardi and Carvalho 2008, 2009; Dunning et al. 2016, hereafter D16; Misra et al. 2017; Bombardi et al. 2017; B20). Other methods include a relative mean rainfall rate that measures the contrast rate between a specific date and a corresponding season (Wang and LinHo 2002; Seregina et al. 2018), a wavelet transform methodology applied to precipitation time-series (García-Franco et al. 2021), and fitting a two-phase linear regression model on accumulated precipitation within the annual rainfall cycle to find wet and dry season transitions (Cook and Buckley 2009). There are also some meteorological methods that use a combination of variables pertinent to the atmospheric dynamics that drive a regions’ rainfall pattern such as temperature gradients, upper vs. lower-level wind patterns, and moisture fluxes to calculate the timing of the annual rainfall cycle (Webster and Yang 1992; Fasullo and Webster 2003; Joseph et al. 2006; Garcia and Kayano 2009; Fitzpatrick et al. 2015; Gouirand et al. 2020; B20).

Most meteorological methods have biases in characterizing the timing of the annual rainfall cycle in regions with complex rainfall regimes. The main limitation in the Liebmann and Marengo (2001) method is that the method has to have consistent above normal precipitation in order to show an identifiable change in the accumulated precipitation anomaly. Any intermittent or light rainfall before or after the main portion of the wet season is given a negative daily rainfall anomaly, potentially reducing the length of the wet season. Adaptations of the Liebmann and Marengo (2001) method experience this limitation; however, since most of these studies worked with regions that have unimodal rainfall patterns with distinct transitions between their dry and wet season (Camberlin and Diop 2003; Bombardi and Carvalho, 2008; 2009; Bombardi et al. 2017; Misra et al. 2017), the limitation is not pertinent for them. However, for regions that have gradual transitions into and out of the wet season, this can skew the timing of the onset and demise. Studies that adapt the Liebmann and Marengo (2001) method to investigate regions with multi-modal rainfall regimes acknowledge this (D16; B20). A common limitation seen in several meteorological methods is using a climatological annual mean to determine the onset and demise of the rainfall cycle (Liebmann and Marengo 2001; Camberlin and Diop 2003; Cook and Buckley 2009; Moron and Robertson 2014; Carvalho et al. 2016; Dunning et al. 2016; Bombardi et al. 2017; Obarein and Amanambu 2019; B20). A climatological annual mean works well for unimodal or multi-modal regimes with clear wet and dry seasons. However, using a climatological annual mean for regions with asymmetrical rainfall seasons (e.g., Martinez et al. 2019, hereafter M19; B20) can skew the timing of the onset(s) and demise(s) in these regions because the annual mean can be biased towards the season within the annual rainfall cycle with the largest amount of rainfall.

The other type of method for calculating temporal characteristics of rainfall are agronomical methods. Agronomical methods use a set of criteria or threshold(s) to determine the timing of the rainfall season relative to some crop (Moron and Robinson 2014; Nieto-Ferreira and Rickenbach 2011; Marengo et al. 2001; Li and Fu 2004; Fitzpatrick et al. 2015; Obarein and Amanambu 2019; B20). Agronomical methods commonly use a millimeter (mm) threshold and a criterion for persistence of rainfall in order to determine the timing of the rainfall onset and demise (B20). However, the threshold values and criteria are different for each agronomical study as the values are specific to their region, commodity of interest, or atmospheric water demand. Therefore, it would likely be unsuitable to apply the same values for a different region or crop. In addition, many agronomical studies have fixed dates to their rainfall season that may not be applicable for other regions. Hence, there is a need to develop a method that is flexible for the user, such that the user can input their values that are relative to their annual rainfall cycle of interest.

Agronomical and meteorological methods have different purposes and benefits. Agronomical methods are advantageous for farmers and decision makers as it relates to the physical needs of their crops or livestock (Fitzpatrick et al. 2015). In addition, agronomical methods can be applied for real-time monitoring and forecasting (Moron and Robertson 2014). However, agronomical methods do not focus on large-scale or monsoonal features, as pre-monsoon or transient activity may be enough to satisfy the required criteria or thresholds pertaining to the crop. If a researcher desires to investigate the variability and timing of monsoonal or large-scale features, a meteorological method is better suited for this purpose. Meteorological methods are advantageous for diagnostic studies: they focus on monsoonal or regional to large-scale dynamical patterns that typically separate wet and dry seasons to assess what dynamical mechanisms affect the timing of the annual rainfall cycle (Fitzpatrick et al. 2015; B20). However, there has yet to be a single method that can be used for both agronomical and meteorological contexts. It would be beneficial to develop an agronomical/meteorological hybrid method given their respective benefits.

Most studies do not detect intermittent dry periods, calculate its characteristics, use them to categorize rainfall modalities, and consequently, determine whether multiple onsets and demises can be calculated for a given region. Some studies classify rainfall modalities by defining rainfall seasons. For example, Seregina et al. (2018) defined a rainy season when at least five consecutive pentads exceed their pre-defined rainfall threshold. D16 used a ratio between the first and second peak amplitudes to determine whether or not a season is bimodal. Studies that classify rainfall modalities based solely on the rainfall season; however, can oversimplify complex rainfall patterns. There are regions with neither a classic unimodal or bimodal rainfall pattern (e.g., Cameroon, Vietnam, Taiwan, southwestern Ethiopia, South Africa, Central America, and Caribbean) (Wang and LinHo 2002; Herrmann and Mohr 2011; M19; B20). Instead, these regions experience patterns that are referred to as single wet season bimodal (Herrmann and Mohr 2011), or as this study will refer to as unimodal dual maxima. Their distinction comes from their subtle intermittent dry period (e.g., the Mid-Summer Drought (MSD; mid-June to late August; Magaña et al. 1999) in portions of the Caribbean), where its weak strength prevents multiple onsets and demises from being calculated. Unlike unimodal patterns, the onset and demise of unimodal dual maxima patterns are likely influenced by two separate sets of dynamical mechanisms that are associated with each rainfall maximum. Subtle intermittent dry periods are difficult to predict and are highly variable (Hellin et al 2017; Bellante 2019). As a consequence, methods that use dry periods to determine the modality of rainfall cycles in order to calculate onsets and demises classify rainfall patterns with subtle intermittent dry periods as unimodal (e.g., B20). Yet subtle intermittent dry periods and their characteristics are important for farmers and water management as the period can impact the end of the preceding rainfall season and start of the subsequential rainfall season (Anderson et al. 2019). There has yet to be a method that (1) utilizes intermittent dry periods to classify rainfall modalities and determine whether multiple onsets and demises can be calculated and (2) distinguishes unimodal dual maxima patterns and calculates its temporal and intermittent dry period characteristics.

The asymmetry of the annual rainfall cycle, variations in modality across sub-regions, intermittent dry periods that vary in magnitude, and unclear transitions between wet and dry seasons make the Caribbean annual rainfall cycle a prime example of a region with a complex rainfall regime that current rainfall characteristic methods would find difficulty in describing. The rainfall pattern in the Caribbean is not uniform; there are five sub-regions, all of which have complex rainfall regimes (M19). The Northwestern, Western, and Central Caribbean regions have non-homogenous unimodal dual maxima patterns with a short duration Early-Rainy Season (ERS; mid-April to mid-June) and a longer duration Late-Rainy Season (LRS; late August to late November). Separating the ERS and LRS is the MSD. The Eastern Caribbean and Guianas experience a unimodal and bimodal rainfall pattern, respectively. Each sub-region has a different set of regional to large-scale dynamical mechanisms that are responsible for their distinct rainfall characteristics (M19). In addition, the interannual variabilities of the ERS and LRS are independent of each other due to differences in large-scale climate drivers that affect each subset of dynamics mechanisms corresponding to each seasonal component (Gouirand et al. 2020; Martinez et al. 2020, hereafter M20). Therefore, the temporal characteristics associated with the ERS are independent of those of the LRS.

This study presents a new and comprehensive method for calculating rainfall characteristics, especially for regions that have complex annual rainfall cycles. The new method aims to (1) include both meteorological and agronomical considerations (2) classify common and uncommon rainfall modalities (e.g. unimodal dual maxima), and (3) frame characteristics based on the modality of the annual rainfall cycle. Given the complexity of the Caribbean rainfall pattern, the Caribbean will be used to showcase this method.

2 Data

There are a few important considerations on what data to use in order to effectively utilize the method. This method requires daily data, in order to accurately capture the timing of the rainfall characteristics. Spatially, the method can be applied to local- or regionally-averaged time series. Both have their advantages and disadvantages. For example, use of individual stations or grid points allows one to investigate local forcings and transient activity, but missing values can cause issues when smoothing or filtering the data. Grouping stations or grid-points reduces rainfall ‘noise’ and missing values, but that averaging can dampen ‘transient’ features and local forcings. If a region does have sub-regional rainfall heterogeneity, it may be beneficial to further subset the data into smaller, but more homogenous regions. For the Caribbean region example that will be employed to demonstrate the method, daily rainfall data is obtained from the Caribbean Institute for Meteorology and Hydrology (CIMH) for the period, 1969–2017 and from NOAA’s Global Historical Climatological Network (GHCN) for 1960–2016. Several stations from Guatemala are also included in this study, provided by the Guatemalan National Meteorological Service (INSIVUMEH). In total, the daily rainfall from 41 stations is used in this study. Stations are grouped by sub-region based on the classified Caribbean sub-regions from M19. A summary of the stations used to showcase this method can be found in Table 1.

Table 1 List of rainfall regions, and their corresponding stations used in the study

Additional steps are suggested to prepare the daily data ahead of the analysis. In the Caribbean, stations are data-stitched across the CIMH and GHCN datasets by replacement of missing data in one station’s dataset by the other dataset (M19) when the stations’ coordinates are within a 0.05-degree margin from each other. The data are also checked for uniformity by analysis of overlapping years from each dataset. A smoothing filter on the daily data is also recommended in order to reduce noise. Gaussian windows are used here, as they simplify delineation of transient vs. non-transient activity, and have been used in other similar studies (e.g., B20). A 10-day Gaussian window was found to best suit the Caribbean: it reduced noise but did not substantially modify signals seen in the daily data.

3 Methods

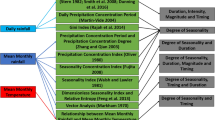
The methodology comprises three parts: creating the annual cycle climatology of rainfall and determining intermittent dry periods, identifying seasonal windows, and calculating temporal and intermittent dry period rainfall characteristics for each year. For temporal characteristics, one context is examined in this section and a summary of the methodology in this context can be found in Fig. 1. In addition, Fig. 1 includes a summary of the adaptations of the methodology in other contexts (e.g. Absolute Meteorological Characteristics, and Agronomical Characteristics), which can be found in Sects. 4 and 5, respectively.

Fig. 1

Summary of methodology under various contexts to calculate onset. Blue boxes highlight the steps. Green boxes are details of the blue boxes. The upper-half of the calculation of yearly rainfall characteristics are steps to calculate meteorological characteristics. The lower-half of the calculation of yearly rainfall characteristics are steps to calculate agronomical characteristics. Demises follow the same steps except in (2a) the candidate demise is only determined if the day is below the mm threshold. For Meteorological Demises, in (2b, c) the maximum of S(n) is found and the Candidate Demise is later than the date of the maximum of S(n). For Agronomical Demises, in (2b-d) number of wet days, and above agronomical mm threshold are used

3.1 Create annual cycle climatology of rainfall and determine intermittent dry periods

The annual cycle climatology of rainfall is calculated from the raw daily (unsmoothed) data, excluding leap days. A harmonic filter then smooths the annual climatology. Harmonic filters have been used to investigate the number of wet seasons over a given region (e.g. Wang 1994; Wang and LinHo 2002; Liebmann et al. 2012). The number of harmonics used depends on the region under study. Previous studies suggest the use of the first 4 to 12 Fourier harmonics (Wang 1994; Wang and LinHo 2002; Liebmann et al. 2012). Here, a five harmonic (5-term Fourier) filter is used to smooth the climatology.

For the purposes of the analysis, the calendar year should be shifted also, to better capture the full cycle of the annual climatology and all transitions between wet and dry seasons (e.g., Bombardi et al. 2017; B20), particularly for regions where a rainfall season bridges two calendar years. The shift is determined by the peaks and troughs of the rainfall cycle that are identified in the smoothed annual climatology. In the smoothed annual climatology, the minima that separates the dry and wet seasons, and the final maximum of the rainfall season are identified. The former denotes the beginning of the climatological annual rainfall cycle. Next, the start and end dates of the analysis are determined. Selecting the start and end dates are subjective choices. Recent studies used 20–50 days before the beginning of the climatological annual rainfall cycle as their start date (D16; B20). However, some determine the start date from tradition (e.g. Allen and Mapes 2017; CIMH deems the start of the Caribbean rainfall season as April 1st). The same steps are applied to determine the end date for the analysis; the end date must be some days after the final climatological peak of the annual rainfall cycle. Recent studies use 20–50 days after the final climatological peak of the annual rainfall cycle to determine the end date (D16; B20), or use a traditional date that is commonly used to describe the end of the rainfall cycle (e.g. M19, M20). These dates will also be used in the year-to-year analysis. For the Caribbean, the data is shifted such that Day 1 is March 1st and Day 365 is February 28th of the following year. For the Guianas, the data is shifted such that Day 1 is February 1st and Day 365 is January 30th of the following year. Daily data for each sub-region was calculated by averaging their stations’ daily data. The start date for the Northwestern and Western Caribbean is April 1st. Since the transition from less-wet to wet rainfall season begins in late March/early April for the Central and Eastern Caribbean (M19), the start date is March 1st. The start and end date in the Guianas is the day of the climatological minima of the annual cycle prior to the first rainfall season, or March 1st, through March 5th of the following year. The end date is November 30th in the Northwestern Caribbean. The Central Caribbean end date is December 30th and in the Eastern and Western Caribbean the end date is January 30th of the following year, as the demise of their rainfall cycles is later in the year than in the Northwestern Caribbean (M19). A summary of the start and end dates for each sub-region can be found in Table 1.

Intermittent dry periods in the smoothed annual climatology are identified in order to determine the modality of the annual climatology. Between the start and end dates, an intermittent dry period is identified if the difference between either rainfall peak and the minima between peaks is greater than 1 mm, following similar steps from B20. Next, any identified intermittent dry period is classified as subtle or distinct. If the intermittent dry period minimum is 1 mm less than the climatological annual mean, the intermittent dry period is distinct. Otherwise, the intermittent dry period is subtle. A step-by-step example of the process for identifying and classifying intermittent dry periods using the smoothed annual climatology is given for the Northwestern Caribbean (Fig. 2a) and Guianas (Fig. 2b). In the Northwestern Caribbean there are two rainfall peaks with a minimum between peaks. The difference between the minimum and either rainfall peak is greater than 1 mm; therefore, the Northwestern Caribbean experiences one intermittent dry period. The intermittent dry period is not 1 mm less than the climatological annual mean (~ 3.8 mm/day); therefore, the intermittent dry period is subtle. Similarly, the Guianas has two rainfall peaks with an intermittent dry period. However, the intermittent dry period minimum in the Guianas is 1 mm less than the climatological annual mean (~ 6 mm); therefore, the intermittent dry period is distinct. The number of intermittent dry periods and their classification determines the modality of the climatological mean annual rainfall cycle. The Northwestern Caribbean experiences one subtle intermittent dry period; therefore, the modality of the rainfall cycle is unimodal dual maxima, or a subtle bimodal rainfall cycle. The Guianas experiences one distinct intermittent dry period; therefore, the modality of the rainfall cycle is bimodal. Whether or not an intermittent dry period is subtle or distinct determines whether one is able to calculate multiple onsets and demises between the start and end dates of the interannual analysis (Sect. 3.3). For example, in the Northwestern Caribbean, only one onset and demise can be determined in the interannual analysis because the intermittent dry period is subtle. In the Guianas, two onsets and two demises can be determined in the interannual analysis because the intermittent dry period is distinct. A summary of the classified modalities for each sub-region can be found in Table 1.

Fig. 2

Calculating the climatological rainfall cycle, determining the presence of intermittent dry periods, classifying intermittent dry periods, and setting seasonal windows for the Northwestern Caribbean (a) and the Guianas (b), where Day 1 is March 1st and February 1st, respectively. Blue line denotes the smoothed climatology averaged over all stations for each region. Seasonal windows are shaded: first rainfall season (green), and second rainfall season (yellow). The darkened green/yellow window is the intermittent dry period window, or mid-summer drought (MSD) for the Northwestern Caribbean

3.2 Identify seasonal windows

Using the smoothed annual climatology, seasonal windows are introduced for the calculation of interannual characteristics associated with each rainy season of the annual rainfall cycle. For unimodal regimes, the seasonal window is the analysis start and end dates. For unimodal dual maxima and bimodal regimes, the first window is set between the start date to the date of the smoothed annual climatology rainfall minimum within the intermittent dry period. The second window is set between the smoothed annual climatology minimum within the intermittent dry period and the end date. An intermittent dry period window is set by determining the midpoints between the smoothed annual climatology rainfall peaks and the minima of the smoothed annual climatology intermittent dry period. For example, two seasonal windows are set for the Northwestern Caribbean (Fig. 2a): the ‘Early Rainfall Season’ window, which is between the analysis start date and the date of the climatological intermittent dry period rainfall minimum, or Day 141 (July 18th), and the ‘Late Rainfall Season’ window, which is between the date of the climatological intermittent dry period rainfall minimum and the analysis end date (Fig. 2a). The intermittent dry period window, or Mid-Summer Drought window, is Day 117 (June 26th) to Day 164 (August 12th).

3.3 Calculate rainfall characteristics for each year

First, the temporal location, amplitude, and width of every peak and trough in the gaussian-filtered (smoothed) daily data for each year is calculated. Second, inflection points are determined in the year-to-year smoothed daily data, and are classified as candidate meteorological onset or demise dates. For candidate onsets, the method considers every trough-to-peak within the smoothed daily data, and finds the minimum day, if any, that has both of the following user-input conditions: (1) the day is above an inflection point mm threshold, and (2) the rate of change between the inflection point and X days exceeds a given mm/day threshold. The latter is done to avoid inflection points in which no clear changes in slope above the mm threshold exist in subsequent days. For candidate demises, the method inspects every peak-to-trough and finds the minimum day, if any, that has its value below the inflection point mm threshold. To define a wet vs. non-wet day, most studies use a threshold value from 0.85 mm (Stern et al. 1981) to 1 mm (Moron and Roberstson 2014), but in some regions with unclear dry seasons, values as high as 2.5 mm are used (Nandargi and Mulye 2012). Therefore, it is recommended to set the inflection point mm threshold between 0.85 mm and 2.5 mm. For the onset calculation, the rate of change requirement is similar to methods that use a criterion to check for persistence of rainfall, and typically check approximately 10 days out. However, those methods do not check for slope and only ask how many days after the date are also at or above the mm threshold. Onsets are associated with a change in intensity of rainfall; hence they should also depend on the change in slope. This method is the first to put a mm/day tendency threshold. In the application of this method, the tendency is calculated as the average change in daily rainfall amount between the smoothed annual climatology trough and peak that is associated with the onset.

To demonstrate the calculation of the accumulated precipitation anomalies, onsets, and demises, a step-by-step illustration of the method using the 2011 rainfall cycle in the Northwestern Caribbean (Fig. 3) and the 1985 rainfall cycle in the Guianas (Fig. 4) are shown. In the Northwestern Caribbean, a candidate onset is determined between any trough to peak if the inflection point is above 1 mm and if there is a rate of change of 0.102 mm/day between the date of the inflection point and 10 days out (Fig. 3a). The latter was determined by taking the difference between the smoothed climatological peak (7 mm) and trough (1.9 mm) that is associated with the onset divided by the number of days between the smoothed climatological trough to peak associated with the onset (50 days). A demise inflection point is determined between any peak to trough if the inflection point is below 1 mm (Fig. 3a). A similar procedure is done for the Guianas (Fig. 4a), except (1) the inflection point threshold is 1.5 mm because it is common for the region to not have consistent rainfall values below 1 mm, and (2) determining candidate onsets are different between the first and second rainfall seasons, as the second rainfall season has a separate mm tendency threshold.

Fig. 3

Schematic summary of using the method to calculate Relative Meteorological Onsets and Demises for the 2011 Northwestern Caribbean rainfall cycle using smoothed daily data (orange line). (a) Determining onset and demise candidates using the mm threshold and rate of change threshold. (b) the minimum and maximum of the accumulated precipitation anomalies (light blue and maroon lines) using raw daily data for each seasonal window (green and yellow boxes) are calculated. (c) locate the nearest candidate onset and demise from min/max S(n) (light blue and maroon squares) that satisfy conditions for Relative Meteorological Onset (green star) and Demise (yellow star)

Fig. 4

Schematic summary of using the method to calculate Relative Meteorological Onsets and Demises for the 1985 Guianas rainfall cycle using smoothed daily data (orange line). (a) Determining onset and demise candidates using the mm threshold and rate of change threshold. (b) the minimum and maximum of the accumulated precipitation anomalies using raw daily data (light blue and maroon lines) for each seasonal window (green and yellow boxes) are calculated. (c) locate the nearest candidate onset and demise from min/max S(n) (light blue and maroon squares) that satisfy conditions for Relative Meteorological Onset (green star) and Demise (yellow star)

The context examined in this section is an adaptation of the approach used in Liebmann and Marengo (2001) and Bombardi et al. (2017). Unlike their methods, the present method does not calculate interannual onsets and demises using a mean threshold that is based on the climatology of the annual rainfall cycle. Onsets and demises using the present method will be referred to as the Relative Meteorological Onset (RMO) and Demise (RMD). Using the unsmoothed data for each year, the same equation from Bombardi et al. (2017) is applied with some modifications to calculate year-to-year RMOs and RMDs:

$${S}_{\mathrm{window}}\left(n\right)=\sum_{i={t}_{\mathrm{window}}}^{n}P\left(i\right)-{P}_{\mathrm{window}}$$

(1)

where S_window(n) is the anomalous accumulated precipitation at precipitation day “i” to day “n”. P(i) is the daily precipitation at day “i”. P_window is the mean daily value of the rainfall in that year calculated over the particular seasonal window; this differs from other methods that use P_window as the annual climatological daily precipitation rate (Liebmann and Marengo 2001; Bombardi et al. 2017; D16; B20). Finally, t_window is the date related to the start, or before the start, of the seasonal window being used. Similarly to Bombardi et al. 2017, for onsets it is recommended to place t_window in the dry season that precedes the rainfall season in order to accurately depict the transition from dry to wet seasons. Depending on the modality of the smoothed annual climatology, one or multiple S_window (n) are used when calculating interannual onsets and demises. For unimodal patterns, only one S_window(n) is used and is used for calculating both onset and demise. For unimodal dual maxima patterns, two S_window(n) are used: one is used for the onset, and the other is used for the demise. For bimodal patterns, four S_window(n) are used: each for each onset and each demise calculation. For onset, the minimum of S_window(n) is identified. Next, the candidate onsets from the given year’s smoothed daily data are utilized by finding the candidate onset that relates to the date of the minimum of S_window(n). This is done by finding the latest date of a candidate onset that is (1) earlier than the date of the minimum of S_window(n), and (2) the magnitude of the rainfall on the candidate onset day is within the Rth percentile of the rainfall amount, relative to that year, over the window. The first criterion does not include the location of the onset to be later than the start date of the seasonal window, as this would restrict the location of the onset to be solely after the climatological intermittent dry period minima (for multi-modal cases) or start date. The latter is done in case the smoothing filter has several “kinks” between the date of the minimum of S_window(n) to the actual onset. A recommended value for the onset Rth percentile is the 33rd to 50th percentile. The candidate onset that satisfies both criteria is deemed the RMO.

The approach to find the RMDs follows that for the RMOs, with a few key differences. The maximum of S_window(n) is found. Using the candidate demises, the timing of the RMD is determined by finding the minimum candidate demise that: (1) is later than the date of the maximum of S_window(n), and (2) the candidate demise value is within the Rth percentile of the rainfall amount, relative to that year, over the window. The first criterion does not include the location of the demise to be earlier than the end date of the seasonal window, as this would restrict the location of the demise to be solely before the climatological intermittent dry period minima (for multi-modal cases) or end date. The second criterion is done in case the smoothing filter has several “kinks” from the date of the maximum of S_window(n) to the actual demise. A recommended value for the demise Rth percentile is the 10th to 33rd percentile.

In the Northwestern Caribbean, two S_window(n) are determined:

$${S}_{\mathrm{ERS}}\left(n\right)=\sum_{i={t}_{\mathrm{ERS}}}^{n}P\left(i\right)-{P}_{\mathrm{ERS}}$$

(2)

$${S}_{\mathrm{LRS}}\left(n\right)=\sum_{i={t}_{\mathrm{LRS}}}^{n}P\left(i\right)-{P}_{\mathrm{LRS}}$$

(3)

t_ERS is Day 1 (March 1st) and t_LRS is the date of the climatological intermittent dry period minima, or Day 141 (July 18th). Since the Northwestern Caribbean has a unimodal dual maxima pattern in its smoothed annual climatology, only the first window is used to determine yearly onsets, and the second window is used to determine yearly demises. The date of the minimum of S_ERS(n) is calculated, and is on day 90 (May 30th) (Fig. 3b). The date of the minimum of S_ERS(n) is used as a reference date to determine the timing of the RMO (Fig. 3c). There is one candidate onset that is before the date of the minimum of S_ERS(n) and its value is within the 33rd percentile of the rainfall amount, relative to the year, over the ERS window. Therefore, the RMO is on day 80 (May 20th). The date of the maximum of S_LRS(n) is calculated, and is on day 248 (November 4th) (Fig. 3b). There are two candidate demises that are after the date of the maximum of S_LRS(n) and its value is within the 10th percentile of the rainfall amount, relative to the year, over the LRS window (Fig. 3c). Therefore, the RMD is the earlier of the two candidate demises, or day 255 (November 11th).

The Guianas experience a bimodal pattern in its smoothed annual climatology; therefore, four S_window(n) are determined in the interannual analysis (Fig. 4b). In the interannual analysis, when finding the onset of the first rainfall season and demise of the second rainfall season, Eq. 1 is used. For finding the demise of the first rainfall season and onset of the second rainfall season, Eq. 1 is altered, such that the mean daily value of the rainfall in that year calculated over the intermittent dry period window, or P_IDP(n), is used. For bimodal patterns the demise of the first rainfall season (RFS1) and onset of the second rainfall season (RFS2) fall under the intermittent dry period window, where using P_IDP(n) better characterizes the transition between each rainfall season. The minimums of S_RFS1(n) and S_RFS2(n) are calculated and RMOs for each season are determined (Fig. 4c). The maximums of S_RFS1(n) and S_RFS2(n) are calculated and RMDs for each season are determined.

3.4 Characteristics related to the intermittent dry period

The intermittent dry period window is used to calculate the magnitude and duration of intermittent dry periods in the interannual analysis. For each year, the magnitude of the intermittent dry period is estimated from the unsmoothed data as the mm/day average within the intermittent dry period window. For each year, the duration of the intermittent dry period is the total number of unsmoothed data days within the intermittent dry period window that has a mm value less than the 66th percentile of the unsmoothed intermittent dry period magnitude from the annual climatology. For the Northwestern Caribbean, the unsmoothed annual climatology magnitude of the intermittent dry period is 4.70 mm, and the dates categorized as less than the 66th percentile of the unsmoothed intermittent dry period magnitude from the annual climatology would be those with amounts less than 5.60 mm.

4 Results

The mean and variability of temporal characteristics have been used to investigate their relationship with other characteristics of rainfall in order to determine its predictability with rainfall characteristics or dynamical phenomena (e.g. Liebmann and Marengo 2001; Moron and Robertson 2014; D16; B20). Some examples are, but not limited to, rainfall amount, frequency of wet days, and intensity of rainfall. One relationship that varies with regions around the world is the relationship between temporal rainfall characteristics and seasonal or annual rainfall totals. Some regions have little to no correlation between seasonal rainfall totals and onset/demise (Drosdowsky 1996; Nicholls et al. 1982; Marengo et al. 2001), while other regions have strong correlations (Liebmann and Marengo, 2001; Moron et al. 2009; Camberlin et al. 2009; Mugo et al. 2016). A factor in determining whether a relationship exists between onset/demise and rainfall amount is whether a sizable amount of rainfall in the seasonal or annual totals are attributed to pre or post rainfall season activity. However, whether or not the relationship is attributed to how an onset and demise is defined has yet to be determined. For example, would onsets and demises that are based on the climatological mean, as D16 and B20 use, have a different relationship with rainfall amount than those that are based on means relative to a particular year’s rainfall season, as this study uses? Below this method and other methods are applied to the Caribbean data to investigate the climatology and variability of temporal characteristics of rainfall. Additionally, the present method is examined to understand relationships between temporal/intermittent dry period characteristics and the dynamical mechanisms that shape the regional climate of the Caribbean. Information on the atmospheric/oceanic indices used in the analysis can be found in Table 2.

• (a) Onset climatology and variability

  
  

  There is a large spread in dates determined by the methods for the mean of the onset for all years across each of the four sub-regions in the Caribbean, and in the Guianas (Table 3). The onset means from this study show that the RMOs progress from east-to-west, starting earliest in the Central Caribbean / first rainfall season in the Guianas and latest in the Western Caribbean. A notable exception is the Eastern Caribbean; however, the dates of the RMO means are at the start of the wetter season, not the rainy season, as this region experiences substantial rainfall throughout the year. The Guianas experience a second rainfall season in the boreal Fall; therefore, its second mean onset is later than the other sub-regions’ mean onsets.

  
  

  The evolution of the RMO across the 5 sub-regions, shown in Table 3, is similar with the evolution of the start of the ERS / first rainfall season found in M19. Hence, the estimates of ERS start dates using the RMO are consistent with that dynamical view of the rainfall climatology over the Caribbean. When applying the method from Liebmann and Marengo (2001), the mean onsets are identified further into the rainfall season. This is because Liebmann and Marengo (2001) uses the entire calendar year which includes the post-rainfall dry season. Including the post-rainfall dry season when calculating accumulated precipitation anomalies can cause the minimum of S(n), and consequently the onset, to occur well after the wet season. Several methods attempt to fix this issue. Bombardi et al. (2017) use the derivative of S(n) and determine the onset as the first day where the dS(n)/dt changes from negative to positive and is positive for 4 consecutive days. When using the Bombardi et al. (2017) method, however, the mean onset begins well before the start of the climatological wet season in the Caribbean (M19). This is due to transient activity occurring in the Caribbean prior to the rainfall season, which induces multiple days of rainfall that satisfy the criteria in Bombardi et al. (2017). Unless modified, the Liebmann and Marengo (2001) and Bombardi et al. (2017) methods are configured for unimodal regimes alone; therefore, onsets and demises in the Guianas could not be calculated under these methods. Additional adaptations of the method from Liebmann and Marengo (2001) include the methods from D16 and B20, both of which calculate the start and end of the hydrological cycle (d_s, d_e) first. Then to determine the year-to-year variability for unimodal patterns, they set t₀ as d_s – N to d_e + N, where N is 45 days (B20), and 50 days (D16). For bimodal patterns, t₀ is d_s1 – N to d_e1 + N for the first rainfall season and d_s2 – N to d_e2 + N for the second rainfall season, where N is 20 days (D16). This reduces the chances of finding the onset after the demise, or the demise before the onset. The mean onset in the Northwestern Caribbean and first rainfall season in the Guianas using their method is comparable with this study, though the interannual variability of the onsets show the present method to have onsets that are earlier than D16/B20 (Fig. 5a, c). The mean onset in the Western (Fig. 5b), Central (Fig. 5d), and Eastern Caribbean (Fig. 5e), and second rainfall season in the Guianas (Fig. 5f) are earlier in the present method than in D16/B20.

  
  

  A closer examination of several cases in the Caribbean helps explain the onset date differences between the present method and D16/B20 method. In the 1974 rainfall cycle in the Northwestern Caribbean (Fig. 6a), the minimum of S(n) is the same between the present method and the D16/B20 method. This implies that differences in the definition of the time period used to calculate the mean threshold and accumulated rainfall between methods did not affect the date of the S(n) minimum. However, D16 and B20 solely use the date of the S(n) minimum to define the onset. The minimum of S(n), which is where previous methods deem is the onset of the rainfall cycle, is not the start of the rainfall season in all cases, but rather when rainfall reaches the calculated seasonal yearly threshold or the calendar year climatological threshold. As a result, portions of the rainfall season are missed. The present method mitigates this limitation by not defining the onset as the minimum of S(n), but defines the onset based on the candidate onset that is associated with the minimum of S(n). This difference largely explains why the Northwestern Caribbean onset dates are earlier in the present method than in D16/B20. The Guianas first rainfall season (e.g., Fig. 6d) show similar differences between onsets that are largely attributed to how S(n) is utilized to find the onset. In the Eastern Caribbean, the onsets in the present method are several weeks to months earlier than in D16/B20. Since the transition of the less-wet to wet seasons in the Eastern Caribbean is gradual (e.g., Fig. 6b), the minimum of S(n), regardless of the time period or mean threshold parameter used, is usually well into the wet season. Hence, the large difference between the onset dates in the Eastern Caribbean is predominantly due to placing the onset as the minimum of S(n) vs. utilizing the minimum of S(n) as a benchmark to find the onset.

  
  

  In some cases and sub-regions, the window and mean threshold parameters also contribute to differences in onset dates between methods. The 1975 rainfall cycle in the Central Caribbean (Fig. 6c), and 2015 rainfall cycle in the Western Caribbean (Fig. 6e), experienced a weaker than normal ERS and a normal LRS. The D16/B20 missed the onset seen in the ERS (Fig. 6e) or placed the onset as d_e + N (Fig. 6d). Using the ERS window with ERS mean thresholds for the given year, the present method captured onsets in the weaker than normal ERS for both sub-regions. As noted in M19 and M20, the ERS is shorter in duration than the LRS, and the variabilities of the ERS and LRS are independent of each other. When applying a mean threshold that is based on the climatology of the entire hydrological cycle, the mean threshold is biased towards the season with a larger amount of rainfall. Hence, the accumulated precipitation anomalies miss the ERS, resulting in onsets that are either during the LRS, or post-rainfall dry season, especially during dry ERS years. Similar findings are seen in the Guianas, where its second rainfall season is shorter in duration and less in magnitude than its first rainfall season. A climatological mean threshold skews the second onset further into the second rainfall season (e.g., Fig. 6d). The S(n) for the second rainfall season in the present method finds onsets that are typically where the transition between the intermittent dry period and second rainfall season are seen. Alongside differences in selecting the minimum of S(n) as the onset, the time and window parameter differences explain why the mean onset standard deviations of D16 and B20 are larger than those estimated in this study, and highlights how previous methods may not capture the transition of the rainfall season(s) in (1) years where the magnitude of the rainfall season is significantly less than its climatology, and (2) sub-regions with non-symmetrical rainfall cycles.

  
  

  The methodology is replicated for each station in order to determine whether sub-regional RMO dates are representative of their respective stations, and to better compare the station precipitation climatologies in M19. All sub-region RMO means using station-averaged daily data reflect their corresponding stations’ RMO mean. The evolution of the RMO means across the 41 stations in the Caribbean/Guianas closely resembles the evolution of the start of the rainfall cycle found in M19 (Fig. 7a). The Central Caribbean, Northern Antilles, and Guianas experience its onset first, with dates ranging from early-April to early May. Onset dates migrate westward onto the Northwestern Caribbean, where a SE-to-NW evolution of its onset dates is seen ranging from early May (e.g., Jamaica) to late May (e.g., Florida Keys). The Western Caribbean experiences its onset dates last, with dates ranging from late-May to mid-June. The findings follow the dynamical evolution of the ERS across the Caribbean, where the western flank of the North Atlantic Subtropical High (NASH) convergence band initiates rainfall over the Central Caribbean and Northern Lesser Antilles and progresses northwestward into the Northwestern Caribbean and in the Western Caribbean in conjunction with convergence from the northward migrating Eastern Pacific Intertropical Convergence Zone (ITCZ) (M19). The Central and Southern Lesser Antilles also experience later onsets—ranging from mid-May to mid-June. The western flank of NASH convergence band does not reach the Central and Southern Lesser Antilles; therefore, the Eastern Caribbean experiences its onset later via convergence from the northward migrating Atlantic ITCZ during the boreal summer (M19). Before the boreal summer, the Atlantic ITCZ is over the Guianas, which is why the Guianas experience its first rainfall season earlier than most of the other sub-regions. The second mean onset dates in the Guianas (not shown) also resemble its regional mean onset date and is in mid-October as a result of the Atlantic ITCZ migrating southward from the Eastern Caribbean.

  
  

  Nearly all correlations between rainfall amounts/dynamical indices and onsets are weaker and statistically non-significant with RMOs than onsets from D16/B20 (Table 4). The contrast is due to how each is calculated. RMOs are independent of the climatology since the mean threshold used to determine S(n) is based on each year’s rainfall. Under D16 and B20, the mean threshold to calculate S(n) is based on the climatology; the mean threshold is building the rainfall amount vs. timing relationship into the methodology by investigating anomalous precipitation respective to the mean normal. To better compare with D16 and B20 onsets, onsets that are determined by the climatological mean threshold are calculated using the present method. These onsets will be called the absolute meteorological onsets. The absolute meteorological onset follows the same steps as the RMO except: (1) when calculating S_window(n), P_window becomes ${\overline{\mathrm{P}} }_{\mathrm{window}}$ or the precipitation from the climatology averaged over the seasonal window, and (2) when determining the absolute meteorological onset, the candidate onset must be within the Rth percentile of the magnitude of the climatology over the seasonal window.

  
  

  Generally, absolute onsets have a similar or stronger relationship with the known atmospheric/oceanic modes of variation that shape the regional climatology and variability of ERS rainfall in the region than D16/B20 onsets. All sub-regions have high negative correlations between first seasonal rainfall totals and onset dates. The winter-time North Atlantic Oscillation (NAO) has moderate positive correlations with onset dates for all sub-regions except the Northwestern Caribbean. Moderate negative and positive correlations are seen across the Central Caribbean, Eastern Caribbean, and to an extent Guianas’ first rainfall season between onsets and southern Tropical North Atlantic ERS sea-surface temperatures (SSTs) and sea-level pressures (SLPs), respectively. ERS zonal 925mb winds over the Caribbean Sea, or the Caribbean Low-Level Jet (CLLJ; Amador 1998), has negative correlations with onset dates across the Western, Central and Eastern Caribbean. The meridional component of 925mb winds during the ERS in the Caribbean Sea and during the first rainfall season in the North South American Coastline have moderate to high negative correlations with onset dates across the Northwestern Caribbean and Guianas, respectively. The winter-time NAO is the main driver of ERS variability; the winter-time NAO induces a persistent anomalous SST and SLP pattern over the southern Tropical North Atlantic and Caribbean Sea that affects the ERS across the Caribbean (M20). During a winter-time positive-NAO, cold SSTs and above-normal SLP are seen over the southern Tropical North Atlantic and persist into the ERS. Alongside stronger easterlies, the anomalous signals weaken moisture convergence over the Caribbean basin and result in a weaker-than normal ERS (M20). Given the strong inverse relationship between absolute or D16/B20 onsets and ERS/first rainfall season totals, the winter-time NAO induced anomalous SST/SLP pattern is likely responsible for the variability of these onset dates (e.g., positive winter-time NAO = later-than-normal ERS absolute onset). However, since RMOs are not statistically significant with most indices, the findings from the correlations suggest the variability of the rainfall seasons are consequences of changes to rainfall seasonal amount rather than changes to rainfall seasons’ timing.

  
  

  The start of the second rainfall season in the Guianas is in the fall, which is also where the demise of the LRS is seen over the Caribbean; therefore, atmospheric/oceanic indices that are known to impact tropical Atlantic rainfall LRS variability are investigated. Onset dates for the second rainfall season are negatively highly correlated with its seasonal rainfall totals. Although weak, some positive correlations are seen between summertime El Niño–Southern Oscillation (ENSO) / Eastern Pacific SSTs and second onset dates.

• (b) Demise climatology and variability

  
  

  The spread between Liebmann and Marengo (2001), Bombardi et al. (2017), and the present method on the mean of the demise for all years across each of the four sub-regions in the Caribbean, and the Guianas is smaller than the spread of onsets (Table 5). The opposite is found between D16/B20 and the present method. The regional RMD mean dates mostly follow the NW to SE progression of the demise of the rainfall season in the Caribbean: the Northwestern Caribbean demise is first, followed by the Western and Central Caribbean, and then the Eastern Caribbean and Guianas’ second rainfall season (M19). The exception is the first rainfall season in the Guianas where its demise is the earliest than the other sub-regions.

  
  

  When applying the method from Liebmann and Marengo (2001), the mean demise dates are earlier than the climatological transition from wet-to-dry seasons (M19), as a result of years with abnormally dry rainfall seasons that cause the maximum of S(n) to be the first date of the calendar year (not shown). Bombardi et al. (2017) also shows a demise that is too early, largely because there are multiple years in Caribbean sub-regions that have breaks in their rainfall season that satisfy the criteria set in their method to determine the demise. The mean demise dates from D16 and B20 are closer to this study’s, yet are also earlier than the climatological wet-to-dry season transition found in M19. This is due to several reasons. First, D16 and B20 set the demise as the maximum of S(n), but this does not accurately depict the end of the rainfall season, as the date of the maximum of S(n) is when rainfall is below the seasonal yearly or climatological mean threshold. This can limit the length of the rainfall season or inaccurately depict the demise by not including portions of the rainfall season that have gradual demises or intermittent rainfall that is post-peak of the rainfall season (e.g. Fig. 6). The 1974 Northwestern Caribbean (Fig. 6a), 1997 Guianas (Fig. 6d) and 2015 Western Caribbean (Fig. 6e) rainfall cycles all show the maximum date of S(n) to be the same in the present method and D16/B20 methods, which means the time period and window parameters did not affect the maximum date of S(n). However, the present method utilizing the candidate demise dates finds demises that are located during the transition from wet-to-dry season, and includes post-rainfall season peak intermittent rainfall or rainfall that is gradually decreasing from the date of the maximum of S(n). Second, in years where the rainfall season is anomalously dry, using a mean threshold based on the climatology, as D16 and B20 use, can skew the demise to be d_s – N or before the onset, because the accumulated precipitation anomalies will be negative throughout the year and the maximum of S(n) would be at the start date. Third, using a window that encompasses the entire hydrological cycle, as D16 and B20 use, can skew the demise date if the rainfall season is non-symmetrical or if components of the rainfall season (e.g. ERS and LRS) are independent of one another. Setting the window as the entire hydrological year when one season is anomalously dry and the other is not, or vice versa, can skew the S(n) calculation and cause the demise to be d_s – N or before the onset. For example, the 1975 Central Caribbean rainfall cycle (Fig. 6c) has the demise using the method D16 and B20 near d_s – N. Since the ERS was anomalously dry that year, using a mean threshold based on the climatology and calculating S(n) over the entire hydrological cycle caused the maximum of S(n) to be near ds – N. The present method found the demise during the wet-to-dry season transition using the LRS window and mean threshold relative to that year’s LRS. These three reasons explain why the standard deviations of the mean demise dates are larger in D16 and B20 than in the present method (Table 5), and how demise dates in the present method are later than in D16 and B20 (Fig. 8).

  
  

  The evolution of the RMD mean dates across stations in the Caribbean match the evolution of the regional RMD mean dates and resembles the dynamical evolution of the end of the rainfall cycle across the Caribbean (Fig. 7b). Generally, the evolution of the RMD mean dates follows a NW-to-SE pattern. The demise of the rainfall cycle in the Caribbean begins in the northwestern corridor, with RMD means between mid-October (e.g. Nassau, Bahamas) to early November (e.g. Worthy Park, Jamaica). The RMD dates migrate southeastward onto the Central Caribbean, with RMD means ranging from late October (e.g. Guaynama, Puerto Rico) to mid-November (e.g. Ensenada, Puerto Rico). M19 finds the earliest climatological demise of the rainfall season beginning in the Northwestern Caribbean and later the Central Caribbean. This is due to divergence from NASH and transience from the continental United States that infiltrates the Northwestern Caribbean and progresses into the Central Caribbean during the LRS (M19). The western Caribbean experiences a large range of demise dates, with inland stations experiencing early-November RMD dates and coastal stations experiencing late-November to December RMD dates. M19 finds the Western Caribbean during the LRS influenced by convergence from the jet exit region of the CLLJ and by the Eastern Pacific ITCZ (M19), which during the LRS slowly migrates southward. It is likely that the later RMD demise dates seen on coastal stations of the Western Caribbean are a result of lingering convergence seen from these dynamical features. The Eastern Caribbean experiences the latest RMD dates out of any Caribbean region, ranging from early to mid-December. The finding resembles the climatological end of the rainfall season across the Eastern Caribbean from the slowly southward migrating Atlantic ITCZ that influences the region during the LRS (M19). In the Guianas, both the first (Fig. 7b) and second (not shown) RMD mean dates are a result of the migration of the Atlantic ITCZ (M19). The Atlantic ITCZ migrates away from the Guianas by August/September and migrates northward into the Eastern Caribbean to provide the Eastern Caribbean with its rainfall peak during its rainfall season. The second demise is when the Atlantic ITCZ moves south of the Guianas during the boreal winter.

  
  

  Similarly with onsets, absolute demises have a comparable or stronger relationship with the atmospheric/oceanic modes of variation that shape the Fall portion of the rainfall season than D16/B20 demises, and relative demises have non-significant and weak correlations with the atmospheric/oceanic modes of variation (Table 4). All sub-regions have high positive correlations between seasonal rainfall totals and demise dates. ENSO and Eastern Pacific SSTs during the rainfall seasons are negatively correlated with demise dates in the Northwestern, Central, and Eastern Caribbean, and Guianas. Eastern Pacific SLP and CLLJ during the LRS are positively correlated with demise dates in the Northwestern Caribbean, Central Caribbean, and to a lesser extent Eastern Caribbean. In the Guianas, both rainfall season demises have a positive correlation, though weak, with Eastern Pacific SLP, and the first rainfall season demise is negatively correlated with the meridional component of the 925mb winds across Northern South America. Central Caribbean and Northwestern Caribbean demise dates are negatively correlated with 925mb wind direction. ENSO is the main driver of LRS variability; the onset of ENSO during the boreal summer and fall induces an anomalous see-saw SLP pattern between the Eastern Pacific and Caribbean basins through an ENSO atmospheric bridge (Giannini et al. 2000) that affects the LRS across the Caribbean (M20). During a warm ENSO, cold SSTs, stronger easterlies, and above-normal SLP are seen over the Caribbean Basin during the LRS, which results in weaker moisture convergence over the Caribbean (M20). Given the strong mutual relationship between absolute or D16/B20 demises and LRS totals, the ENSO induced see-saw SLP pattern is likely responsible for the variability of the Caribbean demise dates under these methods. For the Guianas, the first rainfall season demise falls during the LRS; therefore, the effect of ENSO on the Caribbean likely affects the Guianas similarly. Since the second rainfall season of the Guianas is during the winter-time, it is likely the mature-phase of ENSO impacts the demise dates during the second rainfall season. The correlation differences between demises that are based on a climatological mean threshold such as the absolute and D16/B20 demises vs. demises that are not based on a climatological mean threshold such as the RMDs suggests the variability of the rainfall seasons are a consequence of changes to the rainfall seasonal amount rather than changes to the rainfall seasons’ timing.

• (c) Intermittent dry period characteristics

  
  

  Table 6 highlights the relationship between intermittent dry period characteristics and atmospheric/oceanic indices for sub-regions with intermittent dry periods. In the Caribbean, most sub-regions have statistically significant correlations between magnitude or duration of the intermittent dry period and seasonal rainfall totals, the winter-time NAO, summertime ENSO, southern Tropical North Atlantic SST and SLP during the intermittent dry period, and Caribbean Sea zonal and meridional components of the 925mb winds during the intermittent dry period. There are some notable sub-regional differences. For example, the Western Caribbean and Central Caribbean have higher correlations between their intermittent dry period characteristics and ERS totals/winter-time NAO than LRS totals/summertime ENSO. For these sub-regions, the variability of the intermittent dry period may be more associated with variability of the ERS than LRS. For example, the Central Caribbean experiences little to no ERS during dry ERS years (M20), which results in a longer and more intense intermittent dry period. The correlations between the intermittent dry period characteristics and various indices suggest that above-normal magnitude and below-normal duration of the intermittent dry period are associated with (1) above-normal ERS and LRS, (2) a preceding winter-time negative NAO, and summertime cold ENSO state, (3) warmer SSTs and above-normal SLP over the southern Tropical North Atlantic, and (4) anomalous westerlies. Since the variabilities of the ERS and LRS are largely influenced by the Southern Tropical North Atlantic persistent SST/SLP anomalous signal induced by the preceding winter-time NAO and the summertime onset of ENSO (M20), respectively, the variability of the intermittent dry period in the Caribbean is likely driven by competing interactions of the anomalous signals induced by both preceding winter-time NAO, and summertime ENSO over the region.

Table 2 Atmospheric/oceanic indices and rainfall characteristics used to correlate with temporal, and intermittent dry period rainfall characteristics for the Caribbean/Guianas

Table 3 Comparison of onset means (and standard deviations) of different methods

Fig. 5

Regional station averaged onset dates from 1960/70–2015 in the (a) Northwestern Caribbean, (b) Western Caribbean, (c) Guianas first rainfall season, (d) Central Caribbean, (e) Eastern Caribbean, and (f) Guianas second rainfall season using several methods. Blue squares denote the relative meteorological onset. The orange stars denote onset dates replicating the Dunning et al. 2016 or Bombardi et al. 2020 method

Fig. 6

(a) is similar to Fig. 3c, but for the year 1974 over the Northwestern Caribbean. Similar analysis is applied to other subregions of the Caribbean: (b) Eastern Caribbean in 2003, (c) Central Caribbean in 1975, and (e) Western Caribbean in 2015. (d) is similar to Fig. 4c., but for the year 1997 over the Guianas

Fig. 7

Climatological Relative Meteorological Onset (top) and Demise (bottom) dates across stations in the Caribbean

Table 4 Correlations between various atmospheric/oceanic indices and onset dates (first two columns) and demise dates (last two columns) from 1979–2015

Table 5 Comparison of demise means (and standard deviations) of different methods

Fig. 8

Same as Fig. 5 but for demise dates

Table 6 Correlations between Intermittent Dry Period Magnitude or Duration and several atmospheric/oceanic indices and rainfall characteristics from 1979–2015

In the Guianas, seasonal rainfall totals, summertime ENSO, and Eastern Pacific SST and SLP are correlated with statistical significance with its intermittent dry period characteristics. The intermittent dry period of the Guianas is during the onset of ENSO in the Fall; therefore, the effects of ENSO on the Caribbean in the Fall similarly affect the Guianas as ENSO displaces the Atlantic ITCZ (M20).

Correlations between RMOs and intermittent dry period characteristics are small and insignificant for most of the Caribbean, with the exception being moderately negative correlation between Central Caribbean RMD and magnitude of the intermittent dry period, and moderately positive correlation between the RMD and dry period duration. The lack of correlations between timing characteristics and intermittent dry period characteristics for most of the Caribbean suggest that changes in the timing of the onset and demise may not impact or be impacted by changes in the intermittent dry period, but rather changes in the magnitude of the rainfall season as suggested by the correlation between rainfall amount and intermittent dry period characteristics.

5 Adaptability of the method to an agronomical context

The method can also be adapted to investigate agronomical onsets and demises. An example summary of the thresholds used for the agronomical context, in addition to the meteorological contexts, can be found in Table 7. Of the studies that investigate agronomical onsets, there are two criteria that are universal: a crop-related mm threshold, and a criterion to check for the persistence of rainfall above that threshold. Both of these criteria are incorporated into the present method, but their values can be inputted by the user. The agronomical mm threshold is typically based on the soil water requirements of the crops of interest, which may consider rates of evapotranspiration in a given region. For example, Moron and Robertson (2014) used a 5-mm threshold based on evapotranspiration rates in India which can be 4–7 mm/day during their rainfall season (Bandyopadhyay et al. 2009). Marteau et al. (2009) used a 5-mm total over a 7-day period as the threshold to determine a dry spell. Note that the agronomical mm threshold is not the inflection point mm threshold that is in the present method. Although it is not required, it is recommended to have the agronomical mm threshold be at equal to or greater than the inflection point mm threshold because inflection points are the basis for determining candidate onsets and demises. Hence, if the agronomical mm threshold is less than the inflection point threshold, one could miss inflection points that would otherwise satisfy the agronomical mm threshold.

Table 7 A summary of the user-input/calculated thresholds used to calculate temporal characteristics of the annual rainfall cycle in the Northwestern Caribbean

The criterion for persistence of rainfall below and above the agronomical mm threshold is used to determine any false agronomical onsets and demises, respectively. Using the unsmoothed daily data, a false agronomical onset is determined if the candidate onset meets one of the following user inputs: (1) Dry spell of length “C” consecutive days are below the agronomical mm threshold; or, (2) the total number of days between the candidate onset date and “N” days out that are below the agronomical mm threshold is no more than X% of the total number of days between the candidate onset and “N” days out. A typical “C” value is 5 to 10 days (e.g. Diop, 1996; Moron and Robertson, 2014), and a typical “N” days out is 15 to 30 days (Moron and Robertson, 2014), depending on whether one looks for dry spells or wet spells. The X% of the total number of days is a new criterion, and it mitigates the issue of dealing with years where there is not persistent rainfall above the agronomical mm threshold, even if there were consecutive days that produced rainfall above the threshold. A value of 50–60% is recommended, as it provides at least half of the window to have rainfall above the agronomical mm threshold; however, the value can be changed according to the crop of interest, or other agronomical criteria. Similarly, the false agronomical onsets are filtered out and the agronomical onset is the earliest candidate onset after the start of the window. The false agronomical demises are filtered out and the agronomical demise is the earliest candidate demise after the peak of rainfall within the window.

Illustration of the onset and demise calculations for the agricultural context (Fig. 9) uses an onset agronomical threshold of 2 mm and a demise agronomical threshold of 1 mm, for the entire Caribbean. A daily rainfall value of 1–2 mm is generally the minimum of rainfall in the annual climatological cycle across the Caribbean sub-regions. In the Guianas, the thresholds are 3 mm for onset and 1.5 mm for demise, as the minimums of their annual climatological rainfall cycle is typically between 1.5 and 3 mm. For the persistence check, a dry and wet spell of length 9 days, with 30 days out of the onset candidate, and 15 days out of the candidate demise are used to check for false onsets and demises. The method delineates false and actual agronomical onsets and demises under the values used. For example, the Northwestern Caribbean experienced multiple false agronomical onsets because there were multiple dry spells which did not meet the requirements for the agronomical onset until the start of the ERS (Fig. 9a). The Guianas experienced multiple false demises due to intermittent rainfall throughout the first rainfall season (Fig. 9d). The ability to delineate false versus true agronomical onsets and demises is valuable for end-users such as farmers and forecasters when determining whether pre- or post-monsoon or transient activity is likely to produce a false wet signal, which helps avoid preparing for the spring growing season too soon or finishing the fall harvest season too early (Marteau et al. 2009; Osorio and Galiano 2012).

Fig. 9

Agronomical onsets and demises for (a) Northwestern Caribbean in 1998, (b) Eastern Caribbean in 1987, (c) Central Caribbean in 1976, (d) Guianas in 1971, and (e) Western Caribbean in 2013

6 Discussion

The present method has several advantages, such as the ability to distinguish unimodal dual maxima patterns and calculate its temporal and intermittent dry period rainfall characteristics. Previous methods classify regions with unimodal dual maxima patterns as unimodal patterns, because the intermittent dry period between the rainfall maximums is not distinguishable. However, unimodal dual maxima patterns are a distinct rainfall cycle mode: the pattern appears unimodal, but the sets of dynamical mechanisms and climate drivers influencing each rainfall maximum can be different. Classifying unimodal dual maxima patterns as solely unimodal (1) limits the ability to calculate its intermittent dry period characteristics, and (2) implies that the variabilities of onsets and demises are similar to one another, which may not be the case. This is seen in some sub-regions of the Caribbean, where the ERS and LRS of the rainfall cycle are independent of each other because they are influenced by two separate and largely independent climate drivers and sets of dynamical mechanisms (M20). The present method is able to classify unimodal dual maxima patterns by distinguishing the climatological behavior of its intermittent dry period, and consequently, configure how temporal and intermittent dry period rainfall characteristics are calculated under this modality.

Detecting candidate onset and demise dates through the usage of inflection points that are related to the troughs and peaks of the annual rainfall season provide several gains. The candidate onset and demise dates can be used to determine both meteorological and agronomical onsets and demises, hence the method is universally applicable for both contexts. In the meteorological context, using candidate onsets and demises to find the onset and demise that relates to the minimum or maximum of the accumulated precipitation anomalies, or S(n), addresses the main limitation when using the Liebmann and Marengo (2001), as the min and max of S(n) can miss portions of the rainfall season that has intermittent or light rainfall before or after the main portion of the rainfall season.

The present method incorporates time and seasonal window parameters which have numerous benefits and mitigates limitations seen in previous methods. As most studies deal with unimodal or monsoonal rainfall regimes, they use the annual cycle as a whole to investigate temporal characteristics. However, not all regions experience rainfall regimes that are unimodal, and the characteristics in non-unimodal regimes differ between its multiple rainfall seasons. Methods that have dealt with non-unimodal regimes do not consider regions that experience different modalities year-to-year, a limitation D16 acknowledges. This method mitigates these limitations by establishing seasonal windows that are determined by the modality of the climatological annual rainfall cycle, and setting the analysis based on each window. This characterizes temporal characteristics that pertain to each window, and prevents biases, as showcased in the Caribbean. Furthermore, the intermittent dry period window offers a novel way to characterize subtle and distinct intermittent dry periods. The intermittent dry period characteristics this method offers (magnitude and duration) can be used regardless of whether the intermittent dry period is distinct or not, and is a way to investigate its variability and relationship with atmospheric/oceanic modes of variability and other rainfall characteristics.

Specific to the Caribbean, some important implications are found when using the present method. In Gouirand et al. 2020, Caribbean-wide mean winter-to-summer and summer-to-winter dates, which resemble the onset and demise of the rainfall season, are May 13th and October 26th, respectively. However, this study finds that there are many stations and sub-regions with onsets and demise dates that are well before or after the Caribbean-wide mean onset and demise dates found in Gouirand et al. (2020). The sub-regional differences are attributed to how the dynamical mechanisms that shape the regional rainfall climate of the Caribbean evolve differently in space and time across each of the sub-regions (M19; M20). Using the present method, the findings from this study emphasizes the importance of investigating the Caribbean on a sub-regional scale. Anderson et al. (2019) and García-Franco et al. (2021) did not detect a MSD across the Western Caribbean under their methodologies, and consequently, did not calculate characteristics of the MSD in this region; however, the present method does show the MSD, though subtle, across the Caribbean coastlines of Belize, Guatemala, Nicaragua and San Andrés. Because their methods used gridded datasets, the no MSD detection could be due to coastal grid points that incorporate some ocean, which, as M19 found, can mask the magnitude of the subtle MSD. The newly-founded/stronger relationships between several atmospheric/oceanic modes of variability and onsets/demises/intermittent dry period characteristics across all sub-regions found in the present method are valuable for diagnosis and prediction of these rainfall characteristics. There are also sub-regional differences between which atmospheric/oceanic modes of variation have a strong relationship with onsets, demises, and characteristics of the intermittent dry period. Investigating the prediction of the associated dynamical mechanisms and rainfall characteristics in the Caribbean and tailoring subseasonal-to-seasonal rainfall forecasts on a sub-regional scale may enhance the prediction of the Caribbean rainfall cycle.

7 Conclusion

A novel approach to determine temporal and intermittent dry period rainfall characteristics of unimodal, unimodal dual maxima, and bimodal rainfall patterns are proposed and showcased using rainfall station data in the Caribbean. The method first classifies the modality of the climatological annual rainfall cycle through its intermittent dry period in order to set seasonal windows and time parameters for the yearly analysis. Then information on rainfall and the rate of change of rainfall in the yearly analysis is utilized in order to determine dates of candidate onsets and demises. The method is shown under two lenses: a meteorological context by adapting the Liebmann and Marengo (2001), D16, and B20 methods, and an agronomical context. The method addresses limitations and challenges from previous methods such as (1) the ability to distinguish unimodal dual maxima rainfall patterns and calculate its characteristics, (2) calculate characteristics of subtle and distinct intermittent dry periods, (3) dealing with years that have abnormally dry rainfall seasons, and (4) dealing with false meteorological and agronomical onsets and demises. As temporal and intermittent dry period characteristics are important variables of the rainfall cycle for numerous stakeholders such as agriculture and water management (Boyard-Micheau et al. 2013; Anderson et al. 2019), the method provides a way to investigate the variability and change of the growing and harvesting seasons.

Specific to the Caribbean, the following conclusions are made:

• 1. Generally, onsets and demises that are calculated using yearly mean thresholds are not correlated with rainfall amounts associated with either the ERS or LRS, nor the dynamical mechanisms that shape each rainfall season. However, onsets and demises that are calculated using a climatological mean threshold are correlated with rainfall amounts associated with either the ERS or LRS and the dynamical mechanisms that shape each rainfall season. This difference suggests that the variability of the rainfall seasons are influenced by changes in the magnitude of the rainfall seasons, rather than shifts in rainfall season timing.

• 2. Intermittent dry period characteristics are correlated with rainfall amounts and with dynamical mechanisms that shape the ERS and LRS, but not with onsets and demises that are calculated using yearly mean thresholds. This suggests a relationship exists between the magnitude of the rainfall seasons and the strength and duration of the intermittent dry period, and intermittent dry periods in the Caribbean are influenced by dynamical changes from both the ERS and LRS.

The method has important implications for other rainfall modalities, prediction, modeling capabilities, and the understanding of the variability of rainfall across timescales. A few regions yield rainfall cycles with other rainfall modalities such as trimodal patterns (Herrmann and Mohr 2011; Seregina et al. 2018; B20); the method could be applied to investigate trimodal or other multi-modal patterns that experience a variety of subtle and distinct intermittent dry periods. Although time filtering in the method limits computation of the onsets and demises in real-time, year-to-year onsets and demises can be utilized to investigate their relationship with dynamical mechanisms or weather types that are known to influence the annual rainfall cycle. Understanding what mechanisms or weather types influence temporal characteristics of rainfall can be used for predicting future rainfall. The usage of seasonal windows can be utilized to investigate intraseasonal variability, by assessing how the season evolves between its beginning and end stages. Other rainfall characteristics, such as the intensity or frequency of wet and dry days, wet-spells, dry-spells, and extreme wet days, can be calculated with the usage of seasonal windows. The ability to assess characteristics of the intermittent dry period can also advance in the understanding of its variability, what dynamical mechanisms shape it, and how it influences the rainfall seasons. This method can also be utilized under a modeling diagnostic framework. For example, the method can be used in models in order to determine their ability in simulating the observed behavior of the temporal and intermittent dry period characteristics of rainfall, and consequently detect biases in models in order to improve representation of observed physical mechanisms related to rainfall characteristics, through a process-based diagnostic approach such as the one reported by Muñoz et al (2017).