1 Introduction

The global water cycle is expected to intensify due to global warming (Held and Soden 2006; Huntington 2006; Greve et al. 2014), and such intensification is already taking place (Durack et al. 2012; Markonis et al. 2019; Pascolini-Campbell et al. 2021). In this context, the Mediterranean-Black Sea system has been identified as one of the most important responsive regions to climate change (Giorgi 2006). On the other hand, the flux of warm and salty water from the Mediterranean Sea to the Atlantic Ocean influences the variability of the Atlantic Meridional Overturning Circulation (AMOC; Reid 1979; Artale et al. 2006; Pérez-Asensio et al. 2012). Among other tracers, the AMOC distributes heat within the Earth system and influences temperature and precipitation patterns worldwide (Vellinga and Wood 2002), and it is expected to weaken in the twenty-first century leading to profound climatic and ecological changes over vast regions (Collins et al. 2019). For these reasons, it is critical to monitor the hydrological cycle in the Mediterranean-Black Sea system, as well as its temporal variability, not only due to its important influence in the ecologic and socio-economic conditions of such a densely populated area, but also because it can be useful to gain new insights into global climate change.

The Mediterranean Sea is a semi-enclosed sea of 2.5 × 106 km2, where evaporation (E) exceeds precipitation (P), and the deficit of water mass must be replenished by horizontal water fluxes, namely, continental fresh waters input, and salty waters inflow from the Atlantic Ocean and Black Sea. The connection with the Atlantic takes place through the Strait of Gibraltar (14 km at the narrowest point and 300 m depth at the shallowest one), and with the Black Sea through the Turkish Straits. The Dardanelles Strait is 62 km in length, between 1.2 and 7 km in width, 55 m in mean depth, and connects the Mediterranean Sea to the Sea of Marmara. The latter is connected to the Black Sea through the Bosphorus Strait, which is nearly 31 km in length, between 0.7 and 3.5 km in width, and 35 m in mean depth. Thus, the Mediterranean Sea water budget equation can be written as

$$dW = P - E + R + G + T,$$
(1)

where dW is the change of water content; R consists of river runoff, ice melting, and submarine groundwater discharges into the ocean; G and T are the net water mass fluxes through the Gibraltar and Turkish Straits, respectively, whose positive (negative) values are considered as Mediterranean inflows (outflows).

The Black Sea is another semi-enclosed basin, but with 0.44 ×106 km2, that is less than a fifth of the Mediterranean Sea extension. Here, the water budget equation is simpler, since salty water can only be exchanged through the Turkish Straits. Therefore, the Black Sea water budget equation is obtained from Eq. 1 by setting G = 0. Here, positive (negative) values of T are considered as Black Sea inflows (outflows).

In the continents, the drainage basins discharging into the Mediterranean and Black seas are defined according to the global continental runoff pathways scheme (Oki and Sud 1998), and they cover 5.34 × 106 and 2.43 × 106 km2, respectively (Fig. 1). In the Mediterranean Sea, the area of the continental drainage basin doubles the oceanic area, while the former quintuples the latter in the Black Sea. In both cases, the water budget equation can be applied by cancelling the salty water inputs in Eq. 1, that is setting G = 0 and T = 0, and replacing “ + R” by “ − R”. Knowing P, E, and dW in a continental drainage, the corresponding R can be estimated as a residual in Eq. 1.

Fig. 1
figure 1

Mediterranean-Black Sea system. Light red: Mediterranean Sea; dark red: continental basins draining to the Mediterranean Sea; Light blue: Black Sea; dark blue: continental basins draining to the Black Sea. The locations of both Strait of Gibraltar and Turkish Straits are indicated by black rectangles

Full size image

The general picture of the Mediterranean-Black Sea system is as follows. Net precipitation in the catchment regions flows to the sea after a time-variable period of residence. In both Mediterranean and Black seas, E exceeds P, which contributes to a net loss of water vertically. In the Black Sea, the continental inflow not only replenishes such loss, but produces a surplus of water that is transported superficially to the Mediterranean Sea. At the same time, near the bottom saltier Mediterranean waters go into the Black Sea. Altogether these fluxes accumulate a net water mass transport from the Black Sea to the Mediterranean Sea of 0.0087 ± 0.0019 Sv (275 ± 59 km3/year), as reported in a literature revision by Jordà et al. (2017).

In the Mediterranean Sea the situation is different since continental inflow is not sufficient to replenish the water mass lost via net evaporation. When the contribution from the Black Sea is accounted for, net evaporation is not yet balanced, and an inflow of Atlantic waters is needed to keep the Mediterranean water budget. The Atlantic waters get saltier and denser in the Mediterranean Sea due to the excess of evaporation (which also explains the higher salinity in the Mediterranean Sea). In this sense, the Mediterranean Sea is considered an inverse estuary or concentration basin that increases water density and stimulates deep water formation. As a consequence of the increase in density, Atlantic waters, once in the Mediterranean Sea, sink forming the Levantine Intermediate Water (LIW) in the Rhodes Gyre region, the Eastern Mediterranean Deep Water (EMDW) in the Adriatic Sea, and the Western Mediterranean Deep Water (WMDW) in the Lions Gyre (for further information on Mediterranean Sea circulation we refer the reader to Millot and Taupier-Letage 2005; Bergamasco and Malanotte-Rizzoli 2010). This more saline nutrient-rich water is transported to the Atlantic Ocean through the Strait of Gibraltar below the less dense and nutrient-poor input from the Atlantic (McGill 1953; Coste et al. 1988; Gómez et al. 2000). Altogether, the Mediterranean Sea receives a net inflow of 0.065 ± 0.033 Sv (2050 ± 1041 km3/year) from the Atlantic Ocean as reported in a literature revision by Jordà et al. (2017).

In this work we apply the recent method developed by García-García et al. (2020) to track water flux changes in the Mediterranean-Black Sea system. This knowledge provides new insights on the seasonal and inter-annual water mass exchanges between continents and oceans, and between the oceans themselves. Additionally, these results represent a new source of data based on observations potentially useful to validate oceanic and atmospheric models, as well as other type of observations, especially in geographically complex straits such as the Gibraltar or the Turkish Straits.

The article is organized as follows. Data and methods are described in Sect. 2. Section 3 analyzes the water transport (WT) components in terms of mean values, seasonal and non-seasonal variability, and the influence of the North Atlantic Oscillation (NAO) in them. Discussion of results and conclusions are presented in Sect. 4.

2 Data and methods

2.1 Data

Net precipitation, P–E, is obtained from ERA5 reanalysis (Hersbach et al. 2018), which assimilates observational data into general-circulation modelling provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). It has a global coverage of both continents and oceans at monthly (and hourly) intervals. Data are 0.25º regular grids for years 2002–2020. Grids have been homogenized to 1ºx1º to match the spatial resolution of the continental drainage basin data.

Water mass budget variations, dW, are estimated from the RL06 GRACE mascon (mass concentration) v2 solution provided by the Center of Space Research of University of Texas (Save et al. 2016; Save 2019) for the period May 2002–October 2020, with missing values between the end of GRACE mission and the beginning of GRACE Follow-On, that is from July 2017 to May 2018. Besides, the values of 12 single months and 5 pairs of consecutive months were missing and have been linearly interpolated. Data are on a 0.25º regular grid, but we have re-gridded them to 1º regular grids as we did for P–E. Note that the obtained spatial resolution is still finer than the ~ 300 km (~ 3º near the Equator) resolution of GRACE, which measures gravity anomalies from month to month with respect to a dynamic geophysical model that accounts for solid and ocean tides, among other factors. Assuming that the gravity changes are produced by mass changes on Earth’s surface, such as in the oceans, the mascon solution can be interpreted as water mass (W) budget anomalies (Chao 2016). Time variations of W (that is dW) are estimated as the discrete central derivative of W,

$$dW\left( t \right) = \frac{{dW\left( {t + 1} \right) - dW\left( {t - 1} \right)}}{2},$$

where t refers to any given month. As a result, dW data span from June 2002 to June 2017 and from June 2018 to September 2020. The same months are selected for P–E data.

Usual corrections are applied to GRACE data: C20 coefficient was replaced by a solution from Satellite Laser Ranging (Cheng and Ries 2017), C30 coefficient was also replaced in GRACE Follow-On data, estimates for degree-1 coefficients were used (Swenson et al. 2008; Sun et al. 2016), a correction of glacial isostatic adjustment was applied (GIA) (Peltier et al. 2018), and the GAD product, which accounts for non-tidal variations of the atmosphere and ocean, was added back with the mean value of the ocean set to zero. The latter is done for consistency with the treatment of the Stokes coefficients anomalies of degree-0, ∆C00, which account for variations of the total mass of the Earth. Including the atmosphere, the total mass of the Earth is constant, and then ∆C00 are null. Excluding the atmosphere, the mass of the Earth is not constant since there is an exchange of water-mass between the surface and the atmosphere at a global scale, and in that case ∆C00 are not null. During GRACE processing, atmospheric and dynamic oceanic mass changes are removed, and ∆C00 are set to zero. However, these coefficients should not be zero due to the mentioned global water-mass exchange between Earth’s surface and the atmosphere. To diminish this inconsistency, the ∆C00 term from an atmospheric model could be added to GRACE (Chen et al. 2019; García-García et al. 2020). In this study, we add the ∆C00 term from ERA5 P–E to dW. Errors in the estimate of ∆C00 term propagate to the values of dW, but they do not affect to the estimates of R, T and G from Eq. 1, since the ∆C00 term vanishes due to the residual estimate between dW and P − E. In fact, adding ∆C00 from P−E to GRACE is numerically equivalent to set ∆C00 of P−E to zero as far as Eq. 1 is concerned. In addition, any mismodelling of the ocean basin (“container”) volume change due to GIA would masquerade as WT variations. However, it is not critical as far as our non-secular analysis is concerned.

Note that P−E units are mm/month, which multiplied by the surface of a cell grid in m2 yields volume transport units. GRACE units are kg/m2 and the units for dW are (kg/m2)/month, which multiplied by the surface of a cell grid in m2 gives mass transport units. In order to make P−E and dW comparable, dW units are transformed to volume transport units assuming a water density of 1000 kg/m3 for fresh water and 1025 kg/m3 for ocean water. In what follows, all results will represent volume transport and will be given in km3/year. However, since volume transport through the Strait of Gibraltar in the literature is usually reported in Sv (1 Sv = 106 m3/s), to ease the comparison with previous studies, the estimates of G will be provided both in km3/year and Sv.

2.2 Methods

The annual and semiannual components of the WT time series have been estimated by applying a least-squares fitting to the model

$$C_{t} = p_{0} + p_{1} \cdot \, t + A_{a} \cos (\omega_{a} \cdot \, t \, - \phi_{a} ) + A_{sa} \cos (\omega_{sa} \cdot \, t - \phi_{sa} ),$$
(2)

where t represents time, Ct the value of the time series of interest at time t, (ω, A, Φ) = (frequency, amplitude, phase) and the suffix a and sa denotes annual and semiannual terms, respectively. The obtained results are identical when a third cosine term is included to account for the 161-day signal due to the S2 aliasing in GRACE data.

The reported standard deviations (SD) and 95% confidence intervals (CI) for the averages, trend and seasonal signals of the components of the WT, as well as for correlations have been evaluated using the stationary bootstrap scheme of Politis and Romano (1994) with the optimal block length selected according to Patton et al. (2009). Note that each time series comprises 208 observations and can be seen as the union of two evenly spaced time series (with 181 observations from June 2002 to June 2017, and 27 observations from June 2018 to September 2020) separated by a gap of 11 months. Since the stationary bootstrap assumes evenly spaced data, the distributions and the SD of the estimators of the quantities of interest were obtained by applying the bootstrap to the first series (of length 181). In all cases the distribution of the estimator was approximately normal and thus the corresponding 95% CI can be obtained as the mean of the bootstrap estimates plus/minus 2 SD. In order to make full use of the data, in the calculation of 95% CI, averages of the bootstrap estimates based on the reduced series (with 181 observations), were replaced by the estimate of the quantity of interest based on the original time series (with 208 observations). In most of the cases the correction is minor. To simplify notation all the results in the paper are presented in the form: estimate ± SD. The implementation of the stationary bootstrap used here is very similar to the one used in García-García et al. (2020). The number of bootstrap replications was set to 2000. A more detailed description follows.

2.2.1 SD and CI for the mean, trend and seasonal signals

For each time series corresponding to a certain component of the WT, the harmonic regression model in Eq. 2, with annual and semiannual component plus a linear trend, was fitted to the data (by least-squares). The bootstrap was applied to the residuals of the fitted harmonic regression (to meet the stationarity conditions required by the method). For each time series corresponding to a certain component of the WT, the stationary bootstrap produced 2000 samples of the residuals that were added back to the fitted harmonic regression yielding 2000 bootstrapped time series of the component of interest. For each of these 2000 bootstrapped time series the mean of the component was evaluated and a harmonic regression model with annual and semiannual component plus a linear trend was fitted to the data producing 2000 estimates of the mean, the trend and seasonal signals of the components. These estimates were used to compute the SD and the distributions of the estimators of the quantities of interest.

2.2.2 SD and CI for correlation

In order to avoid spurious correlation, for a given pair of variables of interest trend and seasonal component should be removed before computing the correlation. This can be done in several ways. Here we used two different approaches:

  • Approach 1: For a given pair of variables of interest, the harmonic regression model in Eq. 2, with annual and semiannual component plus a linear trend, was fitted to the data (by least-squares) corresponding to each variable and the residuals of the harmonic regression were computed. This produces a bivariate series of residuals with no trend and no seasonality.

  • Approach 2: For a given pair of variables of interest, the climatology corresponding to each component of the bivariate time series is computed and subtracted from the original time series. Since the trend component is in general not statistically significant, this alternative approach also produces bivariate residuals with approximately no trend and no seasonality and is more robust since it does not require the seasonal component to be approximately sinusoidal.

In both cases, the bootstrap was applied to the bivariate series of residuals. For each bivariate time series corresponding to the given pair of variables of interest, the stationary bootstrap produced 2000 samples of bivariate residuals. For each of these 2000 bootstrapped bivariate series of residuals the Pearson correlation coefficient was computed and these estimates were used to obtain the SD and the distributions of the sample correlation coefficient. In this article we only present the results corresponding to the second approach since those obtained using the first approach are very similar. Since the second approach is based on time series where the seasonal component was removed, we refer to the corresponding results and correlations as “non-seasonal signals” in Sect. 3.3.

In order to understand the relative importance of the seasonal signal in the coupling observed between pairs of variables, correlation between the original series (without removing trend and seasonality) was also computed (having in mind that sometimes this might correspond to spurious correlation). For that purpose, the 2000 samples of bivariate residuals from approach 2 were added back to the climatology of each variable yielding 2000 bootstrapped bivariate time series of the pair of variables of interest. For each of these 2000 bootstrapped bivariate series of residuals the Pearson correlation coefficient was computed and these estimates were used to obtain the SD and the distribution of the sample correlation coefficient. Again, very similar results (not shown) are obtained if residuals are evaluated using approach 1 and added back to the fitted harmonic regression models.

3 Results

In this section we present the mean estimates for each term of Eq. 1 applied to the drainage and oceanic basins of both Mediterranean and Black seas, as well as their temporal variability (Fig. 2). The results are discussed in the context of existing literature, and compared against estimates from previous studies. The seasonal and non-seasonal signals of water mass fluxes are also studied, and for the latter the influence of the North Atlantic Oscillation (NAO) on the temporal evolution of each term is explored.

Fig. 2
figure 2

Water transport (WT) components of Eq. 1 in the Mediterranean (first row) and Black seas (second row) and their drainage basins. First column: drainage basins; second column: ocean basins. Thick lines depict the 12-month running mean. Positive G and negative T correspond to Mediterranean Sea inflows

Full size image

3.1 Mean values of WT

A schematic representation of the mean water cycle in the Mediterranean-Black Sea system is depicted in Fig. 3. According to our estimates, the Black Sea drainage basins receive 378 ± 31 km3/year of net precipitation that produces a near identical amount of R = 391 ± 12 km3/year (Table 1). This value of R is in the upper range of previous studies and agrees, within error estimates, with their averaged value, which is 360 ± 43 km3/year (Table 2). In the Black Sea, about one third of the water supplied by R goes to the atmosphere via net evaporation, and the rest, 248 ± 22 km3/year, goes to the Mediterranean Sea through Turkish Straits (T, Table 1). This value is in the middle range of previous estimates and agrees, within error estimates, with their averaged value, which is 235 ± 72 km3/year (Table 3). The lowest estimates of T based on in situ observations are 111 ± 98 km3/year from September 2008 to February 2009 (Jarosz et al. 2011a, b), and 158 km3/year from September 2008 to August 2009 (Jarosz et al. 2013). For these time periods our estimates are 198 ± 133 km3/year and 194 ± 88 km3/year, respectively, which are within the huge error estimate.

Fig. 3
figure 3

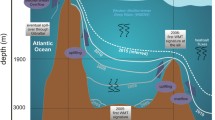
Schematic representation of the mean water cycle in the Mediterranean Sea (reddish) and Black Sea (bluish) shown in Table 1. Units are km3/year. Reported values are mean values, based on the original time series (with 208 observations) plus/minus the standard deviation estimated by stationary bootstrap based on the reduced series (with 181 observations)

Full size image
Table 1 Mean, annual and semiannual signal of WT components in Fig. 2 estimated from Eq. 2
Full size table
Table 2 Runoff from continents to Mediterranean and Black seas as estimated by previous studies
Full size table
Table 3 Turkish Straits flux (T) as estimated by previous studies
Full size table

For the Mediterranean Sea our results confirm that the mean water budget remains approximately constant in time (dW = 14 ± 11 km3/year), though it is characterized by a yearly important loss of water mass (1787 ± 23 km3/year) through net evaporation, that is compensated by the total flow into the Mediterranean Sea. This inflow comes from: (i) continental runoff that contributes around a fourth of that budget (502 ± 27 km3/year); (ii) water transported from the Black Sea that accounts for half of the riverine contribution (248 ± 22 km3/year); and (iii) water coming from the Atlantic Ocean through the Strait of Gibraltar that accounts for the remaining 1020 ± 56 km3/year (0.0323 ± 0.0018 Sv). Note that mean G is four times mean T.

Again, the estimated fluxes are similar to those reported in the literature. First, our estimate of R, 502 ± 27 km3/year, is in the upper range of previous studies for the Mediterranean Sea, and compatible, within error estimates, with their averaged value, which is 392 ± 100 km3/year (Table 2). However, this comparison should be interpreted with caution since the period of study seems to be relevant when estimating R. For example, the average of R for studies covering a time window ending prior to 2002 is 329 km3/year, while the corresponding value for studies ending after 2002 is greater than 500 km3/year. Second, our estimate of P–E in the Mediterranean Sea, −1787 ± 23 km3/year, is larger in absolute value, than the −1475 km3/year reported by Boukthit and Barnier (2000). Finally, our estimate of G, 1020 ± 56 km3/year (0.0323 ± 0.0018 Sv), is in the lower range of previous estimates and in agreement, within error estimates, with their averaged value, which is 1796 ± 948 km3/year (0.057 ± 0.030 Sv; Table 4). The discrepancy between our estimate and reported values of G from previous studies should be expected. For example, the larger value of G (0.055 Sv; 1734 km3/year) reported in García-García et al. (2010), is the result of differences not only in datasets and time periods, but also in the climatology used for R (with a lower mean of 0.0095 Sv; 300 km3/year) and the neglection of T in that study. These two terms (R and T) accounted together for a Mediterranean input deficit of 0.0175 Sv (552 km3/year) with respect to the present study, and such amount was erroneously attributed to G in García-García et al. (2010). The same reasoning can be applied to the 0.057 Sv (1798 km3/year) estimated by Boutov et al. (2014).

Table 4 Strait of Gibraltar flux (G) as estimated by previous studies
Full size table

It is worth noting the regional dependence of E. Although the mean value of E is similar in both Mediterranean Sea and associated drainage regions, the sea surface is less than half of land surface, which means that on sea E per m2 is twice that on land. On the contrary, E in Black Sea drainage regions is four times that in the Black Sea, but E per m2 is similar in both regions.

3.2 Seasonal signal of WT

In the Mediterranean Sea fresh water inputs are lower than net evaporation. The water budget balance achieved thanks to the surplus of water from the Black Sea to the Mediterranean Sea via T, and the inflow from the North Atlantic Ocean to the Mediterranean Sea via G. However, the water mass imbalance is not compensated instantaneously in the Mediterranean nor in the Black seas, and a climatological signal arise in all WT components and in water mass budgets. To analyze such climatology, an average year of each WT component is estimated averaging the signal of all Januarys, all Februarys, and so on. Figure 4 shows the average year or climatology for all WT components displayed in Fig. 2.

Fig. 4
figure 4

Climatology (monthly averages) of signals shown in Fig. 2

Full size image

Regarding the Black Sea drainage basin, P–E shows a clear annual cycle, mainly driven by E. The Pearson correlation between the P–E and E original time series is − 0.85 ± 0.03, while there is no significant correlation between P–E and P (Fig. 4c). The climatology of P–E shows a maximum in January of 1473 ± 94 km3/year and a minimum in July of − 697 ± 90 km3/year (Fig. 4c). The climatology of dW mimics that from P–E, and their original time series show a correlation coefficient of 0.90 ± 0.02, meaning that the water budget variability is driven by P–E (and E). On the other hand, P and R show a similar intra-annual variability (correlation coefficient of the original time series shown in Fig. 2c is 0.57 ± 0.09), meaning that R variability is mainly driven by P.

In the Mediterranean catchment region, the situation is somewhat different, since P–E reaches two local maxima (Fig. 4a). The first one (700 ± 95 km3/year) is in April, and contributes to an annual maximum of 982 ± 108 km3/year for R. The surplus comes from stored water, since dW shows a minimum in the same month of − 283 ± 77 km3/year. The second maximum of P–E (1156 ± 105 km3/year) is in August and produces an annual maximum of 720 ± 115 km3/year for dW. This means that the excess of water in spring mainly runs away via runoff, unlike the excess of water in summer when 2/3 of it is stored in land.

In the Black Sea, P slightly exceeds E from January to April (Fig. 4d). The month-to-month variability of T is mainly driven by R inflow. The correlation coefficient between the T and R original time series is − 0.91 ± 0.02. The correlation is negative since R is always positive and negative values of T indicate a flow from Black Sea to the Mediterranean Sea. During the first half of the year, riverine inputs to the Black Sea directly flow to the Mediterranean Sea at a mean rate of 448 ± 35 km3/year (428 ± 32 km3/year if July is included). During the second half of the year, the intra-annual variability of T is still driven by R, but the mean value of T is reduced to one tenth, mainly due to a great increase of E (maxima in August and September) and changes in the water budget (maxima of dW from October to December). In August and November, T even reverses, bringing water from the Mediterranean to the Black Sea at a mean rate of 185 ± 63 km3/year, which compensates the minimum contributions of R (Fig. 4d). This relationship between R and T would explain the lack of contribution of R to sea level variability in the Black Sea (Volkov and Landerer 2015), and it agrees with the role of P–E as the main driver of sea level variation in the Black Sea (Tsimplis et al. 2004). The reversal of T has also been related to wind-induced mass transport in the region (Stanev et al. 2000; Jarosz et al. 2011a, b).

In the Mediterranean Sea, there is an excess of E over P throughout the year (Fig. 4b). It produces a deficit of water mass that is balanced by the R, T and G inflows, although not instantaneously since there exists a delay in the response of the water budget. Although with different amplitude, the component G mirrors the variability of P–E, yielding a correlation coefficient between the original time series of − 0.77 ± 0.05. G shows an oceanic water mass inflow from June to February of 1913 ± 107 km3/year, with a maximum flux of 2726 ± 113 km3/year in August and September. However, in April and May, G reverses showing a mean net outflow of 407 ± 140 km3/year from the Mediterranean Sea to the Atlantic Ocean, which is very close to the 414 ± 77 km3/year Black Sea inflow during those months. This reversal of G is favoured by the maximum of R and the minimum of E.

Regarding the annual and semiannual signals of the inflow/outflow fluxes, we have found that the annual amplitude of T is 249 ± 32 km3/year and peaks on October 1, which agrees, within error estimates, with a similar study performed by Fenoglio-Marc et al. (2012) with GRACE data. They estimated T for the period 08/2002–07/2008 from previous versions of GRACE and atmospheric data, and R was derived from a hydrological model, reporting an annual signal of T peaking on September 27 (–T peaks on March 28) with an amplitude of 409 ± 91 km3/year. Our estimate for the same period produces an even smaller annual amplitude of 204 ± 44 km3/year and peaks on October 11 (phase is 280 that corresponds to October 7) with a SD of 13 days. Similarly, our estimate of the annual signal of G peaks on September 24 (263º ± 7º) with an annual amplitude of 1513 ± 182 km3/year (0.048 ± 0.006 Sv), which is within the middle range of previous estimates and agrees with their averaged value, 0.048 ± 0.020 Sv (Table 4).

3.3 Non-seasonal signal of WT

The non-seasonal signal is obtained subtracting the climatology from the original signal. This way is more appropriated than fitting an annual sinusoid since the average year is not always sinusoidal in shape (Fig. 4). In general, E shows very low non-seasonal variability, except in the Mediterranean Sea, where month-to-month variability is 3 times larger than in other regions (Fig. 5). In contrast, P shows larger non-seasonal variability everywhere except in the Black Sea.

Fig. 5
figure 5

Non-seasonal signal of WT components shown in Fig. 2

Full size image

In the Black Sea catchment region, the non-seasonal variability of P is propagated to P–E, dW, and R. The Pearson correlation coefficients between P and P–E, R, and dW are 0.98 ± 0.01, 0.61 ± 0.09, and 0.57 ± 0.09, respectively (Fig. 6b). The correlation between P–E and E for non-seasonal time series is not statistically significant, which confirms that non-seasonal variability of P–E is driven mainly by P. The inter-annual variability of P–E is quite large. For example, in 2005, a maximum mean value of P–E = 600 km3/year produced a maximum R = 510 km3/year, while in 2011, a minimum P–E = 153 km3/year produced a minimum R = 326 km3/year. Note that the excess of R over P–E in 2011 came from water extraction from land reserves, when dW presented an anomalous deficit of –173 km3/year. On the other hand, the correlation between R and T increases in magnitude from − 0.91 ± 0.02 (original series in Fig. 2) to − 0.97 ± 0.01 for the non-seasonal signals in Fig. 7. This means that R into the Black Sea goes almost simultaneously, or with a lag of less than a month, to the Mediterranean Sea. The maximum of R in 2005 produced a maximum transport of water mass from the Black Sea to the Mediterranean Sea of 438 km3/year. On the other hand, the minimum of R in 2011 halved T (212 km3/year). The differences between R and T are due to variations of water mass in the Black Sea, meaning that R is not the only factor driving T. Note that T is also forced by sea level changes in the Aegean Sea, sea level pressure variations over the Black Sea, and by winds blowing near Turkish Straits (Ducet et al. 1999; Jarosz et al. 2011b; Volkov and Landerer 2015; Volkov et al. 2016). Finally, the inter-annual variability of T has been reported in previous studies (Tsimplis et al. 2004; Peneva et al. 2001).

Fig. 6
figure 6

Correlation coefficients among all the WT components in Fig. 2 (a), and Fig. 5 (b). White squares represent correlations that are not statistically significant (the corresponding 95% CI contains the zero)

Full size image
Fig. 7
figure 7

Non-seasonal oceanic water exchange between the Mediterranean Sea and a the Black Sea (T), and b the Atlantic Ocean (G). Black curves are a − T, and b G; and red curves are a) R in Black Sea, and − R in the Mediterranean Sea. As T is multiplied by − 1, positive (negative) values of black curves represent Mediterranean inflows (outflows). Note the negative signs in the depicted curves. Correlations between R in the Black Sea and T, and between R in the Mediterranean Sea and G are both negatives

Full size image

In the Mediterranean catchment region, the situation is similar. The non-seasonal variability of P is propagated to P–E and R, with which shows a correlation coefficient of 0.96 ± 0.01 and 0.64 ± 0.09, respectively (Fig. 6). The correlation of P and dW is still significant, although decreases from 0.61 ± 0.08 (original time series, Fig. 2) to 0.38 ± 0.11 (non-seasonal time series). As in the Black Sea catchment region, the inter-annual variability of P–E in the Mediterranean catchment region is also quite large. For example, in 2010, P–E reached a maximum of 736 km3/year that produced a maximum R = 665 km3/year, while in 2008, P–E reached a minimum of 432 km3/year that produced a minimum R = 410 km3/year. Once again, the differences between R and P–E are balanced by variations in water land reserves.

On the other hand, the correlation between G and P–E in the Mediterranean Sea decreases in magnitude from − 0.77 ± 0.05 for the original time series in Fig. 2 to − 0.41 ± 0.12 for the non-seasonal time series in Fig. 5. Conversely, the correlation between G and Mediterranean R increases in magnitude from − 0.56 ± 0.08 for the original time series to − 0.78 ± 0.05 for the non-seasonal time series (Fig. 7). This may be interpreted as that P–E drives the climatology of G, but R is more important regarding the non-seasonal variability of G, which agrees with the fact that large unpredictable cyclones, especially in the Western Mediterranean, are accompanied by low-pressure systems. Altogether increases captured rainfall (and hence river runoff) and may rise Mediterranean sea level by means of the inverse barometer effect (Lionello et al. 2019). This interpretation is supported by the significant correlation of 0.34 ± 0.08 and − 0.40 ± 0.06 observed between the non-seasonal signals of the mean sea level pressure (from ERA5), and (i) G, and (ii) Mediterranean R, respectively. This interpretation is not in contradiction with the reported influence of winds near the Strait of Gibraltar on G (Landerer and Volkov 2013), since water mass blown by winds must overcome the hydraulic pressure produced by riverine waters. The larger R, the lower G as the sea level gradient decreases between both sides of the Strait of Gibraltar. Then, the maximum R in 2010 reduced the inflow from the Atlantic Ocean to the Mediterranean Sea to 706 km3/year (0.0224 Sv), while the minimum of R in 2008 increased such transport to 1262 km3/year (0.0400 Sv). Note that G in 2008 almost doubled the value in 2010. However, a strong inter-annual variability of G has been previously reported in the literature, e.g. Boutov et al. (2014) provided estimates of G = 0.023 Sv in 1996 and G = 0.082 Sv in 2000.

Linear trends have been estimated according to Eq. 2. However, only four WT components showed a statistically significant linear trend (the 95% confidence interval for the trend does not contain 0): dW in the continental catchment region of the Mediterranean Sea, trend = 117 ± 35 km3/year2; R in the Black Sea, trend = − 84 ± 36 km3/year2; P–E in the Black Sea, trend = − 48 ± 18 km3/year2; and T, trend = 129 ± 58.5 km3/year2. As negative values of T represent water transport from the Black Sea into the Mediterranean Sea, the reported positive linear trend of T represents a reduction of mass transport.

3.4 Influence of NAO on WT

The NAO is a climate atmospheric index characterized by sea level air pressure differences between the high-pressure system located over the Azores islands and the low-pressure system over Iceland. The NAO oscillates between positive and negative phases, which have a great influence in weather conditions on Europe and the Mediterranean Sea (Hurrell 1995), as well as in sea level (e.g., Vigo et al. 2011, Ozgenc Akoy 2017). However, we did not find any significant Pearson correlation between the NAO index estimated by NOAA (https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml), and the non-seasonal time series in Fig. 5. The situation is different when the NAO index is averaged over winter months (December–March). In that case, the NAO influence is revealed. A positive (negative) NAO phase produces drier (wetter) than average conditions in the region (Hurrell 1995). The correlation between winter NAO and (i) the annual averages, and (ii) the winter averages of signals in Fig. 5 have been estimated. The reported SD have been obtained applying ordinary bootstrap to the bivariate series of annual/winter averages. It should be noted that, in this case, the estimated sampling distribution of the correlation coefficients is often skewed. In the first case, only five components show a statistically significant correlation: − 0.62 ± 0.15 for E on Mediterranean catchment region; − 0.44 ± 0.18 and − 0.49 ± 0.16 for R and P–E in Black Sea; 0.50 ± 0.15 for T; and 0.51 ± 0.18 for G. Similarly, in the second case only four winter averaged components show a statistically significant correlation: − 0.65 ± 0.23, and − 0.55 ± 0.12, for P and E on Mediterranean catchment region; − 0.49 ± 0.16 and − 0.54 ± 0.20 for E and dW on Black Sea catchment region. Note that only the correlation of E on Mediterranean catchment region is significant for both annual and winter averages.

The correlation of the annual averages of R in the Black Sea is close to the − 0.47 similarly estimated by Stanev and Peneva (2002) for the period 1923–1997. Among the 5 largest rivers discharging into the Black Sea (Danube, Dnepr, Dnestr, Don, and Kuban), the Danube is the most important, accounting for 60% of the mean R in the Black Sea, and its catchment region is the most influenced by NAO. In fact, if the R in the Black Sea is estimated without accounting for the Danube, the correlation with NAO becomes not significant.

Mariotti et al. (2002) found significant correlations between NAO and both annual and winter averages of both P and P–E in a box (latitude, longitude = [25º N, 52º N], [10º W, 40º E]) covering both the Mediterranean and Black seas. In our case, we only found significant correlation between NAO and the components P (Mediterranean catchment region) and P–E (Black Sea) when winter averages are considered. Besides, we found a significant correlation between NAO and E on Mediterranean catchment region for both annual and winter averages. However, there are important differences with respect to our region (see Fig. 1) that may explain the distinct correlation coefficients. For example, they included continental regions corresponding to the Atlantic catchment region, but not the Nile River basin, which extension is more than half of the total Mediterranean catchment region and it is out of the NAO area of influence (Struglia et al. 2004).

It is known that the NAO influences the large-scale sea level pressure patterns over the Mediterranean and Black seas. In particular, NAO modulates the winds near: (1) the Strait of Gibraltar, which influences the non-seasonal water mass transport and the Mediterranean sea level variations (Landerer and Volkov 2013); (2) the Turkish Straits, which influence the water mass transport and the Black Sea level variations (Volkov and Landerer 2015; Jarosz et al. 2011a; 2011b). Then, the connection between NAO and the annual averages of G and T can be explained by these processes.

4 Discussion and conclusions

In this work we present an estimate of the hydrological cycle of the Mediterranean-Black Sea system, for the period 2002–2020, based on atmospheric reanalysis and time-variable gravity data and the water budget equation (Eq. 1). In particular, we provide a time variable estimate of G, which is crucial to understand the dynamics of the Mediterranean Sea (Malanotte-Rizzoli et al. 2014). We report a mean net flux of G = 0.0323 ± 0.0018 Sv (1020 ± 56 km3/year), which accounts for 58% of the water lost by net evaporation in the Mediterranean Sea. In addition, G shows a clear annual cycle, increasing to 0.0844 ± 0.0035 Sv (2660 ± 111 km3/year) in August/September, and reversing to − 0.0129 ± 0.0044 Sv in (− 407 ± 140 km3/year) April/May, when a net WT from the Mediterranean Sea to the Atlantic Ocean takes place. On top of the climatology, G shows a significant inter-annual variability with annual means ranging from 0.0224 (706 ± 56 km3/year) to 0.0400 Sv (1262 ± 56 km3/year) during the studied period.

Previous studies have attempted to estimate the components of WT in the Mediterranean and/or Black Sea using Eq. 1, either assuming that dW is null (Ünlüata et al. 1990; Bryden and Kinder 1991; Boukthir and Barnier 2000), or estimating dW from steric-corrected altimetry (Stanev et al. 2000; Soto-Navarro et al. 2010; Volkov and Landerer 2015) and from GRACE (García et al. 2006; García-García et al. 2010; Fenoglio-Marc et al. 2012). In all these approaches, the continental fresh water input R has been estimated with climatologies obtained from historical runoff measurements, or from hydrological models (as listed in Tables 3 and 4). The main novelties of our approach are: (i) the combination of the latest versions of GRACE and ERA5 datasets to obtain more reliable estimates of the water cycle in the region; and (ii) the indirect monthly estimates of R for the period of study. This represents a critical improvement due to the important differences in R from year to year (a mean decrease of ~ 15% and a mean increase of ~ 30% of R has been observed in some years in both Mediterranean and Black seas, respectively, though not always simultaneously). Consequently, years with above-average (low-average) R in the Black Sea produced above-average (below-average) T, while years with above-average (below-average) R in the Mediterranean produced below-average (above-average) G. This variability should be kept in mind when comparing estimates of G and T from studies performed in different periods. However, the indirect estimate of R is not perfect. As GRACE missions cannot distinguish the signal at length scales below ~ 300 km, and the diameter of some river basins in the Mediterranean-Black Sea system are smaller than that distance, some errors are expected to arise. In particular, for certain months R takes negative values (Fig. 4), which has no physical meaning.

Our climatology of R in the Black Sea is quite different to that estimated by Volkov and Landerer (2015), where R showed a more sinusoidal shape with maximum in April/May and minimum in September/October. Their R was estimated from a reconstruction of discharge measurements of the 5 largest rivers discharging into the Black Sea, and our R is calculated using a larger continental area. We re-estimated R using the 5 largest rivers as in Volkov and Landerer (2015) (not shown) and the signal was quite close to that shown in Fig. 4d which means that the continental area considered is not the source of the discrepancy between our and Volkov and Landerer’s estimates. A possible explanation for this discrepancy may reside in the fact that our R component includes surface running water out of the major rivers and underground water transport. In particular, the intra-annual signal of R, and so the lack of sinusoidal waveform, is mainly produced by the more irregular P in the continental catchment region of the Black Sea (Figs. 4c and 6a). On the other hand, as R drives the intra-annual variability of T, our climatology of T shows a less clear annual cycle than that estimated by Peneva et al. (2001), although both show the maximum transport during the first half of the year, and the minimum during the second one. However, the shape of our climatology of T is similar to that reported by Stanev et al. (2000). In any case, it should be highlighted that the methodologies and periods of study were different. For example, instead of GRACE data (not available prior to 2002), both Stanev et al. (2000) and Peneva et al. (2001) used altimetric measurements, whereas steric estimates from climatic heat fluxes between the Black Sea and the atmosphere came from ECMWF data and were combined with historical records of R prior to the studied periods.

In the Mediterranean Sea, our climatology of R is closer to two sinusoidal cycles (with one maximum in spring and another in autumn), than to one annual cycle with maximum in spring as reported in previous studies (Boukthir and Barnier 2000; Mariotti et al. 2002). However, as it happened in the Black Sea, those climatologies of R are estimated from historical observations of rivers discharge. Then, differences may be produced by distinct periods of time or non-river continental discharges. Besides, in addition to winds near the Strait of Gibraltar (Landerer and Volkov 2013), we report that low-pressure systems over the Mediterranean Sea also influence the non-seasonal variability of G (and of R).

An important feature of the here proposed methodology is that the water cycle of the Mediterranean-Black Sea system has been estimated using only two datasets, and these are expected to be available and periodically extended and updated for the scientific community in the coming years. In this regard, our approach offers the opportunity to continuously monitor the long-term variability of the water cycle in the region, which is important to understand the seasonal and the inter-annual variabilities, and their regional and global implications. Although in general the linear trends of WT components are not significant for the studied period, the inter-annual variability has been shown to be significant. Knowing such variability is not only important to better identify the physical mechanisms, but also at biological level, since, for example, the water transported through the Strait of Gibraltar conditions the exchange of nutrients. On the other hand, long time series would allow to detect possible variations in the seasonal signal that are expected as a consequence of the climate changes produced by the global warming (Held and Soden 2006; Huntington 2006; Greve et al. 2014).