1 Introduction

As the strongest seasonal-to-interannual variability in the tropical Pacific, El Niño and the Southern Oscillation (ENSO) has major impacts on weather and climate in many parts of the world via the atmospheric bridge effect (Cai et al. 2020; Chen et al. 2004; Duan and Mu 2018; Li et al. 2019; Timmermann et al. 2018; Yeh et al. 2018; Zhang et al. 2021). Considerable progress has been made in the understanding and prediction of ENSO over the past few decades (Chen et al. 2004, 2015; Kirtman 2003; Latif et al. 1998; Wang et al. 2017; Xie et al. 2016; Zebiak and Cane 1987). Nevertheless, ENSO prediction remains challenging. The reliability of forecasts of ENSO events has been reported as being relatively lower in the early twenty-first century than in the 1980s and 1990s, even with the ongoing improvement of forecast models. Decadal variations in ENSO forecasting skill have been identified in several analyses of numerical model predictions (Balmaseda et al. 1995; Chen et al. 2004; Kumar et al. 2017; Tang et al. 2008). The variation may be associated with the deficiencies of the ENSO prediction models, but it also depends strongly on ENSO predictability itself (Chen and Cane 2008; Duan and Mu 2018; Kirtman and Schopf 1998; Tang et al. 2008).

Many previous studies have examined decadal variations in ENSO predictability (Duan et al. 2018; Kirtman and Schopf 1998; Tang et al. 2008; Zhao et al. 2016; Zheng et al. 2016) using two common approaches: the diagnostic approach and the prognostic approach. The prognostic approach is based on hindcast experiments and widely used to explore ENSO predictability (Kirtman and Schopf 1998; Latif et al. 1998; Tang et al. 2008). The diagnostic approach uses the signal-to-noise ratio. The variance of a variable is decomposed into a signal component—which is potentially predictable—and an unpredictable noise component (Lopez and Kirtman 2014). Potential predictability at a given scale is analyzed using the ratio of the signal variance to the noise variance. However, for the signal-to-noise method, determining which part of the variance is signal and which part is noise remains somewhat subjective. This method can only qualitatively give the relative size of the predictability, not the predictability limit (PL) (Chen et al. 2006). In the prognostic approach, the predictability is estimated from the prediction skill of dynamical models and is usually model-dependent (Tang et al. 2008). These studies have significantly improved our understanding of ENSO predictability. However, forecast models are always imperfect analogs of the real ENSO dynamical system, which leads to some uncertainties in estimating ENSO predictability. Conclusions on ENSO predictability using the prognostic approach may give a rather confusing explanation of the decadal variations in ENSO forecast skill (Duan and Mu 2018). The predictability of the real ENSO system is concealed in the observational/reanalysis dataset. Thus, challenges remain in ENSO predictability studies in eliminating the negative impact of model deficiencies, deriving robust and general conclusions directly from the observational dataset, and quantitatively obtaining the PL.

The nonlinear local Lyapunov exponent (NLLE) method has been introduced to investigate atmospheric and oceanic predictability using observational data (Ding and Li 2007; Ding et al. 2008, 2016; Hou et al. 2018a; Li and Wang 2008; Li and Ding 2011, 2013, 2015; Li et al. 2018). As a nonlinear extension of the traditional Lyapunov exponent concept, the NLLE measures the nonlinear growth rate of the initial error of a nonlinear dynamical model (Chen et al. 2006). With the NLLE and its derivatives, the limit of atmospheric and oceanic predictability over various timescales can be determined quantitatively by exploring the evolution of the distance between initially local dynamical analogs (LDA) from the observational time series (Li and Ding 2011). Therefore, the ENSO PL can be assessed using the NLLE method with observational/reanalysis data (Hou et al. 2018b). In this paper, we use the NLLE method to estimate the seasonal PL of sea surface temperature (SST) in the tropical Pacific and investigate its decadal variation. The different key Niño regions will be considered, and the performances of their decadal variations of PL are explained from the perspective of error growth dynamics.

This paper is structured as follows: Sect. 2 briefly introduces the NLLE method and describes the data used in this study. Section 3 first examines the decadal variation of SST predictability in the tropical Pacific from 1900 to 2015, then Sect. 3.2 analyzes the error growth represented by the NLLE. The possible mechanisms responsible for the decadal variations in ENSO predictability are discussed in Sect. 3.3. A summary and discussion are given in Sect. 4.

2 Method and data

2.1 The NLLE method

An n-dimensional nonlinear dynamical system is described by

$$ \frac{d}{dt}{\mathbf{x}} = {\mathbf{F}}\left( {\mathbf{x}} \right), $$
(1)

where F denotes the dynamical system and \({\mathbf{x}} = \left[ {x_{1} \left( t \right),x_{2} \left( t \right), \ldots \ldots ,x_{n} \left( t \right)} \right]^{{\text{T}}}\) is the state vector at the time t. The evolution of an error \({{\varvec{\updelta}}} = \left[ {\delta_{1} \left( t \right),\delta_{2} \left( t \right), \ldots ,\delta_{n} \left( t \right)} \right]^{{\text{T}}}\), superimposed on a state x, is given by the equation:

$$ \frac{d}{dt}{{\varvec{\updelta}}} = {\mathbf{J}}\left( {\mathbf{x}} \right){{\varvec{\updelta}}} + {\mathbf{G}}\left( {{\mathbf{x}},{{\varvec{\updelta}}}} \right), $$
(2)

where \({\mathbf{J}}\left( {\mathbf{x}} \right)\) is the tangent linear evolutional operator and \({\mathbf{G}}\left( {{\mathbf{x}},{{\varvec{\updelta}}}} \right)\) is the high-order nonlinear term. There are some difficulties in solving the nonlinear term, so in most previous studies the initial perturbations were assumed to be sufficiently small for their evolution to be approximated by the tangent linear model of the nonlinear dynamical system (Eckmann and Ruelle 1985; Karamperidou et al. 2014; Lorenz 1969). However, the tangent linear approximation has many limitations in predictability problems involving finite-amplitude initial errors (Ding and Li 2007; Lacarra and Talagrand 1988; Li and Ding 2011; Mu and Duan 2003). Therefore, the nonlinear behavior of error growth should be considered. Without making the linear approximation, solutions of Eq. (2) can be obtained by numerical integration from \(t={t}_{0}\) to \({t}_{i}\),

$$ t_{i} = t_{0} + \tau , $$
$$ {{\varvec{\updelta}}}\left( {t_{i} } \right) = {{\varvec{\upeta}}}\left( {{\mathbf{x}}\left( {t_{0} } \right),{{\varvec{\updelta}}}\left( {t_{0} } \right),\tau } \right){{\varvec{\updelta}}}\left( {t_{0} } \right), $$
(3)

where \({{\varvec{\upeta}}}\left( {{\mathbf{x}}\left( {t_{0} } \right),{{\varvec{\updelta}}}\left( {t_{0} } \right),\tau } \right)\) represents the error propagator. The definition of the NLLE is:

$$ {\uplambda }\left( {{\mathbf{x}}\left( {t_{0} } \right),{{\varvec{\updelta}}}\left( {t_{0} } \right),\tau } \right) = \frac{1}{\tau }\ln \frac{{\left\| {{\mathbf{\delta }}\left( {t_{i} } \right)} \right\|}}{{\left\| {{\mathbf{\delta }}\left( {t_{0} } \right)} \right\|}}, $$
(4)

where \({\uplambda }\left( {{\mathbf{x}}\left( {t_{0} } \right),{{\varvec{\updelta}}}\left( {t_{0} } \right),\tau } \right)\) is a function of the initial state \({\mathbf{x}}\left( {t_{0} } \right)\), the initial error \({{\varvec{\updelta}}}\left( {t_{0} } \right)\), and the evolution time increment \(\tau \). The NLLE measures the nonlinear growth rate of the initial errors of a dynamical model without linearizing the model’s governing equations. For a specific class of states \(\Omega \), the ensemble average NLLE, obtained by averaging \(\uplambda \left(\mathbf{x}({t}_{0}),{\varvec{\updelta}}\left({t}_{0}\right),\tau \right)\),

$$ {\overline{\lambda }}\left( {{\Omega },{{\varvec{\updelta}}},\tau } \right) = \frac{{\mathop \smallint \nolimits_{{{\text{x}} \in {\Omega }}}^{{}} {\uplambda }\left( {{\mathbf{x}}\left( {t_{0} } \right),{{\varvec{\updelta}}}\left( {t_{0} } \right),\tau } \right)d{\mathbf{x}}}}{{\mathop \smallint \nolimits_{{{\text{x}} \in {\Omega }}}^{{}} 1d{\mathbf{x}}}} = {\uplambda }\left( {{\mathbf{x}},{{\varvec{\updelta}}},\tau } \right)_{{{\text{x}} \in {\Omega }}} = \frac{1}{\tau }\ln \frac{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{i} } \right)}} } \right\|_{{{\text{x}} \in {\Omega }}} }}{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{0} } \right)}} } \right\|_{{{\text{x}} \in {\Omega}}} }} $$
(5)

where \({\langle \rangle }_{\mathrm{x}\in\Omega }\) denotes the ensemble average of state sample set \(\Omega \) and \({\overline{} }_{\mathrm{x}\in\Omega }\) represents the geometric mean of the errors from state sample set \(\Omega \). The ensemble mean NLLE reflects the evolution of mean error growth and can represent the predictability of the specific set. Based on the definition of NLLE, the mean relative growth of the initial error (RGIE, \(\mathrm{ln}\overline{\mathrm{E} }\)) may be obtained from,

$$ \ln {\overline{\text{E}}}\left( {{\mathbf{x}},{{\varvec{\updelta}}},\tau } \right) = \left[ {{\overline{\lambda }}\left( {{\Omega },{{\varvec{\updelta}}},\tau } \right)\tau } \right] = \ln \frac{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{\tau } } \right)}} } \right\|_{{{\text{x}} \in {\Omega }}} }}{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{0} } \right)}} } \right\|_{{{\text{x}} \in {\Omega }}} }}. $$
(6)

The concept of RGIE can be extended as the mean relative growth during a specific period. Considering the period from \(\tau_{i}\) to \(\tau_{j}\), the mean relative growth may be written:

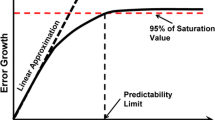
$$ \ln {\overline{\text{E}}}\left( {{\mathbf{x}},{{\varvec{\updelta}}},\tau_{i} \to \tau_{j} } \right) = \ln {\overline{\text{E}}}\left( {{\mathbf{x}},{{\varvec{\updelta}}},\tau_{j} } \right) - \ln {\overline{\text{E}}}\left( {{\mathbf{x}},{{\varvec{\updelta}}},\tau_{i} } \right) = \ln \frac{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{{\tau _{{\text{j}}} }} } \right)}} } \right\|_{{{\text{x}} \in {\Omega }}} }}{{\left\| {\overline{{{\mathbf{\delta }}\left( {t_{{\tau _{i} }} } \right)}} } \right\|_{{{\text{x}} \in {\Omega }}} }}$$
(7)

According to dynamical systems error growth theory, \(\overline{\mathrm{E} }\left(\mathbf{x},{\varvec{\updelta}},\tau \right)\) will converge to a saturation level with increasing \(\tau \) (Ding and Li 2007). Using the theoretical saturation level, the predictability limit can be quantitatively determined (Ding and Li 2007; Li and Ding 2011). The RGIE grows with increasing evolution time and reaches the saturation error level when the information from the initial state is completely lost; this evolution time is regarded as the PL. A schematic illustration of the determination of the PL using the NLLE method is shown as Fig. 1 in Ding et al. (2016).

Fig. 1
figure 1

a Spatial distribution of the mean seasonal predictability limit (PL) of SST and b its standard deviation on the decadal scale over the tropical Pacific from January 1900 to December 2015

Full size image

For dynamical systems, whose governing equations are known explicitly, the mean NLLE and RGIE may be calculated directly by numerical integration of their error evolution equations (Ding and Li 2007). However, the dynamical equations of the atmosphere and ocean are explicitly unknown, but abundant observational/reanalysis data are available, so we can estimate the mean NLLE by using these data with the local dynamical analog (LDA) method (Hou et al. 2020, 2021; Li and Ding 2011). The general purpose of the LDA method is to find the analogues for each base trajectory from the observational time series based on initial and evolved features at two different states (time points) in the time series, then estimate the exponential divergence rate between the base trajectories and their analogues as the NLLE. The mean RGIE can also be calculated. To reduce the effect of error fluctuations, the predictability limit in this study is defined as the time at which the error reaches 95% of its saturation value. The saturation value is obtained by taking the average of the mean error growth after the error almost stops increasing, following the work of Ding et al. (2016). More detailed descriptions and a derivation of the NLLE and LDA method can be found in Li and Ding (2011) and Ding et al. (2016).

Data in geophysical time series always have a certain persistence and are not completely independent. Thus, the effective degrees of freedom for the samples must be considered when computing statistics (Bretherton et al. 1999). In this method, the effective degrees of freedom for significance tests with autocorrelations sequences \({\rho }_{XX}(j)\) and \({\rho }_{YY}(j)\) are derived as follows (Li et al. 2013, 2021; Pyper and Peterman 1998):

$$ \frac{1}{{N^{eff} }} \approx \frac{1}{N} + \frac{2}{N}\mathop \sum \limits_{j = 1}^{N - 2} \frac{N - j}{N}\rho_{XX} \left( j \right)\rho_{YY} \left( j \right), $$
(8)

where \(N^{eff}\) is the effective number of degrees of freedom used in the significance calculation, \(N\) is the sample size (unadjusted number of degrees of freedom), and \(\rho_{XX} \left( j \right)\) and \(\rho_{YY} \left( j \right)\) are the autocorrelations of two sampled time series \(X\) and \(Y\) at time lag \(j\), respectively.

2.2 Data

The monthly SST dataset used in this study is version 5 of the Extended Reconstructed SST (ERSST.v5) generated by the National Oceanic and Atmospheric Administration (NOAA) on a 2° × 2° spatial grid (Huang et al. 2017), covering the period January 1854 to December 2019. The associated subsurface ocean temperatures were investigated using the Simple Ocean Data Assimilation dataset (SODA; available online at http://www.atmos.umd.edu/~ocean/). Version 2.2.4 of the SODA dataset consists of monthly-mean data spanning 1871–2008 with 0.5° × 0.5° horizontal resolution. The monthly mean ocean temperature data from The National Center for Environmental Prediction Global Ocean Data Assimilation System from January 1979 to the present are also used (GODAS; Behringer 2007). Using the ocean temperature and depth of the 20 °C isotherm (D20) from both SODA and GODAS, a warm water volume (WWV) index is defined as the average of D20 over the region 5° S–5° N, 120° E–80° W (Meinen and McPhaden 2000). The WWV index from GODAS and that from SODA are normalized separately, and have good consistency in their common periods. Therefore, we produced a new WWV index by combining that from SODA before 2008 and from GODAS since 2008 to the present.

Before calculating the PL, the climatological mean annual cycle and quadratic trend were first removed from the SST data to obtain the sea surface temperature anomaly (SSTA) at each grid point. The quadratically detrended process is expected to reduce the effects owing to global warming. To extract the seasonal to interannual components of the SSTA, a 9-year high-pass Gaussian filter is applied. The PL and RGIE at each grid point can be determined from the SSTA time series by applying the NLLE method. The mean NLLE and RGIE are calculated using a (9 × 12 + 1)-month moving window from 1900 to 2019. The moving window moves forward every month. The time axis indicates the middle month of the (9 × 12 + 1) month moving window. The seasonal predictability limit of SSTA for different decades is estimated from the mean NLLE. To highlight the decadal component, a 9-year high-pass Gaussian filter is applied to the monthly PL. We also use other SST datasets (OISST, Hadley and Kaplan SST; Kaplan et al. 1998; Rayner et al. 2003; Reynolds et al. 2007), with different moving windows (from 7- to 13-year), and the results are similar.

3 Results

3.1 Predictability limit of the tropical Pacific

The spatial distribution of the mean PL of monthly SST from 1900 to 2015 over the tropical Pacific is shown in Fig. 1a. The mean PL over the tropical and subtropical Pacific (110° E–70° W, 30° S–30° N) is 6.95 months. Zonally averaged, the PL in the equatorial Pacific is higher than that off the equator. From east to west along the equatorial Pacific, the PL in the central and eastern Pacific (exceeding 12 months) is relatively higher than that in the western tropical Pacific (5–7 months). The highest PL (> 14 months) is in the region east of the equatorial international dateline, and another high PL region (> 13 months) occurs in the South Pacific cold tongue off the equator (SPT; 5°–15° S, 140° W–100° W). Of the different Niño key regions, the PL is the highest in the Niño 3.4 region (5°S–5° N, 170°–120° W; > 12 months), followed by the Niño 3 region (5° S–5° N, 150°–90° W; 10–13 months), and then the Niño 1 + 2 region (10° S–0°, 90°–80° W; 8–9 months); these values are consistent with the results of Li and Ding (2013). The spatial structure of the PL in the tropical Pacific at seasonal to interannual time scales is associated with the ENSO dynamics system. The regions related to the ENSO oceanic process have relatively high PL, such as the Niño key regions—including Niño 6 region (8°–16° N, 140°–160° E)—implying the important role of the ENSO mechanism in the predictability of SSTA through the physical processes described by the delayed oscillator and recharge–discharge theory (Jin 1997; Wang et al. 1999; Wang 2018; Wyrtki 1985).

Tang et al. (2008) performed ENSO hindcasts from 1881 to 2000 and highlighted that the prediction skill for different dynamical models showed consistent interdecadal variation; this is the decadal variation of ENSO predictability represented by SST from models rather than the real physical system. In Fig. 2, we display the decadal variation of the mean PL from observational/analysis data in several key Niño regions and the SPT region. The curves in Fig. 2 are the seasonal PLs of SST under a (9 × 12 + 1)-month-low-pass filter and reflect the variation of seasonal predictability in different decades. The mean PL over the period from 1900 to 2015 is highest in the SPT (13.2 months) and Niño 3.4 (12.0 months) regions, followed by the Niño 4 (11.4 months) and Niño 3 (11.0 months), Niño 1 + 2 (8.9 months), and Niño 6 (7.3 months) regions, and lastly by the Niño 5 region (6.2 months), which is consistent with the values shown in Fig. 1. The PLs in these regions show decadal variation. The standard deviation over the period from 1900 to 2015 reflects the magnitude of decadal variation; in the SPT (1.40 months), Niño 3.4 (1.17 months), and Niño 4 (1.37 months) regions it is higher than that in the Niño 3 (0.83 months) and Niño 6 (0.87 months) regions. The decadal variation in the Niño 1 + 2 region is 0.56 months, and the lowest variation occurs in the Niño 5 region (0.47 months).

Fig. 2
figure 2

Decadal variation of the seasonal PL in the Niño 1 + 2 region (10° S–0°, 90°–80° W; brown), Niño 3 region (5° S–5° N, 150°–90° W; cyan), Niño 3.4 region (5° S–5° N, 170°–120° W; deep-sky-blue), Niño 4 region (5°S–5°N, 160°E–150°W; green), Niño 5 region (5° S–5° N, 120° E–140° E; dark violet), Niño 6 region (8°–16° N, 140° E–160° E; deep pink), the South Pacific cold tongue off the equator (SPT region; 5°–15° S, 140°–100° W; orange)

Full size image

The spatial features of decadal variability of the PL are shown in terms of the standard deviation on a decadal scale of the seasonal PL in each grid cell of the tropical Pacific in Fig. 1b. Its spatial distribution is consistent with that of Fig. 1a, and there is larger variability in the equatorial region than in the off-equator regions. The mean standard deviation over the whole tropical Pacific is 1.08 months. The maximum values (> 2.4 months) are found in the central tropical Pacific (5° S–5° N, 170° E–150° W) and the SPT region off the equator. The decadal variation of the seasonal PL in the central Pacific is larger than that in the eastern and western Pacific, consistent with the results in Fig. 2. Relative to the subtropical regions and western tropical Pacific regions, the PL decadal variability in the Niño 6 region is high, which implies the important role of ENSO dynamical processes in the PL of SST.

The seasonal PLs in the central and eastern tropical Pacific regions share some features of decadal variation. As shown in Table 1, the correlation coefficients between the PLs in the Niño 1 + 2 region and in the Niño 3, Niño 3.4, and Niño 4 regions are 0.84, 0.73, and 0.46, respectively, all of which reach the 90% confidence level. The correlation coefficients between Niño 3, Niño 3.4, and Niño 4 are all greater than 0.5 and significant at the \(\alpha =0.1\) level. The high correlation coefficients between the PL curves of the Niño 1 + 2, 3, 3.4, and 4 regions suggest that the same oceanic and atmospheric processes contribute to the PL of SST in the central and eastern Pacific. Interestingly, the decadal variability of the PL in the western tropical Pacific has relatively low consistency with that in the central and eastern Pacific. The PLs of the western Pacific, such as the Niño 5 and 6 regions, have low correlation with those of other Niño regions (Table 1). However, the PLs in the Niño 5 and 6 regions, whose SSTs are representative of those in the western Pacific, have highly consistent decadal variability.

Table 1 Correlation coefficients between the decadal variations of seasonal PLs in different Niño regions from 1900 to 2015. Niño 1 + 2 region (10° S–0°, 90°–80° W), Niño 3 region (5° S–5° N, 150°–90° W), Niño 3.4 region (5° S–5° N, 170°–120° W), Niño 4 region (5° S–5° N, 160° E–150° W), Niño 5 region (5° S–5° N, 120° E–140° E), Niño 6 region (8°–16° N, 140° E–160° E)
Full size table

Considering the difference in PL between the western and central/eastern Pacific, we choose the Niño 3.4 region to represent the central/eastern Pacific and the Niño 6 region for the western Pacific. The correlation coefficient between the PL in the Niño 3.4 region and PLs over the tropical Pacific is shown in Fig. 3a. Dotted regions indicate where the correlation coefficients pass the 90% confidence level. As mentioned above, the PL of the central and eastern tropical Pacific agrees well with the decadal variability of the PL of the Niño 3.4 region. However, the PLs of the western tropical and subtropical Pacific

Fig. 3
figure 3

Spatial field over the tropical Pacific of PL correlation with those over the a Nino 3.4 and b the Nino 6 regions. The dotted region represents correlation coefficients exceeding the 90% confidence level

Full size image

have low correlation with the decadal variability of the PL of the Niño 3.4 region. Figure 3b shows the correlation pattern between the PL of the Niño 6 region and those over the tropical Pacific. There is significant correlation in the western Pacific, where the PLs have insignificant correlation with those of the central/eastern Pacific, such as in the Niño 3.4 region. Thus, the results of Table 1 and Fig. 3 imply that the decadal variation of the PL in the central/eastern tropical Pacific is inconsistent with that in the western tropical and subtropical Pacific, and the decadal variation of the PLs in the Niño 6 and Niño 3.4 regions can be regarded as representative of that in the central/eastern, and western tropical Pacific, respectively.

In the central/eastern tropical Pacific, the PLs in the Niño 3.4 region have larger values (> 13 months) in the early 1900s, mid-1930s, mid-1960s and mid-1990s, along with lower values (< 11 months) around the 1920s, mid-1940s and mid-2010s, as shown in Fig. 2. Since the mid-1990s, the PLs in the Niño 1 + 2, 3, 3.4, and 4 regions have declined, as verified by the reduced forecast accuracy in ENSO operational models (Barnston et al. 2012; Zhao et al. 2016; Zheng et al. 2016). In contrast to the decadal variation of the PL in the Niño 3.4 region, the larger PLs (> 7.0 months) of the Niño 6 region in the western Pacific appear in the mid-1910s, 1940s, mid-1980s and mid-2010s. The PLs of the Niño 6 region are lower (< 7.0 months) in the 1930s, 1950s and mid-1990s. Interestingly, the PLs in the Niño 5 and 6 regions have increased since the mid-1990s. In fact, the model forecast skill from the North American Multi-Model Ensemble performs better in the western tropical Pacific since mid-1990s.

More detail of the decadal variability of the equatorial Pacific is shown in the longitude–time evolution of PL in the equatorial Pacific (5° S–5° N) in Fig. 4. The average PLs for different longitudes show that the seasonal PL is larger in the eastern and central tropical Pacific than in the western tropical Pacific, and the highest PLs (~ 14 months) are found from 180° to 150°W, consistent with Figs. 1 and 2. In addition to the lowest PL, seen in the western tropical Pacific, there are low PL values (< 8 months) east of 90° W from 1900 to 2015, which may be due to the influence of offshore current processes. The different values of the PL in the western, central, and eastern Pacific mean that the zonal gradient of PL in the tropical Pacific changes with longitude. Relative to other longitude regions, the zonal gradient of PL is larger near 170° E, which is a key area of air–sea coupling including wind divergence and the zonal advection of SST in ENSO dynamics.

Fig. 4
figure 4

Hovmöller diagram of the predictability limit zonally averaged from 5° S to 5° N in the tropical Pacific. The ordinate is the time from 1900 to 2015 and the abscissa is the longitude from 110° E to 70° W

Full size image

Like the decadal variation described by the PL curves in Niño regions shown in Fig. 2, the decadal variability of the PL for the whole tropical Pacific in Fig. 4 is more evident in certain decades. The PLs for almost all of the equatorial Pacific are lower in the 1920s and mid-1940s. The high PL areas (> 14 months) from 180° W to 150° W also vary on a decadal basis and occur mainly in the 1900s, mid-1930s, mid-1960s and mid-1990s. The central longitudes of the high PL areas also differ with decade; for example, 150° W in the 1900s, 170° W in the mid-1930s, and 160° W in the mid-1960s and mid-1990s. The high PL areas (> 14 months) in the central and eastern equatorial Pacific are larger and more sustained in the period from the 1980s to 2000s. The decline of the PL in the tropical Pacific since the mid-1990s occurs mainly in the central and eastern Pacific and corresponds to a reduction in the area where PL is greater than 11 months. The reduction of the high PL toward the central Pacific started in the mid-1990s and is ongoing. Meanwhile, the PL in the western tropical Pacific has increased since the mid-1990s, and this is more obvious near 150° E. The region with PL > 8 months has expanded from 140° E to 130° E near the eastern border. Compared with the low PL period of the 1920s and mid-1940s in the tropical Pacific, the PL decline in the central tropical Pacific since the 2000s is slightly weaker but has lasted longer.

3.2 Error growth in the tropical Pacific

From the perspective of error growth dynamics, the PL depends on the growth rate of the initial error and the error saturation level. The error saturation level represents the signal intensity, and the error growth rate determines how long the initial error takes to reach an error saturation value. Therefore, we focus on the error growth estimates from NLLE, such as \(\overline{\uplambda }\left(\Omega ,{\varvec{\updelta}},\tau \right)\) and \(\mathrm{ln}\overline{\mathrm{E} }\left(\mathbf{x},{\varvec{\updelta}},\tau \right)\), to clarify the reasons for the spatial pattern and decadal variation of the seasonal PL in the tropical and subtropical Pacific.

Figure 5 shows the mean error growth values as a function of evolution time, represented by NLLE, RGIE, and the errors in the Niño 3.4 and Niño 6 regions from 1900 to 2015. The mean PL in the Niño 3.4 region (12.0 months) is larger than that in the Niño 6 region (7.3 months). As a measure of error growth rate, the NLLE \(\overline{\uplambda }\left(\Omega ,{\varvec{\updelta}},\tau \right)=\frac{1}{\tau }\mathrm{ln}\frac{{\overline{\Vert {\varvec{\updelta} }\left({t}_{\tau }\right)\Vert }}_{\mathrm{x}\in\Omega }}{{\overline{\Vert {\varvec{\updelta} }\left({t}_{0}\right)\Vert }}_{\mathrm{x}\in\Omega }}\) and represents the logarithmic growth rate of error relative to initial error during a period of evolution. As shown in Fig. 5a, the NLLE in the Niño 6 region is always larger than that in the Niño 3.4 region over evolution periods from 1 to 10 months, which implies that the initial error grows faster in the Niño 6 region than in the Niño 3.4 region. Initial information is lost more rapidly with increasing evolution time in the Niño 6 region, which corresponds to the low PL. The RGIE or \(\mathrm{ln}\overline{\mathrm{E} }\)=\(\mathrm{ln}\frac{{\overline{\Vert {\varvec{\updelta} }\left({t}_{\tau }\right)\Vert }}_{\mathrm{x}\in\Omega }}{{\overline{\Vert {\varvec{\updelta} }\left({t}_{0}\right)\Vert }}_{\mathrm{x}\in\Omega }}\) and represents the error size relative to an initial error as a function of evolution period. The RGIE values in the Niño 3.4 and Niño 6 regions are shown in Fig. 5b. The RGIE values increase with increasing evolution time and reach the saturation level. The RGIE of the Niño 3.4 region is lower than that of the Niño 6 region and grows more slowly over the evolution time from 1 to 10 months. The dashed lines indicate the PL of the Niño 3.4 and Niño 6 regions, showing the period when the RGIE grows to the saturation level (95%). It is interesting that the saturation level of RGIE in the Niño 6 region is almost equivalent to that in the Niño 3.4 region, although the standard deviation of SST in the two regions is quite different. As well as the relative error described by \(\mathrm{ln}\overline{\mathrm{E} }\left(\mathbf{x},{\varvec{\updelta}},\tau \right)\), the actual error values in both regions also grow with increasing evolution time and reach saturation levels, as shown in Fig. 5c. The error values in the Niño 6 region are always lower but grow faster and reach the saturated error level earlier than those in the Niño 3.4 region. The actual saturated error level is almost proportional to the standard deviation of the system (Li et al. 2018). The higher standard deviation and lower error growth rate in the Niño 3.4 region contribute to the higher PL compared with that in the Niño 6 region. Note, however, that high standard deviation of SST does not correspond exactly to high PL.

Fig. 5
figure 5

Error growth in the Niño 3.4 (blue) and Niño 6 (pink) regions averaged from 1900 to 2015: a NLLE, b mean relative growth of the initial error (RGIE, \(\mathrm{ln}\overline{\mathrm{E} }\left(\mathbf{x},{\varvec{\updelta}},\tau \right)\)), c actual error values (°C)

Full size image

Figure 6b shows the spatial pattern of the actual saturated error level in the tropical Pacific over the period 1900–2015, which is very similar to the spatial pattern of the SST standard deviation. The actual errors at the saturation time are high (> 0.7 °C) in the central/eastern equatorial Pacific, and low (< 0.4 °C) in the western and subtropical Pacific. The initial error (Fig. 6a) ranges from 0.008 to 0.04 °C over the whole tropical Pacific, which is reasonable due to the constraint of adjacent states in phase space from the NLLE theory (Castro et al. 2008; Penland and Sardeshmukh 1995; Reynolds and Smith 1994). The initial error presents a similar spatial pattern to the error saturation level pattern, as the SST standard deviation pattern not only determines the spatial pattern of the saturated error value but also affects the spatial mode of the initial error. However, the differences between the spatial pattern of the actual error and that of the mean PL are large; for example, the maximum of the error is in the equatorial Pacific region near the east coast but that of the PL is in the central tropical Pacific. This implies that the absolute error does not fully determine the spatial pattern of PL values in the tropical Pacific. In fact, the error growth rate (NLLE) and RGIE play important roles in the PL.

Fig. 6
figure 6

Spatial distribution of error growth: a initial error at \(\tau =0 \mathrm{month}\); b error at the saturation time; c RGIE at \(\tau =1 \mathrm{month}\); d RGIE at the saturation time; e NLLE at the evolution time of 3 months; f NLLE at the evolutional time of 6 months. Values shown are multiplied by the mean value of each variable shown in the top right corner of the diagram

Full size image

The RGIE is the key variable describing relative error growth and is used to calculate the PL of the dynamical system. Figure 6d displays the saturated RGIE values. As shown in Eq. (6), the saturated RGIE depends on the saturated and initial errors. The regions corresponding to large saturated error values often have large initial errors (Fig. 6a, b). Therefore, the distribution of the saturated RGIE will differ from the spatial pattern of the saturated or initial error. The saturated RGIE in the tropical Pacific ranges from 2.76 to 3.16—which corresponds to 0.93 to 1.08 times the mean saturated RGIE value (2.958) in the tropical Pacific—and has a horseshoe-shaped distribution: small values appear in the equatorial tropical Pacific around the dateline, and in the northeast and southeast Pacific near the equator, and are surrounded by large saturated RGIE. Note that the spatial variation of the saturated RGIE is small (0.93 to 1.08 times the mean). A comparison with the spatial distribution of the mean PL (Fig. 1a) shows that regions with high saturated RGIE values have low PL, which suggests that the spatial distribution of saturated RGIE cannot explain the spatial pattern of the PL of SST in the tropical Pacific.

Meanwhile, the RGIE from 0 to 1 month also has a horseshoe shape (Fig. 6c), with low values in the central and eastern tropical Pacific and high values in the western tropical and subtropical Pacific. In contrast to the saturated RGIE that represents information signal intensity, the RGIE from 0 to 1 month is equivalent to the NLLE in the evolutional time of 1 month (from \({\tau }_{i}=0 \mathrm{month}\) to \({\tau }_{j}=1 \mathrm{month}\)) and represents the error growth over the first month. The values of RGIE from 0 to 1 month range from 0.6 to 1.3, suggesting the error grows to 1.8 (i.e. \({e}^{0.6}\)) to 3.6 (\({e}^{1.3}\)) times the initial error in 1 month. Thus, the high 0 to 1 month RGIE means faster forecast signal loss and low PL. Compared with the spatial range of saturated RGIE (0.93/1.08) in the tropical Pacific, the spatial variation of the 0 to 1 month RGIE is larger (0.65/1.4), which indicates that the spatial pattern of NLLE has a greater impact on the mean PL. Meanwhile, the spatial distribution of the 0 to 1 month RGIE is consistent with the pattern of mean PL in the tropical Pacific. Figure 6e and f display the mean error growth rate or NLLE at 3 and 6 months over the period 1900–2015. The NLLE for different evolution times has low values in the central and eastern tropical Pacific and high values in the western tropical and subtropical Pacific. A high value for NLLE represents fast error growth over the given evolution time, thus corresponding to low PL, whereas low NLLE corresponds to high PL. The NLLE at evolution times of 3 (6) months has high spatial correlation coefficients with the PL pattern shown in Fig. 1a of − 0.77 (− 0.82), both of which reach the 90% confidence level. The similar pattern of the NLLE and PL implies that the error growth rate is the key factor determining the spatial pattern of the PL.

The main factor affecting the spatial distribution of PL in the tropical Pacific is therefore error growth rate, whereas the RGIE at the time of saturation has little influence. The PL in different regions shows decadal variation; how does the error growth rate and saturated RGIE affect this decadal variability? As shown in Fig. 2, the Niño 3.4 and Niño 6 regions are the key regions where the ENSO dynamical systems develop, and their decadal variations, to an extent, represent the PL variation in the central/eastern tropical Pacific and the western tropical Pacific, respectively. Therefore, we first analyze the decadal variability of error growth of the Niño 3.4 and Niño 6 regions.

Figure 7 shows the decadal variation of saturated RGIE and error growth rate (NLLE) from 1900 to 2015 in the Niño 3.4 and Niño 6 regions. The PL, RGIE, and NLLE curves are normalized for better clarity. The NLLE, saturated RGIE, and error also have obvious decadal variations. The RGIE at the saturated time of the Niño 3.4 region (blue–violet curve in Fig. 7a) has larger values in the 1900s, mid-1930s, mid-1960s, and 1980s to 2000s, which is generally consistent with the decadal variation of the PL of the Niño 3.4 region. In fact, the correlation coefficient between the PL and RGIE at the saturated time is 0.81 (passing the 90% confidence level), which indicates that the decadal variation of RGIE at the time of saturation plays an important role in the PL and explains almost 66% of the PL decadal variance of the Niño 3.4 region. The strong linkage between the decadal variation of saturated RGIE and that of the PL of the Niño 3.4 region agrees with results from the signal-to-noise method: highly saturated RGIE represents large signal intensity and high PL. However, the decline of PL around the 2000s appears to be an exception: the PL in the Niño 3.4 region started to decline from the mid-1990s to mid-2010s, but the saturated RGIE value grew consistently from the mid-1990s to mid-2000s. Therefore, other factors affect the decadal variability of the PL. Interestingly, the error growth rate, especially NLLE (6) (that is, NLLE over months 0 to 6), increased at the beginning of the mid-1990s, which contributes to the decline of the PL in the Niño 3.4 region from mid-1990s to mid-2010s, whereas the saturated RGIE value increased from the 2000s to mid-2000s. Thus, there is decadal variation in the error growth rate, which also has a large influence on the decadal variation of PL. The NLLE over months 0 to 3 (NLLE (3); forest-green curve in Fig. 7a) represents the mean error growth rate relative to an initial error during the evolution time of 3 months, and NLLE (6) (deep-pink curve) represents the growth rate during the evolution time of 6 months. Clearly, high NLLE corresponds to low PL, such as in the 1920s and 1950s, whereas low NLLE corresponds to high PL, such as in the 1990s. The correlation coefficient between the PL and NLLE (3) or NLLE (6) is − 0.70 or − 0.63, both of which the 90% confidence level, which confirms the important role of the error growth rate in the decadal variation of the PL.

Fig. 7
figure 7

Decadal variations of error growth variables for the a Niño 3.4 and b Niño 6 regions. The black curve is the PL in Niño regions, the blue–violet curve is RGIE at the saturation time, green represents the error relative growth rate (NLLE) from 0 to 3 months, and deep-pink is the NLLE from 0 to 6 months

Full size image

Similar to the results for the Niño 3.4 region, the decadal variation of the PL of the Niño 6 region is consistent with the decadal variability of the RGIE at the time of saturation, represented by the black and blue–violet curves in Fig. 7b, respectively. The correlation coefficient between the PL and saturated RGIE is 0.90 (passing the 95% confidence level), which implies that high (low) RGIE at the time of saturation always gives a high (low) PL value. In addition, the error growth rate (NLLE) has an opposing effect on the PL of the Niño 6 region. When NLLE (3) and NLLE (6) are high in the 1930s and mid-1950s, the PL is low. The decadal variation of PL in the Niño 6 region has a correlation coefficient of − 0.66, with NLLE (3) that passes the 90% confidence level, as the fast error growth rate in the evolution time reduces the PL. We also calculate the correlation coefficient between the PL and NLLE (6) in the Niño 6 region. The coefficient is − 0.12, which does not pass the 90% confidence level, as a result of the low PL value (~ 5–6 months) of the Niño 6 region. When the evolution time for NLLE (6) is greater than the PL value, the error growth rate is less constrained. Compared with the relationship of the PL and RGIE or NLLE of the Niño 3.4 region, the Niño 6 region shows a stronger correlation between the PL and saturated RGIE, which implies that the decadal variation of PL depends more on the change of saturated RGIE of the Niño 6 region; this may result from the different physical mechanisms and greater atmospheric noise in the western tropical Pacific.

A more striking representation of error evolution at different longitudes is given by the Hovmöller diagram of the RGIE at the saturation time and NLLE at different evolution times in Fig. 8. The NLLE in the western Pacific is higher than that in the central and eastern Pacific, which is consistent with the result that PL is high in the central and eastern Pacific and low in the western Pacific. The decadal variation of saturated RGIE and NLLE in the central and eastern Pacific differs from that in the western tropical Pacific. There are high values of saturated RGIE (Fig. 8a) in the 1900s, mid-1930s, and 1970s to 2000s for the central and eastern tropical Pacific and in the 1910s, mid-1930s, 1960s, 1990s, and mid-2010s for the western tropical Pacific, consistent with the decadal variability of PL. As shown in Fig. 8b, c, and d, the NLLE patterns for these evolution times have similar decadal variation. The NLLE of the central and eastern tropical Pacific is higher in the mid-1940s, which contributes to the lower PL. In the last decade, NLLE (6) has increased at 165° W since the mid-1990s, which is consistent with the decadal decline of PL of the Niño 3.4 region.

Fig. 8
figure 8

Hovmöller diagram of the saturated RGIE (a), and NLLE at the evolution times of b 1, c 3, and d 6 months, meridionally averaged from 5° S to 5° N in the tropical Pacific. The ordinate is the time from 1900 to 2015 and the abscissa is the longitude from 110° E to 70° W

Full size image

In terms of NLLE theory, the decadal variation of saturated RGIE and NLLE determines that of the PL, as shown in Figs. 7 and 8. To illustrate the role of NLLE and saturated RGIE on the PL at different longitudes over the equatorial Pacific, we calculate the correlation coefficient between saturated RGIE or NLLE at different evolution times and the PL at different longitudes in Fig. 9 (solid dots indicate coefficients that pass the 90% confidence level). The correlation coefficients between PL and saturated RGIE at different longitudes are always positive and pass the 90% confidence level, which indicates that the decadal variations of the PL are closely tied to the variation of saturated RGIE. The decadal variability of saturated RGIE can explain 60% of the decadal variation of PL in the equatorial Pacific. Compared with the relationship between saturated RGIE and PL, the influence of NLLE on the PL is more variable, varying with evolution time and longitude. The correlation coefficients between NLLE and PL are significantly negative in the regions from 170° E to 125° W, which implies that high error growth rates lead to low values of the PL in the central and eastern tropical Pacific. In regions west of 165° E and east of 120° W, the relationship between NLLE and PL is not significant, which may result from the role of stochastic physical processes such as atmospheric convection on SST in the region west of 165° E or offshore currents in the region east of 120° W. Interestingly, the PL in the regions west of 150° E has a significant positive correlation with NLLE (6), which contradicts the idea that larger error growth rate decreases the PL. In fact, the region west of 150° E has low PL (lower than 6 months). Therefore, NLLE (6), representing the error growth rate at the evolution time of 6 months, has some features in common with the variation of the saturated RGIE. Comparing the effect of the decadal variation of saturated RGIE and NLLE on PL, we find that the decadal variation of the PL of SST in the tropical Pacific is caused by the change in saturated RGIE, while the error growth rate may affect some longitudinal regions.

Fig. 9
figure 9

Correlation coefficients between the decadal variation of error growth rate (NLLE) or RGIE (saturated) and PL meridionally averaged from 5° S to 5° N in the tropical Pacific during the period 1900 to 2015. Solid dots indicate the correlation passes the 90% confidence level. The abscissa is the longitude from 110° E to 70° W

Full size image

3.3 Physical processes responsible for the decadal variation of the predictability limit

In the previous subsection, we analyzed the influence of error growth on the PL based on the NLLE theory. However, it is not clear which physical processes affect the characteristics of error growth. As the primary source of seasonal-to-yearly climate variability in the tropical Pacific, ENSO events can be predicted up to three seasons in advance owing to the slow equatorial heat content recharge/discharge in the upper ocean (Cane and Zebiak 1985; Wang et al. 2017) that arises from the disequilibrium between zonal winds and WWV. The WWV, describing upper Pacific Ocean heat content, usually leads the ENSO SST evolution by a quarter of the ENSO period and acts as a useful predictor for ENSO SST (McPhaden 2003). Therefore, WWV is an important predictability source for the SST field in the tropical Pacific. However, this phase-lag relationship between the WWV and ENSO SST varies on decadal timescales (Bunge and Clarke 2014); for example, the significant shift around 2000 when the lead time shortened from approximately two to three seasons to approximately one season (Bosc and Delcroix 2008; Neske and McGregor 2018; Neske et al. 2021). It seems plausible to link the variation of WWV–ENSO SST lead time and the decadal variability of SST predictability in the tropical Pacific because the upper ocean heat content provides the ocean memory for the long-lead predictability of SST in the tropical Pacific. From the viewpoint of NLLE theory, the RGIE at the time of saturation and the error growth rate determine the PL of SST. Thus, we will explore how the RGIE (saturated) and error growth rate (NLLE) are affected by the phase-lag relationship between the WWV and SST in the tropical Pacific. We focus here on the Niño 3.4 region, which is an important component of the ENSO dynamical system.

Figure 10a shows the phase-lag relationships between the WWV and the Niño 3.4 index from 1900 to 2015 within a (9 × 12 + 1)-month running window. We find pronounced decadal variability, which is consistent with the results of Zheng (2019). The correlation coefficients between WWV and the Niño 3.4 index are low during the period 1940–1960 at lead times of 0 to 6 months. The phase-lag relationship has weakened at lead times of 6–9 months since the 2000s. Considering that the predictability barrier of ENSO is in spring (March to May, the spring predictability barrier; SPB) and ENSO’s mature phase occurs in winter (December–February), there are between 7 (May–December) to 12 (March–February) months from spring to winter. Therefore, we calculate the mean correlation between the WWV index and Niño 3.4 at lead times of 7 to 12 months as Corr (WWV-Niño, 7–12) (red curve in Fig. 10b) to quantitatively characterize the relationship between WWV and the Niño 3.4 index and explore its effect on error growth and the PL. Corr (WWV-Niño, 7–12) represents the predictability information that WWV contributes to the Niño 3.4 index. When Corr (WWV-Niño, 7–12) is high, WWV can be regarded as a skillful predictor of the Niño 3.4 index, increasing the predictability limit of SST in the tropical Pacific. Consistent with the decadal variation shown in Fig. 10a, Corr (WWV-Niño, 7–12) (red curve in Fig. 10b) is high from the mid-1980s to 2000s, which corresponds to high PL (black curve in Fig. 7a), and is low from the 1940s to 1960s with low PL. Corr (WWV-Niño, 7–12) declines from the start of the twenty-first century with the decrease of PL in the Niño 3.4 region. The correlation coefficient between Corr (WWV-Niño, 7–12) and PL is 0.69 (exceeding the 90% confidence level), which supports the important role of the phase-lag relationships between the WWV and the Niño 3.4 index in the decadal variability of PL.

Fig. 10
figure 10

a Correlation between the warm water volume (WWV) and Niño 3.4 index as a function of WWV lead month (vertical) and time (horizontal), within a (9 × 12 + 1)-month running window. The time shown is the middle month of each (9 × 12 + 1)-month window. A 9-year running average is applied to the correlation to reduce small fluctuations. b Average correlation between the WWV and Niño 3.4 at lead times of 7 to 12 months. The blue represents that at least half of the correlation coefficients used for averaging have passed the significant level of α = 0.1

Full size image

From the perspective of error growth, the variation of the phase-lag relationships between WWV and Niño 3.4 index has an impact on the saturated RGIE and error growth rate. The decadal variation of Corr (WWV-Niño, 7–12) is consistent with the saturated RGIE. In periods with strong phase-lag relationships between WWV and Niño such as in the 1900s, 1930s, 1970s, and 1990s, saturated RGIE is larger, which promotes high PL. Saturated RGIE is relatively low when Corr (WWV-Niño, 7–12) is lower, such as in the 1920s and 1950s. In fact, the correlation between Corr (WWV-Niño, 7–12) and saturated RGIE (blue–violet curve in Fig. 7a) is 0.44, which also passes the 90% confidence level under the effective degrees of freedom described in Sect. 2.1. Meanwhile, NLLE at lead times of 1, 3, and 6 months is more rapid when Corr (WWV-Niño, 7–12) is low, such as during the 1920s and 1950s. When Corr (WWV-Niño, 7–12) is high, NLLE is lower and the predictability limit is larger, such as from the 1980s to 2000s, because with high correlation, WWV can provide more information to predict SST and reduce the error growth rate. Further confirmation is provided by the correlation between Corr (WWV-Niño, 7–12) and NLLE (3) (coefficient is − 0.60), and the correlation between Corr (WWV-Niño, 7–12) and NLLE (6) is − 0.55, both of which pass the 90% confidence level.

Based on the correlation between WWV and SST in the Niño 3.4 region, we calculate the composite results of NLLE, saturated RGIE, and error for composites of high (> 0.3) and low (< 0.3) correlation. For early lead times (< 5 months), the error growth rate (NLLE) is lower where the correlation between WWV and Niño is higher. In particular, the NLLE difference between the high and low correlation periods reaches 0.1 at a lead time of 1 month, meaning that the error growth rate of SST in the low correlation period is 1.10 (\({e}^{0.1}\)) times that in the high correlation period. At lead times of 1–5 months, the error growth rate contributes to the difference of RGIE between high and low correlation periods (Fig. 11b). The value of RGIE in the low correlation period is greater than that in the high correlation period, which reduces the PL. However, the high RGIE in the low period decreases with increasing lead time. Unlike the RGIE for early lead times, the saturated RGIE of the high correlation period is higher than that of the low correlation period (Fig. 12b), which shows the high predictability signal in the high correlation period. Thus, the slow growth of RGIE in early lead times and the high value of RGIE at the saturated time together contribute to the high PL in the high correlation period and low PL in the low correlation period. The composite error as a function of lead time in the high and low correlation periods is also shown in Fig. 11c. The faster error growth rate at early lead times gives a larger error in the low correlation period than in the high correlation period. With increasing lead time, the error in the low correlation period is always larger, which corresponds to low PL.

Fig. 11
figure 11

Composited error growth lines based on the correlation coefficient between the Niño 3.4 index and WWV index. The brown lines represent the low correlation period and deep-sky-blue lines the high correlation period

Full size image
Fig. 12
figure 12

Composite differences between high and low correlation periods of the a predictability limit, b RGIE (\(\mathrm{ln}\overline{\mathrm{E} }\)) at the saturated time, and NLLE at lead times of c 1 month, d 3 months, and e 6 months. The dotted region passes the 90% confidence level

Full size image

The relationship between WWV and the Niño 3.4 index not only affects the PL in the Niño 3.4 region, but also plays an important role in the PL of SST in other regions of the tropical Pacific. Figure 12 displays the spatial field of the difference of the PL, saturated RGIE and NLLE at different evolution times between the high and low correlation periods. Compared to the PL pattern in low correlation periods, the PL of SST in high correlation periods is larger over almost the entire tropical Pacific except the tropical Pacific warm pool. The maximum difference of PL reaches 3 months near the dateline and 165°W in the equatorial Pacific (Fig. 12a). The saturated RGIE in the high correlation period has larger values than in the low correlation period over almost all of the tropical Pacific (Fig. 12b), which indicates that stronger forecast signal contributes to the high PL. In addition to the maximum difference of saturated RGIE at the dateline in the equatorial Pacific being similar to the difference pattern of the PL, the saturated RGIE also has an extreme center in the northeast Pacific where the difference of PL is small. The NLLE represents error growth rate, whose pattern changes with evolution time. The NLLE at a lead time of 1 month (Fig. 12c) is smaller in the equatorial Pacific but larger in the northeast Pacific in the high correlation period than in the low correlation period. The difference pattern of NLLE for an evolution time of 3 months (Fig. 12d) is similar to the pattern of NLLE at an evolution time of 1 month. The larger NLLE in the high correlation period in the northeast Pacific reduces the effect of increasing PL caused by the increase of saturated RGIE, so that the PL of the northeast Pacific increases less during the high correlation period. Unlike the difference pattern of NLLE between the high and low correlation periods at evolution times of 1 and 3 months, the NLLE (6) in the equatorial west Pacific is larger in the high correlation period than in the low correlation period, leading to a low PL in the west Pacific warm pool.

4 Conclusions and discussion

In this paper, we have investigated the mean PL of SST and its decadal variation in the tropical Pacific from 1900 to 2015 using observational SST data. The average PL in the tropical Pacific from 1900 to 2015 is high in the central and eastern Pacific (over 13 months) and is lower than 7 months in the western tropical Pacific. There are decadal variations in the PL in the tropical Pacific that can be as large as 2 months as measured by the standard deviation of the PL. These decadal variations differ between the western and central/eastern Pacific, as shown by the time series of PL in the different key Niño regions: the decadal variation is larger in the Niño 3.4 region than in the Niño 6 region. The Niño 3.4 region, representative of the central/eastern Pacific, has high PL in the 1900s, mid-1930s, mid-1960s, and mid-1990s and low PL in the 1920s, mid-1940s, and mid-2010s. The PL of the western tropical Pacific can be represented by the PL of the Niño 6 region and is higher in the mid-1910s, 1940s, 1980s, and mid-2010s and lower in the 1930s, 1950s, and mid-1990s. The decadal variations of PL in the central and eastern tropical Pacific are consistent and are well represented by those in the Niño 3.4 region; they differ from those in the western tropical Pacific, represented by the Niño 6 region. The difference between the decadal variability of PL in the central/eastern tropical Pacific and that in the western tropical Pacific is more obvious in the Hovmöller diagram of PL. The lower PL in the western Pacific is probably ascribed to the local air-sea interaction. There is also a low PL in the eastern tropical Pacific near the coast, which may result from the influence of offshore currents. The whole equatorial Pacific also shows more obvious decadal variation.

With the NLLE method, the PL is determined by the error growth rate and saturated RGIE. Thus, we investigated their spatial pattern and decadal variability in the framework of error growth dynamics. We found that the main factor affecting the spatial distribution of mean PL in the tropical Pacific is error growth rate (NLLE) when the RGIE at the saturated time has little influence. Regions with low error growth rate have higher PL, and vice versa. Note that the spatial pattern of actual error is clearly different from that of the mean PL, which suggests that the traditional method of estimating PL by a constant mean square error is inappropriate. The different PLs in the western Pacific and central/eastern Pacific may result from the different atmospheric and oceanic dynamical processes. The oceanic processes are slow, which favors the longer PL in the central/eastern Pacific. SST in the western Pacific is affected by atmospheric activity, which introduces more atmospheric noise to SST and reduces the PL of SST.

To investigate the decadal variation of PL, we chose the average of the Niño 3.4 region to represent the central/eastern Pacific and that of the Niño 6 region as the western tropical Pacific and analyzed their decadal variation of saturated RGIE and error growth rate (NLLE). The RGIE at the saturated time of the Niño 3.4 region has larger values in the 1900s, mid-1930s, mid-1960s, and 1980s to 2000s, which is overall consistent with the decadal variation of the PL of the Niño 3.4 region. The high correlation coefficients show that the decadal variation of saturated RGIE plays an important role in the PL and explains almost 66% of the PL decadal variance of Niño 3.4 region. In addition, there is decadal variation of the error growth rate, which also has a big influence on the decadal variation of PL. In particular, the NLLE at the evolution time of 6 months has increased since the mid-1990s, which contributes to the decline of the PL in the Niño 3.4 region from the mid-1990s. Compared with the relationship between the PL and RGIE or NLLE of the Niño 3.4 region, there is stronger correlation between the PL and saturated RGIE in the Niño 6 region, which implies that the decadal variation of PL is more dependent on the change of saturated RGIE in the Niño 6 region. This may result from the different physical mechanisms and greater atmospheric noise in the western tropical Pacific. Comparing the roles of the decadal variation of saturated RGIE and NLLE in the PL, we find that the decadal variation of the PL of SST in the tropical Pacific is due to the change of saturated RGIE, whereas the error growth rate may have an effect in some longitudinal regions of the equatorial Pacific.

The SST on a seasonal scale in the tropical Pacific is affected by the ocean heat capacity, for example, as described by the ENSO recharge–discharge theory. Further analyses indicate that the interdecadal variation in predictability is closely related to the interdecadal variation of the relationship between WWV and SST. From the perspective of error growth, the variation of the phase-lag relationships between WWV and Niño has an impact on the saturated RGIE and error growth rate. In the period with high phase-lag relationships between WWV and Niño, saturated RGIE is larger and NLLE is lower for lead times of 3 and 6 months, which favors high PL, such as in the 1900s, 1930s, 1970s, and 1990s. When the correlation between WWV and SST is lower, the saturated RGIE is relatively low and NLLE at lead times of 3 and 6 months is higher, such as in the 1920s and 1950s. A possible explanation is that the high correlation between WWV and Niño suggests a greater contribution of the slowly varying oceanic signal to the evolution of SST, leading to a longer cycle and stronger intensity of ENSO, which corresponds to high RGIE at the saturated time and increases the PL. The PL behavior in the western Pacific is not well explained by the WWV-SST relationship because of active atmospheric convection. In this paper, we display the decadal variability of seasonal PL in the tropical/subtropical PL over the period from 1900 to 2015 based on observation/analysis data, which increases our understanding of ENSO. The current climate model has some shortcomings in the simulation of SST, thus the performance of the climate model needs to be evaluated in the predictability, which is helpful to improve the capacity of the model.